Commonly used FRET fluorophores promote collapse of an otherwise disordered protein

Significance

Proteins adopt disordered ensembles prior to folding and sometimes as a part of their function. Simulations and FRET studies often described disordered conformations as more compact than the random coil states observed at high denaturant, whereas small-angle X-ray scattering (SAXS) indicates that these conformations remain expanded. Resolving this discrepancy improves our understanding of the properties of proteins, such as whether water is a sufficiently poor solvent to drive nonspecific collapse. We achieve reconciliation by showing the addition of FRET fluorophores reduces the disordered protein’s dimensions. Detailed analysis of FRET and SAXS, along with accounting for fluorophore-induced contraction, demonstrates that disordered and unfolded proteins often remain solvated and expanded without denaturant, properties that minimize misfolding and aggregation.

Abstract

The dimensions that unfolded proteins, including intrinsically disordered proteins (IDPs), adopt in the absence of denaturant remain controversial. We developed an analysis procedure for small-angle X-ray scattering (SAXS) profiles and used it to demonstrate that even relatively hydrophobic IDPs remain nearly as expanded in water as they are in high denaturant concentrations. In contrast, as demonstrated here, most fluorescence resonance energy transfer (FRET) measurements have indicated that relatively hydrophobic IDPs contract significantly in the absence of denaturant. We use two independent approaches to further explore this controversy. First, using SAXS we show that fluorophores employed in FRET can contribute to the observed discrepancy. Specifically, we find that addition of Alexa-488 to a normally expanded IDP causes contraction by an additional 15%, a value in reasonable accord with the contraction reported in FRET-based studies. Second, using our simulations and analysis procedure to accurately extract both the radius of gyration (R_g) and end-to-end distance (R_ee) from SAXS profiles, we tested the recent suggestion that FRET and SAXS results can be reconciled if the R_g and R_ee are “uncoupled” (i.e., no longer simply proportional), in contrast to the case for random walk homopolymers. We find, however, that even for unfolded proteins, these two measures of unfolded state dimensions remain proportional. Together, these results suggest that improved analysis procedures and a correction for significant, fluorophore-driven interactions are sufficient to reconcile prior SAXS and FRET studies, thus providing a unified picture of the nature of unfolded polypeptide chains in the absence of denaturant.

Protein disorder is an essential component of diverse cellular processes (1–4). Unlike well-folded proteins, which populate a well-defined functional state, unfolded and intrinsically disordered proteins (IDPs) sample a broad ensemble of rapidly interconverting conformations (3–8) with biases that are poorly understood and difficult to measure. Of particular interest is the extent to which IDPs contract under physiological conditions (i.e., in the absence of denaturants). Such contraction would have broad implications for our understanding of protein folding, interactions, and stability as well as the action of denaturants. Moreover, understanding the extent to which disordered ensembles contract has profound implications for the development of realistic folding simulations and the interpretation of small-angle X-ray scattering (SAXS) and FRET measurements (9, 10).

Our understanding of the physiochemical principles that underlie whether a polypeptide chain will fold, adopt a disordered but nevertheless relatively compact ensemble, or behave as an expanded, fully solvated, self-avoiding random walk (SARW) is insufficient to explain existing data. Most of this understanding is derived from studies of proteins unfolded by high concentrations of denaturants such as urea and guanidine hydrochloride (Gdn). Under these conditions the consensus is that proteins behave as SARWs, with a Flory exponent (ν) of 0.60 in the relationship R_g ∝ N^ν (N = chain length). In contrast, consensus is lacking regarding the behavior of IDPs at lower or no denaturant. Specifically, while numerous FRET (11–25) and computational studies (11, 14, 18, 23, 26–29) have argued that the expanded, disordered ensemble detected at high denaturant contracts significantly [typically 25–50% upon transfer to low or no denaturant (ν < 0.5)] (11, 14, 18, 23, 26–28, 30–35), a similar number of SAXS studies report little or no contraction under these same conditions (10, 36–41).

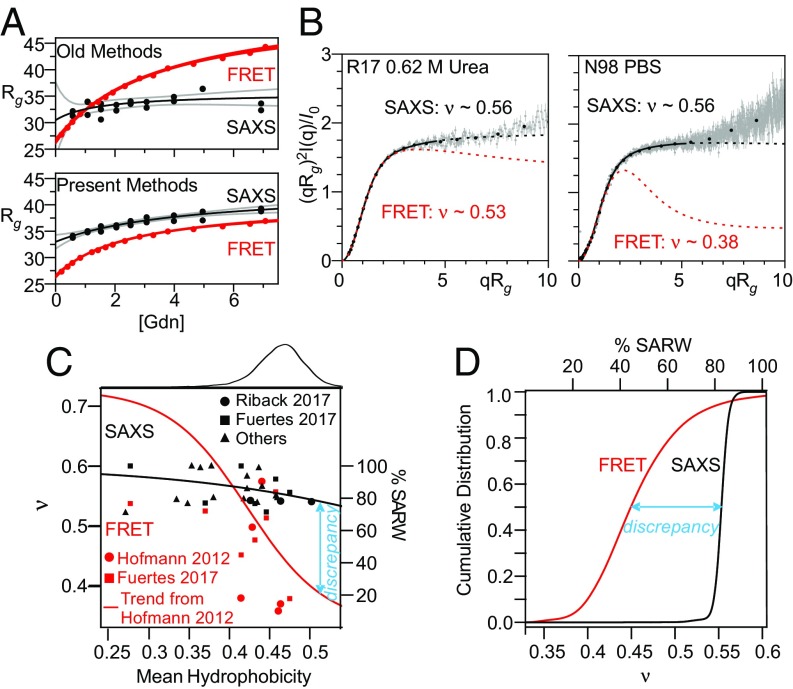
A variety of recent studies have attempted to reconcile this discrepancy (Fig. 1A), which has profound implications in the physics of protein folding. The application of more realistic simulations and analytical models resulted in FRET-derived distances having a smaller denaturant dependence (Fig. 1A, Bottom) (40, 42–44). In parallel, improved SAXS data and analysis, including the use of the dimensionless Kratky plot to emphasize changes in ν rather than R_g, (which is important, as the addition of fluorophores near the ends of a chain will increase R_g due to their mass), likewise provided evidence for a minor contraction below 2 M Gdn (Fig. 1A, Bottom) (45, 46). Nevertheless, significant discrepancies persist in the absence of denaturant, even when the same approaches are used to analyze the same protein under identical conditions (Fig. 1, SI Appendix, Figs. S1 and S2, and Movie S1). Recent studies have proposed that this discrepancy can be eliminated by using a holistic analysis (42, 43), emphasizing a decoupling between the normally fixed, proportional relationship between R_g (determined from SAXS measurements) and R_ee (determined from FRET measurements) without any need to invoke a perturbation due to the presence of the fluorophores (42).

Fig. 1.

Improved analysis procedures do not eliminate discrepancy between SAXS- and FRET-derived measurements of IDP dimensions. (A) R17 SAXS and FRET data (from ref. 43). (A, Top) Comparison of results obtained when FRET data are fit assuming a Gaussian chain and SAXS data are fit using the Guinier approximation. (A, Bottom) SAXS and FRET data fit using our MFF analysis method and a similar approach (45). Black line is best fit hyperbolic trend line; gray lines are 95% confidence intervals. (B) SAXS profiles for R17 (Left, data from Ref. 43) and N98 (Right, data from ref. 42) fit with the MFF are significantly different from the expected behavior using values of ν taken from similar analysis of FRET data. Solid lines denote the region used in the fitting procedure; dashed lines represent extrapolation to higher values of q. Although ∼500 points per scattering curve were fit (gray), most data shown were binned for presentation purposes only (black points). The upturns or kinks in the data at higher values of qR_g are most likely due to errors in buffer subtraction, which is more challenging at high q, low sample concentration, and/or reduced scattering contrast (e.g., at high denaturant, see Materials and Methods). (C) Trends of hydrophobicity (Kyte–Doolittle) versus ν in the absence of denaturant derived from SAXS by applying the MFF to published data collected from foldable protein sequences (42, 45, 67–82). Also shown are results from FRET studies calculated as in ref. 20 for published data (20, 42). Red trend line for FRET data from ref. 20. Black trend line is best fit to SAXS results shown. (C, Top) Histogram of hydrophobicity of representative proteins in the PDB (dataset from ref. 45). (D) Cumulative distributions of ν for the representative proteins from the PDB, inferred from the trend lines shown in C.

To comprehensively compare the results of SAXS and FRET studies, we collected published datasets for a variety of IDPs (Fig. 1 C and D and SI Appendix, Table S3). When analyzed using our simulations and molecular form factor (MFF), SAXS studies consistently find ν > 0.53 (mean = 0.55), whereas ν derived from FRET studies typically falls below 0.50 (mean = 0.46). This 0.09 discrepancy is substantial, relative to the entire range of ν, which varies only from 0.6 (for a SARW) through 0.5 (where intrachain interactions are equally favorable to solvent-chain interactions) to 0.33 (for compaction into a sphere; it is somewhat higher for nonspherical compact states). In general, SAXS results suggest that the conformational ensembles of a majority of unfolded proteins and IDPs with protein-like sequence composition are highly expanded (ν > 0.5) and water is a good solvent, whereas FRET suggests otherwise (Fig. 1D).

The above and other results have led us and others to search for factors that might contribute to the persistent discrepancy between SAXS- and FRET-based views of IDP dimensions (9, 29, 39, 42, 43, 47–50). One alternative, herein denoted the “heteropolymer-decoupling hypothesis,” posits that the heteropolymeric nature of proteins leads to variation in the relationship between R_g and R_ee, a relationship that is fixed (i.e., independent of chain length) at a ratio of 6.3 for a homopolymer SARW. Recent simulations suggest that this ratio may not be fixed for unfolded proteins, which are more complex than homopolymers (29, 39, 42, 43). This “decoupling” offers a possible explanation for the discrepancy between SAXS (which is sensitive to R_g) and FRET (which is sensitive to R_ee). In contrast, a second hypothesis, herein denoted the “fluorophore-interaction hypothesis,” suggests that, in the absence of denaturant, the FRET fluorophores interact with each other and/or the polypeptide chain, causing the conformational ensemble of fluorophore-modified constructs to contract more than they would in the absence of these fluorophores (9, 45, 47, 50, 51).

Here we address both the decoupling and fluorophore-interaction hypotheses. We used SAXS to characterize the radius of gyration of an IDP before and after the addition of a commonly employed fluorophore. We find that such fluorophore modification alters the conformational ensemble in the absence of denaturant, decreasing its SAXS-measured dimensions by 10–20%. When coupled with improved analysis procedures employing realistic simulated ensembles for both SAXS and FRET, this fluorophore-induced collapse is sufficient to bring results from SAXS and FRET studies into agreement. In parallel, we present SAXS measurements on polyethylene glycol (PEG), confirming prior reports that the addition of fluorophores likewise causes the contraction of this otherwise SARW polymer (9), a finding that was recently questioned (42). Moreover, we show that SAXS can extract R_g, ν, and R_ee with accuracies above 97% when analyzed using a new MFF developed for heteropolymers. These simulations are accurate enough to reproduce scattering data without the need to select only a subensemble of conformations, as commonly used in other data fitting procedures. Finally, we demonstrate the extent that one can use small deviations from ideality in SAXS data to infer biases within the heteropolymer conformational ensemble.

Results

Fluorophore Labeling Induces Collapse.

To directly test the fluorophore-interaction hypothesis, we measured SAXS profiles of an unmodified IDP and the same IDP site-specifically modified with one or two copies of the commonly employed FRET fluorophore Alexa-488. We chose this fluorophore because it is relatively small and hydrophilic, thus rendering it less likely than most of the other FRET fluorophores to form interactions that would alter the unfolded ensemble (43). As our test protein, we used PNt, a well-behaved IDP comprising the amino terminal 334 residues of pertactin (52). To produce mono- and dualfluorophore-modified PNt, we used a thiol-reactive Alexa-488 to modify cysteine residues at either position 117 (PNtC-Alexa488) or positions 29 and 117 (PNtCC-Alexa488). As controls, we used the unmodified parent protein (PNt) and alkylation to produce constructs lacking fluorophores (PNtC-Alkd and PNtCC-Alkd).

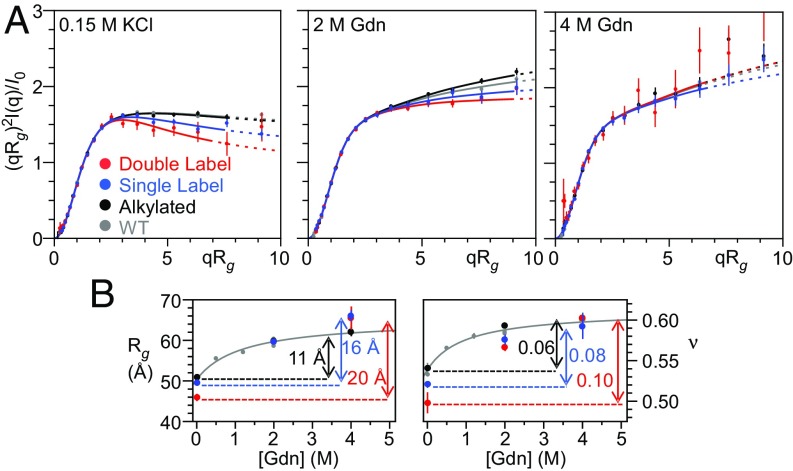
The addition of Alexa-488 reduces the SAXS-measured dimensions of PNt both in the absence of Gdm and at intermediate concentrations (Fig. 2A and SI Appendix, Table S1). Specifically, upon transitioning from 4 to 0 M Gdn, R_g and ν decrease nearly twice as much for the fluorophore-modified PNtCC-Alexa488 as for either PNtCC-Alkd or PNt (Fig. 2B and SI Appendix, Table S1). These data indicate that the presence of Alexa-488 leads to contraction of the PNt conformational ensemble. Of note, whereas 2 M Gdn is a good solvent (ν > 0.50) for the unlabeled protein, fluorophore-labeling leads to measurable intramolecular interactions even at this relatively high denaturant concentration (Fig. 2B, Right). Consistent with a common origin for the effect, the magnitude of this denaturant-dependent expansion is qualitatively similar to that observed by FRET for a variety of other proteins (Fig. 1B) (42, 43). We also observed a fluorophore-dependent decrease in average R_g and ν for the single-labeled construct PNtC-Alexa488 (Fig. 2), indicating that, in addition to presumptive fluorophore–fluorophore interactions, fluorophore–protein interactions also contribute to the observed contraction.

Fig. 2.

The addition of Alexa-488 alters the scattering of PNt. (A) Dimensionless Kratky plots of wild-type PNt (gray), PNtCC-alkylated (black), PNtC-Alexa488 (single label, blue), and PNtCC-Alexa488 (double label, red) in 0.15 M KCl, 2 M Gdn, and 4 M Gdn. Error bars represent the propagated error from the SD calculated assuming counting (Poisson) statistics where σ = √counts. Data were fit and displayed following the procedure described in Fig. 1 (see also Materials and Methods). Results for alkylated PNt are indistinguishable from wild-type PNt but there are significant differences for PNt labeled with Alexa-488 fluorophores. (B) R_g and ν as a function of Gdn concentration. Gray curves data from ref. 45.

Of note, this contraction occurs despite steady-state fluorescence anisotropy values for PNtCC-Alexa488 of 0.11 and 0.08 in 0 and 2 M denaturant, respectively (SI Appendix, Table S2), below the threshold typically considered as evidence of free rotation of protein-attached fluorophores (42, 53). From these results, we conclude that addition of even one of the smaller, more hydrophilic fluorophores commonly employed for FRET measurements can significantly reduce the dimensions of a disordered polypeptide chain (42, 43, 53), an observation that helps reconcile the SAXS–FRET discrepancy.

The SAXS-Derived Dimensions of PEG Are Independent of Polymer Concentration.

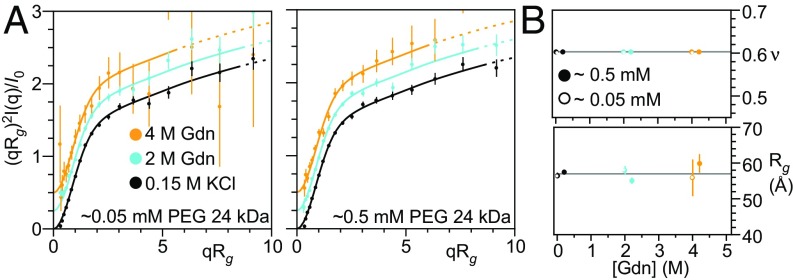
In an earlier study we reported that addition of Alexa-488/594 to PEG resulted in a denaturant-dependent change in FRET (9), similar to that seen in unfolded proteins. No contraction was observed, however, when the equivalent unlabeled polymer was studied using small-angle neutron scattering. It has been proposed that the high (3 mM) concentrations of PEG used in this scattering study mask what would otherwise be a denaturant-dependent change in R_g (42). To test this, we measured SAXS profiles over a range of PEG and denaturant concentrations and found no evidence for a significant change in the dimensions of this highly hydrophilic polymer (Fig. 3). Likewise, under all conditions we observed a Flory exponent of 0.60, further confirming that PEG behaves as a SARW independent of denaturant concentration. Fluorophore effects, and not chain contraction, thus remain the simplest interpretation of the denaturant-dependent changes in FRET previously observed for fluorophore-labeled variants of this polymer (9).

Fig. 3.

SAXS profiles of PEG are denaturant independent. (A) Dimensionless Kratky plots of 24 kDa PEG at 0.5 mM and 0.05 mM in 0.15 M KCl, 2 M Gdn, and 4 M Gdn. The normalized scattering profile of 24 kDa PEG is unchanged from 0 to 4 M Gdn over a broad range of PEG concentrations. Scattering profiles have been offset vertically for clarity. Data were fit and displayed using the procedure described in Fig. 1. (B) R_g and ν as functions of Gdn concentration for 0.5 mM and 0.05 mM PEG. Open and closed points are offset horizontally for clarity.

Testing the Heteropolymer-Decoupling Hypothesis.

Taken together, the above observations indicate that fluorophores added to an IDP lead to significant contraction, contributing to the different conclusions drawn from prior SAXS and FRET studies. These observations, however, do not rule out the possibility that, as previously argued (42), heteropolymer-decoupling (i.e., the relationship between R_ee and R_g deviating from the fixed proportionality seen for homopolymers) could also contribute to the SAXS–FRET discrepancy.

To investigate whether the conformational ensemble of a realistic heteropolymer results in a significant nonproportionality between R_ee and R_g, we used Upside, our Cβ-level simulations (54, 55), to simulate the scattering for unfolded ensembles of 50 protein of 250–650 residues randomly chosen from the Protein Data Bank (PDB). In its simplest version, Upside represents the polypeptide backbone with six atoms per residue (N, Cα, C, H, O, and Cβ) and uses neighbor-dependent Ramachandran maps derived from a coil library (56). Such models are able to reproduce the R_g and NH residual dipolar couplings (RDCs) observed in unfolded proteins; these two parameters are sensitive to global and local properties of the backbone, respectively (57, 58). To generate heteropolymer ensembles, we assigned each Cβ as either hydrophobic or polar (H/P). Favorable interaction profiles (shape shown in ref. 45, SI Appendix, Fig. S3A) are introduced only between Cβ atoms of the hydrophobic residues and self-avoidance is imposed on all atoms. For each of the 50 sequences, we employed 30 different Cβ interaction strengths. After creating these 1,500 H/P ensembles of backbone conformations, we added explicit side chains (59) and then calculated the scattering profiles of the hydrated versions of the proteins (60).

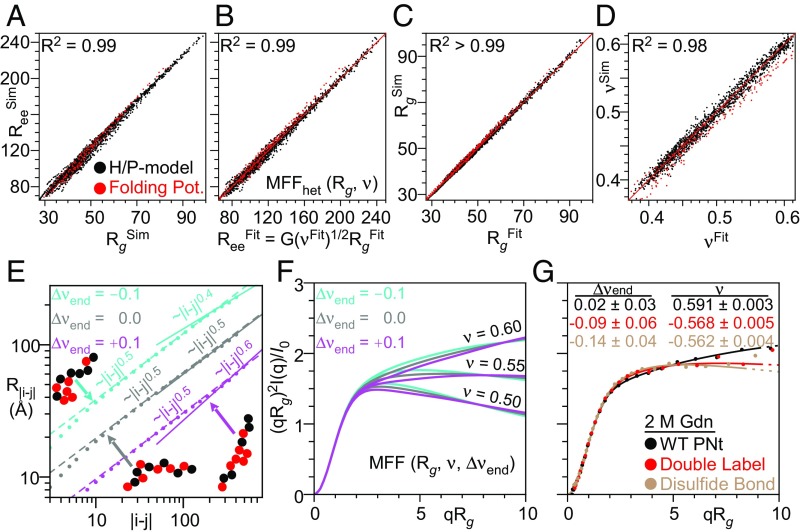
For these 1,500 ensembles, we compared the true R_g, ν, and R_ee values calculated directly from the atomic coordinates with those obtained by fitting the simulated scattering (with added realistic random errors) using our original MFF designed for homopolymers (45). As is true for homopolymers, we find that the values of R_ee and R_g seen in these simulations are proportional (i.e., remain coupled), with a correlation coefficient of R² = 0.99 (Fig. 4A). We next fit the simulated scattering profiles to determine R_g^fit, ν^fit, and R_ee^fit, with the latter obtained using the relationship (R_ee/R_g)² = G(ν), where G(ν) was calibrated using our original homopolymer simulations (SI Appendix, Fig. S1D). We found a mean absolute deviation of only 1.3 Å, 0.011, and 4.2 Å, respectively, representing a 3%, 2%, and 4% mean absolute error in R_g, ν, and R_ee (SI Appendix, Fig. S3). The largest deviations are observed for more compact structures; for more extended conformations (ν > 0.54) the error is ∼2%. The correlation R_g^fit and R_ee^fit remained high, R² > 0.99.

Fig. 4.

Simulations find a strong coupling between R_g and R_ee, and SAXS profiles are a robust measure of R_g, ν, and R_ee while also informing on the degree of heterogeneity. (A) Coupling between R_g and R_ee obtained from the simulated ensembles using the H/P model (black) or our potential used to fold proteins (red). (B–D) Comparison of R_g, ν, and R_ee calculated from coordinates of simulated ensembles versus values obtained from fitting with our MFF_het(R_g, ν) to SAXS profiles of the ensembles with randomly added experimental errors. (E) Deviations in ν_ends are observed for heteropolymers with less well-mixed H/P patterns (obtained by a fit to the slope of the dependence of the intrachain distance, R_{|i − j|}, on sequence separation, |i − j| where |i − j| > N/2). (F) Effects of Δν_end at different values of ν. (G) Experimental data fit to MFF(R_g, ν, Δν_end) demonstrates fluorophore labeling and loop formation via disulfide bonds in PNt induces significant and measurable deviations.

To further reduce the small error associated with the application of our MFF derived from homopolymers to the scattering of heteropolymers, we generated a new molecular form factor, MFF_het, using the H/P simulations described above and the same general procedure as described in ref. 45. Application of this slightly modified MFF_het lowers errors in fitted R_g, ν, and R_ee to 0.5 Å, 0.005, and 2.7 Å, respectively, representing 1%, 1%, and 2% mean absolute error (Fig. 4 B–D). These results demonstrate that our MFF-based analysis procedure returns accurate values for R_g and R_ee, which remain proportional (i.e., coupled), even for heteropolymers.

We next considered whether our conclusions are sensitive to the details of our model or energy function. To test this, we conducted additional simulations using a more detailed version of the Upside algorithm that is capable of de novo folding of proteins with <100 residues (54, 55). In this version, each of the 20 side chains is represented by a multiposition eccentric bead that allows for detailed packing of the core. The energy function includes hydrogen bonds, side chain–side chain and side chain–backbone interactions, amino acid-dependent dihedral angle potentials, and a desolvation term. Using this model, we generated 30 ensembles for each of six proteins (PNt and five other proteins randomly selected from the 50 described above), using short simulations that sample only the unfolded state. We obtained ensembles by running replica exchange simulations over a temperature range from 280 to 320 K, as described previously (54, 55). Values of ν obtained from these ensembles ranged from 0.4 to 0.6, depending on the simulation temperature. Significantly, values of R_ee, R_g, and ν obtained directly from these more realistic ensembles are in close agreement with values determined after fitting with our MFF_het, with nearly the same accuracy as for the simpler H/P ensembles (Fig. 4 A–C, red points). Furthermore, the directly computed values for R_g and R_ee for the ensembles remain proportional, with a correlation coefficient of R² = 0.99. Hence our conclusion that R_g and R_ee remain coupled even for heteropolymers is robust to the details of our simulations.

Measuring Deviations from Ideality in Heteropolymers.

MFF_het accurately captures the overall dimensions of disordered heteropolymers for protein-like H/P sequence patterns and can be used in most instances. Nevertheless, small but measurable deviations are observed for proteins in our test set with less well-mixed H/P patterns (SI Appendix, Fig. S4). These differences can be seen in the intramolecular distance distribution plot, where the slope at separation distances |i − j| > N/2 can be different from the average slope, which defines the global ν value (Fig. 4D). We define change in slope as Δν_end (Fig. 4D). Negative values of Δν_end correlate with a preponderance of hydrophobic residues at the ends of the polypeptide sequence (Fig. 4D and SI Appendix, Fig. S4C) and with deviations in G(ν) (SI Appendix, Fig. S4A) (R² ∼ 0.84). The SAXS profile is most sensitive to Δν_end at low qR_g (Fig. 4E).

To quantify the nonidealities in heteropolymers from the SAXS data, we generated a more general, three-parameter form factor, MFF_general(R_g, ν, Δν_end) (Fig. 4 E and F and Movie S2). To demonstrate its ability to yield useful information, we fit data from PNt, PNtCC-Alexa488 and a circularized (disulfide-bonded) PNtCC at 2 M Gdn (Fig. 4F). Δν_end decreases from ∼0 for PNt to approximately −0.1 for PNtCC-Alexa488 and to approximately −0.2 for circularized PNtCC, consistent with the increase in interactions at the amino terminus of the chain. Less drastic perturbations, such as less well-mixed H/P patterns, and shorter amino acid sequences with a lower useful qR_g range, may require a higher signal-to-noise ratio to measure Δν_end. Nevertheless, these data demonstrate the potential of SAXS to identify, for disordered polymers, sequence-dependent deviations from homopolymer behavior (Fig. 4 E and F) while still accurately measuring R_g and ν (Fig. 4 A–C).

In the infinite chain length limit, the Flory scaling exponent ν has values of 0.33, 0.50, and 0.60, corresponding to globules, random walks, and SARW, respectively. Nevertheless, we and others take a pragmatic approach and allow ν to assume intermediate values; e.g., as obtained from the slope of the scaling plots of R_g versus chain length, or R_ij versus |i − j| (SI Appendix, Fig. S6). In support of this approach, one observes upon increasing the intrachain interaction strength, a decrease in both I(q) at high q and the slope in the scaling plots for proteins of 100–1,000 residues (Fig. 4). Accordingly, we believe that the use of ν values beyond the three canonical values provides a legitimate and practical approach to compare solvent quality for different-sized systems and classify whether water is a good or poor solvent for finite length polymers.

Discussion

Whereas SAXS measurements point to water being a good solvent (ν > 0.5) for unfolded polypeptides, FRET-based studies typically report the opposite (ν < 0.5). We find here, however, that a combination of improved analysis procedures and more careful consideration of fluorophore–fluorophore and/or fluorophore-chain interactions is sufficient to explain this discrepancy. These findings lead to a unified picture in which the unfolded state of proteins is a SARW at high denaturant and contracts only slightly (much less so than previously been reported in the FRET literature) in the absence of denaturant. Specifically, we find that labeling with Alexa-488, a commonly used FRET fluorophore, can alter the conformational ensemble of an IDP, decreasing R_g and ν even when the fluorescence anisotropy is low, relative to accepted limits for free fluorophore rotation (42, 53). In combination with prior studies (9), similar conclusions can be inferred for PEG, a known SARW. These findings, along with our prior result that disordered chains undergo a mild expansion in denaturant (45) and improved methods for extracting R_g values from FRET data (40, 42–44), now provide a sufficient framework for resolving discrepancies between SAXS and FRET on the dimensions of disordered proteins. The fundamental and significant conclusion of the resulting unified picture is that, even in the absence of denaturant, water remains a good solvent for most unfolded proteins.

Our findings of fluorophore-induced effects are consistent with prior findings that the molecular dimensions inferred from FRET can depend on the fluorophore pair used, with more hydrophobic fluorophores leading to more contraction (43). MD simulations with a Alexa-488/594 fluorophore pair, for example, resulted in a 10% contraction of an IDP even in 1 M urea (61). Likewise, a recent study found that single-molecule FRET (smFRET) signals from both DNA and PEG are dependent on solvent conditions under which the dimensions of the chains were expected to be invariant (51). In apparent disagreement with our data, however, Fuertes et al. (42) conducted SAXS measurements on five IDPs with and without Alexa-488/594 and concluded that, on average, the alterations seen upon the addition of fluorophores were minimal. When considered for each protein separately, however, the differences appear significant, relative to the narrow range of possible values. Specifically, for the five proteins characterized in that study, ν_unlabel − ν_label = 0.08, 0.03, 0.03, −0.02, and −0.04 (or 0.09, 0.06, 0.03, −0.02, and −0.08 when analyzed using our procedures; SI Appendix, Fig. S5). Although Fuertes et al. (49) assert that only one protein (NLS), exhibits fluorophore-induced contraction, in fact four of the five proteins they tested had statistically significant fluorophore-induced changes in ν, with more than half exhibiting a fluorophore-induced contraction (42) of similar magnitude to the contraction we observed for fluorophore-labeled PNt in water (45) (SI Appendix, Fig. S5). Together, these data support a consistent picture of fluorophore-induced perturbations, contributing to differences in the magnitude and denaturant dependence of R_g inferred from SAXS and FRET.

The other factor that has been suggested to contribute to the discrepancy between SAXS and FRET results is deviations from the proportional relationship between R_g and R_ee that may arise when analyzing heteropolymers versus homopolymers (42). Underlying this view is the observation that, if one reweights the ensemble (i.e., calculates R_g using only a subset of conformations), many possible values of R_ee are consistent with any given R_g (and vice versa). Rather than selecting a subensemble of conformations to fit a couple of parameters, we have taken an alternative approach (45). We generate physically plausible ensembles at the outset, create a MFF using these entire ensembles, and examine whether it fits the data in its entirety. We find that our MFF accurately matches the entire scattering profile (rather than just the R_g), which provides strong support for our procedure. Since we can calculate the values of R_g and R_ee directly from the underlying ensembles, we have a procedure to obtain these two parameters by fitting the SAXS data with our MFF. We find that for realistic denatured ensembles of foldable sequences, the simulated R_g and R_ee pairs as well as their counterparts determined from the scattering profiles are proportional (R² > 0.99). This leaves the dyes as the source of the remaining discrepancy between SAXS and FRET.

The MFF we employ is imperfect in the sense that slightly different ensembles can be fit using the same R_g and ν parameters. But the error is very low for these two parameters relative to their true values (Fig. 4 A–C). Inclusion of heteropolymer effects does not alter this conclusion. From these results, we conclude that SAXS is well suited to extract both R_g and R_ee for disordered heteropolymers, while circumventing potential artifacts due to fluorophore interactions with polypeptide chains. This conclusion does not negate the potential of FRET to measure dynamics, binding, and conformational changes; it does, however, emphasize that caution must be exercised when employing FRET to infer quantitative distances in the original, unlabeled biomolecule.

Nearly a dozen IDP SAXS datasets reported here and previously (45) have been shown to fit well to our general MFF (SI Appendix, Tables S1 and S3). This finding suggests that the interactions that drive chain contraction are spread along protein sequences. Water-soluble, well-folded protein sequences tend to be well-mixed heteropolymers, with relatively small stretches of consecutive hydrophobic residues (62). These well-mixed sequences tend to behave as homopolymers when measured by global, low-resolution methods such as SAXS. Indeed, we have demonstrated that, with sufficient data quality, poorly mixed sequences can be identified by their deviation from our MFF (Fig. 4 D–F). Larger deviations can occur for some IDPs, especially those with partial folding, unusual sequence patterning (e.g., block copolymers) and/or under crowded conditions that may serve specific functions (63, 64).

The unified picture presented here regarding SAXS and FRET studies of the unfolded state in the absence of denaturant reinforces the view that water is a good solvent for most unfolded polypeptides, a property that should reduce misfolding and aggregation while simultaneously facilitating synthesis and transport. That most proteins nevertheless readily fold in water suggests that the interactions that drive folding are more stabilizing—i.e., overcome the ability of water to solvate the unfolded state—than those that promote nonspecific collapse. Indeed, the observation that, despite the minimal evidence of significant unfolded-state contraction even in the complete absence of denaturant, some proteins remain stably folded in up to 6 M Gdn (41, 65) suggests that native interactions are far more favorable than any nonspecific interactions associated with collapse. Given, however, the highly specific nature of the interactions formed in native proteins, their ability to overcome the solvation of the unfolded chain is perhaps not surprising.

Materials and Methods

PNtCC and PNtC were expressed in Escherichia coli BL21(DE3)pLysS and purified from inclusion bodies as described previously (45, 52, 66), with the following modifications. After inclusion-body solubilization, PNt constructs were refolded in 50 mM Tris pH 7.2 with 50 mM β-mercaptoethanol (βME). Before the final size exclusion chromatography step, 20 mM βME was added to the protein stock solution.

Further information on protein alkylation and Alexa-488 labeling, as well as steady-state anisotropy measurements, SAXS data analysis and simulations can be found in SI Appendix.

Note Added in Proof.

During review, a study was published that implicated fluorophores in the strengthening of the binding affinity between two IDPs (83).