Disconnection description of triple-junction motion

Significance

Many materials of industrial and scientific interest (including metals and ceramics) are polycrystalline. The defect microstructure of these materials has a profound impact on their properties and utility. Microstructure engineering yields materials with greatly enhanced qualities, but the microstructure typically evolves over time via the motion of grain boundaries and triple junctions. One must understand and guide this evolution to produce reliable enhanced materials. Much has been discovered in recent decades regarding the motion of grain boundaries—less so regarding triple junctions. This work presents observations of triple-junction migration from atomistic simulations, explains these observations by extending recent developments in grain boundary theory to triple junctions, and presents a continuum model of triple-junction migration based on this theory.

Abstract

Grain boundary (GB) migration in polycrystalline materials necessarily implies the concurrent motion of triple junctions (TJs), the lines along which three GBs meet. Today, we understand that GB migration occurs through the motion of disconnections in the GB plane (line defects with both step and dislocation character). We present evidence from molecular dynamics grain growth simulations and idealized microstructures that demonstrates that TJ motion and GB migration are coupled through disconnection dynamics. Based on these results, we develop a theory of coupled GB/TJ migration and use it to develop a physically based, disconnection mechanism-specific continuum model of microstructure evolution. The continuum approach provides a means of reducing the complexity of the discrete disconnection picture to extract the features of disconnection dynamics that are important for microstructure evolution. We implement this model in a numerical, continuum simulation and demonstrate that it is capable of reproducing the molecular dynamics (MD) simulation results.

Grain growth has long been described as motion by mean curvature (i.e., curvature flow) (1–3); grain boundaries (GBs) migrate toward their center of curvature, reducing the total GB area and energy. Triple junctions (TJs) (lines along which three GBs meet), in turn, migrate to balance the surface tensions (and torques) exerted by the constituent GBs (4, 5), leading to a set of equilibrium dihedral angles. As GBs migrate, the TJs migrate to maintain these angles; the whole microstructure evolves via this tandem motion. While extensions exist that account for GB anisotropy (6–12), this has been the conceptual core of grain growth theory over the past half century. This theory rests on the assumption that TJs can migrate much faster than GBs (13–15). However, substantial experimental (13, 16, 17) and atomistic simulation (18) evidence demonstrates that this is often not true. Finite TJ mobility causes TJ drag, which leads to dynamic TJ dihedral angles that differ from their thermodynamic values (14, 15, 18–20). When the grain size is sufficiently small, grain growth is controlled by TJ drag rather than curvature flow (13, 14, 20–22). While mechanistic models of GB migration have gained prominence (23–28), particularly in the past decade (29–39), mechanistic models for TJ migration are only just being established (40).

Shear can drive the migration of many grain boundaries. Conversely, migrating GBs often induce shears as they migrate. Each GB is characterized by a temperature-dependent shear-coupling factor $\beta =\dot{B}/\dot{H}$, where $\dot{H}$ is the GB velocity and $\dot{B}$ is the shear velocity (30). This was first observed by Li et al. (41) and Bainbridge et al. (42). Shear coupling in high-angle GBs has been reported in experiments (28, 32, 43–45), ab initio calculations (46–49), and atomistic simulations (50–54). Recent theoretical predictions (33, 35–37) and transmission electron microscopy (TEM) observations (55, 56) connect shear coupling to the motion of line defects/disconnections; disconections are characterized by both a step height $h_i$ and Burgers vector ${\mathbf{b}}_i$ (25, 27, 57–61). This step-mediated migration mechanism was first proposed by Bollmann (62), Ashby (63), and Hirth and Balluffi (24). For each GB, there is an infinite set of possible disconnection modes $\left\{{\mathbf{b}}_i,h_i\right\}$ determined by the crystal structure and the relative orientations of the grains meeting at the GB (64). The ratio between the GB migration velocity $v_{\perp }$ and shear displacement rate (across the GB) $v_{\parallel }$, $\beta =v_{\parallel }/v_{\perp }$, can be related to the ratio ${\beta }_i={\mathbf{b}}_i/h_i$ for disconnection-mode $i$ (while ${\mathbf{b}}_i$ is a vector quantity, it is generally parallel to a symmetric tilt inclination of the GB; it is often used interchangeably with the scalar quantity $b_i$, where sign indicates direction).

The effective $\beta$ and GB mobility represent thermal averages over the available disconnection modes (34, 36, 38, 55, 65). Shear coupling tends to vanish at high temperature (i.e., grain boundary sliding or migration without shear); this is associated with the nucleation and migration of multiple disconnection types with different signs of ${\beta }_i$.

Just as GBs migrate via the nucleation and migration of disconnections, TJ migration is also associated with disconnection motion, i.e., the flux of disconnections into/out of the TJ along their constituent GBs. The finite step height and Burgers vector of these disconnections constrain TJ motion. A TJ can migrate only such that all three GBs remain connected at the TJ; this leads to a zero displacement incompletion condition associated with the flux of steps (40, 66). Since disconnections also carry Burgers vectors, the flux of disconnections into/out of TJs can lead to Burgers vector accumulation (Burgers vector is a conserved quantity). Since there is a long-range stress field associated with a Burgers vector, the accumulation of a Burgers vector at a TJ can create a back stress on the disconnections on the GBs, leading to disconnections being repelled from the TJ and possibly to TJ stagnation.

Nonetheless, experiments do show that grain growth routinely occurs and consequently that triple junctions do migrate. The implication is that TJs may accommodate these constraints either through disconnection dynamics within the GB network or by some form of bulk plasticity (dislocation emission/absorption, twinning, …). The conditions outlined above can be satisfied within the GB network only by requiring that the GBs conspire to produce the necessary disconnections to eliminate the net flux of Burgers vector into the TJ. This is, in general, not possible with single disconnection modes on each GB (38). More commonly, this can occur by the constituent GBs contributing (or the TJs emitting) disconnections with multiple coupling modes. The ability to access multiple coupling modes is temperature dependent and different for each GB; GBs with disconnections of disparate activation energies imply extremely slow TJ motion and highly temperature-sensitive migration kinetics. If the net zero Burgers vector flux condition at the TJ cannot be met, then some form of plasticity must operate to dissipate the accumulated Burgers vector; such lattice dislocation emission into the surrounding grains has been observed both in experiment (67–69) and in simulation (70). Another possibility is the relaxation of the TJ through twinning; both molecular dynamics (MD) simulations (71–73) and experiments (74) show that coherent twin boundaries may form at TJs during microstructural evolution (in the absence of external stress). While the origin of annealing twins remains a topic of considerable debate (23, 75–80), these observations suggest that annealing twins may be a natural outcome of and/or may facilitate TJ migration.

In this paper, we present results from MD simulations of polycrystalline grain growth that elucidate the connection between TJ migration and grain boundary migration in terms of the underlying disconnection dynamics. Based on these observations, we construct a disconnection-mediated TJ migration model that is consistent with disconnection dynamics-controlled GB migration. Finally, we implement this mechanistic model in a continuum framework suitable for large-scale microstructure evolution simulations.

Grain Growth

As discussed above, normal grain growth is widely described as capillarity-driven GB motion, where each point on a GB migrates toward its local center of curvature with velocity

$$v=M_G\gamma \kappa ,$$ [1]

where $\gamma$, $\kappa$, and $M_G$ are the GB energy (per area), mean curvature, and GB mobility at this point on the GB (1). Triple junctions, in turn, migrate to maintain a set of equilibrium dihedral angles that balance the surface tension (and torques) from their constituent GBs. If ${\gamma }^{\left(i\right)}$ is inclination independent, this condition reduces to the classical Herring angles

$$\frac{{\gamma }^{\left(1\right)}}{\sin {\mathrm{\Theta }}^{\left(1\right)}}=\frac{{\gamma }^{\left(2\right)}}{\sin {\mathrm{\Theta }}^{\left(2\right)}}=\frac{{\gamma }^{\left(3\right)}}{\sin {\mathrm{\Theta }}^{\left(3\right)}},$$ [2]

where ${\mathrm{\Theta }}^{\left(i\right)}$ is the dihedral angle opposite the GB with interfacial energy ${\gamma }^{\left(i\right)}$. If triple junctions can move sufficiently rapidly to remain in equilibrium with respect to the GBs, then the microstructure evolves by pure curvature flow with fixed angle junctions. This type of motion may be viewed as a two-step process whereby (i) GBs migrate in accordance with Eq. 1, thereby pulling the TJs out of equilibrium, and (ii) the TJs migrate to restore the equilibrium angles (if GBs have an inclination-dependent energy, new terms arise that account for the torque on GBs at TJs). Experimental (16, 17, 19, 22) and simulation (18) observations show that TJs do indeed have finite mobility, as indicated by steady-state dihedral angles of migrating TJs that differ from their equilibrium values (14, 15, 18–20).

Atomistic simulation permits an examination of grain growth free of any of the normal grain growth theory assumptions described above. We performed MD simulations of polycrystalline embedded atom method nickel (84) in an NPT ensemble (Nosè–Hoover thermostat) at 1,200 K ($\sim 0.85T_m$) under zero external stress. The initial microstructure was created by generating a steady-state curvature-flow microstructure (85), assigning grain orientations at random, and populating each grain with atoms in a face-centered cubic (FCC) structure with the corresponding orientation (see ref. 73 for more details). This was done instead of using the more common Voronoi tessellation, which produces flat GBs, unrealistic TJ angles, and grain size distributions inconsistent with normal grain growth microstructures (72). A cross-section of one such simulation is depicted in Fig. 1, which compares the microstructure between two simulation times. Over this 2-ns timespan, the mean linear grain size [i.e., ${\left(V/N\right)}^{1/3}$, where $V$ is the system volume and $N$ is the number of grains] increases from 40 Å to 140 Å. It is apparent from Fig. 1 that while some triple junctions migrate significantly, others do not. Grain growth is also accompanied by the formation of many defects in the grain interiors; these include dislocations and coherent twin boundaries.

Fig. 1.

Cross-section of a 1,200-K MD polycrystal grain growth simulation, comparing microstructures at 400 ps (blue) and 2,400 ps (red) after initial relaxation. FCC-structure atoms [as determined by common neighbor analysis (81)] are not shown. Coherent twin boundaries are highlighted in a lighter shade and black rectangles indicate dislocations. Triple junctions that are nearly stationary relative to the microstructure are circled. The visualization was performed using OVITO (82).

Fig. 2 shows finite-thickness cross-sections from the same MD simulation along with corresponding schematic illustrations. Here, a migrating TJ emits a pair of partial dislocations. All dislocations in this simulation (that are not part of low-angle tilt GBs) are emitted from TJs or GBs. The direct emission of dislocations from triple junctions has also been observed experimentally (67–70). Fig. 3 shows a migrating TJ leaving behind a set of closely spaced coherent twin boundaries. As with dislocations, nearly all of the twin boundaries that did not form during the initial relaxation of the GB network formed at triple junctions during grain growth. While twinning at TJs has been proposed as a mechanism for relaxing the total energy of the GB network (74), this does not explain the successive twinning during TJ motion/grain growth observed here. It is possible, however, that twin formation may relax internal stresses [as has already been suggested to explain successive deformation twinning in the vicinity of two GBs (86)]. This begs the question, What is the origin of these internal stresses?

Fig. 2.

(A–D) The 5-nm-thick cross-sections from the MD polycrystal grain growth simulation shown in Fig. 1. FCC atoms (common neighbor analysis) are not shown and the remaining atoms are colored by centrosymmetry (83). The white lines depict the simulation cell boundaries. A–D, Insets are schematic representations of the microstructure (lines are GBs; roman numerals label grains)—a pair of partial dislocations (red) separated by a stacking fault (gray) is emitted from the I/II/IV TJ that migrates up and left.

Fig. 3.

Cross-section from a polycrystalline MD grain growth simulation, colored by centrosymmetry. (A–D) A TJ (circled) migrates up and to the right, leaving behind multiple, parallel, coherent twin boundaries (thin yellow lines of atoms).

TJ Migration Simulations

While the MD simulations of polycrystal grain growth faithfully represent TJs and GBs as they occur in the “wild” (i.e., in a polycrystal) without the need for all of the simplifying assumptions made in grain growth theories, the complexity of the polycrystalline microstructure confounds attempts to draw precise conclusions on how TJs move. We therefore perform two sets of MD simulations in more “tame” circumstances, where TJ kinetics may be more directly probed. The first one employs a tricrystal configuration, where the microstructure relaxes from an initial, nonequilibrium geometry toward equilibrium via coupled GB and TJ migration. The second set consists of a single, initially elongated grain spanning an otherwise flat GB; for a sufficiently elongated grain this will lead to steady-state TJ migration as long as the grain width is small compared with the TJ separation (according to a curvature flow model, Eq. 1). Similar geometries were used both in experiment (17, 19) and in atomistic simulations studies of the TJ drag effect (18, 87).

In the tricrystal simulations (Fig. 4), a cylindrical simulation cell (radius $R\approx 37.5$ nm) was divided into three grains, all sharing a common [210] axis parallel to the TJ line which initially lies along the cylinder axis. The vertical GB, labeled 1, is a symmetric tilt GB ($\mathrm{\Sigma }9$, $96.38^{○}$ misorientation). The other GBs, labeled 2 and 3, are also initially symmetric tilt GBs ($\mathrm{\Sigma }15$, $\pm 48.19^{○}$ misorientation)—see SI Appendix, Note 3 for more detail. The ends of GBs 1, 2, and 3 were fixed on the perimeter of the cylindrical simulation cell by fixing the atomic positions in a thin shell along the circumference (the effect of pinning the ends is discussed in SI Appendix, Note 2). The system inside this shell then evolves via molecular dynamics in an NPT ensemble with zero stress along the axial direction. Multiple simulations were performed, varying both simulation temperature (at 800 K, 1,000 K, and 1,200 K) and pinning-point (2 and 3) locations.

Fig. 4.

(Lower Left) Time series of a 1,200-K tricrystal MD simulation. The FCC atoms were removed and the remaining atoms were colored by time after initial relaxation. The atoms on the surface of the cylindrical simulation cell (black) were held fixed, pinning GBs 1 and 2 at the simulation cell perimeter. This simulation is represented by the red open circles in Fig. 5. The GBs and TJs migrate such that the TJ is at position $z\left(t\right)$. Replacing the actual GB profile with straight lines from points 2 and 3 to the TJ, the TJ angle $\varphi \left(t\right)$ is related to the TJ position $z\left(t\right)$ as in Eq. 3, as indicated in the schematic (Upper Right).

Triple-junction dihedral angles are difficult to measure reliably in an MD simulation because of the discreteness of the lattice and thermal fluctuations. Therefore, we directly measure an effect of dihedral/TJ angle $\varphi \left(t\right)$ and TJ location $z\left(t\right)$ from the triangle formed by the pinning points 2 and 3 and the TJ, as shown schematically in Fig. 4, Upper Right. The triple-junction angle $\varphi \left(t\right)$ and the TJ position $z\left(t\right)\le 0$ are related through

$$\tan \left(\frac{\varphi \left(t\right)}{2}\right)=\frac{\sin \left(\frac{\varphi \left(0\right)}{2}\right)}{\cos \left(\frac{\varphi \left(0\right)}{2}\right)+\frac{z\left(t\right)}{R}},$$ [3]

where $\varphi \left(0\right)$ is the initial TJ angle [its initial position is along the cylinder axis, $z\left(0\right)=0$] that also describes the location of the pinning points. If the GBs are nearly flat as they migrate (Fig. 4), then $\varphi$ is approximately equal to the dihedral angle ${\mathrm{\Theta }}^{\left(1\right)}$ [in equilibrium $\varphi \left(\infty \right)={\mathrm{\Theta }}^{\left(1\right)}$].

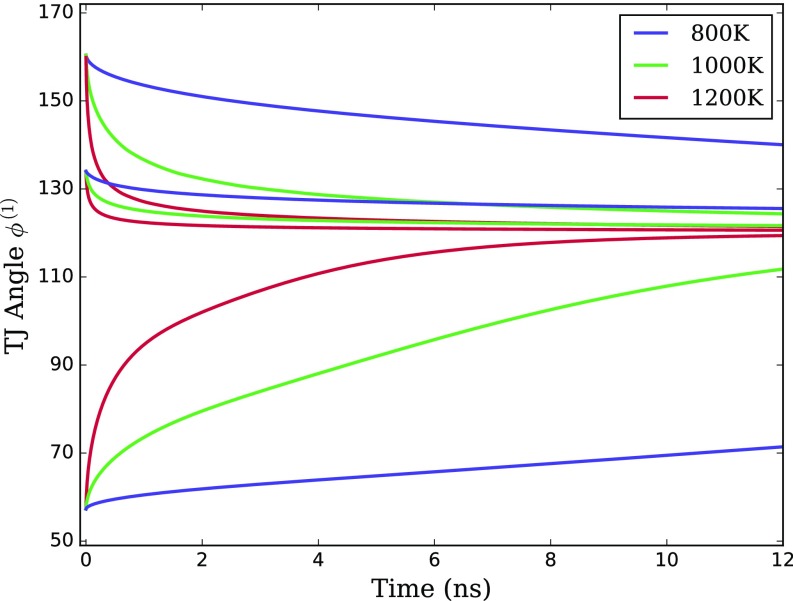
The time evolution of $\varphi$ is shown in Fig. 5A at the highest temperature, 1,200 K. At this temperature, the TJ migrates slower and slower as time passes, asymptotic at late time to $\varphi \left(\infty \right)\approx 100^{○}$ (achieved during the 12-ns simulations) for all initial-angle TJ angles (i.e., location of the pinning points 2 and 3). The fact that the TJs in all simulations at this temperature converge to the same angle suggests that the TJ reaches equilibrium, $\varphi \left(\infty \right)={\mathrm{\Theta }}^{\left(1\right)}$. On the other hand, at the intermediate (1,000 K) and lowest (800 K) simulation temperatures, the TJ moves slowly and continues to move at the end of the 12-ns simulation time. This suggests that equilibrium has yet to be achieved. This is supported by the observation that simulations starting with different initial TJ angles $\varphi \left(0\right)$ do not achieve the same values by the end of the simulation. However, $\varphi \left(t\right)$ moves toward the same value for different initial conditions, even if they do not reach it within the simulation time when $T<\mathrm{1,200}$ K. Fig. 5 B and C shows the details of migration during the initial nanosecond for several simulations. At the very earliest times, the TJs all move at comparable rates for all temperatures; at low temperatures, the TJ subsequently stagnates to the velocity seen at long times.

Fig. 5.

(A) Triple-junction angle $\varphi$ as a function of time for a variety of temperatures with different initial ${\mathrm{\Theta }}^{\left(1\right)}$. The colors indicate simulation temperature and the symbol types indicate initial triple-junction angles $\varphi \left(0\right)$. (B and C) Early time (initial 1.0-ns) behavior of the triple-junction angle $\varphi$ for the simulations with initial dihedral angles of $160^{○}$ and $57^{○}$ (indicated by the black dashed lines), respectively. Since the GBs are nearly flat during the migration (Fig. 4), $\varphi \left(t\right)$ is approximately equal to the dihedral angle ${\mathrm{\Theta }}^{\left(1\right)}$.

Fig. 6A shows the higher-resolution image of the region around the TJ from the 800 K, $\varphi \left(0\right)=134^{○}$ simulation at 0.2 ns and 5 ns. In this case, the TJ is moving very slowly. In Fig. 6A we see that the TJ is not symmetric and that a disconnection that is initially present on the GB in the lower left moves into the TJ, shifts the GB in the lower left downward, and displaces the TJ (toward the right). This is a unit step of the disconnection-mediated TJ migration. Fig. 6B shows the shear stress field near the TJ for the same two configurations. The very fine-scale features in Fig. 6 B1 are associated with the structure of the GB itself. Note that when the disconnection in Fig. 6 B1 moves into the TJ in Fig. 6 B2, the stress field around the TJ changes dramatically on a large scale compared with the stress features of the GBs themselves. Analysis of the stress field around the TJ after disconnection absorption shows that this stress is associated with the net addition of the disconnection Burgers vector. This observation suggests that disconnection flux into the TJ both conserves Burgers vector and builds the TJ stress field.

Fig. 6.

Stress accumulation at a migrating triple junction from a tricrystal MD simulation performed at 800 K with an initial TJ angle $\varphi \left(0\right)=134^{○}$. (A1 and A2) The red lines in A2 (5.0 ns from initial) indicate the GB and TJ positions in A1 (0.2 ns from initial). B1 and B2 show shear stress ${\sigma }_{xy}$. There is some visible stress in B2 due to the initial relaxation. These images are taken from the corresponding simulation depicted in Fig. 4.

We now turn to the motion of the elongated grain embedded into the bicrystal simulations. Fig. 7A shows a time series of one of the embedded-loop simulations. These simulations are reminiscent of simulations performed by Upmanyu et al. (18, 87); however, unlike those simulations, these are fully 3D, are performed over a range of temperatures, and focus on a high-angle tilt GB in place of a low-angle GB for ${\mathrm{G}\mathrm{B}}^{\left(1\right)}$. In these simulations, periodic boundary conditions are applied in the $y$ and $z$ directions with free surfaces in the $x$ direction. Over the course of the simulation, GBs 2 and 3 facet; the system remains in this state for an extended period. Eventually, the upper TJs suddenly and very rapidly migrate, annihilating the central grain. Repeating this simulation under exactly the same conditions (except different initial velocities) and for a wide range of temperatures demonstrates that this result is repeatable; see Fig. 7B where we plot the $y$ coordinate of the upper TJ vs. the logarithm of the time. At the highest temperature (1,200 K), the waiting period is very short (0.3 ns) and grows quickly with decreasing temperature. In most simulations, once the upper TJ starts to migrate, it does so smoothly. In all cases, GBs 2 and 3 strongly facet and these faceted GBs do not migrate inward before TJ migration. We do not report the results for the few cases (6 of 40) in which either the lower TJ migrates first or both begin migrating simultaneously.

Fig. 7.

(A) Time series of an embedded loop simulation at 800 K. After the GBs facet, the microstructure is stationary for a period and then suddenly migrates rapidly. (B) TJ position vs. time for multiple simulations at different temperatures. Series with the same color are from simulations performed at the same temperature. The Xs at the bottom show the time $\tau$ that the TJ crossed the dotted line at the corresponding temperature. (C) Arrhenius plot of $\ln {\tau }_0/\tau$, where ${\tau }_0=1$ ns and $\tau$ is the time after initial relaxation that the TJ passes the dotted line in B, averaged over six simulations at each temperature. This plot gives an activation energy of $0.57\hspace{0.17em}\text{eV}\pm 0.02$ eV.

The motion of the TJ appears to depend on two timescales—one that characterizes the wait or stagnation time for the TJ to start moving and the other associated with the finite TJ migration velocity. Once the TJ begins migrating, the grain shrinks and the capillarity-driving force for migration increases (hence the TJ accelerates). At this point, the evolution becomes complex, consisting of simultaneous inward motion of the two TJs as well as changes in the facet sizes of the vertical GBs. We can quantify the time before the TJ begins migrating by a wait time $\tau$; we measure this from the time of the initial relaxation (faceting) to the time the TJ passes a particular point (i.e., the dotted line in Fig. 7B). $\tau$ was averaged over eight simulations at the same temperature. Fig. 7C shows an Arrhenius plot of $\tau$ vs. inverse temperature (${\tau }_0=1$ ns). The fact that these data fall on a straight line demonstrates that the wait time for the initiation of TJ migration is thermally activated with an activation barrier of approximately 0.57 eV. Since the timescale associated with the actual TJ migration is short, this estimate is insensitive to the choice of the dashed line in Fig. 7B. The magnitude of this activation barrier is comparable to nudged elastic band (NEB) calculations for disconnection nucleation (36, 88). However, this agreement should be viewed with caution since these NEB calculations were performed for GBs other than those in our simulations and they were based on zero temperature energy surfaces (no entropy effects). Nonetheless, the agreement suggests (rather than proves) that the “liberation” of the previously stagnant TJ may be associated with disconnection nucleation on one of the GBs. The wait time for TJ motion is long compared with the migration time, suggesting that the initial disconnection nucleation may be slow compared with subsequent nucleation events. Perhaps this indicates a change in disconnection nucleation (e.g., heterogeneous rather than homogeneous).

The polycrystal simulations and TJ kinetics simulations yield a number of important observations. Triple junctions are the source of many defects that form during grain growth, among them dislocations and twins. Some triple junctions migrate much more readily than others. At high temperatures, TJs appear to migrate consistent with conventional theory (smoothly until they reach a consistent set of equilibrium dihedral angles). At low temperature, TJs may migrate a short distance and stagnate. This stagnation may be associated with the stresses generated by disconnection adsorption. Stagnated TJs can migrate, but the process that facilitates this migration appears to be thermally activated and much slower than the initial and subsequent TJ migration. We now examine these observations in light of a disconnection dynamics approach.

Theory

Grain boundaries migrate via the nucleation and motion of GB step defects known as disconnections (38) which are characterized by a step-height $h_i$ and Burgers vector ${\mathbf{b}}_i$. The set of all possible disconnection modes $\left\{{\mathbf{b}}_i,h_i\right\}$ is determined by the bicrystallography [specifically the displacement shift complete (DSC) lattice (62)]. For each ${\mathbf{b}}_i$, there is a set of $h_i$ separated by translation vectors in the coincident site lattice (CSL). At low temperatures, and when large shear deformations may occur, many GBs strongly favor a particular disconnection mode. This is the origin of shear-coupled GB migration—the dominant disconnection mode determines the shear-coupling factor ${\beta }_i=b_i/h_i$. Since GBs migrate via disconnections, it follows that triple junctions must migrate via the flux of disconnections from and into their constituent GBs. The finite step size and Burgers vector of these disconnections imply constraints on TJ migration that can explain many of the observations from our MD simulations. The first constraint is the zero displacement incompletion condition (40, 66). Simply stated, TJs may migrate only such that the three GBs all meet along the TJ line. As disconnections are GB steps with fixed height and direction, arbitrary combinations of disconnections do not satisfy this condition. The disconnection fluxes $J^{\left(i\right)}$ from each GB must combine at the TJ, satisfying the expression

$$\sum _{i=1}^3{J}^{\left(i\right)}{h}^{\left(i\right)}\sin {\mathrm{\Theta }}^{\left(i\right)}=0,$$ [4]

where ${\mathrm{\Theta }}^{\left(i\right)}$ is the dihedral angle opposite ${\mathrm{G}\mathrm{B}}^{\left(i\right)}$ (SI Appendix, Note 1). This condition holds for a TJ in 2D or any cross-section of a TJ normal to the TJ line in 3D. The resulting TJ velocity is then

$$v_{\text{tj}}=\frac{1}{3}\sum _{i,j,k}{ϵ}_{ijk}\left[\frac{J^{\left(k\right)}{h}^{\left(k\right)}}{\sin {\mathrm{\Theta }}^{\left(j\right)}}-\frac{J^{\left(i\right)}{h}^{\left(i\right)}}{\sin {\mathrm{\Theta }}^{\left(k\right)}}\right]{\mathbf{t}}^{\left(i\right)},$$ [5]

where ${ϵ}_{ijk}$ is the permutation operator and ${\mathbf{t}}^{\left(i\right)}$ is a unit vector aligned with the plane of GB $\left(i\right)$, pointing toward the TJ. Normally, this condition is simply a description of how TJ and GB motions are related.

When disconnections flow into a TJ, satisfying the zero displacement incompletion condition, the disconnection step content annihilates, moving the TJ. However, the disconnection Burgers vectors do not simply vanish; the total Burgers vector is conserved. This implies that in all but very special cases, the net result of disconnection-mediated TJ motion is the accumulation of Burgers vector at the TJ. However, as the residual Burgers vectors accumulate, the resulting stress fields will repel subsequent disconnections, stagnating TJ migration. Long-distance TJ migration is possible only if there is no accumulation of stress, implying an additional Burgers vector cancellation condition

$$\sum _{i=1}^3{J}^{\left(i\right)}{\mathbf{b}}^{\left(i\right)}=0.$$ [6]

This equation represents three conditions on the three variables $J^{\left(i\right)}$. Combined with the zero displacement incompletion condition, the system is overdetermined—there are more equations than variables and valid solutions exist only for (very) special cases (e.g., pure step disconnections, disconnections with parallel Burgers vectors, etc.). However, since experiments and MD simulations show that triple junctions do migrate long distances, something else must happen; several mechanisms can facilitate triple-junction migration, either by adding degrees of freedom or by relaxing the resulting stresses.

Bicrystallography permits a discrete, infinite set of disconnection modes to any GBs. While GB migration favors disconnection modes with low nucleation/migration barriers, each disconnection mode responds differently to driving forces on the boundary. A GB can switch to secondary modes under a given set of driving forces [e.g., when there are competing driving forces for migration (65)]. Secondary-mode nucleation is associated with GB sliding as well as GB migration without shear coupling, but it may also facilitate TJ migration. If ${\mathrm{G}\mathrm{B}}^{\left(i\right)}$ is populated with $N_i$ types of disconnections, then Eq. 6 becomes

$$\sum _{i=1}^3\sum _{j=1}^{N_i}{J}_j^{\left(i\right)}{\mathbf{b}}_j^{\left(i\right)}=0,$$ [7]

where the summation on $j$ represents all disconnection modes of each GB. This modification adds many degrees of freedom for TJ migration, and the conditions of TJ migration are easily satisfied. TJ migration by this means implies that TJs may migrate rapidly at first by the primary modes and then accumulate stress and stagnate (barring the extremely rare/special case in which the primary disconnections can satisfy both conditions simultaneously), after which their migration is controlled by the formation of secondary disconnections.

At high temperature, when the population of secondary disconnections is larger, stagnation is easily overcome. This is consistent with the GB simulations in TJ Migration Simulations. However, the same simulations showed that GB migration may stagnate at low temperature; this is associated with the large energetic penalties associated with forming secondary-mode disconnections. This explains the TJ stagnation observed in the 800-K GB simulations.

As described above and seen in the polycrystal simulations (Figs. 1–3), stresses can be relaxed during microstructure evolution by dislocation and twin emission from GBs and TJs. If the TJ can emit dislocations along $N$ distinct slip planes, then Eq. 6 becomes

$$\sum _{i=1}^3{J}^{\left(i\right)}{\mathbf{b}}^{\left(i\right)}+\sum _{m=1}^N{J}^{L_m}{\mathbf{b}}^{L_m}=0,$$ [8]

where $J^{L_m}$ and ${\mathit{b}}^{L_m}$ denote fluxes and Burgers vectors of lattice dislocations, respectively. With the additional degrees of freedom provided by lattice dislocation flux, TJ migration may occur without new disconnection-mode activation. Likewise, sequential twinning at TJs may be a deformation process (89) that relaxes the accumulating internal stress.

Dislocation emission into the grains is a viable accommodation mechanism only if the slip planes in the crystal are suitably oriented to dissipate the accumulated Burgers vector. Coherent twin boundaries form on a restricted set of lattice planes and so may assist TJ migration only for particular lattice orientations and migration directions. This leaves secondary disconnection nucleation as the general determiner of TJ migration. In this framework, TJ mobility $M_{\text{TJ}}$ is no longer an intrinsic property of a TJ, but rather must be determined directly in terms of disconnection types, densities, and mobilities. At low temperature, some TJs should be highly mobile while others are effectively sessile, depending on the availability of secondary disconnection modes. This disparity should vanish at high temperature where the formation of multiple disconnection types is likely. More fundamentally, this implies that through the disconnection mechanism, GB and TJ migrations are deeply intertwined and disconnection theory can yield a unified framework for microstructure evolution. In the next section, we build a continuum description of microstructure evolution accounting for GB and TJ migration within the context of disconnection motion.

Continuum Model

Zhang et al. (40) developed an equation of motion for the evolution of GB profiles based on a single disconnection-mode model. In this model, the disconnection density is a continuous variable and the dynamics account for both disconnection nucleation and migration. We extend this method to consider both multiple disconnection modes and disconnection-mediated TJ motion. The profile of ${\mathrm{G}\mathrm{B}}^{\left(i\right)}$ is described by $z^{\left(i\right)}$, which measures the GB “height” above some reference plane parallel to the symmetric GB; it evolves as

$$z_{,t}^{\left(i\right)}=-\sum _{j\hspace{0.17em}=\hspace{0.17em}\mathrm{1,2}}{v}_j^{\left(i\right)}\left(\left|{\rho }_j^{\left(i\right)}\right|h_j^{\left(i\right)}+2{\eta }_j^{\left(i\right)}\right),$$ [9]

where $z_{,t}^{\left(i\right)}$ denotes the derivative of $z^{\left(i\right)}$ with respect to time. $v_j^{\left(i\right)}$ is the glide velocity of $j\mathrm{t}\mathrm{h}$-mode disconnections on ${\mathrm{G}\mathrm{B}}^{\left(i\right)}$ and is given by

$$v_j^{\left(i\right)}=M_d\left[\left(\mathit{\sigma }+\mathit{\tau }\right){\mathbf{b}}_j^{\left(i\right)}+\mathrm{\Psi }{h}_j^{\left(i\right)}-\gamma z_{,xx}{h}_j^{\left(i\right)}\right],$$ [10]

where $M_d$ is a disconnection mobility, $\mathit{\sigma }$ is the contribution to stress from other disconnections, and $\mathit{\tau }$ is any external stress. The $\left(\mathit{\sigma }+\mathit{\tau }\right){\mathbf{b}}_j^{\left(i\right)}$ term represents an appropriate summation over stress and Burgers vector components as in the Peach–Koehler force (90). In the limit that the GB is close to a symmetric inclination, such that ${\mathbf{b}}_j^{\left(i\right)}$ lies parallel to the GB plane, we can consider the shear stresses resolved along the GB plane $\sigma$ and $\tau$, as well as the scalar $b_j^{\left(i\right)}=\left|{\mathbf{b}}_{\mathbf{j}}^{\left(\mathbf{i}\right)}\right|$. Finally, the background thermal density of disconnections (scaled by step height) ${\eta }_j^{\left(i\right)}$ is

$${\eta }_j^{\left(i\right)}=\frac{h_j^{\left(i\right)}}{a}{e}^{-E_j^{\left(i\right)}/\left(k_{B}T\right)},$$ [11]

where $a$ is an atomic spacing, and $E_j^{\left(i\right)}$ is half the disconnection pair formation energy (40).

We consider three grain boundaries ${\mathrm{G}\mathrm{B}}^{\left(1\right)}$, ${\mathrm{G}\mathrm{B}}^{\left(2\right)}$, and ${\mathrm{G}\mathrm{B}}^{\left(3\right)}$, which meet at a triple junction $P\hspace{0.17em}=\hspace{0.17em}{\mathit{x}}_0$. We further assume that each ${\mathrm{G}\mathrm{B}}^{\left(i\right)}$ has two possible disconnection modes $\left(b_1^{\left(i\right)},h_1^{\left(i\right)}\right)$ and $\left(b_2^{\left(i\right)},h_2^{\left(i\right)}\right)$, such that $b_1^{\left(i\right)}{b}_2^{\left(i\right)}>0$ and $h_1^{\left(i\right)}{h}_2^{\left(i\right)}<0$ (${\beta }_1$ and ${\beta }_2$ have opposite sign). The TJ migrates to reduce the total energy of the system via the exchange of disconnections between the TJ and its constituent GBs. TJ motion is therefore related to the step flux into/from the GB,

$$J_1^{\left(i\right)}{h}_1^{\left(i\right)}+J_2^{\left(i\right)}{h}_2^{\left(i\right)}=-{\mathbf{v}}_{\text{TJ}}\cdot {\mathbf{n}}^{\left(i\right)},$$ [12]

where $J_j^{\left(i\right)}$ is the flux of $j\mathrm{t}\mathrm{h}$-mode disconnections from the $i\mathrm{t}\mathrm{h}$ GB and ${\mathbf{n}}^{\left(i\right)}$ is the normal to the $i\mathrm{t}\mathrm{h}$ GB symmetric inclination. The Burgers vector flux into the TJ is then

$$\frac{d}{dt}{\mathbf{b}}_{\text{TJ}}=\sum _{i=\mathrm{1,2,3}}{J}_1^{\left(i\right)}{\mathbf{b}}_1^{\left(i\right)}+J_2^{\left(i\right)}{\mathbf{b}}_2^{\left(i\right)},$$ [13]

where ${\mathbf{b}}_{\text{TJ}}$ is the total Burgers vector at the TJ.

The change in total energy due to TJ motion has contributions from both the disconnection step and the Burgers vector. When a net Burgers vector is present at the TJ, the TJ will tend to absorb nearby disconnections (or emit disconnections) to cancel this accumulated Burgers vector and reduce the $\parallel {\mathbf{b}}_{\text{TJ}}{\parallel }^2$ energy contribution. This cancellation happens very quickly and, in the continuum limit, we assume that the zero accumulated Burgers vector condition ${\mathbf{b}}_{\text{TJ}}=0$ holds during TJ motion. Thus, the driving force on TJ motion is solely described by the variation of the energy associated with surface tension (from the disconnection step character and the GB energy itself),

$${\mathbf{v}}_{\text{TJ}}=M_{\text{TJ}}\sum _{i=\mathrm{1,2,3}}{\gamma }^{\left(i\right)}{\mathbf{t}}^{\left(i\right)},$$ [14]

where $M_{\text{TJ}}$ is the TJ mobility, ${\gamma }^{\left(i\right)}$ is the GB energy, and ${\mathbf{t}}^{\left(i\right)}$ is the unit vector tangent to ${\mathrm{G}\mathrm{B}}^{\left(i\right)}$. In particular, ${\mathbf{v}}_{\text{TJ}}=0$ defines the equilibrium angles in Eq. 2. While this equation of motion merges with the classical continuum form of TJ motion, the TJ mobility is not an intrinsic (well-defined) property of the TJ. The TJ mobility is ultimately governed by the disconnection availability and mobility.

The problem of TJ migration reduces to the optimization problem (where $M_{\text{TJ}}\ge 0$)

$$max\left|{\mathbf{v}}_{\text{TJ}}\right|=M_{\text{TJ}}\parallel \sum _{i=\mathrm{1,2,3}}{\gamma }^{\left(i\right)}{\mathbf{t}}^{\left(i\right)}\parallel ,$$ [15]

subject to constraints

$$\sum _i{J}_1^{\left(i\right)}{\mathbf{b}}_1^{\left(i\right)}+J_2^{\left(i\right)}{\mathbf{b}}_2^{\left(i\right)}=\mathbf{0}$$ [16]

$$J_1^{\left(i\right)}{h}_1^{\left(i\right)}+J_2^{\left(i\right)}{h}_2^{\left(i\right)}=-{\mathbf{v}}_{\text{TJ}}\cdot {\mathbf{n}}^{\left(i\right)}$$ [17]

$$\left|J_j^{\left(i\right)}{h}_j^{\left(i\right)}\right|\le M_d\left|{\eta }_j^{\left(i\right)}{\mathbf{n}}^{\left(i\right)}\cdot \sum _{k=\mathrm{1,2,3}}{\gamma }^{\left(k\right)}{\mathbf{t}}^{\left(k\right)}\right|,$$ [18]

where $i=\left\{\mathrm{1,2,3}\right\}$ and $j=\left\{\mathrm{1,2}\right\}$. Eqs. 16 and 17 refer to the zero Burgers vector accumulation and zero displacement incompletion conditions. The inequality Eq. 18 implies that not all nucleated (positive or negative) disconnections can contribute to TJ motion due to the above two constraints, where the right-hand side describes the maximal possible disconnection flux (scaled by step height). The driving force acting on a disconnection at the TJ is ${\mathbf{n}}^{\left(i\right)}\cdot {\sum }_{k=\mathrm{1,2,3}}{\gamma }^{\left(k\right)}{\mathbf{t}}^{\left(k\right)}$, and the available disconnections are limited by the scaled thermal density ${\eta }_j^{\left(i\right)}$. Use of the maximal TJ velocity is consistent with the assumption that TJ motion is overdamped and occurs in the direction of the maximum force on the TJ.

Focusing now on the TJ migration case of Fig. 4, the symmetry of the problem implies that there should be no net motion of the TJ in the $x$ direction [i.e., ${\mathbf{n}}^{\left(1\right)}\cdot {\sum }_k{\gamma }^{\left(k\right)}{\mathbf{t}}^{\left(k\right)}=0$]. Therefore, there is no flux of disconnections into/out of the TJ from ${\mathrm{G}\mathrm{B}}^{\left(1\right)}$ and $J_1^{\left(1\right)}=J_2^{\left(1\right)}=0$. This permits an analytic solution to the optimization problem,

$${\mathbf{v}}_{\text{TJ}}\hspace{0.17em}=\hspace{0.17em}{M}_{\text{TJ}}\sum _{i=\mathrm{1,2,3}}{\gamma }^{\left(i\right)}{\mathbf{t}}^{\left(i\right)}$$ [19]

$$M_{\text{TJ}}=\left\{\begin{array}{c}{M}_d{\eta }_2^{\left(2\right)}\left(\frac{b_2^{\left(2\right)}{h}_1^{\left(2\right)}}{b_1^{\left(2\right)}{h}_2^{\left(2\right)}}-1\right),\text{if}\frac{{\eta }_1^{\left(2\right)}{b}_1^{\left(2\right)}}{h_1^{\left(2\right)}}\ge \frac{{\eta }_2^{\left(2\right)}{b}_2^{\left(2\right)}}{h_2^{\left(2\right)}}\text{,}\hfill \\ M_d{\eta }_1^{\left(2\right)}\left(1-\frac{b_1^{\left(2\right)}{h}_2^{\left(2\right)}}{b_2^{\left(2\right)}{h}_1^{\left(2\right)}}\right),\text{if}\frac{{\eta }_1^{\left(2\right)}{b}_1^{\left(2\right)}}{h_1^{\left(2\right)}}<\frac{{\eta }_2^{\left(2\right)}{b}_2^{\left(2\right)}}{h_2^{\left(2\right)}}\text{,}\hfill \end{array}\right.$$ [20]

where $b_i^j=\left|{\mathbf{b}}_i^j\right|$.

Eq. 20 highlights a fundamental aspect of this analysis; the dynamics that occur at the triple junction during disconnection annihilation are very fast relative to the kinetics of disconnection nucleation and migration along the GBs (otherwise the TJ would not be able to migrate rapidly in Fig. 7). The TJ mobility is a result of the cooperation of available disconnections subject to certain constraints that account for the complex effects of the crystallography of grains and grain boundaries. The resultant TJ motion may be limited by the disconnection availability and mobility and involves competition between disconnection modes with different characteristics (step height and Burgers vector). If secondary-mode nucleation is the limiting factor for TJ migration, then Eq. 20 implies a connection between TJ and GB mobility; these are both manifestations of the more fundamental disconnection nucleation terms ${\eta }_i$ and mobility $M_d$ (likely more important at low temperature).

Fig. 8 shows the results of a tricrystal simulation (same geometry as Fig. 4) performed using the continuum model (for model assumptions and input data, see SI Appendix, Note 3). Here, the nucleation barriers describing ${\eta }_1^{\left(i\right)}$ and ${\eta }_2^{\left(i\right)}$ for each GB are 0.3 eV and 0.6 eV, respectively. The trends here are in excellent agreement with the MD simulation results in Fig. 5. At high temperature, the TJs rapidly migrate until they reach the equilibrium triple-junction angle [i.e., ${\mathrm{\Theta }}^{\left(1\right)}=120^{○}$ here where we assumed that the GB energies are isotropic]. At lower temperature, the migration is significantly slower, limited by the barrier to secondary disconnection nucleation [expressed via the ${\eta }_2^{\left(i\right)}$ terms]. While the MD simulations show that TJ stagnation is possible at low temperature in the course of a finite-time simulation, given sufficient time for secondary disconnection modes to activate, these too should approach equilibrium. In the continuum model, which implicitly assumes statistical averaging, this simply manifests as very slow kinetics (approaching equilibrium).

Fig. 8.

Triple-junction migration (same geometry as Fig. 4) via the continuum model [i.e., $\varphi \left(t\right)$] for comparison with the MD simulation results (Fig. 5). Unlike in the MD simulation the radius of the simulation cell $R=\infty$.

The advantages of the continuum simulation approach over molecular dynamics are twofold. First, it provides a direct connection between the theory and the microstructure evolution that is not accessible to MD because of assumptions required on simulation cell geometry and simulation timescale. Second, it highlights the fundamental conclusion that TJ mobility is governed by the same kinetics as GB mobility by geometric necessity.

Discussion

TJ migration follows from GB migration; ultimately, TJs migrate via the reaction of GB disconnections along the TJ line. Disconnections determine how and how fast TJs migrate. Specifically, a TJ may migrate only if disconnections annihilate in appropriate ratios that preserve the connectivity of GBs along the TJ line and do not accumulate significant residual Burgers vector. This condition cannot, in general, be met if each GB migrates only by a single disconnection mode. If only single disconnection modes are available on the GBs meeting at a TJ, such a TJ should migrate a small distance, accumulate stress, and stagnate. However, all GBs have access to multiple disconnection modes. Since secondary disconnection modes are necessary (in most cases) for continued TJ migration, TJ motion will be slow if the formation/motion of such secondary modes is difficult. This means that while GBs in bicrystals may move via single disconnection modes, such single-mode dominance is rare in the wild (i.e., polycrystalline materials). We also note that since the relative ease of nucleating different disconnection modes varies dramatically from GB to GB, TJs are also expected to show considerable anisotropy in their mobilities. As noted by Holm and Foiles (91), a minority of slow GBs may lead to grain growth stagnation (so too for TJs). This may play a significant role in abnormal grain growth.

While the present results point to the mechanism by which GB and TJ motions are coupled, the results presented here also point to an important coupling between microstructure evolution and the mechanical response of a material. While the temperature-dependent shear coupling of GB migration and strain (65) associated with disconnection motion can produce significant stresses in constrained bicrystals, this effect may be both magnified and ameliorated in polycrystal microstructure evolution. Disconnection pile-up at triple junctions can produce significant back stresses, but such pile-ups can be relaxed by emission of dislocations or twins into grain interiors. This pile-up mechanism at TJs may be one of the dominant mechanisms for emission of defects into the lattice in nanocrystalline materials (67–70).

Finally, we note that while a disconnection picture of grain boundary and triple-junction dynamics appears to add complexity to how we view microstructure evolution, it is through examination of detailed mechanisms and reducing these to physically based, mechanism-specific continuum models, as we propose here, that we learn how to systematically simplify our understanding of GB dynamics while retaining the important features that affect microstructure evolution. To misquote Einstein “everything should be made as simple as possible, but not simpler” (ref. 92, p. 475).