PROTOSOLAR AMMONIA AS THE UNIQUE SOURCE OF TITAN’s NITROGEN

Abstract

The origin of Titan’s nitrogen-rich atmosphere is thought to be ammonia ice, but this has not yet been confirmed. Furthermore, it is uncertain whether the building blocks of Titan formed within the Saturnian subnebula or in the colder protosolar nebula (PSN). Recent measurements of the nitrogen isotope ratio in cometary ammonia, combined with evolutionary constraints on the nitrogen isotopes in Titan’s atmosphere provide firm evidence that the nitrogen in Titan’s atmosphere must have originated as ammonia ice formed in the PSN under conditions similar to that of cometary formation. This result has important implications for the projected D/H ratio in cometary methane, nitrogen isotopic fractionation in the PSN and the source of nitrogen for Earth’s atmosphere.

1. INTRODUCTION

The origin of Titan’s nitrogen-rich atmosphere is still uncertain (Niemann et al. 2010). The ratio of light to heavy nitrogen (¹⁴N/¹⁵N) in molecular nitrogen, the most abundant constituent in Titan’s atmosphere, has been measured to be (Niemann et al. 2010), a value close to the one recently measured in cometary ammonia (Rousselot et al. 2014; Shinnaka et al. 2014). Here we show that the ¹⁴N/¹⁵N ratio in Titan’s nitrogen did not significantly evolve over the satellite’s history, irrespective of the atmospheric escape process considered, and remained close to the value in cometary ammonia. This implies that nitrogen was captured in the form of ammonia present in Titan’s building blocks when they formed in the protosolar nebula (PSN). Soon after Titan’s formation, the conversion of ammonia into nitrogen may have been induced by photolysis (Atreya et al. 1978) or shock chemistry (McKay et al. 1988) in the satellite’s atmosphere, or resulted from its thermal decomposition in the interior (Glein et al. 2009). It has already been shown that none of these conversion processes could have significantly changed the ¹⁴N/¹⁵N ratio (Berezhnoi 2010).

Nitrogen in the PSN was primarily in the form of N₂ (Marty et al. 2010) with trace amounts of NH₃, HCN and organic material. The reduction of N₂ in the warmer subnebula (a gravitationally trapped region of higher density gas) around Saturn is expected to have led to a much greater abundance of NH₃ relative to N₂ (Prinn & Fegley 1981). If the planetesimals that were the building blocks for Titan formed in the Saturnian subnebula, they would therefore have contained a higher abundance of NH₃ than those formed in the PSN. The idea that NH₃ might have been more abundant than N₂ in Titan’s building blocks was supported by the low non-radiogenic argon (³⁶Ar) abundance measured by the Huygens probe Gas Chromatograph Mass Spectrometer (GCMS; Niemann et al. 2010) which suggested that only NH₃ was trapped in Titan’s building blocks because N₂ and ³⁶Ar are trapped in ice at much colder temperatures than NH₃ (Owen & Bar-Nun 1995). However, laboratory studies have shown that aerosols formed in Titan’s atmosphere can trap sufficient amounts of ³⁶Ar to remove enough of it from the atmosphere over the lifetime of Titan to reduce the ³⁶Ar/N₂ ratio from the solar value to the current measurement (Jacovi & Bar-Nun 2008). Hence the low ³⁶Ar abundance is not conclusive in arguing for ammonia as the source of Titan’s nitrogen. Furthermore, an alternative model proposed recently that Titan’s planetesimals formed in the cold PSN and later migrated into the warmer Saturnian subnebula where some of the volatiles in these planetesimals were partly devolatilized (Mousis et al. 2009a). In this model, it was not hot enough in the Saturnian subnebula to vaporize all of the ices or induce chemical conversion. Evaluation of the ¹⁴N/¹⁵N in Titan’s atmosphere can provide a more definitive constraint on the nitrogen composition of Titan’s building blocks and hence provide a test of these competing models for Titan’s formation.

2. NITROGEN IN THE PSN

The measurements of ¹⁴N/¹⁵N made throughout the solar system are listed in Table 1 and illustrated in Figure 1. These ratios are either primordial (triangles in Figure 1), or evolved (circles in Figure 1). Primordial ratios are believed to have preserved their value from the early stages of solar system formation. An example of a primordial measurement is ¹⁴N/¹⁵N in the atmosphere of Jupiter, which is interpreted as primordial because Jupiter’s high-gravity, hydrogen-dense atmosphere maintains a closed chemical system. These ratios are, therefore, presumably a direct record of conditions in the PSN. Evolved ratios are interpreted to have changed in value over the history of the solar system.

Table 1.

Measurements of ¹⁴N/¹⁵N Throughout the Solar System

Target	14N/15N	Primorial or Evolved ratio	Form of nitrogen	Primordial form
Solar wind	442 ± 1001	Primordial	N	N2
Jupiter	435 ± 652	Primordial	NH3	N2
Several Jupiter family and Oort cloud comets	157 ± 213	Primordial	HCN	HCN
Summed spectrum of several Jupiter family and Oort cloud comets	127 ± 324	Primordial	NH3	NH3
Comet C/2012 S1 (ISON)	139 ± 385	Primordial	NH3	NH3
Titan’s atmosphere	167.7 ± 1.76	Evolved	N2	NH3
Titan’s building blocks	⩽ 190	Primordial	NH3
Comet 81P/Wild 2 grains	231 ± 387	Primordial	Organics with ice	Organics + HCN & NH3
Chondrites	259 ± 158	Primordial	Organics	Organics
Earth’s atmosphere	272 ± 0.39	Evolved	N2	TBD
Earth’s mantle	270.4 ± 3.39	Unknown	N2
Venus’ atmosphere	273 ± 5610	Unknown	N2
Mars meteorite	280 ± 511	Unknown	Various N-bearing compounds
Mars’ atmosphere	168 ± 1712	Evolved	N2

Notes. We identify the form of nitrogen in which the measurement was made and the likely form of nitrogen when it was delivered to the target body. Sources:

¹Marty et al. (2010)

²Owen et al. (2001)

³Bockelee-Morvan et al. (2008)

⁴Rousselot et al. (2014)

⁵Shinnaka et al. (2014)

⁶Niemann et al. (2010)

⁷McKeegan et al. (2006)

⁸Alexander et al. (2012)

⁹Marty & Zimmerman (1999)

¹⁰Hoffman et al. (1979)

¹¹Mathew & Marti 2001

¹²Wong et al. (2013).

Figure 1.

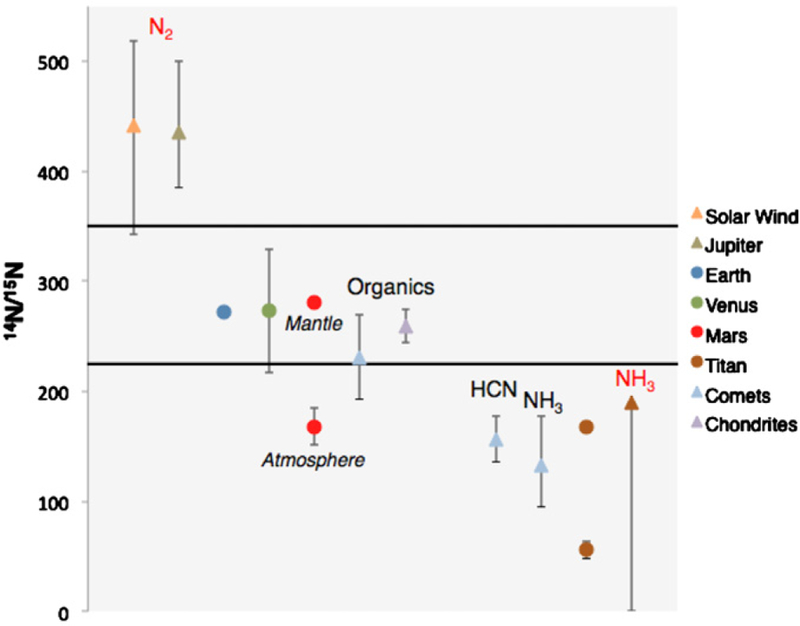
Measurements of nitrogen isotope ratios throughout the solar system. Triangles are primordial values representing ¹⁴N/¹⁵N in the PSN. Circles are isotope ratios that have evolved over the 4.6 Billion year history of the solar system. The primordial value for Titan is inferred from models of atmospheric evolution. The composition of each primordial ¹⁴N/¹⁵N is provided as either the constituent that was measured (black) or inferred (red) based on current understanding of the evolution of the solar system.

The measured ¹⁴N/¹⁵N can be divided into three categories based on their value.

1. The solar wind (Marty et al. 2010) and Jupiter (Owen et al. 2001) have the lightest ratios.

2. Chondrites (Alexander et al. 2012) and grains from comet 81P/Wild 2 (McKeegan et al. 2006), Earth’s atmosphere and mantle (Marty & Zimmermann 1999), Venus (Hoffman et al. 1979) and the mantle of Mars (based on SNC meteorite ratios; Mathew & Marti 2001) have moderately heavy ratios.

3. Saturn’s moon Titan (Niemann et al. 2010), the atmosphere of Mars (Wong et al. 2013) and HCN (Bockelée-Morvan et al. 2008) and NH₃ (Rousselot et al. 2014; Shinnaka et al. 2014) in comets have the heaviest values.

The molecular carrier and the isotopic ratio of nitrogen introduced into Titan during formation was a function of the nebular environment. If Titan’s building blocks formed in an initially warmer and denser Saturnian subnebula, then they would have contained NH₃ formed by N₂ reduction in the gas phase at high temperatures (Prinn & Fegley 1981). This NH₃ would have had a ¹⁴N/¹⁵N similar to N₂ in the PSN because the bulk conversion from N₂ to NH₃ would produce NH₃ with ¹⁴N/¹⁵N reflecting that of its source material—N₂ originating in the PSN. If Titan’s building blocks formed in the colder PSN, then they would have contained either N₂, NH₃, or a combination of both. The primary form of nitrogen in the PSN was N₂ but trace amounts of NH₃ and HCN were also present in the PSN and are preserved in primordial ices in bodies such as cometary nuclei (Hily-Blant et al. 2013). The value for ¹⁴N/¹⁵N in N₂ in the PSN can be determined using ¹⁴N/¹⁵N measured in Jupiter’s atmosphere and the solar wind based on the argument that the Sun and Jupiter derived their nitrogen from N₂ in the PSN (Marty et al. 2010; Owen et al. 2001). The agreement between ¹⁴N/¹⁵N in these two bodies makes this association plausible and gives an estimate for ¹⁴N/¹⁵N in N₂ in the PSN of ~435. If Titan’s nitrogen originated from N₂ or from NH₃ in the Saturnian subnebula, the primordial ratio of nitrogen in Titan’s building blocks would then have been ~435. If Titan’s building blocks formed in the PSN, any N₂ trapped in the ices would have a PSN value of ¹⁴N/¹⁵N, but any NH₃ could have a ¹⁴N/¹⁵N value that differs from ¹⁴N/¹⁵N in N₂. Two recent measurements of ¹⁴N/¹⁵N in cometary NH₃ demonstrate that ammonia ices formed in the PSN are highly fractionated from ¹⁴N/¹⁵N in N₂: 127 ± 32 (Rousselot et al. 2014) using a summed spectrum of 12 comets, and 139 ± 38 (Shinnaka et al. 2014) from the outburst of comet C/2012 S1 (ISON). Therefore, if Titan’s nitrogen originated from NH₃ ice formed in the PSN, its primordial ¹⁴N/¹⁵N would be ~130.

In the past it was assumed that Titan’s primordial ratio was the same as the ¹⁴N/¹⁵N currently measured in Earth’s atmosphere (e.g., Atreya et al. 2009), because comets were suggested to have delivered Earth’s nitrogen in the form of NH₃ (Owen et al. 2001). Prior to the measurements referenced above ¹⁴N/¹⁵N in Earth’s atmosphere was taken to represent ¹⁴N/¹⁵N in cometary NH₃ and was used as the basis for the initial ¹⁴N/¹⁵N for Titan’s atmosphere (e.g., Lunine et al. 1999). If ¹⁴N/¹⁵N in NH₃ was not homogenous throughout the PSN, then it may be possible that Titan’s building blocks could have contained NH₃ with a primordial ratio in the same range as the terrestrial ¹⁴N/¹⁵N, which is measured at 272. We first explore whether it is possible for Titan’s primordial ratio to fractionate from 272 to its current value of 167.7 and then discuss the implications for the origin of Titan’s nitrogen. It has already been demonstrated that the conversion of NH₃ into N₂ by photolysis (Atreya et al. 1978) or shock chemistry (McKay et al. 1988) could not have significantly changed the ¹⁴N/¹⁵N ratio (Berezhnoi 2010) nor could thermal decomposition in the interior (Glein et al. 2009). However, these studies did not consider escape, which is one of the most efficient mechanisms known to substantially fractionate the planetary atmospheres (Pepin 2006). We evaluate this mechanism here to determine if escape can fractionate the ¹⁴N/¹⁵N ratio in Titan’s atmosphere from 272 to 167.7 within the lifetime of the solar system.

3. FRACTIONATION BY ESCAPE

The evolution of isotope ratios in Titan’s atmosphere depends on processes that fractionate the isotopes. Escape preferentially removes the lighter isotope from the atmosphere thus decreasing ¹⁴N/¹⁵N. Photochemistry can also fractionate isotopes by preferentially removing either the lighter or the heavier isotope. Photochemistry in Titan’s atmosphere preferentially removes the heavier isotope from N₂ through self-shielding processes that incorporate more ¹⁵N into HCN relative to ¹⁴N (Liang et al. 2007; Mandt et al. 2009). Because we are looking for a limit on how much Titan’s ¹⁴N/¹⁵N can decrease over the history of the solar system, we will focus only on escape. By doing this, we will define lower limits for the time required to fractionate ¹⁴N/¹⁵N from the terrestrial value of 272 to Titan’s current value of 167.7. In our previous work, we found that hydrodynamic escape of an atmosphere drags too much of both isotopes out of the atmosphere to effectively change the ratio (Mandt et al. 2009), but the assumption was that the loss rate of the heavy isotope depended on that of the primary constituent, which could either be H, H₂ or ¹⁴N₂. We revisit the question of escape-driven fractionation at Titan based on recent studies of escape processes (Volkov et al. 2011) that allow us to consider mass-dependent fractionation during sputtering, Jeans escape and hydrodynamic escape.

The fractionation of isotopes is described by a fractionation factor, f (Mandt et al. 2009). If f is greater than 1.0 there is preferential loss of the heavy isotope, and if f is less than 1.0 the lighter isotope is preferentially removed. The value of ¹⁴N/¹⁵N will not change when f is 1.0. The total inventory of a constituent, in terms of the current inventory (i.e., current atmospheric masses of N₂), n₀/n, required for fractionation from an initial ¹⁴N/¹⁵N, R₀, to the current ¹⁴N/¹⁵N, R, is given as a function of the fractionation factor:

$$\frac{n_0}{n}={\left(\frac{R}{R_0}\right)}^{\frac{1}{1-f}}.$$ (1)

Currently nitrogen escapes from Titan at a small rate due to sputtering (De la Haye et al. 2007). This process efficiently fractionates the isotopes through diffusion as a function of the temperature in the upper atmosphere, T, and the distance between the exobase and the homopause, or r_e − r_h:

$$f=\exp \left[-\frac{(r_e-r_h)GM(m_2-m_1)}{kT{r}^2}\right]$$ (2)

where k is Boltzmann’s constant, G is the gravitational constant, M is the mass of Titan and m is the mass of N₂. A reasonable range of f for Titan is 0.720 to 0.850 based on the extent of the atmosphere and possible temperature ranges in the thermosphere as measured by Cassini instruments (Mandt et al. 2012). Under current atmospheric conditions the fractionation factor for sputtering is f = 0.729. Figure 2 shows the inventory that must be lost by sputtering for the ratio to change from 272 to 167.7 (blue shaded region). The escape rate at the current time due to sputtering is ~10⁸ cm⁻² s⁻¹ (De la Haye et al. 2007), leading to the time limits shown in Figure 3 (blue line).

Figure 2.

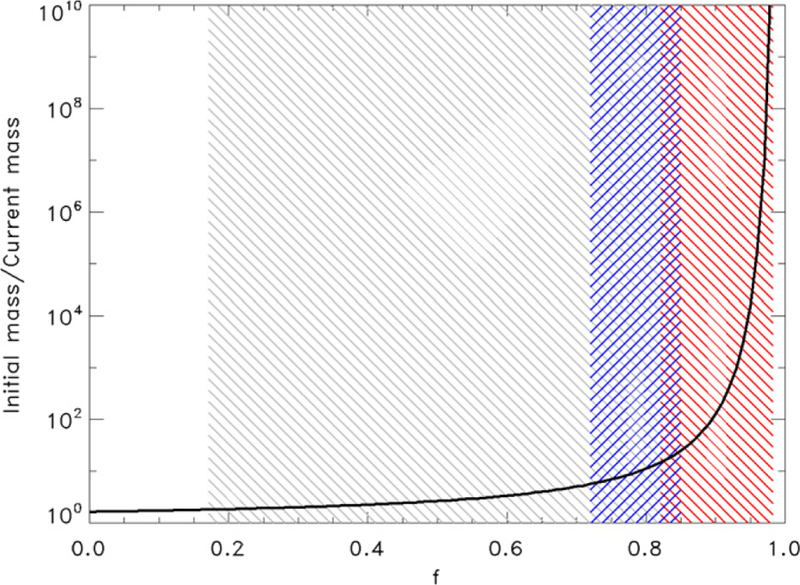
Initial atmospheric mass in terms of the number of current atmospheres required to fractionate ¹⁴N/¹⁵N from 272 to 167.7, and the fractionation factor, f. Hydrodynamic escape (red range) requires loss of between 13 and 10¹⁴ times the current atmosphere, while Sputtering (blue range) only requires loss of 5–24 times the current atmosphere and Jean escape (gray range) requires loss of 0.8–13 times the current atmosphere.

Figure 3.

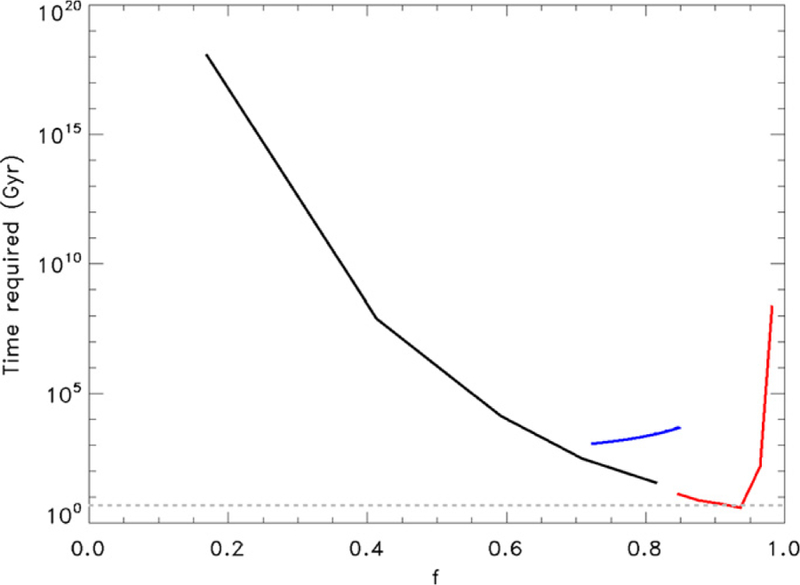
Time required (in billions of years, or Gyr) to change the ratio from 272 to 167.7, shown as a function of f for Hydrodynamic escape (red), Jeans escape (black) and Sputtering (blue). With the exception of one case of Hydrodynamic escape, each type of escape requires longer than the lifetime of the solar system (dashed gray line). The minimum time is ~3.8 Gyr for an escape rate and f that could only have been sustained for 40 Myr.

If we take into account changes in solar activity, sputtering rates early in the history of the solar system could have been up to three orders of magnitude higher for as much as 1 billion years (Gyr) due to the high density and velocity of the solar wind (Penz et al. 2005). These escape rates allow for a total loss of ~0.6 times the current atmospheric mass over the first Gyr of Titan’s lifetime. Although the reasonable range of f for Titan’s current conditions is 0.720–0.850, increased solar extreme ultraviolet (EUV) flux in the early stages of the solar system would increase the temperature and extent of Titan’s atmosphere, increasing f (Equation (2)), and hence reducing fractionation. Thus f of 0.720 is a lower limit, and based on Equation (1) the initial ¹⁴N/¹⁵N must be lower than 190.

Thermal escape due to Jeans escape and hydrodynamic escape must also be considered. The current thermal escape rate at Titan is several orders of magnitude less than the sputtering rate for N₂, and has no effect on atmospheric evolution. However, thermal escape may have been effective in the distant past when the solar EUV flux was much higher (Penz et al. 2005; Mandt et al. 2009). Thermal escape produces mass-dependent fractionation that varies as a function of the Jeans escape parameter, λ:

$$\text{λ=}\frac{GMm}{kT{r}_e}.$$ (3)

The value for λ for N₂ in Titan’s atmosphere is presently ~50 (Volkov et al. 2011). Jeans escape is given as:

$$F_J=n_e\sqrt{\frac{kT}{2\pi m}}(1+\text{λ})e^{-\text{λ}}$$ (4)

where n_e is the density at the exobase. Fractionation due to Jeans escape for N₂ is

$$f=\sqrt{\frac{m_1}{m_2}}\frac{(1+1.036\text{λ})e^{-1.036\text{λ}}}{(1+\text{λ})e^{-\text{λ}}}$$ (5)

The possible values for f due to Jeans escape range between 0.170 when λ = 50 and 0.820 when λ = 6, which is the minimum value for λ before transition to hydrodynamic escape (Volkov et al. 2011). Figure 2 illustrates that 0.8–13 times the current atmosphere (shaded gray area) must be lost through Jeans escape in order to fractionate ¹⁴N/¹⁵N from 272 to 167.7. Jeans escape only becomes more significant than sputtering when λ< 10. We estimate the time required to lose 13 times the current atmosphere through Jeans escape based on the maximum possible rate, which is found when λ = 6 (Volkov et al. 2011). Based on Equation (3), the temperature at the exobase must be between 650 and 1250 K, depending on the extent of the atmosphere, which could have been as far out as three Titan radii (Penz et al. 2005). The exobase temperature decreases with increasing altitude of the exobase. With these constraints, the range of possible N₂ densities at the exobase can be found from the definition that the exobase occurs where the scale height equals the mean free path:

$$\frac{kT{r}_e^2}{GMm}=\frac{1}{\sqrt{2}\sigma n_e}$$ (6)

where σ is the collision cross section for N₂. This limits the density at the exobase to 1–2 × 10⁶ cm⁻³, and gives a maximum Jeans escape rate of ~2.8 × 10⁹ cm⁻² s⁻¹. Based on this, at least 34.5 Gyr are required to fractionate the isotopes, or more than seven times the lifetime of the solar system. When λ = 10, the time required increases to 305 Gyr because the escape rate is lower, as illustrated in Figure 3 (black line).

In hydrodynamic escape λ gradually becomes smaller while f increases to a value of (Volkov et al. 2011):

$$f=\sqrt{\frac{m_1}{m_2}}$$ (7)

as illustrated in Figure 2 (red shaded region). Figure 3 (red line) illustrates estimates for the time required for hydrodynamic escape to fractionate the isotopes. The most effective fractionation occurs when λ = 2, which is the only case where the time required to fractionate the isotopes is within the lifetime of the solar system. In this case we estimate the maximum possible escape rate to be ~4 × 10¹² cm⁻² s⁻¹ assuming an exobase that could range between its current and three times the current altitude (Penz et al. 2005) and temperatures that could be as high as 75,000 K. Other studies estimated a similar energy-limited loss rate of N₂ of 6 × 10¹² cm⁻² s⁻¹ at the earliest stages of the solar system, but found that this loss rate could not be sustained for more than 40 Myr (Penz et al. 2005). This is much less time than what is required for fractionating the isotopes due to hydrodynamic escape, so the time required for hydrodynamic escape is >100 times too long to fractionate the ¹⁴N/¹⁵N from 272 to 167.7.

4. DISCUSSION AND CONCLUSIONS

In the previous sections we demonstrated that sputtering would require too much time to fractionate ¹⁴N/¹⁵N in Titan’s atmosphere from 272 to 167.7, even when taking into account that the early Sun would have allowed higher sputtering rates in the distant past due to a denser solar wind. Fractionation of the isotopes by sputtering would have taken more than 250 times the lifetime of the solar system, as shown in Figure 3. Jeans escape must remove 0.8–13 times the current atmosphere and hydrodynamic escape requires between 13 and 1014 atmospheric masses to be lost. As Figure 3 demonstrates, only one case of hydrodynamic escape provides a timescale that is less than the lifetime of the solar system for an escape process that could have only lasted for ~40 million years (Penz et al. 2005). Therefore, the upper limit for the primordial ratio for Titan is limited to ≤190, which is in agreement with the ¹⁴N/¹⁵N for NH₃ ice in the PSN based on cometary measurements. It is not possible for the primordial ratio of Titan to be the same as the ¹⁴N/¹⁵N in the Earth’s atmosphere, and unlikely that Titan’s primordial ¹⁴N/¹⁵N was ~435, thus demonstrating that Titan’s nitrogen must have originated as NH₃ ice from the PSN, as was also suggested by Rousselot et al. (2014). A further implication of this result is that cometary NH₃ is not likely to be the primary source of Earth’s nitrogen.

Furthermore, a clear difference between ¹⁴N/¹⁵N in N₂ in the PSN and in the NH₃ ices formed in the PSN has been demonstrated by our results for Titan and by the measurements of ¹⁴N/¹⁵N in cometary NH₃. This difference can provide some insight into processes at work in the PSN. Observations of prestellar cores suggest that the formation of nitriles (e.g. HCN) and amines (molecules that form by replacing one or more hydrogen atoms in NH₃) are decoupled and that processes that enrich nitriles in ¹⁵N would not enrich amines in ¹⁵N (Hily-Blant et al., 2013). Self-shielding processes in the PSN can explain the enrichment of ¹⁵N in nitriles such as HCN (Clayton 2008), because HCN in formed from neutral nitrogen atoms produced by dissociation of N₂, while gas–grain chemistry (Charnley & Rodgers 2002; Rodgers & Charnley 2008) provides the best explanation for enrichment of NH₃.

Finally, determining that NH₃ ices formed in the PSN is the unique source of Titan’s nitrogen allows us to make a prediction for the D/H in methane in comets, which should be measured by the Rosetta mission at comet 67P/Churyumov–Gerasimenko (hereafter CG). The D/H in the water of Enceladus’s plume is 2.9 × 10⁻⁴ (Waite et al. 2009), which is in the same range as the enriched values of D/H in water in Oort Cloud comets, suggesting that its building blocks were the same as for this family of comets (Mousis et al. 2009b). Our studies of the evolution of methane in Titan’s atmosphere (Mandt et al. 2012) show that the primordial D/H in Titan’s methane is bracketed between the current value measured by Cassini, 1.6 × 10⁻⁴ (Nixon et al. 2012), and the protosolar D/H of 2.1 × 10⁻⁵ (Geiss & Gloeckler 1998). The scenario for Titan formation therefore predicts that the D/H in methane in Oort Cloud comets should fall within this range. The D/H in methane in short period comets, such as CG, should be less than that of Oort Cloud comets with a lower limit of the protosolar D/H.