Abstract
The origin and evolution of nitrogen in solar system bodies is an important question for understanding processes that took place during the formation of the planets and solar system bodies. Pluto has an atmosphere that is 99% molecular nitrogen, but it is unclear if this nitrogen is primordial or derived from ammonia in the protosolar nebula. The nitrogen isotope ratio is an important tracer of the origin of nitrogen on solar system bodies, and can be used at Pluto to determine the origin of its nitrogen. After evaluating the potential impact of escape and photochemistry on Pluto’s nitrogen isotope ratio (14N/15N), we find that if Pluto’s nitrogen originated as N2 the current ratio in Pluto’s atmosphere would be greater than 324 while it would be less than 157 if the source of Pluto’s nitrogen were NH3. The New Horizons spacecraft successfully visited the Pluto system in July 2015 providing a potential opportunity to measure 14N/15N in N2.
Keywords: Planets and satellites, Atmospheres, Minor planets, Asteroids, Pluto, Planets and satellites: composition
1. Introduction
The New Horizons mission (Stern, 2008a) arrived in the Pluto system in July 2015 and made unprecedented observations of Pluto’s surface and atmosphere. These observations could provide clues to the origin and evolution of Pluto’s atmosphere as well as further constraints on the role of nitrogen in the formation and evolution of the solar system. A key measurement will be the 14N/15N in N2, the primary constituent of Pluto’s atmosphere (Jessup et al., 2013), which could help to constrain the origin of nitrogen on Pluto and the dominant escape process in Pluto’s atmosphere.
Pluto is likely to have formed in the outer solar system (Brown, 2002) and is thought to owe its present orbit to the migration of the giant planets (Levison et al., 2007). Its mass density indicates that Pluto is severely depleted in water ice relative to its rock abundance, which is between 50% and 80% (McKinnon and Mueller, 1988; Olkin et al., 2003). This high rock abundance suggests formation in a CO-rich and ice-poor region of the protosolar nebula (PSN), loss of volatiles by the impact formation of Charon, or a combination of these two factors (McKinnon and Mueller, 1988). The surface of Pluto consists of a spatially heterogeneous mixture of N2, CH4, CO and C2H6 ices (Cruikshank et al., 2014). The most abundant ice on the surface is N2 and is presumed to be the primary constituent in Pluto’s tenuous atmosphere (Owen et al., 1993).
Determining what was the source of Pluto’s nitrogen can provide important information about the temperature and composition of the region of the PSN in which Pluto formed. The most likely source of Pluto’s nitrogen was either N2 or NH3 that were trapped in ices in the PSN. However, it is important to note that significant amounts of nitrogen in the PSN were also bound in refractory organic molecules. As the formation process for these organics is poorly understood, we focus on N2 and NH3 for the sake of this study.
N2 is believed to have been ~10 times greater in the PSN than NH3 (Lewis and Prinn, 1980), but requires much colder temperatures to be trapped in water ices, whether the ices are amorphous (Bar-Nun et al., 1985, 1988) or crystalline (Mousis et al., 2012, 2014). Pluto would have accreted N2 ice in greater abundance than NH3 ice if its formation temperature was less than ~40 K, which may have been possible in the outer solar system. However, comets also formed in the outer solar system and are believed to be deficient in N2 relative to NH3 suggesting either that temperature conditions could have been too warm for N2 to be trapped in icy grains (Iro et al., 2003) or that comets did not retain N2 i) beyond their first pass through the solar system (Owen et al., 1993) or ii) due to internal radiogenic heating at early epochs after formation (Mousis et al., 2012). The recent detection of N2 in comet 67P/Churyumov–Gerasimenko (hereafter 67P/CG) by Rosetta shows that the abundance of N2 relative to CO is a factor of 25.4 lower than the protosolar value (Rubin et al., 2015). This measurement puts a constraint on the formation temperature of 67P/CG of 32–70 K (Lectez et al., 2015). If the composition of 67P/CG, which is believed to be a Kuiper Belt comet, is indicative of the general composition of Kuiper Belt objects, then Pluto could have formed in a similar temperature range and may have retained some N2 from the PSN. As the relative abundance of N2 to NH3 in 67P/CG is not yet known, it is unclear if these results suggest greater retention of NH3 over N2 for Pluto.
It appears, based on the above results, that there is a large uncertainty in the source of nitrogen for Pluto. If temperatures were low enough during formation, the source of Pluto’s nitrogen could have been N2, but if temperatures were above the limits described above (typically 70–80 K for enabling ammonia hydrate formation in the PSN), the source of nitrogen for Pluto’s surface and atmosphere would have been NH3 that was later converted to N2, as was the case for Titan (Mandt et al., 2014).
Stable isotope ratios that are presumed to be primordial, or representative of conditions in the PSN, can help constrain the role of nitrogen in the formation and evolution of the solar system. Measurements of comets, meteorites and giant planet atmospheres are presumed to represent primordial conditions, while the terrestrial planets, Pluto, Saturn’s moon Titan and Neptune’s moon Triton have atmospheres that have evolved over the history of the solar system.
Fig. 1 illustrates 14N/15N measurements throughout the solar system. They are identified as either primordial (triangles), or evolved (circles). The primordial ratios provide constraints for 14N/15N in N2, NH3, HCN and organics in the PSN. The solar wind (Marty et al., 2011) and Jupiter (Owen et al., 2001) have the lightest ratios, with values in the range of ~440, and represent primordial 14N/15N in N2. HCN (Bockelée-Morvan et al., 2008) and NH3 (Rousselot et al., 2014; Shinnaka et al., 2014) in comets give a primordial 14N/15N in HCN and NH3 of ~160 and ~133, respectively. The bulk 14N/15N of organic material found in Ordinary and Carbonaceous Chondrites (Alexander et al., 2012) is intermediate to N2 and HCN and NH3 in the PSN.
Fig. 1.
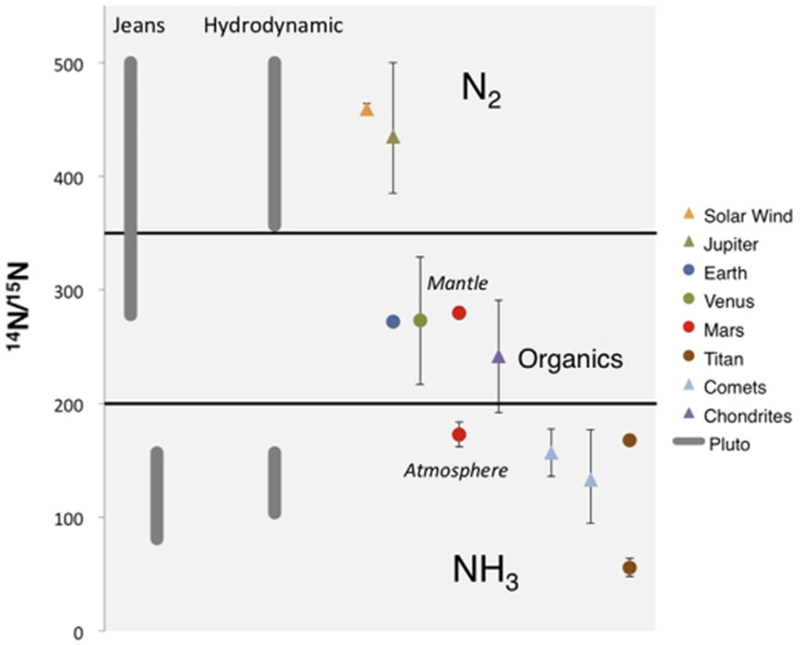
Measurements of nitrogen isotope ratios, or 14N/15N, in the solar wind, comets and the atmospheres of Jupiter, terrestrial planets and Titan. Triangles are primordial values representing 14N/15N in the PSN. Circles are isotope ratios that have evolved over the 4.6 billion year history of the solar system. 14N/15N in the atmosphere of Marsis much lower than in the mantle, although it is unclear if the mantle measurement can be considered as primordial. The primordial value for Titan is inferred from models of atmospheric evolution. Since 14N/15N has not yet been measured for Pluto, we provide a range of values based on the source of the nitrogen and the type of escape as described in Section 3.
Mars, Titan, Venus and the Earth have ratios that are presumed to have evolved over time. The atmosphere of Mars has a much lower 14N/15N (Nier and McElroy, 1977; Wong et al., 2013) than the mantle based on SNC meteorite ratios (Mathew and Marti, 2001) because of extreme fractionation by escape processes that preferentially remove the lighter isotope from the atmosphere (e.g. Fox and Dalgarno, 1983). However, we recently demonstrated (Mandt et al., 2014) that escape could not significantly fractionate the 14N/15N in N2 in Titan’s atmosphere from its current value of 167.7 ± 0.7 (Niemann et al., 2010), which provides a primordial ratio for Titan that is similar to NH3 and HCN in comets. The 14N/15N in HCN in Titan’s atmosphere is ~65 (Vinatier et al., 2007), which results from strong photochemical fractionation by self-shielding of N2 (Liang et al., 2007). Although Earth and Venus are not expected to have experienced much fractionation due to escape, the source of nitrogen for Earth, Venus and Mars is poorly understood (e.g. Hutsemèkers et al., 2009; Alexander et al., 2012) and their ratios are designated as evolved in Fig. 1.
14N/15N in Pluto’s atmosphere has not yet been measured, and the primordial 14N/15N ratio for Pluto it is not presently known. The bulk of the atmosphere (> 99%) is expected to be N2, with trace amounts of CH4, CO and HCN (e.g. Young et al., 1997; Lellouch et al., 2011; Krasnopolsky and Cruikshank, 1999).
At Pluto, several poorly constrained processes could fractionate 14N/15N: sublimation, condensation, escape and photochemistry. It is unknown if, or by how much, sublimation and condensation would fractionate 14N/15N because, to the best of our knowledge, this has never been measured in the laboratory for N2. We therefore assume that the sublimation process releases N2 with a 14N/15N value reflective of the surface ice ratio, and that condensation temporarily removes N2 from the atmosphere, stores it on the surface, and rereleases it without any additional fractionation. The condensed N2 is, therefore, assumed to have a ratio reflective of atmospheric N2 at the time of condensation. We do know that escape preferentially removes the lighter isotope while photochemistry will preferentially remove the heavier isotope due to self-shielding (Liang et al., 2007; Mandt et al., 2009). Of the two known fractionating processes, the dominant process will be escape because it is estimated to have rates as much as three orders of magnitude greater than photochemical loss rates for N2 (Krasnopolsky and Cruikshank, 1999).
The Alice Ultraviolet spectrometer on New Horizons (Stern et al., 2008b) is expected to be able to measure 14N/15N in N2 in Pluto’s atmosphere if the value is ≤ 330 (Jessup et al., 2013). We provide here interpretations for measurements within several ranges of values for 14N/15N based on the source of nitrogen and the type of escape relying on the very limited amount of information presently available for Pluto’s atmosphere.
2. The history of Pluto’s atmosphere
2.1. Current state of knowledge
Because of Pluto’s small size and large distance from the Sun, its atmosphere is difficult to observe from Earth. Observations show that Pluto currently has a tenuous atmosphere with a surface pressure of 6–24 μbar that is composed primarily of N2 (e.g. Young et al., 1997; Lellouch et al., 2011). Pluto’s very high obliquity of 102–126° (Dobrovolskis and Harris, 1983), and eccentric orbit will result in extreme seasonal effects that are poorly understood because Pluto’s atmosphere was first detected in 1988 (Hubbard et al., 1988) and observations of the atmosphere have only covered ~10% of a Pluto year. Model predictions suggest that surface pressures could vary over a Pluto year by as little as a factor of four (Young, 2013; Olkin et al., 2014) or as much as four orders of magnitude (Young, 2013; Hansen et al., 2014).
Based on Pluto’s gravity relative to the energy input to the atmosphere, N2 is expected to easily escape (e.g Krasnopolsky, 1999). Several studies suggest that N2 is escaping hydrodynamically at surface-referenced rates ranging between 1.25 × 1010 and 1.17 × 1011 cm−2 s−1 at perihelion (Krasnopolsky, 1999; Tian and Toon, 2005; Strobel 2008). However, Tucker et al. (2012) suggest that escape is subsonic with rates more reflective of Jeans escape in the range of 6.81 × 109 cm−2 s−1 at perihelion. Although this rate is only a factor of 2–10 less than hydrodynamic escape, the type of fractionation is very different (Volkov et al., 2011; Mandt et al., 2014, 2015, 2012). Furthermore, hydrodynamic escape will produce very different density and temperature altitude profiles compared to an atmosphere experiencing Jeans escape (Tucker et al., 2012).
The only study to evaluate changes in escape over Pluto’s orbit found a yearly averaged escape rate that is a factor of 2 lower than at perihelion (Tian and Toon, 2005). However, Pluto’s surface pressure is predicted to vary significantly and may collapse due to cooling for part of its orbit (see Hansen et al., 2014 and references therein). Studies determining escape rates used lower boundary densities reflective of perihelion conditions and are likely to have overestimated the yearly average escape rate.
We determine here an upper limit and most likely value for fractionation of 14N/15N in Pluto’s atmosphere due to hydrodynamic and Jeans escape using the rates determined for perihelion. Future constraints on Pluto’s atmospheric cycles will enable more precise estimates of fractionation, including seasonal effects.
2.2. Evolution of Pluto’s isotopes
Fractionation of an isotope ratio due to a single process is a function of the initial, n0, and current, n, inventory of the lighter isotope of the constituent and a fractionation factor, f,
| (1) |
where R is the current ratio of 15N to 14N (heavy/light) and R0 is the initial ratio. R/R0 gives the degree of enrichment of the heavier isotope due to fractionation. When R/R0 > 1.0, the current inventory is enriched in the heavy isotope. The fractionation factor, f, describes overall difference in the relative loss or production rates of a heavy and light isotope. If f is greater than 1.0 there is preferential loss of the heavy isotope, while a value less than 1.0 means that the lighter isotope is preferentially removed. The value of R/R0 will not change when f is 1.0. In this relationship, f is presumed to be a representative value for the entire relevant time period.
An upper limit for n0/n is a function of the maximum flux and the amount of time the fractionating process has been in effect:
| (2) |
where ϕ is the maximum flux of the lighter isotope and t is time.
Combining (Eqs. (1) and 2) gives an upper limit for R/R0:
| (3) |
In the case of Pluto, two loss processes play an important role in fractionating R: escape (subscript e) and photochemistry (subscript c). As we demonstrated in Mandt et al., (2015) for Mars and Pluto, the influence of escape and chemistry can be combined because they are both loss processes.
Note that this equation assumes only loss processes are in effect in the atmosphere and that there is no production. This assumption leads to a condition of an initially large atmosphere that decreases with time to the current inventory. However, this is not realistic in the case of Pluto because the escape rate at Pluto relative to the atmospheric abundance is predicted to be significantly higher than at Mars or Titan. For this reason, resupply of the atmosphere by sublimation of fresh unfractionated ice (subscript s) will play an important role in the evolution of R/R0 with time.
In order to illustrate the significance of each of the loss processes, we first evaluate the limit for how much each individual loss process can influence R/R0 over a given time, t, using Eq. (3). We then evaluate the upper limit for fractionation due to combined loss processes. We combine the influence of the two loss processes by (Mandt et al., 2015)
| (4) |
We then evaluate the evolution of R/R0 with time based on the following model that incorporates resupply of the atmosphere due to sublimation.
The basic equations governing the net loss of 14N2 and 14N15N as a function of time, t, are
| (5) |
| (6) |
where is the ratio of 14N15N to 14N2, f is the fractionation factor for each of the three types of loss or production processes, ϕ: sublimation (s), escape (e) and photochemical loss (c). Note that because 14N2 has two 14N atoms, is equal to ½ the value of R. However, also note that .
The change of as a function of time is based on (Eqs. (5) and 6)
| (7) |
No information is available about isotopic fractionation of nitrogen during sublimation or condensation, so we assume that fs = 1.0.
| (8) |
We can simplify this equation by defining a parameter, , which is the ratio of total supply to total loss.
| (9) |
We also make the simplifying assumption that the supply and loss rates are constant over time
| (10) |
| (11) |
Therefore,
| (12) |
We solve Eq. (12) for a range of values for γ to evaluate the role of resupply in the evolution of R/R0. In the simplest case, unfractionated N2 is added to the atmosphere at a rate equal to the total loss of 14N2: ϕs=ϕe+ϕc, or γ = 1. This is a reasonable approximation for resupply at Pluto given the limited understanding of Pluto’s seasonal N2 cycle, which involves migration of N2 ice on the surface through sublimation and condensation rates that must equal or exceed the escape and photochemical loss rates in order to sustain an atmosphere (e.g. Hansen et al., 2014).
It is unclear at this time how the cycle of condensation and resublimation will influence fractionation of the atmosphere beyond storing fractionated N2 ice on the surface. However, it is important to note, that the storing of fractionated N2 ice on the surface removes the fractionated N2 from the atmosphere, reducing the time available for this N2 to fractionate. Modeling the influence of condensation is highly complex and requires an understanding of the condensation and sublimation rates that goes beyond what is available in the literature about Pluto at the present time. However, we note that the process of condensation could reduce the upper limit that we find for fractionation in this study.
The fractionation factor is different for each loss process. For photochemistry, the fractionation factor is a function of R in the reactant and the product (Mandt et al., 2009)
| (13) |
The fractionation factors for Jeans and hydrodynamic escape depend on the escape parameter (or Jeans parameter when r refers to the exobase)
| (14) |
where G is the gravitational constant, M is the mass of Pluto, m is the mass of N2, k is Boltzmann’s constant, T is the temperature and r is the radius of the point at which λ is determined.
The fractionation factor for Jeans escape is (Mandt et al., 2014)
| (15) |
where m1 is the mass of the lighter isotope and m2 is the mass of the heavier isotope. The possible values for f due to Jeans escape range between 0.170 when λ=50 and 0.820 when λ=6, which is the minimum value for λ before transition to hydrodynamic escape (Volkov et al., 2011). The estimated range of values for λ at Pluto is between 5.4 and 8.8 (Tucker et al., 2012) giving f due to Jeans escape of 0.739–0.835. We determine fe for Jeans escape using λ=5.4 because it provides the greatest amount of fractionation in searching for an upper limit. This is likely to be an overestimate of the fractionation due to Jeans escape because the temperature of the atmosphere, and thus λ will vary with time leading to less fractionation.
In hydrodynamic escape λ gradually becomes smaller while f increases to a value of (Volkov et al., 2011; Mandt et al., 2014)
| (16) |
Therefore, if Pluto’s atmosphere is escaping hydrodynamically, f is 0.983.
2.3. Input parameters
Table 1 gives input parameters based on observations and modeling of Pluto’s atmosphere. It is possible that the average column density over a Pluto year was greater in the past than today, which would reduce the upper limit determined by Eq. (3).
Table 1.
Input parameters used to determine the upper limit for fractionation due to escape based on published studies of Pluto. Column density is presumed to be in steady state while the rates for sublimation, escape and photochemistry evolve with time according to Ribas et al. (2005). The total fractionation is constant with time.
| Variable | Jeans escape | Hydrodynamic escape | |
|---|---|---|---|
| Atmospheric column density (cm−2) | n | 3 × 1021 | 3 × 1021 |
| Nitrogen abundance | X | 0.996 | 0.996 |
| Escape rate (cm−2 s−1) | ϕe | 7 × 109 a | 1.8 × 1010 b |
| Escape fractionation | fe | 0.739 c | 0.983 |
| Photochemical loss rate (cm−2 s−1) | ϕc | 2.3 × 107 d | 2.3 × 107 d |
| Photochemical fractionation | fc | 2.6 e | 2.6 e |
| Total loss fractionation | floss | 0.822 | 0.983 |
| Maximum R/R0 | R/R0 | 8.54 | 1.23 |
| Most likely R/R0 | R/R0 | 1.35 | 1.05 |
Krasnopolsky, 1999; Tian and Toon 2005; Strobel 2008;
Assuming λ=5.4 from Tucker et al., 2012, which provides maximum Jeans escape fractionation;
Krasnopolsky and Cruikshank, 1999;
Based on fc determined for Titan by Mandt et al., 2009.
Photochemistry on Titan preferentially removes the heavier isotope from N2 because of complex chemistry that produces aerosols, which fall to the surface leading to a permanent loss of N2. It is unclear if this process will be effective at Pluto, but the estimated 14N2 loss rate due to photodissociation is 2.3 × 107 cm−2 s−1 while production of HCN is ~107 cm−2 s−1 (Krasnopolsky and Cruikshank, 1999) suggesting similar incorporation of nitrogen into HCN to that observed at Titan. Lacking measurements of 14N/15N in N2 and HCN at Pluto, we use the photochemical fractionation factor for Titan to approximate photochemical fractionation at Pluto. However, because the photochemical loss rate is so small compared to the lowest escape rates, f is defined primarily by escape fractionation and the balancing effect of sublimation.
3. Results and discussion
Fig. 2 illustrates the upper limit of enrichment of 14N/15N in Pluto’s atmosphere as a function of time for individual loss processes based on Eq. (3): hydrodynamic escape (black line), Jeans escape (blue line) and photochemistry (red line). Hydrodynamic escape’s fractionation factor is close to 1.0, so it is not efficient at fractionating the isotopes. This process would reduce 14N/15N by a factor of no more than 1.5. Jeans escape, on the other hand, is more efficient at fractionating 14N/15N because f is much lower and would reduce 14N/15N by as much as a factor of ~10. Photochemistry, when considered as an isolated process, is efficient at removing 15N and would increase 14N/15N by a factor of <10−4, which would practically eliminate observable 14N15N from Pluto’s atmosphere.
Fig. 2.
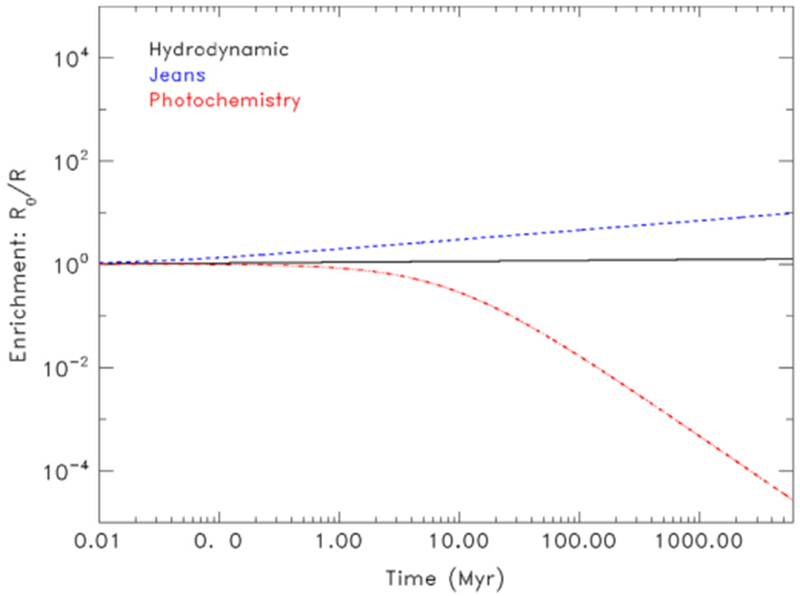
Upper limit for the enrichment of R in the heavy isotope relative to the primordial value for Pluto based on fractionation due to the independent processes of hydrodynamic escape (black solid line), Jeans escape (blue dashed line) and photochemical loss (red dash-dot line). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
However, these processes cannot be taken in isolation. Photochemistry will be accompanied by escape and the atmosphere will be resupplied through sublimation of unfractionated ices. We first illustrate in Fig. 3 the enrichment of 14N/15N in 15N as a function of escape process when combined with photochemistry. We find that photochemistry slightly reduces the fractionation due to escape. Hydrodynamic escape increases the abundance of 15N relative to 14N by a factor of no more than 1.23, while Jeans escape would increase the abundance of 15N relative to 14N by only a factor of 8.54.
Fig. 3. :
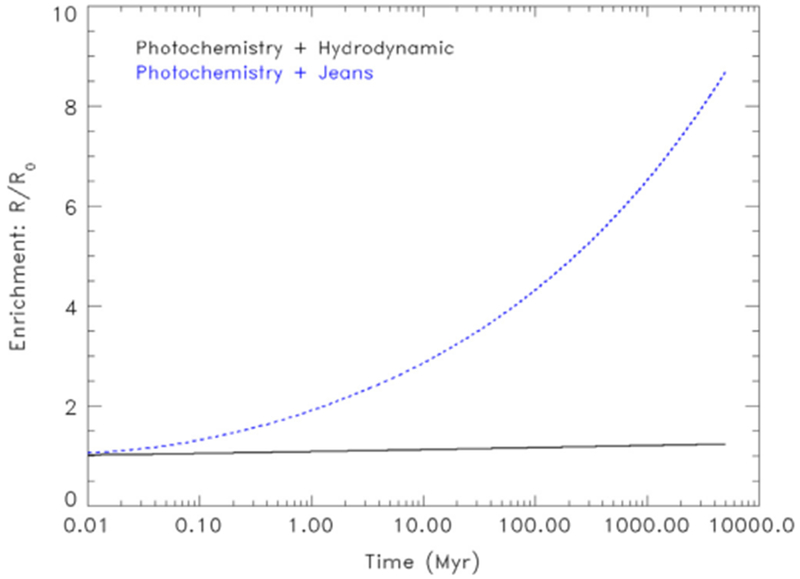
Upper limit for the enrichment of R in the heavy isotope relative to the primordial value for Pluto based on fractionation due to photochemical loss combined with hydrodynamic escape (black solid line) and Jeans escape (blue dashed line). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
Finally, we evaluated R/R0 at the present time using Eq. (12) for a range of γ, or the ratio of supply to loss, as illustrated in Fig. 4. It is first clear from this figure that taking into account resupply of the atmosphere significantly reduces the amount of fractionation that can occur. Furthermore, we find that as γ increases, R/R0 decreases. The maximum R/R0 is 3.63 for Jeans escape and 1.08 for hydrodynamic escape. We also found that if the rate of supply of nitrogen is greater than the rate of loss, the initial density of the atmosphere must be negative due to the rapid rate of atmospheric loss on Pluto due to its weak gravity. In order to sustain an atmosphere on Pluto over geologic timescales the rate of supply of unfractionated nitrogen must be nearly equivalent to the rate of loss, suggesting that the most likely R/R0 is 1.35 for Jeans escape and 1.05 for hydrodynamic escape.
Fig. 4. :
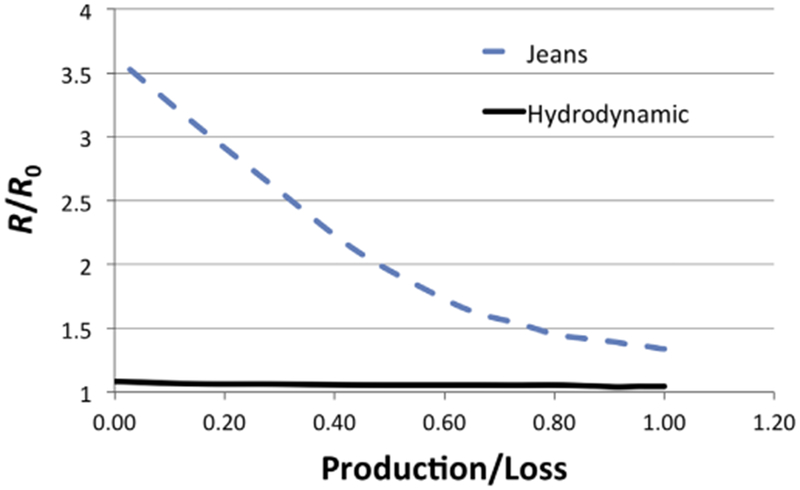
The enrichment of R in the heavy isotope relative to the primordial value for Pluto at the current time based on fractionation due to photochemical loss combined with sublimation and hydrodynamic escape (black solid line) and Jeans escape (blue dashed line). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
The nitrogen in Pluto’s atmosphere is likely to have originated primarily as either N2 or NH3 in the PSN. Table 2 summarizes our predictions for the most likely current 14N/15N ratio in Pluto’s atmosphere based on the source of nitrogen and escape process. These most likely ranges of values are also illustrated in Fig. 1.
Table 2.
Most likely ratio of 14N/15N in Pluto’s atmosphere as a function of the nitrogen source and the process responsible for escape.
| Hydrodynamic | Jeans | |
|---|---|---|
| N2: R0=440 ± 65 | 357–505 | 278–505 |
| NH3: R0=133 ± 24 | 104–157 | 81–157 |
If Pluto’s nitrogen source was N2, then the primordial ratio would have been ~440 ± 65 based on the measurements made in the solar wind (Marty et al., 2011) and Jupiter’s atmosphere (Owen et al., 2001). The current ratio would be greater than 357 if Pluto’s atmosphere is escaping hydrodynamically and between 278 and 505 in the case of Jeans escape. If the source was NH3, then the initial ratio would have been ~133 ± 24 based on the measurements made in comets (Shinnaka et al., 2014; Rousselot et al., 2014). Hydrodynamic escape would give a current ratio of 104–157 while Jeans escape would produce a ratio of 81–157.
4. Conclusions
Our results provide predictions of four possible ranges of values of 14N/15N that could by measured by Alice on New Horizons:
If Alice is not able to detect 14N15N in Pluto’s atmosphere, or measures a value between 278 and 330 (the lower limit for 14N/15N measurable by Alice; Jessup et al., 2013), then Pluto’s nitrogen originated as N2 in the PSN.
If 14N/15N is found to be between 104 and 157 then nitrogen originated as NH3 and the escape process is unconstrained.
A measurement of 14N/15N by Alice of less than 104, can only be explained by an origin as NH3 fractionated by Jeans escape.
Finally, if Alice measures 14N/15N between 157 and 278, the origin of nitrogen is more complex than a bulk source of N2 or NH3 and further investigation is needed to constrain the origin of nitrogen on Pluto. In this case, organics could have served as a major contributor to Pluto’s nitrogen inventory.
It is clear from these results that any information provided by New Horizons Alice could provide a strong indication of whether Pluto’s nitrogen originated as N2 or NH3 or if the source is more complex than a bulk origin as one of these two volatile compounds. It is important to note that the limit determined by Jessup et al. (2013) is based on an atmospheric profile that assumes hydrodynamic escape of N2 (Krasnopolsky and Cruikshank, 1999). As Tucker et al. (2012) demonstrate, the column density that would be observed by Alice under Jeans escape conditions would be significantly greater at distances above 2000 km from Pluto’s center. This may raise the upper limit for Alice to be able to measure 14N/15N.
It is less clear if the isotope ratio can be used to differentiate between hydrodynamic and Jeans escape as the dominant process in Pluto’s atmosphere. Because the density and temperature altitude profiles and the altitude of the exobase are different for an atmosphere escaping hydrodynamically compared to one experiencing Jeans escape (Tucker et al., 2012), a measurement of the density and temperature profiles is the best tool to determine the dominant escape process.
A further constraint on the nitrogen origin can be provided by measuring Argon in Pluto’s atmosphere. Alice has the capability of measuring Ar down to 10% of the Ar/N solar value (Mousis et al., 2012), and since solid Ar exists only at very low temperature in the PSN, either in the form of amorphous ice (Bar-Nun et al., 2007) or a pure condensate (Mousis et al., 2012), its detection in Pluto’s atmosphere would support the idea that the N-dominating species is N2.
Acknowledgments
K.E.M. and A.L.-K. acknowledge support from NASA grant NNX1-3AQ99G. K.E.M. also acknowledges support from JPL Subcontract 1345493. O.M. acknowledges support from CNES. The work contributed by O.M. was carried out thanks to the support of the A*MIDEX project (n° ANR-11-IDEX-0001-02) funded by the « Investissements d’Avenir » French Government program, managed by the French National Research Agency (ANR).
References
- Alexander CMO, Bowden R, Fogel ML, et al. , 2012. Science 337, 721–723. [DOI] [PubMed] [Google Scholar]
- Bar-Nun A, Herman G, Laufer D, Rappaport ML, 1985. ICAR 63, 317–332. [Google Scholar]
- Bar-Nun A, Kleinfeld I, Kochavi E, 1988. Phys. Rev. B 38, 7749–7754. [DOI] [PubMed] [Google Scholar]
- Bar-Nun A, Notesco G, Owen T, 2007. Icarus 190, 655–659. [Google Scholar]
- Bockelée-Morvan D, et al. , 2008. Astrophys. J 679, L49–L52. [Google Scholar]
- Brown ME, 2002. AREPS 30, 307–345. [Google Scholar]
- Cruikshank DP, et al. , 2014. ICAR 246, 82–92. [Google Scholar]
- Dobrovolskis AR, Harris AW, 1983. Icar 55, 231–235. [Google Scholar]
- Fox JL, Dalgarno A, 1983. JGRA 88, 9027–9032. [Google Scholar]
- Hansen CJ, Paige DA, Young LA, 2014. Icar 246, 183–191. [Google Scholar]
- Hubbard WB, Hunten DM, Dieters SW, et al. , 1988. Nature 336, 452–454. [Google Scholar]
- Hutsemèkers D, Manfroid J, Jehin E, Arpigny C, 2009. Icar 204, 346–348. [Google Scholar]
- Iro N, Gautier D, Hersant F, Bockelée-Morvan D, Lunine JI, 2003. Icarus 161, 511–532. [Google Scholar]
- Jessup KL, et al. , 2013. Icar 226, 1514–1526. [Google Scholar]
- Krasnopolsky VA, Cruikshank DP, 1999a. JGR 104, 21979–21996. [Google Scholar]
- Krasnopolsky VA, 1999b. JGR 104, 5955–5962. [Google Scholar]
- Lectez S, et al. , 2015. Astrophys. J 805, L1. [Google Scholar]
- Lellouch E, de Bergh C, Sicardy B, Käufl HU, Smette A, 2011. AA 530, LL4. [Google Scholar]
- Levison H et al. , Icarus 196, 258 10.1016/j.icarus.2007.11.035. [DOI] [Google Scholar]
- Lewis JS, Prinn RG, 1980. Astrophys. J 238, 357–364. [Google Scholar]
- Liang M-C, Heays AN, Lewis BR, Gibson ST, Yung YL, 2007. Astrophys. J 664, L115–L118. [Google Scholar]
- Mandt KE, et al. , 2009. PSS 57, 1917–1930. 10.1016/j.pss.2009.06.005. [DOI] [Google Scholar]
- Mandt KE, et al. , 2012. Astrophys. J 749, 160 10.1088/0004-637X/749/2/160. [DOI] [Google Scholar]
- Mandt KE, Mousis O, Lunine J, Gautier D, 2014. Astrophys. J 788 (2), L24 10.1088/2041-8205/788/2/L24. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mandt KE, Mousis O, Chassefiere E, 2015. Icarus 254,259–261. 10.1016/j.icarus.2015.03.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marty B, Chaussidon M, Wiens RC, Jurewicz AJG, Burnett DS, 2011. Science 332, 1533–1536. [DOI] [PubMed] [Google Scholar]
- Mathew KJ, Marti K, 2001. JGR 106 (E1), 1401 10.1029/2000JE001255. [DOI] [Google Scholar]
- McKinnon WB, Mueller S, 1988. Nature 335, 240–243. [Google Scholar]
- Mousis O, Guilbert-Lepoutre A, Lunine JI, Cochran AL, Waite JH, Petit J-M, Rousselot P, 2012. Astrophys. J 757, 146. [Google Scholar]
- Mousis O, Lunine JI, Fletcher LN, Mandt KE, Ali-Dib M, Gautier D, Atreya S, 2014. ApJ Lett. 796, L28. [Google Scholar]
- Niemann HB, et al. , 2010. J. Geophys. Res 115, E12006. [Google Scholar]
- Nier AO, McElroy MB, 1977. J. Geophys. Res 82, 4341–4349. [Google Scholar]
- Olkin CB, et al. , 2003. Icar 164, 254–259. [Google Scholar]
- Olkin CB, et al. , 2014. Icar 239, 15–22. [Google Scholar]
- Owen TC, et al. , 1993. Science 261, 745–748. [DOI] [PubMed] [Google Scholar]
- Owen T, Mahaffy PR, Niemann HB, Atreya S, Wong M, 2001. ApJ 553, L77–L79. [Google Scholar]
- Ribas I, Guinan EF, Güdel M, Audard M, 2005. Evolution of the solar activity over time and effects on planetary atmosphere. I. High-energy irradiances (1-1700 Å). Astrophys. J 622, 680–694. 10.1086/427977. [DOI] [Google Scholar]
- Rousselot P, et al. , 2014. Astrophys. J 780 (2), L17 10.1088/2041-8205/780/2/L17. [DOI] [Google Scholar]
- Rubin M, et al. , 2015. Science 348, 232–235. [DOI] [PubMed] [Google Scholar]
- Shinnaka Y, Kawakita H, Kobayashi H, Nagashima M, Boice DC, 2014. ApJ 782 (2), L16 10.1088/2041-8205/782/2/L16. [DOI] [Google Scholar]
- Stern SA, 2008a. SSRv 140, 3–21. [Google Scholar]
- Stern SA, et al. , 2008b. SSRv 140, 155–187. [Google Scholar]
- Strobel DF, 2008. Icar 193, 612–619. [Google Scholar]
- Tian F, Toon OB, 2005. GRL 32, L18201. [Google Scholar]
- Tucker OJ, Erwin JT, Deighan JI, Volkov AN, Johnson RE, 2012. Icar 217, 408–415. [Google Scholar]
- Vinatier S, Bezard B, Nixon CA, 2007. Icar 191, 712–721. [Google Scholar]
- Volkov AN, Johnson RE, Tucker OJ, Erwin JT, 2011. Astrophys. J 729, L24. [Google Scholar]
- Wong MH, et al. , 2013. GRL 40, 1–5. 10.1002/2013GL057840. [DOI] [Google Scholar]
- Young LA, Elliot JL, Tokunaga A, de Bergh C, Owen T, 1997. Icar 127, 258–262. [Google Scholar]
- Young LA, 2013. Astrophys. J 766, L22. [Google Scholar]


