A quantitative in silico platform for simulating cytotoxic and nanoparticle drug delivery to solid tumours

Abstract

The role of tumour–host mechano-biology and the mechanisms involved in the delivery of anti-cancer drugs have been extensively studied using in vitro and in vivo models. A complementary approach is offered by in silico models, which can also potentially identify the main factors affecting the transport of tumour-targeting molecules. Here, we present a generalized three-dimensional in silico modelling framework of dynamic solid tumour growth, angiogenesis and drug delivery. Crucially, the model allows for drug properties—such as size and binding affinity—to be explicitly defined, hence facilitating investigation into the interaction between the changing tumour–host microenvironment and cytotoxic and nanoparticle drugs. We use the model to qualitatively recapitulate experimental evidence of delivery efficacy of cytotoxic and nanoparticle drugs on matrix density (and hence porosity). Furthermore, we predict a highly heterogeneous distribution of nanoparticles after delivery; that nanoparticles require a high porosity extracellular matrix to cause tumour regression; and that post-injection transvascular fluid velocity depends on matrix porosity, and implicitly on the size of the drug used to treat the tumour. These results highlight the utility of predictive in silico modelling in better understanding the factors governing efficient cytotoxic and nanoparticle drug delivery.

1. Introduction

The efficient delivery of drugs to solid tumours is determined by a complex system of biophysical factors originating from tumour–host interactions [1–4]. Specifically, growth-induced mechanical stresses exerted by the tumour on the surrounding tissue cause changes in the structure and distribution of the surrounding vasculature, increased interstitial fluid pressure and compromised delivery efficacy [5–7]. These effects occur across multiple length and time scales, with rapid diffusion of single molecule agents—such as cytotoxic drugs—contrasting with convection-dominated transport of larger macromolecules, such as proteoglycans in the extracellular matrix (ECM), and nanoparticles, which have been extensively studied as a potential delivery system for therapeutic drugs [8]. However, progress in developing an effective nanoparticle-based therapy has been slow, largely due to the aforementioned complexity of the tumour–host environment [9]. As such, there is an increasing need for new methodologies that can be used to realistically model tumour–host pathophysiology, and hence estimate the optimal biophysical and material conditions for efficient delivery.

In silico modelling of drug delivery to tumours, whereby the tumour–host system is modelled according to biophysical laws, has been used to predict the effect of blood-borne drugs on pathological tissues. In this paper, we provide an overview of the most recent efforts in this field; for more extensive reviews, see [3,10]. Broadly speaking, in silico models can be split into two categories: (i) static-tissue models, where the tumour and vasculature are treated as a static object in situ and drug delivery is modelled as a separate dynamic process; and (ii) dynamic-tissue models, where both the tumour and surrounding tissue dynamics are coupled with drug kinematics. A static-tissue model was employed by D’Esposito et al. [11], where the authors found good agreement between model predictions of blood flow and the spatial distribution of drug uptake and data acquired from in vivo mouse model images. Sefidgar et al. [12] compared models of static and dynamic vascular networks and found that the dynamic network predicted a more heterogeneous and irregular vascular structure than the static network. More recently, Vavourakis and colleagues [13] developed a dynamic-tissue model of solid tumour growth and angiogenesis, which recapitulated the distribution and structure of pathological vascular networks from in vivo mouse model images. This framework was then extended to include a model of cytotoxic drug delivery [14], which predicted that chemotherapeutic agents have the highest impact when delivered via highly permeable, dense vascular networks.

Here, we generalize the modelling framework to account for drugs of any size, and in particular nanoparticles. We then use the model to make predictions of the effects of both tumour–host and drug properties on delivery efficiency and distribution. Crucially, our dynamic-tissue approach allows us to model how the tumour–host environment changes with time, and hence make predictions of the resulting vascular and tissue distributions post-therapy. This has particular relevance to staged therapeutic approaches, where drugs or combinations of different drugs are administered at intervals in an attempt to maximize delivery efficiency [15]. The article is structured as follows: first, the methodology is reviewed; next, results are presented from multiple simulations of drug delivery to a solid tumour growing into a vascularized host tissue, and concurrently, we discuss the implications of our predictions in the context of optimal drug delivery.

2. Material and methods

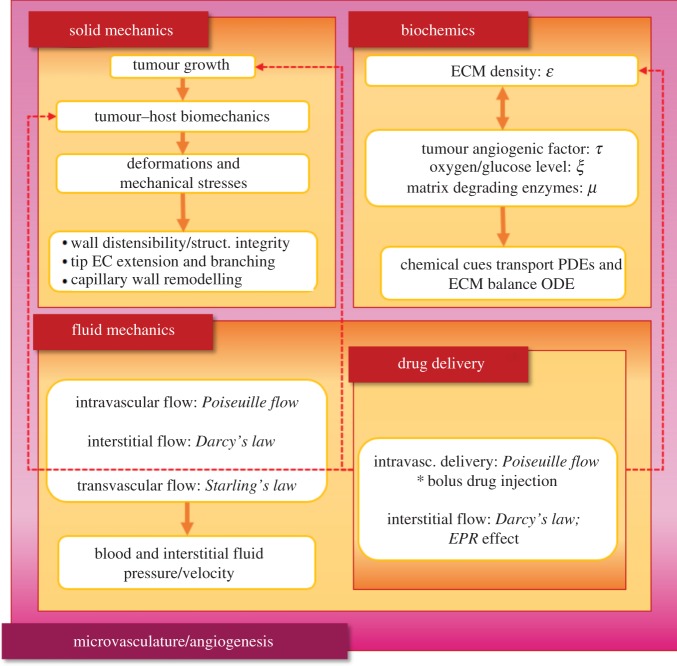
The present in silico cancer modelling methodology is motivated by the tumour growth and angiogenesis model proposed by the authors in [13]; hence, we have adopted here the same notation convention for the presentation of the mathematical models. The in silico cancer modelling framework consists of three interconnected core compartments that encompass different aspects of the mechano-biology of the cancerous and the host tissue, with one sub-compartment and one super-compartment that encapsulates all compartments. The core compartments of the framework are the Solid mechanics, the Fluid mechanics and the Biochemics compartments; whereas, the single sub-compartment of the framework is the Drug delivery one, which impacts the behaviour of the Solid mechanics and the Biochemics compartments.

Finally, the Microvasculature/Angiogenesis compartment is the super-set of all three core compartments, since blood vessels’ structural integrity, perfusion state and ability to branch or/and elongate are affected by both biomechanical and biochemical factors. Figure 1 depicts via a flow chart of the aforementioned compartments of the proposed in silico framework, which are briefly presented in the following subsections.

Figure 1.

Graphical representation of the in silico cancer simulator, showing the core compartments of the coupled modelling approach. The framework consists of the solid mechanics compartment, the biochemics compartment and the fluid mechanics compartment, with the latter also encapsulating the drug delivery modelling component. (Online version in colour.)

2.1. Biochemical model compartment

The Biochemics model encompasses key biological factors associated with the development of a solid tumour and angiogenesis. These include the transport of oxygen and nutrients in the ECM, ξ, the transport of enzymes that degrade the ECM, μ, the balance of tumour-secreted angiogenic factors, τ, and the density of the ECM to connective (structural) tumour/host tissue, ε. The governing equations necessary to describe the first three state variables are defined in detail in [13] (see eqns (12)–(14) therein)—they are unaffected by the addition of the Drug delivery sub-compartment presented in §2.3.2. However, the balance equation of ε that describes the dynamics of the ECM is directly influenced by the drug agent, thus eqn (1) in [13] is modified to reflect this:

$$\dot{ϵ}={\lambda }_{ϵ}\xi \hspace{0.17em}{\text{e}}^{-ϵ/\overline{ϵ}}-{\delta }_{ϵ}\mu ϵ-{\delta }_{\mathrm{d}}{c}_{\mathrm{i}}^{\overline{\alpha }}ϵ,$$ 2.1

with the first term describing the rate at which ECM remodels, where the dot denotes time derivative, $\overline{ϵ}$ is a scaling parameter that modulates the ECM level at which natural remodelling of the host-tissue matrix occurs and ${\lambda }_{ϵ}$ an ECM-remodelling rate parameter. The last two terms in the previous equation describe the ECM degradation due to the presence of matrix-degrading enzymes—secreted by the tumour and the tip-endothelial cells of the tumour vasculature—and the effect of the drugs on the tumour cells’ killing, with ${\delta }_{ϵ}$ and δ_d being the degradation rates, respectively. Also, c_i denotes the drug concentration that has internalized into the cancer cells of the tumour, as clarified in the following subsection, while $\overline{\alpha }$ is a model parameter that controls the cancerous tissue regression.

All continuity equations were discretized using linear finite elements, where we adopted a hexahedral-dominant grid, with zero flux set to all external boundaries for all variables. Numerical solution to the time-dependent equations has been carried out using an explicit time integration scheme, where zero initial values were set for state variables μ and τ while the distribution of ξ and ε was set uniform everywhere in the domain of analysis—to reflect physiological conditions prior to vascularized tumour growth.

2.2. Solid mechanics model compartment

The Solid mechanics compartment encompasses the biomechanics of the tumour and the host tissue, modelled here in three dimensions, and the biomechanics of the microvascular network. The balance of mechanical forces is expressed through the linear momentum equation—formulated in a Lagrangian framework, where both inertia and body forces are considered negligible:

$$\mathbf{\nabla }\cdot [\mathbf{F}\cdot \mathbf{S}]=0,$$ 2.2

where S is the second Piola–Kirchhoff stress tensor. Following the multiplicative decomposition of the deformation gradient tensor into an elastic and an inelastic (growth) component respectively, as in [16]: $\mathbf{F}={\mathbf{F}}_{\mathrm{e}}\cdot {\mathbf{F}}_{\mathrm{g}}$, where ${\mathbf{F}}_{\mathrm{g}}={(2{\vartheta }_{\mathrm{g}}+1)}^{1/2}\mathbf{I}$, with I the identity tensor and ${\vartheta }_{\mathrm{g}}$ the volumetric deformation represented by the product of a Gompertzian growth function (expressed with respect to ξ) and a monomial function (expressed with respect to ε): ${\vartheta }_{\mathrm{g}}={\alpha }_{\mathrm{g}}\{\exp [-{\beta }_{\mathrm{g}}\exp [-{\gamma }_{\mathrm{g}}\xi ]]-\exp [-{\beta }_{\mathrm{g}}]\}\times {ϵ}^{{\delta }_{\mathrm{g}}}$, where α_g, β_g, γ_g, δ_g are dimensionless parameters of the growth function. The constitutive equation of the tissue biomechanics is given by the general form [17] $\mathbf{S}=\mathrm{\partial }\overline{W}/\mathrm{\partial }{\mathbf{E}}_{\mathrm{e}}$, where E_e is the elastic Green–Lagrange strain. The present model assumes a hyperelastic soft tissue biomechanics using the modified neo-Hookean stored energy function (see eqn (6.21) in [18]). From that equation, the structural integrity of the tissue is directly linked to the ECM-related state variable ε via $G(ϵ)={\mu }_{\mathrm{e}}\hspace{0.17em}{ϵ}^{a_{\mathrm{w}}}$, where μ_e represents the material shear modulus, a_w (>0) is a constant parameter that modulates tissue softening/stiffening with respect to the ECM density.

The biomechanical interaction between the tumour–host biomechanics and the capillaries of the microvascular network and the corresponding biomechanical modelling of the capillary wall remodelling is thoroughly explained in our previous work [13]. As in that work, here the balance equation for the solid mechanics of the tumour and the host tissue has been discretized using finite elements. Numerical solution of the unknown displacements has been accomplished via a Newton–Raphson iterative scheme; this was necessitated by the presence of nonlinearities in the tissue biomechanics and the large deformations induced by the growing cancer mass.

2.3. Fluid mechanics model compartment

2.3.1. Microvascular and interstitial fluid flow

Microvascular haemodynamics is taken to obey the Hagen–Poiseuille law, where the capillary blood flow is assumed axial, steady, laminar and viscous [19]. Thus, the flow rate is given by ${\dot{Q}}_{\mathrm{vsc}}=-\pi R^4\hspace{0.17em}\mathrm{\Delta }{p}_{\mathrm{vsc}}/(8\hspace{0.17em}{\mu }_{\mathrm{B}}\hspace{0.17em}{L}_{\mathrm{vsc}})$, where R is the capillary lumen radius, Δp_vsc the vascular pressure drop within a capillary segment, L_vsc, and μ_B the dynamic viscosity of blood which is assumed homogeneous and constant in time. As in [13], the interstitial space is modelled as a porous biofluid-saturated medium, and interstitial fluid flow is modelled using Darcy’s law. Thus, the flow rate at the interstitium is given by [1] ${\dot{Q}}_{\mathrm{int}}=-K_{\mathrm{int}}{A}_{\mathrm{int}}\mathrm{\Delta }{p}_{\mathrm{int}}/L_{\mathrm{int}}$, where K_int and L_int are the average hydraulic conductivity and the relative distance between two material points in the interstitium whose (interstitial fluid) pressure difference is denoted by Δp_int, while A_int denotes the cross-sectional area of the interstitium. Finally, biofluid transport across the endothelium of the capillaries is modelled using Starling’s law [12], with the transvascular flow rate expressed by ${\dot{Q}}_{\mathrm{trv}}=K_{\mathrm{vsc}}{A}_{\mathrm{vsc}}\mathrm{\Delta }{p}_{\mathrm{v}-\mathrm{i}}$, where A_vsc is the surface area of the blood vessel wall, Δp_v-i is the difference between the vascular and interstitial pressure. Also, K_vsc is the hydraulic conductivity of the endothelium and can be expressed as a function of the size of the pores size, r_p, the fraction of vessel wall surface occupied by pores, γ_p, the thickness of the vascular wall, h, and the plasma dynamic viscosity, μ_P, via [20] $K_{\mathrm{vsc}}={\gamma }_{\mathrm{p}}\hspace{0.17em}{r}_{\mathrm{p}}^2/(8{\mu }_{\mathrm{P}}h)$.

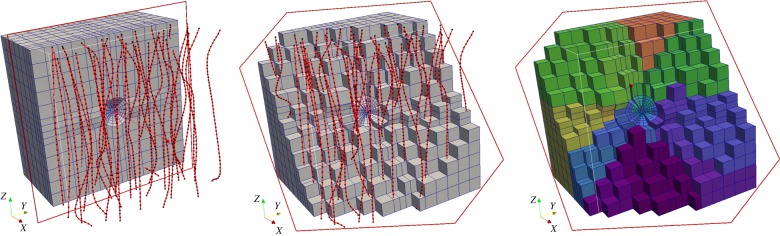
All three flow-rate equations are coupled together in a model for the vascular and interstitial pressures that is formulated as a linear system of equations expressed at the vascular nodes of the network and the interstitial nodes of the three-dimensional finite-element grid (see figure 2). Also, an interconnected grid of tissue and vascular nodes is considered to bridge the two non-conforming meshes, hence, model flow between the vascular and interstitial (extravascular) space. Biofluid flow is solved numerically for the vascular and interstitial pressures while proper pressure/flow boundary conditions are applied on the terminal nodal points of the discretized domains. For more details about the boundary and initial conditions considered in this model, the reader should refer to our previous work [13].

Figure 2.

Cut-through of the three-dimensional finite-element mesh used to discretize the tumour and the host tissue (volume of analysed domain = 1.2 cm³). The solid red lines depict the idealized vascular network used in the simulations (black dots correspond to the vascular nodes) which is relatively evenly distributed in three-dimensional space. Note that the two model discretizations are non-conforming. On the right, the colouring of the hexahedral elements demonstrates the visible partitions of the mesh, as decomposed for the purposes of the scalable in silico executions. (Online version in colour.)

2.3.2. Drug delivery

The continuity equation for the drug concentration in the bloodstream, c_v, is given from [1,19]

$${\dot{c}}_{\mathrm{v}}+{\mathit{v}}_{\mathrm{vsc}}\cdot \mathbf{\nabla }{c}_{\mathrm{v}}=0,$$ 2.3

where the blood mean velocity, v_vsc, is computed after solving the equations governing the intra-, trans- and extravascular flow (as explained above).

Following [21], the drug in the extravascular space is identified in three discrete states: (i) the free-drug state, (ii) the bound-drug state and (iii) the internalized drug state, with their concentrations symbolized as c_f, c_b and c_i respectively. The balance of the free-drug concentration, c_f, is described via the advection–diffusion–reaction equation [12]

$$\begin{array}{c}\dot{c_{\mathrm{f}}}+{\mathit{v}}_{\mathrm{int}}\cdot \mathbf{\nabla }{c}_{\mathrm{f}}-\mathbf{\nabla }\cdot [{\mathbf{D}}_{\mathrm{f}}\cdot \mathbf{\nabla }{c}_{\mathrm{f}}]={\mathit{\Phi }}_{\mathrm{vsc}}+{\mathit{\Phi }}_{\mathrm{lmp}}-k_{\mathrm{on}}{ϵ}^{\overline{\beta }}{c}_{\mathrm{f}}\\ +k_{\mathrm{off}}{c}_{\mathrm{b}}-{\delta }_{\mathrm{f}}{c}_{\mathrm{f}},\end{array}$$ 2.4

while the mass balance of the other two variables is described through a pair of ordinary differential equations

$${\dot{c}}_{\mathrm{b}}=k_{\mathrm{on}}{ϵ}^{\overline{\beta }}{c}_{\mathrm{f}}-k_{\mathrm{off}}{c}_{\mathrm{b}}-k_{\mathrm{int}}{c}_{\mathrm{b}}$$ 2.5

and

$$\dot{c_{\mathrm{i}}}=k_{\mathrm{int}}\hspace{0.17em}{c}_{\mathrm{b}}-{\delta }_{\mathrm{i}}{c}_{\mathrm{i}},$$ 2.6

where v_int is the interstitial fluid velocity vector (calculated through Darcy’s law after evaluating p_int; see §2.3.1) and $\overline{\beta }$ is a model parameter that controls the drug association to the cancerous cells. The diffusion tensor of the drug molecule or drug-borne nanoparticle is D_f (assumed here isotropic, i.e. =D_dI), while k_on, k_off and k_int are the association (binding), disassociation and internalization rate coefficients, respectively, and δ_f/δ_i is the half-life of the free drug and the decay rate of the drug—owing to the depletion of the cancer cells after the drug has found its target and the drug natural decay—respectively. The last two source terms in equation (2.4) come from the contribution of the vascular and the lymphatic network. Using Starling’s law, the rate of solute transport per unit volume through the microvascular endothelial wall can be expressed as [22] Φ_vsc = P_vsc,dS_vsc(c_v − c_f) + K_vsc S_vsc (1 − σ_f,vsc) Δp_v-ic, where c = c_v if p_vsc > p_int, else c = c_f; lymphatics contribution is expressed as Φ_lmp = K_lmpS_lmp(1 − σ_f,lmp)(p_lmp − p_int)c_f, where P_vsc,d is the diffusive permeability of the blood vessels with respect to the solvent (drug molecule), K_lmp the hydraulic permeability of the lymphs’ wall and σ_f,vsc/σ_f,lmp the solvent drag reflection coefficient at the blood vessel/lymphatic wall. Both latter quantities can be estimated numerically as a function of the drug size to the size of the pores of the vessel wall [20], while S_vsc is microvascular density, i.e. the vessels’ surface area per unit volume of tissue, and S_lmp the lymphatic vessels’ density. For simplicity, the fluid pressure at the lymphatic vessels is assumed p_lmp = 0 everywhere in the domain of analysis.

Assuming the absence of interactions of the free drug with other macromolecules or/and enzymes, drug diffusion is controlled by the size of the drug; thus, it can be described through the Stokes–Einstein equation [23]—valid for when modelling chemotherapy transport: D_d = k_B T/(3πμ_Is_c), where k_B the Boltzmann constant, T the absolute (reference) temperature and s_c the size of the molecule (or hydrodynamic diameter if assumed spherical) of the free drug. However, for rigid particles (e.g. polymer vesicles, nanoparticles), Phillips et al. [24] proposed a modified diffusion formula that accounts for the hydrodynamic interactions of the drug with a fibrous matrix (here the collagenous matrix of the host stroma) that reads $D_{\mathrm{d}}=D_0/(1+\sqrt{3r_{\mathrm{c}}}+r_{\mathrm{c}})$; D₀ is calculated from the previous equation, $r_{\mathrm{c}}=s_{\mathrm{c}}^2/3\kappa$, while the matrix permeability, κ, can be expressed with respect to the hydrodynamic diameter of the free drug and the porosity of the ECM, ɛ_s, through κ = ɛ_s s_c/k_Y, with k_Y being the Kozeny factor [25].

Equation (2.3) is discretized using two-node line elements that represent blood vessel segments of the microvascular network. For the outlet boundary nodes, zero-flux outflow condition is prescribed, i.e. dc_v/dL = 0, while for the inlet boundary nodes, c_v is prescribed explicitly to effectively model bolus injection of the drug through the exponential decay function: c_v(t) = c_v-max exp[−t/τ_c], where c_v-max is the maximum dose concentration of the drug that has reached the microcirculation system at the tumour site and τ_c the half-time of the drug. Similarly to the Biochemics model, differential equations (2.4)—(2.6) were discretized using the same finite element grid while time integration was accomplished via the forward Euler method using a ‘lumped mass’ capacity matrix to substantially speed up the numerical simulations.

2.4. Microvasculature/Angiogenesis compartment

A detailed description of this compartment can be found in the methodology description in [13]; here we present a brief overview. The Microvasculature/Angiogenesis compartment encompasses: (a) the elongation and extension of the tip capillary branches, the sprouting of existing blood vessels and the formation of vascular anastomoses, and (b) the remodelling of the capillaries’ endothelial wall, the lumen size, the thickness of the wall, and the structural integrity of the vessels. As explained in the Bioechemics model above, the drug permits degrading the ECM only, whereas pruning of tumour vessels, disruption of the vascular remodelling, or modulation of the permeation of the endothelium is not accounted for in the present in silico framework; we leave this for future work.

2.5. Cancer model solution strategy

Numerical solution of the different compartments (as shown in figure 1) of the proposed in silico cancer modelling framework is accomplished in a staggered manner. The solution strategy employs five different time discretization scales, with each core or sub-compartment having a separate timestep. We iterate in time and we solve the equations involved in each compartment based on the timestep adopted for each one of them. Firstly, the balance equations for the Biochemics compartment are solved numerically, the solution of which is projected into the Solid mechanics compartment. Secondly, equilibrium is sought numerically in the Solid mechanics compartment, and then the numerical solution (strain, stress) is projected into the Microvasculature/Angiogenesis. At this point, within Microvasculature/Angiogenesis, the structural integrity of the vessels is evaluated and the tree is updated (i.e. sprouting, branching, vessel compression, etc.) accordingly. Subsequently, the flow equations of the Fluid mechanics compartment are solved to compute interstitial, intra- and transvascular flow (eqns (2)–(4) in [14]); then equations (2.3)–(2.6) of the Drug delivery sub-compartment are solved to compute drug concentrations, the solution of which is distributed in the Biochemics and Solid mechanics models. The above steps are repeated until the simulation time has reached the desired end time point. However, it is important to highlight here that—regardless of the timestep adopted for the Solid/Fluid mechanics and Microvasculature/Angiogenesis compartments respectively—after solving the solid mechanics equations we enforce checking the vascular integrity, and subsequently the (bio)fluid flow equations are solved.

3. Results

We run simulations of tumour growth to replicate the development of a mammary carcinoma xenograft in immunodeficient mice [16]. In this study, we employed data of an in vivo murine syngeneic mammary MCaIV adenocarcinoma, as in [26,27]. The in silico cancer growth and angiogenesis model has been tested and validated in our previous paper [13]. Here, we model and simulate the single-dose administration of cancer cell killing drugs. The drugs investigated here varied with respect to their hydrodynamic size, i.e. the molecule/particle diameter was set approximately equal to 1 nm, 10 nm and 50 nm in order to mimic chemotherapy and nanomedicine transport in the animal model, respectively. All drugs were assumed to possess identical pharmacokinetic properties, i.e. excretion, absorption, internalization, decay. To simplify this study, the amount of in silico intravenous administration of the chemical was set the same for all drugs. We note, however, that this assumption is not representative of experimental protocols using laboratory mice; usually, the amount of drug administered varies with respect to the type of the drug. For example, administration of doxorubicin can span between 3 and 8 mg kg⁻¹ while for nanoparticles this can vary from greater than 10 mg kg⁻¹ [28]. The sole parameter that varied with respect to the drug pharmacokinetics was the half-time of the drug, τ_c, and was set based on experimentally measured clearance and drug circulation times in the bloodstream: 4 h, 10 h and 16 h, respectively [26]. In view of modelling flow in the capillaries using Poiseuille’s law and the inflow/outflow boundary conditions considered in the simulations, the numerically evaluated average blood flow rate at the healthy capillaries is approximately 2.5 cm³ h⁻¹. Thus, the amount of drug supplied over the period of the time-window of observation of the tumour development corresponded to 10, 25 and 40 times the maximum (intravenous) dose concentration of the drug, c_v−max.

Furthermore, in order to investigate the relationship between drug size and interstitial tissue hydraulic conductivity, simulations were also conducted with two different ECM hydraulic permeabilities: $\kappa =6.4\times {10}^{-15}$ m² (Pa s)⁻¹, henceforth termed ‘high porosity’; and $\kappa =6.4\times {10}^{-16}$ m² (Pa s)⁻¹, henceforth termed ‘low porosity’.

The model parameters required to simulate drug transport from equations (2.4)–(2.6) were taken from relevant works in the literature (e.g. [12,29]). We note that the adopted model parameters for the Solid mechanics, Fluid mechanics and Biochemics compartments are summarized in the electronic supplementary material. All simulations were carried out using our in-house developed in silico modelling framework—details about the numerical implementation of the framework are provided in the electronic supplementary material of our previous paper [14]. The C++ code of the in silico framework can be accessed online from the Bitbucket project: Finite Element Bioengineering in 3D (FEB3).

3.1. Drug size and interstitial porosity affects spatial distribution of delivery

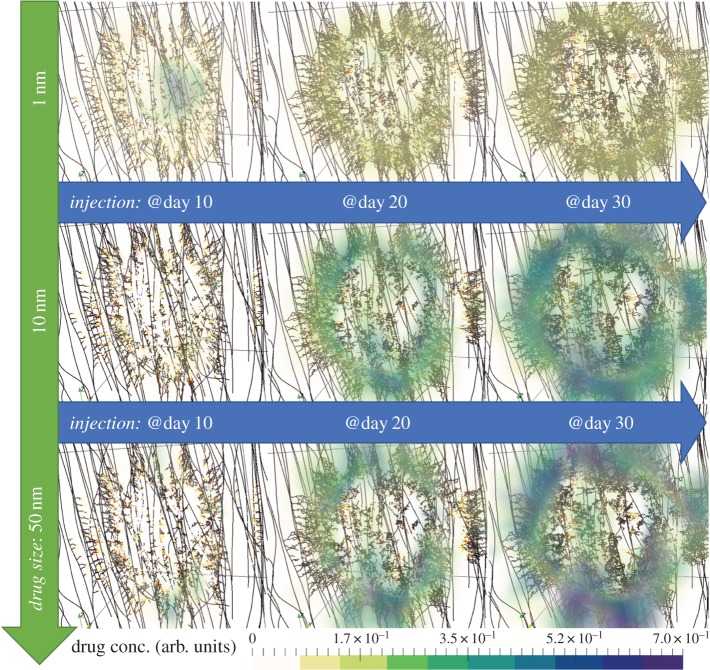
Images of the predicted spatial distribution of the three drugs after single-dose injections at days 10, 20 and 30 are shown in figures 3 and 4, for high porosity and low porosity, respectively. Clear differences are observed between the two porosities, for all drug sizes; for high ECM porosity, the drug concentration is higher both inside and outside the tumour, while for low ECM porosity, the drug concentration is lower and approximately uniform throughout the volume (see electronic supplementary material, figure S1). Interestingly, both porosities produce an approximately uniform distribution of the cytotoxic drug (1 nm), but a highly heterogeneous distribution of the larger drugs (10 and 50 nm). This heterogeneity is driven by the spatially and time varying interstitial fluid velocity field in the ECM (see electronic supplementary material, figure S2), upon which the larger drugs are more dependent due to their motion being primarily governed by convective motion [3]. The accumulation of large molecules, such as nanoparticles, in non-tumour tissue is a hallmark of the enhanced permeability and retention (EPR) effect, a topic of heated debate [30,31].

Figure 3.

Snapshots of the in silico predicted drug distribution for the three drug cases (in rows). Each column corresponds to time-instants of tumour response to treatment 5 days after the time of drug injection. All simulation results correspond to the high porosity extracellular matrix case. The coloured cloud represents the drug concentration (as a fraction of the total drug administered) that has been associated with the tumour and the host tissue. For illustration purposes, the internal structure of the three-dimensional domain of analysis is transparent, while the microvascular network is coloured such that the well-perfused vessels are shown dark whereas the poorly perfused vessels are lightly coloured. (Online version in colour.)

Figure 4.

Snapshots of the in silico predicted drug distribution and the microvascular network for the three drug cases (in rows) and for the three injection times (in columns). All simulation results correspond to the low porosity extracellular matrix case. For detailed interpretation of the graphics, the reader is referred to the caption of figure 3. (Online version in colour.)

3.2. Nanoparticles require high interstitial porosity to reduce tumour volume

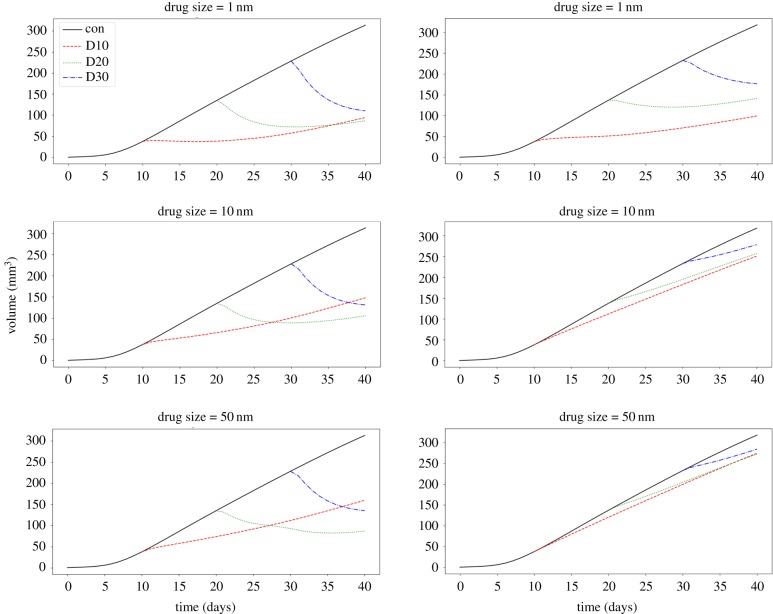
To test the relationship between drug delivery efficacy and ECM hydraulic conductivity, figure 5 shows tumour volume over time for the control case and injections at days 10, 20 and 30, for each drug type, for high porosity (left column), and low porosity (right column) ECMs. A clear dependency of efficacy on porosity is observed, with low porosity reducing the efficacy of all three drug types. However, the cytotoxic drug (1 nm) is able to regress the tumour at both porosities, while the nanoparticles (10 and 50 nm) require high porosity to cause tumour regression; at low porosity, only the rate of growth is affected, and for the largest nanoparticle the effect is almost negligible. This prediction recapitulates experimental observations of improved delivery efficacy as a result of ECM-modifying treatment with the anti-fibrotic drug tranilast; specifically, that reducing matrix density—or, equivalently, increasing matrix porosity—improves delivery of drugs in a size-independent manner [32]. It has been also documented that drugs targeting ECM-remodelling enzymes, such as FAK and hyaluronidase inhibitors, effectively slow tumour growth [33]. A similar effect was also observed with a cytotoxic drug when reducing the concentration of the high molecular weight glycosaminoglycan hyaluronan and hence increasing matrix porosity [34]. Here, we further predict that there is a regime where cytotoxics are effective, but not nanoparticles. Interestingly, the model also predicts that nanoparticles benefit from later injection times at high porosity; here this is due to the elevated interstitial fluid pressure produced by larger tumours increasing the magnitude of the convective flow. The phenomenon of growth-induced increases in interstitial fluid pressure has been previously reported in in vivo mouse experiments [35].

Figure 5.

Line plots of the relative tumour volume (V = Vol.(t)/Vol.(t = 0) − 1) versus time, for control simulations (black solid lines), and treatments administered at days 10, 20 and 30 (D10, D20, D30; coloured dashed lines). The results in the left column correspond to high hydraulic conductivity (‘high porosity’), K_int, and the results in the right column correspond to low hydraulic conductivity (‘low porosity’). (Online version in colour.)

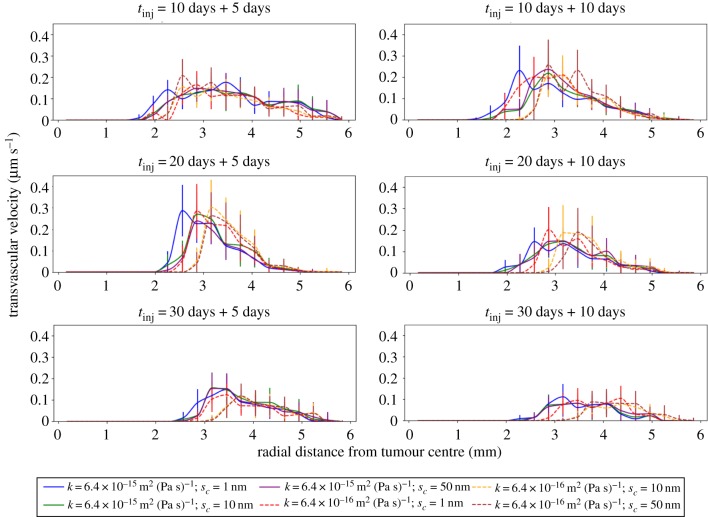
3.3. Transvascular velocity depends on both tissue porosity and drug size

The model was used to predict the transvascular fluid velocity, ${\dot{Q}}_{\mathrm{trv}}$, for different drug types administered separately at days 10, 20 and 30, and for low and high EBM porosity. The resulting mean transvascular fluid velocity as a function of distance from the tumour centre is shown in figure 6, at 5 days (left column) and 10 days (right column) after the respective injection. For the earliest administration (day 10), the distribution is largely independent of drug type at both time points. However, for later administrations (days 20 and 30), there is a dependency of transvascular flow on both drug size and porosity, with low porosity producing a peak closer to the tumour centre than high porosity, and the cytoxic drug peaking closer to the tumour centre than the nanoparticles. This drives the porosity-dependent penetration of the drug observed in figures 3 and 4. Furthermore, the width of the distribution after cytotoxic drug delivery is predicted to be broader than after nanoparticle delivery, which suggests that a broader region of fluid pressure normalization is achieved after cytotoxic delivery. This supports our previous predictions of vascular network structure normalization by cytotoxic drug delivery [14], and given that the effects persist for at least 10 days after injection (as previously highlighted in terms of drug half-time), this prediction has implications for staged drug therapy.

Figure 6.

Line plots of the mean transvascular velocity (TRV) as a function of the radial distance from the centre of the tumour, with standard errors. Each row corresponds to a different time of injection, while each column depicts the TRV radial distribution 5 days and 10 days after drug administration. The legend lists the various simulation combinations based on the hydraulic conductivity of the ECM (κ) and the drug size (s_c). (Online version in colour.)

4. Conclusion

Here we have described an in silico platform for quantitatively simulating the delivery of drugs of varying properties to a dynamically changing tumour–host environment. The proposed platform builds on our previous work [13,14] and generalizes to allow for both diffusive and convective transport mechanisms, hence enabling investigation into the dependency of delivery efficacy on drug size and extracellular matrix density. Future work will integrate our platform with multiscale methods [36] to test how host vasculature and tissue structure affect delivery efficacy of nanoparticles, and hence identify the optimal physiological conditions for size-dependent therapeutic drug delivery.

Data accessibility

The in silico platform can be accessed from the online repository on Bitbucket, FEB3: https://bitbucket.org/vasvav/feb3-finite-element-bioengineering-in-3d/wiki/Home.

Competing interests

We declare we have no competing interests.

Funding

P.A.W. and V.V. were financially supported by EPSRC-funded CMIC Platform Grants (project ID: EP/M020533/1; URL: https://gow.epsrc.ukri.org/NGBOViewGrant.aspx?GrantRef=EP/M020533/1).