Abstract
In statistical modelling with Gaussian process regression, it has been shown that combining (few) high-fidelity data with (many) low-fidelity data can enhance prediction accuracy, compared to prediction based on the few high-fidelity data only. Such information fusion techniques for multi-fidelity data commonly approach the high-fidelity model fh(t) as a function of two variables (t, s), and then use fl(t) as the s data. More generally, the high-fidelity model can be written as a function of several variables (t, s1, s2….); the low-fidelity model fl and, say, some of its derivatives can then be substituted for these variables. In this paper, we will explore mathematical algorithms for multi-fidelity information fusion that use such an approach towards improving the representation of the high-fidelity function with only a few training data points. Given that fh may not be a simple function—and sometimes not even a function—of fl, we demonstrate that using additional functions of t, such as derivatives or shifts of fl, can drastically improve the approximation of fh through Gaussian processes. We also point out a connection with ‘embedology’ techniques from topology and dynamical systems. Our illustrative examples range from instructive caricatures to computational biology models, such as Hodgkin–Huxley neural oscillations.
Keywords: machine learning, multi-fidelity data, multi-resolution simulation
1. Introduction
Recent advances in both algorithms and hardware are increasingly making machine learning an important component of mathematical modelling for physico-chemical, engineering, as well as biological systems (e.g. [1–4]). Part of these developments focus on multi-resolution and multi-fidelity data fusion [5,6]. Fusing information from models constructed at different levels of resolution/fidelity has been shown to enhance prediction accuracy in data-driven scientific computing. Richardson extrapolation, for example, has been widely used to improve the rate of convergence using different resolution discretizations in many practical applications [7]. Also, multi-grid methods in numerical analysis solve numerical PDEs effectively using multi-resolution and linearly dependent discretizations [8–10]. Through advances of machine learning algorithms, if some data from a fine-resolution simulation are missing, it becomes possible to estimate them exploiting data from a low-resolution simulation [11,12].
In addition, if high-fidelity data are costly to obtain (experimentally or computationally) while low-fidelity data are relatively cheap, a combination of a few high-fidelity data and many low-fidelity data can also lead to overall computational efficiency. For example, we may be able to combine few experimental data from a high-resolution measurement with extensive data from a computer simulation or from lower-resolution measurements. Recently, Gaussian process (GP) regression has been widely used to effectively combine multiple fidelity data [13–17]. ‘Classical’ information fusion by GP had focused only on linear dependency between high- and low-fidelity data via auto-regressive schemes such as the coKriging approach of Kennedy & O’Hagan [18]. If two (or more) datasets have nonlinear dependency, such linear-type approaches will lose their effectiveness.
When a high-fidelity model fh(t) has nonlinear dependency with a low-fidelity model fl(t), nonlinear auto-regressive Gaussian process (NARGP) [17] has been observed to achieve highly accurate prediction results by introducing an additional dimension: fh(t) is approximated as a curve on a two-dimensional manifold parametrized by t and a second variable, s. The data points on this manifold are of the form (fh(t), t, s( = fl(t))). More generally, assuming , NARGP finds a smooth manifold in a (d + 1)-dimensional space. In this framework, the low-fidelity model provides the additional ‘latent’ variable of the high-fidelity model.
Deep multi-fidelity GPs were introduced [19] as an improvement, especially in the context of discontinuities in fh with respect to t (and fl). This approach focuses on constructing a useful transformation T(t) of the input variables t through a (deep) neural network. Then, the high-fidelity function fh(t) is approximated as a GP of (just) fl(T(t)). One must now, of course, perform optimization for the additional network hyperparameters.
In this paper, we discuss a connection of NARGP with data-driven embeddings in topology/dynamical systems, and extend it (in the spirit of such data-driven embeddings) in an attempt to improve the numerical approximation of fh in the ‘sparse fh, rich fl’ data setting. In what follows we will (rather arbitrarily) ascribe the characterization ‘high-fidelity’ or ‘low-fidelity’ to different functions used in our illustrations; this characterization is solely based on the number of available data points for each. In the spirit of the Richardson extrapolation or the multi-grid computations mentioned above, one expects that observations/data at multiple fidelities are obtained by a systematic fine/coarse-graining process of studying the same system.
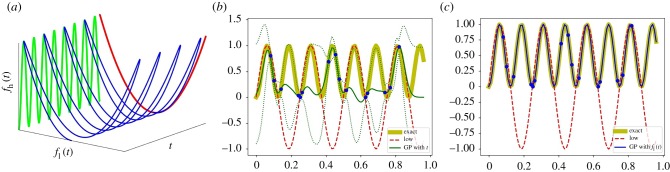
For our first example, the ‘high-fidelity’ function fh, for which we only have a few data points, is a function of t; but it actually also happens that we can describe it as a function of fl (figure 1):
| 1.1 |
Figure 1.
Two alternative GP regressions for the high-fidelity model fh(t) = sin2(8πt) (the highly oscillatory green curve in (a)). The blue curve visually suggests a smooth two-dimensional manifold g(t, fl). If, on the other hand, the high-fidelity function is projected onto fl(t), we can see it is a simple quadratic. (b,c) The prediction results with 2 s.d. (dashed line) for the high-fidelity function by GP regression with only t and with only fl(t), respectively. We employ 15 high-fidelity data points and 100 uniformly distributed low-fidelity data points for the regression. (a) A dependency between fl(t) and fh(t) with t, (b) GP with {t}, (c) GP with {fl(t)}. (Online version in colour.)
In this framework, the high-fidelity datasets (t, fh(t)) can be regarded as ‘ground truth’ obtained from experimental measurements or the high-fidelity model. The low-fidelity datasets (t, fl(t)), on the other hand, are obtained from a model with ‘qualitatively’ correct features—here, the right frequency—yet ‘quantitatively’ inaccurate observations (wrong scaling).
When we choose t as the coordinate parametrizing fh(t) (the green curve in figure 1a), the GP regression fails to represent the high-frequency sine function with just a few training data points as shown in figure 1b. However, as figure 1c shows, if we choose fl as the coordinate of fh(fl) (coloured by red in figure 1a), the GP regression can represent the simple quadratic function quite effectively. If we still need to know the parametrization of fh by t, we can obtain it through the ‘data rich’ fl : fh(t) ≡ fh(fl(t)).
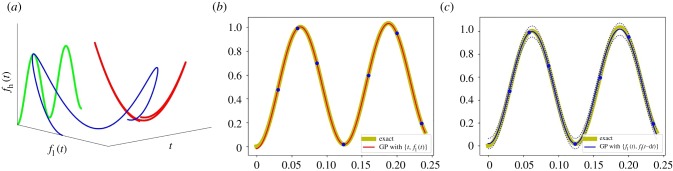
If fh is not a function of fl, however (as has been observed in the literature [17] and as can be seen in figure 2a) more variables are necessary to create a domain over which fh is a function.
Figure 2.
Two alternative GP regressions for the high-fidelity model fh (see equation (2.4)). (a) The multivaluedness of fh with respect to fl is clearly visible when the high-fidelity data (the blue curve) are projected onto fl(t) (the red curve). (b,c) The high-fidelity function (the yellow curve) versus posterior means with two standard deviations (dashed lines) of two alternative GP regressions. We use seven high-fidelity data points and 100 uniformly distributed low-fidelity data points for training GP regression models. (b) GP regression with {t, fl(t)}. (c) GP regression with {fl(t), fl(t − τ)}, τ = 1/400. (Online version in colour.)
In the NARGP framework, the variable used in addition to fl is t itself. In this paper, we will also advocate the use of delays or derivatives of fl as additional variables. This approach can also help remove the explicit dependence of fh on t, since embedding theories in dynamical systems [20–25] guarantee that we can choose any generic observation of t, or derivatives and/or delays of this observation, as a replacement for t; see §2.2 for more details.
In this paper, all examples follow the same problem set-up. We only have a few high-fidelity data points (ground truth), while plentiful data points are available from the low-fidelity model (characterized by fewer modelling terms, or perturbed model parameters when compared with the high-fidelity one). In addition, the high-fidelity function can be written as a simple function of t, fl(t) and its derivatives. With this set-up, we demonstrate the effectiveness of the proposed framework through pedagogical examples in §3.
In §3.4, we apply the proposed framework to the Hodgkin–Huxley model, describing the behaviour of action potentials in a neuron. Here, the high- and the low-fidelity functions are action potentials at two different values of the external current. This is a case where fh is a complicated function of t and does not only depend on fl; yet as we will see, delays of fl will help us construct an accurate approximation of fh.
The paper is organized as follows. In §2, we review the NARGP framework and concepts of ‘embedology’. Also, we illustrate why and when this framework is successful. In §3, we demonstrate the effectiveness of our proposed framework via some pedagogical examples and the biologically motivated application to the Hodgkin–Huxley model. In §4, we summarize our results and discuss open issues for further development of general multi-fidelity information fusion in modelling and simulation practice across scientific domains.
2. Methods
2.1. Nonlinear information fusion algorithms
‘Classical’ multi-fidelity data fusion algorithms require a linear (or almost linear) dependency between different fidelity datasets. Under this constraint, we can merge two or more datasets by using scaling and shifting parameters such as the Kennedy and O’Hagan coKriging approach [18]. However, more generally, nonlinear dependencies may exist between the datasets, typically degrading the quality of the results of linear information fusion algorithms. In order to resolve nonlinear dependencies between datasets, the use of a space-dependent scaling factor ρ(x) [26] or, alternatively, deep multi-fidelity GPs [19] have been introduced; clearly, the improvement they bring requires additional hyperparameter optimization.
When the high-fidelity model fh nonlinearly depends on the low-fidelity model fl, but can be written as a simple function of t and fl, the NARGP [17] is an appropriate choice. In this framework, a one-dimensional high-fidelity function fh is assumed to be a ‘simple’ function g of two variables (t, s), i.e. it is a curve that lies in the two-dimensional manifold described by g. Then, GP regression in the two-dimensional space is performed, where the data for s are the fl(t) data,
| 2.1 |
In [17] the gain in accuracy of NARGP, compared to an auto-regressive scheme with a constant scaling factor, as well as a scaling factor that was modelled as a (space-dependent) Gaussian process, was documented.
Algorithmically, classical autoregressive GPs employ an explicit method such as a scaling constant (ρ) between two covariance kernels, k1 and k2 as
| 2.2 |
The NARGP framework, on the other hand, employs an implicit approach by the automatic relevance determination (ARD) weight [27] in the extended space parametrized by t and s: a different scaling hyperparameter for each of the two dimensions in the kernel. In many applications, a radial basis function (see equation (2.3)) has been used as the covariance kernel (where ARD implies a different scaling hyperparameter θi for each dimension):
| 2.3 |
Figure 2 showcases an example where fh cannot be written as a function of fl:
| 2.4 |
Following the NARGP framework, we choose the low-fidelity data as an additional variable s = fl(t); we then approximate the two-dimensional function
| 2.5 |
Approximating g only requires a few training data point pairs for the GP regression. Then, fh can be written as fh(t) = g(t, s = fl(t)) (figure 2b). Figure 2c demonstrates that we can, alternatively, use delays of fl instead of t as an additional variable. A rationalization of this follows in the next section.
2.2. Data-driven higher-dimensional embeddings
The theorem of Whitney [20] states that any sufficiently smooth manifold of dimension can be embedded in Euclidean space , with the tight bound n ≥ 2d + 1. Nash [21] showed that this embedding can even be isometric if the manifold is compact and Riemannian, even though the bound on n is higher. Many results on the reconstruction of invariant sets in the state spaces of dynamical systems are based on these two theorems [22–25]. Here, the n embedding dimensions are usually formed by n scalar observations of the system state variables. Instead of n different observations, recording n time delays of a single scalar observable is also possible, as originally formulated by Takens [22] (see also [28]).
Given a smooth, d-dimensional manifold M, as well as an observable , it is possible to construct an embedding through
| 2.6 |
In this paper, p = t and the observable is h(t) = fl(t). Figure 2c shows an example where the embedding from delays of fl to t is successful, and figure 3e shows an example where fh is not a function over the manifold that is parametrizable by fl. Sauer et al. [24] specified the conditions on the trajectory of the observable that have to be satisfied, such that the state space can be embedded successfully. They also extended the results on embeddings of invariant sets with fractal dimension. In the context of the dynamical systems that generate the trajectories, the observable and the vector field together build a tuple that has to be generic (Takens [22]) or prevalent (Sauer et al. [24]). The two papers show that ‘almost all’ tuples are admissible, where the notions of genericity and prevalence are defining that probabilistic statement in the respective function spaces. These results are crucial for the numerical exploitation of the embedding theorems, since they show that ‘almost all’ observables of a dynamical system can be chosen for a delay embedding.
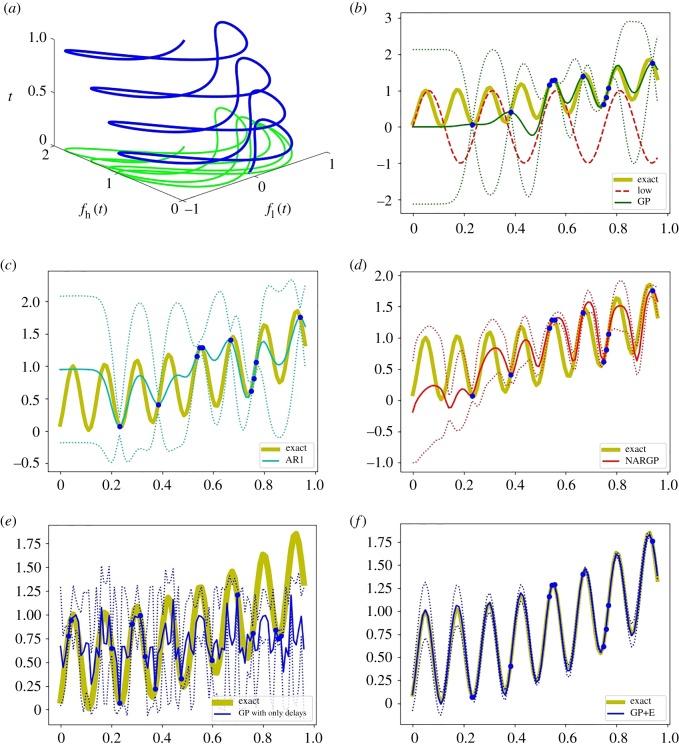
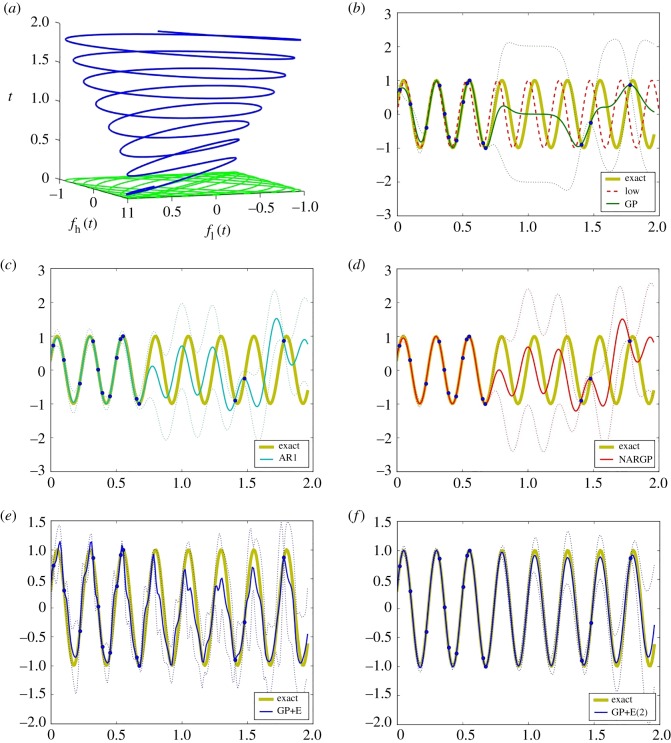
Figure 3.
Examples of phase shifted oscillations. (a) Dependency between fl and fh with t. (b–f) The high-fidelity function (the yellow curve) versus posterior means with 2 s.d. (dashed lines) of 5 compared methods with 10 high-fidelity data points and 100 uniformly distributed low-fidelity data points. (b) GP (Kriging) and low-fidelity data (the red-dashed curve). (c) Auto-regressive GP (AR1 or coKriging). (d) Nonlinear auto-regressive GP (NARGP). (e) GP in the higher-dimensional space with only delays (fl(t), fl(t − τ), fl(t − 2τ)). (f) GP in the higher-dimensional space (GP+E), using (t, fl(t), fl(t − τ), fl(t − 2τ)). (Online version in colour.)
In many applications, the intrinsic dimension d of M is unknown, and n is preemptively chosen large (larger than necessary). Manifold learning techniques are then often capable of reducing the embedding dimension, bringing it closer to the minimal embedding dimension necessary for the given manifold.
We also note that in our framework, if we can obtain low-fidelity data from a (dynamic) process instead of just single measurements, the same embedding and manifold learning techniques can be used even if the ‘independent variable’ t is not known [29].
Let us consider equation (2.4) again. NARGP performs GP regression with two observations {t, fl(t)}. Using embedding theory, we can rationalize (a) why the two observations were necessary and (b) why performing GP regression with an additional delay of the scalar observable, {fl(t), fl(t − τ)}, is equally appropriate for a relatively small time horizon (figure 2c). Note that delay coordinates fl(t) and fl(t − τ) lie on an ellipse with period of 0.25. Hence, if the data are collected over times longer than 0.25, using only delays will fail to represent the high-fidelity function due to multivaluedness (see figure 3e and §3.1); t itself used as an observable will resolve this.
2.3. Extending the formulation through delays
Now we provide a mathematical formulation of the approach. We assume that for two compact sets , fh : A → B and fl : A → B are CK-smooth functions with K ≥ 2, and we want to construct an interpolant of fh with a numerical scheme (here, a GP). The domain A of the functions is chosen to be a subset of (i.e. one dimensional)—because the interpretation of this domain in all our examples can be that of time. To emphasize this, we choose the symbols t and s to denote one-dimensional variables, and x = (x1, x2, …) for variables with more than one dimension. All statements in this section can be made analogously in domains with arbitrary, finite dimension. We chose to present them in one dimension to simplify notation, and because all examples in the following sections are using one input variable for the functions fl and fh. We assume that
-
(1)
only a small number of data points {t, fh(t)} as well as the function fl and its K derivatives are available,
-
(2)fh can be written in the form
where denotes the i-th derivative, i ∈ {1, …, K}, and2.7 -
(3)g : A × BK+1 → B is a CK function with derivatives bounded in the L∞ norm by a small constant cg > 0,
2.8
Assumption (1) outlines the general setting for multi-fidelity modelling, as explained in the introduction. Assumptions (2) and (3) define the relation between the low- and high-fidelity functions. It is difficult to state precisely for which classes of functions fl and fh these assumptions are satisfied. A special case is if the norm of the derivative (∂/∂t)fh is also bounded by cg, in which case g does not need to depend on fl at all. Another case is given if the function fh is in the (linear) span of fl and its derivatives, in which case g is a linear function. More generally, the Taylor series of fh reveals why assumptions (2) and (3) are required for a successful, numerical approximation of g with few data points of fh. Assume we want to evaluate fh in a small neighbourhood of a point t0 ∈ A. Then we can write
| 2.9 |
Since we assume the form (2.7) for fh, we can write
| 2.10 |
| 2.11 |
| 2.12 |
From this, we can see that (∂/∂t)fh(t) can be large (because the derivatives can be large), but if we know all , we only have to estimate g from data fh and . Crucially, we do not approximate the function fh and its derivatives. The derivatives of g are bounded by cg through assumption (2.7), and g is a CK function, so only a few data points are necessary for a good fit. If we have access to function values of fl over ‘delays’ (at discrete shifts, say in the form of a finite difference stencil) in space, rather than its derivatives, we can use the Newton series approximation of fh instead of equation (2.9) for an analogous argumentation. For functions fh that are analytic around the expansion point t0, the function fh can be evaluated at t close to it by
| 2.13 |
| 2.14 |
where Δm fh is the m-th finite difference approximation of fh, with a small step size Δt. By equation (2.7), these differences can be expressed through g and delays of fl (instead of delays of fh), analogously to equations (2.10)–(2.12). Using delays in space compared to derivatives has numerical advantages, especially in cases where fh or fl are not differentiable (or even have discontinuities). It also enables us to estimate the derivatives of fl implicitly, in case only the function fl is available (and not its derivatives). Note that the delays (or derivatives) in this section are used to explain the numerical advantages of assumptions (2) and (3) above. This is different from their use in the previous section on embedology, where delays were used to construct a map back to the domain of the functions fl and fh, in case it is not directly accessible. Figures 1 and 2 show results from the two examples that demonstrate these two approaches.
2.4. Outline of the numerical approach
In order to employ the delay coordinates of the low-fidelity function, it is required to know shifts of it. A necessary condition of the proposed framework is that the low-fidelity function is given explicitly or can be well-learned by given data such that low-fidelity function values can be accurately approximated (interpolated) at arbitrary points. If the state variable t is not available, the low-fidelity model should be a generic observation of t to be useful in employing Takens’ embedding theorem [22,24]. Under these conditions, we now present a summary of the workflow.
If the low-fidelity model is given in the form of (rich) data, we train a GP regression model for it from these data {(tl,i, fl(tl,i))|i = 1, …, nl} via minimizing a negative log marginal likelihood estimation. This data driven process can be circumvented if the low-fidelity model is explicitly given, as in the above examples. After that, we compute predictive posterior means of the low-fidelity model at the points th where the high-fidelity data are available. We also compute a number of shifts of the low-fidelity function at the points th − kτ and at the test points t*. Next, we train another GP regression model for high-fidelity datasets in the higher-dimensional space, and . The number of delays n is strongly linked (in a sense, determines) the simplicity of the function g in equation (2.7). In this paper, observations yh(th,i) are obtained from the high-fidelity model such as yh(th,i) = fh(th,i). Then, we construct and optimize a covariance matrix K using a radial basis function, which is a de facto default kernel function in GP regression (see equation (2.3)). Generally, the choice of a kernel defines the class of functions that the GP can access [27]. Since the correct class may not be known in advance for specific applications, there is no systematic way to choose the kernel. Finally, we compute the predictive posterior mean () and variance (cov(y*)) at all the test points () in the higher-dimensional space by conditioning the joint Gaussian prior distribution with all the training points ():
| 2.15 |
| 2.16 |
| 2.17 |
Here, represents the variance of independent identically distributed Gaussian noise, assumed added to the observations (yh).
Each new delay burdens the optimization by a single additional hyperparameter. For more details, refer to [17,27]. In this paper, all GP computations are performed by the open source Python package GPy [30].
3. Results
We introduce three pedagogical examples to demonstrate our approach. First, we explore the case where fh is a phase shifted version of fl (§3.1). Then, we show that oscillations with different periods (leading to different recurrences) present a more challenging scenario, which however can still be resolved by using shifts of fl. The third example involves discontinuities in fh and fl. After these three examples, in §3.4, we demonstrate the approach in the context of the Hodgkin–Huxley model. We investigate the effectiveness of the proposed framework by comparing it to three established frameworks: (1) single GP regression with high-fidelity data only (GP or Kriging), (2) auto-regressive method with a constant scaling parameter ρ (AR1 or coKriging), and (3) NARGP in the same computational environment.
3.1. Phase shifted oscillations
Using models at different levels of resolution (e.g. for biological oscillators) will often give oscillations that have very comparable periods but are phase-shifted. Let us start by considering two functions with different phases on t ∈ [0, 1],
| 3.1 |
Our ‘high-fidelity function’ can be rewritten by a trigonometric addition formula:
| 3.2 |
Now we can explicitly see how the high-fidelity function can be thought of as a combination of three variables: t2, the low-fidelity function fl(t) = sin(8πt) and its first derivative .
Using delays of fl with a small stepsize τ contains enough information to numerically estimate its derivatives, hence we can also write fh as
| 3.3 |
The GP regression model for g is trained on these four-dimensional data. In addition, we perform GP regression in a three-dimensional space constructed from only three delays:
| 3.4 |
As shown in figure 3b, the single GP regression model provides inaccurate predictive posterior means due to lack of high-fidelity data. While the linear auto-regressive model (AR1) also fails to predict the high-fidelity values, the NARGP (with 10 high-fidelity data points and 100 low-fidelity data points) catches the trend of the high-fidelity data, yet still yields inaccurate results: NARGP is informed only by t and fl(t), but not by . Similarly, the GP regression with only delays (no information about t) in figure 3e fails to represent the high-fidelity function for these long observation windows. Beyond 0.25, t cannot be recovered from the shifts of fl because fl is only a generic observer of t ∈ [0, 0.25].
As shown in figure 3f , the GP using t and three delays of fl provides an excellent prediction with only 10 high-fidelity data points (and 100 low-fidelity data points). This means that, in the four-dimensional space, g (see equation (3.3)) has small derivatives, which then helps to employ GP regression successfully.
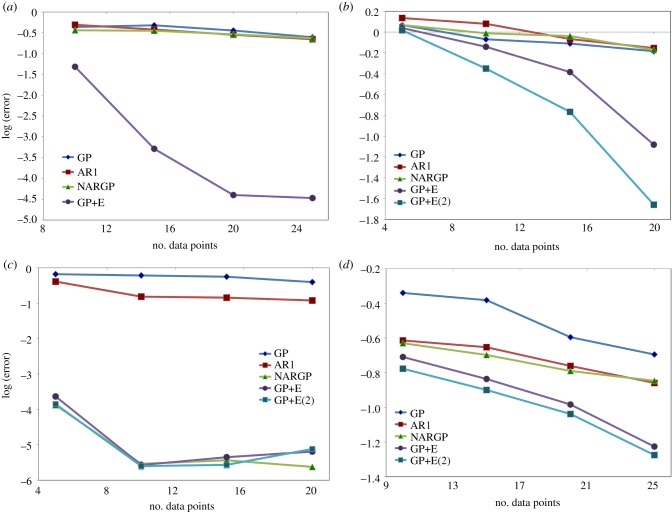
Next, we investigate the sensitivity and scalability of the proposed framework on the number of high-fidelity data points (training data points). We train all GP regression models with 10, 15, 20 and 25 randomly chosen high-fidelity data points and 100 uniformly distributed low-fidelity data points. The error is obtained by averaging 10 trials of random data selections. A log L2 error with respect to the number of high-fidelity data points is presented in figure 4a.
Figure 4.
Log L2 error (y-axis) of prediction for the high-fidelity model by GP (Kriging), AR1 (coKriging), NARGP and GPs in the higher-dimensional space (GP+E and GP+E(2)) with respect to the number of high-fidelity data points (x-axis). The error is obtained by averaging 10 trials of random data selections. In the Hodgkin–Huxley models, we predict action potential for the high-fidelity model. (a) Phase shifted oscillations, (b) different periodicity, (c) models with discontinuities, (d) the Hodgkin–Huxley models. (Online version in colour.)
The two established approaches (AR1 and NARGP) and the GP with only delays have no significant accuracy enhancements as the number of training points increases. The reason for the consistently large errors is the lack of additional information provided by the derivatives. The GP in the higher-dimensional space that includes t, on the other hand, shows a strong correlation between accuracy and the number of training points—more high-fidelity points visibly improve the approximation.
3.2. Different periodicity
In this example, the high- and the low-fidelity model oscillations are not just phase shifted, but they also are characterized by different periods. In applications, this could arise if we tried to match observations of oscillations of the same model at two different parameter values. Different (possibly irrationally related) oscillation periods dramatically complicate the dependency across the two datasets.
We consider two different period and phase shifted data,
| 3.5 |
The high-fidelity function can be rewritten by a trigonometric addition formula
| 3.6 |
In addition, the first term sin(8πt) can be rewritten again by a trigonometric subtraction formula
| 3.7 |
where and . Then,
| 3.8 |
The second term cos(8πt) can be rewritten in the same way. This shows that the high-fidelity function can be written in terms of sin(bt), cos(bt), fl(t) and . Since sin(bt) and cos(bt) have lower frequency compared to the original frequency 8, the bound cg for the derivatives of g (see §2.3) is smaller. It is then reasonable that we can approximate the high-fidelity function in the higher-dimensional space with only a few training data points.
We perform the GP in two different extended spaces: (1) three additional delays, totalling four-dimensional space (GP+E) and (2) five additional delays, totalling six-dimensional space (GP+E(2)), and compare them to a single GP, AR1 and NARGP. Examples of regression results with 15 high-fidelity data points and 200 uniformly distributed low-fidelity data are shown in figure 5. The GP in the four-dimensional space provides better regression results than other established methods, and the GP in the six-dimensional space presents the best results.
Figure 5.
Examples of different periodicity. (a) Dependency between fl and fh with t. (b–f) The high-fidelity function (the yellow curve) versus posterior means with 2 s.d. (dashed lines) of 5 compared methods with 15 high-fidelity data points and 200 uniformly distributed low-fidelity data points. (b) GP (Kriging) and low-fidelity data (the red-dashed curve). (c) Auto-regressive GP (AR1 or coKriging). (d) Nonlinear auto-regressive GP (NARGP). (e) GP in the four-dimensional space (GP+E), using (t, fl(t), fl(t − τ), fl(t − 2τ)). (f) GP in the six-dimensional space (GP+E(2)), using (t, fl(t), fl(t − τ), fl(t − 2τ), fl(t − 3τ), fl(t − 4τ)). (Online version in colour.)
Moreover, as shown in figure 5b, the phase discrepancy between the high- and low-fidelity functions increases as time increases, resulting in larger error for larger values of t (figure 5b–d). However, the GPs in the higher-dimensional spaces provide accurate prediction results over this time observation window.
The sensitivity to the number of high-fidelity data is shown in figure 4b. The GPs in the four- and six-dimensional space show significant computational accuracy gain compared to all other methods. These results demonstrate the capability of the proposed framework for period-shifted and phase-shifted data fusion.
3.3. Models with discontinuities
In general, a smooth stationary covariance kernel cannot capture discontinuous model data. In order to resolve this problem, a non-stationary kernel has been introduced [31,32], with space-dependent hyperparameters. Moreover, nested GPs were also used successfully to alleviate this problem [33]. Both approaches introduce, of course, additional hyperparameters to optimize.
In this example, we introduce a discontinuous function fl on t ∈ [0, 0.5),
| 3.9 |
and on t ∈ [0.5, 1] as
| 3.10 |
and the high-fidelity function fh
| 3.11 |
In the scenario we describe here, the high-fidelity function fh is discontinuous, but can be expressed in terms of a linear function of g in two variables.
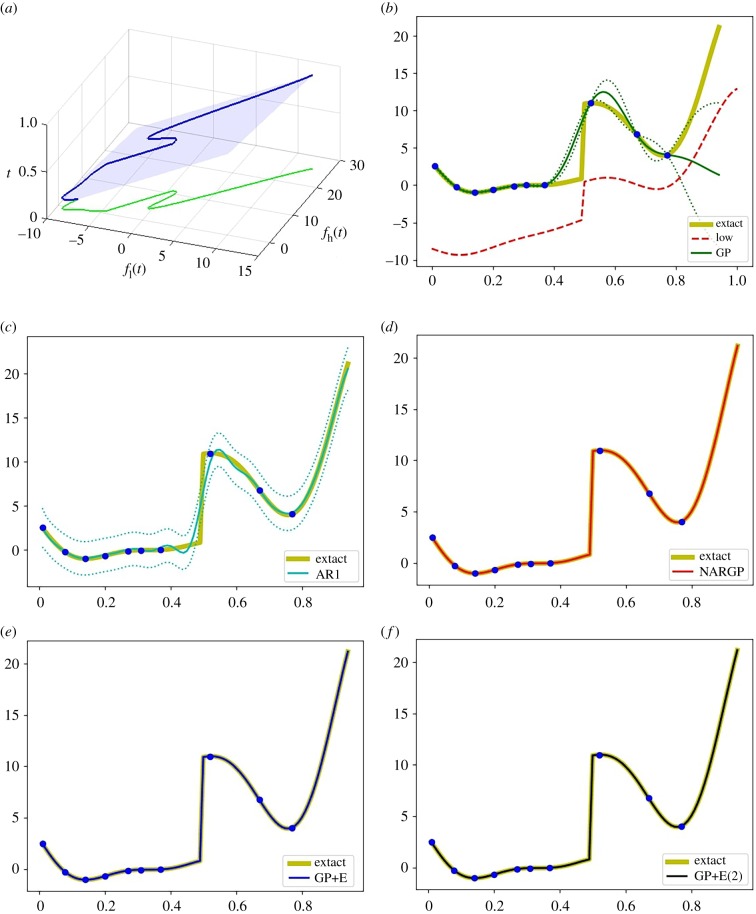
Examples of regression results with 10 high-fidelity data points and 200 uniformly distributed low-fidelity data points are shown in figure 6. Since g is a linear function of t and fl(t), the NARGP, as well as our GPs in the higher-dimensional spaces, provide highly accurate prediction results with just a few high-fidelity data.
Figure 6.
Examples of models with discontinuities. (a) Dependency between fl and fh with t. (b–f) The high-fidelity function (the yellow curve) versus posterior means with 2 s.d. (dashed lines) of 5 compared methods with 10 high-fidelity data points and 200 uniformly distributed low-fidelity data points. (b) GP (Kriging) and low-fidelity data (the red-dashed curve). (c) Auto-regressive GP (AR1 or coKriging). (d) Nonlinear auto-regressive GP (NARGP). (e) GP in the four-dimensional space (GP+E), using (t, fl(t), fl(t − τ), fl(t − 2τ)). (f) GP in the six-dimensional space (GP+E(2)), using (t, fl(t), fl(t − τ), fl(t − 2τ), fl(t − 3τ), fl(t − 4τ)). (Online version in colour.)
In analysing the sensitivity to the number of high-fidelity data points (figure 4c), there is no significant accuracy gain after 10 such high-fidelity data points. That is because 10 training data points are enough to represent a linear function accurately. It is worth noting that, here, the NARGP provides better prediction results with 20 training data points compared to the GPs in the higher-dimensional space, possibly due to overfitting.
3.4. The Hodgkin–Huxley model
Based on the results of our pedagogical examples, we apply the proposed framework to a famous model of a cellular process, a version of the Hodgkin–Huxley equations [34]. In 1952, Hodgkin and Huxley introduced a mathematical model which can describe the initiation and propagation of action potentials in a neuron. Specifically, they invented electrical equivalent circuits to mimic the ion channels, where ions traffic through the cell membrane. The model for intracellular action potentials (Vm) can be written as a simple ODE
| 3.12 |
where Cm is the membrane capacitance and Iion and Iext represent the total ionic current and the external current, respectively.
The total ionic current Iion = INa + IK + IL is the sum of the three individual currents as a sodium current (INa), a potassium current (IK) and a leakage current (IL). In order to calculate the three individual currents in time, the Hodgkin–Huxley model introduced gates which regulate the flow of ions through the channels. Specifically, the three ionic currents are affected by the three different gates n, m and h. Based on these gates, the total ionic currents can be calculated by
| 3.13 |
where represents a normalized constant for the ion channels and represents the equilibrium potential for a sodium (* ≡ Na), a potassium (* ≡ K), and a leakage (* ≡ L), current. The three gates n, m and h can then be modelled by the following ODEs:
| 3.14 |
| 3.15 |
| 3.16 |
In this paper, we set the model parameter values to , , , ENa = 55.17, EK = −72.14 and EL = −49.42 [35]. We assume that we have too few high-fidelity data points to directly estimate the function Vm(t). In addition, we assume that we have many data points from a low-fidelity model which has a slightly perturbed model parameter (Iext) compared to the ‘true’ high-fidelity model. In this paper, we set Iext = 1.0 for the high-fidelity model and Iext = 1.05 for the low-fidelity model, resulting in different oscillation periods (and a phase shift when we start at the same initial conditions). The action potentials Vm of the two different fidelity models are shown in figure 7a,b.
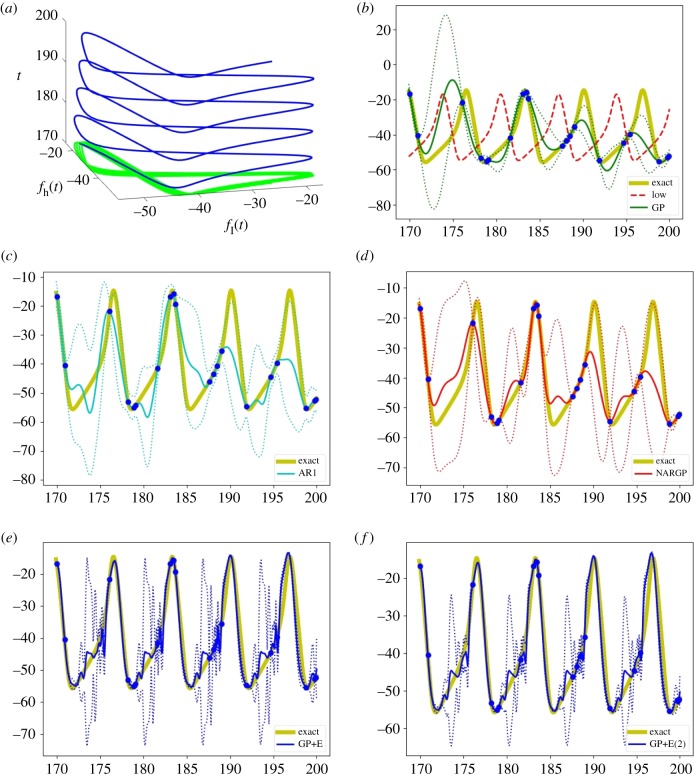
Figure 7.
Examples of the two Hodgkin–Huxley model oscillations obtained with different external currents Iext. (a) Dependency between fl and fh with t. (b–f) The high-fidelity function (the yellow curve) versus posterior means with 2 standard deviations (dashed lines) of 5 compared methods with 20 high-fidelity data points and 300 uniformly distributed low-fidelity data points. (b) GP (Kriging) and low-fidelity data (the red-dashed curve). (c) Auto-regressive GP (AR1 or coKriging). (d) Nonlinear auto-regressive GP (NARGP). (e) GP in the four-dimensional space (GP+E), using (t, fl(t), fl(t − τ), fl(t − 2τ)). (f) GP in the six-dimensional space (GP+E(2)), using (t, fl(t), fl(t − τ), fl(t − 2τ), fl(t − 3τ), fl(t − 4τ)). (Online version in colour.)
Examples of regression results for Vm by 5 different methods with 20 high-fidelity data points and 300 uniformly distributed low-fidelity data points are shown in figure 7b–f . Since the two datasets are phase-shifted, the single GP, AR1, and NARGP fail to accurately approximate the high-fidelity model. However, GPs in the higher-dimensional spaces provide reasonable prediction results. The GP in the six-dimensional space (GP+E(2)) shows significant improvement in the form of large uncertainty reduction as well as high prediction accuracy.
The sensitivity to the number of high-fidelity data is shown in figure 4d. The proposed framework shows computational accuracy gains compared to all other methods, as well as marked improvement when new high-fidelity points are added.
4. Conclusion
In this paper, we explored mathematical algorithms for multi-fidelity information fusion and its links with ‘embedology’, motivated by the NARGP approach. These modifications/extensions of kriging show promise in improving the representation of data-poor ‘high-fidelity’ datasets exploiting data-rich ‘low-fidelity’ datasets. Given that fh may not be a simple function—and sometimes not even a function—of fl, we demonstrated that using additional functions of t, such as derivatives or shifts of fl, can drastically improve the approximation of fh through GP.
The limitations of the proposed framework arise in the form of the curse of dimensionality and of overfitting. As the number of hyperparameters in the GP framework grows in an increasingly higher dimensional input space, the optimization cost grows (and there is always the possibility of converging to local, unsatisfactory minima). Adaptively testing for the ‘best’ number of delays is possible, and will be pursued in future work. The natural option of using multiple low-fidelity models (instead of delays of just one of them) is also being explored. Techniques that systematically find all the local hyperparameter minima (in the spirit of the reduced gradient method [36]) may also be useful in this effort. Another promising research direction involves the construction of data-informed kernels (e.g. through ‘neural-net-induced Gaussian process’ [37]) for more realistic and unbiased predictions. Alternatively, it is interesting to consider transformations of the input space using manifold learning techniques and the so-called Mahalanobis distance [38,39], which has been demonstrated to successfully match different (yet conjugate) models [40,41].
What we believe is a most promising direction for the use of these techniques is the reconciliation of different granularity multi-scale models—having, say, an atomistic ‘high-fidelity’ simulation enhanced by a continuum ‘low-fidelity’ approximate closure. Thus, ‘heterogeneous data fusion’ becomes a version of multi-fidelity data fusion [12]. In this paper, the fusion tools simply ‘filled in the gaps’ in a single manifestation of the high-fidelity data. In a time-dependent context, ‘full space, full time’ low-fidelity simulations can help complete and thus accelerate ‘small space, small time’ high-fidelity simulations—in a form reminiscent of the patch-dynamics approach in equation-free computation [42] (see also [11,12]). Using a qualitatively correct (even though quantitatively inaccurate) low-fidelity model—as opposed to just the local Taylor series that play the role of low-fidelity modelling in patch dynamics—may very much improve the computational savings of such multi-scale computation schemes.
Data accessibility
This article has no additional data.
Competing interests
We declare we have no competing interests.
Funding
S.L., F.D. and I.G.K. gratefully acknowledge the partial support of NSF, NIH and DARPA. G.E.K. gratefully acknowledges the financial support of DARPA (grant no. N66001-534 15-2-4055) as well as the MIT ESRDC grant.
References
- 1.Tarca AL, Carey VJ, Chen Xw, Romero R, Drăghici S. 2007. Machine learning and its applications to biology. PLoS Comput. Biol. 3, e116 ( 10.1371/journal.pcbi.0030116) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Holzinger A, Jurisica I. 2014. Interactive knowledge discovery and data mining in biomedical informatics: state-of-the-art and future challenges. Lecture Notes in Computer Science, vol. 8401 Berlin, Germany: Springer. [Google Scholar]
- 3.Libbrecht MW, Noble WS. 2015. Machine learning applications in genetics and genomics. Nat. Rev. Genet. 16, 321– 332 ( 10.1038/nrg3920) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Villoutreix P, Andén J, Lim B, Lu H, Kevrekidis IG, Singer A, Shvartsman SY. 2017. Synthesizing developmental trajectories. PLoS Comput. Biol. 13, e1005742 ( 10.1371/journal.pcbi.1005742) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Lanckriet GR, De Bie T, Cristianini N, Jordan MI, Noble WS. 2004. A statistical framework for genomic data fusion. Bioinformatics 20, 2626–2635. ( 10.1093/bioinformatics/bth294) [DOI] [PubMed] [Google Scholar]
- 6.Willett P. 2013. Combination of similarity rankings using data fusion. J. Chem. Inf. Model. 53, 1–10. ( 10.1021/ci300547g) [DOI] [PubMed] [Google Scholar]
- 7.Dimov I, Zlatev Z, Faragó I, Havasi Á. 2017. Richardson extrapolation: practical aspects and applications, vol. 2 Berlin, Germany: Walter de Gruyter GmbH & Co KG. [Google Scholar]
- 8.Brandt A. 2001. Multiscale scientific computation: review 2001. In Multiscale and multiresolution methods (eds TJ Barth, T Chan, R Haimes). Lecture Notes in Computational Science and Engineering, vol. 20, pp. 3–95. Berlin, Germany: Springer. ( 10.1007/978-3-642-56205-1_1) [DOI]
- 9.Brandt A. 2005. Multiscale solvers and systematic upscaling in computational physics. Comput. Phys. Commun. 169, 438–441. ( 10.1016/j.cpc.2005.03.097) [DOI] [Google Scholar]
- 10.Brandt A, Brannick J, Kahl K, Livshits I. 2011. Bootstrap AMG. SIAM J. Sci. Comput. 33, 612–632. ( 10.1137/090752973) [DOI] [Google Scholar]
- 11.Lee S, Kevrekidis IG, Karniadakis GE. 2017. A general CFD framework for fault-resilient simulations based on multi-resolution information fusion. J. Comput. Phys. 347, 290–304. ( 10.1016/j.jcp.2017.06.044) [DOI] [Google Scholar]
- 12.Lee S, Kevrekidis IG, Karniadakis GE. 2017. A resilient and efficient CFD framework: statistical learning tools for multi-fidelity and heterogeneous information fusion. J. Comput. Phys. 344, 516–533. ( 10.1016/j.jcp.2017.05.021) [DOI] [Google Scholar]
- 13.Le Gratiet L, Garnier J. 2014. Recursive co-kriging model for design of computer experiments with multiple levels of fidelity. Int. J. Uncertain. Quantif. 4, 365–386. ( 10.1615/Int.J.UncertaintyQuantification.v4.i5) [DOI] [Google Scholar]
- 14.Perdikaris P, Venturi D, Royset J, Karniadakis G. 2015. Multi-fidelity modelling via recursive co-kriging and Gaussian–Markov random fields. Proc. R. Soc. A 471, 20150018 ( 10.1098/rspa.2015.0018) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Perdikaris P, Venturi D, Karniadakis GE. 2016. Multifidelity information fusion algorithms for high-dimensional systems and massive data sets. SIAM J. Sci. Comput. 38, B521–B538. ( 10.1137/15M1055164) [DOI] [Google Scholar]
- 16.Parussini L, Venturi D, Perdikaris P, Karniadakis G. 2017. Multi-fidelity Gaussian process regression for prediction of random fields. J. Comput. Phys. 336, 36–50. ( 10.1016/j.jcp.2017.01.047) [DOI] [Google Scholar]
- 17.Perdikaris P, Raissi M, Damianou A, Lawrence N, Karniadakis G. 2017. Nonlinear information fusion algorithms for data-efficient multi-fidelity modeling. Proc. R. Soc. A 473, 20160751 ( 10.1098/rspa.2016.0751) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Kennedy MC, O’Hagan A. 2000. Predicting the output from a complex computer code when fast approximations are available. Biometrika 87, 1–13. ( 10.1093/biomet/87.1.1) [DOI] [Google Scholar]
- 19.Raissi M, Karniadakis G. 2016 Deep multi-fidelity Gaussian processes. (http://arxiv.org/abs/160407484. )
- 20.Whitney H. 1936. Differentiable manifolds. Ann. Math. 37, 645–680. ( 10.2307/1968482) [DOI] [Google Scholar]
- 21.Nash J. 1966. Analyticity of the solutions of implicit function problems with analytic data. Ann. Math. 84, 345–355. ( 10.2307/1970448) [DOI] [Google Scholar]
- 22.Takens F. 1981. Detecting strange attractors in turbulence. In Dynamical systems and turbulence, Warwick 1980 (eds D Rand, LS Young), pp. 366–381. Berlin, Germany: Springer ( 10.1007/BFb0091924) [DOI]
- 23.Kostelich EJ, Yorke JA. 1990. Noise reduction: finding the simplest dynamical system consistent with the data. Physica D 41, 183–196. ( 10.1016/0167-2789(90)90121-5) [DOI] [Google Scholar]
- 24.Sauer T, Yorke JA, Casdagli M. 1991. Embedology. J. Stat. Phys. 65, 579–616. ( 10.1007/BF01053745) [DOI] [Google Scholar]
- 25.Kennel MB, Brown R, Abarbanel HD. 1992. Determining embedding dimension for phase-space reconstruction using a geometrical construction. Phys. Rev. A 45, 3403–3411. ( 10.1103/PhysRevA.45.3403) [DOI] [PubMed] [Google Scholar]
- 26.Le Gratiet L. 2013. Multi-fidelity Gaussian process regression for computer experiments. Université Paris-Diderot-Paris VII.
- 27.Rasmussen CE, Williams CKI. 2006. Gaussian processes for machine learning. Cambridge, MA: MIT Press. [Google Scholar]
- 28.Packard NH, Crutchfield JP, Farmer JD, Shaw RS. 1980. Geometry from a time series. Phys. Rev. Lett. 45, 712–716. ( 10.1103/PhysRevLett.45.712) [DOI] [Google Scholar]
- 29.Dietrich F, Kooshkbaghi M, Bollt EM, Kevrekidis IG. 2018 doi: 10.1063/1.5133725. Manifold learning for bifurcation diagram observations. (http://arxiv.org/abs/1810.12952. ) [DOI] [PubMed]
- 30.GPy: GPy: a Gaussian process framework in Python, since 2012. http://github.com/SheffieldML/GPy.
- 31.Schmidt AM, O’Hagan A. 2003. Bayesian inference for non-stationary spatial covariance structure via spatial deformations. J. R. Stat. Soc. B 65, 743–758. ( 10.1111/rssb.2003.65.issue-3) [DOI] [Google Scholar]
- 32.Paciorek CJ, Schervish MJ. 2004. Nonstationary covariance functions for Gaussian process regression. In Proc. 16th Int. Conf. on Neural Information Processing Systems, Whistler, Canada, 9–11 December 2003, pp. 273–280. Cambridge, MA: MIT Press.
- 33.Hensman J, Lawrence ND. 2014 Nested variational compression in deep Gaussian processes. (http://arxiv.org/abs/14121370. )
- 34.Hodgkin AL, Huxley AF. 1952. A quantitative description of membrane current and its application to conduction and excitation in nerve. J. Physiol. 117, 500–544. ( 10.1113/jphysiol.1952.sp004764) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Siciliano R. 2012. The Hodgkin–Huxley model: its extensions, analysis and numerics. Montreal, Canada: McGill University. [Google Scholar]
- 36.Quapp W. 2003. Reduced gradient methods and their relaton to reaction paths. J. Theor. Comput. Chem. 2, 385–417. ( 10.1142/S0219633603000604) [DOI] [Google Scholar]
- 37.Pang G, Yang L, Karniadakis GE. 2018 Neural-net-induced Gaussian process regression for function approximation and PDE solution. (http://arxiv.org/abs/180611187. )
- 38.Singer A, Coifman RR. 2008. Non-linear independent component analysis with diffusion maps. Appl. Comput. Harmon. Anal. 25, 226–239. ( 10.1016/j.acha.2007.11.001) [DOI] [Google Scholar]
- 39.Singer A, Erban R, Kevrekidis IG, Coifman RR. 2009. Detecting intrinsic slow variables in stochastic dynamical systems by anisotropic diffusion maps. Proc. Natl Acad. Sci. USA 106, 16090–16095. ( 10.1073/pnas.0905547106) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Dsilva CJ, Talmon R, Gear CW, Coifman RR, Kevrekidis IG. 2016. Data-driven reduction for a class of multiscale fast-slow stochastic dynamical systems. SIAM J. Appl. Dyn. Sys. 15, 1327–1351. ( 10.1137/151004896) [DOI] [Google Scholar]
- 41.Kemeth FP. et al. 2018. An emergent space for distributed data with hidden internal order through manifold learning. IEEE Access 6, 77 402–77 413. ( 10.1109/ACCESS.2018.2882777) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Kevrekidis IG, Gear CW, Hyman JM, Kevrekidis PG, Runborg O, Theodoropoulos C. 2003. Equation-free, coarse-grained multiscale computation: enabling microscopic simulators to perform system-level analysis. Commun. Math. Sci. 1, 715–762. ( 10.4310/CMS.2003.v1.n4.a5) [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
This article has no additional data.