From quantum to subcellular scales: multi-scale simulation approaches and the SIRAH force field

Abstract

Modern molecular and cellular biology profits from astonishing resolution structural methods, currently even reaching the whole cell level. This is encompassed by the development of computational methods providing a deep view into the structure and dynamics of molecular processes happening at very different scales in time and space. Linking such scales is of paramount importance when aiming at far-reaching biological questions. Computational methods at the interface between classical and coarse-grained resolutions are gaining momentum with several research groups dedicating important efforts to their development and tuning. An overview of such methods is addressed herein, with special emphasis on the SIRAH force field for coarse-grained and multi-scale simulations. Moreover, we provide proof of concept calculations on the implementation of a multi-scale simulation scheme including quantum calculations on a classical fine-grained/coarse-grained representation of double-stranded DNA. This opens the possibility to include the effect of large conformational fluctuations in chromatin segments on, for instance, the reactivity of particular base pairs within the same simulation framework.

1. Introduction

Addressing structural and dynamical descriptions of biological processes poses enormous challenges to computational biophysics. Spatio-temporal scales range from subnanometre and femto/picoseconds for enzymatic catalysis or hydrogen bonding [1], to virtually no upper bounds when considering cellular systems. Moreover, life processes occur in a concerted manner, prompting for integrated frameworks to achieve a biologically meaningful description. Contributions coming from mathematical, physical and chemical arenas have furnished a large battery of theoretical tools to address the simulation of biological systems [2,3]. Over the years, theoretical methods ranging from high-level quantum mechanics to classical force fields have provided outstanding insight, becoming solid complements/alternatives to experimental techniques [4–7]. More recently, simplified molecular representations integrating functional groups or degrees of freedom into coarse-grained (CG) moieties that keep the most relevant features have come into fashion because of their remarkable computational efficiency [8,9]. Such cost-effective approaches allow for the study of large macromolecular assemblies on biologically relevant time scales at affordable computational expenses. Not only computational efficiency is gained when applying these methods, but hard drive storage and RAM memory requirements also significantly decrease, thus circumventing major bottlenecks related to data transfer, sharing and analysis. When the electronic or atomic levels cannot be neglected, CG approaches can still make a substantial contribution if integrated into multi-scale frameworks. In such schemes, the high accuracy modelling in small regions of the system is coupled with an effective description of long-range or quaternary structure effects in and from the milieus. In this contribution, we briefly review some of those methods developed in connection to molecular dynamics (MD) simulations, with special emphasis in the recent developments made in our group, associated with the SIRAH force field. Finally, proof of concept calculations integrating quantum, atomistic and CG levels in a double-stranded DNA filament are presented, constituting the first triple-scale simulation scheme in this biomolecule. In that sense, extending multi-scale simulations to quantum mechanical methods opens new pathways for exciting research where the dynamics of extremely large systems can be integrated into electronic level processes.

2. Multi-scaling in molecular dynamics

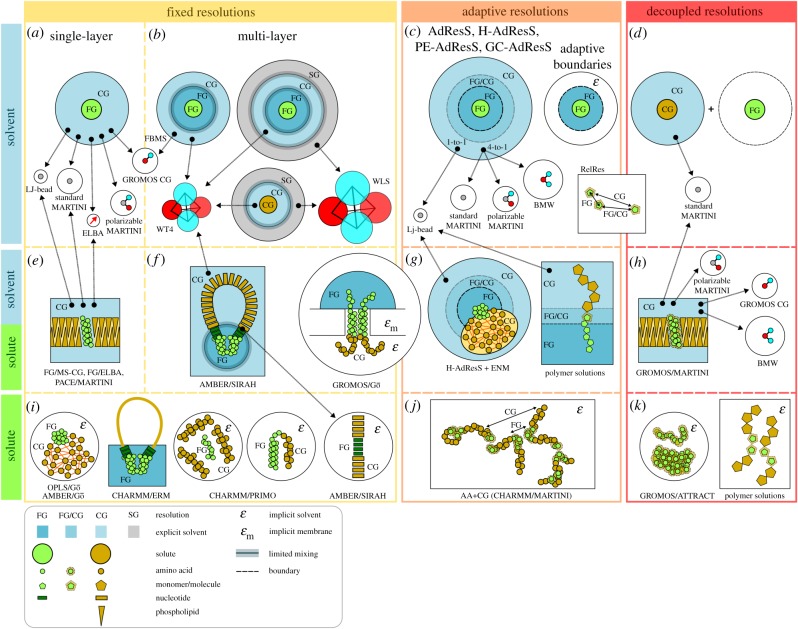
We centre this review on multi-scale approaches applied to MD simulations of biological systems. In this regard, it is possible to distinguish two main multi-scale strategies, which are usually referred to as sequential or serial, and concurrent or parallel [10,11]. In sequential multi-scaling, the entire system is simulated at atomistic resolution for a given amount of time, after which it is mapped to a coarser resolution to speed up the phase space sampling to then go back to the initial resolution to continue the exploration. Remarkable examples of this technique can be found in the work of Sansom and co-workers on high-throughput exploration of the dynamics of membrane proteins [12]. In the case of concurrent multi-scale approaches, different levels of resolutions are simultaneously present in the system during the simulation. These multi-scale frameworks can be classified into three main categories based on the coupling among resolutions, which will be referred to as: fixed resolutions, adaptive resolutions or decoupled resolutions strategies (figure 1). Briefly, in fixed resolutions multi-scale simulations, each molecule in the system is assigned either an atomistic (fine-grained, FG) or CG representation, which is maintained throughout the simulation. In adaptive resolutions simulations, molecules in the system are dynamically treated as FG, CG or hybrid FG/CG according to their position in the box or to their relative distance during the simulation. Finally, in decoupled resolutions simulations, virtual sites are used to add a CG representation on top of FG particles allowing for self-interactions (FG–FG or CG–CG) to be treated at the corresponding level while FG–CG interactions occur only at the CG level.

Figure 1.

A landscape of parallel multi-scale approaches. Presently, available multi-scale approaches are grouped according to the technique used to couple the FG and CG resolutions. Orange frame box: fixed resolutions; light red frame box: adaptive resolutions; and red frame box: decoupled resolutions. This classification applies to solvent, solvent and solute, or only the solute (top, middle and bottom rows within each box, respectively). Molecular models (and some combinations) developed within each resolution coupling technique are shown in (a–k). CG water models are illustrated according to their relative size. ‘LJ-bead’ stands for a water molecule represented by an uncharged (LJ) particle. ELBA represents a water molecule by a LJ particle with a dipole moment. Standard MARTINI represents four water molecules by an uncharged LJ particle. Polarizable MARTINI represents four water molecules by a central uncharged LJ particle bound to two opposite point charges. GROMOS CG represents five water molecules by a central LJ particle of negative charge harmonically bonded to a positive point charge. BMW represents four water molecules using a soft potential with a central negative particle bound to two positive sites. WT4 represents 11 water molecules by a tetrahedral arrangement of four LJ particles of opposing partial charges. WLS represents 55 water molecules in a similar fashion to WT4. (Online version in colour.)

The following sections review the families of concurrent multi-scale schemes applied to describe solute and/or solvent molecules in MD simulations.

3. Multi-scale representations of the solvent

The large amount of water molecules needed to fill big-enough simulation boxes in order to avoid self-image interactions or to correctly describe hydrophobic effects [13] often impairs the computational efficiency of MD simulations. A possible alternative is to use implicit solvent models to increase the computational performance [8,14–16]. However, this comes at the expense of losing atomic solute–solvent details. An intermediate approach is the use of multi-scale approaches where explicit CG solvent models, or a combination between FG and CG solvent models, are used to hydrate a FG solute. In the next sections, a description of the different multi-scale solvation categories will be presented along with a brief summary of the accompanying CG water models. A comparative description of the different available CG water models has been reviewed elsewhere [8,17,18].

3.1. Fixed resolutions single-layer solvation

In single-layer schemes, the solvent is described at a unique CG level (figure 1a). Although different schemes for direct coupling of a FG solute with a CG solvent have been proposed, reproduction of relative stability of peptide conformations and hydrogen bond patterns has posed special difficulties to this multi-scale solvation approach [19–21]. However, two methods worth highlighting use simple Lennard-Jones (LJ) water models [17] or the ELBA CG solvent [22,23]. In the simplest case, FG proteins are solvated by LJ beads, each representing one water molecule, to study peptide aggregation [24]. Alternatively, the PACE model calibrates a united atoms protein force field to directly interact via specific solute–solvent LJ terms with the standard MARTINI water model [25]. This approach has been shown to be effective in folding small proteins. In both cases, setting uniform dielectric constants is mandatory to account for the absence of electrostatic screening generated by the solvent. In the case of the ELBA water model, a dipole is placed at the centre of a LJ bead, allowing to reproduce the experimental hydration free energy of water and amino acids analogues, thus facilitating nearly atomistic accuracy when combined with the CHARMM protein force field [26]. In this case, the solute–solvent coupling is achieved via Lorentz­–Berthelot combination rules supplemented with a shifted-force charge-dipole potential for electrostatic interactions.

3.2. Fixed resolutions multi-layer solvation

This approach implies the presence of regions with progressive decrease of details and specific coupling between different levels of descriptions. Typically, the simulation box contains a FG solute solvated by a shell of FG water, which is then embedded in CG solvent. Eventually, supra CG (SG) layers can further wrap the CG shell (figure 1b). This method requires either limited mixing between the different solvent resolutions or applying additional forces to ensure the phase separation. The latter approach has been implemented for combining the GROMOS CG water model from Riniker et al. [27] with the SPC water [28] and the GROMOS atomistic protein force field [29]. Two restraining potentials have been proposed for this approach. On the one hand, a half-harmonic distance restraint applies a force to any atomistic water molecule moving beyond a certain cut-off from the solute centre of mass [20,30]. This method works well for nearly spherical and rather rigid solutes. Alternatively, for non-spherical solutes, or when conformational changes are of interest, the flexible boundaries for multiresolution solvation (FBMS) method [31] can be applied. This method uses a mixed FG–CG layer buffer between the pure FG and CG regions, serving as reservoir of both FG and CG water molecules. The boundaries are defined by concurrent half-harmonic restraints between the solute surface and the FG water (attractive potential) and the CG water (repulsive potential). Results comparable to full atomistic simulations are obtained for several protein systems. Examples of CG solvent models having limited mixing properties will be discussed in §6.

3.3. Adaptive resolutions solvation

Based on a different formalism, the adaptive resolution method (AdResS) [32,33] proposes an open boundary between the FG and CG solvent regions, allowing the free exchange of molecules. Such exchange is achieved via a space-dependent interpolation between FG and CG intermolecular interactions in a hybrid FG/CG layer region connecting the pure FG and CG domains in the system (figure 1c). The original formulation interpolates the forces between particles, thus rigorously satisfying momentum conservation. The downside is that this approach hampers microcanonical ensemble and Monte Carlo simulations. To overcome this limitation, the interpolation between FG and CG can be formulated at the Hamiltonian level. This has been implemented in a variation of the AdResS method known as H-AdResS [34,35], although it comes at the expense of locally breaking momentum conservation. Closely related to the latter is the recently proposed adaptive boundaries multi-scale approach [36]. This technique also focuses on deriving a Hamiltonian and distribution function for systems where the boundaries between resolutions react to changes in the degrees of freedom during a simulation (e.g. unfolding peptide radius of gyration in a mixed explicit/continuum solvent model). However, some issues arise when dealing with aqueous mixtures like water/methanol, as conformational transitions in the solute may induce fluctuations in local concentrations of the cosolvent. To account for this effect, a variation of the AdResS approach has been proposed, called particle exchange AdResS (PE-AdResS), that couples the FG region to a semi-grand canonical CG solvent reservoir [37]. Worth noting, in the original AdResS formulation the hybrid transition layer only preserves particle density but neither thermodynamic nor structural properties. This can be corrected by applying radial distribution function and thermodynamic force refinements. This allows for a smoother transition between the FG and CG regions, thus avoiding any boundary artefacts. In this formulation, the FG region in AdResS can be interpreted as an effective grand canonical (GC) ensemble. This variation of the method is thus known as GC-AdResS [38,39]. The AdResS approach can be applied both to multi-scale solvents where the CG water has a simple one-to-one mapping as well as to more complex CG models as the case of standard MARTINI, polarizable MARTINI or BMW, which use a four-to-one mapping [40,41]. In the case of standard MARTINI, the four-to-one mapping may be facilitated by the SWINGER dynamics clustering algorithm [42] that allows to concurrently assemble/disassemble water clusters. AddResS in combination with both water-mapping levels has been successfully applied to protein and DNA systems [43–49]. Recent reviews of this method can be found in [46,50].

Reminiscent of the AdResS framework, an approach where the resolution of a certain molecule is relative to the ‘observer’ molecule (FG or CG based on their separation) has been proposed (RelRes [51]). To that end, the potential is described by the sum of a ‘short-range’ contribution mediated by FG interactions and a ‘long-range’ contribution evaluated in terms of CG virtual sites placed on top the FG representation. The RelRes approach, which features adaptive and decoupled resolutions features (see next section), is capable of recovering structural correlations and thermal properties, important for multi-component and multi-phase fluids.

3.4. Decoupled resolutions solvation

The original formulation of this multi-scale approach inherits self-resolution interactions (FG–FG or CG–CG) from pure FG or CG system, without further modifications, while the coupling between resolutions is described at the CG level by means of CG virtual sites placed at the centre of mass of the corresponding atomistic particles (according to the CG mapping scheme) (figure 1d). Forces and torques are conserved by distributing the forces exerted by the CG solvent particles on the virtual sites over the corresponding atomistic components. By excluding explicit interactions between virtual sites, virtual sites and atomistic particles, and the latter with CG particles, a modular description (without FG–CG cross-interactions) is obtained [52]. An extension of this approach including direct Coulomb interactions between FG and CG particles has also been proposed, allowing for explicit dielectric screening of the FG–FG interaction due to charged CG particles [53]. Keeping the virtual CG sites charge to zero, the interaction between the latter and the CG solvent is exclusively based on the LJ potential, as in the original method. This extended approach has been tested combining the GROMOS FG force field [54,55] with a CG environment modelled using the polarizable MARTINI water model [56] or the BMW model [57,58]. Although the structure of different tested protein systems is well maintained throughout short simulations, this approach shows significant deviations from the fully FG or CG simulations regarding thermodynamic calculations such as amino acid analogue potentials of mean force or butane/water partitioning [53]. Indeed, alternative strategies have also been tested to ameliorate the FG–CG coupling [59,60].

4. Multi-scale representations of the solute

In addition to the previously described multi-scale solvation strategies, significant efforts have been devoted to extending the multi-scale approach to the solute. The main challenges reside in coupling intra- and inter-molecular interactions at different granularities within or among solute molecules. In particular, overcoming the loss of information at the interface, which determines the strength and directionality of the interactions, is highly relevant for the correct description of solute flexibility and folding.

Among fixed resolutions strategies describing FG/CG solutes, it is worth highlighting the combination of OPLS or AMBER force fields with Gō-like models (figure 1i) [61,62]. In both approximations, the shape and mechanical stress at CG or FG/CG regions is modelled by distance potentials among particles. A similar idea was applied by Villa et al. [63] to simulate the lac repressor protein (LacI) in complex with a DNA filament. In this case, the binding of the LacI protein to two DNA operator sequences is represented at FG level in explicit solvent, while mechanical tensions on the DNA loop connecting both operators are modelled by an elastic rod model (ERM). During MD simulations forces are transferred from the ERM to the FG level at the connection points, and the new positions are input back to the ERM. The so-called CHARMM/PRIMO model (figure 1i) was developed to access a more detailed multi-scale representation of proteins. This model was initially used to study protein–protein interactions in crowding conditions by mixing FG and CG solutes in implicit solvent [64]. Despite having different Hamiltonians for the FG and CG regions, no special treatment is required to couple the LJ and Coulomb interactions between them as the PRIMO force field is compatible in terms of interaction points and energy with CHARMM. Following the same line, the protein backbone is described at almost atomistic detail in the CG representation, allowing to further extend the CHARMM/PRIMO model to account for intramolecular peptide bonds at the FG/CG frontier. Thus, both levels of description are present at the same polypeptide chain without distorting the folding [65]. An adaptive resolutions model called AA + CG has also been proposed for describing inter- and intra-protein interactions in implicit solvent multi-scale simulations (figure 1j) [66]. The AA + CG formalism is analogous to the RelRes approach mentioned in §3.3, in which particles are described simultaneously at two different resolutions according to their relative distance. At short distances, particles are described at the FG level using CHARMM force field, while the MARTINI force field is used at long distances. At intermediate distances, FG and CG interactions are mixed in a distance-dependent fashion.

Decoupled resolutions strategies have also been applied to represent multi-scale solutes such as proteins [67,68] or polymers [69,70] (figure 1k). The solute is mostly described at CG level while specific particles are represented at fixed FG resolution. As described before for this category of methods, self-resolution interactions (FG–FG or CG–CG) use pure FG or CG potentials, respectively, while virtual sites placed on top of the FG particles are used to couple bonded or non-bonded interactions with CG particles.

A further step in multi-scale modelling of solutes is the explicit description of multi-scale solute/solvent systems. Fixed resolutions strategies are used to study FG proteins or organic molecules within CG membranes and explicit CG solvent (figure 1e). In close analogy to the single-layer multi-scale solvation, FG and CG resolutions are coupled directly by using compatible CG models derived from the MS-CG theory [71], the ELBA force field [72], PACE and MARTINI force fields [73] or other strategies [74,75]. An example of multi-layer solute/solvent representation is provided by the work of Carloni and co-workers (figure 1f) [76]. The model consists of a membrane protein described at FG level around its drug-binding site, and by a Gō-like model outside that region. The membrane and solvent are modelled implicitly, except for a restrained cap of explicit FG waters solvating the exposed FG (extracellular) part of the protein. This model was recently improved by substituting the restraining potential on the FG solvent for an open boundary approach based on the H-AdResS scheme [44]. Using a similar idea, the H-AdResS is combined with an elastic network model (ENM) to represent a FG/CG protein in a FG/CG solvent (figure 1g) [43]. In this case, solute resolutions remain unchanged, while ENM springs are used to mechanically couple both representations. On the other hand, the solvent description around the solute FG region is allowed to change according to the H-AdResS scheme. The adaptive resolutions framework has also been extended to the study of polymers in solution to allow for changes in solute and solvent granularities according to their spatial position (figure 1g) [77,78]. Last but not least, a virtual sites approach has been used to simulate a FG protein embedded in a CG environment composed by a membrane patch solvated with its corresponding CG water (figure 1h) [53].

5. Quantum mechanics in multi-scale approaches

So far we have discussed multi-scale approaches applied to classical or molecular mechanics (MM); however, many problems require a quantum mechanical (QM) level of detail. Owing to the high computational cost of applying QM methods to the study of relatively large biological systems, different multi-scale QM/MM approaches have been derived [79]. In standard QM/MM methods, a small region of the system (where the electronic detail is required) is treated at the QM level, while the rest of the system is modelled using the MM level of theory, usually described at FG resolution. On top of that, the inclusion of CG representations at the MM layer emerges as an appealing strategy [80]. Although the largest share of the computational cost will always be on the QM part, introduction of large CG regions might provide a more realistic representation of quaternary structure environments. The same challenges previously faced by QM/MM approaches are also inherited when a CG representation is introduced into the MM region. In particular, coupling of bonded and/or non-bonded terms to the QM region or a careful treatment of the system temperature and other properties present significant challenges. In addition, different energy expressions need to be properly and efficiently coded in simulation software. Although there are examples in the literature describing the use of effective potentials as CG components in QM/MM calculations [81], we focus here on reviewing the few known examples using explicit CG particles.

To avoid potentially confusing nomenclature, we recall that the acronym QM/MM was historically coined to highlight the difference between quantum mechanics and classical or molecular mechanics levels of theoretical description. As CG regions are in general also modelled using classical mechanics, the MM region may actually contain both FG and CG representations, requiring further nomenclature subtlety to avoid ambiguity and discriminating between different coupling schemes. Unfortunately, there are different approximations using a rather arbitrary nomenclature. In the remainder of this review, we will refer to the literature, keeping the names and acronyms originally proposed by their authors.

A multi-scale formalism called QM/MM/CG has been used to describe drug–protein interactions at QM/MM level in the context of standard or polarizable MARTINI water [82]. This method can be considered as an extension of the previously described decoupled resolutions approach (figure 1d), allowing for the three resolutions (QM, FG and CG) to be simultaneously present. Virtual sites in FG and QM regions are used to account for the LJ interactions with the CG region. In addition, Coulomb electrostatic interactions between FG and CG regions are calculated directly, but the CG particles are included as external point charges in the QM calculation.

An alternative scheme, called QM/(AA + CG), has been derived from the AA + CG adaptive resolution scheme (figure 1j) [83]. In this method, the Hamiltonian of the QM subsystem is preserved, while the QM/MM and MM interactions are described by a multi-resolution scheme according to the relative interparticle distances. In this scheme, the MM region is treated at two different resolutions at the same time. This strategy proved to be as good as QM/MM/CG in the calculation of redox potentials for aqueous ruthenium and iron complexes [83].

So far QM/MM/CG and QM/(AA + CG) schemes have been used to describe intermolecular boundaries at solvent level. A contrasting framework named QM/CG-MM has been recently proposed by Sinitskiy and Voth, in which the entire surroundings of the QM regions are described by a CG potential [84]. The authors derived new expressions for an effective QM Hamiltonian depending on CG variables using the MS-CG formalism [85]. An advantage over usual QM/MM approaches is that QM/CG-MM allows for an explicit definition of a temperature for the whole system. However, routine application of this new formalism on MD simulations remains a challenge.

6. The SIRAH force field for coarse-grained and multi-scale simulations

Our group has developed a generic CG force field for biomolecular systems named SIRAH. This force field follows a top-down approach for parameter development with the distinctive characteristic of using a classical two-body Hamiltonian identical to those employed in popular MD simulation packages. Hence, common-knowledge concepts as atom type, partial charge, bonded and non-bonded interactions are forthrightly incorporated into the CG representation. This allows for a direct implementation in virtually any MD engine, taking profit of computational advances inherent to each code (e.g. GPU acceleration or efficient implementation of long-range electrostatics). Moreover, it is possible to straightforwardly use programs for analysis and visualization contained in common MD packages. Currently, SIRAH has been ported to GROMACS and AMBER and is openly distributed from the Web page http://www.sirahff.com, along with a set of tutorials and analysis/visualization tools [86].

Coarse-graining is performed at the level of chemical functional groups, maintaining the identity of single residues. Moreover, CG beads are placed at the position of real atoms facilitating the mapping, backmapping and the physical interpretation of interactions. This choice makes the force field sensitive to point mutations and environmental conditions, like temperature, pressure, ionic strength and electric fields. In general, CG mapping is guided by physico-chemical knowledge using different bead sizes and partial charges trying to optimize intermolecular interactions needed to capture selected structural features [87].

Currently, SIRAH contains parameters for proteins [88], lipids [89], water, electrolytic ions [90], calcium as a metallic ligand [91] and DNA [92]. It is important to note that the strategy for parameter fitting is mostly oriented to reproduce experimental structures. Interestingly, however, an independent group has recently shown that SIRAH outperforms FoldX in predicting differences in binding free energies upon point mutations in protein–protein complexes [93].

Besides CG simulations, the SIRAH mapping and parametrization are devised because their conception to be compatible with atomistic force fields. The tetrahedral WatFour (WT4 for short) water model used in SIRAH carries partial charges and LJ parameters fitted to reproduce a certain number of water properties [90]. Worth noting, the point charges assigned to WT4 beads are ±0.41e, i.e. identical to those used in the SPC atomistic water model. This has two important consequences. On the one hand, the model creates its own electric permittivity [90], granting the possibility of using long-range electrostatics without imposing artificial uniform dielectric constants. On the other hand, the combination of electrostatic and LJ parameters makes the free energy of mixing with SPC water negative, but less favourable than the mix of either WT4 in WT4 or SPC in SPC species. As a result, FG and CG water models coexist experiencing only limited mixing and creating a smooth transition interface of about 10 Å [94]. Therefore, it is possible to perform fixed resolutions multi-layer solvation using an atomistic solute surrounded by a shell of atomistic water, beyond which WT4 molecules are used to represent bulk solvent [95–98]. Remarkably, it is possible to simulate a desired ionic strength by setting the same ionic concentration in the FG and CG phases without introducing an osmotic pressure imbalance [94]. CG electrolytes in SIRAH (Na⁺, K⁺ and Cl^–) are represented with their corresponding charge and LJ parameters matching their second solvation shell, as determined from neutron diffraction experiments [99]. In order to keep the correct partition of FG and CG ions, differential LJ interactions outside the Lorentz–Berthelot combination rules are set between CG ions and FG water. More precisely, the minimum distance between FG water molecules and CG ions is set to the same distance at which WT4 can approach to the CG ion. This simple trick avoids over stabilization of CG ions by FG water, maintaining the ionic partition without the need for restraining potentials. This approach has also been proven to be transferable to different force fields and three-points water models (namely, TIP3P, SPC and SPC/E) [100]. It is worth noting that, according to the Young–Laplace effect, the very presence of an interphase introduces an interphase pressure. Since simulated systems are usually constituted by a FG core surrounded by CG water, the excess pressure is exerted towards the core. Estimations for small proteins in mixtures of WT4 with different FG water models indicate an increase of about 1 atm at the FG/CG interface, which decreases as the inverse of the radius of the protein [100]. While we could not measure any spurious effect on the conformation or dynamics of well-folded proteins, flexible molecules such as unfolded peptides or polysaccharides might show a higher propensity to visit compact states. Since pressure is an intensive property and the excess of pressure arises as a direct consequence of the presence of the interphase, readers must be aware that this spurious effect is expected to be present in all fixed resolutions multi-scale methods. Besides this, to the best of our knowledge, fixed resolution does not introduce additional artefacts. Moreover, in the particular case of SIRAH, multi-scale simulations are robust to the use of different thermostats, barostats, coupling constants or equilibration procedures.

The good performance of the WT4 model in multi-scale simulations prompted us to develop a cognate SG water model named WatElse (WLS for short, figure 1b), which is also intended to work in combination with atomistic water and WT4 in a fixed resolutions multi-layer solvation scheme [101]. The conception of WLS follows a simple rationale: WT4 is inspired in the structure of an elementary water cluster. If a single water molecule can be viewed as a tetrahedron (with the oxygen at the centre and vertices occupied by two hydrogen atoms and two electron lone pairs), then WT4 can be regarded simply as a higher granularity water molecule. Following this line of reasoning, it is conceivable to homothetically extend the coarse-graining of water to higher granularities. In close similarity with the water/WT4 mix, FG water and WT4 experience only limited mixing with WLS, producing smooth borders at each interface. This simulation scheme is particularly well suited for studying highly solvated systems like viral particles, which require massive amount of bulk water at both internal and external sides of the viral capsid or envelope [102].

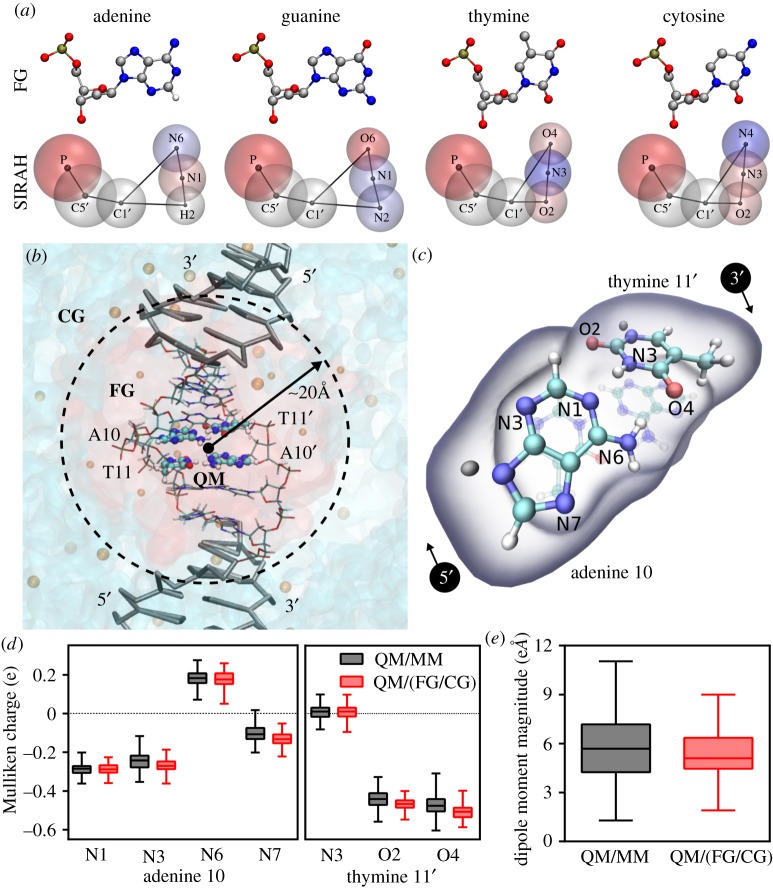
A different multi-scale scheme included in the SIRAH force field involves the double scale modelling of DNA. Currently, SIRAH contains representations for the four canonical DNA nucleotides. Each of them is mapped to a six-beads residue using the positions of the phosphorus, C5′, C1′ and the corresponding atoms at the Watson–Crick edge (figure 2a) [92]. Partial charge distributions add up to −1 for each CG nucleotide and ensures electrostatic recognition of G-C and A-T pairs without the need for additional constraints. Furthermore, the LJ parameters of beads at C1′ and Watson–Crick edge correspond to atomistic ones to avoid clashes with neighbouring nucleotides. The model works for MD simulations using the WT4 model as explicit solvent [90] or generalized Born model as implicit solvent [92]. Bonded and non-bonded parameters are fitted to reproduce the canonical B form of DNA in MD simulations but also sequence induced base-pair openings and the correct persistence length for single-stranded DNA [103]. Moreover, backmapping of CG trajectories resulted in excellent comparison with FG counterparts [104]. The good reproduction of structural and dynamical features added to the use of the position of real atoms to place beads facilitated the direct linking between FG and CG scales choosing only an appropriate set of bonding parameters between both scales, calculating all the interactions within the same Hamiltonian [105]. This dual resolution model for DNA shows a very good conservation of mechanical and electrostatic properties across the FG–CG interface. Indeed, mechanical perturbations into the FG region fade out after only one base pair, while differences in the electrostatic potential became negligible already after two base pairs [105]. This highlighted the good quality of the model and suggested the possibility of implementing a QM, FG, CG simulation scheme for DNA. This is particularly appealing because no approach coupling a FG/CG representation with a QM description has been applied until now for DNA, despite the large repertoire of multi-scale models currently available for this biomolecule [106]. As all the interactions in the SIRAH force field are calculated within the same Hamiltonian used for the FG part, the MM region remains unchanged from a classical point of view. Because of that, we named this approach QM/(FG/CG) to point out that FG and CG representations belong to the same MM region and interact in the same way as the QM part. Worth noting, the latest extension of the FG/CG model to describe the LacI-DNA system in an explicit multi-layer solvation context [107] opens the possibility for new exciting applications.

Figure 2.

Hybrid QM/(FG/CG) calculations in the 5′-CATGCATGCATGCATGCATG-3′ dsDNA. (a) DNA nucleotides at FG (top, only heavy atoms and hydrogen H2, which position is used for mapping in adenine are shown) and SIRAH representation (bottom, including mapped atom names). SIRAH beads are coloured according to their partial charge value, from negative (red) to neutral (white) and positive (blue). (b) Representation of the multi-scale partition of the system: QM treated atoms are shown as balls and sticks, FG base pairs are shown as thin sticks coloured by atom and CG DNA is represented as thick grey sticks. Transparent red and light blue surfaces represent the volume occupied by FG and CG solvent, respectively. FG and CG ions are shown as orange balls with different sizes. Owing to limited mixing of FG and CG solvents just an indicative FG/CG a dashed circle denotes interface. (c) Insight into the QM subsystem indicating the atom nomenclature. Link atoms are depicted in grey. (d) Comparison of Mulliken charges from 2000 single point calculations at QM/MM and QM/(FG/CG) level. (e) Comparison of the calculated dipole moment magnitude at the entire QM subsystems. (Online version in colour.)

As proof of concept, we compared different electronic properties from single point calculations at QM/MM and QM/(FG/CG) levels on a FG and a FG/CG system respectively. To this aim, we used the MD simulations previously presented by us in [107] to describe FG and FG/CG schemes on a double-stranded DNA system with explicit solvent. As detailed in [107], the system consists of a DNA sequence 5′-CATGCATGCATGCATGCATG-3′, where the central GCATGC track is defined as the FG region in the FG/CG system (figure 2b). A shell extending up to 20 Å away from the centre of the FG region is solvated with TIP3P water and Na⁺ ions are set according to Manning's theory of polyelectrolytes [108]. Beyond that volume, WT4 molecules together with 0.15 M of CG electrolytes are added to fill up a simulation box of identical dimensions to that used in the fully FG simulation. Frames each 5 ps from the first 10–20 ns of MD simulations on each system are used in the single point calculations. The QM subsystem is defined as the central AT bases for both QM/MM and QM/(FG/CG) and single point calculations are performed and averaged on both sets of snapshots (figure 2c). The electronic structure calculations are performed at the PM3 semi-empirical level using an 18 Å cut-off for the electrostatic coupling between the QM subsystem and the FG and CG ones, as implemented in the AMBER software suite. This setting has been successfully applied to DNA [109–111].

The distribution of atomic Mulliken charges obtained from QM/MM and QM/(FG/CG) calculations shows excellent agreement between both methodologies. In particular, the charges of donor and acceptor hydrogen bond atoms of the A-T Watson–Crick base pair show practically indistinguishable distributions (figure 2d). Furthermore, the magnitude of the dipole moment in the QM subsystem shows comparable profiles (figure 2e). The notable agreement between these electronic structure properties provides a solid indication of the correct electrostatic coupling between the QM and CG subsystems, most probably due to the well behaved electrostatic potential intrinsic to the SIRAH model. The importance of using a significantly larger cut-off in QM/MM calculations than in classical simulations, together with the increasing efficiency of different QM methodologies [112–114], constitutes a driving force to continue challenging the SIRAH-based QM/(FG/CG) approach, with the aim of integrating different QM levels of theory in large complex systems.

7. Discussion and conclusion

Computational biology is experiencing tremendous advances prompted, on one side, by the ever-growing availability and affordability of computer power; and on the other, by the ‘resolution revolution’ [115]. The introduction of techniques like cryoelectron tomography is bringing astonishing whole cell images with unprecedented structural details of a few nanometres [116]. As illustrated in this contribution, significant efforts are being devoted by the computational biology community to keep pace with the huge amount of information produced by cutting-edge experimental techniques. Concurrently multi-scale methods are acquiring an increasingly predictive power and applicability to concrete biological data.

Although a critical and quantitative comparison of the cost-effectiveness of each method would be highly desirable, we decided to not address this topic. We find it an extremely difficult task in light of the continuous development of ever-faster hardware and software. Indeed, the many possible combinations of computer architecture (e.g. CPU, GPU, fast memories) with software versions, languages, and compilers, just to quote the most obvious, may have a tremendous impact on the performance of a given method. Moreover, quantitative comparisons would be unfair with the newest methods, as usually theoretical developments precede practical and efficient implementations. Obviously, more aggressive coarse-graining and longer time steps used in the simulations are, in general, associated with a higher speed-up. However, users must always select the best-suited method for their problem of interest, which is not necessarily the fastest approach at hand. It must also be noted that some particular applications involve rather intricate strategies for parameter derivation, which may not be transferable between different systems. Extreme care is advised to users adapting or manually tuning interactions, as it may require making arbitrary choices or tampering with in-house codes. In connection to that, a retrospective view shows that methods became popular, in part, due to a user-friendly implementation. However, because multi-scale simulations are at a relatively early stage of development, it is not common to find ‘plug & play’ packages. Table 1 lists those methods sketched in figure 1 along with the MD engines in which they have been implemented.

Table 1.

Implementation and availability of multi-scale methods from figure 1.

panel	model	MD engine
a, e	PACE/MARTINI (https://www.ks.uiuc.edu/~whan/PACE) [25,73]	modified version of NAMD 2.9 GROMACS (http://www.gromacs.org) [117]
a, e	ELBA [26], FG/ELBA [72] (http://www.orsi.sems.qmul.ac.uk/elba)	LAMMPS (https://lammps.sandia.gov) [118]
b	FG/GROMOS CG [31]	GROMOS11 (http://www.gromos.net) [119]
b, f, i	SIRAH (www.sirahff.com)	AMBER (http://ambermd.org) [120] GROMACS (http://www.gromacs.org) [117]
c	AdResS [46]	ESPResSo++ (http://www.espresso-pp.de) [121] GROMACS (http://www.gromacs.org) [117]
c	PE-AdResS [37]	modified version of GROMACS
c	GC-AdResS [38,39]	modified version of GROMACS 5.1.0
c, g	H-AdResS [34,35]	ESPResSo++ (http://www.espresso-pp.de) [121] LAMMPS (https://lammps.sandia.gov) [118]
c	RelRes [51]	GROMACS (http://www.gromacs.org) [117]
d, h	MARTINI virtual sites [52], GROMOS/MARTINI [53] (http://cgmartini.nl)	GROMACS (http://www.gromacs.org) [117]
f	GROMOS/Gō [76]	modified version of GROMACS 4.5
i	OPLS/Gō [61], AMBER/Gō [62]	library-based Monte Carlo (LBMC) (https://www.csb.pitt.edu/Faculty/zuckerman/software.html) [122]
i	CHARMM/ERM [63]	NAMD2 (http://www.ks.uiuc.edu/Research/namd) [123] and in-house code
i	CHARMM/PRIMO [65]	CHARMM c38a2 or later (https://www.charmm.org) [124]
j	AA + CG (CHARMM/MARTINI) [66]	in-house version of QM4D (http://www.qm4d.info)
k	GROMOS/ATTRACT [68]	in-house code
k	polymer solutions [69,70]	modified version of IBIsCO (http://www.theo.chemie.tu-darmstadt.de/ibisco) [125]

Finally, we would like to stress that, despite the diversity of schemes and approximations developed for multi-scale simulations, significant challenges remain unsolved. Those comprise transferability between different representation levels, and efficient handling and sharing of the huge volume of generated data. Addressing such problems will likely necessitate coordinated efforts by the computational biology community [126].

Data accessibility

This article has no additional data.

Authors' contributions

A.Z. and M.M. carried out the molecular simulations. All authors participated in data analysis and drafted the manuscript. All authors gave final approval for publication.

Competing interests

We declare we have no competing interests.

Funding

This work was partially funded by FOCEM (MERCOSUR Structural Convergence Fund), COF 03/11. A.Z and L.D acknowledge Agencia Nacional de Investigación e Innovación (ANII), Institut Pasteur de Montevideo and Universidad de la República for postdoctoral fellowship funding.