SWINGER: a clustering algorithm for concurrent coupling of atomistic and supramolecular liquids

Abstract

In this contribution, we review recent developments and applications of a dynamic clustering algorithm SWINGER tailored for the multiscale molecular simulations of biomolecular systems. The algorithm on-the-fly redistributes solvent molecules among supramolecular clusters. In particular, we focus on its applications in combination with the adaptive resolution scheme, which concurrently couples atomistic and coarse-grained molecular representations. We showcase the versatility of our multiscale approach on a few applications to biomolecular systems coupling atomistic and supramolecular water models such as the well-established MARTINI and dissipative particle dynamics models and provide an outlook for future work.

1. Introduction

All-atom molecular dynamics (MD) simulations in conjunction with modern computers provide us with unprecedented information about the structural and dynamic properties of biomolecular systems at the atomistic length scales. Thus, they can be considered as a virtual microscope to study complex molecular systems with atomistic resolution [1–5]. Owing to the complexity of biomolecular systems, however, molecular simulations still have some limitations in reaching experimentally required spatial and temporal scales. In particular, simulating explicit solvent is computationally the most expensive part in all-atom biomolecular simulations due to a huge number of related degrees of freedom. The associated computational burden is drastically alleviated by implicit solvent models but in many situations, e.g. simulations of dense DNA arrays [6], molecular details play a crucial role and the inclusion of explicit solvent is unavoidable.

One way of circumventing the problem is offered by coarse-graining techniques, which reduce the number of degrees of freedom in the system [7–9]. This can be done either in a bottom-up manner [10–18], where one builds a given coarse-grained (CG) solvent model based on an underlying atomistic (AT) model or in a top-down way [19–25] as in the MARTINI force-field [26] or dissipative particle dynamics (DPD) method [27–34]. Another issue is concerned with the number of molecules that one chooses to be represented by the CG bead [25], for instance, four water molecules in the MARTINI model or an arbitrary number in DPD.¹ In such supramolecular representations, a special challenge is related to the problem of constructing bottom-up supramolecular coarse-grained (SCG) models and clustering algorithms such as the K-means [35,36] or CUMULUS [37] have to be devised to distribute solvent molecules among different SCG beads. This, in turn, leads to a problem of continuous SCG trajectory [38].

In biomolecular simulations, however, one needs the AT resolution usually only in the first few hydration layers around solvated biomolecules to properly account for the interaction between water and macromolecules. The most efficient way to tackle such situations is via multiscale modelling approaches. In this review, we focus on concurrent multiscale methods, which couple fine-grained and CG resolutions at the same time in the simulation box (e.g. [39–56]). Among the most advanced of such multiscale methods is the adaptive resolution scheme (AdResS) [57–59], in which the molecules can change their resolution on-the-fly during the course of an MD simulation. AdResS is hence suitable for systems where the fine-grained AT resolution is required only in some subdomains with the CG level of detail sufficient for the remainder of the system, a typical situation encountered in many biomolecular systems as presented, for example, in figure 1. So far, it has been successfully applied to many biophysical systems such as solvated proteins and DNA molecules [6,60–63]. Because of the fast diffusion of water molecules that takes place on a picosecond timescale the supramolecular coupling represents a major challenge for AdResS. Therefore, if one wishes to map a cluster or a bundle of solvent molecules always to the same SCG bead, the motion of those molecules must be restricted by using additional (artificial) semi-harmonic bonds between water molecules belonging to the same bundle (in the case of MARTINI, four water molecules per bundle) [64–68]. While such bundling of water molecules simplifies the supramolecular coupling to a certain extent, it is also a source of spurious artefacts in certain situations, such as partial unfolding of biomolecules [69].

Figure 1.

Schematic of the multiscale simulation set-up for the simulation of a protein in water where the resolution of the solvent is gradually changed from atomistic to SCG. For supramolecular mappings, the clusters need to be assembled, disassembled and reassembled on-the-fly to accommodate the molecular diffusion from the atomistic to SCG domains and vice versa. To this end, we developed the SWINGER algorithm that acts in the thin layer between the atomistic and hybrid domains. (Online version in colour.)

This review is devoted to a description of the development and applications of the clustering algorithm SWINGER [70], which redistributes molecules into clusters on-the-fly, thus allowing for a seamless coupling between standard AT and SCG water models (figure 1). Note that in the multiscale set-up, there is no need for a continuous SCG trajectory as opposed to the bottom-up SCG [38]. The algorithm was applied to link the AT and the MARTINI SCG force field [70,71], paving the way for efficient biomolecular MD simulations, and also to a concurrent coupling of MD and DPD, thus bridging atomistic and mesoscopic hydrodynamics [72].

The remainder of the review is organized as follows: in §2, we discuss the AdResS scheme in the context of supramolecular coupling and present the main aspects of the SWINGER algorithm. In §3, we revisit three applications of the introduced methodology, namely the coupling of atomistic simple point-charge (SPC) and MARTINI water models, the simulation of the atomistic protein in multiscale SPC/MARTINI solvent, and the coupling of MD and DPD methods for water, followed by conclusions and outlook in §4.

2. Methods

We consider a multiscale simulation where a part of the simulation domain is represented on the AT level and the rest on the SCG resolution level (figure 2). With an SCG model, we denote any model where a cluster of molecules is represented as a single particle. Furthermore, we consider on-the-fly coupling, meaning that the resolution level is adaptively changed depending on the position in the system. For supramolecular mapping, this implies requisition of a concurrent clustering mechanism. In the following, we describe how such simulations can be performed with the combination of AdResS and the clustering algorithm SWINGER.

Figure 2.

Original (a) and ‘reverse’ (b) implementation of AdResS multiscale simulation where an atomistic (AT) model is coupled to an SCG model. The coupling is shown for the special case where the resolution is changed only along one dimension. Only half of the simulation domain is displayed as the system is symmetric. In the original AdResS version, the weighting function w take limiting values of w = 1 and 0 in the AT and SCG domains, respectively. In the ‘reverse’ case, the definition of w is inverted, which permits the exclusion of the intermediate atomistic with bundles (ATwB) region. In both cases, the SWINGER algorithm is applied in a very small region at the edge of the AT domain. Different AdResS domains are shown disjoint only for clarity reasons. (Online version in colour.)

2.1. Adaptive resolution scheme

According to AdResS [58], the total force acting on a cluster α is

$${\mathbf{F}}_{\alpha }={\mathbf{F}}_{\alpha }^{\mathrm{AdResS}}+{\mathbf{F}}_{\alpha }^{\mathrm{TD}}+{\mathbf{F}}_{\alpha }^{\mathrm{thermo}},$$ 2.1

where F^AdResS is the adaptive resolution force that accounts for the AT/SCG resolution change, F^TD is the thermodynamic force and F^thermo is the thermostat contribution. A force interpolation scheme is used to couple the AT and low-resolution SCG regimes, i.e.

$${\mathbf{F}}_{\alpha }^{\mathrm{AdResS}}=\sum _{\beta \ne \alpha }\{\lambda ({\mathbf{R}}_{\alpha },{\mathbf{R}}_{\beta }){\mathbf{F}}_{\alpha \beta }^{\mathrm{AT}}+[1-\lambda ({\mathbf{R}}_{\alpha },{\mathbf{R}}_{\beta })]{\mathbf{F}}_{\alpha \beta }^{\mathrm{SCG}}\}.$$ 2.2

The ${\mathbf{F}}_{\alpha \beta }^{\mathrm{AT}}$ and ${\mathbf{F}}_{\alpha \beta }^{\mathrm{SCG}}$ are the forces between clusters α and β. For MD, the forces are computed from the AT (U^AT) and SCG (U^SCG) potentials as

$${\mathbf{F}}_{\alpha \beta }^{\mathrm{AT}}=-\sum _{i\alpha ,j\beta }\frac{\mathrm{\partial }{U}^{\mathrm{AT}}}{\mathrm{\partial }{\mathbf{r}}_{i\alpha j\beta }}\text{and}{\mathbf{F}}_{\alpha \beta }^{\mathrm{SCG}}=-\frac{\mathrm{\partial }{U}^{\mathrm{SCG}}}{\mathrm{\partial }{\mathbf{R}}_{\alpha \beta }}.$$ 2.3

The sum runs over all pair atom interactions between explicit atoms i of the cluster α and explicit atoms j of the cluster β. The vector R_αβ = R_α − R_β is the relative position vector of the clusters α and β centres-of-mass (CoM), while r_iαjβ = r_iα − r_jβ is the relative position vector of atoms i and j. If, instead, we wish to employ a DPD method in the SCG domain, the ${\mathbf{F}}_{\alpha \beta }^{\mathrm{SCG}}$ is given by

$${\mathbf{F}}_{\alpha \beta }^{\mathrm{SCG}}=a_{\alpha \beta }(1-\frac{R_{\alpha \beta }}{R_c}){\hat{\mathbf{R}}}_{\alpha \beta },$$ 2.4

i.e. the conservative force of the DPD method. A smooth transition from AT to SCG representations and vice versa is enabled with the hybrid (HY) region (R_AT < R < R_SCG; figure 2). Two different interpolations of forces were proposed: the original and the ‘reverse’ definition. The λ is, respectively, given by

$$\lambda ({\mathbf{R}}_{\alpha },{\mathbf{R}}_{\beta })=\{\begin{array}{ccc}w({\mathbf{R}}_{\alpha })w({\mathbf{R}}_{\beta });& w({\mathbf{R}}_{\alpha ,\beta })=\left\{\begin{array}{cc}1,& \mathrm{AT}\hspace{0.17em}\mathrm{and}\hspace{0.17em}\mathrm{ATwB}\\ {\cos }^2\left[\frac{\pi (\parallel {\mathbf{R}}_{\alpha ,\beta }-{\mathbf{R}}_0\parallel -R_{\mathrm{AT}})}{2(R_{\mathrm{SCG}}-R_{\mathrm{AT}})}\right],& \mathrm{HY}\\ 0,& \mathrm{SCG}\end{array}\right\};& \mathrm{original}\\ 1-w({\mathbf{R}}_{\alpha })w({\mathbf{R}}_{\beta });& w({\mathbf{R}}_{\alpha ,\beta })=\left\{\begin{array}{cc}0,& \mathrm{AT}\\ {\cos }^2\left[\frac{\pi (R_{\mathrm{SCG}}-\parallel {\mathbf{R}}_{\alpha ,\beta }-{\mathbf{R}}_0\parallel )}{2(R_{\mathrm{SCG}}-R_{\mathrm{AT}})}\right],& \mathrm{HY}\\ 1,& \mathrm{SCG}\end{array}\right\};& ‘\mathrm{revers}{\mathrm{e}}^{\prime }\end{array}$$ 2.5

In both implementations, the weighting function w is a sigmoid function with extreme values of 0 and 1. However, its definition is turned around in the ‘reverse’ implementation. The two cases are showcased in figure 2. The original implementation of AdResS requires the use of an additional atomistic with bundles (ATwB) domain, where the resolution is atomistic and the SCG interaction sites are well defined. This necessity is due to the non-zero interactions between the AT and HY clusters up to one potential cutoff deep into the AT domain. In the ATwB region, the water molecules in the clusters need to be constrained to remain first neighbours as in, for example, the bundled-SPC water model. From a computational point of view, such implementation is not optimal as one would like to minimize the computationally heavy AT region. Hence, in later applications the ‘reverse’ implementation was adopted, where the ATwB region is omitted. In equation (2.5), R₀ denotes the centre of the AT region, which can be either a fixed point (usually the centre of the simulation box) or a mobile point, as, for example, in a simulation of a macromolecule where it coincides with the macromolecule’s CoM. AdResS can accommodate various geometric boundaries between the resolution regions: splitting in one dimension [70], cylindrical [60], spherical [71]. It also permits the use of flexible domains [73] where the atomistic region is defined as a distance from the surface of the macromolecule which is beneficial for multiscale simulations of macromolecules that change their shape during the simulation, e.g. proteins that fold or unfold.

The thermodynamic force F^TD accommodates the coupling of rather loosely connected molecular representations, i.e. it maintains two different models with, in general, different thermodynamic properties like pressure and chemical potential in thermodynamic equilibrium [74–76]. Typically, there is a preferential tendency of the molecules to migrate into the low-resolution region and change resolution in order to lower the free energy of the system. This effect is manifested as density undulations across the direction of the resolution change. The thermodynamic force amends for these. It is calculated in an iterative manner as

$${{\mathbf{F}}^{\mathrm{TD}}}_{k+1}(\parallel \mathbf{R}-{\mathbf{R}}_0\parallel )={{\mathbf{F}}^{\mathrm{TD}}}_k-C\mathrm{\nabla }{\rho }_k(\parallel \mathbf{R}-{\mathbf{R}}_0\parallel ),$$ 2.6

where k denotes the iteration step. The prefactor $C=M/{\rho }_0^2{\kappa }_T$, where ρ₀ and κ_T are the bulk density and isothermal compressibility, respectively, is in practice empirically adjusted along the process to prevent under/over-correction. To speed up the iteration procedure we simultaneously run at each iteration step several simulations with different prefactors and select the best one for the next iteration. The ${\mathbf{F}}_{\alpha }^{\mathrm{TD}}$ depends on the cluster type, i.e. if the solvent is monocomponent (as in the applications presented below) the force is equal for all SCG particles.

An important point is that the force definition in equation (2.2) satisfies Newton’s Third Law, i.e. F_αβ = −F_βα. However, since the total pair force depends not only on their relative distances but also on the absolute positions of the molecules, it is not conservative and the corresponding potential does not exist. For this reason, the AdResS method requires a local thermostat, which supplies or removes the latent heat caused by the switch of the resolution [57]. Here, we briefly present two local thermostats typically employed in AdResS simulations, that is the Langevin [77] and the DPD [78,79] thermostats, where the thermostat force is decomposed into a random ${\mathbf{F}}_{\alpha }^R$ and a friction ${\mathbf{F}}_{\alpha }^D$ contribution. In the case of the Langevin thermostat, they are given by

$$\begin{array}{rl}{\mathbf{F}}_{\alpha }^D& =-\gamma {\dot{\mathbf{R}}}_{\alpha },\\ ⟨{\mathbf{F}}_{\alpha }^R⟩& =0\mathrm{and}⟨{\mathbf{F}}_{\alpha }^R(t){\mathbf{F}}_{\alpha }^R(t^{\prime })⟩=2\gamma k_{\mathrm{B}}T\delta (t-t^{\prime }),\end{array}$$ 2.7

where γ is the friction coefficient, k_B the Boltzmann constant and T the temperature. The equations satisfy the fluctuation–dissipation theorem and generate a canonical ensemble in equilibrium. However, the linear momentum is not conserved. When hydrodynamic interactions are important a linear momentum conserving DPD thermostat [78] is more appropriate, i.e.

$$\begin{array}{rl}{\mathbf{F}}_{\alpha }^D& =\sum _{\beta \ne \alpha }{\mathbf{F}}_{\alpha \beta }^D{\mathbf{F}}_{\alpha \beta }^D=-\gamma {\omega }^D(R_{\alpha \beta })({\hat{\mathbf{R}}}_{\alpha \beta }{\mathbf{V}}_{\alpha \beta }){\hat{\mathbf{R}}}_{\alpha \beta }\\ \mathrm{and}{\mathbf{F}}_{\alpha }^R& =\sum _{\beta \ne \alpha }{\mathbf{F}}_{\alpha \beta }^R{\mathbf{F}}_{\alpha \beta }^R=\sqrt{2\gamma k_{\mathrm{B}}T}{\omega }^R(R_{\alpha \beta }){\eta }_{\alpha \beta }{\hat{\mathbf{R}}}_{\alpha \beta },\end{array}$$ 2.8

where ${\mathbf{V}}_{\alpha \beta }={\mathbf{V}}_{\alpha }-{\mathbf{V}}_{\beta }$ is the velocity between clusters α and β. The noise η_αβ must satisfy 〈η_αβ〉 = 0 and 〈η_αβ(t)η_kl(t′)〉 = 2(δ_ikδ_jl + δ_ilδ_kj)δ(t − t′) analogous to the Langevin forces. The w^D(R_αβ) and w^R(R_αβ) are R-dependent weight functions that vanish at the predefined cut-off radius. From the fluctuation–dissipation theorem, it follows that (w^R(R_αβ))² = w^D(R_αβ). Equations (2.7) and (2.8) are written only for the SCG domain, since the equations are analogous for the AT domain.

2.2. SWINGER

To facilitate supramolecular coupling, we need an algorithm that will dynamically make, break and remake clusters of water molecules that will form SCG particles. When designing such an algorithm the following factors need to be taken into account

• (i)the algorithm needs to be applied at the boundary between the AT and HY domain, with pure AT domain containing only the unconstrained molecules, whereas the HY domain should contain only the clustered molecules;
• (ii)the number of molecules in a cluster has to be exactly equal to the AT-to-SCG mapping;
• (iii)the clustering should be optimized in terms of minimal distances of molecules within the clusters;
• (iv)the frequency of the algorithm’s initialization should be approximately on the order of timescales of waters’ tetrahedral clusters (≈1 ps);
• (v)the algorithm should leave the coordinates and velocities of atoms intact.

The SWINGER algorithm, whose flowchart is shown in figure 3, was developed with these considerations in mind. It is invoked at every Verlet list update, which in turn is invoked when the maximum displacement of any particle since the last Verlet list update exceeds the value of R_skin. The clusters are made and remade in a thin layer of thickness ΔR_S ≥ R_skin. For the supramolecular mappings thus far considered, i.e. 4-to-1 and 8-to-1 the ΔR_S was set to 0.2, 0.4 nm, respectively. A larger ΔR_S was chosen for the 8-to-1 mapping due to the larger size of the clusters containing eight water molecules. The stages of the algorithm are (i) all clusters in the SWINGER region are disassembled; (ii) initial grouping is performed in an orderly fashion, i.e. the water molecules further from the AT region are grouped first which outputs more optimized clusters closer to the HY region, where each cluster contains exactly the prescribed number of water molecules; (iii) to obtain the optimal clustering the simulated annealing Monte Carlo refinement is performed until the maximum number of iterations is reached or the sum of clusters’ energy (equation (2.9) with Γ = 1) is sufficiently low. The trial moves consist of selecting a random molecule in a random cluster and swapping that molecule with the nearest molecule in the nearest cluster; (iv) all clusters whose CoM resides outside the AT domain are retained while the others are disassembled. A more detailed description can be found in [70].

Figure 3.

Flowchart of the SWINGER algorithm. (Online version in colour.)

When the clusters are formed a half-harmonic spring interaction, given by

$$U_{\mathrm{B}}(r_{ij},\mathbf{R})=\{\begin{array}{rl}& \frac{1}{2}k{(r_{ij}-r_0)}^2\mathit{\Gamma }(\mathbf{R}),r_{ij}>r_0\\ & 0,\mathrm{otherwise}\end{array}$$ 2.9

is added between the oxygen atoms i and j within a cluster. The force-constant k is 1000 kJ mol⁻¹ nm⁻² and r_ij and r₀ = 0.3 nm are the current and equilibrium distances between oxygen atoms, respectively. The bundled interaction is introduced gradually to avoid any large forces due to bundling and to accommodate an easier reclustering. For this purpose, we introduce the function Γ, which has a similar form as the w function used in the AdResS scheme, i.e.

$$\mathit{\Gamma }(\mathbf{R})=\{\begin{array}{cc}\left\{\begin{array}{cc}\cos \left(\frac{\pi (R_{\mathrm{AT}}-\parallel \mathbf{R}-{\mathbf{R}}_0\parallel )}{2(R_{\mathrm{AT}}-R_B)}\right),& R_B<\parallel \mathbf{R}-{\mathbf{R}}_0\parallel <R_{\mathrm{AT}}\\ 1,& R_{\mathrm{AT}}<\parallel \mathbf{R}-{\mathbf{R}}_0\parallel <R_{\mathrm{SCG}}\\ 0,& \mathrm{otherwise}\end{array}\right\};& \mathrm{original}\\ \left\{\begin{array}{cc}\cos \left(\frac{\pi (R_{\mathrm{SCG}}-\parallel \mathbf{R}-{\mathbf{R}}_0\parallel )}{2(R_{\mathrm{SCG}}-R_B)}\right),& R_B<\parallel \mathbf{R}-{\mathbf{R}}_0\parallel <R_{\mathrm{SCG}}\\ 0,& \mathrm{otherwise}\end{array}\right\};& ‘\mathrm{revers}{\mathrm{e}}^{\prime }.\end{array}$$ 2.10

If all water molecules in the cluster are first nearest neighbours, the half-harmonic spring interaction acts between all oxygen pairs. However, special care is needed for higher mappings where the clusters also contain the second neighbours. For the 8-to-1 mapping, for example, we added the interaction between its four nearest oxygens and additionally to oxygen atoms within 0.35 nm thus ensuring that only nearest neighbours are connected and that the cluster is well interconnected, i.e. it does not form, for example, two separate clusters with four water molecules.

The computational cost of the SWINGER algorithm depends on the size of the clustering region. In particular, the algorithm’s complexity scales linearly with the number of water molecules considered in the clustering as the energy of the simulated annealing Monte Carlo involves only intracluster contributions. When the algorithm is executed, the measured computational time of the MD time step is increased by approximately $5\text{\%}$. However, since the SWINGER scheme is not initiated at every MD step but only at every Verlet list update, the overall increase in the computational load due to SWINGER itself is negligible [70].

3. Applications

Now, we showcase three multiscale simulations using a supramolecular coupling and employing the SWINGER algorithm. We demonstrate the successful coupling of SPC and MARTINI water models using a 4-to-1 mapping, where we first consider the pure solvent system [70] and later we immerse a protein into this multiscale solvation [71]. Apart from MARTINI, the SPC water model is also coupled to the DPD water model using 4- and 8-to-1 mappings, which unveils the basics of merging the MD and DPD particle-based methods [72].

3.1. Coupling all-atom and MARTINI solvents

We have performed the multiscale simulation of the SPC/MARTINI water model [70]. The set-up of the system is shown in figure 2a, i.e. we used the original implementation of AdResS and the resolution was changed along one dimension (x-coordinate). The mapping is 4-to-1 since in the MARTINI force field four water molecules are represented as a single particle. As reference systems, we have also performed the pure all-atom simulations with the SPC and bundled-SPC 1 [64] water models. The latter is a modified version of the SPC water model where half-harmonic bonds (equation (2.9) using Γ = 1) are added to oxygen atoms within clusters formed by four water molecules. Additionally, the oxygen–oxygen Lennard–Jones parameters are changed to reproduce the same density as the original SPC model.

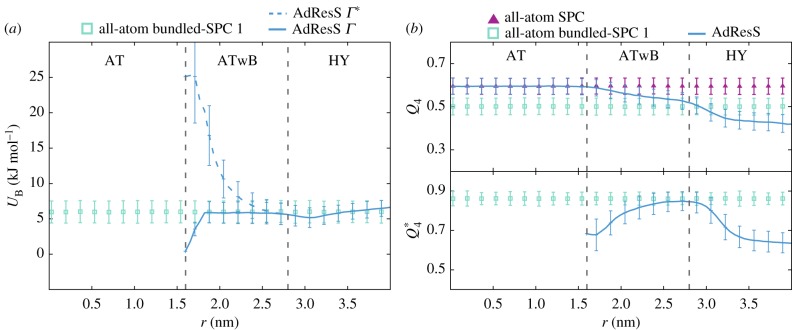
In figure 4a, we show the average bundling energy U_B profile (equation (2.9)) by discretizing the x-coordinate distances of the clusters to the centre of the AT domain (R₀) into bins and taking the average over clusters that fall into a corresponding bin. Comparing the AdResS and all-atom bundled-SPC results, we see that the clusters in the HY region have energies of comparable magnitude as in the bundled-SPC 1 water model. The results for AdResS are computed using Γ given by equation (2.10) and without the use of gradual bundling with Γ* = 1. These plots rationalize our choice of the smooth introduction of the bundling since U_B can be quite high when the clusters are formed and could lead to large forces. The reason why the energies in the cluster formation region are quite high even though the clustering is optimized is that the internal structure promoted by the bundling interaction is not inherent to the standard SPC water. The bundling encourages an internal structure of the bundles, where the water molecules are located at the four vertexes of the tetrahedron and the angle between two molecules and the bundle’s CoM is 109.5°. This ordering can be described with the order parameter $Q_4^{\ast }$ defined by

$$Q_4^{\ast }=1-\frac{3}{8}\sum _{i=1}^3\sum _{\hspace{0.17em}j=i+1}^4{(\cos {\varphi }_{ij}+\frac{1}{3})}^2,$$ 3.1

where i and j are the oxygen atoms of a distinct pair in a bundle and ϕ_ij the angle between the two oxygen atoms and the bundle’s CoM. Figure 4b shows $Q_4^{\ast }$ for the AdResS and reference all-atom bundled-SPC 1 simulations across different resolution regions. As the strength of the bundling is increased in the ATwB region, the promoted order also increases and reaches the value inherent to the bundled-SPC water model. In the HY region, the order parameter declines as a result of the resolution change.

Figure 4.

Average bundling energy of a bundle U_B (a) and tetrahedral order parameter Q₄ and $Q_4^{\ast }$ (b) with standard deviations along the direction of the resolution change (r is the distance from R₀ in direction of the x-coordinate). The AdResS profile is computed separately for Γ (equation (2.10)) and Γ * functions, where Γ * = 1 for R_B < ‖R − R₀‖ < R_SCG. The value of Q₄ = 1 corresponds to a perfect tetrahedral arrangement, whereas Q₄ = 0 describes an ideal gas. The results are plotted for the AdResS simulation and reference all-atom SPC and bundled-SPC 1 [64] water models. Resolution region boundaries are denoted with the vertical dashed lines. Adapted from [70]. (Online version in colour.)

The degree of three-body correlations in water is regularly measured with the tetrahedrality parameter Q₄ as the short-range structure in water is roughly tetrahedral due to the hydrogen-bond network. Q₄ is defined as [80]

$$Q_4=1-\frac{3}{8}\sum _{\hspace{0.17em}j=1}^3\sum _{k=i+1}^4{(\cos {\theta }_{ijk}+\frac{1}{3})}^2,$$ 3.2

where the sum runs over distinct pairs of the four closest neighbours of the reference water molecule i and θ_ijk is the angle between vectors r_ij and r_ik with j and k being the nearest neighbours molecules. The summation is normalized to give the value of 0 for the random distribution, while the value of 1 is obtained for the ideal tetrahedral arrangement. Contrary to the $Q_4^{\ast }$, which considers the arrangement of four water molecules within a bundle, the Q₄ considers five water molecules. For Q₄ = 1, the molecule i is in the centre of the tetrahedron while the four neighbouring molecules are located at the tetrahedron’s vertices. Thus, for bundled-SPC water, the Q₄ involves water molecules of the same cluster and also water molecules of neighbouring clusters. In the AT region, we reproduce the average value of Q₄ of the original all-atom SPC model. Owing to the presence of half-harmonic bonds between oxygen atoms within bundles, the local structure of water is, as expected, distorted in the ATwB and HY regions. In particular, we observe a continuous decrease of the Q₄ parameter as we move away from the AT region. At the boundary between the ATwB and HY regions, the average value of Q₄ is equal to the average tetrahedrality of the bundled-SPC water model (with changed Lennard–Jones parameters according to [64]). Analogously as in the case of $Q_4^{\ast }$, the Q₄ in the HY region also declines due to change of the resolution.

3.2. Biomolecule in a supramolecular solvent

AdResS-type multiscale simulations are particularly advantageous for systems where AT resolution is required only in spatially localized domains whereas a low-resolution level is sufficient for the rest of the system. Typically, such cases are biomolecules in a solvent. Here, we report on the multiscale simulation of an atomistic protein Trp-Cage solvated in a multiresolution water at ambient conditions [71]. The system is schematically illustrated in figure 1. The solvent’s level of representation depends on the distance from the protein’s CoM. For short distances, we resort to the SPC model to properly incorporate the specific hydrogen-bonding pattern. For the description of the water further away, we use the mesoscopic MARTINI SCG model. Water in that region exhibits bulk properties and the high-resolution representation is, therefore, not required. The total simulation domain is a cube with a 9.2 nm long edge containing 25 400 water molecules while the atomistic domain is a sphere with a radius of 2 nm.

The AdResS approach for the present protein–water system has been tested by carrying out the analysis of the structural and dynamic properties of the protein and the multiscale solvent (figure 5). First, we examine the normalized density profile (NDP), i.e. the local density divided by the bulk density, as a function of distance from the protein’s CoM. The NDPs, shown in figure 5a(i), are computed for the water oxygen atoms and MARTINI SCG beads. The AdResS and all-atom SPC NDPs for the water oxygen atoms match well and display similar standard deviations denoted by the error bars. As already mentioned in §2.1, to obtain flat density profile across the resolution region domains we deploy the thermodynamic force. The one used in this work that acts on clusters’ COMs in the HY region is shown in figure 5a(ii).

Figure 5.

Subplot (a) shows the NDP (with standard deviation denoted by the error bars) around the CoM of the protein for water oxygen atoms and MARTINI SCG beads and the thermodynamic (TD) force that acts on CoM of supramolecular bundles in the HY region. In subplot (b), we show the radius of gyration R_g as a function of the simulation time and root-mean-square fluctuations RMSF of the backbone atoms with respect to the crystal structure. The configuration snapshots were prior to RMSD calculation superimposed on the initial crystal structure (1L2Y.pdb). The error bars of RMSF denote the standard deviation computed by block averaging. The multiscale results are compared to all-atom SPC, all-atom bundelled SPC 1 and 2 solvations. Adapted with permission from [71]. Copyright 2018 American Chemical Society. (Online version in colour.)

Next, we plot, in figure 5b, the radius of gyration R_g and the root mean square fluctuations (RMSF) of the protein’s backbone atoms with respect to the crystal initial structure. We use these two properties to demonstrate that the multiscale simulation does not affect the structural properties of the protein. The obtained average values of AdResS simulation match the reference all-atom simulation. The structure of the protein is stable and the protein remains in the folded conformation throughout the simulation. This is true also for the all-atom simulations using the bundled-SPC 1 and 2 [64] water models even though these models were shown to lead to the partial unfolding for the coiled-coil dimer [69].

3.3. Coupling the MD and DPD methods: application to water

Lastly, we turn our attention to the coupling of two particle-based methods: the MD and DPD methods [72]. As a test case, we chose water at ambient conditions. Here, we first introduced the reverse implementation of AdResS and the resolution was changed along one dimension (x-coordinate). The set-up of the simulation is schematically shown in figure 2b. We used the SPC water model in the AT domain, and two different DPD models [81,82] in the SCG domain. DPD models deployed differ in their level of resolution. In the first (denoted as AdResS 4-to-1), each DPD particle represents four water molecules, while in the second (AdResS 8-to-1) it represents eight water molecules. Apart from the multiscale simulations, we performed additional pure all-atom MD and DPD simulations (denoted with MD, DPD 4, and DPD 8, respectively).

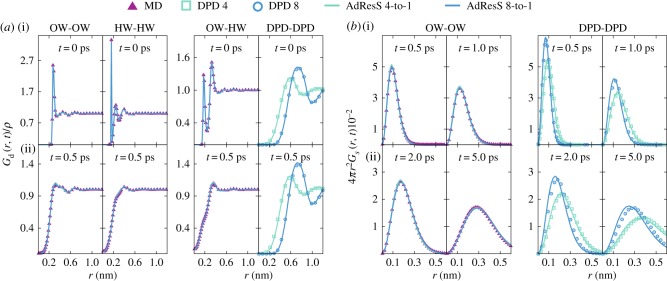
To validate this coupling, we computed the Van Hove function G(r, t), which gives information about the equilibrium structural and dynamical organization of water. For a homogeneous medium, the G(r, t) is given by

$$G(\mathit{r},t)=N^{-1}\sum _{i,j}⟨\delta (\mathit{r}+{\mathit{r}}_{\hspace{0.17em}j}(0)-{\mathit{r}}_i(t))⟩.$$ 3.3

The double sum is performed over all pairs of N particles in the system, r_i,j(t) is the position vector of the i, jth particle at time t, and the brackets 〈 · · · 〉 denote an average over time origins. By differentiating between the cases i = j and i ≠ j the G(r, t) can be separated into two terms, usually referred to as the self and distinct parts, respectively. Both parts are plotted in figure 6. The distinct part G_d gives the probability to find a different particle at position r at time t, given that there was a particle at the origin at time t = 0. For isotropic fluids, the G_d depends only on the scalar quantity r and can thus be simplified as

$$G_d(r,t)={(4\pi r^{2}N)}^{-1}\sum _{i\ne j}⟨\delta (r-|{\mathit{r}}_i(t)-{\mathit{r}}_{\hspace{0.17em}j}(0)|)⟩.$$ 3.4

At t = 0, the G_d reduces to the well-known radial distribution function G_d(r, 0) = ρg(r). The G_s(r, t), given by

$$G_s(r,t)={(4\pi r^{2}N)}^{-1}\sum _i⟨\delta (r-|{\mathit{r}}_i(t)-{\mathit{r}}_i(0)|)⟩,$$ 3.5

probes the equilibrium dynamics of a single particle in terms of its displacement from an initial position.

Figure 6.

Distinct part of the Van Hove function G_d(r, t)/ρ (a) at times 0.0 and 0.5 ps for the oxygen–oxygen (OW-OW), oxygen–hydrogen (OW-HW), hydrogen–hydrogen (HW-HW), and DPD-DPD case. Self-part of the Van Hove function 4πr² G_s(r, t) (b) for water oxygen (OW) atoms and DPD particles at times 0.5, 1.0, 2.0 and 5.0 ps. Adapted with permission from ref. [72]. Copyright 2017 American Institute of Physics (AIP) Publishing. (Online version in colour.)

The distinct part of Van Hove function was computed for all particle types at two different times: 0 and 0.5 ps (figure 6a(i) and (ii) plots, respectively), while the self-part of the Van Hove function G_s(r, t) is evaluated for the water oxygen atoms and DPD particles at times ranging from 0.5 to 5 ps (figure 6b). To make a relevant comparison with the reference simulations, the G_d(r, t) and G_s(r, t) are computed locally for the multiscale simulations, i.e. we only consider the molecules either in the AT or SCG domain. We then compare the Van Hove functions from the MD domain of the AdResS set-up with the corresponding functions from fully MD simulations. Likewise, the Van Hove functions from the SCG domain of the AdResS set-up are compared with the corresponding ones from fully DPD simulations. We find that for both AdResS simulations, all Van Hove functions match the reference results very well, thus demonstrating that, in equilibrium, not only the structural part but also the dynamical part of the water organization is fully preserved in both domains. Note that AdResS force interpolation scheme (equation (2.2)) preserves the local linear momentum by construction. The overall scheme with the included thermodynamic force also conserves the linear momentum, however, on the fluctuating hydrodynamics level.

4. Conclusion and outlook

This contribution presents a review of recent adaptive resolution approaches employing supramolecular coupling. The focus is on the applications employing the SWINGER algorithm that performs an on-the-fly clustering and thus allows for a direct coupling of AT and SCG models. In the presented examples, we coupled the SPC water model with two types of broadly used mesoscopic models: MARTINI and DPD. We discussed two supramolecular mappings, i.e. the 4-to-1 and 8-to-1 molecular mappings. From the methodological point of view, the difference between the two is in clustering only first neighbour molecules versus first and second neighbour molecules. The developed approaches were showcased for pure water systems and a protein–water system. In all cases, we demonstrate that our multiscale approach can faithfully reproduce and thus replace the all-atom simulations. Here, we would like to emphasize that our region of interest is the AT region and the main objective of the AdResS approach is to reproduce the full-blown atomistic simulation properties in the AT region. On the other hand, the agreement with the experimental observations critically depends on the appropriateness of the deployed AT model, which is beyond the scope of this paper.

The presented methodology could be applied to other mappings with a different number of solvent molecules per bundle provided that the mapping is low enough for the legitimacy of the particle-based description, e.g. models employed in [25]. It could also be extended to multi-site supramolecular models such as the PW and BMW models [67]. The all-atom bundled-SPC water model was already coupled with those models, therefore the extension to unconstrained water models should be fairly straightforward. On the other hand, the coupling of MD and DPD methods opens up a range of possible future directions that exploit the DPD method’s capabilities in encompassing the mesoscopic hydrodynamics. Our future efforts will be aimed towards this path and involve testing and applying here presented techniques for non-equilibrium fluid flow simulations.

The computational advantages of AdResS methodology compared to the all-atom simulations were studied in a recent paper by Junghans et al. [83]. In general, the speed-up mostly depends on the AT-to-CG mapping and the volume ratio between the AT and CG domain sizes where the upper bound of the speed-up is given by the fully coarse-grained simulation. Further computational enhancements can be achieved with load-balancing schemes such as heterogeneous domain decomposition approach, which can additionally increase the speed-up by a factor of 1.5 [84] and with multiple time-stepping algorithms [5]. For more detailed discussion on the computational gains, we refer the reader to [61,83].

Data accessibility

This article has no additional data.

Authors' contributions

All authors designed the research, analysed the data and wrote the manuscript. J.Z. performed the simulations. M.P. coordinated the project.

Competing interests

We declare we have no competing interests.

Funding

J.Z. acknowledges financial support as an ETH Zurich Fellow. S.J.M. acknowledges support from the EU via an ERC Advancedgrant COMP-MICR-CROW-MEM. M.P. acknowledges financial support from the Slovenian Research Agency(research core fundings no. P1-0002 and the project J1-7435).