Abstract
In this study the mechanism by which second-sphere residues modulate the structural and electronic properties of substrate-analogue complexes of the Fe-dependent superoxide dismutase (FeSOD) has been explored. Both spectroscopic and computational methods were used to investigate the azide (N3−) adducts of Fe3+SOD (N3-Fe3+SOD) and its Q69E mutant, as well as Fe3+-substituted MnSOD (N3-Fe3+(Mn)SOD) and its Y34F mutant. Electronic absorption, circular dichroism, and magnetic circular dichroism spectroscopic data reveal that the energy of the dominant N3− → Fe3+ ligand-to-metal charge transfer (LMCT) transition decreases in the order N3-Fe3+(Mn)SOD > N3-Fe3+SOD > Q69E N3-Fe3+SOD. Intriguingly, the LMCT transition energies correlate almost linearly with the Fe3+/2+ reduction midpoint potentials of the corresponding Fe3+-bound SOD species in the absence of azide, which span a range of ~1 V (see preceding paper). To explore the origin of this correlation, combined quantum mechanics/molecular mechanics (QM/MM) geometry optimizations were performed on complete enzyme models. The INDO/S-CI computed electronic transition energies satisfactorily reproduce the experimental trend in LMCT transition energies, indicating that the QM/MM optimized active-site models are reasonable. Density functional theory calculations on these experimentally validated active-site models reveal that the differences in spectral and electronic properties among the four N3− adducts arise primarily from differences in the hydrogen-bond network involving the conserved second-sphere Gln (mutated to Glu in Q69E FeSOD) and the solvent ligand. The implications of our findings with respect to the mechanism by which the second-coordination sphere modulates substrate-analogue binding as well as the catalytic properties of FeSOD are discussed.
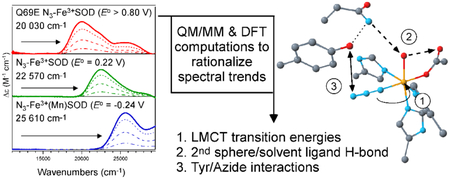
Graphical Abstract:
Spectroscopic and computational methods were used to study the azide (a substrate analogue) complexes of Fe3+ superoxide dismutase (Fe3+SOD), Fe3+-substituted Mn superoxide dismutase (Fe3+(Mn)SOD), Q69E Fe3+SOD, and Y34F Fe3+(Mn)SOD. While all species form a similar azide-Fe3+ adduct, the energy of the dominant azide-to-Fe3+ charge transfer transition varies considerably, correlating almost quantitatively with the corresponding Fe3+/2+ reduction potentials of the azide-free forms. Our results reveal that these spectral differences arise primarily from different hydrogen-bonding interactions between second-sphere residues and the Fe3+-bound solvent ligand.
1. Introduction
Superoxide dismutases (SODs) are metalloenzymes whose function is to protect biological systems from oxidative damage stemming from the superoxide radical anion (O2•–) that is generated by incomplete reduction of O2.1, 2 In the four known types of SODs, the active site contains either Fe, Mn, Ni, or Cu and Zn. The Fe-dependent SODs (FeSODs) are mostly found in prokaryotes, whereas the highly homologous Mn-dependent SODs (MnSODs) are present in both eukaryotes and prokaryotes. The Cu/ZnSOD and NiSOD, which are found in eukaryotes and some bacterial Streptomyces species, respectively, are structurally unrelated to each other as well as the Fe- and MnSODs.3–5 Like all SODs, the Fe- and Mn-dependent enzymes disproportionate O2•– into molecular oxygen and hydrogen peroxide using a ping-pong mechanism. In this proton-coupled electron-transfer process, the metal ion cycles between the +3 and +2 oxidation states (eq 1, where the metal ion M is either Fe or Mn).6, 7 To ensure rapid turnover, the reduction potential, Eº, of the enzyme must lie approximately halfway between the potentials associated with the conversion of O2•– to O2 and H2O2 (−330 mV and +890 mV vs. NHE at pH 7, respectively).8
| (1-a) |
| (1-b) |
FeSOD and MnSOD from Eschericia coli are closely related proteins with very similar amino-acid sequences and virtually identical active-site structures (Figure 1).9–17 In the resting state of each protein, the metal ion is in a trigonal bipyramidal coordination environment consisting of two His residues and an Asp residue in the equatorial plane, and a His residue and a solvent molecule (believed to be OH− and H2O in the M3+ and M2+ states, respectively) in the axial positions.15, 18 Despite their structural similarities, FeSOD and MnSOD display distinct metal specificities; that is, neither Fe-substituted MnSOD (Fe(Mn)SOD), nor Mn-substituted FeSOD (Mn(Fe)SOD) show significant catalytic activity at neutral pH.19–23 A straightforward explanation for this puzzling result was provided by Vance and Miller, who demonstrated that the M3+/2+ reduction potentials of the metal-substituted SODs are drastically altered from those of the native enzymes.24 Specifically, the E° of ~ –240 mV (vs. NHE) measured for Fe(Mn)SOD is depressed too much from FeSOD’s E° of ~20–220 mV to support substrate oxidation activity (eq 1-a).24 Conversely, the E° of >690 mV determined for Mn(Fe)SOD is sufficiently elevated from MnSOD’s E° of 290 mV to preclude O2•– reduction (eq 1-b).25
Figure 1.
Active-site models for FeSOD and MnSOD (prepared using PDB files 1ISA15 and 1VEW,17 respectively). In each case, the E. coli numbering scheme is used and hydrogen-bonding interactions are indicated by dashed lines.
The most striking structural difference between the FeSOD and MnSOD active sites is the different positioning of the second-sphere Gln, which corresponds to residue 69 in FeSOD and residue 146 in MnSOD (Figure 1). Gln69/146 is central to a hydrogen-bond network that also includes the metal-bound solvent molecule and Tyr34 (Figure 1, dashed lines).15, 26, 27 However the hydrogen bond between the Gln69/146 side chain and the coordinated solvent is much stronger in MnSOD than in FeSOD, which may explain the vastly different reduction potentials of the native and metal-substituted enzymes.24, 28 In support of this hypothesis, the Q69E FeSOD mutant, in which the hydrogen-bond donor Gln69 is replaced by a potential hydrogen-bond acceptor, has an E° of >600 mV and thus displays less than 1% of wild-type (WT) FeSOD activity.29–31 A quantitative exploration of the molecular basis for the different metal ion reduction potentials of WT FeSOD, Fe(Mn)SOD, and Q69E FeSOD is presented in the preceding paper.32
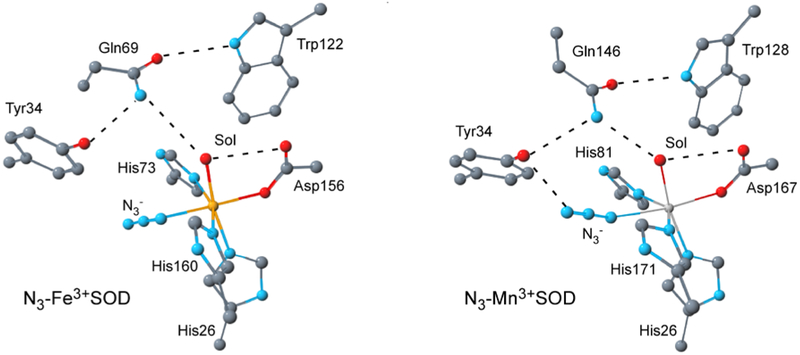
To obtain molecular-level insight into the reaction mechanisms employed by Fe- and MnSODs, it would be desirable to study the nature of the substrate/active-site interactions. However, the rate of O2•– dismutation by SODs approaches the diffusion-controlled limit, making it virtually impossible to trap any intermediates. Therefore, azide (N3−), a competitive inhibitor of SODs that possesses similar frontier orbitals and the same charge as O2•–, has been repeatedly used as a substrate analogue in mechanistic studies of SODs.7, 15, 27, 33–40 X-ray crystallographic data have revealed that in both Fe3+- and Mn3+SODs, azide binds between the two equatorial His residues to form a distorted octahedral complex.15, 41 However, the orientation of the N3– ligand in the corresponding azide adducts is strikingly different (Figure 2), despite the fact that the first coordination spheres of the resting enzymes are virtually identical (Figure 1). In N3-Mn3+SOD from T. thermophilus, azide forms a hydrogen bond with Tyr34, whereas in N3-Fe3+SOD, it points away from Tyr34 and into the substrate access channel. Since oxidation of the superoxide anion by the M3+SODs is believed to follow an inner-sphere mechanism, the different substrate analogue binding modes suggest that the actual substrate could also bind differently and experience different reaction barriers for electron transfer.
Figure 2.
Active-site models for N3-Fe3+SOD and N3-Mn3+SOD (derived from PDB files 1ISC and 1MNG, respectively).15 Hydrogen-bonding interactions are indicated by dashed lines.
In this study, we have characterized the azide-adducts of Fe3+SOD, Fe3+(Mn)SOD, and Q69E Fe3+SOD using electronic absorption (Abs), circular dichroism (CD) and magnetic circular dichroism (MCD) spectroscopies to explore how changes in the Gln69/146∙∙∙O(Sol) hydrogen bond influence the geometric and electronic properties of the active-site azide–Fe3+ complex. Furthermore, to evaluate the possibility that Tyr34 interacts with the azide ligand in N3-Fe3(Mn)SOD, we have also prepared and characterized the azide adduct of the Tyr34 → Phe mutant of Fe(Mn)SOD. As no X-ray crystal structures are available for the N3– complexes of Fe3+(Mn)SOD, Y34F Fe3+(Mn)SOD, and Q69E Fe3+SOD, complete enzyme models for these species were generated by carrying out combined quantum mechanics/molecular mechanics (QM/MM) geometry optimizations. The corresponding active-site models were validated on the basis of our spectroscopic data by using semi-empirical INDO/S-CI and density functional theory (DFT) computations. The results obtained in this combined spectroscopic/computational study provide significant new insight into the mechanism by which second-sphere amino-acids modulate the substrate analogue/active-site interactions in Fe3+SOD.
2. Experimental Section
2.1. Protein Samples.
WT FeSOD, Fe(Mn)SOD, and Q69E FeSOD were prepared according to published procedures,33,37 as outlined in the preceding paper.32 The gene for Y34F MnSOD was constructed by polymerase chain reaction using the megaprimer method.43 Both strands of the mutant gene were sequenced to confirm the presence of the desired mutation and to ascertain that no additional mutations had occurred. Y34F Fe(Mn)SOD was produced by in-vivo metal ion substitution wherein the over-expressing strain was cultured in minimal medium lacking Mn and supplemented with Fe, at low aeration. The resulting Y34F Fe(Mn)SOD contained predominantly Fe (>90%) and displayed ≤10% WT FeSOD activity at neutral pH, consistent with previous reports that Y34F Fe(Mn)SOD possesses low but significant activity.42 Protein and azide concentrations used in our experiments are given in the figure captions.
2.2. Spectroscopy.
Variable-temperature Abs, CD, and MCD spectra were recorded using a Jasco J-715 spectropolarimeter in conjunction with a superconducting magnetocryostat (Oxford Instruments SM-4000 8T). To eliminate contributions from the natural CD to the MCD signal, the difference was taken between data obtained with the magnetic field aligned parallel and anti-parallel to the light propagation axis. Variable-temperature variable-field (VTVH) MCD data were obtained by measuring the signal intensity as a function of applied magnetic field at 2, 4, 8, and 15 K. VTVH MCD data were analyzed using the software developed by Dr. Frank Neese (University of Bonn, Germany).46 All samples were in 50 mM potassium phosphate buffer (pH 7.0) with 55% (v/v) glycerol to ensure glass formation upon freezing.
2.3. Computations:
2.3.1. QM/MM geometry optimizations.
Input files for QM/MM geometry optimizations of entire protein subunits were generated from suitably chosen X-ray crystallographic coordinate files using the pdb2adf program developed by M. Swart (2002). For each model, the QM region included the metal ion, all first-sphere residues (including the coordinated solvent and exogenous azide ligand), along with Tyr34, Trp122 (Trp128 for Fe(Mn)SOD) and Gln69 (Glu69 and Gln146 for Q69E FeSOD and Fe(Mn)SOD, respectively). The MM region included all other atoms as well as the amide moieties of the amino acids that were treated at the QM level. The input coordinates for our N3-Fe3+SOD model were based on the corresponding X-ray crystallographic structure (PDB file 1ISC), using the subunit containing the 6-coordinate, azide-bound Fe3+ center.15 As no X-ray structural data are available for the other three species included in this study, the starting models for QM/MM geometry optimizations were generated as follows. In the case of N3-Fe3+(Mn)SOD, the structure of Fe(Mn)SOD (PDB file 1MMM)47 was used except that the exogenous OH– ligand occupying the sixth coordination site of the Fe center in one subunit was replaced by N3−. This initial structural model was also used for Y34F N3-Fe3+(Mn)SOD, with the modification that the phenol functionality of Tyr34 was replaced with an H atom. For both the N3-Fe3+(Mn)SOD and Y34F N3-Fe3+(Mn)SOD species, two input models were generated: one in which the azide ligand hydrogen bonds to residue 34 as in N3-Mn3+SOD and the other in which it is oriented away from residue 34 as in N3-Fe3+SOD (Figure 2). The Q69E N3-Fe3+SOD input coordinates were generated by substituting the Gln69 in the N3-Fe3+SOD structure (PDB file 1ISC) with a Glu residue, while the positions of all other atoms were initially kept unchanged (but subsequently refined in the full QM/MM geometry optimization).
All QM/MM calculations were performed on an ACE computer cluster using the Amsterdam Density Functional (ADF) 2005 software package,48–51 as described in the preceding paper.32 In short, the QM region was treated with spin-unrestricted DFT, an integration constant of 4.0, and the Vosko, Wilk, Nusair local density approximation52 along with the nonlocal gradient corrections of Becke53 and Perdew.54 For all atoms ADF basis set IV was used and the core orbitals were frozen through 1s (O, C, and N) and 2p (Fe). For the MM region, the AMBER95 molecular mechanics force field as implemented in the ADF program suite was employed,55 and the IMOMM/ADF scheme was used to describe the QM/MM interface.56 The feasibility of each QM/MM optimized protein structure was assessed by computing a quality score with the PROCHECK program.57
2.3.2. Calculation of ground-state and excited-state properties.
The truncated active-site models used for calculating ground-state and excited-state properties were derived from the QM/MM-optimized models and included the first coordination sphere plus the second-sphere residues Tyr34 (Phe34 for Y34F N3-Fe3+(Mn)SOD) and Gln69 (or Glu69 and Gln146 for Q69E N3-Fe3+SOD and N3-Fe3+(Mn)SOD, respectively). Both semi-empirical INDO/S-CI and single-point DFT calculations were performed using the ORCA 2.4 software package developed by Dr. Frank Neese (University of Bonn, Germany).58 ORCA utilizes the INDO/S model of Zerner and co-workers,59, 60 the valence shell ionization potentials and Slater–Condon parameters listed by Bacon and Zerner,61 and the standard interaction factors fpσpσ = 1.266 and fpπpπ = 0.585. Restricted open-shell Hartree-Fock (ROHF) SCF calculations were tightly converged on the S = 5/2 ground state, which served as the reference state for configuration interaction (CI) calculations. Electronic transition energies were calculated by including single-electron excitations among all doubly occupied MOs within 5 eV of the HOMO, the five singly occupied Fe 3d-derived MOs, and all virtual MOs within 3 eV of the HOMO. Ground-state properties were calculated by additionally including double excitations within the 44 highest-energy doubly occupied MOs, the 5 singly occupied MOs, and the 5 lowest-energy virtual MOs, as well as single-electron excitations among the 5 singly occupied MOs for the quartet states. Larger active spaces did not yield significantly different results.
For the DFT calculations performed in ORCA, Becke’s three parameter hybrid functional62, 63 for exchange and the correlation functional of Lee, Yang, and Parr64 were used. The SV(P) basis65 and SV/C auxiliary basis66 were used for all atoms except Fe, for which the TZVP basis67 was chosen. Isosurface plots of the MOs were generated using the gOpenMol program with an isodensity value of 0.04 a.u.68, 69
3. Results and Analysis
3.1.1. Resting states of Fe3+-bound SOD species.
The spectroscopic and electronic properties of Fe3+SOD, Q69E Fe3+SOD, and Fe3+(Mn)SOD have been discussed in detail in the preceding paper.32 In short, despite the fact that Q69E Fe3+SOD and Fe3+(Mn)SOD display negligible catalytic activities at neutral pH,30 their Abs, CD, and MCD spectra are remarkably similar to those obtained for Fe3+SOD. On the basis of this observation and the results obtained from DFT computations, we concluded that the variations in the second coordination spheres among these three Fe-bound SOD species do not notably perturb the electronic properties of the ferric center in their native states.
3.1.2. Spectroscopic characterization of N3−-bound species.
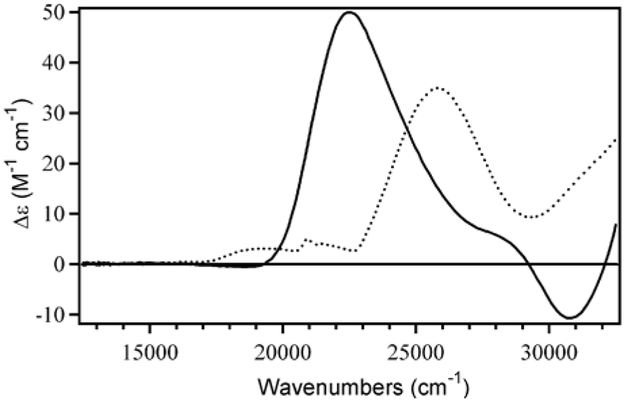
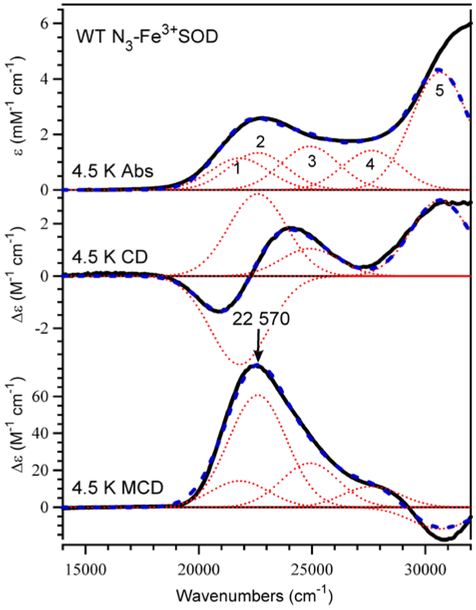
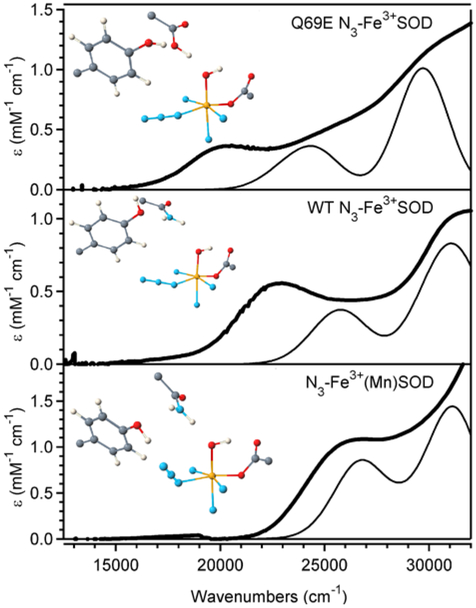
Due to their complementary nature, Abs, CD, and MCD spectroscopic techniques provide an excellent set of tools for probing changes in the protein active site upon azide binding. MCD spectroscopy is particularly well suited for studying paramagnetic species such as Fe3+SOD and N3-Fe3+SOD, because it offers a uniquely sensitive probe of the Fe3+ coordination environment, as exemplified by the large MCD spectral changes accompanying azide binding to Fe3+SOD (Figure 3). While the Fe3+SOD MCD spectrum is dominated by a positive feature at ~25 800 cm−1 attributed to an Asp → Fe3+ charge transfer (CT) transition,70 the MCD spectrum of N3-Fe3+SOD exhibits a new positive feature at 22 500 cm−1 (Figure 3).38 This MCD feature coincides with the dominant Abs band in the visible spectral region (Figure 4), which was previously assigned as an N3− → Fe3+ CT transition on the basis of resonance Raman studies.38 To determine the energies and oscillator strengths of the individual CT transitions of N3-Fe3+SOD, the Abs, CD, and MCD spectra were iteratively fit with a minimal number of Gaussian bands of constant width (Table 1 and Figure 4).
Figure 3.
MCD spectra of Fe3+SOD (dotted line) and N3-Fe3+SOD (solid line) at 4.5 K and 7 T.
Figure 4.
Abs (top), CD (center), and 7 T MCD (bottom) spectra of N3-Fe3+SOD at 4.5 K. Individual Gaussian bands (⋯) and their sums (---) obtained from an iterative fit are shown for each spectrum. Conditions: [Fe3+SOD] = 1.4 mM, [NaN3] = 100 mM; protein was in 50 mM phosphate buffer (pH 7.0) and 55% (v/v) glycerol.
Table 1.
Electronic transition energies (ν, in cm−1) and oscillator strengths (fexp) obtained from Gaussian deconvolutions of the Abs, CD, and MCD spectra of Q69E N3-Fe3+SOD, N3-Fe3+SOD, N3-Fe3+(Mn)SOD, and Y34F N3-Fe3+(Mn)SOD
| Q69E N3-Fe3+SOD | N3-Fe3+SOD | N3-Fe3+(Mn)SOD | Y34F N3-Fe3+(Mn)SOD | |||||
|---|---|---|---|---|---|---|---|---|
| banda | ν | fexp × 103 | ν | fexp × 103 | ν | fexp × 103 | ν | fexp × 103 |
| 1 | 17 700 | 6.02 | 21 800 | 8.28 | 24 600 | 6.77 | 23 640 | 8.28 |
| 2 | 20 000 | 6.77 | 22 600 | 9.78 | 25 680 | 5.27 | 25 150 | 3.99 |
| 3 | 22 700 | 9.78 | 24 900 | 12.0 | 27 400 | 12.0 | 27 370 | 9.78 |
| 4 | 25 950 | 15.8 | 27 622 | 10.5 | 30 350 | 20.3 | 30 500 | 20.0 |
| 5 | 29 500 | 29.4 | 30 642 | 31.6 | ||||
A full width at half maximum of 2914 cm−1 was used for all bands
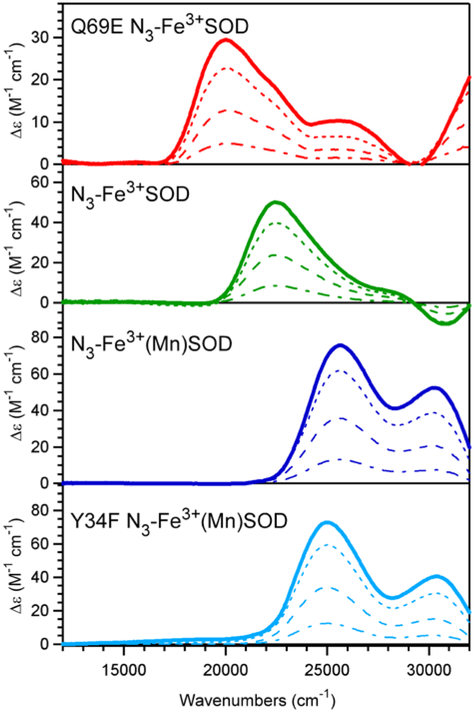
While the Asp → Fe3+ CT transition energies for Fe3+SOD, Fe3+(Mn)SOD, and Q69E Fe3+SOD are nearly identical (see preceding paper),32, 70 the N3− → Fe3+ CT transition energies for the corresponding azide adducts vary significantly (cf. Figure 4 and Figures S1 and S2, Supporting Information). Although in each case the MCD spectrum is dominated by a positively signed MCD feature, the corresponding peak maximum shifts from 22 570 cm−1 for N3-Fe3+SOD to 25 610 cm−1 for N3-Fe3+(Mn)SOD and to 20 030 cm−1 for Q69E N3-Fe3+SOD (Figure 5). Band positions and intensities obtained from Gaussian deconvolutions of the Abs, CD, and MCD spectra of Q69E N3-Fe3+SOD and N3-Fe3+(Mn)SOD are compared with those determined for WT Fe3+SOD in Table 1.
Figure 5.
Variable-field MCD spectra (bold line, 7 T; dashed lines, 3.5 T, 1.5 T, and 0.5 T) at 4.5 K of Q69E N3-Fe3+SOD, N3-Fe3+SOD, N3-Fe3+(Mn)SOD, and Y34F N3-Fe3+(Mn)SOD. Conditions are given in Figures 4 and S1-S3.
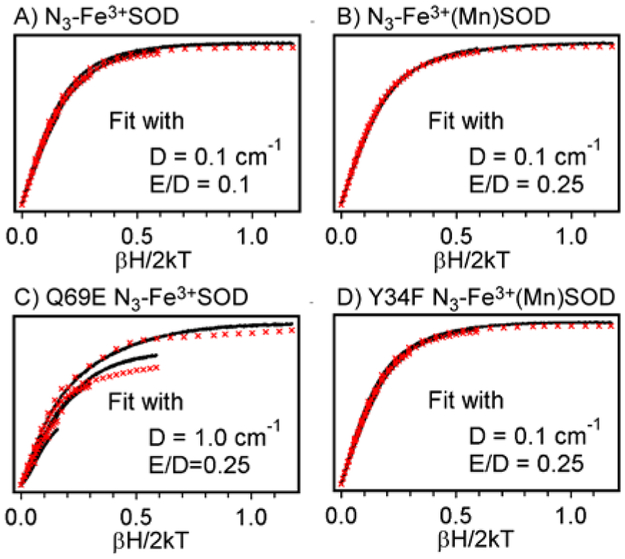
To determine whether structural differences within the Fe3+ coordination environment in N3-Fe3+SOD, N3-Fe3+(Mn)SOD, and Q69E N3-Fe3+SOD may be responsible for the striking variation in N3− → Fe3+ CT transition energies, variable-temperature variable-field (VTVH) MCD data were collected by measuring the MCD signal intensity at a given temperature and fixed wavelength as a function of magnetic field. Because the VTVH MCD data obtained for these three different azide adducts are qualitatively similar (Figure 6, panels A-C), a quantitative analysis was undertaken to disclose possible differences in electronic transition polarizations and ground-state properties.46 In this analysis, the zero-field splitting (ZFS) parameters D and E/D were systematically varied in fixed increments from –2.0 to 2.0 cm−1 and from 0 to 0.3, respectively, and for each set of parameters the three transition-moment products were fit to achieve the best agreement between experimental and calculated VTVH-MCD data. The goodness of fit was judged from the sum of the squares of the differences between the predicted and experimental data, χ2.
Figure 6.
VTVH MCD data obtained for (A) N3-Fe3+SOD at 22 570 cm−1, (B) N3-Fe3+(Mn)SOD at 25 610 cm−1, (C) Q69E N3-Fe3+SOD at 20 030 cm−1, and (D) Y34F N3-Fe3+(Mn)SOD at 25 000 cm−1. In each case, a representative fit of the experimental data is included for comparison (data shown as red x’s).
For N3-Fe3+SOD, the best fits (χ2< 0.10) of the VTVH MCD data were obtained with ∣D∣ < 0.5 cm−1 and E/D = 0.10 – 0.25. For positive D values, the fits required that the transition be polarized predominantly (42 to 100%) along the x-axis, whereas fits performed with negative D values predicted an almost exclusively z-polarized transition. Given that our INDO/S-CI calculations for this species predict that the Fe–azide bond vector is oriented roughly along the x-axis (vide infra), only the polarizations obtained with positive D values are consistent with our assignment of the dominant MCD feature to an N3− → Fe3+ CT transition. A similar analysis for N3-Fe3+(Mn)SOD revealed that the VTVH MCD data are best fit (χ2 < 0.055) with ∣D∣ < 0.3 cm−1 and E/D = 0.10 – 0.30, where the fitted transition polarizations again required that D be positive. Similar results were also obtained in our VTVH MCD data analysis for Q69E N3-Fe3+SOD, ∣D∣ < 2.00 cm−1 and E/D = 0.15 – 0.30, though in this case the quality of the best fits was slightly inferior (χ2 < 1.7). The fact that our VTVH MCD data fits for N3-Fe3+SOD, N3-Fe3+(Mn)SOD, and Q69E N3-Fe3+SOD yielded similar transition polarizations and only small differences in E/D values indicates that differences in the coordination environment of the Fe3+ ion are minor and, thus not a major contributor to the large differences in N3- → Fe3+ CT transition energies.
To explore whether the hydrogen bond between the terminal N atom of azide and Tyr34 observed in the X-ray crystal structure of N3-Mn3+SOD from T. thermophilus (Figure 2)15, 39 is still present in the Fe-substituted enzyme, we have also investigated the azide complex of the Y34F Fe3+(Mn)SOD mutant. The Abs spectrum of this species has been reported previously and was found to be similar to that of N3-Fe3+(Mn)SOD.42 However, our quantitative analysis of the Abs, CD, and MCD spectra of Y34F N3-Fe3+(Mn)SOD (Figure S3) revealed that the N3− → Fe3+ CT transitions are actually red-shifted by as much as 1000 cm−1 from those of N3-Fe3+(Mn)SOD (Table 1), thus suggesting that the Tyr34 residue has significant influence over the azide-Fe3+ bonding interaction. Yet the VTVH MCD data of these two species (Figure 6, panels B and D) are nearly superimposable, ruling out any significant perturbations to the active-site structure upon Tyr34 → Phe mutation.
3.2. Computational Results.
3.2.1. QM/MM geometry optimizations.
To understand the origins of the large shift of N3− → Fe3+ CT transitions energies, complete enzyme models for all four azide adducts investigated were generated via QM/MM geometry optimizations (see Experimental Section). The corresponding active-site structures were then used in single-point DFT computations to obtain a quantitative electronic structure description for each species. To assess the reliability of this approach, it is useful to compare the QM/MM optimized and experimentally determined (PDB file 1ISC)15 structures of N3-Fe3+SOD (Table 2). This comparison reveals that all experimental Fe–ligand bond lengths and angles are remarkably well reproduced in our computational model, the largest differences being a decrease in the Fe–O(Sol) bond length by 0.11 Å and a slight change in the orientation of the azide ligand. Somewhat larger differences are observed within the hydrogen-bonding network, most notably in the O(Tyr)∙∙∙N(Gln) hydrogen-bond distance. However, it should be noted that the position of Tyr34 is somewhat ill-defined crystallographically (as indicated by its higher B-factor relative to the active-site ligands, Gln69, and Trp122), presumably due to its interaction with, and the incomplete (~50%) occupancy of, azide in the crystal structure.15
Table 2.
Bond lengths and bond angles for the N3-Fe3+SOD active site as determined by X-ray crystallography (PDB file 1ISC) as well as for the QM/MM optimized structures of N3-Fe3+SOD, Q69E N3-Fe3+SOD, N3-Fe3+(Mn)SOD, and Y34F N3-Fe3+(Mn)SOD
| 1ISCa | N3-Fe3+SOD | Q69E N3-Fe3+SOD | N3-Fe3+(Mn)SOD | Y34F N3-Fe3+(Mn)SOD | |
|---|---|---|---|---|---|
| Bond lengths (Å) | |||||
| Fe–N(azide) | 2.12 | 2.13 | 2.11 | 2.19 | 2.11 |
| Fe–O (Sol) | 2.00 | 1.89 | 1.97 | 1.89 | 1.90 |
| Fe–O (Asp) | 2.03 | 2.01 | 1.98 | 1.98 | 2.01 |
| Fe–N (His26) | 2.22 | 2.28 | 2.31 | 2.21 | 2.21 |
| Fe–N (His160) | 2.16 | 2.23 | 2.19 | 2.22 | 2.25 |
| Fe–N (His73) | 2.13 | 2.14 | 2.14 | 2.22 | 2.24 |
| H-bond distances (Å) | |||||
| O(Sol)⋯N(Gln)/O(Glu) | 3.29 | 3.27 | 2.65 | 2.82 | 2.75 |
| O(Sol)⋯O(Asp) | 3.15 | 2.91 | 3.35 | 2.78 | 2.78 |
| O(Tyr)⋯N(Gln)/O(Glu) | 3.04 | 3.58 | 3.06 | 3.12 | |
| O(Gln/Glu)···N(Trp) | 3.08 | 2.83 | 2.81 | 2.83 | 2.90 |
| Bond angles (deg) | |||||
| Fe–N–N | 117 | 126 | 125 | 121 | 123 |
| N3–Fe–O(Sol) | 115 | 94 | 100 | 71 | 71 |
| His–Fe–His | 161 | 161 | 163 | 161 | 163 |
Parameters taken from PDB file 1ISC, ref 6.
The integrity of the QM/MM optimized models for the other three azide complexes for which X-ray crystallographic data are not yet available was assessed using the PROCHECK program suite, which computes a score based on the overall quality of the protein structure.57 For our N3-Fe3+SOD, Q69E N3-Fe3+SOD, N3-Fe3+(Mn)SOD, and Y34F N3-Fe3+(Mn)SOD models, the computed scores are 0.08, −0.26, −0.16, and −0.16, respectively, and thus clearly within the acceptable range (i.e., greater than –0.5).
3.2.2. Validation of QM/MM optimized active-site models.
In order to assess the feasibility of our QM/MM optimized active-site models, the INDO/S-CI method was employed to calculate the ZFS parameters and electronic transition energies and intensities for each species. As shown in Figure 7, the INDO/S-CI calculations nicely reproduce the trend in N3− → Fe3+ CT transition energies observed experimentally, predicting a steady red-shift of the dominant Abs feature from N3-Fe3+(Mn)SOD to N3-Fe3+SOD and Q69E N3-Fe3+SOD. Also in accordance with our spectroscopic data, the INDO/S-CI method predicts nearly identical D-tensor orientations for all four models, in each case orienting the z- and x-axes roughly along the O(Sol)–Fe–N(His) and N3–Fe–O(Asp) bond vectors, respectively. Further, the E/D values predicted for the Q69E N3-Fe3+SOD and N3-Fe3+(Mn)SOD models, 0.32 and 0.26, respectively, are substantially larger than the value of 0.10 computed for N3-Fe3+SOD, in agreement with the less rhombic EPR spectrum reported for the WT enzyme and consistent with the ranges of E/D values obtained from our VTVH MCD data analysis presented above.31, 33, 37, 40, 42
Figure 7.
Experimental (bold lines) and INDO/S-CI calculated (thin lines) Abs spectra for Q69E N3-Fe3+SOD, N3-Fe3+SOD, and N3-Fe3+(Mn)SOD; the simulated Abs spectra were uniformly scaled down by a factor of 2.25. Models used for the INDO/S-CI calculations are shown next to their respective Abs spectrum.
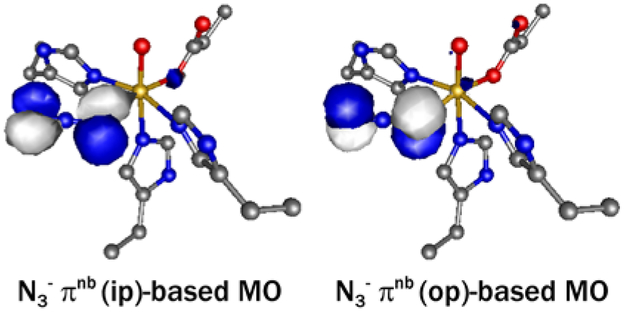
The good agreement between the INDO/S-CI predicted and experimentally determined spectroscopic parameters indicates that our QM/MM optimized active-site models are reasonable and warrants the use of the INDO/S-CI computational results (Table 3) for assigning individual transitions contributing to the experimental Abs spectra. Inspection of Table 3 reveals that the donor molecule orbital (MO) involved in the N3− → Fe3+ CT transitions responsible for the lower energy, broad Abs feature is primarily composed of the azide π non-bonding (πnb) MO that lies in the Fe–azide plane (in plane, ip) (Figure 8). Conversely, the donor MO for the N3− → Fe3+ CT transitions at higher energy is predominantly composed of the azide πnb MO that is oriented perpendicular to the Fe–azide plane (out of plane, op). Thus, the dominant contributors to the Abs features at lower and higher energy, as suggested by our INDO/S-CI results, are the N3− πnb(ip) → Fe3+ 3dx2-y2 CT transition and N3− πnb(op) → Fe3+ 3dz2 CT transition, respectively.
Table 3.
INDO/S-CI calculated N3− → Fe3+ CT transition energies (cm−1) and oscillator strengths (f×103, in parentheses) for Q69E N3-Fe3+SOD, N3-Fe3+SOD, N3-Fe3+(Mn)SOD, and Y34F N3-Fe3+(Mn)SOD
| Q69E N3-Fe3+SOD | N3-Fe3+SOD | N3-Fe3+(Mn)SOD | Y34F N3-Fe3+(Mn)SOD | |
|---|---|---|---|---|
| N3− πnb(ip) → Fe3+ 3d | ||||
| 22 183 (1.4) | 24 657 (4.6) | 25 526 (3.5) | 24 187 (3.2) | |
| 22 891 (1.5) | 25 123 (8.0) | 26 507 (23)a | 25 315 (33)a | |
| 23 146 (17) | 25 791 (7.9) | 26 761 (8.2) | 25 433 (3.9) | |
| 24 655 (42)a | 25 932 (44)a | 26 938 (27)a | 25 651 (3.9) | |
| 26 535 (1.4) | 29 043 (7.0) | 31 011 (70) | ||
| N3− πnb(op) → Fe3+ 3d | ||||
| 28 249 (2.1) | 28 885 (1.2) | 29 019 (14) | 28 087 (1.6) | |
| 29 108 (42) | 30 299 (67)b | 29 214 (7.1) | 28 303 (15) | |
| 29 885 (140)b | 31 516 (120)b | 29 801 (1.8) | 30 212 (20) | |
| 31 506 (52)b | 30 818 (157)b | |||
| Asp → Fe3+ 3dx2-y2 | 39 503 (28) | 38 166 (26) | 36 406 (22) | 36 769 (16) |
Assigned as N3− πnb(ip) → Fe3+ 3dx2-y2 CT transition
Assigned as N3− πnb(op) → Fe3+ 3dz2 CT transition
Figure 8.
Isosurface plots of the azide πnb-based occupied spin-down MOs, obtained from a spin-unrestricted DFT calculation on the N3-Fe3+SOD active-site model.
As noted in section 3.1.2, the Tyr34 → Phe mutation in Fe3+(Mn)SOD causes a substantial red-shift of the N3− → Fe3+ CT transitions in the corresponding azide adducts (Figure 5 and Table 2). The INDO/S-CI computational results for our active-site models of N3-Fe3+(Mn)SOD and its Y34F variant reproduce this red-shift (Figure 7 and Table 3). Interestingly, in the INDO/S-CI computed Abs spectrum for a model of N3-Fe3+(Mn)SOD with the azide oriented away from the Tyr34 residue (data not shown), the N3− → Fe3+ CT transitions now occur at nearly the same energies as in the calculated spectrum for Y34F N3-Fe3+(Mn)SOD. This result supports the proposal that the elimination of the O(Tyr34)∙∙∙N(azide) hydrogen-bond interaction contributes to the red-shift of the N3− → Fe3+ CT transitions from WT to Y34F N3-Fe3+(Mn)SOD.
The INDO/S-CI calculations also provide an estimate of the Asp → Fe3+ CT transition energies that cannot be determined experimentally for the azide adducts because of the strong background absorption by the protein matrices. For the azide-free forms of all four Fe3+-bound SOD species investigated, an intense Asp → Fe3+ CT transition is predicted to occur below 30 000 cm−1 with little variation in energy from one species to another, as observed experimentally.32, 70 In the azide-bound species, the INDO/S-CI computed energy of the analogous Asp → Fe3+ CT transition increases to >34 000 cm−1 due to the large destabilization of the Fe3+ 3d-based MOs upon azide binding. Moreover, the calculated energies for this transition now show a large variation from one species to another, increasing considerably from N3-Fe3+(Mn)SOD and Y34F N3-Fe3+(Mn)SOD to N3-Fe3+SOD and Q69E N3-Fe3+SOD (Table 3). Thus, our calculations suggest that azide binding perturbs the Fe3+ center of each species in a distinct way.
3.2.3. Comparison of QM/MM optimized active-site models.
Because the QM/MM optimized active-site models successfully reproduce the spectral trends observed experimentally, they provide an excellent basis for exploring key structural differences between the four different azide adducts investigated (Table 2). First, from N3-Fe3+SOD to N3-Fe3+(Mn)SOD the optimized Fe–N(azide) bond length increases by 0.06 Å because in the latter the azide ligand forms a hydrogen bond to Tyr34; elimination of this hydrogen-bond interaction via Tyr34 → Phe mutation leads to a shortening of the Fe–N(azide) bond by 0.08 Å. Second, upon substitution of Gln69 in N3-Fe3+SOD by the Glu residue in Q69E N3-Fe3+SOD, the hydrogen-bond distance between residue 69 and coordinated solvent decreases by over 0.60 Å, consistent with the fact that the carboxylic acid functionality of Glu69 is a much stronger hydrogen-bond donor than the –NH2 group of Gln69. Significantly shorter O(Sol)∙∙∙N(Gln) hydrogen-bond distances than in N3-Fe3+SOD are also predicted for N3-Fe3+(Mn)SOD and its Y34F variant (Table 2), as expected on the basis of the closer proximity of the Gln residue to the metal ion in MnSOD than in FeSOD.32 Third, the strong hydrogen-bond interaction between Glu69 and the solvent ligand in Q69E N3-Fe3+SOD results in a lengthening of the Fe–O(Sol) bond by 0.08 Å relative to N3-Fe3+SOD. Lastly, while the optimized Fe–O(Asp) bond lengths are similar in all four active-site models (Table 2), the O(Sol)∙∙∙O(Asp) hydrogen-bond distances vary considerably, decreasing in the order Q69E N3-Fe3+SOD > N3-Fe3+SOD > N3-Fe3+(Mn)SOD ≈ Y34F N3-Fe3+(Mn)SOD. The long O(Sol)∙∙∙O(Asp) hydrogen bond predicted for Q69E N3-Fe3+SOD can again be rationalized in terms of a particularly strong O(Sol)∙∙∙O(Glu) hydrogen-bond interaction that exists in this model, which effectively pulls the solvent ligand away from both the Fe3+ ion and the Asp156 residue to create a more water-like axial ligand. Conversely, the decreased O(Sol)∙∙∙O(Asp) hydrogen-bond length in N3-Fe3+(Mn)SOD can be attributed to the closer proximity of the Gln146 residue to the solvent ligand, which allows the latter to move closer to Asp167.71
3.2.4. DFT computed electronic-structure descriptions.
While INDO/S-CI computations were successfully used for validating our QM/MM optimized active-site models and for developing specific Abs band assignments, they did not permit a direct evaluation of key geometric and electronic differences contributing to the large variation in the corresponding N3− → Fe3+ CT transition energies among the four azide adducts investigated. To overcome this shortcoming, DFT calculations were performed on all four QM/MM optimized active-site models, where in each case the computed electronic-structure description was validated on the basis of our spectroscopic data. Specifically, the energies of the N3− πnb(ip) → Fe 3dx2-y2 and N3− πnb(op) → Fe 3dz2 CT transitions that, according to our INDO/S-CI computations, are responsible for the dominant features in the experimental Abs spectra of the azide-bound Fe3+SOD species (Table 3), were calculated by DFT using the method developed by Slater.72 In this approach, half of an electron is excited from the donor MO to the acceptor MO and the difference in MO energies after SCF convergence is taken as the transition energy. The results obtained using the DFT/Slater method (Table 4) adequately reproduce the trend in N3− → Fe3+ CT transition energies observed experimentally, suggesting a substantial red-shift of both the N3− πnb(ip) → Fe 3dx2-y2 and N3− πnb(op) → Fe 3dz2 CT transitions from N3-Fe3+(Mn)SOD to N3-Fe3+SOD and Q69E N3-Fe3+SOD. Hence, a more detailed analysis of the DFT computed electronic-structure descriptions is justified.
Table 4.
DFT predicted N3− → Fe3+ CT transition energies (cm−1) obtained using the method developed by Slater
| Q69E N3-Fe3+SOD | N3-Fe3+SOD | N3-Fe3+(Mn)SOD | Y34F N3-Fe3+(Mn)SOD | |
|---|---|---|---|---|
| N3− πnb(ip) → Fe 3dx2-y2 | 26 114 | 26 945 | 27 542 | 27 236 |
| N3− πnb(op) → Fe 3dz2 | 28 607 | 30 373 | 31 445 | 30 082 |
Because the occupied Fe3+ 3d-based spin-up MOs are considerably stabilized in energy by spin polarization and thus contain significant ligand orbital character, the dominant metal–ligand bonding interactions were inferred from the compositions of the unoccupied Fe 3d-based spin down MOs. The DFT-computed relative energies and compositions of the occupied azide πnb- and unoccupied Fe3+ 3d-based spin-down MOs for the QM/MM-optimized active-site models are listed in Table 5, and the relevant portions of the corresponding MO diagrams are shown in Figure 9.73 For each species the splitting pattern of the Fe3+ 3d-based spin-down MOs reflects the distorted octahedral ligand-field environment experienced by the metal center. The azide πnb(op)- and πnb(ip)-based MOs are considerably split in energy due, primarily, to the fact that the former is only π-bonding, while the latter is pseudo σ-bonding with respect to the Fe–azide bond (Figure 8).
Table 5.
DFT-computed relative energies and compositions (%) of the occupied azide πnb- and unoccupied Fe3+ 3d-based spin-down MOs for the QM/MM optimized active-site models of Q69E N3-Fe3+SOD, N3-Fe3+SOD, N3-Fe3+(Mn)SOD, and Y34F N3-Fe3+(Mn)SOD
| Fe 3d orbitals |
Azide πnb |
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| MOa | E (eV)b | occc | xy | yz | xz | x2-y2 | z2 | px | py | pz |
| Q69E N3-Fe3+SOD | ||||||||||
| Fe 3dz2 | 4.606 | 0 | 0 | 0 | 0 | 8 | 62 | 2 | 0 | 2 |
| Fe 3dx2-y2 | 4.419 | 0 | 0 | 1 | 14 | 53 | 4 | 2 | 1 | 1 |
| Fe 3dxz | 3.371 | 0 | 5 | 0 | 62 | 16 | 1 | 0 | 5 | 0 |
| Fe 3dyz | 3.331 | 0 | 1 | 82 | 0 | 1 | 0 | 0 | 0 | 1 |
| Fe 3dxy | 3.263 | 0 | 79 | 1 | 3 | 2 | 1 | 0 | 0 | 1 |
| N3− πnb(op) | 0.235 | 1 | 0 | 0 | 3 | 1 | 0 | 1 | 20 | 9 |
| N3− πnb(ip) | 0 | 1 | 0 | 0 | 2 | 1 | 2 | 11 | 8 | 11 |
| N3-Fe3+SOD | ||||||||||
| Fe 3dz2 | 4.954 | 0 | 0 | 0 | 22 | 1 | 43 | 0 | 0 | 0 |
| Fe 3dx2-y2 | 4.516 | 0 | 22 | 2 | 5 | 41 | 1 | 2 | 0 | 0 |
| Fe 3dxz | 3.644 | 0 | 2 | 9 | 41 | 7 | 27 | 0 | 0 | 1 |
| Fe 3dxy/dyz | 3.551 | 0 | 30 | 33 | 2 | 11 | 4 | 0 | 0 | 0 |
| Fe 3dxy/dyz | 3.427 | 0 | 28 | 36 | 6 | 16 | 2 | 0 | 0 | 0 |
| N3− πnb(op) | 0.292 | 1 | 0 | 0 | 2 | 1 | 1 | 3 | 4 | 40 |
| N3− πnb(ip) | 0 | 1 | 0 | 0 | 1 | 4 | 0 | 12 | 33 | 1 |
| N3-Fe3+(Mn)SOD | ||||||||||
| Fe 3dz2 | 5.234 | 0 | 0 | 0 | 0 | 17 | 50 | 0 | 0 | 0 |
| Fe 3dx2-y2 | 4.627 | 0 | 3 | 0 | 0 | 56 | 13 | 1 | 0 | 0 |
| Fe 3dxz | 3.831 | 0 | 0 | 2 | 86 | 0 | 1 | 0 | 0 | 0 |
| Fe 3dyz | 3.736 | 0 | 7 | 67 | 3 | 1 | 0 | 0 | 0 | 0 |
| Fe 3dxy | 3.63 | 0 | 75 | 8 | 0 | 2 | 1 | 0 | 0 | 0 |
| N3− πnb(op) | 0.268 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 23 | 16 |
| N3− πnb(ip) | 0 | 1 | 1 | 0 | 0 | 1 | 2 | 28 | 4 | 9 |
| Y34F N3-Fe3+(Mn)SOD | ||||||||||
| Fe 3dz2 | 5.134 | 0 | 0 | 1 | 0 | 8 | 57 | 0 | 0 | 0 |
| Fe 3dx2-y2 | 4.564 | 0 | 1 | 1 | 0 | 66 | 7 | 1 | 0 | 0 |
| Fe 3dxz | 3.757 | 0 | 0 | 4 | 83 | 0 | 1 | 0 | 0 | 1 |
| Fe 3dyz | 3.633 | 0 | 6 | 68 | 5 | 2 | 0 | 0 | 0 | 0 |
| Fe 3dxy | 3.523 | 0 | 78 | 6 | 0 | 1 | 1 | 1 | 1 | 0 |
| N3− πnb(op) | 0.373 | 1 | 2 | 0 | 2 | 0 | 0 | 0 | 29 | 16 |
| N3− πnb(ip) | 0 | 1 | 0 | 2 | 0 | 1 | 1 | 26 | 4 | 11 |
MOs are labeled according to their principal orbital contributors.
All MO energies are given relative to the energy of the corresponding πnb(ip)-based MO.
MO occupancies.
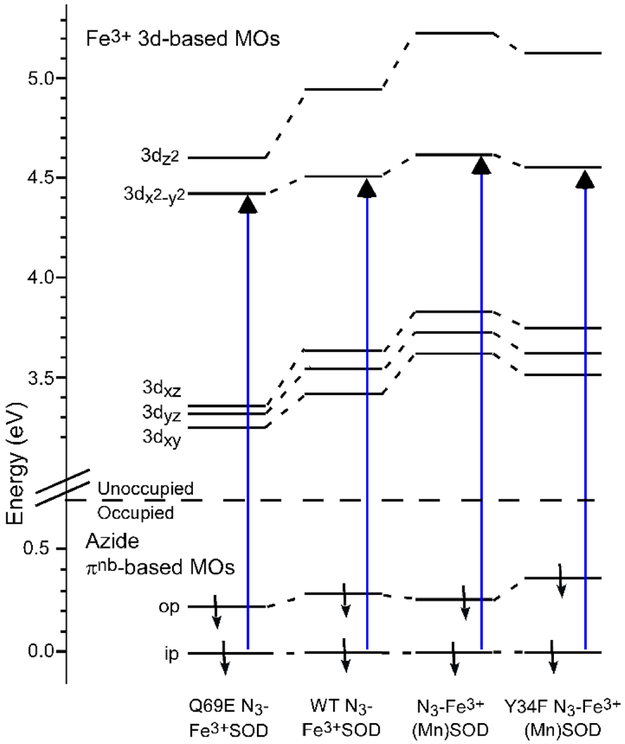
Figure 9.
Relevant portions of the DFT computed MO diagrams for Q69E N3-Fe3+SOD, N3-Fe3+SOD, N3-Fe3+(Mn)SOD, and Y34F N3-Fe3+(Mn)SOD. Only the spin-down MOs are shown, and their energies are given relative to that of the corresponding azide πnb(ip)-based MO. In each case, the N3− → Fe3+ CT transition responsible for the dominant MCD feature in the visible/near-UV spectral region (Figure 5) is indicated by an arrow.
The most notable feature of the DFT-computed MO diagrams in Figure 9 is that the energetic separation of the Fe3+ 3d-based MOs from the azide πnb(ip)-derived MO increases steadily from Q69E N3-Fe3+SOD to N3-Fe3+SOD and N3-Fe3+(Mn)SOD, from where it decreases slightly to Y34F N3-Fe3+(Mn)SOD. This prediction concurs nicely with the trend in N3− → Fe3+ CT transition energies observed experimentally (Figure 5). The computed MO diagrams also disclose a marked increase in the splitting between the Fe 3dz2- and 3dx2-y2-based MOs along the same series. This result can be understood in terms of the large variation in the σ-donor strength of the Fe3+-bound solvent ligand, as discussed in section 3.2.3. In N3-Fe3+(Mn)SOD the solvent ligand has predominant OH– character and interacts strongly with the Fe3+ center, whereas in Q69E N3-Fe3+SOD it is more H2O-like and effectively pulled away from the Fe3+ ion.
4. Discussion
Because of their surprisingly distinct metal requirements for catalytic activity, the highly homologous Fe- and MnSODs have fascinated researchers for several decades. Though numerous other explanations had previously been offered, we have recently demonstrated that the lack of activity displayed by the metal-substituted enzymes can be rationalized in terms of the fact that the two protein matrices impose distinct reduction potentials on their active site metal ion by means of a conserved hydrogen-bonding network that includes the Fe-bound solvent molecule, Gln69 (corresponding to Gln146 in E. coli MnSOD), Trp122 (Trp128 in Fe(Mn)SOD) and Tyr34 (Figure 1).24, 25, 29, 30 In accordance with this hypothesis, alterations in the orientation and identity of the Gln69 residue of FeSOD led to changes in the Fe3+/2+ reduction potential by as much as ~± 500 mV, as illustrated by Fe(Mn)SOD and the Q69E FeSOD mutant.24, 25, 30 While a detailed investigation of the effect of Gln69 on the E° of FeSOD is the subject of the preceding paper, the present study was aimed at elucidating the mechanism by which this second-sphere residue modulates substrate analogue binding in Fe3+-bound SOD species. Below, key findings from our spectroscopic and computational studies of N3-Fe3+SOD, N3-Fe3+(Mn)SOD, Q69E N3-Fe3+SOD, and Y34F N3-Fe3+(Mn)SOD are discussed and their implications for the catalytic mechanism of FeSOD are explored.
4.1. Nature of the different azide-bound Fe3+SOD species.
Despite the fact that the reduction potentials of Fe3+SOD, Fe3+(Mn)SOD, and Q69E Fe3+SOD span a range of ~1 V,24, 30 the Abs, CD, and MCD spectra of these three species are remarkably similar; all exhibiting an Asp → Fe3+ CT transition centered at ~25 800 cm−1. Consistent with this finding, DFT calculations performed on active-site models of Fe3+SOD, Fe3+(Mn)SOD, and Q69E Fe3+SOD yielded virtually identical electronic-structure descriptions.32 However, as the Asp → Fe3+ CT transition energies do not necessarily correlate directly with the reaction barrier for electron transfer between substrate and Fe3+, the use of a substrate analogue such as azide provides a better means for probing the energies and natures of the relevant MOs under turnover conditions. Upon the addition of N3− to the Fe3+-bound SOD species, a new feature attributed to a N3− → Fe3+ CT transition appears in the corresponding MCD spectra. Interestingly, the energy of this feature varies by more than 5000 cm−1 among the different SOD species (Table 1), even though their active sites were shown to be structurally similar on the basis of VTVH MCD data. Specifically, the dominant N3− → Fe3+ CT transition is red shifted from N3-Fe3+(Mn)SOD to N3-Fe3+SOD and Q69E N3-Fe3+SOD, which correlates nicely with the trend observed for the Fe3+/2+ reduction potentials of the corresponding Fe3+-bound SOD species in the absence of azide.
The DFT computed MO descriptions for our active-site models of N3-Fe3+SOD, N3-Fe3+(Mn)SOD, and Q69E N3-Fe3+SOD provide a suitable basis for rationalizing the experimental trend in N3− → Fe3+ CT transition energies (Table 5 and Figure 9). Because the electron donating strength of the axial solvent ligand is strongly influenced by its two hydrogen-bond partners Gln69/146 (Glu69 in Q69E FeSOD) and Asp156/167 (see Figure 1), differences in the second coordination spheres among the azide adducts investigated greatly affect the separation of the Fe 3d-based MOs from the azide πnb-based MOs. The dominant Fe–O(Sol) bonding interaction involves the Fe 3dz2 orbital, and changes in the σ-donating power of the coordinated solvent should therefore primarily affect the Fe 3dz2-based MO while leaving the Fe 3dx2-y2-derived MO essentially unperturbed. Hence, the large increase in the energetic splitting between the Fe 3dz2- and Fe 3dx2-y2-based MOs in the DFT-computed MO diagrams (Figure 9) from Q69E N3-Fe3+SOD (0.15 eV) to N3-Fe3+SOD (0.45 eV) and N3-Fe3+(Mn)SOD (0.60 eV) provides a direct manifestation of the increasing σ-donor strength of the solvent ligand along this series.
In N3-Fe3+(Mn)SOD the O(Sol)∙∙∙N(Gln146) hydrogen bond is 0.45 Å shorter than the O(Sol)∙∙∙N(Gln69) hydrogen bond in N3-Fe3+SOD (Table 2). The closer proximity of the Gln residue and O(Sol) in N3-Fe3+(Mn)SOD allows the solvent ligand to move towards Asp167, thereby causing a decrease in the O(Sol)∙∙∙O(Asp) hydrogen-bond distance by 0.13 Å, from 2.91 Å in N3-Fe3+SOD to 2.78 Å in N3-Fe3+(Mn)SOD (Table 2). As a result of this enhanced hydrogen-bond donation in the latter species, the solvent ligand becomes more electron rich (i.e., more strongly σ-donating), which leads to an overall destabilization of the Fe3+ 3d-based MOs (Figure 9).
The opposite trend is predicted for Q69E N3-Fe3+SOD. The QM/MM optimized O(Sol)∙∙∙O(Glu69) hydrogen bond in Q69E N3-Fe3+SOD is shorter (by 0.62 Å) than the O(Sol)∙∙∙N(Gln69) hydrogen bond in N3-Fe3+SOD, indicating that the Glu69 residue effectively pulls the axial solvent ligand away from both the Fe3+ ion and the Asp156 residue due to the strongly depressed pK of Glu69 relative to Gln69, thereby causing a simultaneous lengthening of the Fe–O(Sol) bond and the O(Sol)∙∙∙O(Asp156) hydrogen bond (by 0.08 and 0.44 Å, respectively). Because the axial solvent ligand in Q69E N3-Fe3+SOD acts as a strong hydrogen-bond acceptor from Glu69 and a weak hydrogen-bond donor to Asp156, it becomes more water-like (i.e., less strongly σ-donating), which leads to an increase in the effective nuclear charge of the iron center and thus an overall stabilization of the Fe3+ 3d-based MOs (Figure 9 and Table 5).
A comparison of the QM/MM optimized active-site models of the N3-Fe3+SOD species investigated reveals that coordination of azide causes relatively major, species-dependent changes within the second coordination sphere. For Fe3+SOD, our computational results predict that azide binding causes the Gln69 residue to move 0.20 Å away from the solvent ligand and the O(Sol)∙∙∙O(Asp156) hydrogen-bond distance to decrease from 3.10 to 2.91 Å; however, both hydrogen-bonding interactions remain fairly weak. Alternatively, upon azide binding to Q69E Fe3+SOD, the Glu69 residue is predicted to move 0.31 Å closer to the solvent molecule (which, therefore, becomes a weaker σ-donor), while the Asp167 residue remains a weak hydrogen-bond acceptor. Lastly, in Fe3+(Mn)SOD the O(Sol)∙∙∙N(Gln146) hydrogen-bond distance remains largely unchanged (at ~2.8 Å) upon azide binding, as Gln146 appears to be held tightly in place by the (Mn)SOD protein matrix; yet, the O(Sol)∙∙∙O(Asp167) hydrogen-bond distance shortens by 0.11 Å, which makes the solvent ligand a better σ-donor. Collectively, these results suggest that the residues involved in the active-site hydrogen-bond network respond to azide coordination to the Fe3+ center in different ways, as dictated by the protein matrix, thereby leading to distinct electronic structures of the three azide complexes. Hence, our computations provide a straightforward explanation as to why the spectroscopic data obtained for the azide adducts of the three Fe3+-bound SOD species investigated are quite different, even though those of their azide-free forms are nearly indistinguishable (see preceding paper).32
4.2. Influence of Tyr34 on substrate analogue binding.
The Tyr34 residue, which is highly conserved in Fe- and MnSODs, resides at the end of the substrate access channel more than 5 Å away from the metal center, and forms a hydrogen bond to the Gln69/146 residue (Figure 1). On the basis of spectroscopic and X-ray crystallographic studies of the native Fe- and MnSODs and their respective Tyr34 mutants, this residue has been suggested to play several roles with regards to SOD activity, such as promoting substrate binding, enhancing substrate specificity, facilitating proton transfer, and providing structural stability.15, 39, 40, 42, 44, 47, 74–80 These studies have also led to the proposal that the Tyr34 residues in the (Fe)SOD and (Mn)SOD protein matrices may be poised for distinct interactions with substrate during catalysis. In particular, X-ray crystallographic data for the six-coordinate azide adducts of E. coli Fe3+SOD and T. thermophilus Mn3+SOD have revealed that the terminal N atom of azide forms a hydrogen bond with the phenolic hydrogen of Tyr34 in the latter enzyme but not in the former.15 Yet in a recently released X-ray crystal structure of Y174F N3-Mn3+SOD, azide appears to be oriented away from Tyr34.81 However, as the Tyr174 → Phe mutation has previously been shown to result in rather extensive disruptions near the active site,75 the substrate-analogue complexes of this species may be very different from those of the WT enzyme.
To explore the possibility that the Tyr34 residue modulates the N3-Fe3+(Mn)SOD electronic structure via hydrogen-bonding interactions, we also included the Y34F N3-Fe3+(Mn)SOD species in our study. Although the Abs spectra of WT and Y34F N3-Fe3+(Mn)SOD were previously described as being similar,42, 75 our analysis of the corresponding CD and MCD spectra obtained in this study (Figures 5 and 7) indicates that the Tyr34 → Phe mutation actually results in a red-shift of the N3− → Fe3+ CT transitions by up to 1000 cm−1. Consistent with this finding, the DFT-computed electronic-structure description for our N3-Fe3+(Mn)SOD active-site model indicates that the O(Tyr34)∙∙∙N(azide) hydrogen bond stabilizes the azide πnb-based MOs (i.e., the donor orbitals in these transitions) by ~0.2 eV (~4.6 kcal/mol). The existence of a similar hydrogen-bond interaction between the actual substrate O2•– and Tyr34 would therefore be expected to lead to a sizable stabilization of the superoxide-based MOs and thus to an even greater barrier for electron transfer to the Fe3+ center for Fe(Mn)SOD.77, 82 Collectively, our spectroscopic and computational data of N3-Fe3+(Mn)SOD and its Y34F variant provide compelling evidence that the hydrogen bond between Tyr34 and the solvent ligand in N3-Mn3+SOD (Figure 2) persists in the Fe-substituted enzyme, suggesting that the different orientations of the azide ligand in N3-Fe3+SOD and N3-Mn3+SOD (Figure 2) are caused by differences in the protein matrices rather than the intrinsic properties of the metal ions.
4.3. Implications for O2•– → Fe3+ electron transfer under turnover conditions.
For an SOD to display high catalytic activity, its metal ion reduction potential must lie about halfway between the midpoint potentials for O2•– oxidation and reduction, E° = –330 and +890 mV (vs. NHE at pH 7), respectively (eqs 1-a and b).8, 83 However, while the metal ion’s E° provides a useful measure for determining whether a given SOD species should be a potent catalyst for O2•– dismutation, it is important to note that the actual species involved in electron transfer from and to substrate may have a significantly different “effective” E°. This is especially true if the electron-transfer process follows an inner-sphere mechanism, which is presumed to be the case for both Fe- and MnSODs during O2•– oxidation. Because the high turnover rates prohibit a direct determination of these “effective” E° values for Fe3+-bound SOD species, azide has been used in this study as a substrate analogue to explore how O2•– binding to the Fe3+ center could potentially modulate the metal ion reduction potential. Though the experimental N3− → Fe3+ CT transition energies only provide a qualitative measure of the energy required for the electron transfer step (eq. 1-a), they nicely complement the information gained from electrochemical studies of the resting enzymes because they reflect the active site electronic structure in the presence of an Fe3+-bound substrate analogue.
Previous studies have led to the proposal that the Gln69/146 residue likely plays an important role in maximizing the catalytic activities of Fe- and MnSODs.12, 24, 25, 28–30, 76, 84 In support of this proposal, our spectroscopic data obtained for the three different azide adducts reveal that the active site electronic structure is quite sensitive to both the position and the identity of this residue. In the case of N3-Fe3+(Mn)SOD, our DFT computational results suggest that the Fe3+ 3d-based MOs are more strongly destabilized than in N3-Fe3+SOD, consistent with the fact that in the former the N3− → Fe3+ CT transitions occur at substantially higher energies. As a result, the thermodynamic barrier for O2•– → Fe3+ electron transfer in the actual reaction intermediate should be considerably larger in Fe3+(Mn)SOD. Consequently, O2•– oxidation (eq 1-a) by Fe3+(Mn)SOD is expected to be thermodynamically highly unfavorable, whereas substrate reduction (eq 1-b) by Fe2+(Mn)SOD should still be possible, as is indeed observed experimentally.24
In contrast, for Q69E N3-Fe3+SOD our computational results suggest that the Fe3+ 3d-based MOs are less strongly destabilized than in N3-Fe3+SOD, consistent with the fact that in the former the N3− → Fe3+ CT transitions now occur at considerably lower energies. Hence, the thermodynamic barrier for O2•– → Fe3+ electron transfer should be greatly depressed in the mutant. Accordingly, Q69E Fe3+SOD is expected to readily catalyze O2•– oxidation, whereas the rate of substrate reduction should be dramatically reduced. Again, these predictions concur nicely with experimental findings: (1) unlike WT FeSOD, which is spontaneously oxidized in air, Q69E FeSOD is isolated in the reduced state, (2) oxidation of as-isolated Q69E Fe2+SOD requires the use of extremely strong oxidants, such as KMnO4, and (3) Q69E Fe2+SOD cannot be oxidized by O2•– and thus lacks substrate reduction activity.30
This study, together with the results presented in the preceding paper, provide compelling evidence that the lack of SOD activity displayed by Fe(Mn)SOD and Q69E FeSOD is neither due to a gross disruption of their active-site structures nor their inability to bind O2•–, as both species retain the ability to bind the substrate analogue azide. Instead, their inactivity is likely caused by an improper tuning of the metal ion reduction midpoint potential E°, a problem that persists – or may get even more severe – upon the coordination of substrate. It will be interesting to extend these studies to the closely related “cambialistic” SODs that are capable of catalyzing O2•– dismutation regardless of whether Fe or Mn is bound to their active site.
Supplementary Material
Acknowledgment.
T.C.B. thanks the N.I.H. (GM 64631) for financial support. A.-F.M. acknowledges support from the N.S.F. (MCB012599) and from the Kentucky Science and Engineering Foundation (K.S.E.F.) for this work.
Footnotes
Supporting Information Available: Cartesian coordinates of all QM/MM-optimized active-site models, Abs, CD, and MCD data obtained for N3-Fe3+(Mn)SOD, Q69E N3-Fe3+SOD, and Y34F N3-Fe3+(Mn)SOD, structural parameters, INDO/S-CI calculated electronic excitation energies and ZFS parameters and DFT predicted MO energies and compositions for the WT and Y34F N3-Fe3+(Mn)SOD active-site models with azide oriented away from Tyr34, and VTVH MCD data fits for N3-Fe3+SOD, N3-Fe3+(Mn)SOD, Q69E N3-Fe3+SOD, and Y34F N3-Fe3+(Mn)SOD. This material is available free of charge via the Internet at http://pubs.acs.org.
References
- (1).Miller A-F; Sorkin DL Comments Mol. Cell. Biophys 1997, 9, 1–48. [Google Scholar]
- (2).Choudhury SB; Lee JW; Davidson G; Yim YI; Bose K; Sharma ML; Kang YM; Cabelli DE; Maroney MJ Biochemistry 1999, 38, 3744–3752. [DOI] [PubMed] [Google Scholar]
- (3).Miller A-F Curr. Opin. Chem. Biol 2004, 8, 162–168. [DOI] [PubMed] [Google Scholar]
- (4).Youn H; Kim E; Roe J; Hah YC; Kang S Biochem. J 1996, 318, 889–896. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (5).Wuerges J; Lee J-W; Yim Y-I; Yim H-S; Kang S-O; Carugo KD Proc. Natl. Acad. Sci. U. S. A 2004, 101, 8569–8574. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (6).Lavelle F; McAdam ME; Fielden EM; Roberts PB; Puget K; Michelson AM Biochem. J 1977, 161, 3–11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (7).Bull C; Fee JA J. Am. Chem. Soc 1985, 107, 3295–3304. [Google Scholar]
- (8).Stein J; Fackler JP Jr.; McClune GJ; Fee JA; Chan LT Inorg. Chem 1979, 18, 3511–3519. [Google Scholar]
- (9).Steinman HM J. Biol. Chem 1978, 253, 8708–8720. [PubMed] [Google Scholar]
- (10).Stallings WC; Powers TB; Pattridge KA; Fee JA; Ludwig ML Proc. Natl. Acad. Sci. U. S. A 1983, 80, 3884–3888. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (11).Schininà ME; Maffey L; Barra D; Bossa F; Puget K; Michelson AM FEBS Lett. 1987, 221, 87–90. [DOI] [PubMed] [Google Scholar]
- (12).Stoddard BL; Howell PL; Ringe D; Petsko GA Biochemistry 1990, 29, 8885–8893. [DOI] [PubMed] [Google Scholar]
- (13).Børgstahl GEO; Parge HE; Hickey MJ; Beyer WF; Hallewell RA; Tainer JA Cell 1992, 71, 107–118. [DOI] [PubMed] [Google Scholar]
- (14).Cooper JB; McIntyre K; Badasso MO; Wood SP; Zhang Y; Garbe TR; Young D J. Mol. Biol 1995, 246, 531–544. [DOI] [PubMed] [Google Scholar]
- (15).Lah MS; Dixon MM; Pattridge KA; Stallings WC; Fee JA; Ludwig ML Biochemistry 1995, 34, 1646–1660. [DOI] [PubMed] [Google Scholar]
- (16).Schmidt M; Meier B; Scherk C; Iakovleva O; Parak F Prog. Biophys. Mol. Biol 1996, 65, PA113–PA113. [Google Scholar]
- (17).Edwards RA; Baker HM; Whittaker MM; Whittaker JW; Jameson GB; Baker EN J. Biol. Inorg. Chem 1998, 3, 161–171. [Google Scholar]
- (18).Han WG; Lovell T; Noodleman L Inorg. Chem 2002, 41, 205–218. [DOI] [PubMed] [Google Scholar]
- (19).Ose DE; Fridovich I J. Biol. Chem 1976, 251, 1217–1218. [PubMed] [Google Scholar]
- (20).Clare DA; Blum J; Fridovich I J. Biol. Chem 1984, 259, 5932–5936. [PubMed] [Google Scholar]
- (21).Beyer WF; Fridovich I, J. Biol. Chem 1991, 266, 303–308. [PubMed] [Google Scholar]
- (22).Schmidt M; Meier B; Parak F, J. Biol. Inorg. Chem 1996, 1, 532–541. [Google Scholar]
- (23).Whittaker MM; Whittaker JW, J. Biol. Chem 1999, 274, 34751–34757. [DOI] [PubMed] [Google Scholar]
- (24).Vance CK; Miller A-F, J. Am. Chem. Soc 1998, 120, 461–467. [Google Scholar]
- (25).Vance CK; Miller A-F Biochemistry 2001, 40, 13079–13087. [DOI] [PubMed] [Google Scholar]
- (26).Ludwig ML; Metzger AL; Pattridge KA; Stallings WC, J. Mol. Biol 1991, 219, 335–358. [DOI] [PubMed] [Google Scholar]
- (27).Tierney DL; Fee JA; Ludwig ML; Penner-Hahn JE Biochemistry 1995, 34, 1661–1668. [DOI] [PubMed] [Google Scholar]
- (28).Schwartz AL; Yikilmaz E; Vance CK; Vathyam S; Miller A-F, J. Inorg. Biochem 2000, 80, 247–256. [DOI] [PubMed] [Google Scholar]
- (29).Yikilmaz E; Xie J; Brunold TC; Miller A-F, J. Am. Chem. Soc 2002, 124, 3482–3483. [DOI] [PubMed] [Google Scholar]
- (30).Yikilmaz E; Rodgers DW; Miller A-F Biochemistry 2006, 45, 1151–1161. [DOI] [PubMed] [Google Scholar]
- (31).Yikilmaz E; Porta J; Grove LE; Vahedi-Faridi A; Bronshteyn Y; Brunold TC; Borgstahl GEO; Miller A-F, J. Am. Chem. Soc 2007, 129, 9927–9940. [DOI] [PubMed] [Google Scholar]
- (32).Grove LE; Xie J; Yikilmaz E; Miller A-F; Brunold TC J. Am. Chem. Soc. 2007. [Google Scholar]
- (33).Slykhouse TO; Fee JA, J. Biol. Chem 1976, 251, 5472–5477. [PubMed] [Google Scholar]
- (34).Misra HP; Fridovich I Arch. Biochem. Biophys 1978, 189, 317–322. [DOI] [PubMed] [Google Scholar]
- (35).Whittaker JW; Whittaker MM, J. Am. Chem. Soc 1991, 113, 5528–5540. [Google Scholar]
- (36).Whittaker MM; Whittaker JW Biochemistry 1996, 35, 6762–6770. [DOI] [PubMed] [Google Scholar]
- (37).Vance CK; Miller A-F Biochemistry 1998, 37, 5518–5527. [DOI] [PubMed] [Google Scholar]
- (38).Xie J; Yikilmaz E; Miller A-F; Brunold TC, J. Am. Chem. Soc 2002, 124, 3769–3774. [DOI] [PubMed] [Google Scholar]
- (39).Jackson TA; Karapetian A; Miller A-F; Brunold TC, J. Am. Chem. Soc 2004, 126, 12477–12491. [DOI] [PubMed] [Google Scholar]
- (40).Miller A-F; Sorkin D; Padmakumar K Biochemistry 2005, 44, 5969–5981. [DOI] [PubMed] [Google Scholar]
- (41).Schmidt M; Scherk C; Iakovleva O; Nolting HF; Meier B; Parak F Inorg. Chim. Acta 1998, 276, 65–72. [Google Scholar]
- (42).Whittaker MM; Whittaker JW Biochemistry 1997, 36, 8923–8931. [DOI] [PubMed] [Google Scholar]
- (43).Barik S In Methods in Molecular Biology; PCR Cloning Protocols: From Molecular Cloning to Genetic Engineering; White BA, Ed.; Humana Press: Totowa N.J., 1989; pp 173–182. [Google Scholar]
- (44).Sorkin DL; Duong DK; Miller A-F Biochemistry 1997, 36, 8202–8208. [DOI] [PubMed] [Google Scholar]
- (45).Carter P Anal. Biochem 1971, 40, 450–458. [DOI] [PubMed] [Google Scholar]
- (46).Neese F; Solomon EI Inorg. Chem 1999, 38, 1847–1865. [DOI] [PubMed] [Google Scholar]
- (47).Edwards RA; Whittaker MM; Whittaker JW; Jameson GB; Baker EN, J. Am. Chem. Soc 1998, 120, 9684–9685. [Google Scholar]
- (48).Baerends EJ; Ellis DE; Ros P Chem. Phys 1973, 2, 41. [Google Scholar]
- (49).Versluis L; Ziegler T, J. Chem. Phys 1988, 88, 322–328. [Google Scholar]
- (50).te Velde G; Baerends EJ, J. Comput. Phys 1992, 99, 84–98. [Google Scholar]
- (51).Guerra CF; Snijders JG; te Velde G; Baerends E, J. Theor. Chem. Acc 1998, 99, 391–403. [Google Scholar]
- (52).Vosko SH; Wilk L; Nusair M Can. J. Phys 1980, 58, 1200. [Google Scholar]
- (53).Becke AD, J. Chem. Phys 1986, 84, 4524–4529. [Google Scholar]
- (54).Perdew JP Phys. Rev. B 1986, 33, 8822–8824. [DOI] [PubMed] [Google Scholar]
- (55).Cornell WD; Cieplak R; Bayly CI; Gould IR; Merz KM Jr.; Ferguson DM; Spellmeyer DC; Fox T; Caldwell JW; Kollman PA, J. Am. Chem. Soc 1995, 117, 5179–5197. [Google Scholar]
- (56).Woo TK; Cavallo L; Ziegler T Theor. Chem. Acc 1998, 100, 307–313. [Google Scholar]
- (57).Laskowski RA; MacArthur MW; Moss DS; Thornton JM, J. Appl. Crystallogr 1993, 26, 283–291. [Google Scholar]
- (58).Neese F (2005) ORCA-An ab Initio, Density Functional, and Semiempirical SCF-MO Package, 2.4, Max-Planck-Institut für Bioanorganische Chemie, Mülheim an der Ruhr, Germany. [Google Scholar]
- (59).Ridley J; Zerner MC Theor. Chem. Acc 1973, 32, 111. [Google Scholar]
- (60).Zerner MC; Loew GH; Kirchner RF; Mueller-Westerhof UT, J. Am. Chem. Soc 1980, 102, 589. [Google Scholar]
- (61).Bacon AD; Zerner MC Theor. Chem. Acc 1979, 53, 21. [Google Scholar]
- (62).Becke AD, J. Chem. Phys 1993, 98, 1372–1377. [Google Scholar]
- (63).Becke AD, J. Chem. Phys 1993, 98, 5648–5652. [Google Scholar]
- (64).Lee C; Yang W; Parr RG Phys. Rev. B 1988, 37, 785–789. [DOI] [PubMed] [Google Scholar]
- (65).Schäfer A; Horn H; Ahlrichs R, J. Chem. Phys 1992, 97, 2571–2577. [Google Scholar]
- (66).Weigand F; Häser M Theor. Chem. Acc 1997, 97, 331–340. [Google Scholar]
- (67).Schäfer A; Huber C; Ahlrichs R, J. Chem. Phys 1994, 100, 5829–5835. [Google Scholar]
- (68).Laaksonen L, J. Mol. Graphics 1992, 10, 33–34. [DOI] [PubMed] [Google Scholar]
- (69).Bergman D; Laaksonen L; Laaksonen A, J. Mol. Graphics Modell 1997, 15, 301–306. [DOI] [PubMed] [Google Scholar]
- (70).Jackson TA; Xie J; Yikilmaz E; Miller A-F; Brunold TC, J. Am. Chem. Soc 2002, 124, 10833–10845. [DOI] [PubMed] [Google Scholar]
- (71).Rulíšek L; Jensen KP; Lundgren K; Ryde U, J. Comput. Chem. 2006, 27, 1398–1410. [DOI] [PubMed] [Google Scholar]
- (72).Slater JC The Calculation of Molecular Orbitals; John Wiley & Sons: New York, 1979. [Google Scholar]
- (73).To facilitate a direct comparison between the different active-site models, all MO energies are given relative to that of the corresponding azide πnb(ip)-based MO.
- (74).Hunter T; Ikebukuro K; Bannister WH; Bannister JV; Hunter G, J. Biochemistry 1997, 36, 4925–4933. [DOI] [PubMed] [Google Scholar]
- (75).Edwards RA; Whittaker MM; Whittaker JW; Baker EN; Jameson GB Biochemistry 2001, 40, 4622–4632. [DOI] [PubMed] [Google Scholar]
- (76).Edwards RA; Whittaker MM; Whittaker JW; Baker EN; Jameson GB Biochemistry 2001, 40, 15–27. [DOI] [PubMed] [Google Scholar]
- (77).Maliekal J; Karapetian A; Vance C; Yikilmaz E; Wu Q; Jackson TA; Brunold TC; Spiro TG; Miller A-F, J. Am. Chem. Soc 2002, 124, 15064–15075. [DOI] [PubMed] [Google Scholar]
- (78).Jackson TA; Yikilmaz E; Miller A-F; Brunold TC, J. Am. Chem. Soc 2003, 125, 8348–8363. [DOI] [PubMed] [Google Scholar]
- (79).Greenleaf WB; Perry JJP; Hearn AS; Cabelli DE; Lepock JR; Stroupe ME; Tainer JA; Nick HS; Silverman DN Biochemistry 2004, 43, 7038–7045. [DOI] [PubMed] [Google Scholar]
- (80).Jackson TA; Karapetian A; Miller A-F; Brunold TC Biochemistry 2005, 44, 1504–1520. [DOI] [PubMed] [Google Scholar]
- (81).Salvador JR, Whittaker MM, Whittaker JW, and Jameson GB Re-Evaluation of the Low-Temperature Azide in Mn-Dependent Superoxide Dismutase. [Google Scholar]
- (82).Miller A-F In Handbook of Metalloenzymes; Messerschmidt A, Huber R, Poulos T, Wieghardt K, Eds.; John Wiley & Sons: Chichester, U.K., 2001; pp 668–682. [Google Scholar]
- (83).Barrette WC Jr.; Sawyer DT; Fee JA; Asada K Biochemistry 1983, 22, 624–627. [DOI] [PubMed] [Google Scholar]
- (84).Leveque VJP; Stroupe ME; Lepock JR; Cabelli DE; Tainer JA; Nick HS; Silverman DN Biochemistry 2000, 39, 7131–7137. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.