On fibre dispersion modelling of soft biological tissues: a review

Abstract

Collagen fibres within fibrous soft biological tissues such as artery walls, cartilage, myocardiums, corneas and heart valves are responsible for their anisotropic mechanical behaviour. It has recently been recognized that the dispersed orientation of these fibres has a significant effect on the mechanical response of the tissues. Modelling of the dispersed structure is important for the prediction of the stress and deformation characteristics in (patho)physiological tissues under various loading conditions. This paper provides a timely and critical review of the continuum modelling of fibre dispersion, specifically, the angular integration and the generalized structure tensor models. The models are used in representative numerical examples to fit sets of experimental data that have been obtained from mechanical tests and fibre structural information from second-harmonic imaging. In particular, patches of healthy and diseased aortic tissues are investigated, and it is shown that the predictions of the models fit very well with the data. It is straightforward to use the models described herein within a finite-element framework, which will enable more realistic (and clinically relevant) boundary-value problems to be solved. This also provides a basis for further developments of material models and points to the need for additional mechanical and microstructural data that can inform further advances in the material modelling.

1. Introduction

In recent years, it has become apparent that in the modelling of fibrous soft biological tissues, the dispersion of the collagen fibres has a significant effect on the mechanical response compared with the case when no dispersion is assumed [1]. Various models have been proposed to take account of different dispersion arrangements on the basis of continuum theory [2–12]. The continuum approach has been shown to be very successful in modelling the elastic behaviour of many types of fibrous tissues, including artery walls [6], cartilage [13], myocardiums [14], corneas [15] and heart valves [4]. In this approach, the material is considered to be a fibre-reinforced composite with the fibres distributed within an isotropic matrix; the models developed within this framework describe the effect of the structural arrangement of the fibres on the mechanical response very well.

To inform the modelling, it is important to have structural data from various imaging techniques in addition to data from mechanical tests. In recent years, advances have been made that improve understanding of the microstructure of fibrous tissues; however, more information, such as the structure of the cross-linking of the collagen fibres and the effect this has on the mechanical response, is still needed to capture more details of the microstructure. Currently, available mechanical tests are insufficiently general to fully characterize the three-dimensional mechanical response [16]. There is, therefore, a need for more general test protocols such as planar biaxial tests combined with in-plane shear and/or through-thickness shear or, as an alternative, extension/inflation tests combined with torsion and azimuthal or axial shear.

One consideration in modelling the collagen fibre structure is whether or not collagen fibres, in view of their very slender nature, can support compression. This is particularly important where the volume fraction of fibres is relatively small and the fibres under compression do not contribute to the mechanical response. In recent years, several models have been proposed for excluding compressed collagen fibres from the mechanical response. To the authors' knowledge the study of Holzapfel & Ogden [17] was the first to analyse the set of orientations for which fibres are compressed and should therefore be excluded, while the study of Li et al. [18] used this theory as a basis for a finite-element (FE) realization. Another approach for excluding compressed fibres is based on the use of a Heaviside function, as suggested by Federico & Herzog [19]. An efficient computational scheme for excluding fibres under compression has been developed more recently by Li et al. [20]. This involves discretizing a unit hemisphere with a finite number of spherical triangles and averaging the fibre density over each triangle.

In view of these recent developments and as a basis for further advances, it is an appropriate time to provide a review of fibre dispersion modelling . This is the purpose of the first part of the present paper, while in the second part, the theory is applied to some representative examples. In particular, §2 provides the equations for transversely isotropic elastic materials and extensions of these to account for fibre dispersion, including the angular integration (AI) [2] and the generalized structure tensor (GST) [1] approaches, and a further extension to allow for excluding compressed fibres. In §3, the theory is applied to the special deformations of biaxial extension, equibiaxial extension and uniaxial extension and provides explicit stress–deformation relations for these cases for both the AI and GST models. In §4, the first numerical example relates to the equibiaxial deformation of a tissue taken from an abdominal aortic aneurysm for which the published structural and mechanical test data of the tissue were used as a basis for fitting each model. The second numerical example relates to the uniaxial extension of two strips taken from the circumferential and longitudinal (axial) directions of a healthy human thoracic aorta. The novel structural and mechanical test data for the elastic domain (as yet unpublished) were used to identify an optimal set of the material parameters for each model. The overall agreement between the model predictions and the data is very good. The final section, §5, concludes this present study and points to the need for further developments.

2. Modelling anisotropy for fibrous materials

In this section, we introduce transverse isotropy and the fibre dispersion for which we critically analyse the AI and GST approaches and model approaches that exclude compressed fibres. For an overview of the main existing continuum mechanical models which take fibre dispersion into account, the reader is referred to Table 1 of Holzapfel et al. [10]. In particular, different approaches, probability density functions, parameters describing the fibre dispersion and the type of dispersion are compared.

(a). Transverse isotropy

We introduce the deformation gradient F relative to an undeformed reference configuration, the right Cauchy–Green tensor C = F^TF and the left Cauchy–Green tensor b = FF^T as the basic kinematic variables. For an incompressible transversely isotropic elastic material, for which $det\mathbf{F}\equiv 1$, with preferred direction M in the reference configuration, which is associated with the direction of a collagen fibre, the strain-energy function Ψ can be expressed in terms of four invariants, typically taken to be

$$I_1=\mathrm{tr}\mathbf{C},I_2=\frac{1}{2}[I_1^2-\mathrm{tr}({\mathbf{C}}^2)],I_4=\mathrm{tr}(\mathbf{C}\mathbf{M}\otimes \mathbf{M})\mathrm{and}{I}_5=\mathrm{tr}({\mathbf{C}}^2\mathbf{M}\otimes \mathbf{M}),$$ 2.1

where M⊗M is referred to as a structure tensor. The Cauchy stress tensor σ is given by (see, e.g. [21])

$$\mathit{\sigma }=-p\mathbf{I}+2{\psi }_1\mathbf{b}+2{\psi }_2(I_1\mathbf{b}-{\mathbf{b}}^2)+2{\psi }_4\mathbf{m}\otimes \mathbf{m}+2{\psi }_5(\mathbf{m}\otimes \mathbf{b}\mathbf{m}+\mathbf{b}\mathbf{m}\otimes \mathbf{m}),$$ 2.2

where m = FM is the preferred direction mapped to the deformed configuration and ψ_i = ∂Ψ/∂I_i, i = 1, 2, 4, 5. For the reference configuration to be stress free, we require

$$2{\psi }_1+4{\psi }_2-p=0\mathrm{and}{\psi }_4+2{\psi }_5=0,$$ 2.3

although, in general, the reference configuration may be residually stressed, but residual stresses are not considered here. For reasons discussed by Holzapfel et al. [22], we consider an energy function Ψ that reflects the isotropy through I₁ and the fibre content through I₄ so that (2.2) reduces to

$$\mathit{\sigma }=-p\mathbf{I}+2{\psi }_1\mathbf{b}+2{\psi }_4\mathbf{m}\otimes \mathbf{m},$$ 2.4

where now Ψ is a function of I₁ and I₄ only, and conditions (2.3) specialize accordingly. For many applications, the strain-energy function Ψ is decoupled in the form

$$\mathit{\Psi }={\mathit{\Psi }}_{\mathrm{iso}}+{\mathit{\Psi }}_{\mathrm{fib}},$$ 2.5

where Ψ_iso is the combined isotropic contribution of the extrafibrillar matrix and the elastic fibres, generally considered to be a function of I₁ alone and frequently characterized by the neo-Hookean model according to

$${\mathit{\Psi }}_{\mathrm{iso}}=\frac{1}{2}\mu (I_1-3),$$ 2.6

where μ > 0 is the reference state shear modulus of the isotropic material. The function Ψ_fib is connected with the energy stored in the collagen fabric and is often given by Holzapfel et al. [22]

$${\mathit{\Psi }}_{\mathrm{fib}}=\frac{c_1}{2c_2}\{\exp [c_2{(I_4-1)}^2]-1\},$$ 2.7

where c₁ > 0 is a parameter with the dimension of stress and c₂ > 0 is dimensionless.

(b). Fibre dispersion

(i). The angular integration approach.

Instead of considering fibres to be locally aligned, we consider now a more realistic situation where there is a distribution of orientations. If a typical fibre has an orientation N in the reference configuration, then a strain-energy function per unit volume associated with the stretching of all the fibres in that direction is given by W(I₄), where I₄ = N · CN≡tr(CN⊗N), with W(I₄) = W^′(I₄) = 0 for I₄≤1 and W^′(I₄) > 0 for I₄ > 1. Suppose that the fibre orientations are distributed according to a probability density ρ(N) so that the total energy associated with the fibres is

$${\mathit{\Psi }}_{\mathrm{fib}}={\mathit{\Psi }}_{\mathrm{AI}}=\frac{1}{4\pi }{\int }_{\mathit{\Omega }}\rho (\mathbf{N})W(I_4)\hspace{0.17em}\mathrm{d}\mathit{\Omega },$$ 2.8

where Ω is a unit sphere. Note that the total strain-energy Ψ also includes an isotropic part as in (2.5), where Ψ_iso depends only on I₁. Several other formulations consider a multiplier n to describe the number of fibres per unit reference volume, but this is now absorbed into W. The factor 1/4π is not always used but is included here so that (2.8) reduces to W(I₄) when there is no dispersion about some fixed direction M with I₄ = tr(CM⊗M). Note that the orientation density function is normalized according to

$$\frac{1}{4\pi }{\int }_{\mathit{\Omega }}\rho (\mathbf{N})\hspace{0.17em}\mathrm{d}\mathit{\Omega }=1.$$ 2.9

This integral formulation is called the AI approach, which was introduced by Lanir [2]. It is worth noting that in the original Lanir AI approach, no isotropic part was included in the energy function and the possibility of different properties for different fibres within the dispersion was allowed for. The Cauchy stress tensor σ has the form

$$\mathit{\sigma }={\mathit{\sigma }}_{\mathrm{iso}}+{\mathit{\sigma }}_{\mathrm{AI}}-p\mathbf{I}\mathrm{and}{\mathit{\sigma }}_{\mathrm{AI}}=\frac{1}{2\pi }{\int }_{\mathit{\Omega }}\rho (\mathbf{N})W^{\mathrm{\prime }}(I_4)\mathbf{n}\otimes \mathbf{n}\hspace{0.17em}\mathrm{d}\mathit{\Omega },$$ 2.10

where n = FN and σ_iso is the isotropic stress contribution from the non-collagenous material.

Some modifications of the AI approach adopted in the literature are as follows: the model of Sacks [23] incorporates a two-dimensional AI distribution in a strain-energy function based on the Beta distribution, while the theory was applied to bovine pericardium. Also using the AI approach the model of Driessen et al. [3], which is based on Billar & Sacks [24] following Lanir [2], studied the biaxial behaviour of arterial walls and aortic valves with a planar fibre dispersion and a Gaussian probability density function. The model documented by Alastrué et al. [25] used an eight-chain model, where the chains are described as worm-like chains together with a repulsive energy function. This is based on the von Mises distribution with a non-symmetric dispersion and a micro-sphere model, and it was applied to artery walls with two fibre families. The study of Ateshian et al. [13] used an ellipsoidal distribution with a power-law strain-energy function to analyse the solid matrix of the cartilage fibres with fibres under compression excluded by use of the Heaviside function. Using the von Mises distribution, the study of Raghupathy & Barocas [26] derived a closed-form solution in terms of modified Bessel functions of the first kind for an exponential fibre stress–strain law. The model was fitted to experimental data and applied to planar biaxial extension of a bioartificial tissue.

The paper of Federico & Gasser [5] documents a computational method for treating AI models using a Heaviside function to exclude compressed fibres and a planar von Mises distribution to examine the in-plane dispersion of collagen fibres. The model and a numerical integration method were implemented into Feap [27] and applied to simulate the response of articular cartilage. The study of Agianniotis et al. [7] examined in-plane dispersion of collagen fibres and was fitted to experimental data on rabbit facial veins obtained from inflation/extension tests. Wavy collagen fibres were modelled so that they engage and bear stress at a critical value of the extension. Elastin was captured by a neo-Hookean term and a term which depends on I₄, while individual collagen fibres were modelled by using quadratic functions of the strain. On the basis of a Bingham distribution, the study of Gasser et al. [28] proposed a constitutive law depending on the collagen fibre orientation and the authors applied the model to predict the biaxial response of abdominal aortic aneurysms and compared with synthetic data. A method for excluding compressed fibres within the AI framework was proposed by Holzapfel & Ogden [17], and a general formulation for the Cauchy stress and the critical angles at the boundary of the region where the fibres are stretched were provided. The review article of Limbert [29] on aspects of the mathematical and computational modelling of skin biophysics refers to several models including the AI model.

(ii). The generalized structure tensor approach.

An alternative approach for describing fibre dispersion, referred to as the GST approach, was developed by Gasser et al. [1] on the basis of a generalized structure tensor H defined by

$$\mathbf{H}=\frac{1}{4\pi }{\int }_{\mathit{\Omega }}\rho (\mathbf{N})\mathbf{N}\otimes \mathbf{N}\hspace{0.17em}\mathrm{d}\mathit{\Omega },$$ 2.11

with trH = 1, which results from the normalization (2.9). A similar tensor was introduced in the context of the rheology of short fibre composites by Advani & Tucker [30] and referred to as an orientation tensor. Therein planar orientation states were discussed with applications to linear elasticity. Advani and Tucker orientation tensors were also considered within the more recent paper of Lanir [31], which concluded that higher-order tensors are needed to better represent the geometrical fibre structure of the material. However, this is a purely geometrical consideration and does not take account of the actual material response, which can be well represented in terms of a second-order orientation tensor.

The tensor H is an averaged version of the individual structure tensors N⊗N of the fibres within the dispersion. A general strain-energy function involving the structure tensor H has the form Ψ_fib = Ψ_GST(C, H) and can be represented in terms of the invariants of C and H. For example, the generalized invariant I^⋆₄ = tr(CH) is analogous to tr(CN⊗N) with N⊗N replaced by its generalized counterpart H, and the generalized invariant I^⋆₅ = tr(C²H) is similarly analogous to I₅. If we suppose that Ψ_GST depends only on I^⋆₄ and I^⋆₅, then the Cauchy stress tensor σ takes on the form

$$\mathit{\sigma }={\mathit{\sigma }}_{\mathrm{iso}}+{\mathit{\sigma }}_{\mathrm{GST}}-p\mathbf{I}\mathrm{and}{\mathit{\sigma }}_{\mathrm{GST}}=2{\psi }_4^{\star }\mathbf{h}+2{\psi }_5^{\star }(\mathbf{b}\mathbf{h}+\mathbf{h}\mathbf{b}),$$ 2.12

where ψ^⋆_i = ∂Ψ_GST/∂I^⋆_i, i = 4, 5, h = FHF^T and σ_iso is the isotropic contribution of the non-collagenous material, as in (2.10).

When specialized to a transversely isotropic distribution where the fibres are distributed symmetrically around a mean direction M, H and h are given by

$$\mathbf{H}=\kappa \mathbf{I}+(1-3\kappa )\mathbf{M}\otimes \mathbf{M}\mathrm{and}\mathbf{h}=\kappa \mathbf{b}+(1-3\kappa )\mathbf{m}\otimes \mathbf{m},$$ 2.13

where I is the identity tensor and κ is the dispersion parameter defined by

$$\kappa =\frac{1}{4}{\int }_0^{\pi }\rho (\mathit{\Theta }){\sin }^3\mathit{\Theta }\hspace{0.17em}\mathrm{d}\mathit{\Theta },$$ 2.14

where ρ(N) is replaced by ρ(Θ). In general, κ is contained in [0, 1/2] but for reasons discussed by Holzapfel & Ogden [6], it is usually restricted to [0, 1/3].

We now represent a general fibre direction N within a dispersion in terms of spherical polar angles Θ and Φ as

$$\mathbf{N}(\mathit{\Theta },\mathit{\Phi })=\sin \mathit{\Theta }\cos \mathit{\Phi }{\mathbf{e}}_1+\sin \mathit{\Theta }\sin \mathit{\Phi }{\mathbf{e}}_2+\cos \mathit{\Theta }{\mathbf{e}}_3,$$ 2.15

with Θ∈[0, π], Φ∈[0, 2π] and where e₁, e₂ and e₃ are fixed rectangular Cartesian unit vectors. We then multiplicatively decompose the density function ρ according to

$$\rho (\mathbf{N})={\rho }_{\mathrm{op}}(\mathit{\Theta }){\rho }_{\mathrm{ip}}(\mathit{\Phi }),$$ 2.16

where ρ_op and ρ_ip denote the orientation densities in the e₃ (out-of-plane) direction and the (e₁, e₂) plane (in-plane), respectively. We impose symmetry conditions, which are based on experiments [32] and have also been used by Holzapfel et al. [10], according to

$${\rho }_{\mathrm{op}}(\pi -\mathit{\Theta })={\rho }_{\mathrm{op}}(\mathit{\Theta })\mathrm{and}{\rho }_{\mathrm{ip}}(\pi +\mathit{\Phi })={\rho }_{\mathrm{ip}}(\mathit{\Phi }).$$ 2.17

Now, in the case when the fibre dispersion is non-symmetric, the structure tensors H and h take on the particular forms [10]

$$\mathbf{H}=2{\kappa }_{\mathrm{op}}{\kappa }_{\mathrm{ip}}\mathbf{I}+2{\kappa }_{\mathrm{op}}(1-2{\kappa }_{\mathrm{ip}})\mathbf{M}\otimes \mathbf{M}+(1-2{\kappa }_{\mathrm{op}}-2{\kappa }_{\mathrm{op}}{\kappa }_{\mathrm{ip}}){\mathbf{M}}_{\mathrm{n}}\otimes {\mathbf{M}}_{\mathrm{n}}$$ 2.18

and

$$\mathbf{h}=2{\kappa }_{\mathrm{op}}{\kappa }_{\mathrm{ip}}\mathbf{b}+2{\kappa }_{\mathrm{op}}(1-2{\kappa }_{\mathrm{ip}})\mathbf{m}\otimes \mathbf{m}+(1-2{\kappa }_{\mathrm{op}}-2{\kappa }_{\mathrm{op}}{\kappa }_{\mathrm{ip}}){\mathbf{m}}_{\mathrm{n}}\otimes {\mathbf{m}}_{\mathrm{n}},$$ 2.19

where M here denotes the mean fibre direction lying in the (e₁, e₂)-plane, M_n is the out-of-plane unit vector e₃, and m_n = FM_n is the push forward of M_n. The parameters κ_op and κ_ip quantify the out-of-plane and in-plane dispersions and are defined by

$${\kappa }_{\mathrm{op}}={\int }_0^{\pi /2}{\rho }_{\mathrm{op}}(\mathit{\Theta }){\sin }^3\mathit{\Theta }\hspace{0.17em}\mathrm{d}\mathit{\Theta }\mathrm{and}{\kappa }_{\mathrm{ip}}=\frac{1}{\pi }{\int }_0^{\pi }{\rho }_{\mathrm{ip}}(\mathit{\Phi }){\sin }^2\mathit{\Phi }\hspace{0.17em}\mathrm{d}\mathit{\Phi },$$ 2.20

with the normalization conditions

$$\frac{1}{2}{\int }_0^{\pi /2}{\rho }_{\mathrm{op}}(\mathit{\Theta })\sin \mathit{\Theta }\hspace{0.17em}\mathrm{d}\mathit{\Theta }=1\mathrm{and}\frac{1}{\pi }{\int }_0^{\pi }{\rho }_{\mathrm{ip}}(\mathit{\Phi })\hspace{0.17em}\mathrm{d}\mathit{\Phi }=1$$ 2.21

and the ranges of values

$$0\le {\kappa }_{\mathrm{op}}\le 1/2\mathrm{and}0\le {\kappa }_{\mathrm{ip}}\le 1.$$ 2.22

The dispersion parameter κ_op corresponds to a rotationally symmetric dispersion about the direction Θ = 0, while κ_ip represents a planar dispersion in the plane Θ = π/2. In the case of a non-symmetric fibre dispersion, the contribution σ_GST to the Cauchy stress tensor is again given by (2.12), but with h now coming from (2.19).

It has been found convenient to use von Mises distributions to represent the probability density functions according to

$${\rho }_{\mathrm{ip}}(\mathit{\Phi })=\frac{\exp (-a\cos 2\mathit{\Phi })}{I_0(a)}\mathrm{and}{\rho }_{\mathrm{op}}(\mathit{\Theta })=4\sqrt{\frac{b}{2\pi }}\frac{\exp (-2b{\cos }^2\mathit{\Theta })}{\mathrm{erf}(\sqrt{2b})},$$ 2.23

where the constants a and b are concentration parameters, I₀(a) is the Bessel function of the first kind of order 0, and erf denotes the error function. The dispersion parameters κ _ip and κ_op then have the explicit forms

$${\kappa }_{\mathrm{ip}}=\frac{1}{2}-\frac{I_1(a)}{2I_0(a)}\mathrm{and}{\kappa }_{\mathrm{op}}=\frac{1}{2}-\frac{1}{8b}+\frac{1}{4}\sqrt{\frac{2}{\pi b}}\frac{\exp (-2b)}{\mathrm{erf}(\sqrt{2b})},$$ 2.24

where I₁(a) is the modified Bessel function of the first kind of order 1. An alternative to the von Mises distribution is the Bingham model used by Gasser et al. [28], although it has not been adopted subsequently to any great extent.

A specific form of Ψ_GST which depends only on I^⋆₄ is commonly used in the form [1]

$${\mathit{\Psi }}_{\mathrm{GST}}=\frac{k_1}{2k_2}\{\exp [k_2{(I_4^{\star }-1)}^2]-1\},$$ 2.25

which, with (2.6), is frequently referred to as the Gasser–Ogden–Holzapfel (GOH) model. Here, it is important to note that the parameters k₁ and k₂ are in general not the same as those involved in (2.7). Note that I^⋆₄ = tr(CH) = trh, and hence, with (2.13)₂ and (2.19), the specifications

$$I_4^{\star }=\kappa I_1+(1-3\kappa )I_4\mathrm{and}{I}_4^{\star }=2{\kappa }_{\mathrm{op}}{\kappa }_{\mathrm{ip}}{I}_1+2{\kappa }_{\mathrm{op}}(1-2{\kappa }_{\mathrm{ip}})I_4+(1-2{\kappa }_{\mathrm{op}}-2{\kappa }_{\mathrm{op}}{\kappa }_{\mathrm{ip}})I_{\mathrm{n}}$$ 2.26

follow, respectively, where I_n = m_n · m_n. The specific expression for σ_GST in this case is

$${\mathit{\sigma }}_{\mathrm{GST}}=2k_1(I_4^{\star }-1)\exp [k_2{(I_4^{\star }-1)}^2]\mathbf{h},$$ 2.27

with h given by (2.13)₂ or (2.19) as appropriate.

We remark in passing that the general structure-like approach provided by Freed et al. [4] has some similarities with that developed here in terms of invariants, and it was applied to aortic heart valves. The paper of Melnik et al. [9] on the modelling of fibre dispersion in fibre-reinforced elastic materials introduced a modified structure tensor H in which compressed fibres are removed from the integral by use of a Heaviside function, as previously suggested by Federico & Herzog [19] with respect to the AI approach, and used by Federico & Gasser [5]. In considering the original GST model, the authors of [9] unfortunately included the isotropic part of the structure tensor when the mean fibre direction was compressed instead of completely omitting the anisotropic contribution to the strain-energy function in this case; see equation (2.26) therein. This is a misinterpretation of a statement on p. 26 by Gasser et al. [1] and leads to unphysical predictions of the uniaxial tension-stretch behaviour in section 2 of their paper. A similar misinterpretation is contained in Latorre & Montáns [33] (see equation (2.17) therein), and the results obtained on that basis are not clear. This misinterpretation motivated the development of a model for excluding fibres in compression. Unfortunately, this model does not achieve this aim because it uses the mean squared stretch of the fibres in the plane transverse to the mean fibre direction, and this does not guarantee the exclusion of all compressed fibres.

On the basis of a GST model, in Roohbakhshan et al. [34], a projection method was presented to reduce three-dimensional constitutive models to membrane formulations, which considerably reduces the number of degrees of freedom compared with the three-dimensional solid FE discretization. The follow-up study of Roohbakhshan & Sauer [35] developed rotation-free shell models by using the GST approach; NURBS-based FEs were used for the FE discretization and pure membrane, pure bending and mixed modes of the shell deformation were examined.

By using the GST model of Gasser et al. [1], Ferreira et al. [36] also incorporated a damage formulation and its non-local averaging of integral type, which seeks to include the effects of the microstructure in order to limit the localization induced by the damage variables. The study of Volokh [37] presents AI-based models using multiple (16 and 8) structure tensors and the author applied the models to analyse uniaxial extension in the circumferential and axial directions of arterial walls.

The motivation of an alternative approach documented by Pandolfi & Vasta [8] and subsequent papers, e.g. by Vasta et al. [38] and Gizzi et al. [39,40], was based on errors in Federico & Herzog [19] and Cortes et al. [41], which have been followed by Pandolfi & Vasta [8] with the conclusion ‘that for all the loading cases for which GST models introduce large errors, such as uniaxial loading, shear and biaxial loading, the proposed model has a better performance, in the sense that it provides results closer to the ones furnished by an exact AI of the fibre orientation distribution’. Holzapfel & Ogden [42,43] have pointed out that the errors of the papers by Federico & Herzog [19] and Cortes et al. [41] are based on incorrect analysis. Part of the motivation of the approach by Pandolfi & Vasta [8] was to incorporate higher-order statistics to try and correct the supposed (but non-existent) errors. We now outline their formulation, which was designed to modify the GST model Ψ _fib = Ψ_GST(I^⋆₄) by including second-order statistics. Consider the AI model (2.8) and expand W(I₄) as a Taylor series around I^⋆₄ as

$$W(I_4)=W(I_4^{\star })+(I_4-I_4^{\star })W^{\mathrm{\prime }}(I_4^{\star })+\frac{1}{2}{(I_4-I_4^{\star })}^2{W}^{\mathrm{\prime }\mathrm{\prime }}(I_4^{\star })+\cdots .$$ 2.28

Since, by (2.11) and the definition of I^⋆₄, $(1/4\pi ){\int }_{\mathit{\Omega }}\rho (\mathbf{N})I_4\hspace{0.17em}\mathrm{d}\mathit{\Omega }=I_4^{\star }$, after substitution into (2.8), the approximation reads

$$\begin{array}{rl}{\mathit{\Psi }}_{\mathrm{fib}}& \simeq W(I_4^{\star })+\frac{1}{2}{W}^{\mathrm{\prime }\mathrm{\prime }}(I_4^{\star })\frac{1}{4\pi }{\int }_{\mathit{\Omega }}\rho (\mathbf{N}){(I_4-I_4^{\star })}^2\hspace{0.17em}\mathrm{d}\mathit{\Omega }\\ & ={\mathit{\Psi }}_{\mathrm{GST}}(I_4^{\star })+\frac{1}{2}{W}^{\mathrm{\prime }\mathrm{\prime }}(I_4^{\star })[(\mathbb{H}\mathbf{C}):\mathbf{C}-I_4^{\star 2}],\end{array}$$ 2.29

where ‘:’ denotes the double contraction. The latter term follows since, from (2.11) and the definition

$$\mathbb{H}=\frac{1}{4\pi }{\int }_{\mathit{\Omega }}\rho (\mathbf{N})\mathbf{N}\otimes \mathbf{N}\otimes \mathbf{N}\otimes \mathbf{N}\hspace{0.17em}\mathrm{d}\mathit{\Omega },$$ 2.30

we obtain

$$\frac{1}{4\pi }{\int }_{\mathit{\Omega }}\rho (\mathbf{N})(I_4^2-2I_4{I}_4^{\star }+I_4^{\star 2})\hspace{0.17em}\mathrm{d}\mathit{\Omega }=(\mathbb{H}\mathbf{C}):\mathbf{C}-{(\mathbf{H}:\mathbf{C})}^2.$$ 2.31

Herein, $\mathbb{H}$ is a fourth-order structure tensor which, without the factor 1/4π, was introduced by Advani & Tucker [30] and referred to as an orientation tensor. It should be emphasized that this approximation is only valid for dispersions for which I^⋆₄ is close to I₄, i.e. for narrow dispersions.

Given the energy function (2.29)₂, we can derive the rather complex Cauchy stress tensor σ_fib, i.e.

$${\mathit{\sigma }}_{\mathrm{fib}}=\{2W^{\mathrm{\prime }}(I_4^{\star })-2I_4^{\star }{W}^{\mathrm{\prime }\mathrm{\prime }}(I_4^{\star })+W^{\mathrm{\prime }\mathrm{\prime }\mathrm{\prime }}(I_4^{\star })[(\mathbb{H}\mathbf{C}):\mathbf{C}-I_4^{\star 2}]\}\mathbf{h}+2W^{\mathrm{\prime }\mathrm{\prime }}(I_4^{\star })\mathbf{F}(\mathbb{H}\mathbf{C}){\mathbf{F}}^{\mathrm{T}}.$$ 2.32

Holzapfel & Ogden have shown in, e.g. [42], that the GST and AI models have very similar predictive powers. It is inappropriate to argue that an additional term of the type considered here is needed to improve accuracy. In addition, the resulting stress tensor and elasticity tensor (not shown here) are relatively complicated to handle and to implement.

(iii). Model approaches excluding compressed fibres.

Collagen fibres are embedded in a matrix material in a wavy form, as can be seen in particular in healthy artery tissues in the unloaded state. During loading, the collagen fibres are straightened and then bear tension, leading to a stiffening response which is typically described by an exponential function. Under compression, however, the collagen fibres store very little or no energy because they are very slender, and the matrix material bears the compressive load. Moreover, for a mathematical model to be well behaved it should satisfy certain convexity conditions, which cannot be guaranteed when compressed fibres store energy [22,44]. For this reason, exclusion of compressed fibres is also important from the mathematical point of view in order to properly reflect the overall behaviour of the tissue.

It appears that the study of Weiss et al. [45] was the first to describe this switch between tension and compression in modelling the human medial collateral ligament. This was followed by Holzapfel et al. [22], who used this switch in a constitutive framework for arterial walls although the model therein does not consider dispersion. The key point is that the anisotropic part of the strain-energy function only contributes when either one or both of the fibre families is/are extended (I₄ > 1 or I₆ > 1 or both). This model was then extended by Gasser et al. [1] to accommodate dispersion based on the stretch in the mean fibre direction. However, using a criterion for which the mean fibre direction is extended does not, in general, allow exclusion of all compressed fibres within a dispersion. In fact, it has been claimed in the literature that it is not possible to exclude compressed fibres in the GST model of Cortes et al. [41], although Holzapfel & Ogden [42] have shown that this is not the case.

The following simple example of homogeneous uniaxial deformation illustrates how some fibres are compressed when the mean fibre direction is extended. Suppose a stretch λ₃ = λ is applied in the mean fibre direction M, which is taken to be the e₃ direction so that by symmetry and incompressibility λ₁ = λ₂ = λ^−1/2. According to (2.1)₁ and (2.1)₃, we have

$$I_1={\mathrm{\lambda }}^2+2{\mathrm{\lambda }}^{-1}\mathrm{and}{I}_4={\mathrm{\lambda }}^2$$ 2.33

and from (2.25) and (2.26)₁, we then obtain

$$I_4^{\star }={\mathrm{\lambda }}^2(1-2\kappa )+2\kappa {\mathrm{\lambda }}^{-1}.$$ 2.34

A plot of this relationship is shown in figure 1 for five different values of κ. As the plot indicates, I^⋆₄ > 1 for λ > 1, but, for some κ, I^⋆₄ can also be greater than 1 when λ is less than 1, which means that the mean fibre direction can also be under compression.

Figure 1.

Plots of the generalized invariant I^⋆₄ as a function of the fibre stretch λ for five different values of the dispersion parameter κ in the range [0, 1/3].

Another point is that there exists a range of the angles of individual fibres for which the fibres are shortened when λ > 1 in the mean fibre direction. Hence, such fibres should be excluded from the energy function. We now consider N, as given by (2.15), which makes an angle Θ with the mean fibre direction M = e₃. Because of symmetry, the square of the stretch in the direction N (i.e. N · (CN)) is independent of Φ, and hence,

$$\mathbf{N}\cdot (\mathbf{C}\mathbf{N})={\mathrm{\lambda }}^2{\cos }^2\mathit{\Theta }+{\mathrm{\lambda }}^{-1}{\sin }^2\mathit{\Theta }\equiv {\mathrm{\lambda }}^{-1}+{\mathrm{\lambda }}^{-1}({\mathrm{\lambda }}^3-1){\cos }^2\mathit{\Theta }=I_4(\mathit{\Theta }),$$ 2.35

which defines the notation I₄(Θ). Thus, for N · (CN) > 1 with λ > 1, we require

$${\cos }^2\mathit{\Theta }>\frac{1}{{\mathrm{\lambda }}^2+\mathrm{\lambda }+1}={\cos }^2{\mathit{\Theta }}_{\mathrm{c}},$$ 2.36

which identifies the range of values of Θ for which the fibres are extended, i.e. −Θ_c < Θ < Θ_c or π − Θ_c < Θ < π + Θ_c. This means that the fibres should only contribute to the strain-energy function if cos²Θ is larger than cos²Θ_c. Thus, if extension of the mean fibre direction of the dispersion is used as a criterion for including the anisotropic term in the strain-energy function, then some compressed fibres will also be included, i.e. those outside these two ranges.

To our knowledge, it was the study of Federico & Herzog [19], which first suggested the possibility, following a comment by Gasser et al. [1] in relation to the GST model, of using a Heaviside function $\mathcal{H}$ in the AI model for excluding compressed fibres, which in our notation reads

$${\mathit{\Psi }}_{\mathrm{fib}}={\mathit{\Psi }}_{\mathrm{AI}}=\frac{1}{4\pi }{\int }_{\mathit{\Omega }}\rho (\mathbf{N})\mathcal{H}(I_4-1)W(I_4)\hspace{0.17em}\mathrm{d}\mathit{\Omega }.$$ 2.37

Subsequently, this approach was pursued by Federico & Gasser [5] and applied to analyse articular cartilage numerically. The idea of considering a Heaviside function in the energy for the collagen fibres was also used in the study of Ateshian et al. [13] and applied to articular cartilage. The more recent paper of Melnik et al. [9] employed a deformation-dependent structure tensor in order to exclude compressed fibres, which the authors applied to uniaxial extension with two families of fibres. The study of Hashlamoun et al. [46] also used a Heaviside function to exclude compressed fibres, and the authors compared the results for three different polynomial expansions of the energy function about I₄ = 1, and they also performed comparisons of the Cauchy stresses σ₁₁ and σ₂₂ as functions of stretch for equibiaxial and biaxial deformations. Note that the comparison in the exponential case was performed with the same parameters c₁ = k₁ and for c₂ = k₂ = 1 for each case. The comparison of the GOH model and the AI-based model is, therefore, erroneous and misleading, as pointed out by Holzapfel & Ogden [42,43].

In the study of Holzapfel & Ogden [17], the effect of using an inappropriate tension–compression switch for excluding the contribution of fibres under compression was analysed. A simple tension illustration indicates that the stiffness of the composite is in general significantly overestimated by not excluding fibres under compression. We have also computed the critical angle of the individual fibres relative to the fibre direction that corresponds to the switch. The subsequent paper of Li et al. [18] documents computational aspects of the model, and in particular expressions for the elasticity tensor and the integration boundary that admits only fibres which are extended were provided. The work of Gizzi et al. [39] introduced a probability density of I₄ to average I₄ itself over the range of values for I₄ > 1 as a means to exclude compressed fibres in the energy function. They also introduced two dispersion parameters, one as for the standard GST model and another one which is related to the second-order approximation. This approach was applied to uniaxial loading in the mean fibre direction in three dimensions and to a planar dispersion for uniaxial loading in the mean fibre direction.

Alternative schemes for omitting compressed fibres in the calculations based on a particular constitutive law have been detailed by Li et al. [20,47,48]. In [47], the exclusion was effected by a restriction of the domain of integration in the AI energy function so that this domain becomes deformation dependent. The method was applied to some representative numerical examples including uniaxial extension, simple shear and extension–inflation of a residually stressed carotid artery. In [48], a new general invariant which depends on only the fibres under tension was introduced, and then used to form the exponential energy function in place of I₄. This approach was applied to simple tension/compression, simple shear and unconfined compression of articular cartilage. A very efficient computational scheme based on discretizing a unit hemisphere with a finite number of spherical triangles and averaging the fibre density over each triangle was recently presented in [20]. The method was again applied to uniaxial extension, simple shear and also to the non-homogeneous extension of a rectangular strip.

3. Applications to specific deformations

(a). Biaxial extension

Here, we consider a sheet of arterial tissue in the e₁ and e₂ plane which is biaxially stretched so as to minimize the amount of shearing. For arterial tissue, two families of fibres are present and we now introduce the necessary equations to describe this.

While the mean fibre direction of the first family of fibres in the reference configuration is denoted by M, that of the second family of fibres is denoted by M^′, and the associated squares of the stretches in these two directions are denoted I₄ and I₆. The corresponding generalized invariants analogous to (2.26) are the same except that I₄ is changed to I₆, and I^⋆₄ to I^⋆₆, while Ψ_GST depends now only on I^⋆₄ and I^⋆₆. The corresponding contribution σ_GST to the Cauchy stress tensor is

$${\mathit{\sigma }}_{\mathrm{GST}}=2{\psi }_4^{\star }\mathbf{h}+2{\psi }_6^{\star }{\mathbf{h}}^{\mathrm{\prime }},$$ 3.1

where ψ^⋆_i = ∂Ψ_GST/∂I^⋆_i, i = 4, 6, and h^′ is given by (2.19), with m is replaced by m^′ = FM^′. By incompressibility the stretch in the thickness direction is λ₃ = (λ₁λ₂)⁻¹. We assume that each mean fibre direction makes an angle α with the direction 1 so that M = cosαe₁ + sinαe₂ and M^′ = cosαe₁ − sinαe₂; for the arrangement in an arterial sheet, see figure 2. The right Cauchy–Green tensor C has diagonal components λ²₁, λ²₂, λ²₃ with respect to Cartesian axes e₁, e₂, e₃. From (2.1), I₁ = λ²₁ + λ²₂ + λ²₃, and from the symmetry, I₄ = I₆ = λ²₁cos²α + λ²₂sin²α, while I_n = λ²₃. By using (2.19), the non-zero components of h and h^′ are given as

$$\begin{array}{rl}{h}_{11}& =h_{11}^{\mathrm{\prime }}=\overline{a}{\mathrm{\lambda }}_1^2,\overline{a}=2{\kappa }_{\mathrm{op}}[{\kappa }_{\mathrm{ip}}+(1-2{\kappa }_{\mathrm{ip}}){\cos }^2\alpha ],\end{array}$$ 3.2

$$\begin{array}{r}\\ h_{22}& =h_{22}^{\mathrm{\prime }}=\overline{b}{\mathrm{\lambda }}_2^2,\overline{b}=2{\kappa }_{\mathrm{op}}[{\kappa }_{\mathrm{ip}}+(1-2{\kappa }_{\mathrm{ip}}){\sin }^2\alpha ],\end{array}$$ 3.3

$$\begin{array}{rl}{h}_{33}& =h_{33}^{\mathrm{\prime }}=\overline{c}{\mathrm{\lambda }}_3^2,\overline{c}=(1-2{\kappa }_{\mathrm{op}})\end{array}$$ 3.4

$$\begin{array}{rl}\mathrm{and}{h}_{12}& =-h_{12}^{\mathrm{\prime }}=2{\kappa }_{\mathrm{op}}(1-2{\kappa }_{\mathrm{ip}}){\mathrm{\lambda }}_1{\mathrm{\lambda }}_2\sin \alpha \cos \alpha ,\end{array}$$ 3.5

where $\overline{a}+\overline{b}=2{\kappa }_{\mathrm{op}}$ and $\overline{a}+\overline{b}+\overline{c}=1$. Consequently, for I^⋆₄ and I^⋆₆, we can write

$$I_4^{\star }=I_6^{\star }=\mathrm{tr}\mathbf{h}=h_{11}+h_{22}+h_{33}.$$ 3.6

The non-zero components of the Cauchy stress tensor σ = σ_iso + σ_GST − pI are obtained as

$${\sigma }_{11}=2{\psi }_1{\mathrm{\lambda }}_1^2+4{\psi }_4^{\star }{h}_{11}-p,{\sigma }_{22}=2{\psi }_1{\mathrm{\lambda }}_2^2+4{\psi }_4^{\star }{h}_{22}-p\mathrm{and}{\sigma }_{33}=2{\psi }_1{\mathrm{\lambda }}_3^2+4{\psi }_4^{\star }{h}_{33}-p,$$ 3.7

where ψ₁ = ∂Ψ_iso/∂I₁, with Ψ_iso now just a function of I₁. Since we are considering a thin sheet under plane stress conditions, we have σ₃₃ = 0 and on elimination of p equations (3.7)₁ and (3.7)₂ can be written as

$${\sigma }_{11}=2{\psi }_1({\mathrm{\lambda }}_1^2-{\mathrm{\lambda }}_3^2)+4{\psi }_4^{\star }(h_{11}-h_{33})\mathrm{and}{\sigma }_{22}=2{\psi }_1({\mathrm{\lambda }}_2^2-{\mathrm{\lambda }}_3^2)+4{\psi }_4^{\star }(h_{22}-h_{33}).$$ 3.8

Now, by using the neo-Hookean model (2.6) and the exponential (2.25) in (3.8), we obtain

$${\sigma }_{11}=\mu ({\mathrm{\lambda }}_1^2-{\mathrm{\lambda }}_3^2)+4k_1(I_4^{\star }-1)\exp [k_2{(I_4^{\star }-1)}^2](h_{11}-h_{33})$$ 3.9

and

$${\sigma }_{22}=\mu ({\mathrm{\lambda }}_2^2-{\mathrm{\lambda }}_3^2)+4k_1(I_4^{\star }-1)\exp [k_2{(I_4^{\star }-1)}^2](h_{22}-h_{33}),$$ 3.10

where h₁₁, h₂₂, h₃₃ are given by (3.2)–(3.4) and I^⋆₄ by (3.6). For the special case of equibiaxial extension λ₁ = λ₂ = λ, λ₃ = λ⁻², $I_4^{\star }=(\overline{a}+\overline{b}){\mathrm{\lambda }}^2+\overline{c}{\mathrm{\lambda }}^{-4}$, and $h_{11}=\overline{a}{\mathrm{\lambda }}^2$, $h_{22}=\overline{b}{\mathrm{\lambda }}^2$, $h_{33}=\overline{c}{\mathrm{\lambda }}^{-4}$.

Figure 2.

Sheet of arterial tissue in the e₁ and e₂ plane which is biaxially stretched (λ₁ in e₁ and λ₂ in e₂ direction). Two families of fibres are present with mean fibre directions M and M^′, each making an angle α with the e₁ direction. The normal direction to the plane is e₃ = M_n.

We now provide the corresponding stress expressions for the AI model. By using expression (2.15) for N, the related vector n = FN in the deformed configuration has the form

$$\mathbf{n}={\mathrm{\lambda }}_1\sin \mathit{\Theta }\cos \mathit{\Phi }{\mathbf{e}}_1+{\mathrm{\lambda }}_2\sin \mathit{\Theta }\sin \mathit{\Phi }{\mathbf{e}}_2+{\mathrm{\lambda }}_3\cos \mathit{\Theta }{\mathbf{e}}_3.$$ 3.11

Then, from (2.10), we obtain

$$\begin{array}{rl}{\sigma }_{11}& =\frac{{\mathrm{\lambda }}_1^2}{2\pi }{\int }_{\mathit{\Omega }}\rho (\mathbf{N})W^{\mathrm{\prime }}(I_4){\sin }^2\mathit{\Theta }{\cos }^2\mathit{\Phi }\hspace{0.17em}\mathrm{d}\mathit{\Omega }+2{\psi }_1{\mathrm{\lambda }}_1^2-p,\end{array}$$ 3.12

$$\begin{array}{r}\\ {\sigma }_{22}& =\frac{{\mathrm{\lambda }}_2^2}{2\pi }{\int }_{\mathit{\Omega }}\rho (\mathbf{N})W^{\mathrm{\prime }}(I_4){\sin }^2\mathit{\Theta }{\sin }^2\mathit{\Phi }\hspace{0.17em}\mathrm{d}\mathit{\Omega }+2{\psi }_1{\mathrm{\lambda }}_2^2-p\end{array}$$ 3.13

$$\begin{array}{rl}\mathrm{and}{\sigma }_{33}& =\frac{{\mathrm{\lambda }}_3^2}{2\pi }{\int }_{\mathit{\Omega }}\rho (\mathbf{N})W^{\mathrm{\prime }}(I_4){\cos }^2\mathit{\Theta }\hspace{0.17em}\mathrm{d}\mathit{\Omega }+2{\psi }_1{\mathrm{\lambda }}_3^2-p,\end{array}$$ 3.14

where the density function ρ(N) is decoupled according to (2.16), with the von Mises distributions (2.23). By symmetry, we have σ₁₂ = σ₁₃ = σ₂₃ = 0. From (3.11), we can now derive an explicit expression for the invariant I₄, i.e.

$$I_4={\mathrm{\lambda }}_1^2{\sin }^2\mathit{\Theta }{\cos }^2\mathit{\Phi }+{\mathrm{\lambda }}_2^2{\sin }^2\mathit{\Theta }{\sin }^2\mathit{\Phi }+{\mathrm{\lambda }}_3^2{\cos }^2\mathit{\Theta }.$$ 3.15

By writing Ψ_fib as W(I₄) from (2.7), we calculate W^′(I₄), which is required in (3.12)–(3.14), as

$$W^{\mathrm{\prime }}(I_4)=c_1(I_4-1)\exp [c_2{(I_4-1)}^2].$$ 3.16

Finally, with the plane stress condition σ₃₃ = 0, the use of the neo-Hookean model (2.6), and on elimination of p equations (3.12) and (3.13) read

$${\sigma }_{11}=\frac{1}{2\pi }{\int }_{\mathit{\Omega }}\rho (\mathbf{N})W^{\mathrm{\prime }}(I_4)({\mathrm{\lambda }}_1^2{\sin }^2\mathit{\Theta }{\cos }^2\mathit{\Phi }-{\mathrm{\lambda }}_3^2{\cos }^2\mathit{\Theta })\hspace{0.17em}\mathrm{d}\mathit{\Omega }+\mu ({\mathrm{\lambda }}_1^2-{\mathrm{\lambda }}_3^2)$$ 3.17

and

$${\sigma }_{22}=\frac{1}{2\pi }{\int }_{\mathit{\Omega }}\rho (\mathbf{N})W^{\mathrm{\prime }}(I_4)({\mathrm{\lambda }}_2^2{\sin }^2\mathit{\Theta }{\sin }^2\mathit{\Phi }-{\mathrm{\lambda }}_3^2{\cos }^2\mathit{\Theta })\hspace{0.17em}\mathrm{d}\mathit{\Omega }+\mu ({\mathrm{\lambda }}_2^2-{\mathrm{\lambda }}_3^2).$$ 3.18

A similar derivation for uniaxial extension and simple shear was documented by Holzapfel & Ogden [43]. For the special case of equibiaxial extension with λ₁ = λ₂ = λ, the above equations apply with I₄ = λ²sin²Θ + λ⁻⁴cos²Θ.

(b). Homogeneous uniaxial extension

We now consider a strip of an incompressible arterial tissue which is loaded by a stretch λ₁ = λ in the e₁ direction. There are two families of fibres symmetrically disposed with respect to the e₁ direction but with non-symmetric dispersion, and mean fibre directions M and M^′, as indicated in figure 3.

Figure 3.

Sheet of arterial tissue in the e₁ and e₂ plane, which is uniaxially stretched (λ₁ = λ in e₁ direction). Two fibre families are symmetrically disposed with mean fibre directions M and M^′, each making an angle α with the e₁ direction.

We introduce the notation

$$f(I_4^{\star })=4{\overline{k}}_1(I_4^{\star }-1)\exp [k_2{(I_4^{\star }-1)}^2]\mathrm{and}{\overline{k}}_1=\frac{k_1}{\mu }.$$ 3.19

Then, with the condition σ₂₂ = 0, we obtain from (3.10) that

$$\frac{{\sigma }_{22}}{\mu }={\mathrm{\lambda }}_2^2-{\mathrm{\lambda }}_3^2+f(I_4^{\star })(h_{22}-h_{33})=0.$$ 3.20

With the expressions for h₂₂ and h₃₃ from (3.3)₁ and (3.4)₁, we then obtain, on suppressing the argument I^⋆₄ in f(I^⋆₄),

$$(1+\overline{b}f){\mathrm{\lambda }}_2^2=(1+\overline{c}f){\mathrm{\lambda }}_3^2.$$ 3.21

We also have the incompressibility condition λ₂λ₃ = λ⁻¹₁ so that from (3.21) and (3.6), we obtain

$${\mathrm{\lambda }}_2^2={\left(\frac{1+\overline{c}f}{1+\overline{b}f}\right)}^{1/2}{\mathrm{\lambda }}_1^{-1}\mathrm{and}{\mathrm{\lambda }}_3^2={\left(\frac{1+\overline{b}f}{1+\overline{c}f}\right)}^{1/2}{\mathrm{\lambda }}_1^{-1}$$ 3.22

and the following cubic for λ₁

$$\overline{a}{\mathrm{\lambda }}_1^3-I_4^{\star }{\mathrm{\lambda }}_1+\frac{\overline{b}+\overline{c}+2\overline{b}\overline{c}f}{{(1+\overline{b}f)}^{1/2}{(1+\overline{c}f)}^{1/2}}=0.$$ 3.23

By recalling (3.9), (3.19), (3.2)₁, (3.4)₁ and (3.22)₂, we find the Cauchy stress σ₁₁ in the e₁ direction is given by

$$\frac{{\sigma }_{11}}{\mu }={\mathrm{\lambda }}_1^2-{\mathrm{\lambda }}_3^2+f(h_{11}-h_{33})=(1+\overline{a}f){\mathrm{\lambda }}_1^2-{(1+\overline{b}f)}^{1/2}{(1+\overline{c}f)}^{1/2}{\mathrm{\lambda }}_1^{-1},$$ 3.24

where λ₁ is provided in (3.23).

Note that if λ₂ = λ₃, then we obtain from (3.21) that $1+\overline{c}f=1+\overline{b}f$. So, either I^⋆₄ = 1, which is a trivial case, or $\overline{b}=\overline{c}$, which, using (3.3)₂ and (3.4)₂ (for $\overline{b}$ and $\overline{c}$), leads to the condition

$$2{\kappa }_{\mathrm{op}}[1+{\kappa }_{\mathrm{ip}}+(1-2{\kappa }_{\mathrm{ip}}){\sin }^2\alpha ]=1.$$ 3.25

This condition can be satisfied for quite a wide range of connections between α, κ_ip and κ_op. For example, if κ_op = 1/3, then sin²α = 1/2 independent of κ_ip. On the other hand, if κ _ip = 1/2, then κ_op = 1/3 independent of α (the isotropic case). If κ_ip = 0, then sin²α = (1 − 2κ_op)/κ_op, which requires 1/4≤κ_op≤1/2. Similarly, κ_ip = 1 requires sin²α = (4κ_op − 1)/2κ_op, which again requires 1/4≤κ_op≤1/2. If κ_ip = 1/4, then sin²α = (2 − 5κ_op)/κ_op, which requires 2/7≤κ_op≤2/5. There is no solution for either κ_op = 0 or κ_op = 1/2, which are limiting cases that are not physiologically relevant.

With (3.25), the cubic equation (3.23) reduces to

$$\overline{a}{\mathrm{\lambda }}_1^3-I_4^{\star }{\mathrm{\lambda }}_1+2\overline{b}=0.$$ 3.26

Since $\overline{a}+\overline{b}=2{\kappa }_{\mathrm{op}}$ and $\overline{b}=\overline{c,}$ we deduce that $\overline{b}=1-2{\kappa }_{\mathrm{op}}$ and $\overline{a}+2\overline{b}=1$ so that (3.26) can be written as

$$I_4^{\star }=\frac{\overline{a}{\mathrm{\lambda }}_1^3+2\overline{b}}{{\mathrm{\lambda }}_1}$$ 3.27

and hence (3.24)₃ gives

$$\frac{{\sigma }_{11}}{\mu }={\mathrm{\lambda }}_1^2-{\mathrm{\lambda }}_1^{-1}+(\overline{a}{\mathrm{\lambda }}_1^2-\overline{b}{\mathrm{\lambda }}_1^{-1})\hspace{0.17em}f(I_4^{\star }),$$ 3.28

which becomes an explicit expression in terms of λ₁ when (3.27) is substituted in (3.19).

We now provide the corresponding equations for the AI approach. For uniaxial extension, we require that σ₂₂ = 0 so that with λ₃ = λ⁻¹₁λ⁻¹₂ we have from (3.18)

$$\frac{1}{2\pi }{\int }_{\mathit{\Omega }}\rho W^{\mathrm{\prime }}(I_4)({\mathrm{\lambda }}_2^2{\sin }^2\mathit{\Theta }{\sin }^2\mathit{\Phi }-{\mathrm{\lambda }}_1^{-2}{\mathrm{\lambda }}_2^{-2}{\cos }^2\mathit{\Theta })\hspace{0.17em}\mathrm{d}\mathit{\Omega }+\mu ({\mathrm{\lambda }}_2^2-{\mathrm{\lambda }}_1^{-2}{\mathrm{\lambda }}_2^{-2})=0,$$ 3.29

which gives λ₂ in terms of λ₁ on noting that I₄ is given by (3.15) with λ²₃ = λ⁻²₁λ⁻²₂. Now, by subtracting (3.18) from (3.17) with σ₂₂ = 0, we obtain

$${\sigma }_{11}=\frac{1}{2\pi }{\int }_{\mathit{\Omega }}\rho W^{\mathrm{\prime }}(I_4)({\mathrm{\lambda }}_1^2{\cos }^2\mathit{\Phi }-{\mathrm{\lambda }}_2^2{\sin }^2\mathit{\Phi }){\sin }^2\mathit{\Theta }\hspace{0.17em}\mathrm{d}\mathit{\Omega }+\mu ({\mathrm{\lambda }}_1^2-{\mathrm{\lambda }}_2^2),$$ 3.30

with λ₂ in terms of λ₁ from (3.29), which gives σ₁₁ as a function of λ₁.

Finally, let us discuss the special case λ₂ = λ₃ = λ^−1/2₁. Then, by using sin²Φ = 1 − cos²Φ and cos²Θ = 1 − sin²Θ, (3.29) gives

$${\int }_{\mathit{\Omega }}\rho W^{\mathrm{\prime }}(I_4){\sin }^2\mathit{\Theta }{\cos }^2\mathit{\Phi }\hspace{0.17em}\mathrm{d}\mathit{\Omega }={\int }_{\mathit{\Omega }}\rho W^{\mathrm{\prime }}(I_4){\cos }^2\mathit{\Theta }\hspace{0.17em}\mathrm{d}\mathit{\Omega },$$ 3.31

so that (3.30) reduces to

$${\sigma }_{11}=\frac{1}{2\pi }({\mathrm{\lambda }}_1^2+2{\mathrm{\lambda }}_1^{-1}){\int }_{\mathit{\Omega }}\rho W^{\mathrm{\prime }}(I_4){\cos }^2\mathit{\Theta }\hspace{0.17em}\mathrm{d}\mathit{\Omega }-\frac{{\mathrm{\lambda }}_1^{-1}}{2\pi }{\int }_{\mathit{\Omega }}\rho W^{\mathrm{\prime }}(I_4)\hspace{0.17em}\mathrm{d}\mathit{\Omega }+\mu ({\mathrm{\lambda }}_1^2-{\mathrm{\lambda }}_1^{-1}),$$ 3.32

where ρ is given by (2.16) and (2.23), and I₄ is given by

$$I_4={\mathrm{\lambda }}_1^2{\sin }^2\mathit{\Theta }{\cos }^2\mathit{\Phi }+{\mathrm{\lambda }}_1^{-1}({\sin }^2\mathit{\Theta }{\sin }^2\mathit{\Phi }+{\cos }^2\mathit{\Theta })=({\mathrm{\lambda }}_1^2-{\mathrm{\lambda }}_1^{-1}){\sin }^2\mathit{\Theta }{\cos }^2\mathit{\Phi }+{\mathrm{\lambda }}_1^{-1},$$ 3.33

which results from (3.15).

4. Numerical examples

In this section, we illustrate the theory in §3 by relating it to sets of data for (a) equibiaxial extension of a tissue sample obtained from an abdominal aortic aneurysm and (b) uniaxial extension of strips from the circumferential and axial directions of a media from a healthy thoracic aorta.

(a). Equibiaxial extension

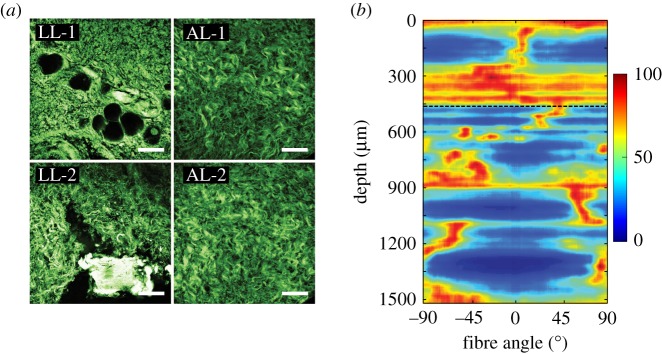
Here, we use experimental data which were obtained from an equibiaxial test of a tissue taken from a human abdominal aortic aneurysm, as documented in fig. 12 of Niestrawska et al. [49] (sample AAA-4.1). The experimental data are shown here in figure 4 in terms of the circumferential Cauchy stress (open squares) and longitudinal Cauchy stress (open circles) as functions of the equibiaxial stretch. As can be seen, the mechanical response is highly anisotropic and nonlinear. A representative set of mechanical and structural data was selected from the sets of data of Niestrawska et al. [49]. Figure 5, which is based on second-harmonic generation (SHG), shows the structure of different layers taken from two adjacently located patches. To the right there is an intensity plot indicating a highly disturbed collagen fibre structure for the luminal layer with 450 μm thickness. The abscissa corresponds to the angle measured from the circumferential direction at the origin (0°), while ±90° refer to the axial direction. The red colour identifies fibre angles at which there are fibres with that orientation, while the blue colour indicates the absence of fibres. More details can be found in the caption and in the study [49].

Figure 4.

Plots of the Cauchy stress versus the stretch for representative data from an equibiaxial test of a tissue taken from an abdominal aortic aneurysm (i.e. sample AAA-4.1, as illustrated in fig. 12 of Niestrawska et al. [49]). Open squares and circles indicate the experimental data, while solid curves show the fitting of (a) the GST model and (b) the AI model.

Figure 5.

SHG images and intensity plot for a tissue taken from an abdominal aortic aneurysm (AAA-4, see fig. 8b of Niestrawska et al. [49]): structure of luminal layer (LL-1 and LL-2), and abluminal layer (AL-1 and AL-2), of two patches taken from adjacent locations. Image LL-1 shows bright ‘stains’ representing a degenerated collagen structure, and image LL-2 indicates a different structure with calcification and wavy collagen fibres. The AL patches are similar to those of a healthy layer. The intensity plot (b) exhibits a highly disturbed structure for the upper 450 μm and an adventitia-like structure with generally two fibre families in the remaining wall thickness. The intensity plot starts at the top with the LL. Scale bar is 100 μm. (Online version in colour.)

The structural parameters for the patient AAA-4 according to [49] are κ_ip = 0.223, κ_op = 0.413 and α = 24.33°. On that basis a GST fitting to the experimental data was performed and achieved the following set of parameters: μ = 1.66 kPa, k₁ = 5.82 kPa and k₂ = 99.91 with R² = 0.98, but the corresponding plot was not shown therein. The R² value can be improved by starting with the dispersion parameters above and the value of μ, but allowing α to be a fitting parameter so that we obtained the fit shown in figure 4a with the values k₁ = 7.68 kPa and k₂ = 91.8 and α = 25.82°, with R² = 0.997. For the fit, the equations (3.9) and (3.10) were used for the special case of equibiaxial extension. Figure 4b shows a corresponding fit of the data for the AI model by using (3.17) and (3.18) with (3.16) for the special case of equibiaxial extension, and with the von Mises distribution (2.23). The integrations were performed numerically using Mathematica [50]. The fitting process achieved the concentration parameters a = 0.9 and b = 13.5 and the mechanical parameters μ = 1.66 kPa, c₁ = 0.46 kPa and c₂ = 37.0. The concentration parameters a and b lead to values of κ_ip = 0.295 and κ_op = 0.491 according to (2.23)₁ and (2.23)₂, respectively, whereas the κ_ip and κ_op for the GST model were based on imaging data, while a and b were obtained as fitting parameters. Thus, if the values a and b are associated with values of κ_ip and κ_op given by (2.23), these are reasonably consistent with the structurally obtained values. The fit is in good agreement with the experimental data and leads to an R² value of 0.998. It should be noted that the values of the stretches and the corresponding stresses obtained for equibiaxial tension are rather low. This is because of the experimental limitations of a biaxial extension test. Larger extensions and correspondingly larger stresses can be obtained in uniaxial extension experiments, as we now discuss.

(b). Uniaxial extension

We now fit each of the GST and the AI models to representative sets of new experimental data obtained from axial and circumferential strips from a media of a healthy human thoracic aorta (59 years, female). The donor sample was separated into layers, and dog-bone specimens of the media with markers for real-time tracking were prepared. The medial strips were preconditioned in five cycles and then extended until failure. The protocol took place within a container which was filled with a phosphate-buffered saline solution and kept at 37°C (as described by Sommer et al. [51]). For the pre-softening elastic domain the data in the form of the Cauchy stress versus stretch are presented in figure 6 as open squares (circumferential) and open circles (longitudinal), while the subsequent softening data in the circumferential case are shown as solid squares.

Figure 6.

Plots of the Cauchy stress versus the stretch for a representative set of data obtained from longitudinal and circumferential strips of a media from a healthy human thoracic aorta. Open circles (longitudinal) and open squares (circumferential) indicate the experimental data for the pre-softening elastic domain; the subsequent softening data in the circumferential case are shown as solid squares. The solid curves show the fitting of (a) the GST model and (b) the AI model.

Structural data were obtained by using SHG according to the protocol documented by Schriefl et al. [52], except that the sampling was set to 0.62 × 0.62 × 5 μm instead of 0.62 × 0.62 × 1 μm. For each strip, the data were obtained separately in two orthogonal planes, namely, the radial/circumferential and radial/axial (out-of-plane), and in the circumferential/axial plane (in-plane). The out-of-plane data from the two orthogonal planes were fitted together using the least-squares method [53], which produced the concentration parameter b, from which the dispersion parameter κ_op was calculated via (2.24)₂. The in-plane data were fitted using a maximum-likelihood estimation [54], which produced the mean fibre angle α and the median concentration parameter a, while the dispersion parameter κ_ip was obtained from (2.24)₁. Then, the values obtained were averaged between the two strips to give the in-plane and out-of-plane dispersion parameters, the concentration parameters, and the mean fibre angle, as represented in table 1.

Table 1.

Structural parameters.

	dispersion	concentration	mean fibre angle
in-plane	κip = 0.227	a = 1.32	α = 8.0°
out-of-plane	κop = 0.484	b = 13.68	—

Figure 7 illustrates contrast enhanced SHG images of the collagen architecture of a circumferential strip using FIJI (http://fiji.sc/Fiji, Ashburn, VA). Figure 7a shows an image obtained from the in-plane stack (axial/circumferential), which corresponds to a depth of 300 μm in the intensity plot (figure 7d). Figures 7b and 7c shows out-of-plane images of the radial/axial and the radial/circumferential planes, respectively. Figure 7d shows an intensity plot through the thickness of the medial strip in the circumferential direction, which is composed of multiple lamellar units. The strip in the axial direction shows a similar intensity pattern. An individual image does not show two families of fibres but the two fibre families can be identified through the stack by the zig-zag characteristic.

Figure 7.

SHG images and intensity plot for a tissue taken from the media of a healthy human thoracic aorta: (a–c) illustrate SHG images of the collagen architecture of the circumferential strip obtained from (a) an in-plane image (axial/circumferential) corresponding to 300 μm depth in the intensity plot, see (d); (b) out-of-plane image of the radial/axial plane; (c) out-of-plane image of the radial/circumferential plane; (d) intensity plot of a circumferential strip through the thickness of the media depicting highly aligned fibres along ±7.2° from the circumferential direction (with 0°). The intensity plot starts at the top with the medial side closer to the adventitia. Scale bar is 100 μm. (Online version in colour.)

We now focus on fitting the data up to the point where softening is initiated. Based on the structural data for the GST fit, we have assumed values of κ_op = 0.48 and κ_ip = 0.25 which are approximations of the measured data (table 1). These two values served as fixed input data for the fitting procedure of the GST model. Noting that $\overline{a}+\overline{b}=2{\kappa }_{\mathrm{op}}$, the fitting produced $\overline{a}=0.385$, and hence $\overline{b}=0.575$, and $\overline{c}=0.04$, then k₁ = 107.0 kPa and k₂ = 0.155, and α = 33.3°. The model results are illustrated as solid curves in figure 6a and show good agreement with the experimental data, with R² = 0.993. While the dispersion parameters used in the fitting are very similar to those obtained from the images, the mean fibre angle α is not so close. However, this can be explained by the fact that there is quite a large range of fibre angles and the averaging within the image stacks to obtain the structural parameters for individual strips and then between the strips has a considerable impact on the values reported in table 1.

As far as the AI model is concerned, the fitted parameters are a = 1, b = 10, c₁ = 4.725 kPa and c₂ = 0.038. For both models, the shear modulus μ used was 1.05 kPa. Figure 6b also illustrates a good agreement with the experimental data, with R² = 0.980.

5. Conclusion and perspectives

We have described both the GST and AI approaches for the modelling of fibrous tissues with dispersed fibre structures. The constitutive equations for each model have then been applied to the special cases of equibiaxial and uniaxial extension of tissue samples obtained from human aortas. For each of the GST and the AI models, the agreement with experimental data has been shown to be very good.

The basic structure of the dispersion model does not take into account interactions between fibres such as cross-linking. There is some evidence that a larger number of collagen cross-links leads to a higher wall stiffness and a larger elastic modulus in older arteries [55]. In addition, the study of Xu et al. [56] shows that the stress–strain responses based on equibiaxial tensile tests of engineered collagen scaffolds with different degrees of cross-linking indicate the influence of the cross-links on the mechanical response; in particular, the response becomes stiffer as the proportion of cross-links increases. A similar conclusion was drawn by Wang & Chesler [57] in respect of the pressure–stretch response of isolated dynamic tests of pulmonary arteries. The more recent study of Tian et al. [58] uses the eight-chain Arruda–Boyce model with a parameter N which corresponds to a number of subunits per chain; the density of cross-links is larger for smaller N which is a basic way to account for cross-links. The study of Xu et al. [56] also attempts to model the effect of cross-links with a model based on Gasser et al. [1] by varying the parameters, although the cross-linking was not explicitly accounted for otherwise. There is a need for more structural data on the fibre arrangement and cross-linking, and for more advanced constitutive models which are able to better capture the cross-link stabilization of the side-by-side packing of collagen molecules and to quantify the effect on the mechanical response. New invariants might also be useful in the modelling of cross-linking and associated in-plane and out-plane dispersion. In this connection, a recent relevant modelling approach aimed at capturing the mechanical response of fibrous biological tissues using a general invariant that excludes compressed fibres is documented by Li et al. [48].

In cardiovascular diseases such as aortic dissection there is evidence that medial weakness forms a basis for an aortic dissection and that weakness is due to the structural abnormalities of elastic fibres; in particular, a marked reduction in interlaminar elastic fibres is observed (see, e.g. Nakashima [59]; for a review of the mechanical assessment of arterial dissection, see Tong et al. [60]). Signs of fibre degradation and/or fragmentation are similarly observed in aortic aneurysms (see, e.g. Borges et al. [61]), a cardiovascular disease in which the elastin content decreases significantly with increasing aneurysm diameter (Tong et al. [62]). Consequently, changes in the architecture of the medial elastic pattern of aortas occur, which play a significant role in the pathogenesis of aortic dissections and aneurysms. Hence, at the microscale, an extension of the dispersion models is required to capture such changes in the medial elastin structure, and to improve constitutive modelling, even though the mechanical response of the non-collagenous material is rather isotropic.

We also need better structural characterizations of tissue components in atherosclerotic plaques in order to inform constitutive models used to predict the mechanical environment of stenotic arteries during interaction with stents [63]. A more accurate consideration of the collagen structure, in particular, of the fibrous cap (i.e. the fibrotic part at the luminal border) is important because this plaque component may become remarkably stressed and may lead to tissue failure and to severe life-threatening clinical consequences such as stroke or myocardial infarction. The recent study of Douglas et al. [64] documents significant differences in the fibre architecture across the luminal region of human coronary atherosclerotic plaques. The study describes a vital pathway for improving our understanding of material stability and rupture mechanisms of plaques on the basis of considering the fibre structure.

Clearly, improved fibre dispersion models when including the nanoscale interactions between the different tissue constituents may advance the development of multiscale modelling methods, an important research area still in its infancy. Multiscale models are able to describe complex processes across multiple length, time or energy scales to inform the macroscopic response of tissues. For a brief summary of the most recent developments on multiscale modelling in biomechanics, see the review article by Bhattacharya & Viceconti [65]. A collection of studies on multiscale soft tissue mechanics and mechanobiology can be found in a book edited by Holzapfel & Ogden [66].

Ethics

The use of donor samples for the uniaxial extension tests was approved by the Ethics Committee at the Medical University of Graz (27-250 ex 14/15).

Data accessibility

The experimental data from the equibiaxial test of the tissue of an abdominal aortic aneurysm (figure 4) and from the uniaxial tests of the media of a healthy human thoracic aorta (figure 6) can be downloaded from doi.org/10.6084/m9.figshare.7667627 [67]. In addition, on that link, we have also provided 106 raw 8-bit *.tif files obtained by SHG imaging used to produce the intensity plot of a circumferential strip through the thickness of the media, as shown in figure 7d. The integrations required for the AI model were numerically solved using Mathematica [50]. All computational results are reproducible.

Authors' contributions

G.A.H. and R.W.O. conceived and designed the research, interpreted the results and drafted the manuscript; S.S. carried out the experimental analyses on human tissues (figure 6), produced the SHG images (figure 7) and analysed the results. All authors edited and revised the manuscript, and gave final approval for publication.

Competing interests

No conflicts of interest, financial or otherwise, are declared by the authors.

Funding

The work of R.W.O. was, in part, funded by the UK EPSRC grant no. EP/N014642/1.