Abstract
Quantitative experimental studies of the thermodynamics with which biopolymers interact with specific surfaces remain quite limited. In response, here we describe experimental and theoretical studies of the change in folding free energy that occurs when a simple biopolymer, a DNA stem-loop, is site-specifically attached to a range of chemically distinct surfaces generated via self-assembled monolayer formation on a gold electrode. Not surprisingly, the extent to which surface attachment alters the biopolymer’s folding free energy depends strongly on the charge of the surface, with increasingly negatively charged surfaces leading to increased destabilization. A simple model that considers only the excluded volume and electrostatic repulsion generated by the surface and models the ionic environment above the surface as a continuum quantitatively recovers the observed free energy change associated with attachment to weakly charged negative surfaces. For more strongly charged negative surfaces a model taking into account the discrete size of the involved ions is required. Our studies thus highlight the important role that electrostatics can play in the physics of surface−biomolecule interactions.
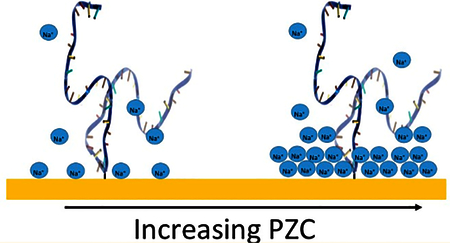
INTRODUCTION
Theoretical studies suggest that biopolymers interact with surfaces via a variety of mechanisms, with often-profound consequences for their folding and function. Attachment to a completely inert surface, for example, should stabilize the folded state by reducing the entropy of the unfolded state.1 Attachment to a charged—but otherwise inert—surface destabilizes the folded state through either electrostatic repulsion,2 which preferentially stabilizes the more expanded unfolded state, or electrostatic attraction, which promotes unfolding and subsequent electrostatic adsorption.3 Finally, attachment to chemically reactive surfaces can alter the folding free energy of a tethered biopolymer via specific interactions which are more easily satisfied by either the folded or unfolded state, leading to stabilization or destabilization, respectively.4
Motivated by the above predictions, we have developed5 an electrochemical method for measuring the extent to which surface interactions alter biomolecular folding free energies (Figure 1). The approach utilizes a biomolecule modified at one end with a methylene blue “redox reporter” and tethered by the other end to a self-assembled monolayer deposited onto a gold surface. The folded biomolecule holds the reporter at a fixed distance from the surface. Chemical denaturation (unfolding) of the biomolecule relaxes this constraint, changing the rate of electron transfer. Following this, via square-wave voltammetry as we titrate the biomolecule with urea we can then determine its folding free energy using the well-established linear relationship between denaturant concentration and stability.6,7 Finally, comparison of this with the stability of the molecule in solution (determined via optically monitored urea denaturation) informs on the free energy of interaction with the surface.
Figure 1.
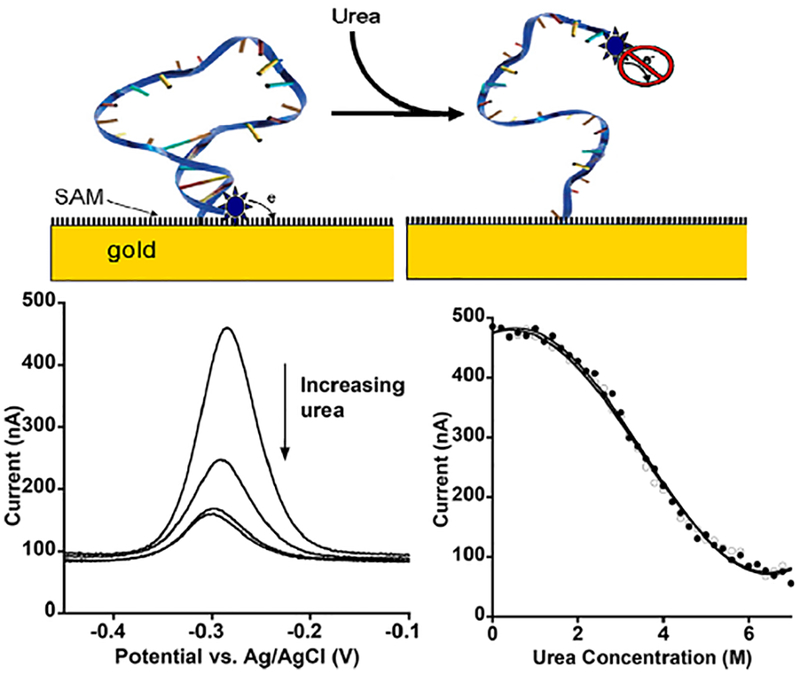
(Top) In this study, we have characterized the folding thermodynamics of a stem-loop DNA site-specifically attached via its 5′ end to a variety of monolayer-coated gold surfaces. The distal terminus of the DNA is modified with a methylene blue redox reporter, electron transfer from which reports on its conformation.5 (Bottom Left) Specifically, when the stem is formed the reporter is held close to the surface, increasing electron transfer efficiency. When the stem-loop is unfolded via the addition of urea, electron transfer is reduced. (Bottom Right) The folding free energy of the stem loop can then be determined by fitting the peak current as a function of urea to a standard linear free energy model.6,7 The open and closed symbols represent forward (low to high denaturant) and reverse titrations, respectively, performed on a single electrode, and serve to illustrate the reversibility that this system exhibits.
Using the above approach, we have previously explored the thermodynamic consequences of site-specifically attaching a DNA stem loop to a hydroxyl-terminated, six-carbon (C6OH) thiol-on-gold self-assembled monolayer (SAM) held at an applied potential matching the −260 mV (versus Ag/AgCl) redox potential of methylene blue.5,8 We selected this model system because (i) DNA folds reversibly on many SAM-coated gold surfaces via a unimolecular two-state folding transition,9 (ii) DNA is structurally well-characterized in solution, and (iii) DNA is uniformly negatively charged, simplifying modeling of any electrostatic interactions. In our prior studies,5 we found that, while at high ionic strength the surface-bound molecule is stabilized (relative to in solution), the reverse is true at ionic strengths below ~130 mM (Figure 2, left). We believe that this occurs due to competition between excluded volume, which stabilizes the folded conformation by reducing the entropy of the unfolded state (at all ionic strengths), and electrostatic repulsion between the DNA and the negatively charged (at the potential applied in our experiments) surface, which destabilizes (repels) the more compact folded state under low ionic strength conditions. In support, a quantitative model of these effects recapitulates our experimental results.5 Specifically, by combining existing theories of the conformation of surface-bound polyelectrolytes10,11 to model the unfolded state, a nuclear magnetic resonance (NMR)-derived solution structure of the folded state,12−14 and theoretical estimates of the excluded volume entropy effect,5,11,15 we generated a simple theory of the effects of surface attachment on this biomolecule that quantitatively recovers our experimental observations.
Figure 2.
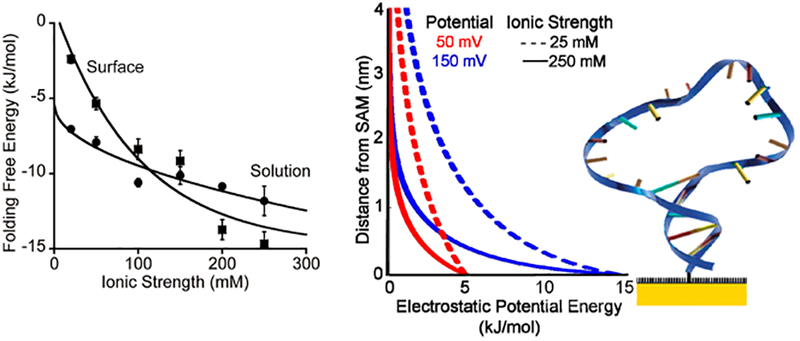
(Left) The folding free energy of a stem-loop site-specifically attached to a C6OH SAM-on-gold surface is more sensitive to ionic strength than that of the same stem-loop in solution. This is because attachment to this negatively charged (at the potential applied in our experiments) surface destabilizes the folded state through electrostatic repulsion.5 (Right) This scheme serves to illustrate the dimensions of the stem loop relative to the potential field that forms above the surface when a potential is applied. Specifically, shown are the electric fields produced if the surface is at a potential of 50 (red) or 150 mV (blue) (versus the potential of zero charge; pzc) at ionic strengths of 25 (dashed lines) or 250 mM (solid lines). At low surface charge and/or high ionic strength the electric field experienced by the stem-loop is minimal. The left-hand panel was adapted from ref 5.
For a complete description of the prior model, see ref 5; in brief it is as follows: We model the change in folding free energy, ΔΔGf, between the biomolecule on the surface and the same molecule free in bulk solution as having two components: ΔΔHEL, the difference between the electrostatic cost of bringing the folded state (ΔHFSol‑Sur) versus the unfolded state (ΔHUSol‑Sur) from solution to the surface, and ΔΔSEV, the difference in the entropy of folding of the surface bound molecule and that of the molecule in solution.
| (1) |
THE ENTHALPIC COMPONENT
We modeled the enthalpy component, which accounts for how each charge moves in the electric field as the stem loop folds, as
| (2) |
where ρ(z) and U(z) are the charge density of the biopolymer and the electrostatic potential, respectively, at height z above the surface. According to the Poisson−Boltzmann equation, the latter is given by
| (3) |
| (4) |
where λD is the Debye length, e is the elementary charge, T is the temperature, and ϕ0 is the potential at the surface of the SAM relative to the potential at which the net surface charge is zero (i.e., relative to the potential of zero charge, pzc). The Debye length (for any given ionic strength) and ρ(z) are predicted by theory.16 Given this, ΔΔHEL is dependent on only a single fitted parameter, the pzc.
THE ENTROPIC COMPONENT
Because the folded state is fairly rigid, we assume that the entropic cost of surface attachment arises solely from the restricted conformational freedom of the unfolded state. Prior analytical theory and simulation-based arguments suggests that this loss in entropy goes logarithmically with the number of persistence lengths in the chain (NK):
| (5) |
where A ≈ 1.5 kBT (ref 15), and B is 0.5 for a Gaussian chain11 and 0.44 for a self-avoiding chain.15 The persistence length for a polyelectrolyte is dependent on ionic strength. In this case, the ionic strength of relevance is that found near the surface, which varies with both the ionic strength of the bulk solution and the surface charge (as ions migrate in response to the electric field), with the latter dependent on the applied potential and the pzc. Because the ionic-strength dependence of the persistence length of single-stranded DNA17 and the effects of surface charge on surface ionic strength18 are well established, the entropic contribution can also be estimated from theory as a function of only the pzc.
Despite depending only on a single fitted parameter, the pzc, our model recovers our observed changes in folding free energy (as a function of ionic strength) quite well.19 Moreover, it produces a best-fit pzc of −206 mV, which is within error of the −210 ± 10 mV previously estimated (using other methods) for the C6OH surface we employed. Together, these observations suggest that, despite its simplicity, our model provides a fairly complete description of the system. In this paper, we expand the experimental testing of this model by measuring the thermodynamic consequences of attaching the same stem-loop DNA to thiol-on-gold monolayers varying greatly in chemistry and surface charge.
MATERIALS AND METHODS
The DNA oligonucleotide employed was synthesized by Bio-Search Technologies (Novato, CA) and were purified by anion exchange HPLC followed by reverse phase HPLC. Its sequence was 5′-ACT CTC GAT CGG CGT TTT AGA GAG G-3′. This was modified with a 6- or an 11-carbon thiol on its 5′-terminus (for use with C6 or C11 SAMs, respectively) and methylene blue attached via amide bond formation to a 6-carbon amine on its 3′-terminus. As the gold surface, we employed polycrystalline gold disk electrodes (2 mm diameter; BAS, West Lafayette, IN).
Prior to depositing the DNA and monolayers on our gold surfaces we first electrochemically cleaned them using a series of oxidation and reduction cycling as follows. (1) Cyclic voltammetry (CV) for 500 cycles at 2 V/s 0.5 M NaOH between −0.4 and −1.35 V. (2) Constant potential at 2 V for 5 s in 0.5 M H2SO4. (3) Constant potential at −0.35 V for 15 s in 0.5 M H2SO4. (4) CV for 120 cycles at 4 V/s between −0.35 and 1.5 V in 0.5 M H2SO4. (5) CV for 4 cycles at 0.1 V/s between −0.35 and 1.5 V in 0.5 M H2SO4. (6) CV, 10 cycles at 0.1 V/s between 0.2 and 0.75 V in 0.01 M KCl/0.1 M H2SO4. (7) CV, 10 cycles, 0.1 V/s between 0.2 and 1 V in 0.01 M KCl/0.1 M H2SO4. (8) CV, 10 cycles, 0.1 V/s between 0.2 and 1.25 V in 0.01 M KCl/0.1 M H2SO4. (9) CV, 10 cycles, 0.1 V/s between 0.2 and 1.5 V in 0.01 M KCl/0.1 M H2SO4.
To prepare the surface we first treated the stem-loop DNA (1 μM) in 20 μM tris (2-carboxyethyl) phosphine hydrochloride before dilution to 50 nM with 180 mM NaCl/20 mM phosphate (pH 7.0) and then incubated the clean gold surface in this solution (5 min, room temperature). The resulting surface was washed with deionized water before being incubated overnight in a solution of the appropriate ω-modified alkanethiol to form the SAM. The relevant solutions were 2 mM 6-mercaptohexanol in water, 40 mM 6-mercaptohexanoic acid in ethanol, 40 mM 11-mercaptoundecanol in ethanol, and 100 mM 6-mercaptohexaneamine in ethanol. These conditions lead to relatively sparse packing of the DNA (the dilute regime), such that neighboring biopolymers do not interact significantly.8
We determined folding free energies using urea melts generated either with a Hamilton 500C titrator or by manual titrations starting at 10 M urea (in buffer) and titrating in buffer. At each urea concentration the system was allowed to equilibrate for 30 s (with stirring) prior to measurement. The buffer employed was 20 mM sodium phosphate (pH 7.0) with sodium chloride added to bring the solution to the desired sodium ion concentration. Surface measurements were conducted using square wave voltammetry from 0 to −0.5 V with a 25 mV step size and a 4 mV interval at a frequency of either 50 or 60 Hz on either a CHI 630 potentiostat (CH Instruments, Austin, TX) or a PalmSens (PalmSens BV, The Netherlands) in a standard cell with a platinum counter electrode and a Ag/AgCl (saturated with 3 M NaCl) reference electrode.
Prior to use, each electrode was washed with 10 M urea in buffer, washed again with buffer, and then incubated in 10 M urea in buffer for at least 1 h prior to the start of the titration. To determine the folding free energy, a plot of peak current versus urea concentration was fitted to a standard two-state unfolding curve with linear, sloping baselines.7 After all titrations, all surfaces were returned to 10 M urea to ensure that the unfolding of the surface-bound biomolecule was reversible. The error bars reported for the free energies represent the standard error of the mean of at least three independently measured titrations.
RESULTS
We have selected as our model system one of the simplest biomolecules that still undergoes an easily measurable unfolding transition: a 25-base DNA that, due to the presence of self-complementary ends, adopts a stem-loop conformation. We monitored the urea-induced unfolding of this stem-loop when free in bulk solution using circular dichroism spectroscopy.5 To monitor its urea-induced unfolding when site specifically attached to a surface we covalently linked it to a gold electrode via an alkanethiol attached to its 5′ terminus (as part of a well-formed self-assembled monolayer20) and attached a methylene blue redox “reporter” on its opposite terminus (Figure 1, Top). The latter provides a ready means of following the unfolding of the stem-loop via square wave voltammetry (Figure 1, Bottom left). We extracted folding free energies from these data by assuming a linear relationship between free energy and the concentration of the denaturant ΔG = ΔG°′ + m[urea], where ΔG°′ is the folding free energy in the absence of denaturant and m is the denaturant strength. The assumption of linearity is well established for the folding of both proteins and nucleic acids.7,21 (For further discussion of the relationship between folding free energy and ionic strength, and how chemical denaturants modulate that relationship, the reader is referred to work by Shelton et al.7 and Hirs.21) The difference between the folding free energy determined under the two conditions then reports on the extent to which interactions with the surface stabilize or destabilize the biomolecule (Figure 2, left).
Following our earlier work on the folding free energy of the same stem-loop on a hydroxyl-terminated, six-carbon mono-layer, we describe here the thermodynamic consequences of attaching it to other monolayers differing in surface chemistry and/or surface charge. The previously reported pzc of two of these new surfaces, 11-mercapto-1-undecanol (C11OH) and 6-mercaptohexanoic acid (C6OOH), are, respectively, −50 ± 10 mV and −130 ± 50 mV (versus Ag/AgCl).19,22 These surfaces thus exhibit potentials of −210 ± 10 mV and −130 ± 50 mV when held at the −260 mV (versus Ag/AgCl) redox potential of methylene blue, rendering them more negatively charged than the −50 mV potential the surface we employed in our original studies adopts under these same conditions (Figure 3). Consistent with this, we find that attachment to the C11OH SAM is more destabilizing than attachment to the C6OOH SAM, which, in turn, is more destabilizing than attachment to the C6OH SAM over all of the ionic strengths we have investigated (Figure 4). The third new monolayer we explored was 6-mercaptohexylamine SAM, HS(CH2)6NH2(C6NH2), which, due to its positively charged headgroup, is likely positively charged under the conditions employed (while experimental determination of its pzc has not been reported, theoretical predictions23 indicate that it is below −300 mV). The urea-induced denaturation of the stem loop, however, is not reversible on this surface (Supporting Information Figure S1).
Figure 3.
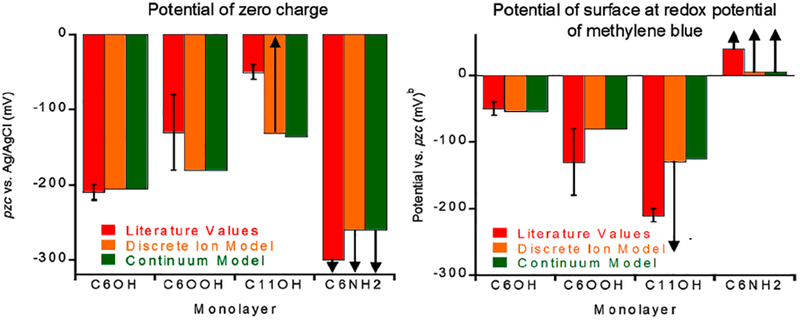
(Left) Shown are the potentials of zero charge (pzc; the applied potential at which the surface is uncharged) of our surfaces both as previously reported literature values and the values produced when the thermodynamic data presented here are fitted to either our discrete ion or continuum models. (Right) The potential of the surface is a function of its pzc and the applied potential. Shown are the potentials our surfaces are estimated to adopt (at an applied potential equal to the redox potential of methylene blue) using either literature values for the pzc or the best-fit pzc estimated from our discrete ion and continuum models. Literature pzc values from refs 19,22,23.
Figure 4.
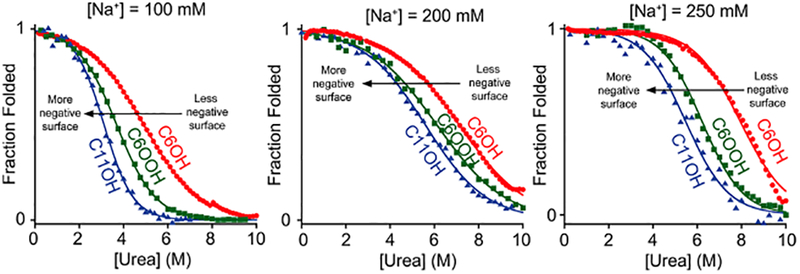
Stability of the stem loop is a strong function of the charge on the surface to which it is tethered. Specifically, the stability of the stem-loop decreases (e.g., the urea-melt midpoint shifts to lower denaturant concentrations) as it is attached to increasingly negatively charged surfaces (surfaces of increasingly positive pzc all held at the redox potential of methylene blue). As ionic strength increases, the DNA is stabilized on all surfaces, but the stability differences between the surfaces remains nearly constant. As derived using previously published pzc,19,22 the potentials the three surfaces adopt when, as is the case here, they are subjected to an applied potential at the redox potential of methylene blue are −50 ± 10 mV, −130 ± 50 mV, and −210 ± 10 mV for C6OH, C6OOH, and C11OH, respectively (values from refs 19,22,23).
We have previously developed5 a model to describe the extent to which attachment to the C6OH SAM alters the folding free energy of a stem-loop DNA. Here we find that it also fits our observations regarding the effects of attachment to the more negatively charged C6OOH SAM (Figure 5). The fit of our model to the latter data produces an estimated pzc of −180 mV (versus Ag/AgCl) for this surface, which is experimentally indistinguishable from the previously reported22 value of −130 ± 50 mV. In contrast, however, our prior model recovers neither the change in folding free energy we observe for the stem loop on a C11OH SAM-coated surface (Figure 3) nor the −50 ± 10 mV pzc previously reported for this surface.19 The origins of this failure are addressed below.
Figure 5.
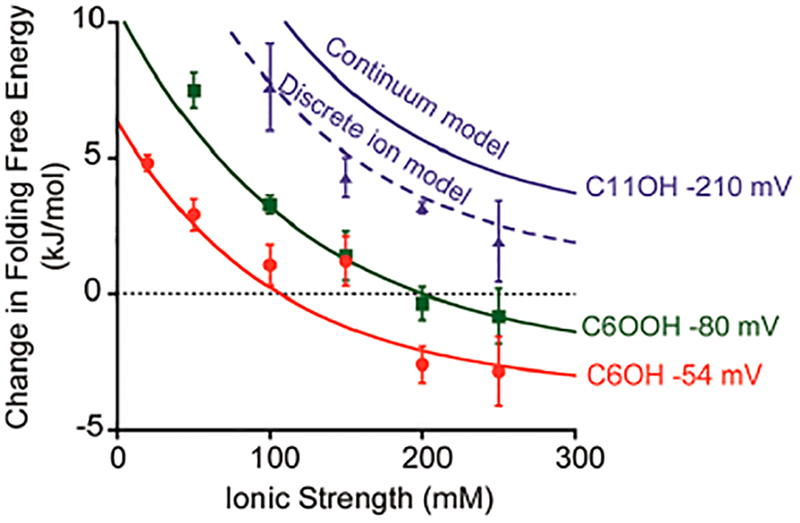
Extent to which surface attachment alters folding free energy depends on both ionic strength and the charge on the surface. The previously described continuum model (solid lines) of these effects5 accurately predicts the change in folding free energy for the two less highly charged surfaces we have characterized. For the C11OH SAM surface (blue), however, which is estimated to be at a potential of −210 mV under the conditions employed here,19 the continuum model fails. A more detailed model that considers the discrete volume of ions (discrete ion model) corrects this error and accurately predicts the free energy of the stem-loop on this surface (dashed line).
The inability of our first-generation model to recapitulate the behavior of our stem loop on a C11OH SAM may occur due its assumption of a Poisson−Boltzmann distribution of counterions near a charged surface18 which, in turn, contains an implicit assumption that the counterions can be accurately described as point charges. This “continuum model” holds well when the volume fraction of counterion at the surface is small, i.e., when
| (6) |
| (7) |
| (8) |
where φ0 is the volume fraction of free counterions in solution, a is the diameter of a free counterion (including its hydration shell), n0 is the number density of ions, and ϕc is the potential on the surface. The continuum model fails, however, when the concentration of counterions near the surface is so great that their nonzero volume limits any further increase in their concentration. This occurs when high surface potentials drive a very high concentration of counterions to the surface and steric repulsion between ions becomes significant. The potential at which this is expected to occur, ϕc, is given by
| (9) |
where the various parameters are as defined above. Under the conditions employed here (applied potential at −260 mV versus Ag/AgCl; sodium ion concentrations between 25 and 300 mM), our first-generation model will fail for surfaces for which the pzc is more positive than about −180 mV (versus Ag/AgCl). This explains why the best-fit pzcs we obtain for C6OH and C6OOH surfaces, both of which fall at or below this limit, are within error of previous reports but our model overestimates the pzc of C11OH (Figure 3).
In contrast to the continuum model, an expansion that explicitly considers ionic volume accurately recapitulates the thermodynamic consequences of surface attachment on all of the negatively charged surfaces we have characterized. The approach in this “discrete ion” model, which is similar to the Gouy−Chapman-Stern model of charged surfaces,24 describes the potential above the charged surface by
| (10) |
where ε is the permittivity constant, ε0 is the relative dielectric constant, and the other parameters are as described above. This modification considers interion steric interactions and effectively ensures that the counterion concentration near the surface remains physically reasonable even at relatively high potentials (Figure 6).
Figure 6.
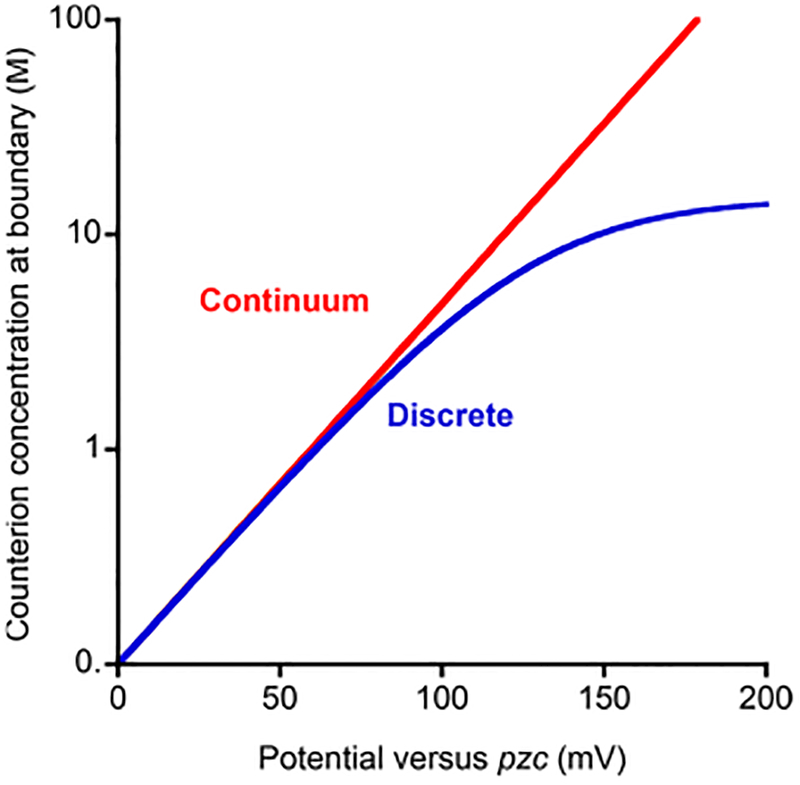
Continuum (red) and discrete ion (blue) models effectively predict identical counterion migration when the applied potential differs from the potential of zero charge by less than ~100 mV. They diverge significantly, however, at potentials farther from the pzc, with the continuum model predicting ion concentrations in this regime that are unphysical; i.e., concentrations are impossible to reach because they exceed the close packing limit of real ions.
While there is no analytical form for this potential, a close approximation is as follows. At sufficiently high surface potential, eq 9 is violated. When this is the case, counterions will pack densely on the surface to compensate for the high charge density. Once the surface charge is sufficiently compensated the potential at the top of the counterion layer satisfies eq 6. That is, the ions above the counterion layer are no longer close-packed, and the point charge approximation of the Gouy−Chapman model is once again valid. This description is similar to the Stern layer,24 but differs in that it allows for the formation of discrete ionic multilayers. The discrete ion model is indistinguishable from the continuum model at charge densities below that corresponding to the cutoff potential. When the cutoff potential is exceeded, however, the two models diverge significantly (Figure 5). Under these conditions, the discrete ion model fits our experimental observations. Specifically, the model based on eq 10 fits the experimental observations we collected on the more highly charged C11OH surface quantitatively (R2 = 0.98) without changing any of its other parameters (Figure 4).
Despite the quality of the fit between the model and experimental data, there is still reason to question its validity in the high-potential regime. The physical picture described here for potentials sufficiently far below the pzc is of a densely packed monolayer of hydrated sodium ions sitting on top of the self-assembled monolayer. While these are treated as discrete objects of finite size, all the other ions in the system are treated as point charges, creating a continuous, differentiable concentration gradient. Likewise, this model ignores the breakdown in the continuum description of the solvent, along with the accompanying breakdown of the continuous model of the dielectric constant. These same criticisms, however, are often applied to the Gouy−Chapman and Gouy−Chapman−Stern models, both of which nevertheless agree well with experiment for a wide range of systems.18 It has been theorized that the ability of these models to accurately predict experimental results despite these potential problems is due to offsetting errors between, for example, the breakdown of the continuum model of the solvent, which leads to underestimating the potential above the surface, and the assumption of immobile hydration shells, which leads to overestimating the potential above the surface.18
DISCUSSION
Here we have measured the thermodynamic effects of attaching a simple biomolecule to a range of negatively charged surfaces. We find that the extent to which attachment to the two less negatively charged surfaces we have explored is accurately recovered using a simple continuum model that includes only excluded volume entropy effects and repulsive electrostatic enthalpic effects. For a more negatively charged surface, in contrast, the continuum model fails, rendering it necessary to move to a more complex model that takes into account the nonzero size of counterions.
In contrast to our findings on negatively charged surfaces, we find that the refolding of the biomolecule is irreversible on a positively charged surface even at very high (1 M) ionic strength (Figure S1). We present two plausible explanations for this result. First, the SAM may degrade due to successive measurements at potentials that induce a high surface charge density. Previous work has shown that E-DNA systems are less stable when the interrogation potential (the potential of the redox reporter) is far from the pzc of the SAM.25 The second possibility is that the irreversability of the signal is due to electrostatic adsorption of the negatively charged DNA to the positively charged surface.26 The latter explanation is consistent with previous theoretical predictions suggesting that electrostatic adsorption may be an important factor in the nonspecific adsorption of proteins to surfaces.27 Since a zwitterion polymer can adopt a conformation such that all the opposite charges are adjacent to the surface, while like charges are some distance away, it will adhere to a charged surface, regardless of the sign of that charge. Because of this, proteins and other zwitterionic biopolymers are likely to strongly adsorb to charged surfaces if their net charge is near zero. For polymers with a high net charge, in contrast, it may be possible to prevent adsorption by using an appropriately charged surface.
Biopolymers interact with surfaces in many and varied ways, producing a range of complex behaviors. This study, for example, shows that excluded volume effects and, more importantly, surface−polymer electrostatics significantly modify the folding free energy of even a homogeneously charged biopolymer attached to chemically inert surfaces (i.e., DNA does not interact with the surfaces employed here via hydrogen bonding or hydrophobic interactions28). Still greater effects will presumably be seen for mixed charged biopolymers and for biopolymer/surface pairs that interact chemically.29,30 Given the simplicity—and thus quantitative theoretical tractability—of the model system explored here, we believe it may prove a valuable vehicle with which to begin to explore these more complex and still more interesting systems.
Supplementary Material
ACKNOWLEDGMENTS
This research was funded by NIH Grants R21EB018617 and 1R01GM118560 and by the Italian Ministry of University and Research MIUR under the PRIN 2015 program (grant no. 2015TWP83Z) (FR). Herschel Watkins is a Whitaker Fellow.
ABBREVIATIONS
- pzc
potential of zero charge
- SAM
self-assembled monolayer
- C6OH
6-mercapto-1-hexanol
- C11OH
11-mercapto-1-undecanol
- C6OOH
6-mercaptohexanoic acid
- C6NH2
6-amino-hexane-1-thiol
ASSOCIATED CONTENT
Supporting Information
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.langmuir.8b01004.
Additional information regarding the irreversible urea unfolding of the DNA stem loop when attached to an amine-terminated SAM (PDF)
The authors declare no competing financial interest.
REFERENCES
- (1).Knotts TA IV; Rathore N; de Pablo JJ An Entropic Perspective of Protein Stability on Surfaces. Biophys. J 2008, 94 (11), 4473–4483. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (2).Zhulina EB; Wolterink JK; Borisov OV Screening Effects in a Polyelectrolyte Brush: Self-Consistent-Field Theory. Macromolecules 2000, 33 (13), 4945–4953. [Google Scholar]
- (3).Pryamitsyn VA; Leermakers FAM; Fleer GJ; Zhulina EB Theory of the Collapse of the Polyelectrolyte Brush. Macromolecules 1996, 29 (25), 8260–8270. [Google Scholar]
- (4).Spiess C; Meyer AS; Reissmann S; Frydman J Mechanism of the Eukaryotic Chaperonin: Protein Folding in the Chamber of Secrets. Trends Cell Biol 2004, 14 (11), 598–604. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (5).Watkins HM; Vallée-Bélisle A; Ricci F; Makarov DE;Plaxco KW Entropic and Electrostatic Effects on the Folding Free Energy of a Surface-Attached Biomolecule: An Experimental and Theoretical Study. J. Am. Chem. Soc 2012, 134 (4), 2120–2126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (6).Greene RF; Pace CN Urea and Guanidine Hydrochloride Denaturation of Ribonuclease, Lysozyme, A-Chymotrypsin, and BLactoglobulin. J. Biol. Chem 1974, 249 (17), 5388–5393. [PubMed] [Google Scholar]
- (7).Shelton VM; Sosnick TR; Pan T Applicability of Urea in the Thermodynamic Analysis of Secondary and Tertiary RNA Folding. Biochemistry 1999, 38 (51), 16831–16839. [DOI] [PubMed] [Google Scholar]
- (8).Watkins HM; Simon AJ; Ricci F; Plaxco KW Effects of Crowding on the Stability of a Surface-Tethered Biopolymer: An Experimental Study of Folding in a Highly Crowded Regime. J. Am. Chem. Soc 2014, 136 (25), 8923–8927. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (9).Li H; Arroyo-Currás,´ N.; Kang, D.; Ricci, F.; Plaxco, K. W.Dual-Reporter Drift Correction To Enhance the Performance of Electrochemical Aptamer-Based Sensors in Whole Blood. J. Am. Chem. Soc 2016, 138 (49), 15809–15812. [DOI] [PubMed] [Google Scholar]
- (10).Carslaw HS; Jaeger JC Conduction of Heat in Solids, 2nd ed.; Oxford University Press: USA, 1986. [Google Scholar]
- (11).Dolan AK; Edwards SF Theory of the Stabilization of Colloids by Adsorbed Polymer. Proc. R. Soc. London, Ser. A 1974, 337 (1611), 509–516. [Google Scholar]
- (12).Robeyns K; Herdewijn P; Van Meervelt L Direct Observation of Two Cyclohexenyl (CeNA) Ring Conformations in Duplex DNA. Artif. DNA PNA XNA 2010, 1 (1), 2–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (13).Fusetti F; Schröter KH; Steiner RA; van Noort PI; Pijning T; Rozeboom HJ; Kalk KH; Egmond MR; Dijkstra BW Crystal Structure of the Copper-Containing Quercetin 2,3-Dioxygenase from Aspergillus Japonicus. Structure 2002, 10 (2), 259–268. [DOI] [PubMed] [Google Scholar]
- (14).Chenoweth DM; Dervan PB Allosteric Modulation of DNA by Small Molecules. Proc. Natl. Acad. Sci. U. S. A 2009, 106 (32), 13175–13179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (15).Chen Y-C; Luo M-B Monte Carlo Study on the Entropy of Tail-like Polymer Chain with One End Attached to Flat Surface. Int. J. Mod. Phys. B 2007, 21 (10), 1787–1795. [Google Scholar]
- (16).Cheng RR; Makarov DE End-to-Surface Reaction Dynamics of a Single Surface-Attached DNA or Polypeptide. J. Phys. Chem. B 2010, 114 (9), 3321–3329. [DOI] [PubMed] [Google Scholar]
- (17).Saleh OA; McIntosh DB; Pincus P; Ribeck N Nonlinear Low-Force Elasticity of Single-Stranded DNA Molecules. Phys. Rev. Lett 2009, 102 (6), 068301. [DOI] [PubMed] [Google Scholar]
- (18).Poon WC; Andelman D Soft Condensed Matter Physics in Molecular and Cell Biology; Taylor & Francis, 2006; Vol. 59. [Google Scholar]
- (19).Rentsch S; Siegenthaler H; Papastavrou G Diffuse Layer Properties of Thiol-Modified Gold Electrodes Probed by Direct Force Measurements. Langmuir 2007, 23 (17), 9083–9091. [DOI] [PubMed] [Google Scholar]
- (20).Lubin AA; Plaxco KW Folding-Based Electrochemical Biosensors: The Case for Responsive Nucleic Acid Architectures. Acc. Chem. Res 2010, 43 (4), 496–505. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (21).Hirs CHW Enzyme Structure; Academic Press, 1986; Vol. 131. [Google Scholar]
- (22).Sanders W; Vargas R; Anderson MR Characterization of Carboxylic Acid-Terminated Self-Assembled Monolayers by Electro-chemical Impedance Spectroscopy and Scanning Electrochemical Microscopy. Langmuir 2008, 24 (12), 6133–6139. [DOI] [PubMed] [Google Scholar]
- (23).Bryant MA; Crooks RM Determination of Surface pKa Values of Surface-Confined Molecules Derivatized with pH-Sensitive Pendant Groups. Langmuir 1993, 9 (2), 385–387. [Google Scholar]
- (24).Stern O Zur Theorie Der Elektrolytischen Doppelschicht. Z. Elektrochem 1924, 30 (21/22), 508–516. [Google Scholar]
- (25).Kang D; Zuo X; Yang R; Xia F; Plaxco KW; White RJ Comparing the Properties of Electrochemical-Based DNA Sensors Employing Different Redox Tags. Anal. Chem 2009, 81 (21), 9109–9113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (26).Erdmann M; David R; Fornof A; Gaub HE Electrically Controlled DNA Adhesion. Nat. Nanotechnol 2010, 5 (2), 154–159. [DOI] [PubMed] [Google Scholar]
- (27).Kalasin S; Santore MM Non-Specific Adhesion on Biomaterial Surfaces Driven by Small Amounts of Protein Adsorption. Colloids Surf., B 2009, 73 (2), 229–236. [DOI] [PubMed] [Google Scholar]
- (28).Lee C-Y; Gong P; Harbers GM; Grainger DW; Castner DG; Gamble LJ Surface Coverage and Structure of Mixed DNA/Alkylthiol Monolayers on Gold: Characterization by XPS, NEXAFS, and Fluorescence Intensity Measurements. Anal. Chem 2006, 78 (10), 3316–3325. [DOI] [PubMed] [Google Scholar]
- (29).Zhuang Z; Jewett AI; Kuttimalai S; Bellesia G; Gnanakaran S; Shea J-E Assisted Peptide Folding by Surface Pattern Recognition. Biophys. J 2011, 100 (5), 1306–1315. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (30).Kang T; Hong S; Choi I; Sung J-J; Yi J Urea-Driven Conformational Changes in Surface-Bound Superoxide Dismutase. Bull. Korean Chem. Soc 2008, 29, 1451–1458. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


