The rise of the X-ray atomic pair distribution function method: a series of fortunate events

Abstract

The atomic pair distribution function (PDF) technique is a powerful approach to gain quantitative insight into the structure of materials where the structural coherence extends only over a few nanometres. In this paper, I focus on PDF from synchrotron X-rays and describe what is the PDF and where it came from, as well as key moments on the journey that have contributed to its enormous recent growth and expanding impact in materials science today. Synchrotron X-ray sources played a starring role in this story.

This article is part of the theme issue ‘Fifty years of synchrotron science: achievements and opportunities’.

1. Introduction

A revolution has taken place in materials science in the past century. A hundred years ago, most materials were natural in origin. Shirts were made of cotton, trousers were wool, shoes and boots were leather and car tyres were natural rubber. There were some exceptions of course. Cement had been manufactured since Roman times, and ceramics go back much further, though largely made from naturally occurring clays. The one type of synthetic material that was rather highly developed was metals. Mankind had been learning metallurgy since the Bronze Age, and already by the turn of the twentieth century, we were quite sophisticated at making ferrous and non-ferrous metals. But we were highly reliant on natural materials. The materials landscape now would be totally unrecognizable to an early twentieth-century person, with so much of what is around us made out of man-made synthetic materials. We continue to seek new materials to provide technological solutions to the most challenging problems facing humanity, from sustainable energy, to environmental remediation, to health. For example, for electric powered transportation, we need higher energy density batteries [1] and for grid storage, higher capacity batteries that are recyclable and made of earth-abundant materials [2]. These need to be cheap and environmentally benign. The challenges that remain are enormous, but our ability to innovate in the materials domain is also unprecedented.

A major contributing factor to this revolution in materials has been X-ray crystallography, which, probably not coincidentally, also began around 100 years ago when the materials revolution began. The knowledge of where atoms are in a crystal is a prerequisite to understanding, and thereafter engineering, materials properties. Crystallography has played a critical role in the materials revolution.

2. Real materials

These days, engineered materials and devices are complex and hierarchical. Examples are modern batteries [3] with intricate arrangements of electrodes, membranes, barely understood thin passivation layers, electrolytes, contacts and packaging. Likewise polymer electrolyte membrane (PEM) fuel cells [4] consist of hierarchical electrodes that consist of nano- and mesco-scale porous supports containing nanoparticles of Pt catalysts, built up into higher order structures also with electrolytes and membranes. To understand the performance of such devices, we desire to study the materials in the device even as it is operating [5], a massive challenge in such a complex, nanostructured but multi-scale device. Beyond this, materials scientists know that materials performance depends on more than just the average crystal structure, which is provided from our powerful crystallographic experiments. There are many other material factors that can have huge effects on the performance, for example

• (i)the morphology (shape and size) which often is nanoscale,
• (ii)surface reconstructions,
• (iii)surface termination/dressing, for example, by hydroxyl groups or by organic ligands,
• (iv)interfaces,
• (v)heterogeneities such as phase separation or engineered heterogeneity such as the electrodes of the PEM fuel cell,
• (vi)point defects,
• (vii)extended defects,
• (viii)chemical short-range order,
• (ix)distortive short-range order

and so on. To make the distinction between crystals (which are idealizations of materials), and materials that contain these meta-characteristics, I refer to the latter in general as ‘real materials’. From a structural perspective, we need methods to yield the atomic arrangements in real materials.

There are many powerful ways to characterize the defects, morphologies and heterogeneities by imaging (for example, transmission electron microscopy) and various spectroscopies. However, we are only beginning to be able to solve their structure, in the sense of obtaining with high precision the three-dimensional coordinates of atoms in defective materials. The reason is that such material attributes are inherently non-periodic in nature and conventional crystallography is not a good starting point in such cases.

3. The nanostructure problem

The problem is especially acute when the structural arrangements are on the nanoscale [6]. I call this the nanostructure problem [7]. The challenge of doing crystallography on nanomaterials is illustrated in figure 1. This figure shows the powder X-ray diffraction (XRD) profile from two phosphate materials, using a standard laboratory XRD approach [8]. The top pattern is from a crystalline sample, and the bottom panel is from a similar material that did not crystallize [8]. In the nanocrystalline case, the peaks become very broad and diffuse. This is known as Scherrer broadening [9], and Scherrer's approximate formula for Bragg peak broadening works well for larger crystallites, but when the range of structural coherence gets very small, a few nanometres, it no longer does a good job of explaining the diffraction line-shape. The approximation of scattering from a finite sized block of perfect crystal is no longer a good one. But most importantly, it is apparent from the figure that the information content in the data has gone down. Since there are fewer peaks, there are fewer bytes of information in the dataset, the critical information that we need to determine structure. When we are looking at powders of nanomaterials, there is an inherent information theoretic problem, that we seek more complex structural solutions than in the simple crystalline case (because we need to know about structural relaxations at the surface and in the core, and ligand binding, etc.) but we have to do it from less information. This means that many nanostructure problems are inverse problems that fall into the category of being chronically or acutely ill-posed.

Figure 1.

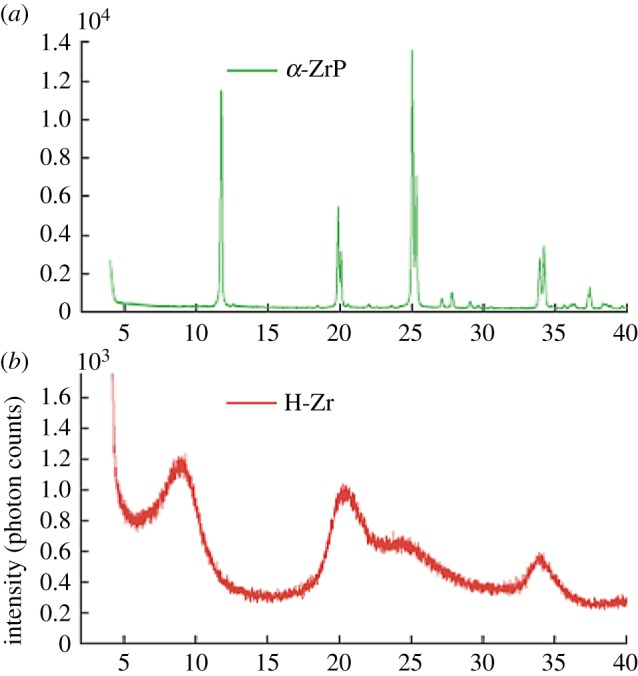
Conventional laboratory powder X-ray diffractometer diffractograms, versus 2θ from (a) a well-crystallized material and (b) a nanomaterial, showing the excessive peak broadening and loss of information in the signal in the case of the nanomaterial. Adapted from [8]. (Online version in colour.)

XRD patterns that look like this are often referred to in the literature as ‘x-ray amorphous’ or simply ‘amorphous’, although we now know that this material in particular, and indeed many materials that return similar signals, is well-ordered locally and nanocrystalline in nature [8,10–12].

We have described here the case where we measured large numbers of nanoparticles in a bulk sample, which is the most common situation. In principle, we could do a ‘single-nanocrystal’ experiment, analogous to the single-crystal experiment contrasted with powder diffraction. Such experiments are exceptionally difficult in practice because the small size of the particle does not produce enough signal of scattered X-rays to detect, even at the most powerful synchrotron sources. Some progress is being made at fourth-generation free-electron laser sources [13], but it is still exceptionally difficult and there are few examples of a single-particle structure solution.

Transmission electron micrscopes and scanning tunnelling microscopes can image single atoms, or columns of atoms [14–17], and with great difficulty can reconstruct atomic coordinates from three-dimensional tomographic reconstructions of atomically resolved images collected at many angles [18]. However, this is far from routine, and many things need still to be sorted out, for example, the effects of beam damage on such delicate samples. The tomographic methods are also not giving positional resolutions with the same precision as we are used to from crystallography, which may never be possible. However, material properties do depend sensitively on bond lengths at levels comparable to, and even much smaller than, a tenth of an ångsrtöm [19].

Finally, it should be noted that many experiments, such as studying catalysts in PEM fuel cells under operating conditions [5], would not be feasible in the single-nanocrystal mode. So as exciting as single-nanoparticle approaches are, we still need to be able to extract as much quantitative structural information as we possibly can from samples that give XRD patterns like figure 1b.

4. The atomic pair distribution function method

One approach to this problem is to use the atomic pair distribution function (PDF) method (defined more explicitly in appendix A and in these references [20,21]). In this method, high energy X-rays (or neutrons or electrons, though these will not be discussed in this paper) are scattered off our nanomaterial and detected, very much like in a conventional powder diffraction experiment. The difference is that the extremely short wavelengths of X-rays that are used, and the wide-angular range over which they are detected, results in a very wide range of reciprocal space to be probed. For this reason (and because we consider both diffuse and Bragg scattering), these experiments are sometimes called total scattering experiments, since we measure all the scattering, throughout all of reciprocal space, from the sample. In these experiments, the variable Q is generally used to measure location in reciprocal space. Q is the magnitude of the scattering vector, Q = 4πsinθ/λ, where θ is half the scattering angle, 2θ, and λ the X-ray wavelength. In total scattering experiments, we like to measure Q to as high as possible, potentially as high as Q = 30 Å⁻¹ or higher. This contrasts with the standard XRD characterization measurements (for example, shown in figure 1) that typically go to a Q_max = 5 Å⁻¹ or so.

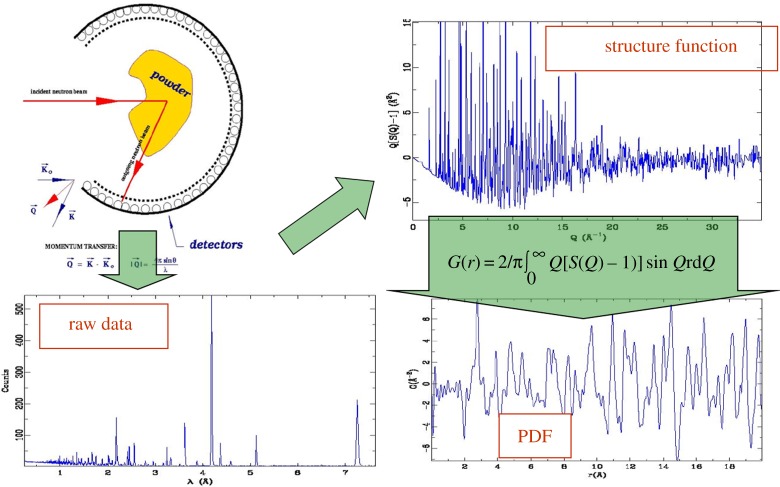
Various corrections are applied to the data, as described in great detail in [20], but to get the PDF, the last step is a Fourier transform. This is shown schematically in figure 2. The PDF function is shown in the bottom right panel. It is a measure of the probability of finding a pair of atoms separated by distance-r. This makes it a very intuitive function to understand and interpret, because peaks in the function are coming from actual interatomic distances in the material.

Figure 2.

Schematic of the process for obtaining atomic pair distribution functions. Top left: a powder or nanoparticulate sample is placed in an intense beam of X-rays or neutrons and intensity is collected as a function of angle. This results in a ‘raw’ diffraction pattern (lower left) that also contains many effects of the measurement. To the extent possible the signal is corrected for the instrumental aberrations and normalized, resulting in the reduced structure function, F(Q) = Q(S(Q) − 1) (top right), where Q is the momentum transferred during the scattering process. The PDF (bottom right), G(r), is obtained from F(Q) through a Fourier transform relationship shown in the schematic. (Online version in colour.)

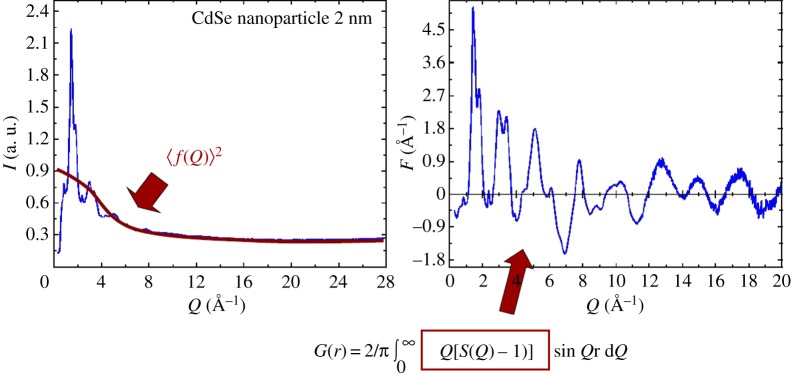
We are now ready to return to the topic of the ill-posedness of the nanostructure inverse problem. Our new measurement has measured all the (coherent) scattering coming from our structure, so it is the best we can possibly do. The mathematics of the approach also has an important effect of naturally amplifying small signals in the data in the high-Q region of scattering. This is because to get the PDF we have to divide the measured scattering by the square of the atomic form factor, which is falling to a small value at high-Q. Dividing a number by a small number results in a large number, and so even difficult to measure weak signals are amplified and become significant. This process is illustrated in figure 3, which shows the scattering pattern before and after dividing by the form factor squared (another multiplication by Q that is required by the mathematics has also been done). In figure 3b, the abundance of a strong new signal as a result of this process is very apparent.

Figure 3.

Raw diffraction data (a) and after dividing by the square of the X-ray atomic form factor and multiplied by Q (b). For many years, the high-Q region in an X-ray experiment was thought to contain little or no information, but the advent of synchrotrons allowed the important weak signals in this region to be measured with good accuracy. As a result, we obtain a signal that contains greatly more information from nanomaterials than in traditional measurements and data treatments. (Online version in colour.)

This does mean that to measure these weak high-Q signals we need very good statistics, and prefer intense synchrotron X-ray sources. PDFs from laboratory-based instruments can be measured, but Q_max tends to be limited, and measurement times are long.

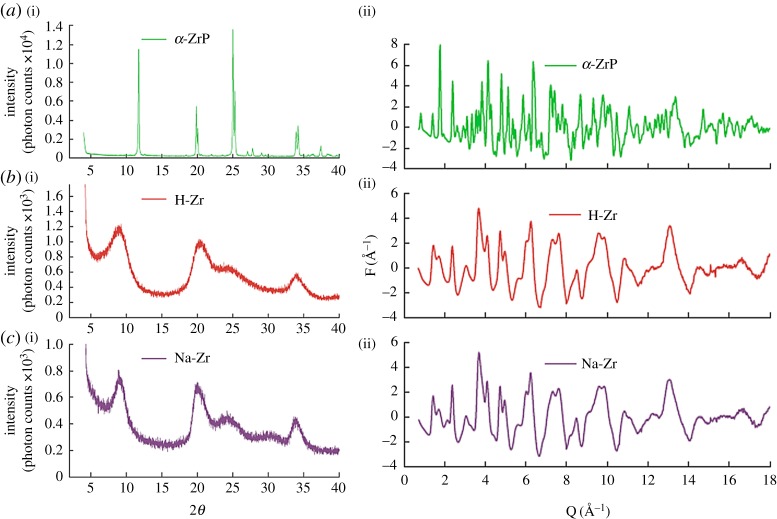
The magic of this data collection and analysis protocol is shown in figure 4, which reprises the crystalline and ‘X-ray amorphous’ XRD patterns from the phosphate materials shown in figure 1 in the left panels, but the signal that we get from the PDF approach on the right. In this case, it was possible to solve the atomic structure of the phosphate layers and to learn about the stacking from the PDF data [8] (but patently not from the traditional XPD data).

Figure 4.

From conventional powder diffraction to the PDF. The patterns on the ((a)(i),(b)(i),(c)(i)) are conventional powder diffraction patterns from three samples, a crystalline material (a), and two nanocrystalline samples (b) and (c). ((a)(ii),(b)(ii),(c)(ii)) The diffraction patterns from the same samples when it is measured and analysed to get the total scattering data suitable for PDF analysis. There is considerably more information in the patterns in the right column. The data in (a) and (b) are shown in figure 1. Adapted from [8]. (Online version in colour.)

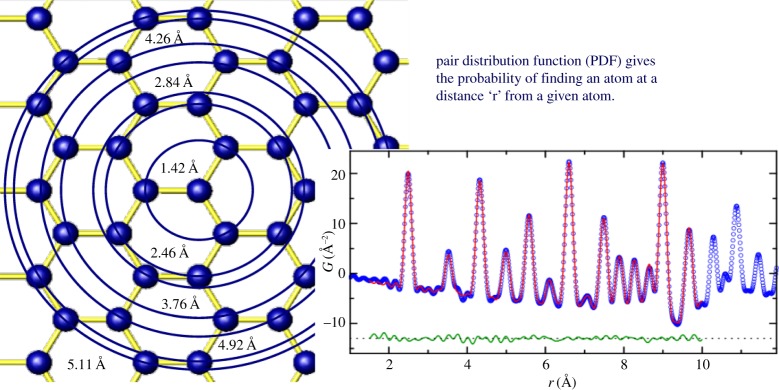
We can calculate PDFs from atomic structure models using computers in a straightforward fashion, as illustrated in figure 5. Each atom is placed at the origin and then delta-functions, broadened into Gaussian functions due to thermal motion effects, are placed at distances where neighbours are found. It is easy to compute the PDF of a structure model [22–28]. The inverse problem of determining the structure model given a PDF is quite a different matter and is currently largely an unsolved problem, though some successes have been lodged [29–31].

Figure 5.

A schematic of the modelling process. Each unique atom is placed at the origin and larger and larger circles are drawn. Whenever a new atom intersects with the circle, a unit of intensity is added to a histogram at the position r that is the radius of the circle at the intersection point. Thermal motion of materials causes the histogram to broaden into a Gaussians, and so the PDF is well represented by a sum of independent Gaussian functions. Lower right: the blue open symbols are the measured PDF from nickel powder and the red solid line is the PDF calculated from the structure of nickel. The green curve, offset below shows the difference, which in this case is dominated by noise in the measurement. (Online version in colour.)

The PDF method is not a new method. Its roots lie in the Debye scattering equation (DSE), which was first published in 1915 [32], soon after the first X-ray diffraction experiments were performed. In 1927, Zernicke & Prins [33] derived the Fourier relationship between the real-space pair density and the DSE and PDF was born. The very first X-ray PDF experiments were carried out by Debye himself, with Menke in 1930 [34]. More aspects of the history of PDF may be found in [20], but here I want to skip to the epoch synchrotron radiation studies.

The first synchrotron X-ray PDF experiments were carried out at the Cornell High Energy Synchrotron Source (CHESS) and the National Synchrotron Light Source (NSLS) at Brookhaven National Laboratory in the USA by Takeshi Egami in the mid-1980s [35,36]. At the early second-generation synchrotrons like the NSLS, the Q_max was somewhat limited by the modest X-ray energy at that source. Experiments were carried out with a germanium point-detector that was moved around the sample in a circle from low to high angles. Each dataset took many hours to measure.

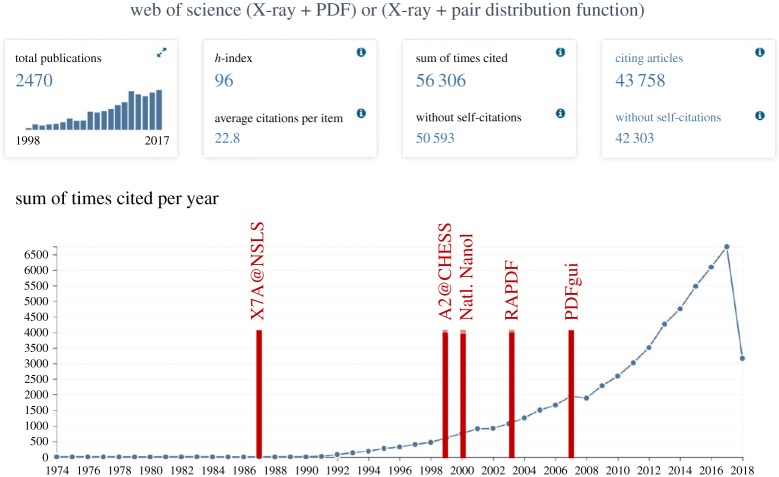
This was the first in a series of fortunate events that paved the way for PDF to become the widely applied and high impact method that it currently has become. If we use publications as a measure of impact, we see enormous growth in publications that mention (X-ray + PDF) or (X-ray + pair distribution function) beginning around 2000 as shown in figure 6.

Figure 6.

A screenshot from a search from ISI web of science for (X-ray AND PDF) OR (X-ray AND pair distribution function), showing the growth in number of papers referencing the technique. The thick red vertical lines indicate methodological developments, and other external factors, which in the author's view have significantly contributed to the growth of the method. The list of factors is not intended to be exhaustive, but rather illustrational. The factors are discussed in the text. (Online version in colour.)

The Cornell High Energy Synchrotron Source (CHESS) operated (and continues to operate) at a much higher energy than NSLS, in principle allowing for experiments to be carried out with shorter-wavelength X-rays and allowing a much higher Q_max and therefore higher real-space-resolution to be obtained. In the late 1990s, we carried out measurements with a record, for X-rays, q_max of 45 Å⁻¹ were made on In_1-xGa_xAs [37,38] semiconducting alloys, allowing the different In–As and Ga–As bond lengths to be directly resolved (they differ in length by 0.14 Å). This experiment was important because it demonstrated unequivocally that the PDF method, which had met with some scepticism to this point when used for studying disorder in crystalline materials, was really working at resolving different bond-lengths in local structures. In the alloys, it was possible to discern two distinct (albeit overlapped) peaks coming from In–As and Ga–As nearest neighbours, even though the average crystal structure just had one bond with a length that was the weighted mean of the two real bonds. At around the same time another breakout experiment also helped to establish that the PDF really was revealing local structure by using neutron PDF to show explicitly the presence, and nature, of polarons (charge induced lattice distortions) associated with the metal-insulator transition in the colossal magneto-resistant manganites [19]. Confidence in the power of PDF for finding broken local symmetries in materials was growing. The CHESS experiment, however, was also important because it allayed scepticism that X-rays, with their atomic form factor that reduces the scattering intensity in the important high-Q region of reciprocal space, could actually be successful for high-resolution PDF work of this nature.

The synchrotron X-ray PDF method was earning a reputation for yielding local structural information difficult to obtain elsewhere, but the difficulty of the experiments, with one dataset taking up to 12 h to collect after days of beamline set-up, meant that it was still considered a niche technique, beloved only by physics who wanted to delve deeply into a single, well-characterized material system where local structural effects were suspected of affecting some interesting property. An attempt by us to measure the PDF of CdSe quantum dot nanoparticles at the advanced photon source (APS) at Argonne National Laboratory, resulted in the discovery at the end of the 12 h scan of a brown-singed hole in the sample: the organic-coated sample was simply burned by the intense X-ray beam. On the other hand, there was a large growth in interest in nanotechnology in the late 1990s, culminating with the announcement in the USA of the National Nanotechnology Initiative (NNI) in 2000 by President Clinton. Making materials nanosized results in them having their own special properties, with the exciting promise of being able to engineer materials at the nanoscale for desired outcomes. But traditional crystallography breaks down for the smallest nanoparticles (below around 10 nm) where much of the interesting nano-physics and chemistry emerges. PDF, which does not presume periodicity, naturally yields a signal from the nanostructure if we could just measure it and interpret the data. Just as the PDF methodologies were starting to mature there came a pressing scientific need for the approach.

In an attempt to raise awareness about the method, we proposed to organize a PDF workshop at the 2001 annual meeting of the American Crystallographic Association (ACA). This was accepted onto the conference programme, and went ahead successfully, but Connie Chidester (now Rajnak) later shared a cartoon that was drawn by her niece, Stacey Morrison, and is reproduced in figure 7, that depicted the deliberations of the Executive Committee of the ACA, highlighting the status the method had at the time in the crystallographic community.

Figure 7.

A cartoon drawn by Stacey Morrison and shared with the author by Connie Chidester (now Rajnak) that depicts the deliberations of the Executive Committee of the American Crystallographic Association (ACA) in response for a request to hold a workshop at the 2001 ACA annual meeting. Apparently, at this time, the method was not widely known in the crystallographic community. The workshop was approved. (Online version in colour.)

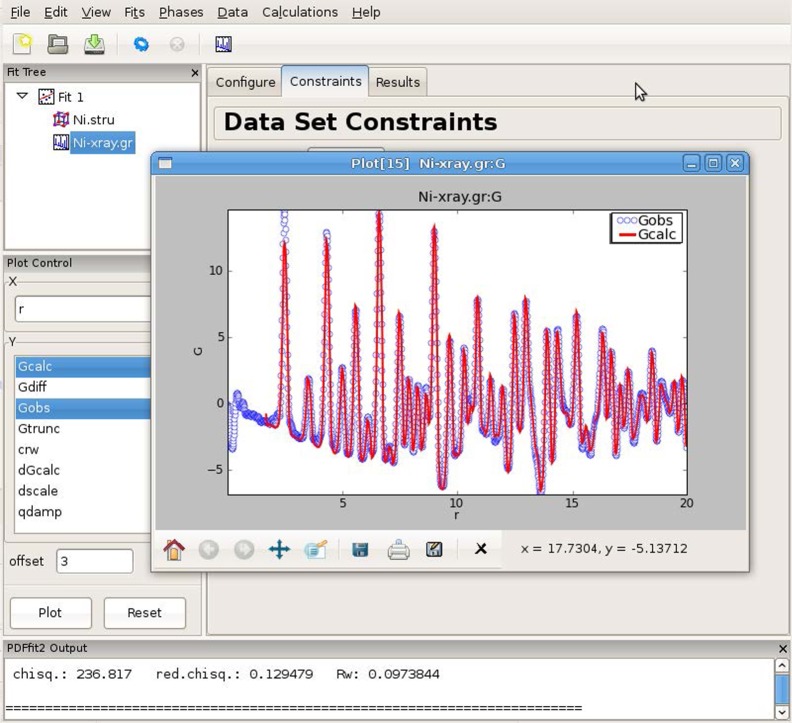
A big experimental breakthrough occurred in 2003 in a collaboration between Peter Chupas, a student of Clare Grey at Stony Brook University, and Xiangyun Qiu, a student in my group at Michigan State University. The accepted wisdom at the time in the PDF community was that careful energy discrimination of the scattered signal was needed to get meaningful results from the weak high-Q coherent scattering signal, due to the dominance of the incoherent Compton scattering in that region (not to mention fluorescence). The challenging and time-consuming synchrotron X-ray experiments we were doing up to that time used a Ge single-crystal point detector with energy discrimination, exactly for this reason. However, around this time with the development of the MAR345 image plate detector with a built-in laser readout, it was becoming easier to collect diffraction data on large area two-dimensional detectors, which could in principle greatly speed up the data acquisition process as the whole diffraction pattern could be collected in just one or two exposures, instead of thousands with the point detector. Not only that, it would result in an entire Scherrer cone of scattering being collected instead of a single cut through the cone, giving an additional parallelization of the data acquisition (with other good side-effects such as better powder averaging for free). But these new detectors were not energy resolving, so the Compton scattering would have to be subtracted from the whole signal. It turned out that the approach worked beautifully. The greatly increased counting statistics that it was possible to collect outweighed the higher incoherent background, and the PDF from a reference nickel sample collected with a 1 s exposure was comparable in quality to one collected in 12 h using the old method, a four order of magnitude increase in experimental throughput [39]. The experimental set-up shown in figure 8, including the veritable original MAR345 detector (which has since made way for detectors based on amorphous silicon [40], and even more recently, single photon counting hybrid pixel array [41] technologies). Together with improvements in powerful, easy to use, software (figure 5) on both the data reduction [42,43] and modelling [43,44] sides, this was to open up synchrotron X-ray PDF studies to a much wider audience of chemists, materials scientists, geologists and earth scientists and even more recently, polymer and pharmaceutical scientists. Synchrotron X-ray PDF was already off the ground, but this development probably more than any other has led to the exponential growth in publications that is indicated in figure 6, and has resulted in multiple beamlines around the world (11IDB at APS in Chicago, XPD and PDF at NSLS-II in New York, ID15 at ESRF in Grenoble, XPDF at the Diamond Light Source in the UK, P07 at DESY in Germany, and multiple others at Spring 8 and elsewhere) optimized for these RAPDF measurements. Finally, the development of easy to use software for extracting structural information from the PDF, such as PDFgui [25] (figure 9), has greatly increased the utility, and utilization, of the PDF technique.

Figure 8.

The rapid acquisition PDF (RAPDF) set-up. A beam of high energy X-rays comes from the right, originating from a synchrotron source and hits the powder sample. The scattering is collected in a single-shot on a large area detector that is pushed, close (typically approx. 200 mm) to the sample position. (Online version in colour.)

Figure 9.

A screenshot of a pdfgui model refinement session illustrating how modern software has facilitated PDF studies. Adapted from the pdfgui manual. (Online version in colour.)

5. A few notable recent developments

As we have discussed, the PDF method is becoming much more widely adopted. New developments in the methodology are also allowing it to be applied in ever greater number of scientific applications. We mention a few here that we have been developing, and which are making full use of the large fluxes of high energy X-rays that are available at modern synchrotron sources.

A significant advance was made in 2015 with the discovery that it was possible to detect very small signals of nanoparticules in acqueous solution [45]. The study was on nanosized pharmaceutical drug particles that are used in an inhaler device. Prior to this, there was a sense in the community that the signal detection limit was around 1–5%, meaning that it was possible to detect minority phases if there were present in quantities greater than 1–5% but not otherwise. This study [45] detected the organic drug molecules (already weakly scattering) in acqueous solvent at the 0.25 wt% level. What was learned was that the previous detection limit was probably due to limitations on the ability to reproduce the experiment exactly when measuring the signal and the background. The approach that is often taken to detect such a small signal was to subtract the signal from the solvent from the total signal of the drug plus solvent. For the first time, we were using the newly developed PDFgetX3 [43] program, which makes ad hoc corrections for experimental aberrations. Small differences in the experimental geometry, such as exactly where the beam hits the sample capillary, would be corrected by this program automatically without affecting the signal. An unintended, but fortunate, consequence of this was that these small differences in experimental geometry could be removed without affecting the nanoparticle or solvent signal itself, resulting in a much greater sensitivity to the weak signal. The, albeit weak, signal from the nanoparticle drug sample is clearly evident in figure 10, compared to measurements from the same drug suspension at much higher concentrations [45]. This development has enabled a raft of new applications for the PDF method where the detection of weak signals is a prerequisite, including the in situ study of hydrothermal nanoparticle synthesis[46–50], the measurement of very thin (approx. 100 nm thick) polycrystalline films on thick substrates [51], detection of nuclei of intermediate phases during recrystallization from the amorphous state [52], and even to the detection and measurement of solvent restructuring in the presence of solute species [53].

Figure 10.

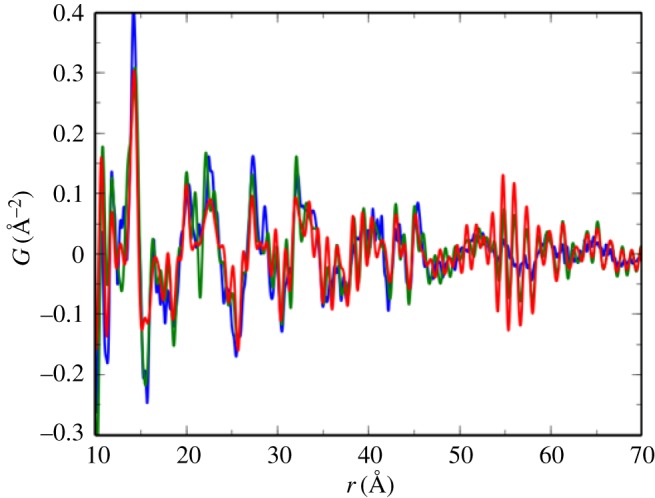
PDFs from a nanosized pharmaceutical drug in an aqueous suspension at different concentrations. The blue (black in print) curve is 5 wt%, the green (darker grey in print) curve is 0.6 wt% and the red (light grey in print) curve is 0.25 wt%, which is the actual dose loading. Adapted from [45]. (Online version in colour.)

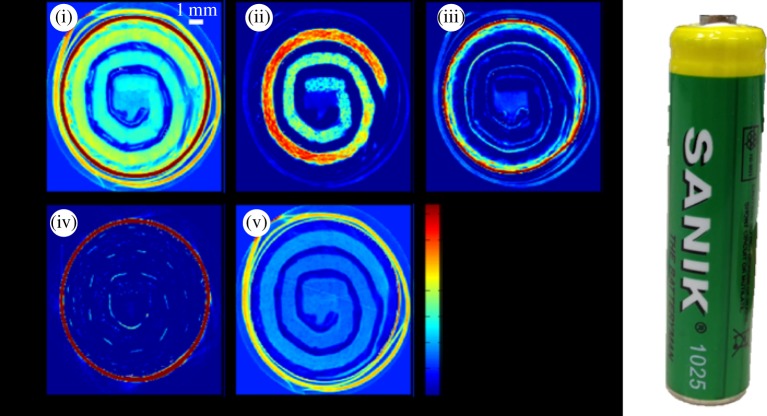
The high throughput nature of the modern-day experiments, enabled by synchrotrons and two-dimensional detectors, has also allowed PDF [54] (and powder diffraction [55,56]) to be coupled with computed tomography to yield nano-structural information at locations buried inside larger objects and devices. The experiments involve taking a line-scan of around 100 points of a small 10–50 μm beam across a sample and recording the whole diffraction pattern at each point. Then the sample (whose axis of rotation is perpendicular to but aligned with the X-ray beam) is rotated by approximately 2 degrees and the line-scan repeated. This ‘outer-loop’ is then repeated itself until the sample has undergone a complete rotation. This results in approximately 100 × 100 = 10⁴ datasets, each of which contains a signal that is the superposition of all the locations in the sample that were illuminated in that measurement. The tomographic reconstruction algorithm takes these 10 000 diffraction patterns and returns back 10 000 diffraction patterns which are the diffraction pattern for 10 000 sample voxels (tiny regions of the sample at some known location). This allows us to peer inside the object and measure a diffraction pattern from a small, approximately 10 μm × 10 μ × 10 μm region deep inside the object. This is illustrated in figure 11 which shows images of a cross-section through a AAA nickel metal-hydride rechargable battery, which is also shown in the figure [57]. Each image contains approximately 10 000 differently coloured pixels, in direct analogy with a standard absorption tomogram. However, instead of a scalar (a single number) in each pixel, we actually have a complete diffraction pattern and PDF, which can be analysed and fit with a model just like any PDF/diffraction pattern. We can then make two-dimensional images that focus on different parameters that we are extracting from the diffraction pattern. In the figure, we show five such channels [57]. (i) is the total incoherent scattering intensity which is directly related to what you would see in a conventional absorption tomogram. It is basically a map of the electron density in this cross-section of the sample. In (ii), we apply a filter to the diffraction data that extracts the signal from the cathode electrode material (in this case, it is a polycrystalline nickel hydride material). (iii) shows a signal from the anode material, (iv) from steel and (v) from a polymer signal. Interestingly, we see a polymer signal in the same region of space as the cathode material. It is the polymer binder that is used to hold the fine-grained cathode material together. We also see the polymeric ‘skin’ on the battery that is the green label apparent in the photograph.

Figure 11.

Diffraction tomography from a AAA spiral wound nickel metal hydride rechargable battery (shown on the right). (i) the high-Q scattering, which approximates the signal you would get from an absorption tomography experiment. The other panels show different signals in the diffraction pattern: (ii) the cathode material, (iii) the anode material, (iv) steel, (v) polymer. We have a complete diffraction pattern, and in principle a complete PDF, in each pixel of the image. Adapted from [57]. (Online version in colour.)

6. Conclusion

We have summarized here the recent history of the atomic PDF technique and the key role that X-ray synchtrotrons have played in the development and widespread adoption of the technique. We also briefly mentioned recent developments and future directions.

Appendix A. The PDF method

The PDF method is a total scattering technique for determining local order in nanostructured materials [20]. The technique does not require periodicity, so it is well suited for studying nanoscale features in a variety of materials [58,59]. The experimental PDF, denoted G(r), is the truncated Fourier transform of the total scattering structure function, F(Q) = Q[S(Q) − 1] [44]:

$$G(r)=\frac{2}{\pi }{\int }_{Q_{\min }}^{Q_{\max }}F(Q)\sin (Qr)\hspace{0.17em}\mathrm{d}Q,$$ A 1

where Q is the magnitude of the scattering momentum. The structure function, S(Q), is extracted from the Bragg and diffuse components of X-ray, neutron or electron powder diffraction intensity. For elastic scattering, Q = 4πsin(θ)/λ, where λ is the scattering wavelength and 2θ is the scattering angle. In practice, values of Q_min and Q_max are determined by the experimental set-up and Q_max is often reduced below the experimental maximum to eliminate noisy data from the PDF since the signal to noise ratio becomes unfavourable in the high-Q region.

Once the experimental PDFs are determined they can be analysed directly or through modelling. A powerful approach is simply to compare experimentally determined PDFs from samples under study and from known control samples [60]. A great deal can be learned simply from visual inspections and by taking differences to look for residual signals. Numerical tools that compare the likeness, or degree of correlation, between two curves also give insight [60,61]. The Pearson correlation coefficient is one such tool [61].

The PDF gives the scaled probability of finding two atoms in a material a distance r apart and is related to the density of atom pairs in the material [20]. For a macroscopic scatterer, G(r) can be calculated from a known structure model according to

$$\begin{array}{rl}G(r)& =4\pi r[\rho (r)-{\rho }_0],\\ \rho (r)& =\frac{1}{4\pi r^{2}N}\sum _i\sum _{j\ne i}\frac{b_i{b}_j}{{⟨b⟩}^2}\delta (r-r_{ij}).\end{array}$$ A 2

Here, ρ₀ is the atomic number density of the material and ρ(r) is the atomic pair density, which is the mean weighted density of neighbour atoms at distance r from an atom at the origin. The sums in ρ(r) run over all atoms in the sample, b_i is the scattering factor of atom i, 〈b〉 is the average scattering factor and r_ij is the distance between atoms i and j.

In practice, we use equation (A 2) to fit the PDF generated from a structure model to a PDF determined from experiment. For this purpose, the delta functions in equation (A 2) are Gaussian-broadened and the equation is modified to account for experimental effects. PDF modelling, where it is carried out, is performed by adjusting the parameters of the structure model, such as the lattice constants, atom positions and anisotropic atomic displacement parameters, to maximize the agreement between the theoretical and an experimental PDF. This procedure is implemented, for example, in PDFgui [25] and Diffpy-CMI [28].

Data accessibility

This article does not contain any additional data.

Competing interests

I declare I have no competing interests.

Funding

This work was supported by US DOE, Office of Science, Office of Basic Energy Sciences (DOE-BES) under contract no. DE-SC0012704.