Ice-binding proteins and the applicability and limitations of the kinetic pinning model

Abstract

Ice-binding proteins (IBPs) are unique molecules that bind to and are active on the interface between two phases of water: ice and liquid water. This property allows them to affect ice growth in multiple ways: shaping ice crystals, suppressing the freezing point, inhibiting recrystallization and promoting nucleation. Advances in the protein's production technologies make these proteins promising agents for medical applications among others. Here, we focus on a special class of IBPs that suppress freezing by causing thermal hysteresis (TH): antifreeze proteins (AFPs). The kinetic pinning model describes the dynamics of a growing ice face with proteins binding to it, which eventually slow it down to a halt. We use the kinetic pinning model, with some adjustments made, to study the TH dependence on the solution's concentration of AFPs by fitting the model to published experimental data. We find this model describes the activity of (moderate) type III AFPs well, but is inadequate for the (hyperactive) Tenebrio molitor AFPs. We also find the engulfment resistance to be a key parameter, which depends on the protein's size. Finally, we explain intuitively how TH depends on the seeding time of the ice crystal in the protein solution. Using this insight, we explain the discrepancy in TH measurements between different assays.

This article is part of the theme issue ‘The physics and chemistry of ice: scaffolding across scales, from the viability of life to the formation of planets’.

1. Introduction: ice-binding proteins

Ice-binding proteins (IBPs) are a class of molecules that are key for the survival of organisms in cold environments. These include antifreeze proteins (AFPs) and recrystallization inhibition proteins, which mitigate the physical damage from ice growth to an organism by suppressing the freezing temperature and the recrystallization inhibition, respectively.

Ice-nucleating proteins can either act to prevent frost injury, such as by initiating freezing in insects at lower super-cooling, where ice grows slower and can be less damaging [1], or lead to frost injury, for example on plant leaves, where bacteria promote infection following the injury [2]. Ice-nucleating proteins are considered to contribute to the induction of precipitation in clouds [3] and are a key ingredient in snow generation machines (Snomax). Owing to the small size of the AFPs, their nucleation ability is expected to be only a few degrees above the homogeneous nucleation [4]. This small shift of the ice nucleation temperature from the homogeneous nucleation temperature by AFPs has recently been observed both experimentally [5] and computationally [6].

Another function of IBPs is to mediate adherence to ice. Bacteria living in cold water use IBP to bind to ice that floats on the water's surface, allowing them access to the nutrient-rich water at the top of the water body they live in [7]. Marinomonas primoryensis bacteria have a 0.6 μm adhesion complex that includes an IBP molecule at the end that allows it to adhere to ice and thrive in the partially frozen water environment [8].

Furthermore, ice crystals grow in the air into complex morphology depending on the temperature and humidity conditions [9]. In a solution, the morphology of ice crystals depends on the solutes, their concentration and the temperature profile. IBPs' interaction with ice crystals, namely, its binding to specific faces of the ice, results in unique ice crystal shapes during freezing and melting in the presence of IBPs [10].

The control of ice growth morphology by IBPs has practical implications [11]. For example, the morphology of ice affects the texture of ice cream and the damage to food from freezing, and to organs during preservation procedures. In addition, IBPs can prevent recrystallization damage to foods during frozen storage.

The preservation of tissues and, eventually, organs by freezing is the holy grail of cryobiology [12]. The main strategy for preservation techniques is to minimize the freezing damage to the sample during the procedure. In cryosurgery, on the other hand, damage to organs during freezing and thawing is used to kill tumours [13]. So, similar principles can be used for both minimizing damage in organ preservation and maximizing damage in cryosurgery. Ice and crystal growth have traditionally been controlled by adjusting the cooling rates and the thermal profile in the sample in the presence of cryoprotectants. IBPs allow another degree of freedom during freezing and thawing, which is independent of temperature, by blocking recrystallization and changing the shape of the ice crystals. IBPs also allow sub-zero non-freezing preservation of tissue [14]. Therefore, IBPs hold great promise as enabling agents for both the preservation of foods and organs as well as for cryosurgery.

In order to study and use IBPs, there is a need to purify them from the organisms that contain them. One of the purification methods that is unique to IBPs is based on their affinity to ice, whereas other solutes are rejected from the growing ice. Slowly, growing ice rejects solutes while the IBPs bind to the surface and are engulfed by the ice. As the IBPs accumulate on the surface of the ice, they are depleted from the vicinity of the ice and, thus, there is a need for stirring in order to reduce the protein concentration gradients. At high growth velocities, the concentration gradient of the solutes in the solution ahead of the growing ice can destabilize the surface and can lead to the incorporation of the solutes into the ice; therefore, slow growth is preferable. Furthermore, the time needed for the protein to accumulate on the surface also requires slow ice growth.

A small concentration gradient of the solutes ahead of the ice front was achieved by setting the ice to grow very slowly (3 cm in 6 h) by inserting a cooled brass finger into the solution and letting the ice grow as a hemisphere around it while gently stirring the solution [15]. Only a small concentration solution (10⁻²–10⁻³ mg ml⁻¹) could be used in this method to purify IBPs. Recently, new methods have been implemented that increase the surface of the ice. One such method, ice shell purification, involves rotating a round vessel that is partially submerged in a sub-zero bath, which increases the ice surface area as well as homogenizing the solution [16]. In another method, falling water purification, the solution flows over the growing ice surface in a commercial ice machine, and solutes are washed from the ice surface [17]. These methods open the way to the purification of large amounts of IBPs, both from natural sources and from proteins cultivated from bacteria containing recombinant IBP.

(a). Antifreeze proteins

AFPs, in mM concentrations, can inhibit ice growth in supercooled conditions for up to a few degrees [18]. This property makes AFPs a key molecule in the adaptive strategies of species to an extremely cold environment as well as a promising agent for the cryopreservation of tissues and foods [19,20]. An equivalent freezing inhibition by colligative equilibrium freezing depression would require a few orders of magnitude higher concentrations of conventional antifreeze agents.

The AFP's activity is kinetic in its nature. AFPs bind to the faces of ice crystals and block the crystal's growth [15,18]. AFPs also increase the melting temperature of ice crystals [21,22]. The difference between the reduced freezing temperature and the increased melting temperature is the thermal hysteresis (TH).

Gibbs–Thompson

The freezing repression mechanism stems from the AFP's ability to bind to the surface of the ice crystals [23]. Ice can then grow only between the proteins. Growing between the proteins forces the ice surface to develop locally significant curvature [24], and high surface curvature reduces the melting point according to the Gibbs–Thomson effect.

This effect can be explained as follows. The curvature is approximately the ratio of the local change in surface to the local change in volume. Thus, as curvature is increased the contribution of the surface energy increases, and the offset of the access surface energy is balanced by a reduced melting point, i.e. an increase in the free energy difference between the water and ice. The Gibbs–Thomson equation for ice is given by Liu et al. [25]

$$T_{\mathrm{m}}(r)=T_{\mathrm{m}}^{\mathrm{flat}}-\frac{50nm}{r}\hspace{0.17em}\mathrm{K},$$ 1.1

where r is the radius of the curvature, and T_m(r) and T^flat_m are the freezing temperatures for the curved surface of radius r and for the flat surface, respectively. The curvature is originated by the fact that the ice is confined to grow between the AFPs on the surface.

(b). Moderate versus hyperactive antifreeze proteins

AFPs can be divided into two categories: moderate and hyperactive. Moderate AFPs, such as type III AFPs (AFPIII), reduce the freezing point by a maximum of 1.5 K at mM concentrations (figure 1) while hyperactive AFPs, such as Tenebrio molitor AFPs (TmAFP), can reduce the freezing point by over 3 K at a 0.1 mM concentration (figure 2). Following which, we describe the mechanism for TH activity for each AFP category.

Figure 1.

The fitting of the kinetic pinning model to the data, with the TH as a function of the concentration. The data for AFPIII, TRX-AFPIII and MBP-AFPIII are from [33] while the data for wsswAFPIII, wlwAFPIII and wlxAFPIII are from [32]. Schematic figures of each protein are drawn near their graphs.

Figure 2.

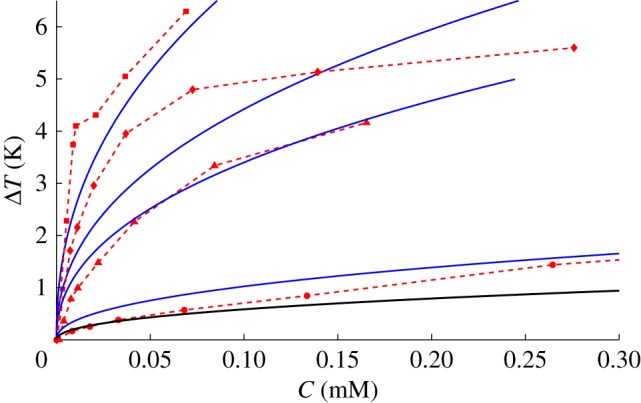
Inadequacy of the kinetic pinning model to the TH of TmAFP: The blue solid lines are the fitting of the kinetic pinning model to the experimental TH of TmAFP of different sizes, as a function of the concentration, plotted in red. The larger proteins have higher activity, as each dataset corresponds to protein size compared to wild-type (WT), which is taken from [34]. The sizes are, WT − 1 coil (circle), WT (triangle), WT + 1 coil (diamond) and WT + 2 coils (box). The fitting parameter χ is found to have the values 1.8, 6.2, 8.4 and 14, which correspond to the proteins according to their size, from small to large. These values are much larger than what was previously measured [35]; therefore, we conclude this model is inadequate for this protein. The black line corresponds to WT with χ = 1, roughly saying it is the highest TH, which the kinetic pinning model can predict for AFPs of TmAFP's size.

AFPs can only bind to specific crystal planes of ice. AFP III binds to the fast-growing prism plane and blocks its growth, leaving the slow-growing basal plane uncovered, as the crystal initially resembles a flat hexagon. The basal plane grows slowly, layer by layer and each new layer nucleates (secondary nucleation) as a step on top of the previous layer. The step then grows rapidly until it is blocked by AFPs, which bind to it from the solution. This process is repeated, resulting in the conic shape of the crystal [7,26]. This explains how AFPs, which bind selectively to only the prism plane, block the growth of a three-dimensional ice crystal that has several different crystal planes on its surface. How AFP blocking of one ice layer affects the next layer is unknown. Even the blocking of a layer on a step has yet to be confirmed.

TmAFPs bind both the basal plane and other non-basal planes so that they cover the whole ice crystal. TmAFPs adsorb slowly on ice, and the measured TH is increased over time. Fast cooling results in a burst of growth that cannot be blocked by the TmAFPs [27]. The high TH activity of TmAFPs can be measured after a long incubation time of the ice crystal in an AFP solution, during which the proteins accumulate on it. After the incubation time, the TH is the same for the presence and the absence of TmAFPs in the solution [27].

It has been shown that AFPs bind to the surface of the ice [27,28]; however, the mechanism of the depression of the freezing point causing TH is still under debate. The Gibbs–Thomson mechanism describes the inhibition of an ice plane, but it is not sufficient to explain the arrest in growth of a three-dimensional crystal, which includes multiple crystal orientations that are not all blocked by the IBPs. Computer simulations allow the study of dynamics on a molecular level and are an efficient supplementary tool for studying AFPs on ice. However, simulations are inherently dependent on the parameters inserted into them. The information gap regarding the AFP-ice-binding energy, their specific positioning on the ice surface, and their orientation makes it difficult to make experimental predictions from computational studies. Thus, this lack of experimental data makes quantitative calculations and models challenging [29,30].

(c). Kinetic pinning model

The kinetic pinning model by Sander & Tkachenko [31] describes the dynamics of AFPs on the surface of growing ice. The model relates the physical properties of the proteins (i.e. their size and shape), their concentration in the solution, and their engulfment resistance (χ, a quantity which we will define later) to the TH activity of the proteins.

AFPs bind to the ice surface and, then, ice is confined to grow between the AFPs, which act as obstacles to its growth. This locally confined growth develops local curvature of the surface that decreases the freezing point according to the Gibbs–Thomson effect. When ice grows between AFPs, the slope of the growing ice surface relative to the surface below an adjacent AFP grows until it reaches a maximum value χ = tan(θ), where θ is the angle between the curved surface near an AFP and the surface to which the AFP is bound. Further growth of the surface causes the surface to grow over the AFP and engulf it. The concentration of AFPs on the surface of the ice, which determines the freezing point repression, changes over time thanks to the adsorption of AFPs from the solution, which increases the concentration and engulfment of adsorbed AFPs into the ice and decreases their surface concentration. If the rate of adsorption is higher than the rate of engulfment of the AFPs into the ice, the ice growth slows down until it stops. The stoppage of the growth is the reduction of the freezing point. Next, we briefly describe the mathematics of the model and present its predictions.

TH is related to the surface curvature according to the Gibbs–Thompson equation. This relation results in a Poisson equation for the height of the surface. Solving the equation and demanding a zero growth speed of the ice surface results in

$$\frac{{\delta }_T^2}{\log (2\chi l_0/b{\delta }_T)}\simeq {(\chi b)}^{2}2\pi l_0\frac{k_{+}}{v_0},$$ 1.2

where δ_T is the dimensionless TH δ_T = (T_m − T)/T_m = TH/T_m, T_m is the melting temperature; l₀ is the capillary length, which is the ratio of the water–ice interface energy per unit area to the latent heat per volume, and is on the order of 0.1 nm; b is the radius of the spherical AFP; χ is the maximal slope of the ice–water interface on the edge of the AFP, without being engulfed by the ice; k₊ is the rate of the absorption of AFPs to the ice surface; and v₀ is a velocity scale for ice surface growth. The absorption rate can be written as k₊ = v_ApC, where C is the AFP concentration in the solution, v_A is a typical diffusion velocity and p is the probability that an AFP that gets to the ice surface actually binds to it. We have inserted the parameter p, which was not in the original model by Sander & Tkachenko [31].

The diffusion velocity v_A scales according to $v_A\sim \sqrt{D}$, where D is the diffusion coefficient. The Einstein–Stokes relation states that D∼1/b, where b is the radius of the AFP. For an asymmetrical AFP, [31], it is approximated by an ellipsoid with a semi-axis a, b, c (a > b = c) and equation (1.2) is modified to

$$\frac{{\delta }_T}{\sqrt{\log (2\chi l_0/b{\delta }_T)-2\beta }}\eqsim \chi b{\left(\frac{\lambda }{a}\right)}^{1/4}\sqrt{2\pi (\beta +1)l_{0}pC},$$ 1.3

where β = log((a + b)/2b) and λ = k_BΛ/6πηκ, where k_B is the Boltzmann constant, Λ is the latent heat of freezing, and η and κ are the viscosity and thermal conductivity of water, respectively. Some of the cases we will consider cannot be accurately approximated in such a way because the height of the protein is bigger than its width (c > a, c > b). In such cases, the size of the AFP that affects the surface curvature b in equation (1.2) is not the same size that affects the diffusion. For that, we modify equation (1.3), assuming the projection on the surface to be circular with radius b = a and that c is the semi-axis perpendicular to the surface

$$\frac{{\delta }_T}{\sqrt{\log (2\chi l_0/b{\delta }_T)}}\eqsim \chi b{\left(\frac{\lambda }{c}\right)}^{1/4}\sqrt{2\pi (\log \frac{b+c}{2b}+1)l_{0}pC}.$$ 1.4

The physical properties of the AFP that affect δ_T are b, c, and its chemical ice interacting properties p and χ. Especially interesting is the relationship between these parameters themselves χ(b, c, p) for a given AFP. We also attempt to shed light on the relation of χ(b, c, p) using published experimental data.

2. Methods

(a). Fitting the experimental data to the kinetic pinning model

To explore the validity of the kinetic pinning model, we have preformed calculations based on the model and compared them to published experimental data for both the moderate AFPIII [32,33] and for the hyperactive TmAFP [34].

In these experiments, AFPIII was fused with other proteins or with itself to vary its physical properties while measuring its TH activity in different concentrations (figure 1). Variations were made of dimers of AFPIII fused together [32]. For instance, wlxAFPIII is a dimer of AFPIII, as one of the AFPs was modified to disable its ice-binding activity. Furthermore, wlwAFPIII and wsswAFPIII are dimers of two AFPs fused together with the ice-binding faces in parallel, facing the same direction and the opposite direction, respectively [32]. Also, AFPIII was linked to either thioredoxin or maltose-binding protein to form larger AFPs, TRX-AFPIII and MBP-AFPIII, respectively [33]. We drew the protein schematically as a box with the ice-binding face in green. Equation (1.3) was fitted to experimental data for AFPIII, wlxAFPIII and wlwAFPIII while equation (1.4) was fitted to the proteins MBP-AFPIII, TRX-AFPIII and wsswAFPIII, which are large in the dimension perpendicular to the ice-binding face.

The TmAFP structure resembles an array of coils with spacing matching the spacing between oxygen atoms on the surface of the ice. Marshal et al. have changed the number of coils in the protein and measured the resulting TH for different concentrations [34] (figure 2).

The main fit parameter is the engulfment resistance χ while other parameters are optimized in parallel for all of the data in relation to their expected values. The protein sizes used in the calculation are systematically smaller than the physical sizes of the proteins, which can be attributed to our schematic representation of the proteins.

3. Results

In figure 1, we show the fitting of the kinetic pinning model to the experimental data of the AFPIII of different sizes and shapes. The model followed the experimental data well, and the parameters used are summarized in table 1. Generally, as the protein became larger so did its TH activity. There were two exceptions to this trend: wlwAFPIII and wsswAFPIII, which are dimers of active AFPs. These two dimers had higher TH than would be expected based on their size. This high TH was made possible by their high probability of binding to the surface p due to the two ice-binding faces, where the wsswAFPIII dimer had a higher p relative to wlwAFPIII because its ice-binding faces covered more potential binding directions.

Table 1.

The fit parameters for the data from figure 1. In the first three rows (AFPIII, wlxAFPIII and wlwAFPIII), the data are fitted to equation (1.3). In the last three rows (wsswAFPIII, MBP-AFPIII and TRX-AFPIII), the data are fitted to equation (1.4).

In figure 2, we show the fitting of the kinetic pinning model to the experimental data of TmAFP of different sizes. The model described the activity of the wild-type TmAFP well while for the other protein sizes, the fitting was not good. The hyperactive TmAFP had a significantly larger TH than the moderate AFPIII. Fitting the kinetic pinning model to the TmAFP TH data resulted in unusually high values of χ: 1.8, 6.2, 8.4 and 14 (figure 2). We concluded that the kinetic pinning model did not describe the activity of the hyperactive TmAFP protein well.

4. Discussion

Type III AFPs do not bind to the basal plane of ice and, therefore, basal plane growth is not inhibited. When a step on the basal plane nucleates, the side of the step, which is a prism face, grows and the proteins from the solution can block it [26,27]. This ice growth inhibition correlates to balance between the protein adsorption and engulfment that causes the ice growth to eventually stop, as described in the kinetic pinning model. Thus, the kinetic pinning model describes the TH activity of AFPIII well (figure 1).

Contrarily, the TmAFP accumulates on the ice crystal both on basal and prism planes. As it accumulates on the ice, the TH increases [28]. Furthermore, it has been shown that the TH of the TmAFP is insensitive to the concentration after the incubation time in a solution of proteins [27]. This increase in TH over time and insensibility to the concentration indicates that the burst limit is not dictated by the rate of absorption but by the concentration of the proteins on the surface. The kinetic pinning predictions are suitable for prediction only when there is a competition between absorption and engulfment. Thus, the kinetic pinning model is not suitable for predicting the TH for the hyperactive proteins, as was also noticed recently by Kozuch et al. [36]. Moreover, the values of χ that allow the model to be on the same scale as the data are above 1 and increase to 14, whereas it was shown previously that for TmAFP, χ < 0.1 [35,37]. Therefore, the kinetic pinning model does not describe the activity of TmAFP.

(a). The effects of the size and shape of the protein on χ

Recently, Naullage et al. [38] showed that the value of χ and the TH for a specific AFP depend on the size of this protein, both upon its projection on the ice surface and its height. We plotted χ as a function of the maximum size $(max(b,c))$ of the protein and showed that χ increases with the size of the AFP (figure 3). When the AFP is larger, ice has to grow around it more in order to engulf it, and the engulfment resistivity is greater [38]. This stems from the fact that engulfing larger particles into a crystal is less favourable energetically [39,40].

Figure 3.

The relationship between the size of the protein and the maximum slope of the ice in its vicinity χ. Near every data point, there is a sketch of the AFP that is related. The green area on the sketch is the ice-binding site. The size is taken as the major semi-axis of an ellipsoid approximation of the protein. χ is deduced from fitting the experimental data to the model from table 1.

In figure 3, there are two obvious exceptions to our claim, wsswAFPIII and TRX-AFPIII. We explain these using the Janus effect. The non-ice-binding face of AFPs (specifically, the back side of the ice-binding domain) suppress ice nucleation, making it ‘ice-phobic’ [41], as opposed to the ice-binding face that promotes ice nucleation and is ‘ice-philic’. This difference between the two faces is called the Janus effect. Recently, it was shown that water near the non-binding face of the AFPs has a short hydrogen bond lifetime, and this is important for achieving high TH [36].

Thus, increasing the size of the AFP by another particle on its non-ice-binding face should, on the one hand, increase χ, as was mentioned before, and, on the other hand, the fused particle should cover the ice-phobic face and reduce the barrier for ice growth over the protein toward its engulfment. As the fused particle becomes larger, the effect on the covering of the ice-phobic face does not change while χ is increased due to the overall increase in size. TRX-AFPIII is a dimer of relatively small protein that is fused to AFPIII, and we found its affect on χ to be negative (figure 3). Covering the ice-phobic face had a more dominant effect than increasing the size of the protein. For the larger MBP-AFPIII, the effect of the increased size increased itself and was more dominant, resulting in increased χ. For wsswAFPIII, the same argument as for TRX-AFPIII can be made. In addition, it has an ice-binding domain on its top side, which we expect should decrease χ even further. This decrease in χ, relative to TRX-AFPIII, was not observed, likely because of its larger size projection on the surface.

5. The accumulation time effect on antifreeze protein activity

The TH for a given protein should depend on its density on the surface of the ice. Recent evidence has shown that the binding of AFPs to ice is irreversible. Therefore, for a stopped surface, i.e. no engulfment, the TH is a function of the density of AFPs on the surface of the ice and is dependent on the surface density of the proteins and not directly on the concentration of the proteins in the solution. Under such conditions, the TH should be expected to increase over time due to the absorption of proteins from the solution and the increase in the density of the proteins on the surface. Such an increase in TH over time was observed for hyperactive AFPs while for type III AFPs, only a small change was recorded [27,28,42].

TH activity stems from the binding of the proteins to the ice surface and their coverage of the surface. The concentration of the proteins on the surface determines the TH of the surface via the Gibbs–Thomson effect. The concentration of the AFPs on the ice surface depends on the AFP's concentration in the solution C, the AFP's adsorption rate k₊, and the accumulation time of the AFPs on the surface t. In this section, we focus on how the AFP TH of a specific ice face depends on the accumulation time of the AFPs on this ice face prior to cooling it below the freezing point.

It has been found that that hyperactive AFPs, i.e. those having a high TH, in cryoscopic (nanolitre) studies [43] are less active in sonocrystallization assays than moderate AFPs [44]. This difference in measured TH values is due to the difference in ice crystal growth and the incubation time in each procedure. In nanolitre osmometers, the ice crystal is slowly cooled in a supercooled AFP solution, where as in sonocrystallization, the supercooled AFP solution is fast frozen through ice nucleation by an ultrasound pulse. Hyperactive AFPs bind slowly to the basal plane as well as to other planes. This allows them to achieve better coverage of the small ice crystals in the cryoscopy assays. On the other hand, in sonocrystallization, ice crystals grow rapidly, and TH is determined by the binding to the fast-growing non-basal planes, at which the hyperactive AFPs are less effective [44,45]. Such a discrepancy in basic TH measurements illustrates that these measurements are sensitive to the measurement conditions. Microscopic direct measurements, therefore, might add to the understanding of the AFP mechanism.

To elaborate on the difference between the sonocrystallization and nanolitre assays, the limits of long and short incubation times can be discussed. When the accumulation time is very small, k₊t≪1, proteins do not adsorb to the surface of the ice and there is no activity, i.e. the TH is small. When increasing the accumulation time, more AFPs are adsorbed to the surface during that time before the temperature is reduced. At some point, the accumulation time is long enough that the concentration of AFPs on the surface is large enough to block ice growth and, hence, suppress freezing (figure 4). Moreover, increasing the time further increases the concentration of AFPs on the ice surface, which increases the TH. Eventually, the accumulation time is large enough that the surface concentration of AFPs is so high that they are saturated on the surface, and no new AFPs can be adsorbed. Then, increasing the accumulation time does not effect the TH, which has reached its maximal value.

Figure 4.

(a) The effect of the accumulation time on TH activity is concentration-dependent. Accumulation time affects the surface concentration on the ice face of the AFPs that are adsorbed from the solution. Both the AFP concentration in the solution and the accumulation time are proportional to the AFP concentration on the surface of the ice. Therefore, increasing the solution concentration reduces the accumulation time needed to achieve the same TH. (b) TH measurement assays allow for different accumulation times, a short time in the sonocrystallization, and a longer time in the nanolitre osmometer.

6. Conclusion

The activity of AFPs is difficult to model due to the multiple macroscopic parameters involved, which include incubation time and temperature, initial ice crystal shape, and temperature profile in addition to the microscopic parameters which include AFP-ice-binding energy, ice topography and growth in the vicinity of an AFP, AFP-specific positioning on the ice surface, and AFP engulfment resistance (χ). The microscopic parameter's values were never measured, and there is large uncertainty regarding their value, making quantitative models and computer simulations challenging [29].

We showed that the kinetic pinning model can be implemented to describe the dependence of type III AFP's TH activity on their concentration in the solution while the model was inadequate for Tenebrio molitor AFPs. The kinetic pinning model describes the growth arrest of an ice surface in an AFP solution. The dynamics of AFPIII adsorbing to the ice to block the slowly growing basal plane resembled the model picture of growing ice, whereas the TmAFPs covering the ice crystal and blocking its growth did not resemble the picture drawn by the kinetic pinning model; the disagreement of the model with experimental data was, therefore, expected.

The engulfment resistance, χ, is a key parameter in the kinetic pinning model. We calculated its value to be in the range 0.5 < χ < 0.9 by fitting the model to published experimental data of the TH as a function of the AFP concentration in the solution for variations of type III AFP of different sizes and shapes. We found evidence that engulfment resistance relates directly to the protein's size, as would be expected for any large particle [39].

Moreover, we showed intuitively how TH activity depends on the incubation time of the ice crystal in an AFP solution. This relationship is general and applies to freezing point suppression of an ice face by AFPs. This insight facilitated understanding of the discrepancy in the TH results for different measurement techniques, which was due to the different accumulation times in each assay [44].

Data accessibility

This article has no additional data.

Authors' contributions

M.C. performed the data analysis and drafted the manuscript. I.B. conceived of and designed the study. All authors read and approved the manuscript.

Competing interests

The authors declare that they have no competing interests.

Funding

I.B. acknowledges support from the Israel Science Foundation, grant no. 930/16. M.C. acknowledges support from The Samuel and Lottie Rudin Scholarship Foundation.