Channel catfish use higher coordination to capture prey than to swallow

Abstract

When animals move they must coordinate motion among multiple parts of the musculoskeletal system. Different behaviours exhibit different patterns of coordination, however, it remains unclear what general principles determine the coordination pattern for a particular behaviour. One hypothesis is that speed determines coordination patterns as a result of differences in voluntary versus involuntary control. An alternative hypothesis is that the nature of the behavioural task determines patterns of coordination. Suction-feeding fishes have highly kinetic skulls and must coordinate the motions of over a dozen skeletal elements to draw fluid and prey into the mouth. We used a dataset of intracranial motions at five cranial joints in channel catfish (Ictalurus punctatus), collected using X-ray reconstruction of moving morphology, to test whether speed or task best explained patterns of coordination. We found that motions were significantly more coordinated (by 20–29%) during prey capture than during prey transport, supporting the hypothesis that the nature of the task determines coordination patterns. We found no significant difference in coordination between low- and high-speed motions. We speculate that capture is more coordinated to create a single fluid flow into the mouth while transport is less coordinated so that the cranial elements can independently generate multiple flows to reposition prey. Our results demonstrate the benefits of both higher and lower coordination in animal behaviours and the potential of motion analysis to elucidate motor tasks.

1. Introduction

Central to the diversity of animal movements, including those of humans, is the coordinated motion of multiple components of the musculoskeletal system. In its colloquial use ‘coordinated’ may describe someone who is adept at a particular task or sport. However, in its technical sense ‘coordination’ refers to the strength of correlated motion among different body parts owing to active, neural processes [1,2], typically measured using cross-correlation or continuous relative phase (CRP) [3]. Because environmental interactions are often unpredictable, the neural system cannot coordinate motion simply by issuing consistently timed motor commands. Rather, the neural system must integrate sensory information, system dynamic properties and motor commands to link the state of one or more effectors to that of one or more other effectors [1,2]. For example, human patients who have lost all sensation (proprioception and touch) in their arm have trouble coordinating motion at different joints during reaching tasks [4], illustrating the need for the neural system to receive sensory input to maintain proper timing of muscle activity.

In its technical sense, higher coordination is not always advantageous. For example, although higher coordination between the left and right leg is desirable during normal walking, if one leg is encumbered by an obstacle, a momentary decrease in coordination (more independent motion of the left and right leg) allows the encumbered leg to free itself while the other leg maintains stride. Accordingly, different behaviours appear to require different levels of coordination [5–8]. For example, in humans, poor ball catching ability can be attributed to arm motions that are too coordinated [7], while poor arm reaching performance in stroke patients can be attributed to arm motions that are not sufficiently coordinated [5]. If human subjects are made to walk such that the left and right legs are on separate treadmills moving at different speeds, subjects change their patterns of interlimb coordination within minutes to restore a symmetric gait pattern [6], and coordination patterns vary among species in association with different behavioural and biomechanical requirements [8], consistent with reinforcement of particular coordination patterns through learning or natural selection.

What general principles, if any, determine the patterns of coordination during motion? One possibility is that coordination patterns are determined by speed. At faster speeds, animals have less time to perform neural computations and must increasingly rely on involuntary control; this shift in control may drive a shift in coordination patterns [9]. Consistent with this, changes in coordination variability have been observed for the same behaviour at different speeds [10] and increasing the speed of motion is used in experiments to trigger a shift in coordination [11]. Another possibility is that the nature of the task determines patterns of coordination [2], specifically that motions of elements in a system are more coordinated when engaged in the same motor task. Consistent with this, coordination patterns among motions of the head, eyes and hand [12] or between the left and right hands [13] in humans differ depending on the behavioural task. These two mechanisms are not mutually exclusive and coordination changes have been observed in motions of the jaw, neck and forelimb of lizards at different speeds and when performing different tasks [8]. What is needed is a test of these two mechanisms on the same dataset: for a given motion sequence does task or speed best explain differences in coordination?

One group of organisms that face a particularly interesting coordination challenge is suction-feeding fishes. Fishes have more moving parts in their skulls (figure 1) than any other vertebrate—well over a dozen [14–16]. These movable elements are not all accessible to active and independent neural coordination: joints and ligaments connect these elements to form a multiloop linkage that passively couples the motion of certain elements [14–16]. Thus, suction-feeding fishes use a combination of active actuation and passive coupling, effectively unfolding and collapsing the skeletal elements that surround the mouth to suck in fluid and prey items [17–20]. Suction feeding consists of at least two main phases, prey capture and intraoral transport (colloquially, ‘swallowing’), and fish use distinct motion patterns for each phase [21–23]. However, whether these different motion patterns constitute distinct coordination patterns, indicating active coordination by the neural system, remains unknown.

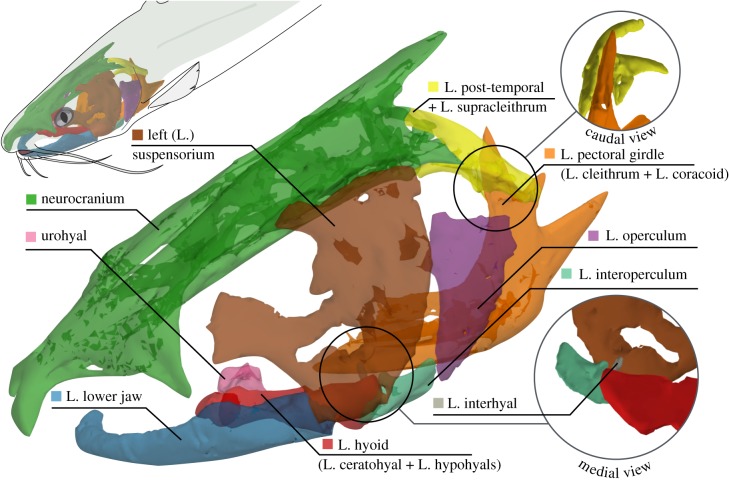
Figure 1.

Mobile skeletal elements of the channel catfish skull (latero-frontal view). The ‘+’ symbol indicates ossifications included within the skeletal element names used in the text. Left (L.).

As a part of a broader investigation into the biomechanics of suction feeding in fishes we measured the three-dimensional, in vivo motion of seven bones in the skull and shoulder of channel catfish (Ictalurus punctatus) during the prey capture and transport phases of suction feeding. We initially chose channel catfish because their body form contrasts with a previously studied species, largemouth bass [24]. However, their cyclical feeding motions subsequently proved advantageous to measuring cross-correlation for the purpose of studying coordination. For motion measurements, we used X-ray reconstruction of moving morphology (XROMM) [25] because the skeletal elements that function directly in expansion of the mouth are not all visible using surface motion capture approaches. Here we use this motion dataset to ask: does this motor system use distinct patterns of coordination and, if so, are these patterns best explained by differences in the behavioural task (prey capture versus transport) or by differences in speed? Distinct patterns of coordination would be consistent with extensive active coordination and sensorimotor integration by the neural system in the skulls of fishes, and whether these patterns are best explained by task or speed would provide a clear test of competing hypotheses for the general determinants of coordination patterns in animal motion.

2. Material and methods

(a). Animal care and surgical procedures

Channel catfish were obtained from Osage Catfisheries, Inc. (Osage Beach, MO, USA), housed individually at room temperature and regularly fed carnivore pellets. Animal care and procedures were approved by the Brown University Institutional Animal Care and Use Committee. Standard lengths (in cm) of Indiv1, Indiv2 and Indiv3 were 31.8, 30.5 and 37.5, respectively. After one to two months of training each fish to feed on demand, we performed surgery to implant tantalum spherical markers in three individuals for X-ray-based motion tracking. We anaesthetized the fish with buffered MS-222 (at 0.09–0.135 g l⁻¹) and administered an analgesic (0.4 mg kg⁻¹ butorphanol). We unilaterally implanted 0.5 and 0.8 mm diameter markers into eight skeletal elements (neurocranium, urohyal and left-side post-temporal, cleithrum, suspensorium, operculum, lower jaw and hyoid) and 0.8 mm diameter markers into the hypaxial muscles (intracranial motions in channel catfish appear to be bilaterally symmetric). Bone markers were implanted by pushing the bead into a hand-drilled hole having the same diameter as the bead. Muscle beads were injected through a hypodermic needle. We also implanted a polyethylene cannula through the rostral neurocranium to insert a pressure probe during experiments. Additional methodological details are provided in the electronic supplementary material, including marker implantation sites (electronic supplementary material, figures S1–S3) and names (electronic supplementary material, tables S1–S3).

(b). In vivo data collection

We recorded synchronous X-ray videos and intraoral pressures during suction feeding. Videos were recorded from two views (biplanar fluoroscopy) at 300 frames s⁻¹. For filming, individuals were given three different prey types: half or whole live earthworms, dead squid pieces and carnivore pellets (electronic supplementary material, movies S1–S2). In choosing prey types, our main objective was to elicit maximal changes in intraoral pressure for a related study quantifying suction power. We began experiments with Indiv1 and Indiv2 using a mix of prey types (Indiv1: eight sinking pellet trials, three worm trials and four squid trials; Indiv2: five sinking pellet trials, nine worm trials and one squid trial). Then, after establishing that worms elicited the greatest intraoral pressure changes we filmed all Indiv3 trials (12 total) using only worms. Although worms elicited the greatest pressure differential, they did so only for some trials. Thus, even though all Indiv3 trials used worm prey, we obtained comparable pressure distributions for all three individuals (electronic supplementary material, table S4).

(c). X-ray reconstruction of moving morphology animation

To convert marker motions into three-dimensional rigid-body transformations for each skeletal element, we used a workflow of marker tracking, reconstruction and computed tomography (CT) mesh unification known as XROMM animation. Marker X-ray trajectories were tracked using automation-assisted tracking tools in XMALab v. 1.3.9 [26]. A total of 36–38 beads were tracked (per individual) over a total of approximately 42 000 frames (all individuals). Hypaxial muscle strain was measured using fluoromicrometry, measuring the distance between the most rostral and the second or third most rostral hypaxial markers [27]. We performed camera calibration and marker reconstruction in XMALab. We segmented each skeletal element of interest from the CT scans and exported marker three-dimensional coordinates in ‘CT space’ using Horos v. 2.0.1 (horosproject.org). We performed all subsequent analyses using a new XROMM animation workflow (matools R package; github.com/aaronolsen) for R [28], including marker smoothing and aligning the smoothed three-dimensional marker coordinates with the corresponding CT marker coordinates (unification; electronic supplementary material, movie S3) to animate each skeletal CT mesh. All mesh animations (e.g. electronic supplementary material, movie S3) were created using the svgViewR R package [29]. The standard deviation in marker-to-marker distances within each skeletal element, one measure of precision, was 0.080 mm on average (electronic supplementary material, table S5).

(d). Joint model fitting

We used joint model fitting to reduce the full joint motion dataset (6 degrees of freedom (d.f.s.) per skeletal element, three translational and three rotational, 36 total d.f.s) to a smaller set of axes that represent the principal motions within the skull. We first trimmed out regions of each trial with little intracranial motion (e.g. swimming towards prey), leaving a total of 32 909 frames (Indiv1: 15 405 frames; Indiv2: 9450; Indiv3: 8054). We then fitted models to the six joints connecting our skeletal elements of interest, fixing one element at each joint to characterize relative motion and concatenated all trials into a single sequence. To each joint, we fitted three models: a one-axis (hinge) joint, a two-axis (saddle) joint and a three-axis (ball-and-socket) joint; here, the number of joint axes is also the number of d.f.s. Model fitting was done using the ‘fitMechanism’ function in the linkR R package [30], which estimates a best-fitting centre of rotation and axis or axes of rotation and the rotations about each axis. Specifically, the algorithm iteratively optimizes orientation and position of each axis, element pose and rotations about each axis until the error or change in error drops below a specified threshold. Fit error was quantified using three landmarks distributed across each element. We then selected the lowest d.f. model with an average maximum error less than 1% of head length (approx. 0.75 mm).

(e). Subsetting and binning data

To compare prey capture and intraoral transport, we identified the capture and transport phase for each trial. The end of capture (and start of transport) was identified as the first time at which the lower jaw fully elevated (closed) after the prey entered the mouth. We also divided each trial into open–close events for the purpose of comparing low- and high-speed motions (Indiv1: 61 events; Indiv2: 64; Indiv3: 45). An open–close event was defined as a single retraction and protraction of the pectoral girdle (each open–close event started and ended with the pectoral girdle in the retracted position). We used the minima of pectoral girdle retraction speed to delineate consecutive events because pectoral girdle retraction occurred consistently with mouth opening. We then binned these events evenly by individual into high- and low-speed bins based on the maximum pectoral girdle retraction speed during each event. The cut-offs separating low- and high-speed bins were set to obtain a similar number of open–close events in each bin and ranged from 48.5 to 66.4° s⁻¹ (electronic supplementary material, table S4). We repeated the same binning procedure based on the maximum intraoral pressure differential during each open–close event to test whether pressure has an effect on differences in cross-correlation. Results of the comparison based on pressure did not differ from those based on speed and so are not discussed further here but can be found in the electronic supplementary material.

(f). Cross-correlation, motion integration and randomizations

From the joint model fitting, we obtained a set of eight significant rotations about each best-fit axis (concatenating all trials). We then measured the pairwise cross-correlation between each set of axis rotations (motion pairs) for a total of 28 motion pairs. Cross-correlation takes as input two time-varying signals and returns the linear correlation coefficient between the two signals over a range of time lags (lags are added by shifting one signal relative to the other). For each pairwise combination, we recorded the maximum cross-correlation across a lag range of −40 to 40 frames (−133 to 133 ms; lag.max = 40 frames), so subsequent uses of ‘cross-correlation’ refer to this maximum value (a re-analysis using a narrower lag range of −83 to 83 ms, lag.max = 25 frames, did not affect the conclusions). Since cross-correlation implies just two signals we use ‘motion integration’ (or simply ‘integration’) to refer to the correlation between two or more motions [31]. This parallels the use of ‘integration’ in shape analysis to describe the correlation among multidimensional shape coordinates. We took the mean of all these pairwise cross-correlations as the total motion integration within the skull. We calculated cross-correlation using ‘ccfDis’ (matools R package), based on the standard cross-correlation function (ccf) but modified for discontinuous time series. The ‘ccfDis’ function inserts buffers of ‘NA’ values between concatenated sequences so that when one signal is slid relative to the other, the edge of one sequence does not overlap with the edge of a different sequence.

We assessed significance by resampling randomizations. The standard cross-correlation function does not return a significance statistic (high-frequency but independent oscillatory patterns can give relatively high, but non-significant, cross-correlation coefficients). Thus, to assess the significance of the cross-correlation coefficient we created a randomized sample by flipping (temporally reversing) one signal in each motion pair for each trial and calculating the cross-correlation, randomly choosing for each trial which of the two signals to flip. This process of flipping the signals creates a null distribution of motions for each pair that preserves the frequency and amplitude characteristics of the original data but removes temporal correspondence between the two signals. We calculated a p-value by dividing the number of iterations for which the randomized cross-correlation was greater or less than the actual cross-correlation (greater if the actual was positive, less if negative) by the number of randomized iterations. We formed a null distribution for assessing the significance of the cross-correlation difference between tasks (capture versus transport) by randomizing the designation of capture versus transport within each trial. The significance of cross-correlation differences between bins (high versus low speed) was assessed in a similar way, randomizing the low and high bin designations by open–close event. Lastly, we assessed whether total integration differed significantly among individuals by randomizing the designation of individual across all 42 trials and calculating cross-correlations. All randomizations were repeated 999 times. We also tested for a difference in cross-correlation during capture versus transport by trial (i.e. calculating the mean cross-correlation for each behaviour and trial and using a t-test to assess significance). Because this approach is more sensitive to spurious cross-correlations given the shorter sequences, the lag range had to be reduced to −83 to 83 ms. However, the conclusions were the same as for the concatenated sequences and only the results from the concatenated sequences are presented here.

(g). Measuring coordination from motion integration

A challenge to measuring coordination is that although coordination produces correlated motion (i.e. motion integration), correlated motion is not produced solely by coordination [31]. We can think of three mechanisms that could cause correlated motion: extrinsic integrators, passive coupling and active coordination. Extrinsic integrators include organism–environment interactions; for example, when trout swim in a flow with vortices, the vortices themselves drive much of the observed body undulations [32]. Passive coupling includes ligaments and other tissues that mechanically link elements. Motion integration not caused by extrinsic integrators or coupling results from active coordination by the neural system. For a fish feeding in still water, it is the skeletal elements that primarily drive fluid flow. Thus, observed motion patterns should result mostly from intrinsic mechanisms (coupling and coordination). Coupling, being structural, should generally be invariant across behaviours while coordination can vary motion integration patterns for different behaviours (we note exceptions in the discussion). Thus, we infer that changes in motion integration patterns are caused by changes in coordination. Because we have used cross-correlation, our results may not be directly comparable to studies using CRP or CRP variability [3]. CRP measures instantaneous correlation, whereas cross-correlation measures correlation over a given time range. Owing to sample size limitations, we cannot measure cross-correlation variability in a manner analogous to CRP variability. We used cross-correlation because, unlike CRP, it can incorporate lags. Lastly, although ‘coordination’ is often used in the literature to refer to what we call ‘integration’, we use ‘coordination’ to refer solely to the active component of motion integration.

3. Results

(a). Behaviour

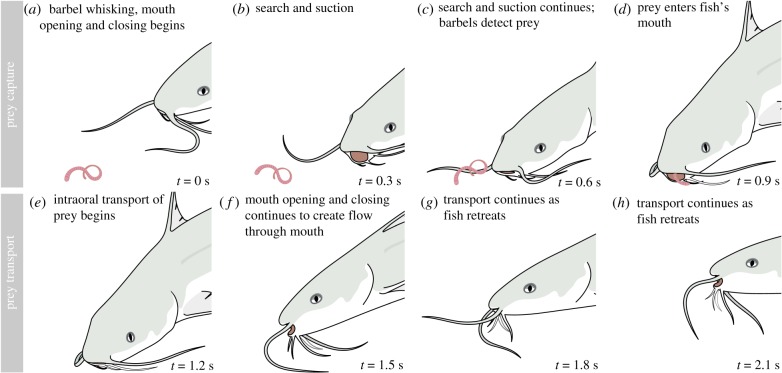
For most trials, we observed channel catfish perform a complete feeding sequence, starting with search for the prey and ending with transport of the prey into the oesophagus (figure 2; electronic supplementary material, movies S4–S5). Throughout the entire sequence (figure 2a–h), we observed repeated opening and closing of the mouth. During prey search, the fish whisked its barbels back and forth while rummaging along the bottom of the tank with its head (figure 2a–c). Only after a barbel made physical contact with the prey did the fish suck the prey into its mouth (figure 2c,d); fish did not appear to make any use of visual cues. After engulfing the prey, the fish retreated by swimming backward while simultaneously beginning intraoral transport of the prey (figure 2e–h). We used the first mouth closure immediately after the prey entered the mouth (figure 2e) to divide each feeding sequence into prey capture (figure 2a–d) and intraoral transport (figure 2e–h).

Figure 2.

Channel catfish feeding behaviour. For this study, we separated feeding into two tasks or phases: (a–d) prey capture and (e–h) prey intraoral transport. The timing of events (lower right corner) is variable; only approximate timings are shown.

(b). Intracranial motion

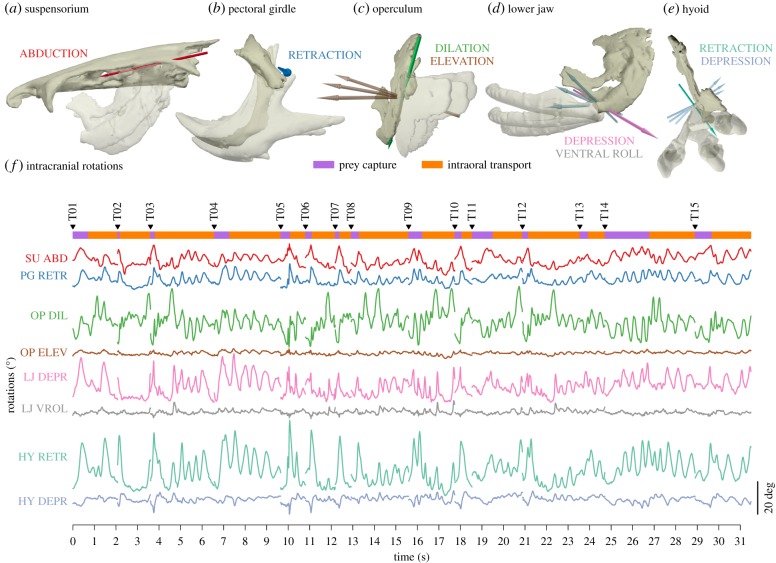
We observed substantial motion (rotations about a primary axis of at least 15°) at five of the six joints of interest in this study during both capture and transport (figure 3; electronic supplementary material, figures S4–S9; movie S3). The exception was the neurocranium-post-temporal joint, where rotations were generally less than 4° (electronic supplementary material, figures S4–S6) and were not correlated with any other intracranial motions (electronic supplementary material, figures S10–S12); for this reason, we excluded motion at the post-temporal joint from subsequent analyses. Based on the magnitude of rotations about each axis and mean maximum model fit errors, we found that one rotational axis (a hinge model) was sufficient to describe motions of the suspensorium and pectoral girdle (figure 3a,b). For the suspensorium, secondary and tertiary rotations were less than 2° (electronic supplementary material, figures S4e–S3e) and one-axis model errors were less than 1% head length for all individuals (electronic supplementary material, figures S4f–S3f). For the pectoral girdle, secondary and tertiary rotations were less than 3° (electronic supplementary material, figures S4 h–S3 h) and one-axis model errors only significantly exceeded 1% head length for Indiv3 (electronic supplementary material, figure S6i).

Figure 3.

Rotations at the principal intracranial joints in channel catfish during feeding for Indiv2. Coloured arrows in (a–e) are best-fit motion axes with corresponding rotations in degrees (f) about each axis across all trials from this individual. Only axes with significant rotations are shown. The mobile body in each pair is shown in the most extreme poses over its range of motion. For the two-axis joint model, the secondary axis moves with the mobile body and is therefore shown in multiple poses. In (f), inverted black triangles indicate the start of each trial (n = 15 trials). The capture and transport phases were identified for each feeding trial. The purple and orange bars indicate the duration of the capture (purple) and transport (orange) phases for each trial. See the electronic supplementary material, figures S7–S9 for corresponding figures for all individuals.

We found that two rotational axes (a saddle joint model) were needed to describe the motions of the operculum, lower jaw and hyoid, all relative to the suspensorium (figure 6c–e). For the operculum, two-axis model errors were less than 1% head length for all individuals (electronic supplementary material, figures S4l–S6l). For the lower jaw, two-axis model errors significantly exceeded 1% head length for Indiv1 (electronic supplementary material, figure S4o). For the hyoid, two-axis model errors significantly exceeded 1% head length for Indiv2 and Indiv3 (electronic supplementary material, figures S5r and S6r, respectively). However, tertiary rotations (oriented approximately along the long axis of the hyoid) may be unreliable given our inability to implant markers far from the long axis of the hyoid. Thus, we used only the first two axes. Motion names for each joint (e.g. suspensorium abduction; figure 3) refer to positive rotations about the corresponding axis (figure 3a–e), following the right-hand rule. The rotations about these eight axes represent the principal motions within the skull (figure 3f; results for all individuals in the electronic supplementary material, figures S7–S9).

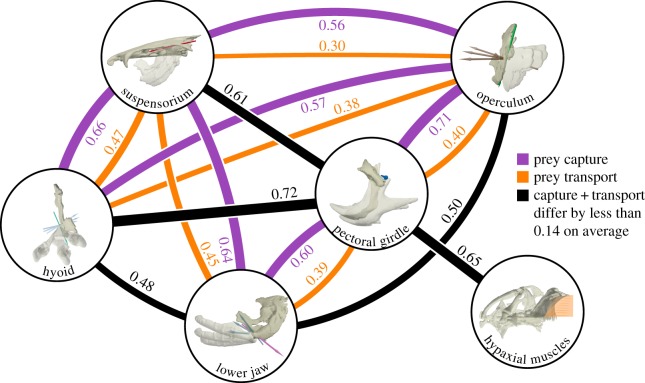
Figure 6.

Summary of coordination changes in the channel catfish skull during feeding. Nodes represent each skeletal element and edges represent the mean motion integration between skeletal elements (mean of all cross-correlations including that element for all individuals). Black edges indicate where integration changes from capture to transport by less than 0.14 (the mean difference for all pairwise comparisons); purple and orange edges indicate integration changes greater than 0.14. Edge thickness is proportional to the associated integration value. See the corresponding electronic supplementary material, table S6 for results by individual.

(c). Motion integration patterns and coordination changes

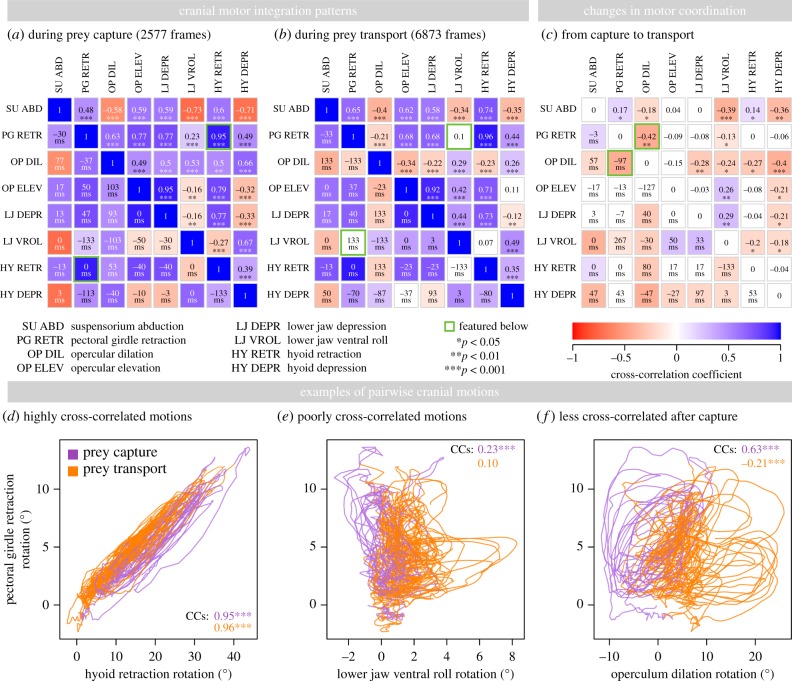
Intracranial motions in channel catfish were highly and significantly cross-correlated throughout feeding (figure 4a,b, upper diagonal; results for all individuals in the electronic supplementary material, figures S13–S15). Of the 28 pairwise motion comparisons, rotations between at least 27 pairs were significantly cross-correlated during capture (p < 0.05; figure 4a) and rotations between at least 23 pairs were significantly cross-correlated during transport (figure 4b) for all individuals. Two motion pairs showed particularly high cross-correlations (figure 4a,b, upper right triangle) and 0 ms lags (figure 4a,b, lower left triangle): pectoral girdle retraction and hyoid retraction (figure 4d) and opercular elevation and lower jaw depression. Among the motion pairs with the lowest cross-correlation was pectoral girdle retraction and lower jaw ventral roll (figure 4e). In spite of significant intracranial motion integration during prey capture and transport, we detected several significant decreases in integration from capture to transport (figure 4c). Of all significant changes during capture versus transport, at least 75% were decreases: 14 of 14 for Indiv1, 13 of 17 for Indiv2 (figure 4c) and 12 of 15 for Indiv3. One motion pair for which this decrease was particularly pronounced was pectoral girdle retraction and opercular dilation (figure 4f).

Figure 4.

Cranial motion integration patterns in channel catfish during feeding for Indiv2. Squares in (a–c) represent pairwise comparisons of intracranial motions, with cross-correlations in the upper right and lag times in the lower left. Positive lag times indicate that the left row label motion precedes the top column label motion; for example, during capture, lower jaw depression precedes pectoral girdle retraction by 47 ms. Negative lag times indicate that the left label follows the top column label. Because motions are generally more integrated during capture (a) than during transport (b), changes in absolute cross-correlation are mostly negative (c). Asterisks indicate significant cross-correlations in (a,b) and significant shifts in cross-correlation in (c), based on randomization tests. Three examples of motion cross-correlation relationships are shown in (d–f). See the electronic supplementary material, figures S13–S15 for corresponding figures for all individuals.

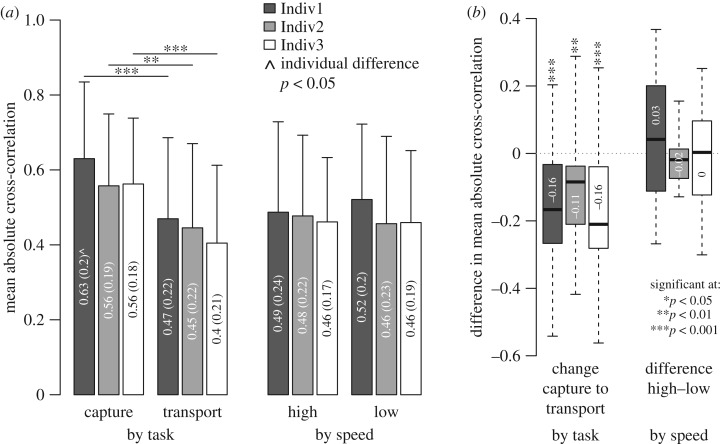
A decrease was also observed in the mean of all pairwise cross-correlations (total intracranial integration): integration dropped significantly by 0.11–0.16 (20–29%) from capture to transport for all individuals (p < 0.01; figure 5a,b). By contrast, no significant differences in total integration were detected between mouth open–close events grouped by high versus low pectoral girdle retraction speed (figure 5a,b). Some differences among individuals were detected in mean integration (figure 5a,b, carets), however no significant individual differences were detected in the motion integration change from capture to transport (figure 5b; p < 0.05). Thus, although individuals showed slight differences in overall intracranial integration, decreases in integration from capture to transport were consistent for all individuals. The decrease in integration from prey capture to transport in channel catfish affected all five cranial skeletal elements of interest in this study (figure 6; electronic supplementary material, table S6). Each cranial element showed a decrease in cross-correlation strength with at least two other elements by a magnitude greater than the mean decrease across all pairwise comparisons (0.14). Pectoral girdle retraction was the motion most strongly cross-correlated with all other motions. Pectoral girdle retraction was also significantly correlated with shortening of the hypaxial muscles (figure 6), with no significant change between capture and transport (p < 0.05). By contrast, suspensorium and operculum motions were among the most variable in their cross-correlation with other elements.

Figure 5.

Mean motion integration differences by task and speed for all individuals. Mean intracranial motion integration was significantly greater (p < 0.01, asterisks) during capture than during transport for all individuals (a,b, left). By contrast, no significant differences in mean integration were found between mouth open–close events grouped by speed (a,b, right). One significant individual difference was identified (p < 0.05, carets) but not in the mean integration differences during capture versus transport (b, left). Values within bars are mean (s.d.) in (a) and mean in (b). Significance was determined by randomization tests.

4. Discussion

In this study, we used a dataset of motions throughout the skull of channel catfish to uncover a significant shift in patterns of motion integration (correlations among two or more motion sequences) during feeding. We argue that this shift in integration is owing primarily to changes in coordination by the neural system. We find that this shift in integration is not explained by speed but rather by behavioural objective (prey capture versus transport), supporting the hypothesis that it is the nature of a task that determines coordination patterns. Specifically, we find that intracranial motions are more coordinated during prey capture than during prey transport. Our finding that shifts in coordination affect all five cranial skeletal elements suggests that the fish cranial linkage, in spite of multiple couplings, has greater d.f.s of motion than generally recognized. And our finding that tightly integrated motions during prey capture are mediated by coordination suggests an important role for sensory feedback in motor control of the fish skull.

Despite only collecting motion data, we can still conclude that most of the motion integration changes that we have observed are owing to coordination. Ruling out extrinsic causes of motion integration, we are left with intrinsic mechanisms: passive coupling and active coordination (see §2g). Although correlated motion owing to coupling should generally be invariant across behaviours (because such couplings are always present), we can think of two ways in which coupling could cause varying motion integration patterns, referred to here as variable passive coupling (VPC). The first is viscoelasticity of coupling elements such as connective tissues. Because of viscoelasticity, a coupling element could provide tighter coupling the faster it is pulled, creating a difference in integration when the system is actuated at different speeds. However, we observed no significant difference in total integration between high- and low-speed motions (figure 5). We would especially expect viscoelastic VPC at direct ligamentous couplings, such as between lower jaw depression and opercular elevation, coupled by the interoperculomandibular ligament. However, the cross-correlation between these motions changes less than 0.03 for low- versus high-speed events (electronic supplementary material, figure S13f–15f). The short length of the ligaments relative to the size of the bones in channel catfish skulls may explain why any length changes in connective tissues have little effect in varying integration patterns.

A second potential VPC mechanism is nonlinear motion transmission between two links in a linkage. For example, in a 1 d.f. four-bar linkage, input link motion relative to output link motion is often nonlinear. If such a four-bar is actuated over a consistent range between two behaviours then the input–output cross-correlation will be consistent. However, if actuated over different ranges, one effectively ‘samples’ different regions of this nonlinear relationship, resulting in variable input–output cross-correlations. Importantly, the linkage must have 1 d.f. so that motion of one link follows directly from the motion of another. None of the skeletal elements investigated here appear to be coupled by 1 d.f. linkages. We recently showed that the lower jaw-operculum linkage in largemouth bass functions as a 3 d.f. three-dimensional four-bar [16] and this linkage appears to have at least as much mobility in channel catfish. Similarly, the pectoral-hyoid linkage [14] forms a six-bar linkage in three dimensions, which should have at least 2 d.f.s. Furthermore, four of the six skeletal element pairs that show the greatest change in integration (figure 6) are not even directly coupled by a linkage.

Not only can we rule out passive mechanisms as a principal cause of the observed changes in integration, but we can also identify active mechanisms that can fully account for these changes. At least 10 different muscles (eight intracranial and two axial muscle groups) attach to the skeletal elements of interest here (figure 6), with at least two muscles attached to each element. Studies of cranial muscle activity in other species of fishes have found that these muscles are active during feeding [21,23,33], and that their activation patterns can differ significantly between prey capture and other feeding behaviours [21,23,33]. Muscle architecture and general patterns of muscle activation across fishes are fully and uniquely congruent with active neural control as the modifier of motion integration patterns between prey capture and transport. For this reason, we conclude that the shift in integration observed here is primarily a shift in coordination.

Our results suggest that sensorimotor integration maintains the effective timing of intracranial motions within the fish skull [34]. Although the fish skull is frequently modelled as a series of two dimensions, 1 d.f. four-bar linkages (e.g. [14,15]) it is also recognized that fish are capable of moving the bones within their heads in multiple, independent ways [33,35]. Based on our results, the channel catfish skull probably has at least 5 d.f.s: we observe significant changes in coordination among five main skeletal elements (figure 6) and the opercular linkage and pectoral-hyoid linkages (which, as mentioned previously, probably have at least 3 and 2 d.f.s, respectively) can account for at least 5 d.f.s. Each d.f. in a system represents an independent dimension along which position and motion must be controlled. Thus, with greater d.f.s comes a greater need for active control and coordination, which in turn requires sensory feedback to maintain the relative timings among moving parts [1,2]. Evidence for sensory feedback in the fish skull has been reported previously, particularly the ability of fishes to modulate their feeding kinematics in response to prey type and position [33–35]. Our findings confirm the role of sensory feedback in modulating kinematics and suggest an additional role in coordinating the relative timing of intracranial motions.

Why are intracranial motions in channel catfish more coordinated during capture than during transport? In suction-feeding fishes intracranial motions function to direct fluid flow. During capture, these motions follow a stereotyped and evolutionarily conserved anterior-to-posterior sequence: lower jaw depression, hyoid retraction and opercular dilation [17,36]. This sequence creates a single, unidirectional flow into the mouth [18,20]. The relative timing of these events is key to performance. Opercular dilation, which allows caudal outflow, enables fish to ingest more water than can be accommodated by the oral cavity [18], and wave-like, rather than simultaneous, expansion prolongs fluid flow so that maximum fluid speed better coincides with peak gape [18,37]. As expected, during capture in channel catfish we find an anterior-to-posterior wave starting with peak lower jaw depression at 0 ms, peak suspensorial abduction at 30 ms, peak hyoid retraction at 36 ms and peak opercular dilation at 76 ms. However, during transport this sequence breaks down: lags become more variable, opercular dilation generally decouples from hyoid retraction and cross-correlations decrease. This attenuation of the anterior-to-posterior wave during transport shows that the wave is not built into the mechanical linkages of the skull [37], but rather results from active neural control. Much of the decrease in coordination that we observe from capture to transport may be owing to a shift away from the stereotyped anterior-to-posterior wave and towards a more variable or modular pattern of timings.

Motions may be less cross-correlated during transport simply because timings during that phase are not as crucial to performance. A relaxation of timing constraints would free the system from adhering to a single coordination programme, increasing variability and decreasing cross-correlations. Additionally, it is possible that alternative ways of partitioning this motion dataset would reveal alternative coordination patterns. For example, ‘transport’ may contain multiple discrete coordination patterns, which when grouped together appear as lower coordination. A final explanation relates back to the general question of what determines coordination patterns in motor systems. One hypothesis is that the motions of elements in a system are more coordinated when they are engaged in the same motor task [2]. In the case of fish feeding, the ‘number of flows’ generated by the skull may represent the number of tasks. High coordination during prey capture can then be explained as all of the cranial elements engaged in a single task (a single flow throughout the mouth), whereas lower coordination during transport reflects the cranial elements engaging in multiple tasks, independently accelerating fluid at one or more localized regions within the mouth to reposition and move prey. Future work investigating how intracranial motions relate to intraoral fluid flows and prey transport performance will ultimately resolve these questions and increase our understanding of why particular motor tasks are accomplished by different coordination patterns.

Ethics

Animal care and procedures were approved by the Brown University Institutional Animal Care and Use Committee.

Data accessibility

We deposited data for this publication in the XMAPortal (xmaportal.org) in the study ‘Catfish Suction Feeding’ (permanent ID BROWN61), in accordance with best practices for video data management [38]. Processed kinematic data (.csv format) are published with this study as a supplemental dataset. All custom R functions referenced here can be found at https://github.com/aaronolsen.

Authors' contributions

Designed data collection: A.M.O., L.P.H., A.L.C. and E.L.B. Performed data collection: A.M.O. and L.P.H. Analysed data, conceived this study and wrote the paper: A.M.O. Provided comments on paper: A.L.C., E.L.B. and L.P.H.

Competing interests

We declare we have no competing interests.

Funding

This research was funded by National Science Foundation grant nos. 1612230 to A.M.O., 1655756 to E.L.B. and A.L.C., 1661129 to E.L.B., and the Bushnell Research and Education Fund.