Teacher Math Anxiety Relates to Adolescent Students’ Math Achievement

Abstract

Elementary school teachers’ math anxiety has been found to play a role in their students’ math achievement. The current study addresses the role of teacher math anxiety on ninth-grade students’ math achievement and the mediating factors underlying this relationship. Using data from the National Mindset Study, we find that higher teacher math anxiety is associated with lower math achievement. This relationship is partially mediated by the students’ perception that their teacher believes not everyone can be good at math and is not explainable by teachers’ usable knowledge to teach mathematics. In subsequent analyses, we find that higher teacher math anxiety relates to a reduction in process-oriented (as opposed to ability-oriented) teaching practices, which in turn predict students’ perception of teacher mindset. We argue that math anxious teachers and their use of particular teaching strategies have the potential to shape students’ math achievement and their perceptions of what their teacher believes about math.

High levels of math anxiety can severely undermine an individual’s ability to acquire the mathematical knowledge needed for the 21st-century workplace (Hembree, 1990). Math anxiety is a persistent fear, tension, and apprehension related to situations that require math. Individuals who are math anxious experience intrusive worries that disrupt performance (Ashcraft & Kirk, 2001). These worries manifest in everyday experiences as well as evaluative classroom situations (e.g., taking a test, answering a question in front of peers, etc.). Individuals who are math anxious also engage in avoidance behaviors that lead them to take fewer math classes and participate in majors with fewer math requirements (Hembree, 1990; LeFevre, Kulak, & Heymans, 1992) even if they possess the math skills and course experience to be successful in those majors.

Decades of research have led to a good understanding of the impact of math anxiety among students, but we are only beginning to understand the effects of math anxiety among teachers. One might expect that teachers, who are tasked with being students’ primary mathematics instructors, would feel quite comfortable around math. Unfortunately, many elementary teachers have higher math anxiety than individuals in other fields of study, such as business, physical science, and health sciences (Battista, 1986; Bryant, 2009; Hembree, 1990). The math anxiety that teachers experience carries consequences beyond the individual as teachers who report high levels of math anxiety also report a reduction in the belief that they are capable of successfully carrying out their teaching responsibilities to their students (i.e., teaching self-efficacy and confidence; Bursal & Paznokas, 2006; Gresham, 2008; Swars, Daane, & Giesen, 2006). Teacher math anxiety also impacts their own students’ math learning. Several quantitative (Beilock, Gunderson, Ramirez, & Levine, 2010; Hadley & Dorward, 2011; Maloney, Ramirez, Gunderson, Levine, & Beilock, 2015) and qualitative (Bryant, 2009; Bulmahn & Young, 1982; Furner & Berman, 2003; Hembree, 1990; Karp, 1991; Kelly & Tomhave, 1985; Larson, 1983; Lazarus, 1974; Martinez, 1987; Ring, Pape, & Tittle, 2000; Sloan, Daane, & Giesen, 2002; Swetman, 1994; Vinson, 2001) studies report a negative relationship between teacher math anxiety and growth in student math achievement. In summary, there is a link in how teachers feel about math and the math learning outcomes of their students.

A limitation in past literature about teacher math anxiety is that it has exclusively focused on elementary school and has not been extended to study the pernicious nature of math anxiety among teachers at the middle and high school levels. One reason why teacher math anxiety has been relatively ignored at the high school level is that researchers may have reasoned that math anxiety is not likely to be present among teachers who specialize in math and use it on a daily basis. However, competent and high-performing adults can feel anxious about math as well (Ashcraft & Kirk, 2001; Lee, 2009; Ramirez, McDonough, & Jin, 2017), and individuals in professions that use mathematics on a regular basis are also vulnerable to underperformance in their field of specialization as a consequence of math anxiety. For instance, nurses tasked with making effective drug calculations demonstrate an inverse relationship between math anxiety and drug calculation accuracy (Williams & Davis, 2016). Hence, it seems possible that even high school math teachers may experience anxiety in challenging math situations. If this is the case, their adolescent students might be put at risk for reduced math learning.

Adolescence in particular is an important developmental period for understanding how environmental behaviors and attitudes on behalf of the adults might shape student educational outcomes. Adolescence is a time when students begin to make more autonomous educational decisions and become quite sensitive to status and respect from adults (Yeager, Dahl, & Dweck, in press). Adults’ actions and behaviors often undermine adolescent students’ competency and agency, which can reduce student learning, performance, and persistence (Ryan & Deci, 2000; Vansteenkiste, Simons, Lens, Sheldon, & Deci, 2004). Adolescence is also a time period that has been associated with an increase in fear and anxiety around math (Brush, 1985; Meece, 1981; Meece, Wigfield, & Eccles, 1990; Wigfield & Meece, 1988), making adolescents a vulnerable population to pick up the maladaptive attitudes and beliefs of their teacher.

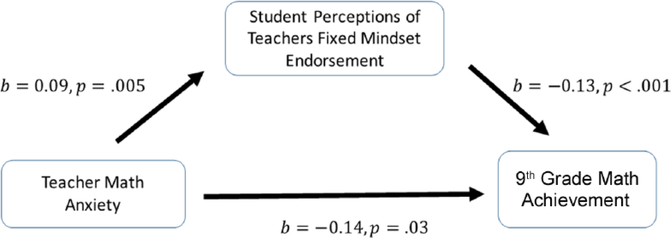
Unfortunately, there have been no studies examining the role of teacher math anxiety during adolescence. Hence, one goal of the current study was to examine the role of teacher math anxiety on the achievement and perceptions of students at the start of their high school years. We begin by attempting to establish whether teacher math anxiety relates to students’ ninth-grade math achievement. As a preview, our main conceptual model is presented in Figure 1. We begin by asking:

Research Question 1: Does teacher math anxiety predict ninth-grade math achievement, controlling for eighth-grade achievement?

FIGURE 1.

The unstandardized effect of teacher math anxiety on student achievement through perceived teacher mindset. Covariates included.

*p < .05. **p < .01. ***p < .001.

We hypothesize that at the ninth-grade level, teachers’ reports of math anxiety will inversely relate to students’ ninth-grade achievement. We control for eighth-grade math achievement to reduce the possibility that math anxious teachers may have simply been assigned low-performing eighth-grade students.

Why Does Teacher Math Anxiety Relate to Student Learning?

We know that elementary school teachers report having high math anxiety and this anxiety hinders student learning. What is less clear is how teachers’ math anxiety affects the math learning of students. Previous investigations suggest that math anxious teachers model a fear around mathematics, which harms learning (Beilock et al., 2010; Stoehr, 2017). In a previous qualitative study, one math anxious teacher reflects that:

One day I was teaching a concept and literally cried in front of my kids because I didn’t get it either. . . . I know that seeing their teacher get frustrated with the math left a long lasting if not lifelong impression on them. (Gresham, 2018, p. 97)

A similar effect has been found by Beilock et al. (2010), who showed that young female students in classrooms with math anxious female teachers were more likely to model themselves after their teachers and endorse the traditional gender stereotype that women are bad at math. Female students presumably observe their own female teacher’s insecurities around math and come to believe that women are not supposed to be good at math. Beilock et al. showed that endorsement of traditional gender stereotypes in turn went on to inversely relate to math learning across the school year.

Other work suggests that math anxious teachers harm student math learning by responding angrily when students request help with mathematics (Cornell, 1999; Fiore, 1999; Jackson & Leffingwell, 1999). Math anxious teachers have also been found to teach in a very inflexible manner that favors traditional and rigid forms of instruction (Chapline, 1980; Chavez & Widmer, 1982; Markovits, 2011), overemphasize rote learning (Trujillo & Hadfield, 1999; Vinson, 2001), and spend less time attending to students’ questions (Bush, 1989) in comparison to teachers with lower math anxiety. We also find that math anxious teachers primarily promote algorithmic thinking (Karp, 1991) and typically ask for a single solution to a problem (Bush, 1989). In summary, the literature suggests that math anxious teachers, through their teaching comments, behaviors, and teaching practices, may create an environment that devalues sense-making and effort in lieu of an emphasis on memorization and innate ability. If this is the case, then students in a classroom with a math anxious teacher might develop maladaptive perceptions about what their teacher believes about math, and these perceptions might relate to their math learning. We discuss the implications of teachers communicating such belief systems in the following.

Classroom mindsets about intelligence.

The belief that ability/intelligence can grow over time with effort is described as a growth mindset (Grant & Dweck, 2003). By contrast, a fixed mindset is the belief that ability/intelligence is a generally unchanging trait that some people inherently have more of than others. These two mindsets are believed to orient individuals to either take on goals focused on learning through effort or goals focused on maintaining perceived ability levels (Dweck & Leggett, 1988). Individuals who hold a fixed mindset rather than a growth mindset have been found to give up faster, avoid opportunities to learn, and interpret failure as a sign that they are simply not competent enough to do math (Blackwell, Trzesniewski, & Dweck, 2007). Students are not only affected by their own mindset beliefs but by the perceptions they have about what others believe as well.

Individuals play an active role in interpreting the world and what those around them believe (Dweck & Molden, 2017). There is evidence that teachers with higher math anxiety report having lower expectations for student achievement than teachers with lower math anxiety, presumably because math anxious teachers project their anxiety on students (Mizala, Martinez, & Martinez, 2015). Students are attuned to cues from their environment to infer their teachers’ beliefs and expectations (Ambady & Gray, 2002; Beilock et al., 2010; Givvin, 2001; Jacobs, 1991; Keller, 2001; Murphy, Steele, & Gross, 2007; Olson & Dweck, 2008; Parsons, Meece, Adler, & Kaczala, 1982). It is also the case that student perceptions of teacher beliefs in general can predict students’ academicrelevant behaviors, cognitions, and subsequent achievement (Ames, 1992; Ames & Archer, 1988; Bandura, 1986; Brown & Bigler, 2005; Gutshall, 2016; Hokoda & Fincham, 1995; Meece et al., 1990; Ryan & Grolnick, 1986; Weinstein, Marshall, Brattesani, & Middlestadt, 1982; Yeager et al., 2014). For instance, students who view the classroom as a place to develop conceptual understanding instead of memorization report more adaptive learning strategies (Young, 1997), learning behaviors (Ames & Archer, 1988; Anderman & Young, 1994), and achievement (Anderman et al., 2001; Kaplan, Gheen, & Midgley, 2002).

Even though math anxious teachers hold explicitly lower achievement expectations for their students (Mizala, Martinez, & Martinez, 2015), we suspect that students make inferences (however accurate they may be) about their teachers’ beliefs and expectations based on the actions and behaviors they witness. Math anxious teachers might engage in classroom actions and behaviors that emphasize memorization and innate ability (i.e., an ability-oriented approach), which aligns with a fixed mindset. Indeed, actions and behaviors implemented by math anxious teachers may show little resemblance to a process-oriented approach that emphasizes effort, reasoning, and sense-making, which aligns better with a growth mindset. Hence, classrooms with math anxious teachers may subject students to greater ability-oriented teaching practices versus process-oriented teaching practices, and students may pick up on the possible mindset that guides their teachers’ use of these practices. Thus, we hypothesized that teacher math anxiety will relate to students’ perceptions of their teacher’s fixed mindset, which in turn relates to student achievement. Given our interest in students’ perceptions of their teacher’s mindset, rather than students’ mindsets, we also measured students’ mindset beliefs, which serve as a covariate in the model (see model in Figure 1). Hence, the second question we ask is as follows:

Research Question 2: Do students’ perceptions of their teachers’ mindsets explain the relationship between teacher math anxiety and student math achievement (controlling for students’ mindset)?

Math anxious teachers’ knowledge and practices.

Based on a review of previous work on teacher math anxiety, we evaluate two factors that might account for the relationship between teacher math anxiety and students’ perceptions of their teachers’ fixed mindsets. First, we asked about math anxious teachers’ use of process-oriented teaching practices. We previously outlined that math anxious teachers might be overly focused on rote learning and other rigid forms of instruction (Bush, 1989; Chapline, 1980; Chavez & Widmer, 1982; Markovits, 2011; Trujillo & Hadfield, 1999; Vinson, 2001). Students make inferences about the possible mindset guiding these classroom practices (Lee, 1996; Pomerantz & Moorman, 2010; Rattan, Savani, Naidu, & Dweck, 2012). For instance, Park, Gunderson, Tsukayama, Levine, and Beilock (2016) found that teachers’ self-reported use of performance-oriented instructional practices, such as pointing out the best-performing students, was indirectly related to students’ achievement growth (via a change in the students’ own motivational framework). Hence, teachers’ math anxiety might relate to student perceptions of teacher mindset via instructional practices that indirectly communicate beliefs about what it takes to be successful in mathematics.

A second and perhaps more parsimonious account is that math anxious teachers may simply not have adequate mathematical knowledge or knowledge for teaching mathematics in the first place (Bursal & Paznokas, 2006; Hembree, 1990; Kim, 2014; Novak & Tassell, 2017). Since ninth-grade math teachers specialize in mathematics, we did not anticipate that teacher math anxiety would be associated with reduced math knowledge or knowledge for teaching mathematics in general. It has been well established that many math anxious adults actually have the necessary math knowledge and strategies to be successful in math, but concerns about failure make it difficult to effectively access and use knowledge during the situations when it matters most (Ashcraft & Kirk, 2001; Beilock, 2008; Ramirez, 2017; Ramirez, McDonough, & Jin, 2017). Therefore, rather than focusing on ninth-grade teachers’ math knowledge, we instead ask whether teacher math anxiety might relate to the knowledge that teachers are able to access and use in a classroom. In a previous qualitative study, one math anxious teacher commented: “I learned effective teaching methods during my preservice days. However, when it came to teaching I sometimes struggled. I hated the math and my math anxiety screamed at me” (Gresham, 2018, p. 98).

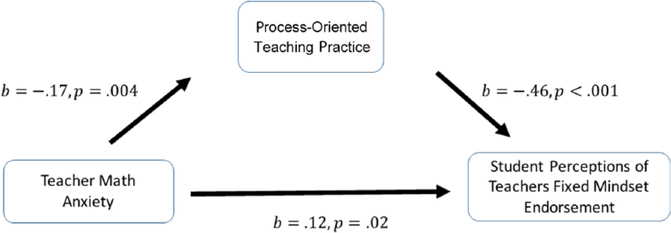
Hence, we sought to address whether teachers who are anxious about math might display more general difficulties accessing and using the knowledge they have (see model in Figure 2) using a classroom video analysis instrument (Kersting, 2008; Kersting, Sherin, & Stigler, 2014) that elicits usable teaching knowledge by asking teachers to analyze teaching episodes shown in video clips of authentic mathematics instruction. To obtain measures of usable mathematics teaching knowledge, teachers’ written responses to the video clips are scored according to four rubrics that reflect common teaching tasks and competencies (analysis of the mathematics, analysis of student thinking, suggestions for improvement, and overall depth of the interpretation).

FIGURE 2.

The unstandardized effect of perceived teacher mindset on student achievement through perceived process-oriented teaching practice. Covariates included.

*p < .05. **p < .01. ***p < .001.

Our third research question is as follows:

Research Question 3: Does teacher math anxiety predict student perceptions of teacher mindset through (a) process-oriented teaching practices or (b) teachers’ usable knowledge for teaching mathematics?

In summary, our work is the first to address whether teacher math anxiety relates to student math achievement as well as the mediating factors that underlie this relationship. By examining both teacher-level and student-level factors, we paint a more comprehensive picture of the effects of teacher math anxiety. We focus on actual course performance rather than performance on a standardized achievement battery to better ascertain how authentic course grades and the effort that students make to obtain those course grades might be undermined by learning in classrooms with math-anxious teachers.

Methods

Participants

Students.

Student participants were 1,886 ninth-grade students from 11 public high schools from an intentionally diverse national convenience sample in California, New York, Texas, Virginia, and North Carolina. Participants were drawn from a large national experimental study, the National Mindset Study, which was conducted with the purpose of investigating the effect of a growth mindset intervention program on student achievement. Student-level survey data were collected approximately three months after the start of the school year, which allowed sufficient time for students to familiarize themselves with their teachers’ practices. All the survey data were collected, cleaned, and merged by a third-party firm. All data are housed at the University of Texas at Austin Population Research Center (PRC) and will be disseminated to the public in the future. For the purpose of the current analyses and to avoid any influence from the treatment, only control group participants were used. Participants were racially and ethnically diverse: 31% self-identified as White, 29% as Hispanic/Latino, 17% as African American, 6% as Asian, 4% as Native American, 4% as Middle Eastern, 1% as Pacific Islander, and the rest identified as multiracial or did not self-identify. Half (48%) were female.

Math teachers.

Math teachers who taught more than 10 ninth-grade students were invited to complete our survey. Sixty teachers completed the survey approximately four months into the school year. Most of the math teachers were female (65%), and race/ethnic information was not collected. The teachers in the ninth grade were different from those who taught students during eighth grade. Teachers within our data set had a minimum of 3 students. The maximum number of students assigned was 75, and the average number of students assigned was 21.

Measures

The data come from three sources: official school records, a teacher survey, and a student survey of teachers’ teaching practices and mindsets. Descriptive statistics and the main study variables appear in Table 1.

TABLE 1.

Descriptive Statistics of Main Study Variables

Variables	N	Mean	SD	Minimum	Maximum
Teacher math anxiety	60	1.9	0.77	1	4
Student perceptions of teacher fixed mindset endorsement	1,553	2.24	0.95	1	5
Ninth-grade math GPA	1,613	2.27	1.32	0	4.3
Process-oriented teaching practice	1,549	2.6	0.82	1	5

Teacher math anxiety.

Given time limitations in working with teachers, we opted to use a single-item measure to assess teacher math anxiety. Single-item measures have been found to show good reliability and validity for assessing math anxiety (Núñez-Peña, Guilera, & Suárez-Pellicioni, 2014) as well as other attitudes (Bergkvist & Rossiter, 2007; Fishbein & Ajzen, 1974; Wanous, Reichers, & Hudy, 1997). For instance, the single-item math anxiety scale (Núñez-Peña et al., 2014) has been shown to correlate strongly (i.e., r = .77) with the more widely used 25-item short mathematics rating scale (Alexander & Martray, 1989). The single-item math anxiety scale also predicts performance on addition and subtraction just as well as the short mathematics rating scale. We adapted the single-item math anxiety scale to our sample of math teachers. Our single-item measure was, “In general, how much math anxiety do you experience when you do very challenging math?” The response options were 1 = none at all, 2 = a little, 3 = a moderate amount, 4 = a lot, and 5 = an extreme amount. We emphasized the phrase challenging math because we reasoned that ninth-grade math specialists would likely not be made anxious by everyday use of math outside of the classroom.

Teachers’ usable knowledge for teaching mathematics.

Teachers’ usable mathematics teaching knowledge was measured using the Classroom Video Analysis (CVA) assessment procedure (Kersting, 2008; Kersting et al., 2014; Kersting, Givvin, Sotelo, & Stigler, 2010). This measure is based on research in expertise (Berliner, 2001; Carter, Cushing, Sabers, Stein, & Berliner, 1988; Carter, Sabers, Cushing, Pinnegar, & Berliner, 1987) and teacher noticing (Sherin & van Es, 2005). It has been shown to relate to traditional measures of teacher knowledge, including the Mathematics for Teaching (MKT) instrument (Kersting et al., 2014).

We created a short version of the CVA scale on variables, expressions, and equations by selecting three video clips (two video clips on patterns and one clip on modeling), which had been shown to function well psychometrically and positively predict student learning (Kersting et al., 2014). The CVA scores teachers’ written analyses of three short video clips of classroom instruction via trained raters and machine learning techniques according to four rubrics. Each rubric consists of three categories (0–2) that capture different aspects of teachers’ written responses to the video clips: (1) analysis of the mathematical content shown in the clip, (2) analysis of student thinking or understanding, (3) suggestions for improving the observed teaching episode, and (4) the overall depth of interpretation. In broad terms, responses that did not analyze the mathematics or student thinking, include any suggestions for improvement, and provide any interpretation of the observed teaching episode (but simply recounted the teaching episode) received a score of 0. Responses that did address the mathematics and student thinking but did not provide a deeper analysis of the mathematics or students’ mathematical understanding received a score of 1. Similarly, responses that did include some pedagogical suggestions for improvement and provide some interpretations but without connecting them to form a coherent argument received a score of 1. Responses that analyzed the mathematics and students’ mathematical understanding in depth, provided mathematically based suggestions for improvement, and provided a coherent in-depth analysis were scored as 2. Score reliability, as measured by internal consistency, based on the individual rubric scores was α = .82 for rater-assigned scores and α =. 89 for the computer-generated scores. Internal consistency based on clip sum scores was α = .76 for rater-assigned scores and α = .66 for computer-generated scores. Teachers’ usable mathematical teaching knowledge was indicated by a human coding index and computer coding index. Both the human coding and computer coding indexes have been shown to be valid and reliable measures of teaching knowledge (Kersting et al., 2014).

Student perception of teacher fixed mindset.

We measured students’ perceptions of their teacher’s mindset by asking students to think about their current high school math class and rate the extent to which the following statements were true of their math teacher: “My math teacher believes that everybody in my class can be very good at math,” “My math teacher seems to believe that only a few students will understand the hardest problems,” and “My math teacher seems to like you better if you are good at math.” These items came from a previous study examining organizational mindset (Hooper, Yeager, Wright, Haimovitz, & Murphy, 2016). They were written by experts in mindset theory and informed by the work on the socialization theory of mindsets (Haimovitz & Dweck, in press; Sun, 2015). For these three items, response options were 1 = not at all true, 2 = slightly true, 3 = somewhat true, 4 = very true, and 5 = extremely true. Answers to the first item were reverse-coded, and all items were then averaged, with higher values corresponding to the perception that the teacher endorsed a more fixed mindset (α = .61).

Process-oriented teaching practices.

We used a set of items from the Tripod 7Cs of effective teaching scale (Ferguson & Danielson, 2015; Kane, McCaffrey, Miller, & Staiger, 2013) to examine students’ perception of their math teacher’s practices. The items required students to rate the following statements regarding their experiences with their math teacher: “My math teacher accepts nothing less than our full effort,” “My math teacher asks questions to be sure we are following along when s/he is teaching,” “In my math class, we learn a lot almost every day,” “My math teacher doesn’t let people give up when the work gets hard,” and “My math teacher wants us to use our thinking skills, not just memorize things” (α = .84). Response options were 1 = not at all true, 2 = slightly true, 3 = somewhat true, 4 = very true, and 5 = extremely true. These perceptions of teaching items were selected because they are logically consistent with a process-oriented growth mindset and inconsistent with a person/performance-oriented fixed mindset. We also selected these items because they are items in the Tripod 7Cs index for Challenge, which has been found in the Bill and Melinda Gates Foundation Measures of Effective Teaching (MET) project to be a strong predictor of value-added achievement gains among children in Grades 4 through 8 (Kane et al., 2013).¹ Higher values indicated more process-oriented teaching practices.

Ninth-grade math GPA.

The schools provided the students’ final grades for math class for the first semester of ninth grade. All grades were converted to letter grades (F– A+), which were then converted to scale grades (0–4.33). Students’ ninth-grade math GPA served as our primary outcome of interest.

Covariates.

Covariates were prior (eighth grade) math GPA (centered within schools), prior (eighth grade) state test score (tests varied across states; centered within schools), student-reported mindset (i.e., whether students believe their abilities are malleable; Grant & Dweck, 2003), dummy variables indicating gender, and dummy variables indicating racial/ethnic group membership. We also added variables for both missing test scores and prior math GPA to address the missing data issue. All models included school fixed effects.

Analysis Plan

All path analyses and mediation analyses were conducted within the SEM framework using the lavaan package in R (Rosseel, 2012). The standard errors were calculated using the delta method. Students are nested within classrooms. Thus, students belonging to the same classroom are correlated, and the independent assumption is violated. To take into account this clustering nature of the data structure, we defined the clustering structure in the svydesign function, and all the standard errors were adjusted accordingly (lavaan. survey package; Oberski, 2014).

Results

Research Question 1: Does Teacher Math Anxiety Predict Higher Ninth-Grade Math GPA?

Our first question was whether teacher math anxiety predicted greater student math achievement, controlling for students’ prior achievement. We conducted a SEM model with the clustering structure to test the effect of math teacher anxiety on ninth-grade math GPA with and without covariates. Results were consistent with and without covariates, and thus, we only reported the results with covariates. With covariates, teacher anxiety had a significant inverse effect on ninth-grade math GPA, b = –.16, p = .007, 95% CI [–.27, –.04]. Higher teacher math anxiety was associated with worse math GPA among students regardless of student prior achievement and mindset.

To ensure the reliability of the results, we also ran a “falsification test,” which rests on the logic that you can discredit a finding if the same statistical model produces an impossible result (Rothstein, 2010). In the present case, we reasoned that if teacher math anxiety among ninth-grade students predicts the same students’ eighth-grade achievement, then this would be an impossible causal path. Reassuringly, teacher math anxiety among ninth-grade teachers did not predict the same students’ eighth-grade math GPA, b = –.11, p = .35. In summary, we show for the first time that higher teacher math anxiety is inversely related to how well students perform in their ninth-grade math course, even after adjusting for prior achievement and students’ own mindset.

Research Question 2: Will Students’ Perceptions of Their Teacher’s Fixed Mindset Beliefs Explain the Relationship Between Teacher Math Anxiety and Student Math Achievement After Controlling for Students’ Own Mindset?

We tested our structural model examining the direct and indirect relationships among teacher math anxiety, students’ perceptions of their teacher’s fixed mindset, and students’ ninth-grade math achievement. Results were consistent with and without covariates, and thus, we only reported the results with covariates. With all the covariates in the model, the model fit was acceptable: χ²(18) = 27.04, p = .08; Comparative Fit Index (CFI) = .99; root mean square error of approximation (RMSEA) = .02, 90% CI [.015, .022]; standardized root mean square residual (SRMR) = .03. Results showed that teacher math anxiety was related to students’ perceptions of their teacher’s fixed mindset beliefs, which further undermined students’ math achievement (see Figure 1). More interestingly, the indirect effect of teacher math anxiety on ninth-grade math achievement through perceived teacher fixed mindset was significant, b = –.02, p = .03, 95% CI [–.03, –.002]. This suggests that the relationship between teacher math anxiety and student achievement is partially mediated via students’ perceptions of their teacher’s fixed mindset.

Research Question 3: Does Teacher Math Anxiety Predict Students’ Perceptions of Their Teacher’s Mindset Through Process-Oriented Teaching Practices or Teachers’ Usable Teaching Knowledge More Generally?

To address our third research question, we began by first testing the direct and indirect relationships among teacher math anxiety, students’ report of their teachers’ process-oriented teaching practices, and students’ perceptions of their teacher’s mindset. When all the covariates were included in the model, the model fit was acceptable: χ²(18) = 33.69, p = .01; CFI = .98; RMSEA = .03, 90% CI [.02, .03]; SRMR = .04. As shown in Figure 2, teacher math anxiety was negatively related to students’ report of their teachers’ process-oriented teaching practices, which was inversely associated with students’ perceptions of their teacher’s fixed mindset. Additionally, we tested the indirect effect of math teacher anxiety on students’ perceptions of their teacher’s mindset through students’ reports of their teachers’ process-oriented teaching practices. The indirect effect was significant, b = .08, p = .007, 95% CI [.02, .14]. The results indicate that higher teacher math anxiety is related to a decrease in students’ report that their teachers engage in process-oriented teaching practices, which partially explains why students perceived these teachers as having a more fixed mindset.

We next tested whether teachers’ usable mathematical teaching knowledge plays a role in the relationship between teacher math anxiety and student perceptions of teachers’ fixed mindset endorsement. Using two indexes of the CVA, we found that teacher math anxiety does not predict either the human coding index or the computer coding index of teachers’ usable mathematical teaching knowledge, b = −0.61, p = .59 and b = −1.41, p = .39. In addition, teachers’ usable mathematical teaching knowledge does not predict student perceptions of teachers’ fixed mindset endorsement, b = −0.01, p = .39 for human coding index and b = −0.001, p = .92 for computer coding index. Therefore, we conclude that the effect of teacher math anxiety on student perceptions of teachers’ fixed mindset endorsement is independent of how much usable mathematical teaching knowledge teachers have.

Overall Model

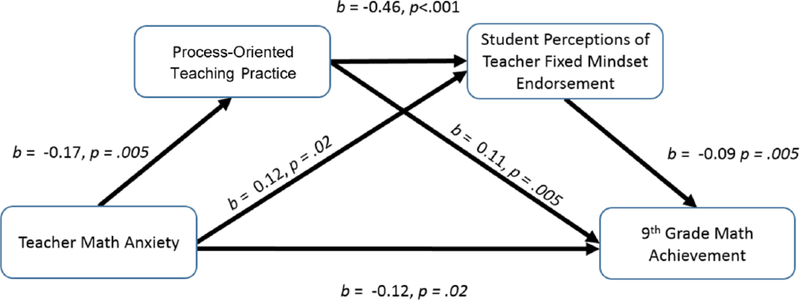
Overall, we established the effect of teacher math anxiety on teachers’ process-oriented teaching practices, which then influenced student perceptions of teachers’ fixed mindset endorsement. Student perceptions of teachers’ fixed mindset in turn relates to student GPA. Combining all variables, we tested our final SEM model (see Figure 3). With covariates, the model fit was acceptable: χ²(19) = 36.93, p = .008; CFI = .98; RMSEA = .03, 90% CI [.02, .03]; SRMR = .04. We found direct links from teacher math anxiety to teacher process-oriented teaching practices, to student perceptions of teachers’ fixed mindset endorsement, and finally, to students’ ninth-grade GPA. Again, we found an indirect effect from teacher math anxiety to student perceptions of teachers’ fixed mindsets endorsement through teacher process-oriented teaching practices, b = .08, p = .007, 95% CI [.02, .14], and an indirect effect from teacher process-oriented teaching practices to students’ GPA through student perceptions of teachers’ fixed mindset, b = .04, p = .005, 95% CI [.01, .07].

FIGURE 3.

Overall model showing the relationships among teacher math anxiety, process-oriented teaching practice, student perceptions of teachers fixed mindset endorsement, and ninth-grade math achievement. Unstandardized coefficient reported. Covariates included.

*p < .05. **p < .01. ***p < .001.

Discussion

Adolescence is a stressful time period in which students take on additional responsibilities and make more autonomous educational decisions. For adolescent students to be successful in school, they must possess a high subjective judgment of their capacity to learn and reach their educational goals (Bandura, 1986; Blackwell et al., 2007; Claro, Paunesku, & Dweck, 2016). Unfortunately, adults’ own fears and beliefs can influence them to act in ways that undermine adolescents’ desire for autonomy and respect (Bhanot & Jovanovic, 2005; Pomerantz & Eaton, 2001; Yeager et al., in press). For instance, previous research indicates that a high degree of math anxiety is common among teachers, but much of this work has been limited to small samples of elementary school teachers. The current study extends previous research by drawing on a large national data set of ninth-grade classrooms to test several models that focus on the role of student perceptions of teacher beliefs and practices in accounting for the relationship between teacher math anxiety and student achievement.

We begin by demonstrating that adolescents placed in a classroom with a math anxious teacher show lower achievement than those placed in a classroom with a non–math anxious teacher. Establishing a relationship between teacher math anxiety and student math achievement is in itself significant since ninth-grade teachers are primarily math specialists who shouldn’t experience math anxiety to begin with. And yet, the results revealed that even among a group of math teaching specialists, higher math anxiety was associated with reduced math achievement. While our evidence is correlational in nature, it suggests that the impact of math anxiety may extend beyond the individual and into the learning context where teachers work hard to develop student math abilities.

Why might teacher math anxiety relate to lower achievement among their students? In previous work, it has been reported that math anxious teachers model negative attitudes around math (Beilock et al., 2010), provide harsh negative feedback (Cornell, 1999; Fiore, 1999; Jackson & Leffingwell, 1999), and show an overreliance on ineffective teaching practices (Chapline, 1980; Chavez & Widmer, 1982; Markovits, 2011; Trujillo & Hadfield, 1999; Vinson, 2001). These various factors create an aversive learning experience and may indirectly communicate to students the belief their teacher holds about math learning, which in turn affects student achievement (Beilock et al., 2010; Bush, 1989; Karp, 1991).

In line with this account, we found that students’ perceptions that their teacher holds a fixed mindset belief partially explains the relationship between teacher math anxiety and student math achievement. Students in classrooms with a math anxious teacher may be receiving instructions that convey the expectation that not everyone can be good at math. Previous work finds that math anxious teachers hold explicitly lower achievement expectations for their own students (Mizala, Martinez, & Martinez, 2015). Students are quite adept at decoding cues from the social world and making rich social inferences from limited interactions with teachers (Ambady & Gray, 2002; Jacobs, 1991; Keller, 2001; Parsons et al., 1982) to interpret the actions of their teachers in an educational context (Yeager et al., 2014).

To more accurately understand why higher teacher math anxiety is associated with students’ perceptions of their teacher’s fixed mindset, we examined the extent to which teachers engaged in process-oriented teaching practices that are generally better aligned with a growth mindset. We reasoned that although ninth-grade math anxious teachers may not appear insecure in their teaching practices or even explicitly endorse particular math ability beliefs, they may be less likely to employ process-oriented teaching practices that send a message that all students are capable of being good at math. Our results revealed a negative relationship between teacher math anxiety and students’ perception that their teacher employs process-oriented teaching practices.

Of course, a more parsimonious account of our results is that math anxious teachers may simply lack knowledge for teaching mathematics or the ability to access and use math in a classroom. We addressed this issue by examining individual differences in teachers’ usable knowledge for teaching mathematics using a well-validated measure (Kersting et al., 2010, 2014). We found that teachers’ usable knowledge for teaching mathematics was not related to teacher math anxiety or students’ perceptions of teacher mindset. To be sure, past investigations have also found that after controlling for knowledge for teaching math, a relationship between teacher math anxiety and student learning persists (Beilock et al., 2010).

Thus, it seems that teachers’ lack of process-oriented teaching strategies (rather than usable knowledge for teaching mathematics) appears to send the message to students that not everyone is capable of understanding difficult math concepts. Our findings are consistent with Bush (1989), who found that math anxious teachers spent less time entertaining student questions, a practice that has the potential to communicate to students that math is either something you know or do not know. Karp (1991) also found that elementary teachers with poor attitudes toward math use more algorithmic teaching that makes the teacher the primary source of information rather than encouraging student-level reasoning, which further promotes a process-based classroom environment. Our results for the overall model suggest that students who perceive more ability-oriented (as opposed to process-oriented) teaching practices may infer how their potential is regarded by the teacher and the environment (e.g., Haimovitz & Dweck, 2016; Murphy et al., 2007), which goes on to shape their own achievement.

Our results align with the teacher expectancy literature that has shown that low expectations on the part of teachers, whether expressed explicitly (Rattan et al., 2012) or inferred (Graham, 1984; Graham & Barker, 1990), can change student-level beliefs (Young, 1997) and performance (Rosenthal & Jacobson, 1968). For instance, teachers’ use of instructional practices focused on student ability/performance (rather than the process of learning) predict subsequent learning approaches (Urdan, Midgley, & Anderman, 1998), motivational frameworks (Park et al., 2016), and achievement (Anderman et al., 2001). Our work adds to previous mindset literature on organizational incremental theory, which suggested that the growth or fixed mindset messages conveyed by the environment affect students’ motivation and learning (Hooper et al., 2016; Murphy & Dweck, 2010). The results reported here bridge research on teacher math anxiety, organizational incremental theory, and teacher expectations to suggest a novel account by which teachers’ own affective disposition toward math shapes the perceptions and achievement of their students.

To combat these “Golem” effects, teachers must have the conviction that math material can be learned by everyone and use instructional strategies that emphasize learning rather than memorization and abilities (Ashton, Webb, & Doda, 1982; Clauset & Gaynor, 1982; Park et al., 2016). Teachers whose classroom practices communicate high expectations for math as well as personal assurance in their students’ ability to meet those expectations (Yeager et al., 2014) may position their students to respond more adaptively to struggle experiences that shape mathematics learning (National Council of Teachers in Mathematics, 2014).

The current study is not without limitations. Even though we drew from a large-scale national sample, the conclusions we make are still based on correlational data, which prevents us from inferring causality. One way to experimentally test the effects of teacher math anxiety would be to randomly assign teachers to teach under a high- versus low-stakes context. When similar manipulations have been performed in a laboratory environment, we find that individuals placed in a high relative to low anxiety context revert to using prepotent responses rather than novel solution methods (Jamieson & Harkins, 2007; Ramirez, Chang, Maloney, Levine, & Beilock, 2016). A similar mechanism may be at play among math specialists who have the necessary usable math knowledge to teach mathematics but revert to using more rudimentary teaching strategies when under the duress of math anxiety.

We also know little about the longitudinal implications of adolescents when they perceive their teacher as endorsing a growth or a fixed mindset. Follow-up longitudinal research will allow us to identify the critical timing of perceiving a growth mindset environment as well as the long-term consequences of being exposed to a fixed mindset environment. Our study could have also benefited from the use of objective measures rather than self-report, which can be prone to social desirability bias. We were, however, able to avoid some of the biases that would have arisen from asking teachers themselves to report on their practices by instead focusing on students’ perceptions of their teachers’ practices, which is likely a more meaningful measure of how classroom climate affects achievement outcomes (Meece, Herman, & McCombs, 2003; Murayama & Elliot, 2009). Lastly, our study would have been strengthened if we obtained baseline measures of several of our key constructs, such as student perception of their teacher’s growth mindset, and measured other student-level motivation variables that have been shown to predict student achievement (i.e., math self-efficacy).

Conclusion

The present research makes a significant contribution to the math anxiety and mindset literature by highlighting the importance of student-perceived teacher mindset in understanding the negative relation between teacher math anxiety and student performance. The current research also underscored that it is the extent to which teachers engage in process-oriented teaching practices, not teachers’ usable knowledge for teaching mathematics, that matters in terms of determining students’ perceptions of their teacher’s mindset. Our take-home message is that the way teachers feel in the classroom and the indirect messages they convey through their practice may be an important factor shaping student math learning.