Weighted NPMLE for the Subdistribution of a Competing Risk

Abstract

Direct regression modeling of the subdistribution has become popular for analyzing data with multiple, competing event types. All general approaches so far are based on non-likelihood based procedures and target covariate effects on the subdistribution. We introduce a novel weighted likelihood function that allows for a direct extension of the Fine-Gray model to a broad class of semiparametric regression models. The model accommodates time-dependent covariate effects on the subdistribution hazard. To motivate the proposed likelihood method, we derive standard nonparametric estimators and discuss a new interpretation based on pseudo risk sets. We establish consistency and asymptotic normality of the estimators and propose a sandwich estimator of the variance. In comprehensive simulation studies we demonstrate the solid performance of the weighted NPMLE in the presence of independent right censoring. We provide an application to a very large bone marrow transplant dataset, thereby illustrating its practical utility.

1 Introduction

Competing risks occur when subjects are exposed to multiple, mutually exclusive event types. The model may formally be defined as a jump process, with a single transient state and several absorbing states that we refer to as the competing events. In such settings one only observes the time of the first event, denoted by T, and the type of that event, denoted by ε ∈ {1, …, k}. As an example, in the bone marrow transplant dataset analyzed in Section 5, recurrence of leukemia and death in remission are the competing events of interest.

Let C denote a possible censoring time and Z a vector of covariates. It is assumed that C is independent of (T, ε) given Z. A common approach is to model the cause specific hazards, defined as ${\alpha }_j^{\ast }(t\mid Z):={lim}_{\mathrm{\Delta }t\to 0}P\{t<T\le t+\mathrm{\Delta }t,\epsilon =j\mid T>t,Z\}$ for j = 1, …, k, which can be interpreted as the instantaneous risk of dying from the event of type j at time T conditional on not having experienced any of the competing events prior to T. Modeling the cause specific hazard for the event of interest is straightforward from the point of view that it relies on a traditional risk set of individuals not having experienced any of the k events. In many applications however, the cumulative incidence function (CIF), defined as F_j(t|Z) = P(T ≤ t, ε = j|Z) and also referred to as the absolute risk of an event over time, is of interest. An efficient prediction of the CIF may be achieved by modeling the cause specific hazards of all event types, see e.g. Kalbfleisch and Prentice (1980, 2002). The relation between the cause specific hazards and the CIF, however, is complex and an accurate prediction of F_j(t|Z) requires correctly specified models with appropriate sample sizes for all cause specific hazards ${\alpha }_1^{\ast }(t\mid Z),\dots ,{\alpha }_k^{\ast }(t\mid Z)$.

A common pitfall in the analysis of competing risks is the use of a product limit estimator based on the cause specific hazard to estimate the corresponding CIF, as illustrated e.g. by Tai at al. (2001). This generally leads to a systematic overestimation of the CIF in the presence of competing events. Similar issues arise in regression modeling on the cause specific hazard, since the effect of a covariate on the cause specific hazard for a specific event type is not interpretable with regard to the corresponding CIF, see Latouche et al. (2013). In extreme cases a covariate may have a strong effect on ${\alpha }_j^{\ast }(t\mid Z)$ but no effect on F_j(t|Z).

For modeling the cause specific hazard, competing risk events are removed from the risk set in the same way as censored individuals, despite a conceptual difference between censorings and competing events: per definition, a competing risk event precludes the possibility of a subsequent event of interest, while for independently censored individuals it is assumed that an event of interest will occur with the same probability as for the individuals with no prior event.

An alternative approach to competing risks regression modeling is based on the idea that individuals are retained in the risk set instead of being removed. Gray (1988) has first defined the subdistribution hazard

$$\alpha (t\mid Z):={lim}_{\mathrm{\Delta }t\to 0}P\{t<T\le t+\mathrm{\Delta }t,\epsilon =1\mid (T>t)\cup (T\le t,\epsilon \ne 1),Z\},$$

which may be interpreted as the hazard of the improper random variable T^* = T · 𝟙{ε = 1}+∞·· 𝟙{ε ≠ 1}, as in Fine and Gray (1999). The risk set for the subdistribution hazard is unconventional but interpretable with a cure model intuition, where individuals are no longer exposed to the event of interest after a competing risk event and therefore regarded as cured with regard to the event of interest. For statistical inference on F₁(t|Z), cured individuals are included in the risk set, as is typically done in cure modeling without competing risks. The resulting risk set consists of those individuals who either did not experience an event of interest in the past or will never experience an event of interest in the future. Fine and Gray (1999) propose a proportional hazards regression model for the subdistribution hazard based on a weighted partial likelihood function. For the Fine-Gray model, estimated regression parameters are directly interpretable with regard to the corresponding CIF, as with $F_1(t\mid Z)=1-exp\left(-{\int }_0^t\alpha (u\mid Z)du\right)$, the usual one to one relationship between the hazard and the failure probability is obtained.

It should be emphasized that neither for the cause specific hazard, nor for the subdistribution hazard approach, the dependency structure between the different event types is of relevance.

The extension of the Fine-Gray model to a larger class of semiparametric regression models is of particular interest as the proportional hazards assumption is not valid in general, as exhibited in Section 5, where alternative models are shown to yield improved model fit for leukemic relapse. Theoretical concerns have been expressed regarding the ability to simultaneously model multiple CIFs using the Fine-Gray approach. For example, with two event types, one requires F₁(t|Z) + F₂(t|Z) ≤ 1 for all t and all Z, with equality at t = ∞. The condition may hold for finite t but not at t = ∞. By considering a general class of semiparametric regression models this constraint can be considerably relaxed. In Section 3, we propose such a general class to address potential lack of fit in practice and theoretical issues of model compatibility. This class includes the models of Fine (2001), Klein and Andersen (2005), Scheike, Zhang and Gerds (2008), and others. Unlike these earlier approaches which model F₁(t|Z), our model directly targets the subdistribution hazard, accommodating time-dependent covariates in the hazard model. This modeling strategy permits likelihood based inferences, which have not been possible with previous approaches to direct competing risks regression.

In Section 2, a weighted nonparametric likelihood for competing risks data is developed from the cure model point of view that the contribution of individuals with a competing event is the probability of not having an event of interest until the endpoint of the study. The proposed weighted likelihood function yields a Nelson-Aalen type estimator of the subdistribution hazard in the absence of covariates and enables parameter estimation in regression models targeting the subdistribution hazard in the presence of Z, as further discussed in Section 3. The method is widely applicable to models for the subdistribution hazard, in particular to the classes of Box-Cox transformation models and logarithmic transformation models that include the Fine-Gray model and the proportional odds model. The estimators are shown to be uniformly consistent and weakly convergent to a Gaussian distribution. We present a sandwich variance estimator that is theoretically justified by a new lemma in connection to the proof of weak convergence, as provided in Section A.3.

Comprehensive simulation studies are conducted in Section 4 to assess the performance of the weighted NPMLEs in finite sample sizes. The bone marrow transplant data is reanalyzed in Section 5.

2 Competing risks analysis based on pseudo risk sets

The subdistribution hazard is related to a cure model interpretation of the competing risks setting, where competing risk events are assigned to the risk set in a similar way as cured individuals. For statistical inference about the CIF via the subdistribution hazard, an adjustment for cured individuals is required to account for unobserved censoring. Fine-Gray (1999) propose a weight function that induces the appropriate pseudo risk set. In the following paragraphs we derive a Nelson-Aalen type estimator for the subdistribution hazard from the weighted Doob decomposition of the underlying counting process for the events of interest. The same Nelson-Aalen type estimator is then obtained from a pseudo likelihood function that reduces to the common counting process likelihood for settings without competing risks.

2.1 Complete data

Let T_i denote the event time and ε_i the failure type of the i–th individual, i = 1, …, n. All data is observed on a time interval [0, τ] with τ denoting the duration of the study. With N_i(t) = 𝟙{T_i ≤ t, ε_i = 1}, let $N(t)={\sum }_{i=1}^n{N}_i(t)$ denote the process counting the events of interest and define Y_i(t) = 1 − N_i(t−). Then $Y(t)={\sum }_{i=1}^n{Y}_i(t)$ is the cardinality of the risk set ℛ(t) = {i : (T_i ≥ t) ∪ (T_i ≤ t, ε_i ≠ 1)}. Notice that ℛ(t) contains those individuals who have not experienced any event until t or who will never experience an event of interest. It is easy to check that $\mathrm{\Lambda }(t):={\int }_0^t\alpha (u)Y(u)du$ is the compensator of N(t) with respect to the filtration ℱ(t) := σ{N_i(s), s ≤ t, i = 1, …, n}. From the Doob decomposition dN_i(t) = Y_i(t)α(t)dt + dM_i(t) we obtain the Nelson-Aalen estimator of the cumulative subdistribution hazard, $\widehat{A}(t):={\int }_0^t{\{Y(u)\}}^{-1}dN(u)$.

This estimator can also be derived from a novel likelihood function. Defining the increments of the cumulative subdistribution hazard by A{T_i} := A(T_i) − A(T_i−1), the contribution for an event of interest at T_i is P(T^* ∈ (T_i−1, T_i], ε = 1) = A{T_i}S₁(T_i−1), while the contribution for a competing risk event is P(T^* ≥ τ) = S₁(τ). The likelihood function therefore takes the form

$$\begin{gathered} L_n=\prod _{i=1}^n{[A\{T_i\}{S}_1(T_{i-1})]}^{𝟙\{{\epsilon }_i=1\}}·{\left[S_1(\tau )\right]}^{𝟙\{{\epsilon }_i\ne 1\}} \\ =\prod _{i:T_i\le \tau }\left[{[Y_i(T_i)A\{T_i\}]}^{d{N}_i(T_i)}·exp\left(-{\int }_0^{\tau }{Y}_i(u)dA(u)\right)\right]. \end{gathered}$$

2.2 Model with administrative censoring

We consider a setting where the censoring time C is observed even for individuals with a previous competing risk event. Such data arises for example in administrative databases where all individuals are censored at a fixed calendar time with complete follow-up to that time point.

Let C_i denote the censoring time of the i-th individual, X_i = T_i ∧ C_i and Δ_i = 𝟙{T_i ≤ C_i ∧ τ}. The process counting the events of interest is denoted by $N^a(t)={\sum }_{i=1}^n{N}_i^a(t),N_i^a(t)={\int }_0^t𝟙\{C_i\ge u\}d{N}_i(u)$. The process $Y^a(t)={\sum }_{i=1}^n{Y}_i^a(t)$ with $Y_i^a(t)=1\{C_i\ge t\}{Y}_i(t)$ is the cardinality of the risk set ℛ^a(t) = {i : (X_i ≥ t)} ∪ {i : (X_i < t,Δ_i = 1, ε_i ≠ 1, C_i ≥ t)}. In this case ${\mathrm{\Lambda }}^a(t)={\int }_0^t\alpha (u)Y^a(u)du$ is the compensator of N^a(t) with respect to ${\mathcal{A}}^a(t)=\sigma \{N_i^a(s),𝟙(C_i\ge s),s\le t,i=1,\dots ,n\}$ and the Nelson-Aalen estimator $\widehat{A}(t)={\int }_0^t{\{Y^a(u)\}}^{-1}d{N}^a(u)$ can be derived from the likelihood function

$$L_n^a=\prod _{i:X_i\le \tau }\left[{[Y_i^a(X_i)A_n\{X_i\}]}^{d{N}_i^a(X_i)}·exp\left(-{\int }_0^{\tau }{Y}_i^a(u)d{A}_n(u)\right)\right].$$

2.3 Model with independent right censoring

For the Fine-Gray approach, individuals with a competing risk event are regarded as a cure fraction of the risk set, as they are no longer exposed to the event of interest. This slightly differs from the ordinary cure model, where individuals in the cure fraction would be subject to independent right censoring which, per definition, cannot be observed after a competing risk event. To maintain the common cure model structure, Fine and Gray (1999) use inverse probability of censoring weighting (IPCW) technique, thereby applying the estimated weight w_i(t) := 𝟙{C_i ≥ T_i ∧ t}· Ĝ_C (t)/Ĝ_C (T_i ∧ t) in place of w̃_i(t) := 𝟙{C_i ≥ T_i ∧ t}· G_C (t)/G_C (T_i ∧ t), where Ĝ_C is the product limit estimator of G_C (t) = P(C > t).

A Nelson-Aalen type estimator for the subdistribution hazard can be derived from the weighted Doob decomposition w_i(t)dN_i(t) = w_i(t)Y_i(t)α(t)dt+w_i(t)dM_i(t), with

$$\sum _{i=1}^n{w}_i(t)Y_i(t)=\sum _{i=1}^n𝟙\{X_i\ge t\}+\sum _{i=1}^n𝟙\{X_i<t,{\mathrm{\Delta }}_i=1,{\epsilon }_i\ne 1\}·{\widehat{G}}_c(t)/{\widehat{G}}_c(T_i)$$

representing the expected number of individuals in the pseudo risk set. Alternatively Â_n can be derived from the pseudo likelihood function

$$\begin{gathered} L_n=\prod _{i=1}^n\left\{{[A\{X_i\}]}^{{\mathrm{\Delta }}_i𝟙\{{\epsilon }_i=1\}}·\prod _{\ell :X_{\ell }<X_i}(1-A\{X_{\ell }\})\times \prod _{\ell :X_{\ell }\ge X_i}{(1-A\{X_{\ell }\})}^{{\mathrm{\Delta }}_i𝟙\{{\epsilon }_i\ne 1\}\widehat{G}(X_{\ell })/\widehat{G}(X_i\wedge X_{\ell })}\right\} \\ =\prod _{i=1}^n\left[{[w_i(X_i)Y_i(X_i)d{A}_n(X_i)]}^{{\mathrm{\Delta }}_{i}d{N}_i(X_i)}exp\left(-{\int }_0^{\tau }{w}_i(u)Y_i(u)dA(u)\right)\right]. \end{gathered}$$

Our proposed likelihood function is consistent with the general likelihood function in Andersen et al. (1993) and it can be ascertained that the product limit estimator based on the estimated cumulative subdistribution hazard is equivalent to the fully efficient Aalen-Johansen estimator, see e.g. Antolini, Biganzoli and Boracchi (2007), Zhang, Zhang and Fine (2009), Geskus (2011). This indicates that the weighted likelihood is a promising candidate for inference in semiparametric regression models, an idea which is explored in subsequent sections.

3 General subdistribution hazard regression model

Fine-Gray (1999) propose a proportional hazards model for the subdistribution with an estimation procedure based on a weighted partial likelihood function. The method accommodates time-varying covariate effects on the subdistribution hazard and yields the usual nonparametric estimators in the absence of Z.

Various other approaches have been developed based on modeling F₁(t|Z) instead of α(t|Z). Fine (2001) proposed a general regression model for F₁(t|Z) in which the subdistribution is assumed to satisfy a generalized linear model after transformation, with a time-varying intercept. Pairwise rank estimators were utilized, again using inverse probability of censoring weighting. A simple method for estimation of the model based on F₁(t|Z) was proposed by Andersen and Klein (2007). Using jackknife ideas, pseudo values may be employed, which enable the construction of estimating equations. While computationally appealing owing to its ease of implementation in standard software, the approach is ad hoc, requiring choices of time points at which to evaluate the pseudo-values, and its general theoretical properties with right censoring, including efficiency, are unclear. Scheike et al (2008) adapted binomial regression techniques to regression modeling of F₁(t|Z), also using inverse probability of censoring weighting. None of the above methods adapt easily to time-varying covariates, which are most naturally accommodated in models for the hazard function, as with survival data without competing risks. Moreover, these methods do not reduce to the usual nonparametric estimators without covariates.

3.1 Model formulation

As a general model for the cumulative subdistribution hazard we propose

$$A(t)=\mathcal{G}\left({\int }_0^t{e}^{{\beta }^{T}Z(s)}d{A}_0(s)\right),$$

where β ∈ ℝ^d is a vector of unknown regression parameters, A₀ is an unspecified increasing function, Z(s) is a vector of possibly time dependent covariates of bounded variation and 𝒢 is a thrice continuously differentiable and strictly increasing function with 𝒢(0) = 0, 𝒢′(0) > 0 and 𝒢(∞) = ∞. Additional regularity conditions for the existence of the weighted NPMLE, which are considerably weaker than those in Zeng and Lin (2006), are specified in Section A.1. In particular, our general model entails not only the class of Box-Cox transformation models with link function 𝒢(x) = {(1 + x)^ρ − 1} /ρ for ρ ≥ 0 but also the class of logarithmic transformation models with link function 𝒢(x) = log(1+rx)/r for r ≥ 0 (Chen, Jin, Ying, 2002). Important special cases of these classes are firstly the Fine-Gray model, which is the Box-Cox transformation model with ρ = 1 and the limiting logarithmic transformation model for r → 0 and secondly the proportional odds model as the logarithmic transformation model with r = 1 and the limiting Box-Cox transformation model for ρ → 0.

With independent right censoring our general model is related to the multiplicative intensity process

$$\alpha (t,Z)w(t)Y(t)={\alpha }_0(t)w(t)Y(t)e^{{\beta }^{T}Z(t)}{\mathcal{G}}^{\prime }\left({\int }_0^t{e}^{{\beta }^{T}Z(s)}d{A}_0(s)\right),$$ (1)

while in the case of administrative right censoring the multiplicative intensity process

$$\alpha (t,Z)𝟙(C>t)Y(t)={\alpha }_0(t)𝟙(C>t)Y(t)e^{{\beta }^{T}Z(t)}{\mathcal{G}}^{\prime }\left({\int }_0^t{e}^{{\beta }^{T}Z(s)}d{A}_0(s)\right)$$

is obtained, which yields the cumulative intensity

$$\mathrm{\Lambda }(t)=\mathcal{G}\left({\int }_0^t𝟙(C>t)Y(t)e^{{\beta }^{T}Z(s)}d{A}_0(s)\right),$$

akin to the model proposed by Zeng and Lin (2006) for settings without competing risks.

The model incorporates time-dependent covariates into a general subdistribution hazard regression model, extending Fine and Gray’s (1999) formulation to the non-proportional hazard setting. Challenges arise for individuals with a competing event, where the covariate process Z(t) should be well defined for t ∈ [X, τ]. This is always the case for baseline covariates and for external time dependent covariates, where Z(t) can be observed after a competing risks event. For internal time dependent covariates, the issues are more complicated, as discussed in Section 6.

3.2 Weighted nonparametric maximum likelihood estimation

With independent right censoring, the observed data needed for estimation consists of iid samples of (X,Δ,Δε, Z(t), t ≤ (X ∧τ ) 𝟙(Δε ∈ {0, 1})+τ 𝟙(Δε ∉ {0, 1})) denoted by {(X_i,Δ_i,Δ_iε_i, Z_i(t), t ≤ (X_i ∧ τ ) · 𝟙(Δ_iε_i ∈ {0, 1})+ τ · 𝟙(Δ_iε_i ∉ {0, 1})), i = 1, ...., n}. Notice that the covariate process Z_i(t) is observed on [0,X_i] for all individuals and observed on [X_i, τ] for those individuals with Δ_iε_i ∉ {0, 1}. We thus obtain the weighted log-likelihood function under the general semiparametric regression model:

$$\begin{gathered} \ell (\beta ,A_0)=\sum _{i=1}^n[{\int }_0^{\tau }log\left(e^{{\beta }^T{Z}_i(t)}{\alpha }_0(t){\mathcal{G}}^{\prime }\left({\int }_0^t{e}^{{\beta }^T{Z}_i(u)}d{A}_0(u)\right)\right)𝟙(C_i\ge t)Y_i(t)d{N}_i(t) \\ -{\int }_0^{\tau }{w}_i(t)Y_i(t)e^{{\beta }^T{Z}_i(t)}{\mathcal{G}}^{\prime }\left({\int }_0^t{e}^{{\beta }^T{Z}_i(u)}d{A}_0(u)\right)d{A}_0(t)]. \end{gathered}$$ (2)

Decomposition of the weighted risk set $w_i(t)Y_i(t)=𝟙(X_i\ge t)+w_i^{\ast }(t)𝟙(X_i\le t,{\mathrm{\Delta }}_i{\epsilon }_i\notin \{0,1\})$ with a simplified weight function $w_i^{\ast }(t)=𝟙(C_i\ge T_i){\widehat{G}}_c(t)/{\widehat{G}}_c(T_i)$ yields the equivalent representation

$$\begin{gathered} \ell (\beta ,A_0)=\sum _{i=1}^n\left[{\int }_0^{\tau }log\left(e^{{\beta }^T{Z}_i(t)}{\alpha }_0(t){\mathcal{G}}^{\prime }\left({\int }_0^t{e}^{{\beta }^T{Z}_i(u)}d{A}_0(u)\right)\right)𝟙(C_i\ge t)Y_i(t)d{N}_i(t)\right] \\ -\sum _{i=1}^n\mathcal{G}\left({\int }_0^{X_i\wedge \tau }{e}^{{\beta }^T{Z}_i(t)}d{A}_0(t)\right) \\ -\sum _{i:{\mathrm{\Delta }}_i{\epsilon }_i\ne 1,X_i\le \tau }\left[{\int }_{X_i}^{\tau }{w}_i^{\ast }(t)e^{{\beta }^T{Z}_i(t)}{\mathcal{G}}^{\prime }\left({\int }_0^t{e}^{{\beta }^T{Z}_i(u)}d{A}_0(u)\right)d{A}_0(t)\right]. \end{gathered}$$ (3)

The cumulative baseline hazard A₀ is approximated by a sequence of step functions $A_n^0$, with jumps at the observed events of interest. Those increments are interpretable as a finite dimensional parameter. Let {0 < T̃₁ < T̃₂ < … < T̃_k(n) < τ} denote the ordered times and k(n) the number of the observed events of interest. Replacing A₀ by $A_n^0$ we obtain a modified likelihood function ${\ell }_n(\beta ,{\widehat{A}}_n^0)$ and maximization yields an estimator ${\widehat{\theta }}_n^{\ast }=({\widehat{\beta }}_n,{\widehat{A}}_n^0\{{\stackrel{\sim }{T}}_1\},\dots ,{\widehat{A}}_n^0\{{\stackrel{\sim }{T}}_{k(n)}\})$, with $A_n^0\{{\stackrel{\sim }{T}}_i\}=A_n^0({\stackrel{\sim }{T}}_i)-A_n^0({\stackrel{\sim }{T}}_{i-1})$ and β̂_n ∈ ℝ^d. An estimator for the parameter of interest ${\widehat{\theta }}_n=({\widehat{\beta }}_n,{\widehat{A}}_n^0({\stackrel{\sim }{T}}_1),\dots ,{\widehat{A}}_n^0({\stackrel{\sim }{T}}_{k(n)}))$ is obtained by the linear transformation ${\widehat{\theta }}_n^T=C{\widehat{\theta }}_n^{\ast T}$, with C being specified in our technical report.

For 𝒢(x) = x, corresponding to the proportional subdistribution hazard model, the weighted log-likelihood function takes the simple form

$$\ell (\beta ,A_0)=\sum _{i=1}^n\left[{\int }_0^{\tau }log\left(e^{{\beta }^T{Z}_i(t)}{\alpha }_0(t)\right)𝟙(C_i\ge t)Y_i(t)d{N}_i(t)-{\int }_0^{\tau }{w}_i(t)Y_i(t)e^{{\beta }^T{Z}_i(t)}d{A}_0(t)\right]$$

and in the same way as for the proportional hazards model without competing risks, it can be factorized into the Fine-Gray partial likelihood function and a second term,

$$L_n=\prod _{i:{\mathrm{\Delta }}_i{\epsilon }_i=1}\left[\frac{w_i(X_i)Y_i(X_i)e^{{\beta }^T{Z}_i(X_i)}}{{\sum }_{j=1}^n{w}_j(X_i)Y_j(X_i)e^{{\beta }^T{Z}_j(X_i)}}\right]·\left(\sum _{j=1}^n{w}_j(X_i)Y_j(X_i)e^{{\beta }^T{Z}_j(X_i)}{A}_0\{X_i\}\right)\times exp\left(-{\int }_0^{\tau }{w}_i(u)Y_i(u)e^{{\beta }^T{Z}_i(u)}d{A}_0(u)\right).$$

Accordingly parameter estimates derived from the weighted log-likelihood function with 𝒢(x) = x are identical to those derived from the Fine-Gray model.

For administratively censored data we obtain the log-likelihood function

$$\begin{gathered} {\ell }^a(\beta ,A_0) \\ =\sum _{i=1}^n[{\int }_0^{\tau }log\left(e^{{\beta }^T{Z}_i(t)}{\alpha }_0(t){\mathcal{G}}^{\prime }\left({\int }_0^t{e}^{{\beta }^T{Z}_i(u)}d{A}_0(u)\right)\right)𝟙(C_i\ge t)Y_i(t)d{N}_i(t)-\mathcal{G}\left({\int }_0^{\tau }𝟙(C_i\ge t)Y_i(t)e^{{\beta }^T{Z}_i(t)}d{A}_0(t)\right)], \end{gathered}$$ (4)

with the same structure as in Zeng and Lin (2006) for the model without competing risks. Because there are no estimated weights, the estimators inherit those same asymptotic properties. In particular efficiency is obtained, and the variance estimator simplifies to the empirical inverse Fisher information.

3.3 Asymptotic inference and variance estimator

Theorem 1

The estimator ${\widehat{\theta }}_n=({\widehat{\beta }}_n,{\widehat{A}}_n^0)$ derived from maximizing the weighted likelihood function is uniformly consistent.

To prove consistency we adapt arguments established by Murphy (1994), (1995) and developed e.g. by Parner (1998), Kosorok, Lee and Fine (2004) and by Zeng and Lin (2006), (2010). An additional challenge for our model are the estimated weights that require an application of IPCW technique. To our knowledge this issue has not previously been addressed in connection with nonparametric maximum likelihood estimation of parameters in semiparametric regression models. As in Fine and Gray (1999), we first prove consistency for settings with administrative censoring. It is then argued that the weighted NPMLEs for settings with independent right censoring are asymptotically equivalent.

Theorem 2

$\sqrt{n}({\widehat{\beta }}_n-{\beta }_0,{\widehat{A}}_n-A_0)$ converges weakly to a Gaussian process.

To establish weak convergence we apply our new Lemma 3, as stated in Section A.3, that is based on Theorem 3.3.1. of van der Vaart and Wellner (1996).

We consider linear functionals of the form $\sqrt{n}({\widehat{\theta }}_n-{\theta }_0)(h)=\sqrt{n}{h}_1^T({\widehat{\beta }}_n-{\beta }_0)+\sqrt{n}{\int }_0^{\tau }{h}_2(t)d\left({\widehat{A}}_n(t)-A_0(t)\right)$, with h = (h₁, h₂), h₂ being an arbitrary element in the Skorohod space 𝒟[0, τ] and h₁ ∈ ℝ^d. Defining a corresponding vector h̃₂ ∈ ℝ^k(n) with ${\stackrel{\sim }{h}}_2^j=h_2({\stackrel{\sim }{T}}_i)$, Ã₀{T̃_i} = A₀(T̃_i) − A₀(T̃_i−1) for i = 1, …, k(n) and $\stackrel{\sim }{h}\equiv (h_1,{\stackrel{\sim }{h}}_2^1,\dots ,{\stackrel{\sim }{h}}_2^{k(n)})$, we propose the sandwich estimator

$$\widehat{\text{Var}}\sqrt{n}({\widehat{\theta }}_n-{\theta }_n)(\stackrel{\sim }{h})={\stackrel{\sim }{h}}^T{\mathcal{I}}_n^{-1^T}{\widehat{\mathrm{\sum }}}_n{\mathcal{I}}_n^{-1}\stackrel{\sim }{h}$$

for the asymptotic variance of $\sqrt{n}{h}_1^T({\widehat{\beta }}_n-{\beta }_0)+\sqrt{n}{\sum }_{j=1}^{k(n)}{\stackrel{\sim }{h}}_2^j({\widehat{A}}_n\{{\stackrel{\sim }{T}}_j\}-{\stackrel{\sim }{A}}_0\{{\stackrel{\sim }{T}}_j\})$, where ℐ_n is the observed Fisher information with respect to β and jump sizes, and ${\widehat{\mathrm{\sum }}}_n=n^{-1}{\sum }_{i=1}^n{({\widehat{\eta }}_i+{\widehat{\psi }}_i)}^{\otimes 2}$ is the estimator for the variance of the score with respect to β and jump sizes, with η̂_i and ψ̂_i denoting the components of the iid decomposition as given in Section A.4. Analogously we obtain that a consistent estimator for the covariances is $\widehat{\text{Cov}}\left(\sqrt{n}({\widehat{\theta }}_n-{\theta }_0)(\stackrel{\sim }{h}),\sqrt{n}({\widehat{\theta }}_n-{\theta }_0)(\stackrel{\sim }{g})\right)={\stackrel{\sim }{h}}^T{\mathcal{I}}_n^{-1^T}{\widehat{\mathrm{\sum }}}_n{\mathcal{I}}_n^{-1}\stackrel{\sim }{g}$.

The sandwich estimator contains a term that reflects the additional variability resulting from estimating the weights. Similarly to Fine and Gray (1999), this additional variability cannot be ignored, even though in practice the adjusted sandwich estimator may be quite close to the empirical inverse Fisher information.

4 Simulation studies

Simulation studies were conducted for the Fine-Gray model and for the proportional odds model with sample sizes n = 50, 200 and 500. Event times were generated using the model formulations in Fine and Gray (1999) and in Fine (2001), with two distinct failure types. For each setting, 1000 samples were generated. We defined censoring times uniformly distributed on subsets of [0, τ]. Covariates Z_i1 and Z_i2 were generated independently from a standard normal distribution for i = 1, …, n. The subdistribution for the events of interest was defined by F₁(t|Z_i) = P(T_i ≤ t, ε_i = 1|Z_i) = 1 − [1 − p{1 − exp(−t)}]^{exp(Z_i1β₁₁+Z_i2β₁₂)} for the Fine-Gray model and by F₁(t|Z_i) = exp[p + log{1 − exp(−1)} + Z_i1β₁₁ + Z_i2β₁₂] (1 + exp [p + log{1 − exp(−t)}]+Z_i1β₁₁ +Z_i2β₁₂)⁻¹ for the proportional odds model. The subdistribution for the competing risk events was in both scenarios obtained from the conditional distribution P(T_i ≤ t|ε_i = 2, Z_i) being exponential distributed with rate exp(Z_i1β₂₁ + Z_i2β₂₂) and by taking P(ε_i = 2|Z_i) = 1 − P(ε_i = 1|Z_i). The parameter vector was defined as (p, β₁₁, β₁₂, β₂₁, β₂₂) = (0.3, 0.5,−0.5, 0.5, 0.5).

In Tables 2 and 3 we report the average deviation from the true parameter values (bias), empirical standard errors, the mean of the Fine-Gray sandwich estimator and of the inverse Fisher information, and the coverage probabilities for both variance estimators. The bias is generally small, the standard errors decrease at rate $\sqrt{n}$ with the empirical and model based variances in agreement, and the coverage probabilities are close to the nominal level 0.95, particularly with sample sizes n = 200 and 500. The solid performance of the weighted NPMLE with realistic sample sizes indicates that the proposed method is reliable for use in real applications. For the Fine-Gray model, the estimated parameters and variances were identical with those derived from the crr function (cmpsrk package). Interestingly, the performances of the proposed sandwich estimator and of the inverse Fisher information, which lacks theoretical justification, are rather similar for all sample sizes, with both approaches yielding diminished coverage with n = 50. Additional simulation studies, histograms and qq-plots of the parameter estimates are presented in our technical report.

Table 2.

Simulation studies for the Fine-Gray model, parameter of interest (β₁₁, β₁₂) = (0.5,−0.5). Censorings were uniformly distributed on [a, b], with [τ ] denoting that there was only administrative censoring at τ. Bias),%) deviation from true parameter (absolute values and in %), SE) empirical standard error, SEE₁) sandwich estimator, SEE₂) inverse Fisher information, Cov₁, Cov₂) coverage probability of 0.95 confidence intervals for the variance estimators.

			Bias and Standard errors					Coverage
size	[a, b]	parameter	Bias	%	SE	SEE1	SEE2	Cov1	Cov2
50	[τ]	β11	0.023	4.7	0.295	0.269	0.280	0.936	0.956
		β12	−0.029	5.8	0.295	0.267	0.279	0.936	0.952
		An(τ/4)	−0.006	3.0	0.074	0.069	0.070	0.888	0.894
		An(τ/2)	−0.006	1.9	0.093	0.088	0.090	0.908	0.916
		An(τ )	−0.008	2.3	0.103	0.097	0.099	0.918	0.923
200	[τ]	β11	0.004	0.7	0.131	0.129	0.130	0.950	0.960
		β12	−0.009	1.8	0.127	0.128	0.130	0.954	0.959
		An(τ/4)	−0.002	1.1	0.035	0.035	0.035	0.935	0.938
		An(τ/2)	−0.003	1.1	0.044	0.044	0.045	0.948	0.952
		An(τ )	−0.005	1.3	0.048	0.049	0.049	0.950	0.946
500	[τ]	β11	−0.002	0.4	0.080	0.081	0.081	0.954	0.953
		β12	−0.001	0.2	0.086	0.081	0.081	0.932	0.938
		An(τ/4)	−0.001	0.3	0.023	0.022	0.022	0.938	0.939
		An(τ/2)	0.000	0.2	0.028	0.028	0.028	0.941	0.940
		An(τ )	−0.001	0.4	0.031	0.031	0.031	0.951	0.952
50	[1, 2]	β11	0.047	9.5	0.360	0.298	0.317	0.920	0.935
		β12	−0.048	9.7	0.362	0.303	0.319	0.913	0.940
		An(τ/4)	−0.008	6.9	0.050	0.048	0.048	0.866	0.869
		An(τ/2)	−0.013	6.3	0.072	0.068	0.069	0.890	0.897
		An(τ )	−0.013	4.5	0.110	0.101	0.100	0.880	0.888
200	[1, 2]	β11	0.004	0.7	0.153	0.143	0.145	0.928	0.936
		β12	−0.012	2.4	0.147	0.143	0.145	0.943	0.952
		An(τ/4)	−0.002	2.0	0.026	0.025	0.025	0.928	0.927
		An(τ/2)	−0.004	2.1	0.036	0.035	0.035	0.934	0.934
		An(τ )	−0.012	4.0	0.048	0.048	0.048	0.920	0.924
500	[1, 2]	β11	0.000	0.1	0.091	0.089	0.090	0.940	0.047
		β12	0.000	0.1	0.092	0.089	0.090	0.944	0.951
		An(τ/4)	0.001	0.5	0.016	0.016	0.016	0.956	0.954
		An(τ/2)	0.000	0.1	0.022	0.022	0.022	0.952	0.955
		An(τ )	−0.007	2.3	0.030	0.031	0.031	0.938	0.940
50	[0.5, 1]	β11	0.041	8.2	0.438	0.361	0.385	0.916	0.944
		β12	−0.044	8.7	0.417	0.354	0.383	0.902	0.941
		An(τ/4)	−0.017	26.3	0.124	0.040	0.042	0.832	0.847
		An(τ/2)	−0.010	8.3	0.051	0.049	0.050	0.855	0.864
		An(τ )	−0.016	7.9	0.085	0.079	0.081	0.865	0.860
200	[0.5, 1]	β11	0.003	0.6	0.173	0.170	0.172	0.932	0.949
		β12	−0.007	1.3	0.172	0.170	0.172	0.948	0.954
		An(τ/4)	−0.001	1.6	0.018	0.018	0.018	0.935	0.930
		An(τ/2)	−0.002	2.0	0.026	0.026	0.026	0.931	0.934
		An(τ )	−0.003	1.5	0.045	0.043	0.043	0.912	0.914
500	[0.5, 1]	β11	0.004	0.7	0.110	0.106	0.107	0.936	0.939
		β12	−0.004	0.8	0.105	0.107	0.107	0.954	0.957
		An(τ/4)	−0.001	1.5	0.011	0.011	0.011	0.935	0.935
		An(τ/2)	−0.001	1.0	0.016	0.017	0.017	0.941	0.941
		An(τ )	−0.001	0.4	0.028	0.028	0.028	0.941	0.943

Table 3.

Simulation studies for the proportional odds model, parameter of interest (β₁₁, β₁₂) = (0.5,−0.5). Censorings uniformly distributed on [a, b], with [τ ] denoting that there was only administrative censoring at τ. Bias),%) deviation from true parameter (absolute values and in %), SE) empirical standard error, SEE₁) sandwich estimator, SEE₂) inverse Fisher information. Cov₁, Cov₂) coverage probability of 0.95 confidence intervals for the variance estimators.

size	[a, b]	parameter	Bias	%	SE	SEE1	SEE2	Cov1	Cov2
50	[τ]	β11	0.010	2.0	0.285	0.276	0.287	0.942	0.965
		β12	−0.020	3.9	0.296	0.278	0.288	0.937	0.955
		An(τ/4)	−0.005	0.6	0.239	0.237	0.241	0.920	0.923
		An(τ/2)	0.007	0.7	0.344	0.339	0.346	0.917	0.920
		An(τ )	0.001	0.0	0.390	0.399	0.408	0.923	0.925
200	[τ]	β11	0.007	1.4	0.137	0.136	0.138	0.956	0.959
		β12	0.000	0.0	0.139	0.137	0.138	0.941	0.943
		An(τ/4)	−0.004	0.5	0.113	0.117	0.117	0.951	0.951
		An(τ/2)	0.005	0.5	0.169	0.167	0.167	0.948	0.950
		An(τ )	−0.001	0.0	0.198	0.196	0.197	0.943	0.944
500	[τ]	β11	0.002	0.5	0.085	0.084	0.087	0.934	0.949
		β12	−0.002	0.4	0.085	0.083	0.087	0.950	0.961
		An(τ/4)	0.002	0.3	0.068	0.066	0.068	0.947	0.951
		An(τ/2)	0.003	0.3	0.099	0.096	0.099	0.944	0.949
		An(τ )	0.004	0.3	0.122	0.117	0.122	0.940	0.947
50	[0.75, 1.5]	β11	0.009	1.8	0.310	0.289	0.301	0.938	0.956
		β12	−0.023	4.7	0.315	0.291	0.303	0.934	0.957
		An(τ/4)	−0.013	3.3	0.130	0.127	0.129	0.908	0.914
		An(τ/2)	−0.012	1.8	0.211	0.205	0.209	0.917	0.918
		An(τ )	0.012	1.1	0.467	0.383	0.386	0.898	0.904
200	[0.75, 1.5]	β11	0.004	0.8	0.147	0.143	0.144	0.947	0.951
		β12	−0.011	2.3	0.145	0.142	0.144	0.943	0.950
		An(τ/4)	−0.005	1.4	0.063	0.064	0.065	0.940	0.940
		An(τ/2)	0.000	0.1	0.103	0.103	0.104	0.946	0.945
		An(τ )	0.005	0.5	0.183	0.178	0.178	0.943	0.944
500	[0.75, 1.5]	β11	−0.002	0.3	0.091	0.089	0.090	0.944	0.946
		β12	0.000	0.1	0.087	0.089	0.090	0.961	0.963
		An(τ/4)	−0.003	0.6	0.041	0.041	0.041	0.937	0.940
		An(τ/2)	−0.003	0.4	0.066	0.065	0.065	0.940	0.939
		An(τ )	−0.005	0.5	0.109	0.111	0.110	0.935	0.937
50	[0.5, 3.5]	β11	0.005	0.9	0.294	0.285	0.296	0.945	0.959
		β12	−0.019	3.9	0.298	0.289	0.297	0.944	0.953
		An(τ/4)	−0.011	1.8	0.194	0.190	0.193	0.909	0.918
		An(τ/2)	0.007	0.7	0.322	0.302	0.309	0.926	0.925
		An(τ )	0.039	3.1	0.479	0.450	0.454	0.917	0.920
200	[0.5, 3.5]	β11	0.004	0.9	0.137	0.140	0.141	0.953	0.960
		β12	−0.004	0.8	0.143	0.140	0.141	0.954	0.956
		An(τ/4)	−0.006	0.9	0.094	0.095	0.095	0.935	0.938
		An(τ/2)	−0.009	0.9	0.145	0.147	0.147	0.942	0.944
		An(τ )	−0.009	0.7	0.197	0.210	0.206	0.948	0.944
500	[0.5, 3.5]	β11	0.001	0.3	0.089	0.088	0.088	0.948	0.948
		β12	−0.005	1.0	0.091	0.088	0.088	0.946	0.950
		An(τ/4)	−0.001	0.1	0.059	0.060	0.060	0.952	0.951
		An(τ/2)	0.000	0.0	0.092	0.093	0.093	0.951	0.951
		An(τ )	0.002	0.2	0.129	0.133	0.130	0.955	0.954

For the proportional odds model, we compare in table 4 weighted NPMLEs for β₁ with the corresponding parameter estimates derived from the regression model of the competing crude failure probability, as reported in Fine (2001). Bias and variances of the weighted NPMLEs are smaller, with comparable coverage probabilities.

Table 4.

Weighted NPMLEs for the proportional odds model in comparison to Fine (2001). Censorings uniformly distributed on [a, b], with [τ ] denoting administrative censoring at τ. Bias),%) deviation from true parameter (absolute values and in %), SE) empirical standard error, SEE) sandwich estimator, Cov) coverage probability of 0.95 confidence intervals for the sandwich estimator.

		weighted NPMLE					Fine (2001)
size	[a, b]	Bias	%	SE	SEE	Cov	Bias	%	SE	SEE	Cov
50	[τ]	0.010	2.0	0.285	0.276	0.942	0.029	5.8	0.409	0.377	0.955
150	[τ]	0.003	0.7	0.163	0.159	0.940	0.017	3.4	0.205	0.197	0.938
50	[0.75, 1.5]	0.009	1.8	0.310	0.289	0.938	0.093	18.6	0.567	0.482	0.956
150	[0.75, 1.5]	0.003	0.7	0.165	0.164	0.948	0.036	7.2	0.239	0.230	0.954

This is somewhat expected for a likelihood based procedure, which is efficient with complete data and with censoring complete data.

5 Bone marrow transplant dataset

A common side effect of a bone marrow transplant (bmt) as a treatment of leukemia is the occurrence of graft-versus-host disease (GVHD), where white blood cells from the donor attack cells in the patient’s body. This complication is closely related to the matching of the human leukocyte antigen (HLA) type between recipient and donor.

We reanalyzed bmt data of 1715 patients who received stem cells from either an HLA-identical sibling, an HLA matched or an HLA mismatched unrelated donor. During 74 months of follow-up, 311 patients had a relapse and 557 patients died in remission. As in Gerds et al. (2011), the main objective was to determine how the transplant of stem cells from unrelated donors would influence the risk for relapse and for death in remission, in comparison to having an HLA matched sibling as a donor.

We defined binary covariates “match” and “mism” indicating if the donor was HLA matched and unrelated or HLA mismatched and unrelated. Seven additional covariates were included in the analysis as displayed in Tables 5 and 6.

Table 5.

Bmt dataset, weighted NPMLEs for Relapse.

	Box-Cox transformation		Logarithmic transformation
model		Fine-Gray	prop. odds
parameter	ρ = 0.5	ρ = 1	r = 1	r = 2	r = 5
loglik	2449.68	−2452.46	−2446.21	−2442.00	−2437.43
match	−0.233(0.174)	−0.236(0.162)	− −0.222(0.191)	−0.181(0.215)	0.001(0.272)
mism	−1.392(0.404)	−1.326(0.381)	−1.473(0.437)	−1.573(0.499)	−1.678(0.628)
AML	−0.273(0.163)	−0.249(0.150)	−0.305(0.179)	−0.342(0.200)	−0.380(0.248)
CML	−0.803(0.166)	−0.752(0.158)	−0.869(0.176)	−0.976(0.193)	−1.240(0.239)
wtime	−0.010(0.004)	−0.010(0.004)	− −0.011(0.004)	−0.013(0.005)	−0.015(0.006)
sex	−0.068(0.126)	−0.068(0.118)	−0.066(0.135)	−0.065(0.148)	−0.082(0.182)
karn	0.156(0.167)	0.179(0.153)	0.108(0.183)	0.019(0.204)	−0.223(0.254)
sint	0.733(0.178)	0.689(0.169)	0.785(0.189)	0.873(0.208)	1.129(0.267)
sadv	1.700(0.166)	1.557(0.155)	1.885(0.182)	2.173(0.204)	2.835(0.264)
Ân(τ/4)	0.184(0.042)	0.172(0.037)	0.244(0.067)	0.244(0.074)	0.395(0.134)
Ân(τ/2)	0.231(0.053)	0.212(0.046)	0.324(0.090)	0.324(0.099)	0.580(0.200)
Ân(τ)	0.286(0.066)	0.258(0.056)	0.330(0.084)	0.424(0.119)	0.841(0.297)

Table 6.

Bmt dataset, weighted NPMLEs for Death in remission.

	Box-Cox transformation			Logarithmic transformation
model			Fine-Gray	prop. odds
parameter	ρ = 2	ρ = 1.5	ρ = 1	r = 1	r = 2
loglik	−4457.15	−4457.05	−4457.21	−4460.64	−4467.04
match	0.598(0.085)	0.638(0.092)	0.685(0.099)	0.811(0.125)	0.905(0.170)
mism	0.940(0.113)	1.005(0.122)	1.086(0.134)	1.274(0.166)	1.384(0.232)
AML	−0.036(0.129)	−0.043(0.137)	−0.054(0.147)	−0.100(0.178)	−0.147(0.228)
CML	0.329(0.109)	0.342(0.116)	0.355(0.124)	0.363(0.152)	0.350(0.198)
wtime	0.006(0.001)	0.007(0.001)	0.008(0.002)	0.010(0.002)	0.012(0.003)
sex	0.003(0.076)	0.003(0.081)	0.002(0.087)	−0.006(0.106)	−0.019(0.138)
karn	−0.349(0.091)	−0.387(0.098)	−0.437(0.106)	−0.595(0.136)	−0.733(0.188)
sint	0.250(0.094)	0.267(0.100)	0.287(0.108)	0.337(0.131)	0.382(0.175)
sadv	0.367(0.114)	0.398(0.121)	0.438(0.132)	0.567(0.164)	0.678(0.220)
Ân(τ/4)	0.224(0.034)	0.239(0.038)	0.258(0.044)	0.326(0.067)	0.425(0.112)
Ân(τ/2)	0.238(0.036)	0.255(0.041)	0.276(0.047)	0.356(0.072)	0.472(0.124)
Ân(τ)	0.244(0.037)	0.262(0.042)	0.286(0.049)	0.370(0.075)	0.496(0.131)

Tables 5 and 6: Parameter estimates and estimated standard errors (in brackets) for different link functions from the classes of logarithmic- and Box-Cox transformation models. Covariates included were “match” and “mism” indicating if the type of donor was HLA matched and unrelated or HLA mismatched and unrelated in comparison to a having an HLA matched sibling as a donor, “AML” and “CML” indicating the type of leukemia in comparison to ALL, waiting time until transplant (“wtime”), “sex” indicating if the patient was female, “karn” indication if the Karnovsky index was ≥ 90, “sint” and “sadv” indicating if the stage of the disease was intermediate or advanced in comparison to early.

Weighted NPMLEs were calculated for transformation models from the logarithmic-and the Box-Cox class. As a simple tool for model selection we applied the Akaike criterion, by ranking models based on the value of the weighted log-likelihood.

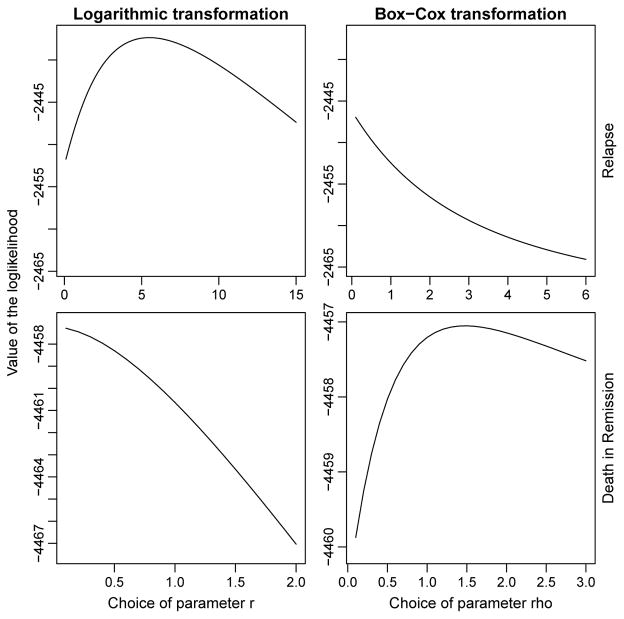
As illustrated in Figure 1, the logarithmic transformation model with parameter r ≈ 5 is the best fitting model for relapse, while the optimal choice for death in remission is the Box-Cox transformation model with parameter ρ = 1.5, which is only slightly different from the Fine-Gray model. In Tables 5 and 6 we report the estimated regression parameters for different link functions. Pp-plots, as displayed in our technical report, indicate that none of the models selected by the Akaike criterion exhibits a significant lack of fit. For the Fine-Gray model the estimated values were identical with the results from the crr function.

Figure 1.

Model selection with Akaike criterion for the bmt dataset. Value of the loglik in relation to the choice of parameter r for the logarithmic transformation models (left hand side) and of parameter ρ for the Box-Cox class of transformation models (right hand side). First row: relapse, second row: death in remission.

For relapse and r = 5 we can see in Table 5 that “match” is not significant while “mism” is significant with a negative estimated parameter value, indicating that an HLA mismatched and unrelated donor will decrease the risk of relapse in comparison to an HLA matched sibling. This was somewhat expected since GVHD might decrease the risk of relapse, if white blood cells from the donor attack the patients cancer cells.

For death in remission and r = 0 the covariates “match” and “mism” are both significant with positive estimated parameter values, as displayed in Table 6. This indicates that an HLA matched unrelated donor will increase the risk of dying in remission in comparison to an HLA matched sibling. For patients receiving stem cells from an HLA mismatched and unrelated donor, the increase in the risk of dying is greater.

The magnitude of the parameter and standard error estimates in Tables 5 and 6 vary across models with different choices of parameter r, owing to the fact that the parameters are defined on different scales. The ratios of the parameter estimates and the estimated standard errors are, however, relatively constant across these models. As established by Kosorok, Lee and Fine (2004) such constancy holds under regularity conditions for misspecified models within classes of semiparametric regression models.

The logarithmic transformation model may be regarded as a proportional hazards frailty model for the CIF, in which the frailty has gamma distribution with parameter r. The estimated covariate effects are thus interpretable as subdistribution hazard ratios in a frailty regression model, where the frailty accounts for important covariates that are omitted from the regression model.

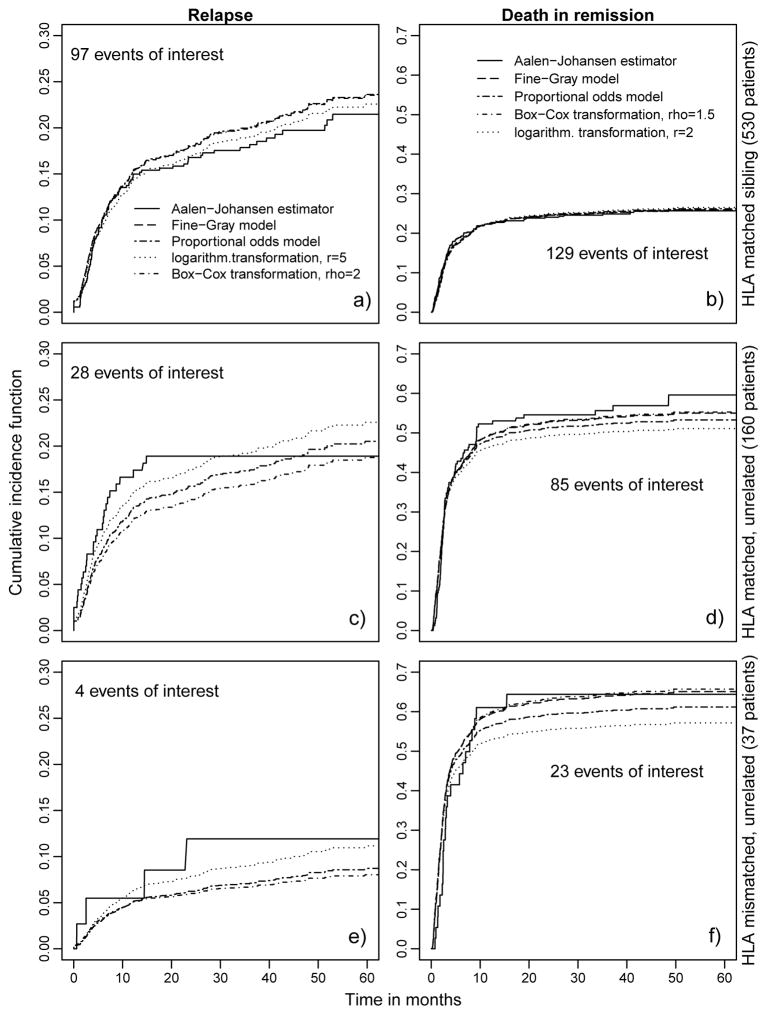
To illustrate the importance of model selection in prediction, we plotted in figure 2 the aggregated CIFs for subgroups of the 727 female patients from different regression models in comparison to the Aalen-Johansen estimator. The baseline hazards for the events relapse and death in remission were obtained by maximizing the weighted log-likelihood functions over the entire population.

Figure 2.

Prediction plots for the bmt dataset for different subsets of the 727 female patients. For 530 female patients the donor was an HLA matched sibling, for 160 female patients the donor was HLA matched and unrelated, for 37 female patients the donor was HLA mismatched and unrelated.

Aggregated CIFs for both events were then obtained for the three subgroups by averaging the predicted probabilities across individuals in the subgroup.

For relapse it seems that the prognosis of female patients with a sibling as a donor and female patients with an HLA matched donor is similar. Having an HLA mismatched unrelated donor seems to decrease the probability of a relapse in comparison to the other two subgroups. For the largest subgroup of 530 female patients with an HLA matched sibling as a donor and for the subgroup of 37 female patients with an HLA mismatched donor, the CIFs from the logarithmic transformation model with r = 5 are located closest to the nonparametric Aalen Johansen estimator. This means that the prediction of the best model under AIC, r = 5, clearly improves on the Fine-Gray model. For the second group of 160 female patients with an HLA matched donor, the performance of the prediction for the logarithmic transformation model is better for the first 30 months. For this subgroup no relapse was observed at a time later than t = 15 months.

For death in remission the plots for the three subgroups illustrate how the choice of an unrelated donor leads to a dramatic increase in the risk of dying in remission. For the largest subgroup of 530 female patients with a sibling as a donor and 129 events of interest, all regression models perform equally well, evidenced by good agreement with the Aalen-Johansen estimator. For the subgroups of female patients with an HLA matched unrelated donor or an HLA mismatched unrelated donor, the Fine-Gray model and the Box-Cox transformation model with ρ = 1.5 perform similarly well and are clearly superior to the other preselected models. The prediction curves for both subgroups were closest to the Aalen-Johansen estimator.

6 Discussion

We propose a novel weighted likelihood function and establish a general semiparametric regression model for the subdistribution hazard. We thereby provide a flexible likelihood framework for the Fine-Gray model that is extendable in several directions.

The new approach is applicable to a general class of semiparametric transformation models, as previously considered by Zeng and Lin (2006) for simple survival settings without competing events. A major point is that in cases where the proportional hazards assumption cannot be validated, nonproportionality may be captured via the choice of the link function. Alternatively, the use of interaction terms in the proportional hazards model can lead to an improvement with regard to the fit of the model. We present results from such a regression analysis with interaction terms for the bmt dataset in Section B.5.2 of our technical report. Difficulties in interpretation arise from the fact that covariates and the corresponding interaction terms have in many cases opposing directions. With our proposed general regression model nonproportionality can be addressed more parsimoniously and estimated covariate effects are immediately interpretable.

A useful feature of the weighted likelihood approach is that the Akaike criterion can easily be adapted as a simple tool for model selection, as we demonstrate for the bmt dataset. To address the overall question of fit we propose a method based on pp-plots in Section B.5.1 of our technical report. Another method to check the fit of the model might be to compare the prediction plots for different transformation models to the Aalen-Johansen estimator within particular subgroups of the dataset, as conducted in Section 5. Investigating other model selection techniques for semiparametric transformation models would be an important topic for further research.

Furthermore, the weighted likelihood approach enables modeling time-dependent covariate effects on the subdistribution hazard, as opposed to earlier work on direct regression modeling for competing risks, where covariate effects target the CIF.

The one-two-one correspondence between the subdistribution hazard and the CIF holds with either time-independent, eg, baseline covariates, or with external time-dependent covariates in the same way as for the survival model without competing risk (Kalbfleisch and Prentice, 2002). External time-dependent covariates might include interactions of time-independent covariates and time used to capture nonproportionality or exogenous covariates. As an example of a nontrivial external covariate, in evaluating hospital performance, where death serves as a competing risk for discharge, operational characteristics of the hospital, including staffing factors and level of hospital utilization, change over time. The cumulative incidences of discharge and death may be derived from the subdistribution hazard conditionally on these covariates, which are observed after a patient’s event.

For internal time-dependent covariates, it is not possible to establish a direct relation between the subdistribution hazard and the CIF. The problem is well known even for survival settings without competing risks, where regression parameters for the hazard rate in the presence of internal time-dependent covariates are not interpretable with regard to the underlying distribution, see Kalbfleisch and Prentice (2002). For procedures which directly model the absolute risk conditionally on time-dependent covariates instead of the subdistribution hazard, similar problems occur. Regression modeling of the subdistribution hazard with internal time-dependent covariates is a more delicate issue as covariates are not generally available after a competing risk event. Similar challenges arise when directly modeling the absolute risk of an event by a particular time point conditionally on the value of internal time-dependent covariates, see Klein and Andersen (2005) and Scheike, Zhang and Gerds (2008). The approach proposed by Beyersmann and Schumacher (2008) or alternative methods of extrapolation may be applied in our weighted NPMLE procedure. In contrast to that, modeling the cause specific hazard with internal time dependent covariates is straightforward. The approach, however, does not alleviate the problem of interpretability of the estimated regression parameters with regard to the CIF.

A heuristic approach to the subdistribution hazard modeling is elaborated in Section 2. The idea of modeling the subdistribution hazard from a cure model perspective leads to a hazard ratio interpretation which has been accepted by many practitioners, with widespread application in substantive biomedical papers.

To evaluate the options of either modeling the subdistribution hazard or the cause specific hazard, the main consideration should be the scientific objectives of a clinical trial. Modeling the cause-specific hazards is considered as intuitive with regard to a traditional risk set of individuals with no prior event. The sum of the cause specific hazards is the total hazard, which is directly related to the overall survival function.

An advantage of a regression models targeting either the subdistribution hazard or directly the CIF is that it quantifies the absolute risk of a particular event type. Lau et al (2009) suggest that cause specific hazard models are “better suited for studying the etiology of diseases, while the subdistribution hazard model has use in predicting an individual’s absolute risk”. Similarly, Wolbers et al (2009) suggested that subdistribution hazard methods are preferable when the focus is on actual risks and prognosis, which are not captured by a single cause specific hazard function.

With regard to the theoretical foundation of the weighted NPMLE, several new results are presented in Section A.2 and in our technical report. A proof for the existence of the weighted NPMLE and the uniform boundedness of the baseline hazard is provided that requires only one of the weak model assumptions M4a) or M4b), whereas Zeng and Lin’s model assumptions are rather restrictive. A challenge thereby is that the fundamental theorem of calculus cannot be routinely applied, which has previously been neglected in theoretical work on NPMLE.

The proposed sandwich estimator is theoretically justified by a new lemma for weighted 𝒵–estimators that may be regarded as a Wald type argument in the light of Theorem 3.3.1 of van der Vaart and Wellner being based on a Taylor series expansion in abstract spaces. The arguments for weighted NPMLEs are similar but considerably more complex than those for weighted parametric maximum likelihood estimators.

Finally, an extension of the weighted NPMLE to the clinically relevant setting of recurrent events with competing terminal events appears to be an obvious next step. Let D denote the time of the competing terminal event and let N(t) denote the process counting the number of recurrent events before D. The marginal mean intensity, defined as λ(t) = E[dN(t)|N(s), s < t], has the desirable property that the usual relationship with the marginal mean is retained, that is $E[N(t)]={\int }_0^t\lambda (u)du$. With a weight function defined as in Ghosh and Lin (2002) the general model (1) in Section 3.1 may be proposed for the marginal mean intensity. Even for the particular choice of the link function 𝒢(x) = x, this approach does not represent a Markov model and, as for the Andersen Gill model, it would be suitable in cases where the dependency structure between the recurrent events for a particular individual can be mediated by time dependent covariates. A general regression model for the marginal mean intensity is then obtained from the modified weighted log-likelihood function. It will be of interest for further research to investigate a general regression model for the marginal mean intensity in greater depth.

Table 1.

Simulations studies for the weighted NPMLE with (β₁₁, β₁₂) = (0.5,−0.5). Censorings were uniformly distributed on [a, b], with b = [τ ] indicating that there was only administrative censoring at τ. Columns 5–7: events of interest, competing risk events and censorings in %.

Model	𝒢(x)	a	b	τ	type 1	type 2	cens.
Fine-Gray	x	-	[τ]	4	33	62	5
Fine-Gray	x	1	2	1.9	26	49	25
Fine-Gray	x	0.5	1	0.95	18	36	46
prop.odds	log(1 + x)	-	[τ]	3.5	56	39	5
prop.odds	log(1 + x)	0.75	1.5	1.4	47	29	24
prop.odds	log(1 + x)	0.5	3.5	2.5	51	33	16

A Appendix

A.1 Model conditions

• M1)The cumulative baseline A₀(t) is a strictly increasing and continuously differentiable function and β₀ lies in the interior of a compact set 𝒞.
• M2)The vector of covariates Z(t) is P-almost surely of bounded variation on the observed interval [0, τ].
• M3)The endpoint of the study τ is chosen in a way that P-almost surely there exists a constant δ > 0 such that P(C ≥ τ|Z) > δ and P(X ≥ τ|Z) > δ.
• M4)𝒢 is a thrice continuously differentiable and strictly increasing function with 𝒢(0) = 0, 𝒢′(0) > 0 and 𝒢(∞) = ∞. In addition to that one of the following conditions is required:

  1. ) 𝒢″(x) ≤ 0 for x > 0 or

  2. 𝒢″(x) ≥ 0 for x > 0. In addition to that for any a ∈ (0,∞) and for any sequence (x_n) ⊂ ℝ with x_n → ∞ as n → ∞,

     $$\underset{n\to \infty }{lim}\mathbb{P}(X\le \tau ,\mathrm{\Delta }\epsilon =1)\left[\frac{log(a{x}_n)}{\mathcal{G}(a^{-1}{x}_n)}+\frac{log{\mathcal{G}}^{\prime }(a{x}_n)}{\mathcal{G}(a^{-1}{x}_n)}\right]<P(X\ge \tau ).$$ (*)
• M5)Identifiability condition: If h₁ ∈ ℝ^d and h₂ ∈ 𝒟[0, τ] exist such that $h_1^{T}Z(t)+h_2(t)=0$ P-almost surely, then h₁ = 0 and h₂(t) = 0 ∀t ∈ [0, τ].
• M6)
  For any h₁ ∈ ℝ^d and for any h₂ ∈ 𝒟[0, τ] exists a subset 𝒮 ⊂ [0, τ] of nonzero Lebesgue measure such that ∀t ∈ 𝒮

  $$h_1^{T}Z(t)+h_2(t)\ne -\frac{{\mathcal{G}}^{″}\left({\int }_0^t{e}^{{\beta }_0^{T}Z(u)}{dA}_0(u)\right)}{{\mathcal{G}}^{\prime }\left({\int }_0^t{e}^{{\beta }_0^{T}Z(u)}{dA}_0(u)\right)}{\int }_0^t{e}^{{\beta }^{T}Z(u)}(h_1^{T}Z(u)+h_2(u)){dA}_0(u).$$

For the consistency of the weighted NPMLE, model conditions M1)-M5) and twice continuous differentiability of 𝒢 are sufficient. Model conditions M1)-M2),M5)-M6) and thrice continuous differentiability of 𝒢 are sufficient to obtain weak convergence. For the proportional hazards (Fine-Gray) model conditions M5) and M6) are equivalent. Condition M4a) is satisfied for example for the class of logarithmic transformation models and for the Box-Cox transformation models with ρ ∈ [0, 1]. M4b) holds for the Box-Cox transformation models with ρ > 1. It is sufficient for (*) to prove that log(ax_n)/𝒢(a⁻¹x_n) → 0 and log 𝒢′(ax_n)/𝒢(a⁻¹x_n) → 0 for x_n → ∞.

A.2 Consistency

We show that ${\widehat{A}}_n^0(\tau )$ is bounded P-almost surely, thereby ascertaining the existence of the weighted NPMLE. Then ${\widehat{A}}_n^0(t)$ is bounded on [0, τ] uniformly P-almost surely. From Helly’s selection theorem it is then obtained that $\exists n_k\subset \mathbb{N}:{\widehat{A}}_{n_k}^0\stackrel{\ast }{\to }{A}^{\ast }$, for a limit A^*, with * denoting outer almost sure convergence. With a Kullback-Leibler argument it is ascertained that every subsequence (β̂_nk, ${\widehat{A}}_{n_k}^0$) converges to the true parameter (β₀, A₀). Â_n(t) is a sequence of monotone increasing functions, and the limit A₀(t) is continuous. From this ||Â_n − A₀||_{ℓ^∞[0,τ]} → 0 [P] and |β̂_n − β₀| → 0 [P] where ℓ^∞[0, τ] denotes the space of bounded functions on [0, τ].

Existence of (β̂_n, ${\widehat{A}}_n^0$) and boundedness of ${\widehat{A}}_n^0(\tau )$ under model condition M4a)

We define ${\stackrel{\sim }{A}}_n^0(t):=n^{-1}{\sum }_{i=1}^n{N}_i(t)$. By Jensen’s inequality it is ascertained that

$$n^{-1}[\ell ({\widehat{A}}_n^0,{\widehat{\beta }}_n)-\ell ({\stackrel{\sim }{A}}_n^0,{\beta }_0)]\le \left[{\mathbb{P}}_n𝟙\{X\le \tau ,\mathrm{\Delta }\epsilon =1\}\frac{log\mathcal{G}\left(e^{-M}{\widehat{A}}_n^0(\tau )\right)}{\mathcal{G}\left(e^{-M}{\widehat{A}}_n^0(\tau )\right)}-{\mathbb{P}}_n𝟙\{X\ge \tau \}\right]\mathcal{G}(e^{-M}{\widehat{A}}_n^0(\tau ))+O_p(1).$$

Existence of (β̂_n, ${\widehat{A}}_n^0$) and boundedness of ${\widehat{A}}_n^0(\tau )$ under model condition M4b)

$$n^{-1}[\ell ({\widehat{A}}_n^0,{\widehat{\beta }}_n)-\ell ({\stackrel{\sim }{A}}_n^0,{\beta }_0)]\le \left\{{\mathbb{P}}_n𝟙\{X\le \tau ,\mathrm{\Delta }\epsilon =1\}\left[\frac{log{\mathcal{G}}^{\prime }(e^M{\widehat{A}}_n^0(\tau ))}{\mathcal{G}(e^{-M}{\widehat{A}}_n^0(\tau ))}+\frac{log(e^M{\widehat{A}}_n^0(\tau ))}{\mathcal{G}(e^{-M}{\widehat{A}}_n^0(\tau ))}\right]-{\mathbb{P}}_n𝟙\{X\ge \tau \}\right\}\times \mathcal{G}(e^{-M}{\widehat{A}}_n^0(\tau ))+O_p(1).$$

The conclusion in both cases is that if ${\widehat{A}}_n^0(\tau )$ became infinitely large, the right hand side would go to − ∞, which contradicts the definition of (Â_n, β̂_n) as a maximum likelihood estimator.

Competing risks setting with administrative censoring

From differentiating the discretized log-likelihood with respect to jumps sizes we obtain

$${\widehat{A}}_n^0(t)=\sum _{i:X_i\le t,{\mathrm{\Delta }}_i{\epsilon }_i=1}{\left[n·{\mathrm{\Phi }}_n^a(X_i,{\widehat{A}}_n^0,{\widehat{\beta }}_n)\right]}^{-1}={\int }_0^t\frac{\frac{1}{n}{\sum }_{i=1}^n𝟙(C_i\ge s)d{N}_i(s)}{\mid {\mathrm{\Phi }}_n^a(s,{\widehat{A}}_n^0,{\widehat{\beta }}_n)\mid },$$

with ${\mathrm{\Phi }}_n^a(s,{\widehat{A}}_n^0,{\widehat{\beta }}_n)$ as provided in our technical report. Substituting estimated parameters by the true model parameters we obtain

$${\stackrel{\sim }{A}}_n^a(t)={\int }_0^t\frac{\frac{1}{n}{\sum }_{i=1}^n𝟙(C_i\ge s)d{N}_i(s)}{\mid {\stackrel{\sim }{\mathrm{\Phi }}}_n^a(s,A_0,{\beta }_0)\mid },$$

and by Doob decomposition of the counting process N_i(t)

$${\stackrel{\sim }{\mathrm{\Phi }}}_n^a(s,{\beta }_0,A_0)=\frac{1}{n}\sum _{i=1}^n𝟙(C_i\ge s)Y_i(s)e^{{\beta }_0^T{Z}_i(s)}{\mathcal{G}}^{\prime }\left({\int }_0^s{e}^{{\beta }_0^T{Z}_i(u)}{dA}_0(u)\right)+o_p(1).$$

By the Glivenko-Cantelli theorem ${\stackrel{\sim }{\mathrm{\Phi }}}_n^a(s,{\beta }_0,A_0)$ converges uniformly to E[η(s, β₀, A₀)] with

$$\eta (s,{\beta }_0,A_0)\equiv 𝟙(C\ge s)Y(s)e^{{\beta }_0^{T}Z(s)}{\mathcal{G}}^{\prime }\left({\int }_0^{s}Y(u)e^{{\beta }_0^{T}Z(u)}{dA}_0(u)\right)$$

and another application of Doob decomposition implies

$${\stackrel{\sim }{A}}_n^a(t)=A_0(t)+n^{-1}\sum _{i=1}^n{\int }_0^t\frac{𝟙(C_i\ge s){dM}_i(s)}{E[\eta (s,{\beta }_0,A_0)]+o_p(1)}+o_p(1).$$

By the Glivenko-Cantelli theorem ${\stackrel{\sim }{A}}_n^a(t)\to A_0(t)$ for n → ∞ uniformly almost surely in t. Further the Glivenko-Cantelli theorem implies that ${\mathrm{\Phi }}_n^a(s,{\widehat{A}}_n^0,{\widehat{\beta }}_n)$ converges uniformly to a continuously differentiable function Φ_*(s, A_*, β_*) and the limit is bounded away from zero. ${\widehat{A}}_n^0(t)$ is absolutely continuous with respect ${\stackrel{\sim }{A}}_n^a(t)$ and ${\widehat{A}}_n^0(t)/{\stackrel{\sim }{A}}_n^a(t)$ converges to α_*(t) = E[η(s, β₀, A₀)]/Φ_*(s, A_*, β_*). Therefore,

$${\widehat{A}}_n^0(t)\to A_{\ast }(t)={\int }_0^t\frac{E[\eta (s,{\beta }_0,A_0)]}{{\mathrm{\Phi }}_{\ast }(s,A_{\ast },{\beta }_{\ast })}{dA}_0(s).$$

With a Kullback-Leibler argument it is then obtained that the limit A_*(t) is P-almost surely the true baseline hazard A₀(t). For the setting with administrative censoring we define the Kullback-Leibler distance

$${\mathcal{K}}_a({\theta }_0,{\theta }_{\ast })=E_{F_{{\theta }_0},G}\left[log\left\{{\left(\frac{f_{{\theta }_0}(X)}{f_{{\theta }_{\ast }}(X)}\right)}^{\mathrm{\Delta }𝟙(\epsilon =1)}{\left(\frac{S_{{\theta }_0}(C\wedge \tau )}{S_{{\theta }_{\ast }}(C\wedge \tau )}\right)}^{1-\mathrm{\Delta }}{\left(\frac{S_{{\theta }_0}(C\wedge \tau )}{S_{{\theta }_{\ast }}(C\wedge \tau )}\right)}^{\mathrm{\Delta }𝟙(\epsilon \ne 1)}\right\}\right],$$

thereby denoting θ₀ = (β₀, A₀) and θ_* = (β_*, A_*) and with f_θ(t) = α_θ(t)S_θ(t) being the subdensity for the event of interest. As derived in Section B.3 this Kullback-Leibler distance is nonnegative. On the other hand, as ${\widehat{\theta }}_n=({\widehat{\beta }}_n,{\widehat{A}}_n^0(t))$ maximizes the log-likelihood function it is obtained that 𝒦_a(θ₀, θ_*) ≤ 0 and thus 𝒦_a(θ₀, θ_*) = 0. It is then ascertained Section B.3 of our technical report that the Kullback-Leibler distance takes the value zero if and only if β_* = β₀ and A_* = A₀. From this we conclude that β̂_n → β₀ P-almost surely and ${\widehat{A}}_{n_k}^0\to A_0$ uniformly P-almost surely.

Competing risks setting with independent right censoring

From maximizing the discretized likelihood function we obtain

$${\widehat{A}}_n(t)=\sum _{i:X_i\le t,{\mathrm{\Delta }}_i{\epsilon }_i=1}{\left[n·{\mathrm{\Phi }}_n(X_i,{\widehat{A}}_n,{\widehat{\beta }}_n)\right]}^{-1}={\int }_0^t\frac{\frac{1}{n}{\sum }_{i=1}^n𝟙(C_i\ge s)d{N}_i(s)}{\mid {\mathrm{\Phi }}_n(s,{\widehat{A}}_n,{\widehat{\beta }}_n)\mid },$$

with Φ_n(s, Â_n, β̂_n) as provided in our technical report. Substituting estimted parameters by the true model parameters we define

$${\stackrel{\sim }{A}}_n(t)={\int }_0^t\frac{\frac{1}{n}{\sum }_{i=1}^n𝟙(C_i\ge s)d{N}_i(s)}{\mid {\stackrel{\sim }{\mathrm{\Phi }}}_n(s,A_0,{\beta }_0)\mid }.$$

With an application of empirical process theory it is ascertained that ${\stackrel{\sim }{\mathrm{\Phi }}}_n(s,{\beta }_0,A_0)={\stackrel{\sim }{\mathrm{\Phi }}}_n^a(s,{\beta }_0,A_0)+o_p(1)$ and thus Ã_n(t) → A₀(t). By the Glivenko-Cantelli theorem Φ_n(s, β̂_n, Â_n) converges uniformly to a continuously differentiable function Φ^*(s, A^*, β^*) with Φ^*(s, A^*, β^*) > 0 for s ∈ [0, τ] and

$${\widehat{A}}_n(t)\to A^{\ast }(t)={\int }_0^t\frac{E[\eta (s,{\beta }_0,A_0)]}{{\mathrm{\Phi }}^{\ast }(s,{\beta }^{\ast },A^{\ast })}{dA}_0(s).$$

A^*(t) is absolutely continuous with respect to the Lebesgue measure and the Radon–Nikodym derivative takes the form α^*(t) = E[η(t, β₀, A₀)]/Φ^*(t, β^*, A^*)α₀(t).

We define the Kullback-Leibler distance corresponding to the weighted log-likelihood function as

$$\begin{gathered} {\mathcal{K}}_{w^{\ast }}({\theta }_0,{\theta }_{\ast }) \\ =E_{F_{{\theta }_0},G}\left[log\left\{{\left(\frac{f_{{\theta }_0}(X)}{f_{{\theta }_{\ast }}(X)}\right)}^{\mathrm{\Delta }𝟙(\epsilon =1)}{\left(\frac{S_{{\theta }_0}(C\wedge \tau )}{S_{{\theta }_{\ast }}(C\wedge \tau )}\right)}^{1-\mathrm{\Delta }}\times {\left(\frac{exp(-{\int }_0^{\tau }\stackrel{\sim }{w}(t){dA}_{{\theta }_0}(t))}{exp(-{\int }_0^{\tau }\stackrel{\sim }{w}(t){dA}_{{\theta }_{\ast }}(t)}\right)}^{\mathrm{\Delta }𝟙(\epsilon \ne 1)}\right\}\right]. \end{gathered}$$

From the asymptotic equivalence of 𝒦_a(θ₀, θ_*) and 𝒦_w^* (θ₀, θ_*) it can be concluded that β_* = β₀ and A_* = A₀.

A.3 Weak convergence

Let ℋ denote the space of elements h = (h₁, h₂) with h₁ ∈ ℝ^d and h₂ ∈ 𝒟[0, τ]. A norm on ℋ is then defined by ||h||_ℋ = ||h₁||+||h₂||_v, with ||·|| denoting the Euclidean norm and ||·||_v denoting the total variation norm. For p < ∞ we define ℋ_p = {h ∈ ℋ : ||h||_ℋ ≤ p}. The parameter space is denoted by Θ = {θ = (β, A₀), with β ∈ ℝ^d andA₀ being a monotone increasing element of 𝒟[0, τ]}. For h ∈ ℋ_p we define $\theta (h)=h_1^T\beta +{\int }_0^{\tau }{h}_2(u){dA}_0(u)$, so that Θ ⊂ ℓ^∞(ℋ_p). One-dimensional submodels of the form $t\to {\theta }_t=\theta +t(h_1,{\int }_0^{(·)}{h}_2(u){dA}_0(u))$ are considered with h ∈ ℋ_p to define the empirical score operator

$${\mathrm{\Psi }}_n(\theta ,h,w)={\frac{\partial }{\partial t}{\ell }_n({\theta }_t,h,w)|}_{t=0}={\mathbb{P}}_n\psi (\theta ,h,w)={\mathbb{P}}_n({\psi }_1(\theta ,h,w)+{\psi }_2(\theta ,h,w)),$$

for a measurable function ψ(θ, h,w), where ${\mathrm{\Psi }}_{n1}^w(\theta ,h,w)={\mathbb{P}}_n{\psi }_1(\theta ,h,w)$ is the component related to the derivative with regard to β and ${\mathrm{\Psi }}_{n2}^w(\theta ,h,w)={\mathbb{P}}_n{\psi }_2(\theta ,h,w)$ is the component related to the derivative along the submodel for A₀. The limiting version Ψ is defined by replacing the empirical measure ℙ_n by the probability measure ℘.

Weak convergence is ascertained by a new lemma for weighted 𝒵–estimators, that is based on Theorem 3.3.1. of van der Vaart and Wellner (1996):

Lemma 3

Let the parameter set Θ be a subset of a Banach space. Let w̃(t) be a bounded deterministic weight function and let ŵ_n(t) be a sequence of bounded random weight functions with values in ℝ₊. Let Ψ_n and Ψ be a linear random map and a linear deterministic map, respectively from Θ × ℝ₊ into a Banach space such that

$$a)\sqrt{n}({\mathrm{\Psi }}_n-\mathrm{\Psi })({\widehat{\theta }}_n,{\widehat{w}}_n)-\sqrt{n}({\mathrm{\Psi }}_n-\mathrm{\Psi })({\theta }_0,{\widehat{w}}_n)=o_p^{\ast }(1+\sqrt{n}\Vert {\widehat{\theta }}_n-{\theta }_0\Vert ),$$

such that $\sqrt{n}({\mathrm{\Psi }}_n-\mathrm{\Psi })({\theta }_0,\stackrel{\sim }{w})$ converges to a tight limit 𝒵₁ and $\sqrt{n}\left(({\mathrm{\Psi }}_n-\mathrm{\Psi })({\theta }_0,{\widehat{w}}_n)-({\mathrm{\Psi }}_n-\mathrm{\Psi })({\theta }_0,\stackrel{\sim }{w})\right)$ converges to a tight limit 𝒵₂, and the sequences jointly converge to (𝒵₁,𝒵₂).

Let (θ, w) → Ψ(θ, w) be Fréchet-differentiable at (θ₀, w̃) with a continuously invertible derivative ${\stackrel{.}{\mathrm{\Psi }}}_{{\theta }_0}^{\stackrel{\sim }{w}}$. If Ψ(θ₀, w̃) and θ̂_n satisfies ${\mathrm{\Psi }}_n({\widehat{\theta }}_n,{\widehat{w}}_n)=o_p^{\ast }(n^{-1/2})$, if Ψ_n(θ̂_n, w̃) = Ψ_n(θ̂_n, ŵ_n) + o_p(1) and if Ψ_n(θ̂_n, w̃) converges in outer probability to Ψ(θ₀, w̃), then

$$\sqrt{n}{\stackrel{.}{\mathrm{\Psi }}}_{{\theta }_0}^{\stackrel{\sim }{w}}({\widehat{\theta }}_n-{\theta }_0)=-\sqrt{n}\left(({\mathrm{\Psi }}_n-\mathrm{\Psi })({\theta }_0,\stackrel{\sim }{w})+({\mathrm{\Psi }}_n-\mathrm{\Psi })({\theta }_0,\widehat{w})-({\mathrm{\Psi }}_n-\mathrm{\Psi })({\theta }_0,\stackrel{\sim }{w})\right)+o_p^{\ast }(1)$$ (5)

and $\sqrt{n}({\widehat{\theta }}_n-{\theta }_0)\rightsquigarrow -{\left[{\stackrel{.}{\mathrm{\Psi }}}_{{\theta }_0}^{\stackrel{\sim }{w}}\right]}^{-1}({\mathcal{Z}}_1+{\mathcal{Z}}_2)$, with ↝ denoting weak convergence.

As our model is based on iid observations, for condition a) in the above Lemma 3 it is sufficient to verify the two conditions of Lemma 5 in our technical report.

By the Donsker theorem $\sqrt{n}({\mathrm{\Psi }}_n-\mathrm{\Psi })({\theta }_0,\stackrel{\sim }{w})$ converges in distribution to the tight random element 𝒵₁. Also by Donsker theorem $\sqrt{n}\left(({\mathrm{\Psi }}_n-\mathrm{\Psi })({\theta }_0,{\widehat{w}}_n)-({\mathrm{\Psi }}_n-\mathrm{\Psi })({\theta }_0,\stackrel{\sim }{w})\right)$ converges in distribution to a tight random element 𝒵₂. Joint convergence follows from the asymptotic linearity of the two components marginally, combined with the fact that the composition of two Donsker classes is also Donsker. Per definition Ψ_n(θ̂_n, ŵ_n) = 0. As argued in Parner (1998) from the Kullback-Leibler information being positive and by interchanging expectation and differentiation we obtain Ψ(θ₀, w̃) = 0. Arguments for the continuous invertibility of Ψ̇₀ and ${\stackrel{.}{\mathrm{\Psi }}}_0^a$ under model conditions M6),M7) are provided in our technical report.

From Lemma 3 we obtain weak convergence of $\sqrt{n}({\widehat{\theta }}_n-{\theta }_0)$ and the covariances for the limiting process $-{\stackrel{.}{\mathrm{\Psi }}}_0^{-1}({\mathcal{Z}}_1+{\mathcal{Z}}_2)$, with 𝒵₁(h) = lim_n→∞ ℙ_n ψ(β̂_n, Â_n, h, w̃) and 𝒵₂(h) = lim_n→∞ ℙ_n[(ψ(β̂_n, Â_n, h, ŵ_n) − ψ(β̂_n, Â_n, h, w̃)], are given by

$$\mathcal{P}\left\{\left[({\mathcal{Z}}_1+{\mathcal{Z}}_2)\left({\stackrel{.}{\mathrm{\Psi }}}_0^{-1}(g)\right)\right]\left[({\mathcal{Z}}_1+{\mathcal{Z}}_2)\left({\stackrel{.}{\mathrm{\Psi }}}_0^{-1}(h)\right)\right]\right\}$$

for g, h ∈ ℋ (Kosorok, 2008, page 302).

A.4 Variance estimation

The middle part of the sandwich variance estimator, as proposed in section 3.3, is obtained from the iid decomposition of the score with ${\eta }_{i,n}=\left({\eta }_i^1,\dots ,{\eta }_i^{d+k(n)}\right)$ and ${\psi }_{i,n}=\left({\psi }_i^1,\dots ,{\psi }_i^{d+k(n)}\right)$ defined as

$$\begin{gathered} {\eta }_{i,n}^{\ell }=\left[Z_{i\ell }(X_i)+\sum _{\begin{array}{c}j:X_j\le X_i\\ {\mathrm{\Delta }}_j{\epsilon }_j=1\end{array}}{Z}_{i\ell }(X_j)e^{{\beta }^T{Z}_i(X_j)}{A}_n\{X_j\}\frac{{\mathcal{G}}^{″}\left({\int }_0^{X_i}{e}^{{\beta }_0^T{Z}_i(u)}{dA}_n(u)\right)}{{\mathcal{G}}^{\prime }\left({\int }_0^{X_i}{e}^{{\beta }^T{Z}_i(u)}{dA}_n(u)\right)}\right]𝟙({\mathrm{\Delta }}_i{\epsilon }_i=1) \\ -\sum _{\begin{array}{c}j:X_j\le X_i\wedge \tau \\ {\mathrm{\Delta }}_j{\epsilon }_j=1\end{array}}{Z}_{i\ell }(X_j)e^{{\beta }^T{Z}_i(X_j)}{A}_n\{X_j\}{\mathcal{G}}^{\prime }\left({\int }_0^{X_i\wedge \tau }{e}^{{\beta }^T{Z}_i(u)}{dA}_n(u)\right) \\ -\left[{\int }_{X_i}^{\tau }{\stackrel{\sim }{w}}_i^{\ast }(t)e^{{\beta }^T{Z}_i(t)}{Z}_{i\ell }(t){\mathcal{G}}^{\prime }\left({\int }_0^t{e}^{{\beta }^T{Z}_i(u)}{dA}_n(u)\right){dA}_n(t)\right]𝟙({\mathrm{\Delta }}_i{\epsilon }_i=2) \\ -\left[{\int }_{X_i}^{\tau }{\stackrel{\sim }{w}}_i^{\ast }(t)e^{{\beta }^T{Z}_i(t)}\left({\int }_0^t{Z}_{i\ell }(u)e^{{\beta }^T{Z}_i(u)}{dA}_n(u)\right){\mathcal{G}}^{″}\left({\int }_0^t{e}^{{\beta }^T{Z}_i(u)}{dA}_n(u)\right){dA}_n(t)\right]\times 𝟙({\mathrm{\Delta }}_i{\epsilon }_i=2) \end{gathered}$$

for ℓ ∈ {1, …, d} and

$$\begin{gathered} {\eta }_{i,n}^{\ell }=[𝟙(X_{\ell }=X_i){[A_n\{X_{\ell }\}]}^{-1}+𝟙(X_{\ell }\le (X_i\wedge \tau ))e^{{\beta }^T{Z}_i(X_{\ell })}\times {\mathcal{G}}^{″}\left({\int }_0^{X_i}{e}^{{\beta }^T{Z}_i(u)}{dA}_n(u)\right)/{\mathcal{G}}^{\prime }\left({\int }_0^{X_i}{e}^{{\beta }^T{Z}_i(u)}{dA}_n(u)\right)]𝟙({\mathrm{\Delta }}_i{\epsilon }_i=1) \\ -𝟙(X_{\ell }\le (X_i\wedge \tau ))e^{{\beta }^T{Z}_i(X_{\ell })}{\mathcal{G}}^{\prime }\left({\int }_0^{X_{\ell }}{e}^{{\beta }^T{Z}_i(u)}{dA}_n(u)\right) \\ -𝟙(X_i\le X_{\ell })\left[{\stackrel{\sim }{w}}_i^{\ast }(X_{\ell })e^{{\beta }^T{Z}_i(X_{\ell })}{\mathcal{G}}^{\prime }\left({\int }_0^{X_{\ell }}{e}^{{\beta }^T{Z}_i(u)}{dA}_n(u)\right)\right]𝟙({\mathrm{\Delta }}_i{\epsilon }_i=2) \\ -\left[e^{{\beta }^T{Z}_i(X_{\ell })}{\int }_{X_i\wedge X_{\ell }}^{\tau }{\stackrel{\sim }{w}}_i^{\ast }(t)e^{{\beta }^T{Z}_i(t)}{\mathcal{G}}^{″}\left({\int }_0^t{e}^{{\beta }^T{Z}_i(u)}{dA}_n(u)\right){dA}_n(t)\right]𝟙({\mathrm{\Delta }}_i{\epsilon }_i=2) \end{gathered}$$

for ℓ ∈ {d + 1, …, d + k(n)}. To calculate ${\psi }_{i,n}^{\ell }$ we apply

$$\frac{{\widehat{G}}_c(t)}{{\widehat{G}}_c(X_j)}-\frac{G_c(t)}{G_c(X_j)}=-\frac{G_c(t)}{G_c(X_j)}\sum _{i=1}^n{\int }_{X_j}^t\frac{1}{{\sum }_{k=1}^n𝟙(X_k\ge u)}\times {dM}_i^c(u)+o_p(n^{-1/2}),$$

where $M_i^c(t)=𝟙(X_i\le t,{\mathrm{\Delta }}_i=0)-{\int }_0^t𝟙(X_i\ge u)d{A}^c(u)$ is the martingale associated with the censoring process and A^c(t) is the cumulative hazard of the censoring distribution. From this we obtain the representation

$$\begin{gathered} {\psi }_{i,n}^{\ell }={\int }_0^{\infty }{q}_n^{\ell }(u){\{{\pi }_n(u)\}}^{-1}{dM}_i^c(u),\text{with} \\ {q}_n^{\ell }(u)=\frac{1}{n}\sum _{j:{\mathrm{\Delta }}_j{\epsilon }_j=2}\left[{\int }_0^{\tau }{\stackrel{\sim }{w}}_j^{\ast }(t)𝟙(X_j\le u\le t)e^{{\beta }^T{Z}_j(t)}{Z}_{j\ell }(t){\mathcal{G}}^{\prime }\left({\int }_0^t{e}^{{\beta }^T{Z}_j(s)}{dA}_n(s)\right){dA}_n(t)\right] \\ +\frac{1}{n}\sum _{j:{\mathrm{\Delta }}_j{\epsilon }_j=2}[{\int }_0^{\tau }{\stackrel{\sim }{w}}_j^{\ast }(t)𝟙(X_j\le u\le t)e^{{\beta }^T{Z}_j(t)}\left({\int }_0^t{Z}_{j\ell }(s)e^{{\beta }^T{Z}_j(s)}{dA}_n(s)\right)\times {\mathcal{G}}^{″}\left({\int }_0^t{e}^{{\beta }^T{Z}_j(s)}{dA}_n(s)\right){dA}_n(t)]\text{for}\ell \in \{1,\dots ,d\}, \\ {q}_n^{\ell }(u)=\frac{1}{n}\sum _{j:{\mathrm{\Delta }}_j{\epsilon }_j=2}\left[{\stackrel{\sim }{w}}_j^{\ast }(X_{\ell })𝟙(X_j\le u\le X_{\ell })e^{{\beta }^T{Z}_j(X_{\ell })}{\mathcal{G}}^{\prime }({\int }_0^{X_{\ell }}{e}^{{\beta }^T{Z}_j(s)}{dA}_n(s))\right] \\ +\frac{1}{n}\sum _{j:{\mathrm{\Delta }}_j{\epsilon }_j=2}\left[e^{{\beta }^T{Z}_j(X_{\ell })}{\int }_0^{\tau }𝟙(X_{\ell }\le t)𝟙(X_j\le u\le t){\stackrel{\sim }{w}}_j^{\ast }(t)e^{{\beta }^T{Z}_j(t)}{\mathcal{G}}^{″}({\int }_0^t{e}^{{\beta }^T{Z}_j(s)}{dA}_n(s)){dA}_n(t)\right] \end{gathered}$$

for ℓ ∈ {d + 1, …, d + k(n)} and ${\pi }_n(u)=n^{-1}{\sum }_{j=1}^n𝟙(X_j\ge u)$.