Precision Medicine

Abstract

Precision medicine seeks to maximize the quality of healthcare by individualizing the healthcare process to the uniquely evolving health status of each patient. This endeavor spans a broad range of scientific areas including drug discovery, genetics/genomics, health communication, and causal inference all in support of evidence-based, i.e., data-driven, decision making. Precision medicine is formalized as a treatment regime which comprises a sequence of decision rules, one per decision point, which map up-to-date patient information to a recommended action. The potential actions could be the selection of which drug to use, the selection of dose, timing of administration, specific diet or exercise recommendation, or other aspects of treatment or care. Statistics research in precision medicine is broadly focused on methodological development for estimation of and inference for treatment regimes which maximize some cumulative clinical outcome. In this review, we provide an overview of this vibrant area of research and present important and emerging challenges.

1. INTRODUCTION

The idea of improving health outcomes by tailoring treatment to individual patient characteristics is centuries old and remains a core component of medical practice. The scientific method began to impact medical treatment through the use of statistical inference by the late 1700s, but advances began to dramatically increase after the success of the first randomized controlled clinical trial, conducted by Austin Bradford Hill in 1946, which demonstrated the efficacy of streptomycin for treating tuberculosis (Stusser 2006). Following Hill’s trial was a period of rapid methodological progress in the design and analysis of clinical trials as well as observational studies. Systematic study of the integration of data, experience, and clinical judgment into the clinical decision process led to the concept of ‘evidence-based medicine’ wherein clinical decision making is based on (to the extent possible) empirical evidence with randomized controlled trials being a gold-standard for generating such evidence (Eddy 1990). However, the primary scientific aim in most clinical trials is the identification of the best treatment for a given disease area with any heterogeneity in patient characteristics or outcomes being viewed as a nuisance to the research process.

Awareness that patient heterogeneity was important in evaluating treatments–and not just a nuisance–began to emerge late in the 20th century, among both clinicians (Sorensen 1996) and biostatisticians (Longford and Nelder 1999). That patient heterogeneity implied the need to individualize therapy in the context of evidence-based medicine was nicely articulated in Kravitz et al (2004). These constituent concepts, combined together, yield the modern concept of precision medicine, the paradigm wherein patient heterogeneity is leveraged through data-driven approaches to improve treatment decisions so that the right treatment is given to the right patient at the right time. Precision medicine became a national priority with President Obama’s announcement of the Precision Medicine Initiative in his 2015 State of the Union Address (The White House 2015). We note that precision medicine is conceptually the same as stratified medicine (Lonergan et al 2017) and personalized medicine (Kosorok and Moodie 2016).

The goal of this paper is to provide a review of the current state-of-the-art in statistical research for precision medicine. The chief priority of statistical research in precision medicine is to use data to inform decision making in healthcare; thus, this encompasses a wide range of tasks including drug-discovery, biomarker identification, estimation and inference for causal treatment effects, modeling health communication and shared decision making, and study design. However, our focus in this review is on estimation and inference for treatment regimes which prescribe interventions based on individual patient characteristics. An estimated optimal treatment regime might be used as part of a decision support system within a healthcare organization or to generate new clinical hypotheses for future study. Thus, it is critical that statistical methodology for precision medicine be rigorous, transparent, reproducible, and generalizable.

We view precision medicine as fitting within the broader concepts of precision public health and data-driven decision science. However, the focus on data-driven patient-centered care with its inherent challenges, e.g., patient heterogeneity, implementation cost, causal confounding, etc., distinguishes precision medicine as its own field of study. To this point, precision medicine has led to new methodologies and insights in semi-parametric modeling, causal inference, non-regular asymptotics, clinical trial design, and machine learning (see Murphy 2003; Robins 2004; Chakraborty and Moodie 2013; Laber et al 2014; Zhao et al 2015a; Kosorok and Moodie 2016, and references therein). There have also been major advancements in genetics driven by the vision for precision medicine (see, e.g., Torkamani et al 2018); however, our focus will be broader in that while the biomarkers used to inform treatment selection could be genetic or genomic factors, we also allow that these could be demographic and physiological measurements, co-morbid conditions, individual patient preferences, lifestyle, and so on.

The remainder of the paper is as follows. In Section 2, we formalize the goals of precision medicine and catalog different decision settings. In Section 3, we discuss biomarker discovery as an important supporting task in constructing an optimal treatment regime. In Section 4, we review the methodological underpinnings of precision medicine including regression-based and direct-search estimation, managing multiple outcomes, and inference for estimated optimal regimes. We conclude with a summary and discussion of pressing open problems.

2. GOALS OF PRECISION MEDICINE

In this section, we formalize an optimal dynamic treatment regime and contrast estimation of an optimal regime with subgroup identification and causal effect estimation. We also discuss generalizations of the dynamic treatment regime framework and how decision problems in precision medicine fit into precision public health and data-driven decision science. Note that we view decision support—especially the estimation of optimal or near-optimal treatment regimes and those endeavors which directly support this—to be the primary goal of precision medicine. Accordingly, we view modeling the disease process per se to be of secondary importance in precision medicine, except when it is directly supportive of dynamic treatment regime discovery.

2.1. Discovering dynamic treatment regimes

As stated previously, the goal in precision medicine is to use data to improve decision making in healthcare. Dynamic treatment regimes formalize decision making as a sequence of decision rules, one per decision point, that map available information to a recommended intervention. The decision points may either be fixed in calendar time or driven by patient outcomes. Thus, the timing and number of decision points may be random and can vary considerably across patients in some application domains. Furthermore, the set of allowable interventions at any given time point may vary according to a patient’s health status, availability, or other factors (Bembom and van der Laan 2008; Schulte et al 2014; Laber and Staicu In press; Laber et al 2018); however, for simplicity, in describing methods for estimation and inference in Section 4, we will not do so in complete generality. We formalize the notion of an optimal treatment regime using the language of potential outcomes (Rubin 1978, 2005; Dawid 2015).

2.1.1. The single-decision setting.

In the single decision setting the observed data are assumed to be of the form ${\left\{\left(X_i,A_i,Y_i\right)\right\}}_{i=1}^n$ which comprise n i.i.d. triples (X, A, Y) where: $X\in \mathcal{X}$ denotes baseline patient characteristics; $A\in \mathcal{A}$ denotes the assigned treatment; and $Y\in ℝ$ denotes the outcome coded so that higher values are better. For each $x\in \mathcal{X}$ define $\psi \left(x\right)\subseteq \mathcal{A}$ to be the set of allowable treatments for a patient presenting with X = x. A dynamic treatment regime in this context is a map $d:\mathcal{X}\to \mathcal{A}$ which satisfies d(x) ∈ ψ(x) for all $x\in \mathcal{X}$; under d, patients presenting with X = x would be assigned treatment d(x). An optimal treatment regime yields the maximal mean outcome if applied to select treatments in the population of interest. Let Y* (a) denote the potential outcome under treatment $a\in \mathcal{A}$ and subsequently for any regime, d, define the potential outcome under d to be $Y^{*}\left(d\right)={\displaystyle \sum }_{a\in \mathcal{A}}{Y}^{*}\left(a\right)1_{\left\{d\left(X\right)=a\right\}}$. The optimal regime, say d^opt, satisfies: (i) d^opt(x) ∈ ψ(x) for all $x\in \mathcal{X}$; and (ii) EY* (d^opt) ≥ EY* (d) for all d such that d(x) ∈ ψ(x) and all $x\in \mathcal{X}$. There are other notions of optimality including maximizing quantiles of the outcome distribution (Linn et al 2017; Wang et al In press); maximizing efficacy subject to constraints on risk/harm (Linn et al 2015; Laber et al 2018; Wang et al In press); and maximizing the mean outcome subject to cost or logistical constraints (Luedtke and van der Laan 2016a; Lakkaraju and Rudin 2017).

The optimal dynamic treatment regime, d^opt, is defined in terms of potential outcomes; however, in order to construct an estimator of d^opt we need to identify it in terms of the data-generating model. In Section 4, we present causal conditions under which such identifiability holds. We note that the term ‘dynamic’ refers to the individualization of treatment to patient characteristics, not time; hence, the term ‘dynamic treatment regime’ is used even with a single decision point. One could also assume that the clinicians assigning treatment are already making nearly optimal choices, and thus a potentially good dynamic treatment is one obtained by mimicking the clinicians’ decisions Wallace et al (2018). We will consider this in Section 5 for the special case where physicians make the optimal decision at least for a small portion of the time.

2.1.2. The multi-decision setting.

In the multi-decision setting there are two or more opportunities for treatment change for some subset of the population. Examples include the treatment of small-cell lung cancer where two or more lines of chemotherapy may be required (Zhao et al 2011). A key concept in the multi-decision setting is that interventions can affect a patient’s health status in multiple ways including: (immediate effects) it may make an immediate impact on their health status; (moderating effects) it may generate information that is useful for subsequent decisions, e.g., failure to respond to a drug in a given class may indicate that other drugs belonging to the same class may also perform poorly; and (delayed effects) it may change the patient’s health status so as to set them up for future success, e.g., providing a patient with cognitive behavioral therapy at one stage may allow them to reap greater benefits from tele-therapy at later time points. Thus, applying a treatment that leads to a suboptimal proximal effect may lead to better longterm outcomes if there are strong delayed or prognostic effects (Thall et al 2007; Kidwell 2016).

In the multi-decision setting, we assume that the observed data are of the form ${\left\{\left(X_{1,i},A_{1,}{}_i,Y_{1,i},\dots ,X_{T,i},A_{T,i},Y_{T,i}\right)\right\}}_{i=1}^n$ which comprise n i.i.d. replicates of (X₁, A₁, Y₁, … , X_T, A_T, Y_T) where: $X_1\in {\mathcal{X}}_1$ denotes baseline information and $X_t\in {\mathcal{X}}_t$ denotes interim information collected during the course of the stage t − 1 treatment for t = 2, …, T; $A_t\in {\mathcal{A}}_t$ denotes the assigned treatment; and Y_t denotes a proximal outcome measured after the treatment at stage t for t = 1, … , T . Define H₁ = X₁ and H_t = (H_t−1, A_t−1, Y_t−1, X_t) so that H_t is the available patient history at time t. Let ${\mathcal{H}}_t=dom{H}_t$ and let ${\psi }_t\left(h_t\right)\subseteq {\mathcal{A}}_t$ denote the set of allowable treatments for a patient presenting with H_t = h_t at time t. A dynamic treatment regime in this setting is a sequence of functions d = (d₁, … , d_T) such that $d_t:{\mathcal{H}}_t\to {\mathcal{A}}_t$ satisfies d_t(h_t) ∈ ψ_t(h_t) for all h_t for t = 1, … , T. An optimal treatment regime maximizes the expectation of some (prespecified) cumulative outcome measure Y = y(Y₁, … , Y_T ), e.g., $y\left({\upsilon }_1\dots ,{\upsilon }_T\right)={\displaystyle \sum }_{t=1}^T{\upsilon }_T$ or y(v₁, … , v_T ) = max_t v_t, or y(v₁, … , v_T ) = v_T, etc.

Interventions applied at time t affect both the proximal outcomes Y_t and interim measurements X_t+1; thus, to define the optimal treatment regime we need to consider both potential proximal outcomes and potential interim measurements. We use an overline to denote history so that ${\overline{a}}_t=\left(a_1,\dots ,a_t\right)$. Define $X_t^{*}\left({\overline{a}}_{t-1}\right)$ to be the potential interim measurements at time t under treatment sequence ${\overline{a}}_{t-1}\in {\mathcal{A}}_1\times \cdots \times {\mathcal{A}}_{t-1}$, where products of sets are interpreted as cartesian products, and define $Y_t^{*}\left({\overline{a}}_t\right)$ to be the potential proximal outcome under ${\overline{a}}_t\in {\mathcal{A}}_1\times \cdots \times {\mathcal{A}}_t$. The potential outcome under ${\overline{a}}_T\in {\mathcal{A}}_1\times \cdots \times {\mathcal{A}}_T$ is therefore $Y^{*}\left({\overline{a}}_T\right)=y\left\{Y_1^{*}\left(a_1\right),Y_2^{*}\left({\overline{a}}_2\right),\dots ,Y_T^{*}\left({\overline{a}}_T\right)\right\}$. For any regime, d, the potential outcome is

$$Y^{*}\left(d\right)={\displaystyle \sum _{{\overline{a}}_T}{Y}^{*}\left({\overline{a}}_T\right){\displaystyle \prod _{t=1}^T{1}_{\left[d_t\left\{H_t^{*}\left({\overline{a}}_{t-1}\right)\right\}=a_t\right]}},}$$

where we have defined $H_1^{*}\left(a_0\right)\equiv H_1$ and 1_B is the indicator of B. An optimal regime, d^opt, satisfies: (i) $d_t^{opt}\left(h_t\right)\in {\psi }_t\left(h_t\right)$ for all $h_t\in {\mathcal{H}}_t$ and t = 1,…,T; and (ii) EY*(d^opt) ≥ EY* (d) for all d satisfying d_t(h_t) ∈ ψ_t(h_t) for all $h_t\in {\mathcal{H}}_t$ and t = 1, … , T.

As in the single-decision setting, the optimal regime is defined in terms of potential outcomes and is only identifiable in terms of the data-generating model under additional assumptions; we discuss such assumptions in Section 4. The preceding development assumes that future patients will be treated over the same time horizon as the patients in the sample; however, this need not be the case. In some settings, e.g., diabetes (Ertefaie 2015; Luckett et al 2017) or cystic fibrosis (Tang and Kosorok 2012), interventions are applied over an indefinite time horizon. This structure would also be applicable to precision screening for cancer (Olsen and Lund 2017), among other applications. Thus, the objective in these settings is often to estimate a treatment regime that can potentially be applied beyond the time horizon over which the training data are collected. Such extrapolation typically requires additional structure to be imposed on the data generating model; a common assumption is that the decision process is (perhaps after some suitable transformation) heterogeneous and Markov (Puterman 2005). We discuss this further in Section 4.

2.1.3. Other decision settings.

The decision settings described above assume: (S1) the observed data consist of i.i.d. replicates; (S2) the data-generating model is fixed and indifferent to the actions of the decision maker; and (S3) the observed data are used to construct treatment regimes for application with yet unobserved future patients. However, these assumptions may need to be relaxed in some application domains. For example, in the context of managing the spread of an emerging infectious disease over a network of individuals, spatial dependence and spillover effects preclude treating the individuals as independent replicates; furthermore, in this setting, one must manage the disease in real-time (Laber et al In press). Thus, neither (S1) nor (S3) hold in this setting. In the context of adversarial decision making wherein one faces an intelligent (and adaptive) opponent, the data-generating model can change in response to the decision makers actions, e.g., imagine playing poker repeatedly against the same shrewd player (Cesa-Bianchi and Lugosi 2006).

There are potentially other decision settings not covered by the above structures, however, the methods and ideas presented in this review are readily extensible to new domains. There are also additional complications associated with estimation of optimal treatment regimes that occur more generally in statistical modeling and thus we will not discuss them here; e.g., missing data (Shortreed et al 2011; Shortreed and Moodie 2012; Shortreed et al 2014; Kosorok and Moodie 2016); measurement error (Shani et al 2013), and model-building (Biernot and Moodie 2010; Rich et al 2010; Henderson et al 2010; Gunter et al 2011; Lu et al 2013; Laber et al 2014; Song et al 2015; Luedtke and van der Laan 2016b).

2.2. Treatment effect estimation and subgroup identification

Estimation of an optimal treatment regime is closely related to subgroup identification and estimation of the conditional average treatment effect (CATE). For simplicity, we use a single-decision problem with binary treatments, so that the data for a generic subject are (X, A, Y ), where $X\in \mathcal{X}\subseteq {ℝ}^p$ denotes baseline patient information; $A\in \mathcal{A}=\left\{-1,1\right\}$ denotes the assigned treatment; and $Y\in ℝ$ denotes the outcome coded so that higher values are better. We assume that $\psi \left(x\right)\equiv \mathcal{A}$ for all $x\in \mathcal{X}$. In this setup, the CATE is defined as Δ(x) = E {Y*(1) – Y*(−1)|X = x}. For any regime d it can be seen that

$$\begin{gathered} E{Y}^{*}\left(d\right)=E\left[Y^{*}\left(1\right)1_{\left\{d\left(X\right)=1\right\}}+Y^{*}\left(-1\right)1_{\left\{d\left(X\right)=-1\right\}}\right] \\ =E\left\{Y^{*}\left(1\right)-Y^{*}\left(-1\right)\right\}{1}_{\left\{d\left(X\right)=1\right\}}+E{Y}^{*}\left(-1\right) \\ =E\Delta \left(X\right)1_{\left\{d\left(X\right)=1\right\}}+E{Y}^{*}\left(-1\right) \\ \le E\Delta \left(X\right)1_{\left\{\Delta \left(X\right)>0\right\}}+E{Y}^{*}\left(-1\right) \\ =E\left[Y^{*}\left(1\right)1_{\left\{\Delta \left(X\right)>0\right\}}+Y^{*}\left(-1\right)1\left\{\Delta \left(X\right)\le 0\right\}\right], \end{gathered}$$

whence it can be seen that d^opt(x) = sign {Δ(x)}is optimal, where sign(x) = ±1 according to whether x > 0 or < 0. Thus, a natural approach to estimating an optimal treatment regime in this context is to first construct an estimator ${\widehat{\Delta }}_n\left(x\right)$ of Δ(x) and subsequently to use the plug-in estimator ${\widehat{d}}_n\left(x\right)=sign\left\{{\widehat{\Delta }}_n\left(x\right)\right\}$ of d^opt(x); we discuss this approach in more detail in Section 4. We note this can be developed for more than two treatments, but we focus here on two treatment for simplicity.

Subgroup identification seeks to find a subgroup in the target population with an en hanced treatment effect; sometimes this is referred to as finding ‘the right patient for the right treatment.’ Given a threshold, $\eta \in ℝ$, one way to operationalize a subgroup is through the level set $\mathcal{T}(\eta )=\{x\in \mathcal{X}:\Delta (x)\ge \eta \}$. Thus, one could estimate this level set using the plug-in estimator ${\widehat{\mathcal{T}}}_n(\eta )=\{x\in \mathcal{X}:{\widehat{\Delta }}_n(x)\ge \eta \}$, where ${\widehat{\Delta }}_n(x)$ is an estimator of Δ(x). We note that while much of clinical research focuses on estimating the CATE, precision medicine seeks to go further by tailoring treatments to subgroups (as reflected in x) to benefit each subgroup and thereby further benefit the population on average.

To illustrate the differences between estimation of an optimal treatment regime, estimation of the CATE, and subgroup identification consider the following generative model: X ~ Normal(0, τ²), A ⊥ X and A ~ Uniform (−1, 1}, ∈ ⊥ (X, A), ∈ ~ Normal(0, σ²), and Y = g(X, A) + ∈, where $g(X,A)=\text{exp}({\alpha }_0^{*}+{\alpha }_1^{*}A+{\alpha }_2^{*}X+{\alpha }_3^{*}AX\text{)}$ and ⊥ denotes independence. The optimal treatment can be seen to equal $d^{\text{opt}}(x)=\text{sign}\text{{}{\alpha }_1^{*}+{\alpha }_3^{*}X\text{}}$, the CATE is given by $g(x,1)-g(x,-1)=\text{exp}\text{{}\text{exp}\text{{}{\alpha }_0^{*}+{\alpha }_1^{*}+({\alpha }_2^{*}+{\alpha }_3^{*})x\text{}\hspace{0.17em}}-\text{exp}\text{{}\text{exp}\text{{}{\alpha }_0^{*}-{\alpha }_1^{*}+({\alpha }_2^{*}-{\alpha }_3^{*})x\text{}}$, the subgroup corresponding to the level-set with threshold η is given by $\mathcal{T}(\eta )=\{x\in ℝ:g(x,1)-g(x,-1)\ge \eta \}$ which, provided it is nonempty, is an interval [ℓ, u] with −∞ ≤ ℓ ≤ u ≤ ∞. The optimal regime in this toy example is linear. Suppose that one attempted to estimate an optimal linear decision rule by postulating a linear model of the form g(x, a; β) = β₀ + β₁a + β₂x + β₃ax so that Δ(x; β) = 2β₁ + 2 β₃x which is to be estimated using least squares. It can be shown that the projection of g(x, a) onto g(x, a; β) is given by g(x, a; β*), where

$$\begin{gathered} {\beta }_0^{*}=\frac{1}{2}\exp \left\{{\alpha }_0+{\alpha }_1+\frac{{\left({\alpha }_2+{\alpha }_3\right)}^2{\tau }^2}{2}\right\}+\frac{1}{2}\exp \left\{{\alpha }_0-{\alpha }_1+\frac{{\left({\alpha }_2-{\alpha }_3\right)}^2{\tau }^2}{2}\right\} \\ {\beta }_1^{*}=\frac{1}{2}\exp \left\{{\alpha }_0+{\alpha }_1+\frac{{\left({\alpha }_2+{\alpha }_3\right)}^2{\tau }^2}{2}\right\}-\frac{1}{2}\exp \left\{{\alpha }_0-{\alpha }_1+\frac{{\left({\alpha }_2-{\alpha }_3\right)}^2{\tau }^2}{2}\right\} \\ {\beta }_2^{*}=\frac{\left({\alpha }_2+{\alpha }_3\right)}{2}\exp \left\{{\alpha }_0+{\alpha }_1+\frac{{\left({\alpha }_2+{\alpha }_3\right)}^2{\tau }^2}{2}\right\}+\frac{\left({\alpha }_2-{\alpha }_3\right)}{2}\exp \left\{{\alpha }_0-{\alpha }_1+\frac{{\left({\alpha }_2-{\alpha }_3\right)}^2{\tau }^2}{2}\right\} \\ {\beta }_3^{*}=\frac{\left({\alpha }_2+{\alpha }_3\right)}{2}\exp \left\{{\alpha }_0+{\alpha }_1+\frac{{\left({\alpha }_2+{\alpha }_3\right)}^2{\tau }^2}{2}\right\}-\frac{\left({\alpha }_2-{\alpha }_3\right)}{2}\exp \left\{{\alpha }_0-{\alpha }_1+\frac{{\left({\alpha }_2-{\alpha }_3\right)}^2{\tau }^2}{2}\right\}. \end{gathered}$$

Thus, it can be seen that β^*can be far from α^* and subsequently the linear rule obtained by estimating g(x, a) with a linear model need not lead to a high-quality linear decision rule, e.g., if τ = 1 and α^*= (4.176, 1.720, −4.704, 0.320)^T then the optimal rule $d^{\text{opt}}(x)=\text{sign}\text{{}{\alpha }_1^{*}+{\alpha }_3^{*}x\text{}}$ and the rule $\text{sign}\text{{}\Delta (x;{\beta }^{*}\text{)}\hspace{0.17em}=\hspace{0.17em}}\text{sign}({\beta }_1^{*}+{\beta }_3^{*}x\text{)}$ disagree on more than 60% of the population.

2.3. Dynamic data-driven decision science

Estimation of an optimal treatment regime is an example of a reinforcement learning problem in that one must learn about optimal decision making using data on the interactions between one or more decision makers and the environment. There is an expansive literature on reinforcement learning in computer science and engineering (e.g., Sutton and Barto 1998; Si 2004; Powell 2007; Szepesvari 2010; Busoniu et al 2010). This literature was developed with a focus on algorithmic efficiency, computational scalability, and empirical performance; state-of-the-art reinforcement learning algorithms are expected to identify complex and subtle patterns from massive data sets. In contrast, in the precision medicine literature, methodology was developed with a focus on casual validity, generalizability, and interpretability within a domain context; state-of-the-art methodologies for precision medicine are expected to be transparent, rigorous, and to generate new scientific knowledge from (relatively) small data sets. However, cross-pollination is rapidly increasing due to technological advancements facilitating the collection and curation of massive amounts of patient-level data in real (or near-real) time and the emergence of mobile-health (Tewari and Murphy 2017; Nahum-Shani et al 2017; Luckett et al 2017).

Precision medicine is also closely connected with control theory and operations research. Within these areas there is a rich history of modeling the underlying system dynamics (i.e., the generative model) and using simulation-optimization to inform decision making; standard texts include Hillier (1990) and Macia and Thaler (2005). Introducing stochasticity into dynamic systems to address various forms of uncertainty has led to many rich developments in stochastic differential equations (Nisio 2015) and in Markov Decision Processes (Puterman 2005). Simulation-based approaches which use interactions between complex agents, such as agent-based modeling, have also been developed which allow for studying situations of greater complexity than normally achievable through systems of mathematical equations (Wilensky and Rand 2015). These approaches can be effective when there is rich scientific theory to inform the construction of the underlying models; however, such information is rarely available in the context of precision medicine making these methods diffcult to apply directly.

3. BIOMARKERS

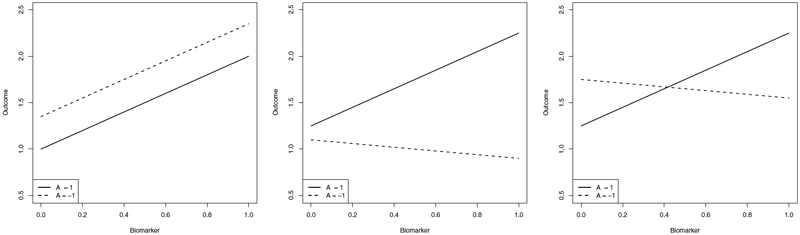
In precision medicine research a common clinical goal is the identification of patient biomarkers that are important for choosing an optimal treatment. We use the term biomarker generically to represent a scalar feature constructed from current patient information; thus, a biomarker could be a single component of the available history or a composite measurement constructed from multiple components. A biomarker may provide valuable clinical information by being: (i) prognostic, i.e., the biomarker is useful in predicting the mean outcome of a patient; (ii) moderating, i.e., the biomarker is useful for predicting contrasts of the mean outcome across different candidate treatments; and (iii) prescriptive, i.e., the biomarker is useful in selecting the treatment that maximizes the mean outcome (see Teran Hidalgo et al 2016, for additional refinements on biomarker classification). We focus here on the mean for simplicity, but other distributional summaries, such as the median, could also be used. Figure 1 shows conceptual schematics for each of the three biomarker types. Below we formalize these notions and show that they are nested so that prescriptive biomarkers are moderating and prognostic while moderating biomarkers are prognostic but need not be prescriptive. We focus on the single-decision setting; analogs for the multi-decision setting can be derived based on the approximate dynamic programming methods described in Section 4.

Figure 1.

Left: schematic for a prognostic biomarker. Center: schematic for a moderating biomarker. Right: schematic for a prescriptive biomarker.

3.1. Prognostic biomarkers

Consider the single-decision binary treatment setting with $A\in \mathcal{A}=\{-1,1\}$ Then it follows that E {Y*(a)|X = x} = μ(x) + aΔ(x)/2, where μ(x) = E {Y*(1) + Y* (−1)|X = x}. We note that these ideas can be generalized to more than two treatments, but we restrict ourselves here to the two treatment situation for ease of exposition. To illustrate key concepts, we first assume models of the form $\mu (x;{\beta }_0^{*})=x^{⊺}{\beta }_0^{*}$ and $\Delta (x;{\beta }_1^{*})=x^{⊺}{\beta }_1^{*}$ and biomarkers under consideration are the components of X = (X₁, … , X_p)^T; a more general definition is given below. Under this model, the biomarker X_j is a prognostic biomarker if either ${\beta }_{0,j}^{*}$ or ${\beta }_{1,j}^{*}$ is not zero. Under the causal conditions presented in Section 4, one can estimate the vectors ${\beta }_0^{*}$ and ${\beta }_1^{*}$ using ordinary least squares and whether a biomarker is prognostic using standard methods. The regression features found in many predictive models in medical research, such as, for example, a Cox regression model used to predict survival of non-Hodgkin’s lymphoma patients (Non-Hodgkin’s Lymphoma Prognostic Factors Project 1992), are examples of prognostic biomarkers.

Now consider the setting where one has a set of candidate biomarkers $\mathcal{B}=\{B_j:j=1,\dots ,q\}$ where $B_j=B_j(X)\in ℝ$ is a possible composite summary of X.For any $\mathcal{J}\subseteq \{1,\dots ,q\}$, we say that $\mathcal{J}$ is sufficient for prognosis if $\sigma \{\mu (X),\Delta (X)\}\subseteq \sigma \{B_j:j\in \mathcal{J}\}$, where σ(U) denotes the σ-algebra generated by U. We define a set of biomarkers, $\mathcal{J}$, to be minimal sufficient for prognosis if it is sufficient for prognosis and $\#\mathcal{J}\le \#{\mathcal{J}}^{\prime }$ for any other sufficient set ${\mathcal{J}}^{\prime }$, where $\#\mathcal{B}$ denotes the number of elements in $\mathcal{B}$.We define a biomarker B_j to be prognostic if $j\in \mathcal{J}$ for some minimal sufficient set $\mathcal{J}$. As in the linear setting, a general approach to identifying predictive biomarkers is to model μ(x) and Δ(x) as functions of the candidate markers and to apply standard methods for variable selection. One could also use methods for feature construction in regression to identify the set of candidate features $\mathcal{B}$ (Cook and Ni 2005; Li 2007; Lee and Verleysen 2007).

3.2. Moderating biomarkers

Moderating biomarkers are predictive of the contrast between two treatments. In the linear model example, where $\mu (x;{\beta }_0^{*})=x^{⊺}{\beta }_0^{*}$ and $\Delta (x;{\beta }_1^{*})=x^{⊺}{\beta }_1^{*}$ we say that X_j is a moderating biomarker if ${\beta }_{1,j}^{*}$ is not zero. Thus, it can be seen immediately that a moderating biomarker is also prognostic. As with identifying prognostic biomarkers, under appropriate causal conditions, one can use ordinary least squares to estimate ${\beta }_1^{*}$ and test whether ${\beta }_{1,j}^{*}$ is zero to identify moderating biomarkers. Under the postulated linear model with unbounded biomarkers, every moderating biomarker is also prescriptive; however, this does not hold in general. In the more general setting with candidate biomarkers $\mathcal{B}=\{B_j:j=1,\dots ,q\}$ we say that subset of biomarkers $\mathcal{J}\subseteq \{1,\dots ,q\}$ is sufficient for moderation if $\sigma \{\Delta (X)\}\subseteq \sigma \{B_j:j\in \mathcal{J}\}$ and furthermore minimal sufficient if $\#\mathcal{J}\le \#{\mathcal{J}}^{\prime }$ for any other sufficient set ${\mathcal{J}}^{\prime }$.

3.3. Prescriptive biomarkers

To illustrate the difference between moderating and prescriptive biomarkers, consider the model $\Delta (x;{\beta }_1^{*},{\beta }_2^{*})=\text{exp}(x^{⊺}{\beta }_2^{*})x^{⊺}{\beta }_1^{*}$ and suppose that the support of X is ${ℝ}^p$. Then we say that X_j is a prescriptive biomarker if ${\beta }_{1,j}^{*}$ is not zero. It can be seen that if ${\beta }_{1,j}^{*}$ is zero but ${\beta }_{2,j}^{*}$ is nonzero then X_j is moderating but not prescriptive. More generally, under the setting with candidate biomarkers $\mathcal{B}=\{B_j:j=1,\dots ,q\}$ we say that $\mathcal{J}\subseteq \{1,\dots ,q\}$ is sufficient for prescription if $\sigma [\text{sign}\{\Delta (X)\}]\subseteq \sigma (B_j:j\in \mathcal{J})$ and we say that $\mathcal{J}$ is minimally sufficient for prescription it if further satisfies $\#\mathcal{J}\le \#{\mathcal{J}}^{\prime }$ for all sufficient ${\mathcal{J}}^{\prime }$.The identification of prescriptive biomarkers has been studied as a subtopic within precision medicine with early approaches seeking to identify ‘qualitative interactions’ (Gail and Simon 1985; Gunter et al 2011) and more recent approaches focused on identification of variables that are informative for identification of an optimal treatment regime (Song et al 2015; Zhang and Zhang 2016; Fan et al 2016).

A concrete example of both moderating and prescriptive biomarkers can be found in Gail and Simon (1985) who analyze data from the National Surgical Adjuvant Breast and Bowel Project (Fisher et al 1983). They find that a patient’s age and progesterone receptor level (PR) are informative of the effect of adding tamoxifen to chemotherapy. Thus both age and PR are moderating biomarkers. Now define the composite biomarker D to be 1 if both age< 50 and PR< 10 and to be −1 otherwise. Gail and Simon found that if D = 1, tamoxifen should be added, but it should not be added otherwise. In this setting D is both a moderating and a prescriptive biomarker. We note that the FDA identifies a biomarker as predictive if it is predictive of the contrast between active treatment and a control; thus, a predictive variable is prescriptive for a contrast involving a control (FDA-NIH Biomarker Working Group 2016).

4. ESTIMATING DYNAMIC TREATMENT REGIMES

4.1. The single-decision setting

In the single-decision setting, as described in section 2.1.1., the goal is to estimate a regime, d^opt, that satisfies EY* (d^opt) ≥ EY^* (d) for any other regime d. In order to construct an estimator, we need to express d^opt in terms of the data-generating model. To do this, we make the following assumptions: (i) positivity, P (A =a |X = x) > 0 for all a ∈ ψ(x) for all $x\in \mathcal{X}$; (ii) consistency, Y = Y* (A); and (iii) strong ignorability, $\{Y^{*}(a):a\in \mathcal{A}\}\perp A|X$. These assumptions are standard (Kidwell 2016) though they are not as general as possible (Robins et al 2000; Petersen et al 2012).

Define Q(x, a) = E(Y|X = x, A = a), then under the preceding assumptions, d^opt(x) = arg max _a∈ψ(x) Q(x, a) is an optimal regime. This immediately suggests a regression-based estimator wherein one first constructs an estimator ${\widehat{Q}}_n(x,a)$ of Q(x, a) and subsequently uses the plug-in estimator ${\widehat{d}}_n(x)=\text{\hspace{0.17em}arg\hspace{0.17em}}{\text{max}}_{a\in \psi (x)}{\widehat{Q}}_n(x,a)$. For example, one might posit a linear model of the form $Q(x,a;\beta )={\displaystyle {\sum }_{a^{\prime }\in \mathcal{A}}{x}_{a^{\prime }}^{⊺}{\beta }_{a^{\prime }}}1\{a=a^{\prime }\}=x_a^{⊺}{\beta }_a$, where $\beta =\{{\beta }_a:a\in \mathcal{A}\}$ and x_a, $a\in \mathcal{A}$ are features of x. Define ${\mathbb{P}}_n$ to be the empirical measure. Let ${\widehat{\beta }}_n=\text{\hspace{0.17em}arg\hspace{0.17em}}{\text{min}}_{\beta }{\mathbb{P}}_n{\{Y-Q(X,A;\beta )\}}^2$ and subsequently ${\widehat{Q}}_n(x,a)=Q(x,a;{\widehat{\beta }}_n)$ so that the plug-in estimator is ${\widehat{d}}_n(x)=\text{\hspace{0.17em}arg\hspace{0.17em}}{\text{max}}_{a\in \psi (x)}Q(x,a;{\widehat{\beta }}_n)=\text{\hspace{0.17em}arg\hspace{0.17em}}{\text{max}}_{a\in \psi (x)}{x}_a^{⊺}{\widehat{\beta }}_{a,n}$. Linear models are commonly used because they are regarded as being easy to interpret, e.g., the coefficients of ${\widehat{\beta }}_{a,n}$ can be used to identify what biomarkers are likely to impact a patient’s outcome under treatment a. However, while linearity lends itself to interpretation, this may come at the cost of misspecification; thus, as with any regression model, one should apply model diagnostics and interactive model-building techniques to ensure a high-quality model.

To mitigate misspecification, one can use a flexible class of models to estimate Q(x, a), e.g., trees (Taylor et al 2015; Zhang et al 2012b), boosting (Kang et al 2014), generalized additive models (Moodie et al 2014), or non-linear basis expansions (Qian and Murphy 2011). However, using a flexible model for Q(x, a) can render the estimated rule $x\mapsto \arg {\max }_{a\in \psi (x)}{\widehat{Q}}_n(x,a)$ unintelligible—thereby obscuring the scientific content of the estimated regime and limiting its value as a decision support tool. This issue led to the development of regression-based policy-search methods wherein the class of regimes is decoupled from the class of estimators used for Q(x, a). For any regime d it follows under the preceding causal conditions that EY^* (d) = EQ {X, d(X)}; thus, if $\mathcal{D}$ is a pre-specified class of regimes then the optimal within this class is $d_{\mathcal{D}}^{\text{opt}}=\arg {\max }_{d\in \mathcal{D}}EQ\left\{X,d(X)\right\}$ Let ${\widehat{Q}}_n(x,a)$ be an estimator of Q(x, a) then the plug-in estimator of $d_{\mathcal{D}}^{\text{opt}}\text{\hspace{0.17em}is\hspace{0.17em}}{\widehat{d}}_{\mathcal{D},n}=\arg {\max }_{d\in \mathcal{D}}{\mathbb{P}}_n{\widehat{Q}}_n\left\{X,d(X)\right\}$Because the class $\mathcal{D}$ is chosen independently of the class of models for Q(x, a), one can use nonparametric regression estimators while maintaining control of the form of the estimated optimal regime. Furthermore, because this approach is built upon regression, it is easily extensible to settings with complex data structures, censored data, measurement error or other settings for which regression models have been developed.

Regression-based estimators were derived from a regression based representation of the optimal treatment regime, an alternative representation based on importance sampling leads to another class of estimators termed direct-search or classification-based estimators. For simplicity, we assume that treatment is binary and coded so that$A\in \mathcal{A}=\left\{-1,1\right\}$. Under the causal conditions stated above, the marginal mean outcome under a regime d is

$$V\left(d\right)\triangleq E{Y}^{*}\left(d\right)=E\left\{\frac{Y{1}_{d\left(X\right)=A}}{\pi \left(A;X\right)}\right\},$$

where π(a; x) = P (A = a|X = x) is the propensity score (Qian and Murphy 2011). Thus, the optimal regime satisfies d^opt = arg max_d V (d). Given an estimator${\widehat{\pi }}_n(a;x)of\text{\hspace{0.17em}π(}a;x\text{)}$, which might be obtained using logistic regression, the inverse probability weighted estimator of V (d) is given by ${\widehat{V}}_n(d)={\mathbb{P}}_n\{Y{1}_{d(X)=A}/{\widehat{\pi }}_n(A;X)\}$ Given a class of regimes, $\mathcal{D}$, one could construct an estimator of $d_{\mathcal{D}}^{\text{opt}}$ by direct maximization, i.e.,${\widehat{d}}_{\mathcal{D},n}=\arg {\max }_{d\in \mathcal{D}}{\widehat{V}}_n(d)$; however, because of the discontinuous indicator function, direct optimization is not computationally feasible save for settings where $\mathcal{D}$ is small. However, it can be see that

$$V\left(d\right)=-E\left\{\frac{\left|Y\right|1_{Asign\left(Y\right)d\left(X\right)<0}}{\pi \left(A;X\right)}\right\}+E\left\{\frac{\left(Y\right)+}{\pi \left(A;X\right)}\right\},$$

where sign(u) = 1_u>0 − 1_u<0 is the sign function and (u)₊ = max(0, u) is the positive part function. Thus, given a class of regimes, $\mathcal{D}$, the optimal regime within this class satisfies

$$d_D^{opt}=\arg \underset{d\in D}{\min }E\left\{\frac{\left|Y\right|1_{Asign\left(Y\right)d\left(X\right)<0}}{\pi \left(A;X\right)}\right\},$$

hence, it can be seen that $d_{\mathcal{D}}^{\text{opt}}$ minimizes a cost-sensitive classification problem (Elkan 2001; Zadrozny et al 2003; Zhou and Liu 2006; Pires et al 2013) with cost function |Y|/π(A; X), class label A sign(Y), and input$X\in \mathcal{X}$, over the set of classifiers $\mathcal{D}$ (see Zhao et al 2012; Zhang et al 2012a,b). Thus, one can estimate $d_{\mathcal{D}}^{\text{opt}}$ by applying off-the-shelf classification algorithms using the estimated cost $\left|Y\right|/{\widehat{\pi }}_n(A;X)$ in place of |Y|/π(A; X); for a discussion of converting cost-sensitive classification problems into standard (i.e., constant cost) classification problems see (Zadrozny 2003 and references therein). Outcome Weighted Learning (OWL, Zhao et al 2012) uses this framework with support vector machines (see, e.g., Chapter 12 of Hastie et al 2009) to estimate an optimal treatment regime; convergence rates for OWL were among the first to establish the mathematical underpinnings of direct-search estimation for optimal treatment regimes and led to a series of refinements including residual outcome weighted learning (Laber and Zhao 2015; Wang et al 2016; Zhou et al 2017) and improved bounds based on efficiency theory (Athey and Wager 2017). More generally, policy-search methods based on maximizing an estimator ${\widehat{V}}_n(d)ofV(d)$ over a prespecified class of regimes have been extended to a wide range of settings including: ordinal treatments (Chen et al In press); right-censored outcomes (Zhao et al 2015b; Cui et al 2017) (see also (Bai et al 2017)); continuous treatments (Laber and Zhao 2015; Chen et al 2016b; Kallus 2018); and high-dimensional data (Song et al 2015; Jeng et al 2018).

4.2. The multi-decision setting

The multi-decision setting is complicated by the need to account for delayed treatment effects and prognostic effects, e.g., information gain that improves decision making at subsequent decision points. We consider two multi-decision settings: (i) a finite time horizon wherein the number of decision points is small and finite; and (ii) an indefinite time horizon wherein the number of decision points is large or indeterminate. There are, of course, many intermediate settings but these two encompass many commonly encountered settings in precision medicine. The methods we discuss apply to both observational and randomized studies.

4.2.1. Finite time horizon.

In the finite horizon setting, we can estimate the optimal dynamic treatment regimes through a variety of reinforcement learning techniques, including G-estimation (Robins 2004; Stephens 2016), Q- and A- learning (for an overview of these methods, see Schulte et al 2014, wherein G-learning is articulated as a special case of A-learning), modeling of the entire longitudinal process (Xu et al 2016), several extensions of outcome weighted learning (Zhao et al 2015a), among other approaches. Recall that in precision medicine, we are primarily interested in estimating the decision rule, and, in many settings, it is much more robust and feasible to not model the entire process if possible. Many of the learning methods listed above were motivated, at least in part, to obtain the dynamic treatment regime without needing to model the full process. Early seminal work in estimating dynamic treatment regimes includes (Robins 1986), (Robins 1997), (Murphy et al 2001), (van der Laan et al 2001), (Murphy 2003), and (Robins 2004). Because of its flexibility and relative ease in implementation, we will present Q-learning in some detail, followed by a brief discussion of OWL and several related methods, but we will not further discuss other approaches here.

As in the single-decision setting, we will derive regression-based and inverse-weighting or classification-based representations of the optimal treatment regime in terms of the data-generating model and subsequently use these representations to construct estimators of the optimal regime. Using the notation of Section 2.1.1, we make the following assumptions: (i) positivity, P (A_t = a_t|H_t = h_t) > 0 for all$a_t\in {\psi }_t\text{and\hspace{0.17em}}{h}_t\in {\mathcal{H}}_t$; (ii) consistency, $H_t=H_t^{*}({\overline{A}}_{t-1})$ for t = 2,…,T and and$Y=Y^{*}({\overline{A}}_T)$; and (iii) sequential ignorability$\{Y^{*}({\overline{a}}_T),H_T^{*}({\overline{a}}_{T1},\mathrm{...},H_2^{*}(a_1),H_1:{\overline{a}}_T\in {\otimes }_{t=1}^T{\mathcal{A}}_t)\}\perp A_t|H_t$t =1,…,T, where ⊗ denote cartesian product taken over the specified range of indices; see Schulte et al (2014) for additional discussion of these assumptions.

Define Q_T(h_T, a_T) = E (Y|H_T = h_T, A_T = a_T) and for t = T − 1, … , .1 define Q_t(h_t, a_t) = E {max_at+1 Q_t+1(H_t+1, a_t+1)|H_t = h_t, A_t = a_t} then it follows from dynamic programming (Bellman 1957) that

$$d_t^{opt}\left(h_t\right)=\arg \underset{a_t\in {\psi }_t\left(h_t\right)}{\min }{Q}_t\left(h_t,a_t\right),$$ 1.

which we term the regression-based representation of the optimal regime. Q-learning is an approximate dynamic programming algorithm based on (1) which proceeds as follows. Construct an estimator ${\widehat{Q}}_{T,n}(h_T,a_T)of{Q}_T(h_T,a_T)$ obtained by regressing Y on H_T and A_T, subsequently for t = T − 1, … , 1 let ${\widehat{Q}}_{t,n}(h_t,a_t)$ be an estimator of Q_t(h_t, a_t) obtained by regressing ${\max }_{a_{t+1}\in {\psi }_{t+1}(H_{t+1})}{\widehat{Q}}_{t+1,n}(H_{t+1,a_{t+1}})$ on H_t and A_t. The Q-learning estimator of d^opt is thus ${\widehat{d}}_{t,n}(h_t)=argma{x}_{a_t\in {\psi }_t(h_t)}{\widehat{Q}}_{n,t}(h_t,a_t)$for t=1,…,T (Murphy 2005b; Schulte et al 2014).

Because Q-learning relies on a series of regression models, it is easily extensible to a variety of models and data structures (Zhao et al 2009; Goldberg and Kosorok 2012; Moodie et al 2014) and allows the user to interactively construct and critique the models used for the Q-functions (Rich et al 2010; Laber et al 2014). However, as in the single-decision setting, in the above formulation the estimated optimal decision rule is tied to the class of models used for the Q-functions; thus, one may be forced with an unpleasant trade-off between severe model misspecification and an unintelligible black box. Instead one can use Q-learning with policy-search wherein the class of regimes is divorced from the class of models for the Q-functions (see Zhang et al In press; Laber et al 2018). An alternative representation of the optimal decision rule is based on inverse probability weighting. For any regime, d, it follows that

$$V\left(d\right)=-E\left(Y{\displaystyle \prod _{t=1}^T\frac{1_{d_t\left(H_t\right)=A_t}}{{\pi }_t\left(A_t|H_t\right)}}\right).$$

Thus, given estimators${\widehat{\pi }}_{t,n}(a_t;h_t)of{\text{π}}_t(a_t;h_t\text{)}$ for t = 1,…,T, the plug-in estimator of V(d) is

$$\widehat{V}\left(d\right)=-{\mathbb{P}}_n\left(Y{\displaystyle \prod }_{t=1}^T\frac{1d_t\left(H_t\right)=A_t}{{\pi }_{t,n}\left(A_t|H_t\right)}\right),$$

and given a class of regimes $\mathcal{D}$, an estimator of$d_{\mathcal{D}}^{\text{opt}}$ is${\widehat{d}}_{\mathcal{D},n}=\arg {\max }_{d\in \mathcal{D}}{\widehat{V}}_n(d)$. Directly computing ${\widehat{d}}_{\mathcal{D},n}$ is diffcult except in small problems as the indicators make this into a discontinuous optimization problem. This computational issue is ameliorated in Zhao et al (2015a) through the use of a surrogate optimization function for ${\widehat{V}}_n(d)$ which is smooth and has a global optimum.

However, computational issues aside, there is another difficulty with optimizing ${\widehat{V}}_n(d)$ or one of its surrogates when the number of time points T is large as: (i) the product of indicators can rapidly become zero for the majority of subjects, e.g., with binary treatments assigned uniformly at random at each stage, the product of indicators will be zero for all but n(1/2)^T of the original n subjects on average; and (ii) the product of the propensity scores can grow quite small leading to high-variance. For these reasons, direct search estimators based on ${\widehat{V}}_n(d)$ work best for settings where T is small, e.g., T = 2; however, in such settings OWL and related methods can offer significant gains in terms of robustness and marginal mean outcome (see Zhang et al 2013; Zhao et al 2015a). As in the single-decision setting, OWL and other direct search estimators are based on converting ${\widehat{V}}_n(d)$ or a more efficient augmented variant of this estimator into a cost sensitive classification problem. We note that products of indicators across time points share a similar structure to hierarchical classification problems (Gorden 1987; Wang et al 2009) though this connection has yet to be fully explored.

4.2.2. Infinite time horizon.

The infinite horizon setting applies when a sequence of similar decisions need to be made over an extended time as happens for example when treating diabetes or other chronic diseases as mentioned previously. In this setting, decision making is typically modeled as a Markov Decision Process (MDP, Puterman 2005) which encompasses a tremendously broad class of decision problems (Sutton 1997). We assume that the observed data are of the form ${\{(S_{1,i},A_{1,i}{S}_{2,i},\mathrm{...},S_{T-1,i},S_{T,i})\}}_{i=1}^n$ which comprise n i.i.d. replicates of (S₁, A₁, S₂, … , S_T−1, A_T−1, S_T), where: S_t ∈ S denotes a summary of the patient’s health status at time t; and A_t ∈ A denotes the treatment applied at time t = 1, … , T; and T is the observed time horizon. We assume that there exists a momentary reward function $y:\mathcal{S}\times \mathcal{A}\times \mathcal{S}\to ℝ$ so that y(s, a, s^′) captures the momentary goodness for a patient with health status s who receives treatment a and subsequently transitions to a health status s^′: we write Y_t = y(S_t, A_t, S_t+1) to denote the observed momentary outcome at time t. While the observed data are collected over a horizon T the goal may be to estimate a treatment regime that can be applied indefinitely to a new patient, i.e., well beyond T decision points. To this end we assume that the observed data are Markov and Homogeneous so that for any $\sout{\mathcal{Z}}\subseteq \mathcal{S}$ and t ≥ 1

$$P\left(S_{t+1}\in \sout{\mathcal{Z}}|{\overline{S}}_t={\overline{s}}_t,{\overline{A}}_t={\overline{a}}_t\right)=P\left(S_{t+1}\in \sout{\mathcal{Z}}|S_t=s_t,A_t=a_t\right)={\mu }_{st,at}\left(\sout{\mathcal{Z}}\right),$$

where the measure μ_st,at does not depend on time. In application, the raw data may not satisfy these conditions and one must judiciously construct the state S_t as a summary of the raw data to ensure that these conditions hold (at least approximately, see Wang et al 2018, and references therein).

For each $s_t\in \mathcal{S}$ let $\psi (s_t)\subseteq \mathcal{A}$ denote the set of allowable treatments for a patient with status S_t = s_t. A treatment regime in this context is a map $d:\mathcal{S}\to \mathcal{A}$ that satisfies d(s) ∈ ψ(s) for all $s\in \mathcal{S}$ so that under d a patient presenting with state S_t = s_t at time t ≥ 1 would be recommended to receive treatment d(s_t); because d is stationary it can be applied for all t, even if t > T .¹ Let $S_t^{*}({\overline{a}}_{t-})$¹ denote the potential patient status at time t under treatment sequence ${\overline{a}}_{t-1}\in {\otimes }_{v=1}^{t-1}\mathcal{A}$ so that the potential status under a regime d is

$$S_t^{*}\left(d\right)={\displaystyle \sum }_{{\overline{a}}_{t-1}}{S}_t^{*}\left({\overline{a}}_{t-1}\right){\displaystyle \prod }_{\upsilon =1}^{t-1}{1}_{\left[d\left\{S_{\upsilon }^{*}\left({\overline{a}}_{\upsilon -1}\right)=a_{\upsilon }\right\}\right]}.$$

The potential momentary outcome for regime d is $Y_t^{*}(d)=y[S_t^{*}(d),d\{S_t^{*}(d)\},S_{t+1}^{*}(d)]$. Define the conditional discounted marginal mean outcome under d to be

$$V\left(s;d\right)=E\left\{{\displaystyle \sum }_{\kappa \ge 0}{\gamma }^{\kappa }{Y}_{t+\kappa }^{*}\left(d\right)|S_t=s\right\},$$

where γ ∈ [0, 1) is a discount factor that balances the trade-off between immediate and longterm outcomes. An optimal regime, d^opt, satisfies V (s; d^opt) ≥ V (s; d) for all $s\in \mathcal{S}$ and all regimes d. Given distribution R on $\mathcal{S}$ we define the marginal mean outcome with respect to reference R to be V_R(d) =∫ V (s; d)dR(s). One can think of the reference distribution R as the observed sample distribution or the distribution of a potential future population of patients, whichever is of primary interest. In the context of policy-search methods over a pre-specified class of regimes, $\mathcal{D}$, we define the optimal regime within $\mathcal{D}$ with respect to reference R as$d_{d\in \mathcal{D}}^{\text{opt}}=\arg {\max }_{d\in \mathcal{D}}{V}_R(d)$.

Under causal assumptions analogous to those used in the finite horizon case the following recursion holds:

$$V\left(s;d\right)=E\left[\frac{1_{A_t=d\left(S_t\right)}}{{\pi }_t\left(A_t;S_t\right)}\left\{Y_t+\gamma V\left(S_{t+1},d\right)\right\}|S_t=s\right],$$

from which it can be seen that for any function $\varphi :\mathcal{S}\to {ℝ}^q$ that (see Precup 2000; Paduraru 2013; Luckett et al 2017)

$$0=E\left[\frac{1_{A_t=d\left(S_t\right)}}{{\pi }_t\left(A_t;S_t\right)}\left\{Y_t+\gamma V\left(S_{t+1},d\right)-V\left(S_t,d\right)\right\}\varphi \left(S_t\right)\right].$$

The forgoing expression forms the basis for an estimating equation for V (s, d). Let V (s, d; λ) be a postulated class of models for V (s, d) indexed by$\text{λ}\in \wedge \subseteq {ℝ}^q$; we assume that V (s, d; λ) is differentiable in λ for each s and d. Define

$${\Lambda }_n\left(d,\lambda \right)={\mathbb{P}}_n{\displaystyle \sum }_{t=1}^{T-1}\left[\frac{1_{A_t=d\left(S_t\right)}}{{\pi }_t\left(A_t;S_t\right)}\left\{Y_t+\gamma V\left(S_{t+1},d\right)-V\left(S_t,d\right)\right\}{\nabla }_{\lambda }V\left(S_t,d;\lambda \right)\right],$$

and let ${\widehat{\lambda }}_n(d)$ be a solution to Λ_n(d, λ) = 0. The estimated conditional marginal mean outcome is${\widehat{V}}_n(s,d)=V\left\{s,d;{\widehat{\lambda }}_n(d)\right\}$. Furthermore, given a reference distribution, R, a policy-search estimator of $d_{\mathcal{D},R}^{\text{opt}}$ is${\widehat{d}}_{\mathcal{D},R,n}$. Note that this is an infinite horizon variant of OWL (see Luckett et al 2017, for additional description and an online version that uses stochastic regimes). Q-learning in the infinite horizon setting can be derived using analogous arguments (see Ertefaie 2015) and has been applied to manage infection from Pseudomonas aeruginosa in patients with cystic fibrosis (Tang and Kosorok 2012) and to control diabetes (see Ertefaie 2015).

We note that inference for V-learning has been derived based on assuming that the underlying dynamic process is constant or, more precisely, stationary, at least over moderately long stretches of time (see Luckett et al 2017). However, in some practical settings, such as in diabetes, it may be more realistic to expect the dynamics to gradually change as patients age. In this more complicated setting, inference is more challenging and remains on open research question.

4.2.3. Mobile health.

One important motivation for infinite horizon reinforcement learning is mobile health (mHealth) wherein it is feasible to both collect information and provide interventions to patients in real time. This is the case for the work in both Ertefaie (2015) and Luckett et al (2017). Such data can be collected retrospectively or by using SMART designs. A somewhat different approach to precision medicine in mHealth involves using data obtained from a micro-randomized clinical trial developed by (Klasnja et al 2015). These are particularly suited for developing interventions involving prompting people to take healthy actions to improve health behavior (Bekiroglu et al 2017). Often, these are designed to improve proximal outcomes and not necessarily longer term outcomes and can be framed as a contextual bandit problem (Tewari and Murphy 2017). This is an active and exciting area of precision medicine research.

4.3. Data sources and study design

Data for estimating dynamic treatment regimes can come from a range of sources including: convenience samples, planned observational studies, randomized clinical trials, and hybrid study designs (Zatzick et al 2016; Liu et al 2017). In many of these sources, including randomized clinical trials, the primary study objective is not estimation of an optimal treatment regime (Lavori and Dawson 2000, 2004; Murphy 2005a; Laber et al 2016); at best, estimation of an optimal treatment regime is a planned—but strictly exploratory—analysis. However, such data can still be a rich resource for estimation and inference for optimal treatment regimes. Electronic health records (EHR), for example, are collected for administrative or insurance purposes but have been shown to be useful for precision medicine research (see, e.g., Hripcsak et al 2016). Planned observational studies are usually conducted in epidemiology and other fields but usually involve careful design, planning, and execution so that the quality of data is high (see, e.g., (Thiese 2014)). These designs are frequently the inspiration for causal inference research as the absence of randomization treatment assignment complicates identification of causal relationships among treatments and risk factors. These designs can also include careful selection of subsets of convenience samples to improve quality of causal inference, as done, for example in Lund et al (2015).

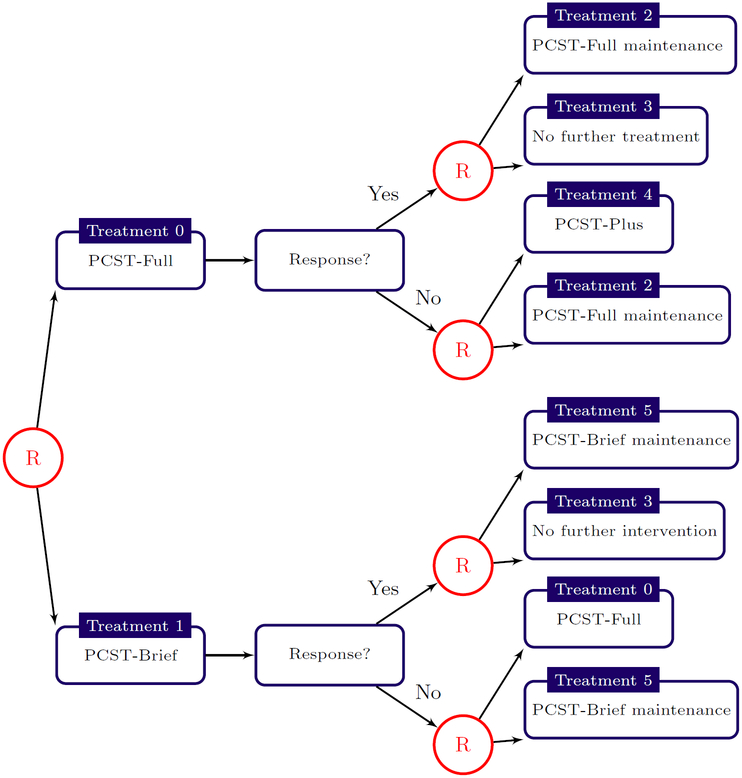
Randomized clinical trials are a gold standard for data collection as they protect against unmeasured confounding and can be designed to ensure efficient estimation of the targeted estimand. For single-stage decision problems, a k-arm randomized clinical trial with equal randomization provides maximal information about average treatment effects across pairs of treatments. For multistage decision problems, Sequential Multiple Assignment Randomized Trials (SMARTs, Lavori and Dawson 2000, 2004; Murphy 2005a) allow for the efficient comparison of treatment sequences and fixed (i.e., not data-dependent) treatment regimes. In a SMART, a patient is randomized at each point in the treatment process where there is clinical equipoise and thus each patient may be randomized multiple times throughout the trial. Figure 2 shows a schematic for a two-stage SMART for evaluating behavioral interventions for cancer pain management (Kelleher et al 2017). In the first stage subjects were randomized with equal probability to one of two variants of Pain Coping Skills Training (PCST); in the second stage, responders were randomized to either a maintenance therapy or no further treatment whereas non-responders were randomized to either maintenance therapy or an intensified treatment. Two-stage SMARTs are among the most common though they are an extremely flexible design with many different variations (Kidwell 2014, 2016; Penn State Methodology Center 2018).

Figure 2.

Two-stage SMART for evaluating Pain Coping Skills Training (PCST) for cancer pain management. In the first stage, subjects are randomized to receive either PCST-Full or PCST-Brief. At the second stage, responders are randomized to a maintenance therapy or no further treatments whereas non-responders are randomly assigned to a maintenance therapy or more intensive treatment. See Kelleher et al (2017) for additional trial details.

For various reasons, randomization at each decision point is not always possible, ethical, feasible or even scientifically optimal, and various hybrid designs can be considered. A pragmatic clinical trial (see, e.g., (Ford and Norrie 2016)) is one in which various design features are carefully incorporated to ensure similarity with treatment conditions to the real world. This can include randomizing clinics instead of patients to ensure that the treatment is the same throughout the clinic as would normally happen in practice, or recruiting a more heterogeneous patient population through liberal inclusion criteria. In a certain sense, a SMART clinical trial is more pragmatic than traditional clinical trials as the treatment decisions being evaluated are more similar to those utilized in practice. Hybrid designs have both randomization and observational components and often have a pragmatic motivation. One example is the enrichment design proposed by (Liu et al 2017) which allows the first treatment assignment to be non-randomized but has the second treatment assignment randomized. There are many other possibilities which we will not explore further here. Two important points we want to make are: first, that heterogeneity is good for precision medicine as this is needed to estimate an optimal treatment regime which is valid for a broad range of possible patients; and, second, that design of studies used for discovering precision medicine is a crucially important aspect of precision medicine research.

5. MANAGING MULTIPLE OUTCOMES

So far, we have considered optimal dynamic treatment regimes in terms of a single scalar outcome that we wish to optimize. In many clinical settings, there are multiple outcomes which need to be considered when managing treatment decisions. For example, in treating schizophrenia, there can be steep trade-off between side-effects and efficacy (Butler et al 2018). As another example, consider bipolar depression in which there is a trade-off between depressive symptoms and risk of mania (Luckett et al 2018). Recent work on precision medicine with multiple outcomes includes set-valuated treatment regimes which recommend a set of ‘acceptable’ treatments given a patient’s history (Fard 2009; Lizotte et al 2012; Laber et al 2014; Lizotte and Laber 2016; Wu 2016); and methods where a primary outcome is maximized while a secondary outcome is constrained to be within an acceptable region, using either regression based or outcome weighted learning methods (Linn et al 2015; Wang et al In press; Laber et al 2018).

In some cases, there is a trade-off between two or more endpoints which depends on patient preferences or other factors that depend on individual patient needs. Butler et al (2018) develop a method for the single-decision setting which uses item response theory to elicit patient preferences and then combines this with Q-learning to optimize the patient-preferred composite utility which is a convex combination of two outcomes. They show that under reasonable regularity and logic conditions, the optimal regime for any utility is equivalent to the optimal regime for a utility expressed as a convex combination of the available outcomes. They also show that the item-response model leads to the optimal patient-preferred treatment decisions under reasonable regularity conditions as the number of items grows and the sample size increases. One caveat of their approach is that the items in the patient preference instrument need to be appropriately calibrated which can be challenging. Extensions allowing calibration to be done empirically and which can be applied to both single- and multi- decision settings are given in Butler (2016).

Luckett et al (2018) study the situation where the trade-offs between two outcomes depend on complex individual-level factors about which clinicians have imperfect information. They consider observational data on clinicians prescribing anti-depressants to patients with bipolar depression and measures of both depression and mania outcomes are observed in the patients. They assume that the clinicians are trying to act optimally and that they sometimes succeed but not always. Based on the estimated Q-functions for each outcome (depression and mania), they estimate the weight in the combined utility of the convex combination of the two outcomes as a function of patient-level covariates as well as the probability of correct treatment assignment also as a function of patient-level covariates. They demonstrate that under reasonable regularity conditions, the asymptotic joint limiting distribution of the parameters are obtained at the $\sqrt{n}$ rate. The limiting distribution is non-Gaussian and requires a non-standard bootstrap for inference. They demonstrate the validity of the inference through simulation studies and apply the method to the STEP-BD study data on bipolar disorder (Sachs et al 2007). They also demonstrate that applying the estimated dynamic treatment regime obtained from this data using the proposed method can lead to a statistically significant increased average patient-specific composite outcome for future patients. Generally speaking, addressing multiple outcomes in precision medicine is crucially important and there is much interesting work yet to be done in this area.

6. STATISTICAL INFERENCE

For many of the methods described above, asymptotic consistency, i.e., the property that the estimated quantities converge to the truth as the sample size grows, has been proven. For the sake of discussion, we refer to asymptotic consistency as zero order inference. However, typically with statistical procedures, it is valuable to be able to also provide first order inference consisting of confidence intervals, hypothesis tests, and sample size calculations. Generally speaking, first order inference is not yet known for many of the machine learning tools used in precision medicine and this is an open and active area of research. Because the focus is to inform decision making, a primary emphasis is on inference for performance of a treatment regime; note that a confidence or prediction set for the marginal mean outcome of an estimated optimal treatment regime is still meaningful even if models underlying estimation of the regime are misspecified.

Although first order inference for many of the machine learning approaches utilized has not been developed, some advances have been made in a number of settings, including for support vector machines (Laber and Murphy 2011) and for random forests (Wager and Athey In press). In addition, computation of error bounds can be a useful assessment of performance which is more precise than the presence or absence of consistency but not precise enough to obtain first order inference. These have been developed for many machine learning tools used in precision medicine, as in (Qian and Murphy 2011; Goldberg and Kosorok 2012; Zhao et al 2012; Cui et al 2017), and, more recently, have been improved for some settings in (Athey and Wager 2017). We also note the sample size formulas for the single-decision setting have been developed based on the value function (Laber et al 2016). Because regression-based approaches applied to the single-decision setting involve standard regression analyses, inference in this setting can sometimes be straightforward. However, in the multi-decision setting, for example with Q-learning involving two or more decision times, the inference is non-regular even if linear regression is used at each decision time (Chakraborty and Murphy 2010; Moodie and Richardson 2010; Chakraborty et al 2013, 2014; Laber et al 2014; Song et al 2015).

Inference for precision medicine is an active and important area of research, and we have only touched on it briefly here. We note that much of the inferential challenges follow from the use of complex machine learning procedures. One could argue that this is a reason to avoid machine learning methods in precision medicine. However, since the primary goal of precision medicine is to find dynamic treatment regimes that perform well on future patients, we need to use the best available tools, and this includes machine learning methods.

7. DISCUSSION

Precision medicine is beginning to emerge as a well-defined discipline with specific goals, areas of focus, and tailored methodology. Specifically, the primary goal is to discover treatment rules which leverage heterogeneity to improve clinical decision making in a manner that is reproducible, generalizable, and which can adapt as needed. We note that patient heterogeneity is a blessing for precision medicine although it may not be convenient for other areas of medical research. We also highlight the focus in precision medicine on discovery, as opposed to confirmatory research, and note that this makes the inferential aspects somewhat distinct from some areas of traditional medical research. Nevertheless, discovery of precision medicine should be confirmed rigorously just as with other medical discoveries. The emphasis on both discovery and heterogeneity makes machine learning tools particularly valuable in this quest, and this means that the inferential challenges are different and in many ways more difficult.

We also note that there are many other important supporting aspects of precision medicine which we have not discussed, including implementation, national policy questions, data storage and management, among many others. We also have not included numerous relevant research contributions to machine learning and other areas in many disciplines, both within statistics as well as outside, including many biomedical sciences, computer science, operations research, engineering, robotics, economics, and others.

Nevertheless, we hope that this review helps to clarify the goals of precision medicine and becomes a catalyst for bringing together the diverse disciplines and perspectives that are needed to make dramatic advances in precision medicine which will yield fundamental changes in human health and well being. This is an exciting and vibrant area of research with many open questions and tremendous opportunities.