Abstract
Cryo-Electron Tomography (cryo-ET) has become an essential technique in revealing cellular and macromolecular assembly structures in their native states. However, due to radiation damage and the limited tilt range, cryo-ET suffers from low contrast and missing wedge artifacts, which limits the tomograms to low resolution and hinders further biological interpretation. In this study, we applied the Model-Based Iterative Reconstruction (MBIR) method to obtain tomographic 3D reconstructions of experimental cryo-ET datasets and demonstrated the advantages of MBIR in contrast improvement, missing wedge artifacts reduction, missing information restoration, and subtomogram averaging compared with other reconstruction approaches. Considering the outstanding reconstruction quality, MBIR has a great potential in the determination of high resolution biological structures with cryo-ET.
Keywords: Model-Based Iterative Reconstruction, cryo-ET, contrast improvement, missing wedge artifacts reduction, missing information restoration, subtomogram averaging
Graphical Abstract

1. Introduction
Cryo-electron tomography (cryo-ET) has emerged as a promising technique that allows us to comprehensively explore macromolecular complexes and cellular architecture in near-native states (Lučić et al., 2005). Using cryo-ET, the 3D tomogram of the biological sample can be reconstructed from a 2D tilt series collected by sequentially tilting the sample at different projection angles around a tilt axis (Herman, 2009). In practice, the quality of reconstruction with cryo-ET remains limited by several challenges in the data acquisition and reconstruction process.
The extremely poor signal-to-noise ratio (SNR) of cryo-ET is the first major challenge in improving cryo-ET resolution (Pilhofer et al., 2010). To prevent significant radiation damage to biological samples by the electron beam, the total dose used for a cryo-ET tilt series is typically less than 100 e/Å2. This low-dose imaging strategy in combination with the increment of sample thickness during tilting results in very noisy, low contrast 2D projections, which poses a challenge in subsequent 2D tilt series alignments and deteriorates the resolution of cryo-ET 3D reconstruction (Turoňová et al., 2015; Vanhecke et al., 2011).
The second major challenge of cryo-ET is the missing wedge artifacts caused by the limited tilt angle range during data collection (Orlova and Saibil, 2011). Since more electrons are lost to inelastic scattering as the effective sample thickness increases when the sample is tilted (Pilhofer et al., 2010), the maximal tilt range of cryo-ET is typically restricted within ±70° to ensure enough electrons can traverse through the sample, generate elastic scattering, and form reliable images (Penczek et al., 1995). Consequently, the absence of the high tilt angles (−90° ~ −70° and +70° ~ +90°) becomes a “missing wedge” of un-sampled information in Fourier space, leading to severe ray artifacts, structural elongation and distortion effects in the final reconstruction (Chen et al., 2016). The missing wedge artifacts dramatically weaken the interpretability of the reconstructed tomogram and limit the achievable resolution of cryo-ET (Lučić et al., 2005).
To address these challenges of cryo-ET, we introduce the Model-Based Iterative Reconstruction (MBIR) method (Venkatakrishnan et al., 2015) for tomographic reconstruction and benchmark the tomogram quality with the state-of-the art algorithms, including Weighted Back Projection (WBP) (Radermacher, 1992), Simultaneous Iterative Reconstruction Technique (SIRT) (Gilbert, 1972), and Iterative Compressed-sensing Optimized Non-uniform fast Fourier transform reconstruction (ICON) (Deng et al., 2016). MBIR method has been previously shown to generate better quality tomograms when applied to tomography applications like CT scan, X-Ray tomography, positron emission tomography (PET), optical diffusion tomography (ODT), and atomic resolution high-dose electron tomography of radiation-resistant material specimens with heavy atoms (Venkatakrishnan et al., 2013). MBIR combines a forward model for image formation with a prior model for the unknown structure to reconstruct tomograms. In this study, tests with both plastic embedded ET dataset and ice embedded low-dose cryo-ET datasets of radiation-sensitive biological samples have shown that MBIR can significantly improve the reconstruction quality with enhanced contrast, reduced missing wedge artifacts, partially restored information in the un-sampled angular region, and improve the resolution of subtomogram averages.
2. Methods
2.1. MBIR Algorithm
In the MBIR framework, the reconstruction is formulated as the maximum a posterior (MAP) estimate of the unknowns, given the measurements
| (1) |
where g represents the data obtained from an imaging system (e.g. cryo-ET tilt series), f represents the unknown 3D structure to be discovered, ∅ represents the unknown nuisance parameters of the system such as beam intensity fluctuations and noise characteristics. p(g|f, ∅) is the likelihood function that models how the observations are related to the unknowns, p(f) is the assumed prior distribution of the unknown structure. Here p(g|f, ∅) and p(f) indicate the forward model of image formation and prior model of the tomogram in MBIR algorithm, respectively (Venkatakrishnan et al., 2015). The goal of MBIR will be to compute a final estimate that represents a balance between fitting the measurements based on the system forward model p(g|f, ∅) while remaining consistent with the prior model p(f).
Fig. 1 illustrates a general framework of MBIR for solving inverse problems in imaging applications. The MBIR method uses probabilistic models to cast the reconstruction as minimizing a cost/energy/fitting function that balances two sets of terms - the data fidelity term (determined from the log-likelihood model logp(g|f, ∅)) and the regularization term (determined from the log-prior model logp(f)). The data fidelity ensures that the reconstructed 3D volume and calibration values match the measurements under the assumption of the appropriate physics-based forward model (e.g., Beer-Lambert’s law with Poisson statistics), while the regularization term encourages the 3D reconstructions to have certain desirable properties (such as local correlations that are common in real-world images/volumes). It is this synergistic combination of models that enable the MBIR method to produce high quality tomograms even from limited-angle and highly noisy datasets. Once the cost function is formulated, the main challenge is to minimize it with respect to all the voxels in 3D and other calibration parameters. Due to the extremely large number of unknowns, an iterative algorithm has to be employed to solve this problem efficiently. Notice that the choice of models typically defines the quality of the final reconstruction while the choice of the iterative optimization determines how fast we can compute this solution (Venkatakrishnan et al., 2015, 2013).
Fig. 1. Graphical scheme of the MBIR algorithm.
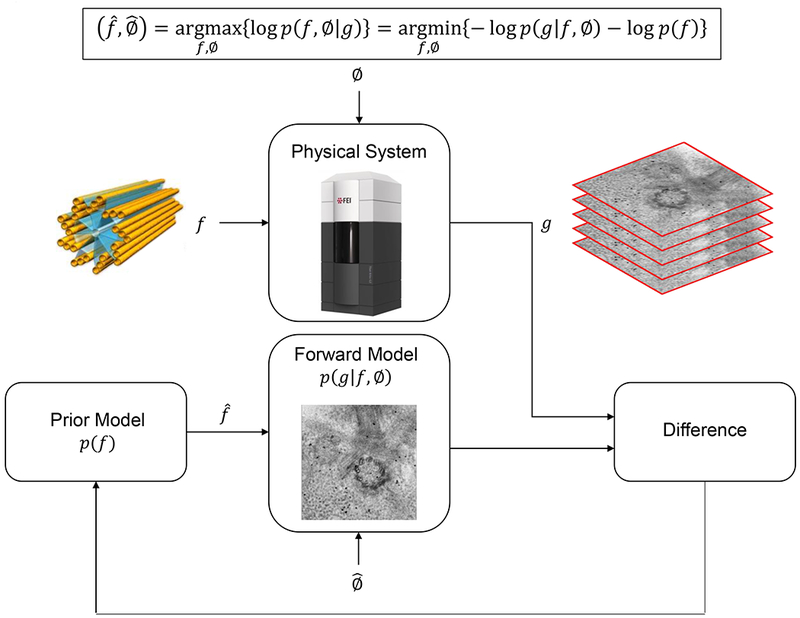
g denotes the tilt series from cryo-ET, f denotes the unknown structure, and ∅ denotes unknown nuisance parameters of the system (e.g. noise characteristics) which needs to be determined in the inverse process. p(.) denotes the probability density function and p(g\f, ∅) and p(f) are the forward model and prior model in the MBIR algorithm, respectively. and denote the estimate of f and ∅, respectively.
2.2. Implementation of MBIR
The MBIR algorithm was implemented into a standalone program with C++ language. It is cross-platform portable and works on Linux, Windows and Mac OS X operating systems. The MBIR software package used for ET is freely available in the form of binary executables and source codes from the authors’ website (https://engineering.purdue.edu/~bouman/OpenMBIR/bf-em). A tutorial of MBIR can be found in the Supplementary Note.
2.3. Simulated datasets
We used the ribosome structure (EMD-8799) (Himes and Zhang, 2017) from the EMDB database (Lawson et al., 2011) to simulate a synthetic 3D phantom (512×512×64 pixels) and generate tilt series with different tilt ranges (e.g. −70°~+70°, −60°~+60°, −50°~+50°), angular intervals (e.g. 1°, 2°, 4°), and Gaussian noises (SNR=0.5, 0.25, 0.125). The synthetic phantom was generated using EMAN2 package (Tang et al., 2007) and the tilt series were generated using the radon function in Matlab. The missing wedges shown in the power spectra of the central XZ-slices (Fig. S2) were calculated using the EMAN2 processor mask.fft.wedge available in the EMAN2 version 2018-11-24 or later.
2.4. Experimental test datasets
We evaluated the performance of the MBIR method on both plastic embedded ET dataset and cryo-ET datasets by comparing its results with three reconstruction techniques used in the cryo-ET community, including WBP and SIRT available in IMOD (Kremer et al., 1996), and ICON. The plastic embedded ET dataset obtained from IMOD tutorial website (Kremer et al., 1996) was originally provided for dual axes reconstruction, but we only used the first tilt series (BBa.st) in our study. Four published experimental cryo-ET datasets (EMPIAR-10037 (Schur et al., 2015), EMPIAR-10045 (Bharat and Scheres, 2016), EMPIAR-10064 (Khoshouei et al., 2017) and EMPIAR-10110 (Chang et al., 2017)) were downloaded from the public database EMPIAR (Iudin et al., 2016). EMPIAR-10064 dataset was collected with the Volta phase plate (VPP). These tilt series were first aligned based on fiducial gold markers using IMOD and then the same aligned tilt series were reconstructed without further alignment by the four reconstruction techniques, respectively. We used 12 iterations for cryo-ET dataset and 20 for the resin embedded dataset in the SIRT method according to the IMOD instruction. The details of these datasets are summarized in Table S1 including data type, biological sample, instrument, defocus, tilt scheme, total dose, and data collection software. In this study, the figures used for comparing the performance of different methods are contrast-normalized to avoid subjectivity of observations and to ensure the reliability of comparison.
2.5. Leave-one-out Fourier Ring Correlation (FRC)
Leave-one-out (FRC) method (Cardone et al., 2005) was used to assess the information restoration capability of the four reconstruction methods. In this test, the FRC is calculated for the raw tilt image X and the corresponding reprojection from a tomogram computed from all other tilts without tilt X. Here the tilde sign represents the reprojection from a tomogram, and the minus sign represents the tomogram used for reprojection is calculated by omitting the tilt X from the original tilt series to avoid bias. We first excluded a raw image X at a certain tilt angle and utilized the remaining images of the tilt series to generate a tomogram. Next, we re-projected this tomogram at the angle of tilt X to obtain a reprojection . Finally, we calculated the FRC curve between the excluded raw image X and the reprojection , and used this FRC curve as a quantitative evaluation of the quality of the recovered information.
2.6. Subtomogram averaging
Single particle cryo-ET dataset of the S. cerevisiae 80 S ribosome (EMPIAR-10045) was also used for the subtomogram averaging tests. EMPIAR-10045 is the tutorial data of the Relion software (Bharat and Scheres, 2016). We followed the standard protocol of Relion subtomogram averaging and completed the tasks using Relion 2.1 package. To reduce the effect of strong signals at low frequencies, we high-pass filtered the MBIR tomograms to 20Å.
Two subtomogram average maps (EMD-3228 (Bharat and Scheres, 2016) and EMD-8799 (Himes and Zhang, 2018)) of the same dataset (EMPIAR-10045) were used as the reference maps to calculate the Fourier Shell Correlation (FSC) with the average subtomograms generated in this study using WBP and MBIR, respectively. These two reference maps with reported resolution of 13Å and 7.8Å, were generated using Relion (Bharat et al., 2015) and emClarity (Himes and Zhang, 2018) packages, respectively.
3. Results
3.1. MBIR performance on simulated datasets
To evaluate the quality of information restoration in the missing wedge, we performed tomogram reconstructions of three tilt series with varying tilt ranges (−70°~+70°, −60°~+60°, −50°~+50°, angular interval = 2°, SNR=0.5) using four different methods (WBP, SIRT, ICON and MBIR), then extracted the missing wedge region from each tomogram in Fourier space. The representative central XY-slices of the phantom and the four reconstructions are displayed in Fig. S1. Fig. S2 shows the central XZ-slice of the power spectra in the region corresponding to the missing wedge in the phantom (Fig. S2A) and WBP (Fig. S2B), SIRT (Fig. S2C), ICON (Fig. S2D) and MBIR (Fig. S2E) tomograms for the tilt angle range from −60° to +60°. Next, we calculated the FSC between the phantom’s missing wedge region (Fig. S2A) and that of each tomogram (Fig. S2B-E). As shown in Fig. S3, MBIR exhibits a considerably better correlation between its recovered missing wedge information and the phantom than other methods for all the tested tilt angle ranges including −70° to +70° (Fig. S3A), −60° to +60° (Fig. S3B), −50° to +50° (Fig. S3C), respectively, indicating the superior ability in restoring the missing wedge information by the MBIR method. Furthermore, we re-plotted the FSC curves of Fig. S3A-C by reconstruction methods and compared the FSC of the same method for varying tilt ranges in Fig. S3D-G. We can see that MBIR (Fig. S3G) is able to restore more missing wedge information when the tilt range becomes larger and the missing wedge becomes smaller (−70°~+70°, red line in Fig. S3G). However, other methods do not show significant improvement in recovering the missing wedge information when the tilt range increases. Fig. S4 displays the FSC curves between the phantom and the whole tomogram of each method. It is noted that MBIR’s FSC is always significantly higher than other methods for the tested tilt ranges (Fig. S4A-C), confirming the best performance by MBIR in restoring the missing information. The results in Fig. S4D-G also confirm that the quality of the tomograms become poorer with reduced tilt ranges.
To test the robustness of MBIR at different noise levels, we generated reconstructions from three tilt series with varying amount of noise added (SNR=0.5, 0.25, 0.125, tilt range is −60°~+60°, angular interval = 2°). Fig. S5 presents the 0° tilt image from each tilt series with SNR 0.5, 0.25 and 0.125, respectively. As described in Fig. S6A-C, MBIR tomogram has the best correlation with the phantom at all tested noise levels, proving its robustness against the noise. The comparisons of the performance at different noise levels (Fig. S6D-G) confirm that, as expected, the tomogram quality degrades at higher noise levels regardless of the reconstruction method.
To assess the effect of angular interval on the tomogram quality, tomograms were reconstructed from three tilt series with varying angular increments (1°, 2°, 4°, tilt range is −60°~+60°, SNR=0.5). The plots in Fig. S7A-C show that MBIR demonstrates the highest FSC with the phantom at all tested angular intervals, implying that MBIR is better at dealing with the limited angular sampling. As can be seen from Fig. S7D-G, the tomogram quality is attenuated for all four methods, as expected, with increased angular intervals. However, the increased angular intervals have relatively less effect on the tomogram quality for MBIR and ICON than WBP and SIRT.
3.2. Missing wedge assessments using gold markers
We then evaluated MBIR using one cryo-ET dataset (EMPIAR-10045) by visually examining the missing wedge artifacts of gold markers in different slice views of the tomograms. Due to the missing wedge problem, the gold markers become elongated along the direction of the missing wedge and suffer from halos and streaking artifacts in the adjacent region. Fig. 2 compares slice views of the reconstructions generated by the four methods using gold markers as an indicator of quality. In each block, three planes represent the XY-slice (middle plane), XZ-slice (top plane) and YZ-slice (right plane) of the tomogram, respectively, intersecting at the same gold marker. The zoomed-in view of the gold markers pointed by white arrows in the three planes are placed at the corner of the corresponding planes. From the XY-slices of tomograms, it is clear MBIR (XY-slice in Fig. 2D) has eliminated the halos artifacts and displays more round, sharp-edged gold markers than other methods. In the XZ and YZ-slices, MBIR (Fig. 2D) significantly reduced the elongation and ray artifacts of gold markers with improved contrast of the biological structures, compared with the tomograms reconstructed by other methods. Hence, MBIR-reconstructed tomograms show less artifacts from the missing wedge problem, better contrast in cryo specimen, and clearer background.
Fig. 2. Comparison of tomograms from an experimental cryo-ET dataset (EMPIAR-10045) reconstructed by WBP(A), SIRT (B), ICON (C) and MBIR (D) methods.
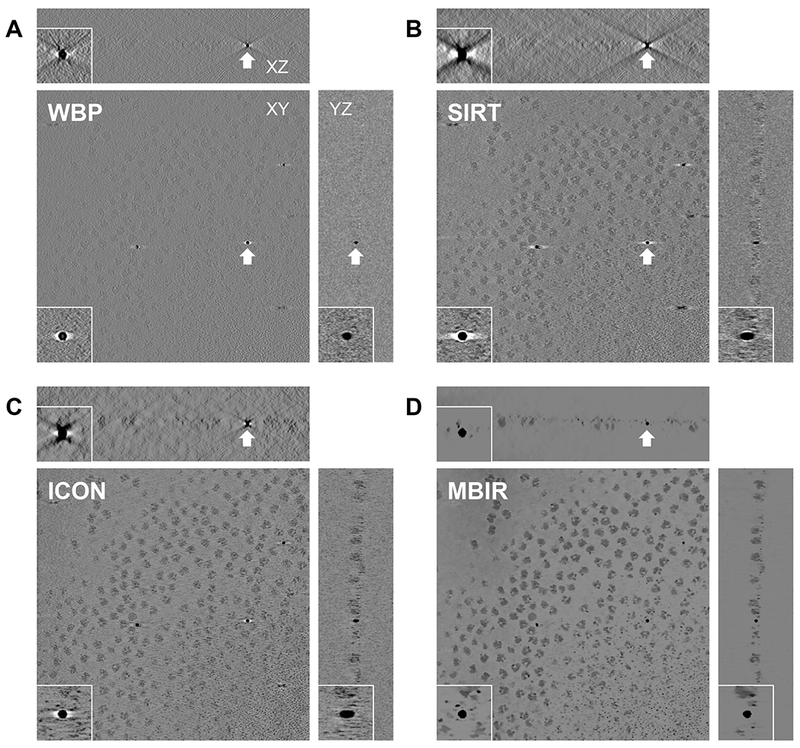
The three planes for each method represent the XY-slice (middle plane), XZ-slice (top plane) and YZ-slice (right plane) of the tomogram intersecting at the same gold marker. In each plane, the gold marker is indicted by a white arrow with corresponding zoomed-in view showing the missing wedge artifacts.
To further examine the performance of MBIR, we applied it to one cryo-ET dataset acquired with VPP (EMPIAR-10064 in Fig. 3A), two cryo-ET datasets without VPP (EMPIAR-10037 and EMPIAR-10110 in Fig. 3B and C), and one plastic embedded ET dataset (IMOD tutorial dataset in Fig. 3D). Fig. 3 shows the slice views of these four datasets in which each row represents the results of one dataset reconstructed by the four methods and each column represents the results of one method applied to different datasets. In Fig. 3B and D, XY-slices are mainly used to reveal the reconstruction quality of sample areas without targeting at a gold marker because the sample and markers are not on the same XY plane. EMPIAR-10037 (Fig. 3B) is challenging due to its small tilt range (−45°~+45°), large angular interval (3°) and low total dose (24~34 e/Å2). For this challenging dataset, it is clear that WBP reconstruction quality is too poor to make the biological sample visible. SIRT and ICON reconstructions contain phantoms of gold markers at the upper left corners in XY-slice (circled by dash lines in Fig. 3B) which is caused by the missing wedge artifacts and should not appear here since gold markers are located in different Z sections of the sample. In stark contrast, MBIR in Fig. 3B is able to drastically reduce the missing wedge problem in XZ-slice and YZ-slice, completely suppress the gold marker phantoms in XY-slice and considerably enhance the contrast of biological samples. In addition, MBIR provides better quality of tomogram in other datasets of Fig. 3, which is in a good agreement with the results shown in Fig. 2. In summary, the comparison of slice views among different methods in Fig. 3 and Fig. 2 gives a clear impression that MBIR has superior performance in boosting contrast of biological specimens, eliminating halos and streaking artifacts, retaining sharp features, and reducing noise. The superior performance of MBIR is evident in both cryo-ET (Fig. 2 and Fig. 3A-C) and plastic-embedded ET (Fig. 3D) datasets.
Fig. 3. Comparison of tomograms from multiple experimental ET datasets reconstructed by different reconstruction techniques.
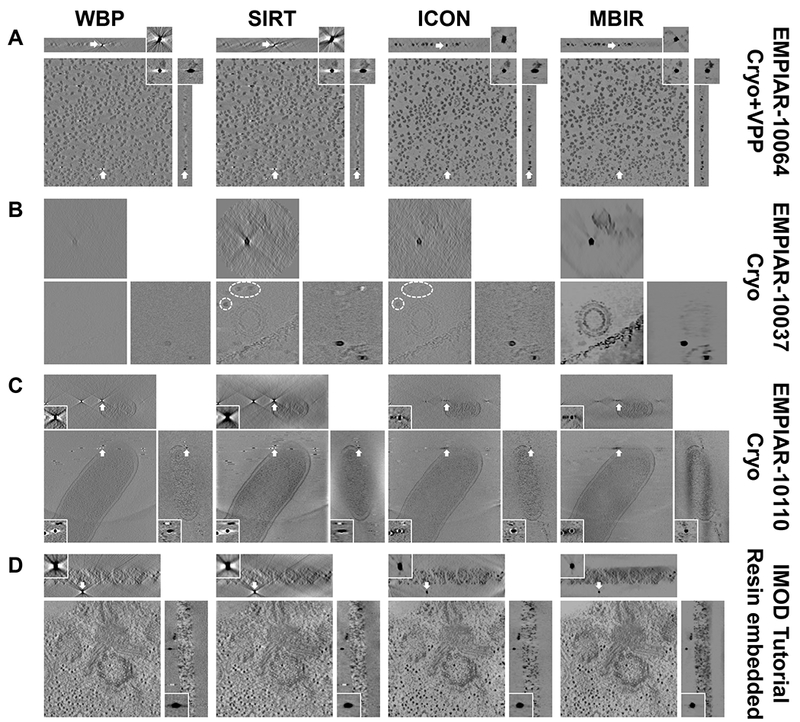
Each row indicates the reconstructions from the same dataset using different methods. Each column indicates the reconstructions from the same method applied to different datasets. The data type and EMPIAR ID are denoted at the right side of each row. The method of comparison in each dataset is the same as described in Fig. 2. Note that the XY-slices of the dataset shown in (B) and (D) are used to show the biological sample area and not targeted at the gold markers since the sample and gold markers are located in different Z sections.
3.3. Power spectra evaluation
To quantitatively evaluate MBIR’s ability in restoring missing information, we calculated the log-scaled power spectrum of the central XZ-slice and used it as a measurement of information restoration in 3D reconstruction. As depicted in Fig. 4, four plots of power spectra correspond to the central XZ-slices of the tomograms reconstructed by the four methods shown in Fig. 2. It is noted that MBIR can fill more un-sampled region in Fourier space than other methods, not only in the region of the missing wedge but also the empty space between two adjacent tilts, suggesting better performance of MBIR in restoring missing information. It is worth noting that the lines at the corners of WBP (Fig. 4A) and SIRT (Fig. 4B) power spectra are due to the aliasing issue. To check if such aliasing issues are unique to our results, we downloaded another four 3D tomograms (Albert et al., 2017; Bykov et al., 2017; Chang et al., 2017; Shahmoradian et al., 2014) from EMDB, calculated their central XZ-slices power spectra, and plotted them in Fig. S8. The results in Fig. S8 suggest that this aliasing issue is a general phenomenon in the cryo-ET field (Kunz and Frangakis, 2014) since it is observed in a variety of data, including data from multiple research groups, varying TEM facilities and imaging conditions, a diverse range of samples, and different reconstruction software.
Fig. 4. Comparison of the central XZ-slice power spectra from the tomograms shown in Fig. 2.

The tomograms were reconstructed by WBP (A), SIRT (B), ICON (C) and MBIR (D) methods, respectively.
We next examined the central XZ-slice power spectra of the datasets displayed in Fig. 3 and compared them in Fig. S9. In general, MBIR and ICON yield more non-zero values in the missing wedge region than WBP and SIRT, except for one challenging dataset (Fig. S9B). However, power spectrum may not be a reliable and complete assessment for the information restoration because it only conveys the amplitude information without considering the phase information. What’s more, various filters can be internally applied to tomograms in different methods to balance the non-uniform sampling in Fourier space (Wei et al., 2005). As a result, further validation is still needed to confirm the advantage of MBIR in restoring not only amplitude but also phase information.
3.4. Cross validation of projections using the leave-one-out FRC method
We used the leave-one-out FRC method described in Section 2.5 to assess the correctness of the information restored by MBIR and compare it with the performance of other reconstruction methods. As shown in Fig. 5A, the first row and the second row are the raw images X (the first image in each row) and the reprojections corresponding to different reconstruction methods at a smaller tilt angle 0° and a larger tilt angle 45°, respectively. The gold markers indicated by white arrows are zoomed in and placed at the lower left corners of each images. It is evident that the gold marker in MBIR reprojection is circular without discernible distortion or blurring, which is nearly identical to the original tilted image, even at a high tilt angle. In contrast, the gold markers in the reprojections of other methods clearly suffer from missing wedge artifacts including elongation, white halos, and blurring. Furthermore, such visual assessments are verified quantitatively by the FRC (Fig. 5B and C) of the raw tilt images and reprojections shown in Fig. 5A. As shown in Fig. 5B and C, the quick drop of WBP (blue curve), SIRT (red curve) and ICON (green curve) FRC curves implies that only low resolution information is reliably restored in the non-sampled angular regions. However, the FRC curve of MBIR exhibits a significantly higher correlation between the reprojection and the original tilt image, confirming the successful restoration of the missing information.
Fig. 5. Comparison of missing information restoration from an experimental cryo-ET data (EMPIAR-10045) reconstructed by different reconstruction techniques using the leave-one-out FRC method.
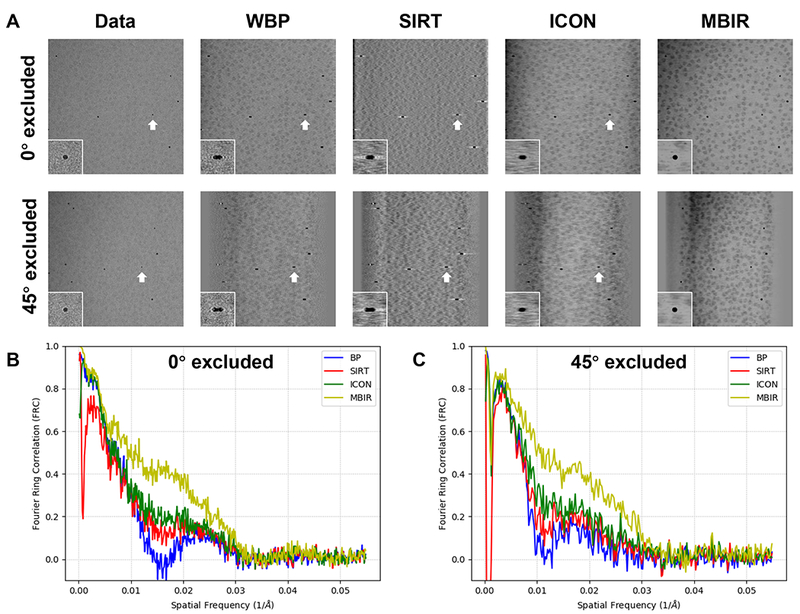
(A) Comparison of reprojections at two tilt angles (0° in the first row and 45° in the second row) using the tomograms generated without the corresponding tilt. The images in the first column are extracted from the tilt series, serving as the ground truth for comparison. In each plane, the gold marker indicted by a white arrow is displayed with corresponding zoomed-in view. (B) and (C) are comparisons of the FRC curves of reprojections against the ground truth as depicted in (A) when 0° and 45° tilt is excluded in the leave-one-out test, respectively.
To further substantiate the capability of MBIR in restoring missing information, we performed the same analysis as described in Fig. 5 on more datasets and summarized the comparisons of raw images and reprojections in Fig. S10–S11 and FRC comparisons in Fig. 6. As can be seen from Fig. S10–S11, MBIR preserved the round shape of gold markers in the leave-one-out reprojections at low (Fig. S10) and high (Fig. S11) tilt angles in both cryo (Fig. S10A-C, Fig. S11A-C) and plastic embedded datasets (Fig. S10D, Fig. S11D), which is consistent with the results shown in Fig. 5A. Fig. 6 shows the FRC comparisons of different methods when 0° (Fig. 6A, C, E, G) and 45° (Fig. 6B, D, F, H) tilts were excluded in the leave-one-out tests, respectively. The FRC curve of MBIR (yellow curve) in Fig. 6 is typically higher than that of other methods, which suggests the superior quality of MBIR in recovering authentic information of biological samples in 3D tomographic reconstructions. As demonstrated in Fig. 6A-B, VPP used in this dataset boosts the signal-to-noise ratio of cryo-ET images and improves the low frequency signal in FRC curve compared with Fig. 5B-C, leading to a smaller difference among the results of the four reconstruction methods than the case shown in Fig. 5. However, the local missing wedge artifacts around the gold markers remained in the tomograms reconstructed by the other three methods but not by MBIR for this cryo-ET dataset with VPP as shown in the corresponding slice views (Fig. 3A) and reprojections (Fig. S10A and Fig. S11A), emphasizing the advantages of MBIR method. Therefore, all the analyses above validate MBIR’s capability to partially restore the missing information in both cryo-ET and plastic embedded datasets.
Fig. 6. Comparisons of FRC curves from multiple experimental ET datasets reconstructed by different reconstruction techniques using the leave-one-out FRC method.
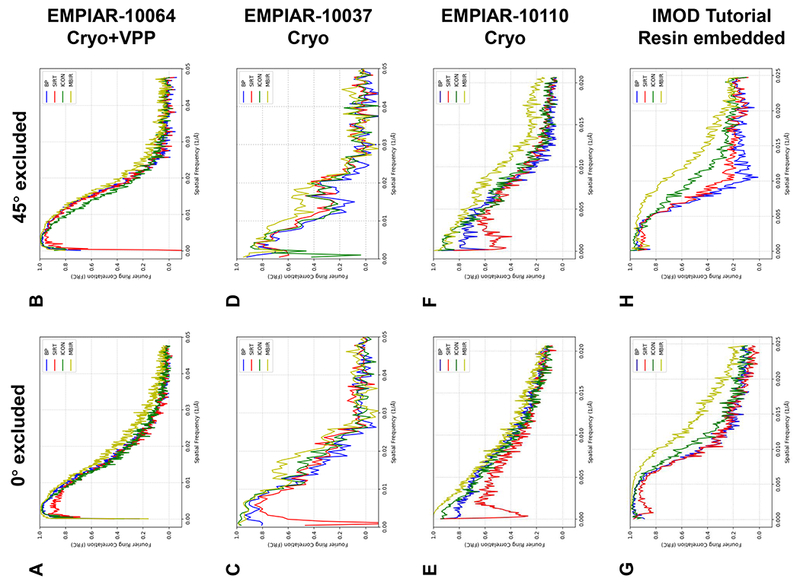
Each row represents the comparison of FRC curves from the same dataset when 0° (left plot) and 45° (right plot) tilt is excluded in the leave-one-out test, respectively. The details of the corresponding reprojections and ground truths are shown in Fig. S10 (0° excluded) and Fig. S11 (45° excluded), respectively.
3.5. Subtomogram averaging
In addition to above tests that demonstrated the excellent performance of MBIR in generating raw tomograms, we have further tested if the improved raw tomogram quality can lead to improved subtomogram averages. We used Relion to obtain the average ribosome maps by using 1600 subtomograms (1003 voxels, voxel size 4.34Å) of the EMPIAR-10045 dataset extracted from WBP and MBIR tomograms with 2X binning, respectively. The averaged subtomograms of WBP, MBIR maps and their “gold standard” FSC curves are shown in Fig. 7A, B and E, respectively. Although the “gold standard” FSC curves (Fig. 7E) indicate a slightly better resolution for the MBIR map (green line in Fig. 7E) than WBP (blue line in Fig. 7E), it is evident that the FSCs do not drop to zero, which is puzzling but consistent with the results included in the EMPIAR-10045 dataset. Therefore, the “gold standard” FSC curves from the half maps may not be a reliable measurement of resolution for this dataset.
Fig. 7. Comparison of subtomogram averages.
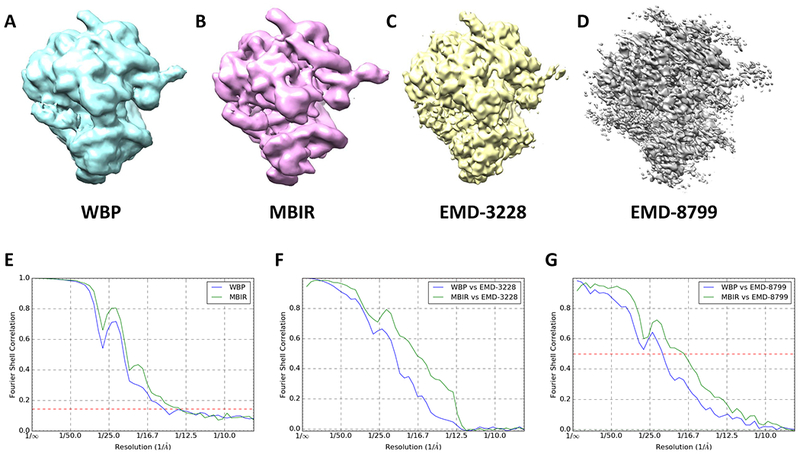
(A) the averaged map of WBP’s subtomograms. (B) the averaged map of MBIR’s subtomograms. (C) the published subtomogram average map EMD-3228. (D) the published subtomogram average map EMD-8799. (E) the comparison of the “gold standard” FSC curves between WBP and MBIR maps. (F) FSC curves between the reference map EMD-3228 in (C) and the averaged subtomograms (WBP in blue and MBIR in green). (G) FSC curves between the reference map EMD-8779 in (D) and the averaged subtomograms (WBP in blue and MBIR in green).
To further assess the quality of the averaged subtomograms from MBIR and WBP tomograms, we calculated the FSCs between them and additional reference maps at higher reported resolutions. The reference shown in Fig. 7C is the published subtomogram average map (EMD-3228) solved by Relion package at 13Å resolution with 3100 unbinned subtomograms of the same dataset (Bharat et al., 2015). The MBIR’s FSC (green line in Fig. 7F) shows significant overall improvement compared with WBP’s FSC (blue line in Fig. 7F), implying the higher reconstruction quality of the subtomogram average from MBIR. Furthermore, another subtomogram average map (EMD-8799, Fig. 7D) with the reported resolution of 7.8Å, which was solved by emClarity package using the same unbinned dataset (Himes and Zhang, 2018), serves as another high-resolution reference to assess the quality of the subtomogram averages. The apparent gap between FSCs in Fig. 7G confirms the better quality of the subtomogram average from MBIR than WBP.
4. Discussion
In addition to the most commonly used WBP method (Radermacher, 1992), many algorithms have been developed for 3D reconstruction of electron tomography data, such as algebra methods (Gilbert, 1972; Gordon et al., 1970; Marabini et al., 1998; Penczek et al., 2018; Wan et al., 2011), Fourier transformation-based methods (Grigorieff, 1998; Penczek et al., 2004; Sandberg et al., 2003; Zhang et al., 2008), Fourier-based interpolation methods (Chen and Forster, 2014; Fessler and Sutton, 2003; Knopp et al., 2007; Matej et al., 2004), compressed sensing-based reconstruction methods (Deng et al., 2016; Goris et al., 2012; Guay et al., 2016; Leary et al., 2013), Monte Carlo-based method (Gregson et al., 2012; Turoňová et al., 2015), nonlinear diffusion filter technique (Chen et al., 2016; Perona and Malik, 1990), statistical reconstruction method (Paavolainen et al., 2014), etc. As a widely explored 2D/3D reconstruction method, MBIR has a growing impact in the medical, industrial, and scientific imaging fields. In the present work, we introduced the MBIR method into biological ET and corroborated the substantial advantages of MBIR over current, state-of-the-art reconstruction methods for both cryo and plastic embedded data. MBIR employs a model of the image formation process and combines it with a prior model of the 3D object to formulate a MAP estimation cost function which rejects measurements that do not fit the model. MBIR is finding a fit that balances between generating a reconstruction that matches the data and constraining it to have some properties that any real world object would have. Our results on both simulated and experimental data have effectively demonstrated the excellent performance of MBIR in contrast enhancement, missing wedge artifacts reduction, and missing information restoration, generating visually and quantitatively accurate tomograms that also allow improved subtomogram averaging.
At the beginning of our subtomogram averaging study, we were puzzled by the “gold standard” FSC curves from the half maps (Fig. 7E) since the improvement of MBIR’s FSC is only marginal despite the dramatic enhancement at the tomogram level. The tails of FSCs in Fig. 7E hover around a correlation at 0.1, rather than completely dropping to zero, which is in general indicative of some artificial correlation. In contrast, the FSC curves in Fig. 7F-G show significant improvements when comparing the averaged subtomograms with independently solved reference maps, and clearly drop to zero at high spatial frequencies. Therefore, we should interpret the “gold standard” FSC from the half maps with caution, instead of blindly trusting it, especially when some artificial correlations prevent the FSC from dropping to zero.
Cryo-ET tomographic reconstruction usually suffers from problems such as a high level of noise, poor contrast, artifacts caused by the missing wedge issue and unreliable restoration of missing information, which poses significant challenges to subsequent analysis of the tomograms. The clear benefits of MBIR should not only help achieve better quality reconstruction as shown in this work, but also facilitate further visualization and computational tasks, such as biological feature interpretation, structure segmentation and ultimately help advance cryo-ET to higher resolution.
While MBIR significantly improves tomography quality, the extensive computational load makes its speed slower compared to other approaches (Table S2) and currently restricts the application of MBIR to small datasets. Recently, a computationally optimized algorithm termed Non-Uniform Parallel Super-Voxel (NU-PSV) has been developed for MBIR 3D reconstruction of CT images which enables rapid and massively parallel reconstruction while ensuring fast convergence (Wang et al., 2017). Thus, it is desirable to implement this powerful parallel algorithm into cryo-ET MBIR reconstruction in the future, using either GPU or multicore CPUs on multiple computer nodes. Furthermore, MBIR should be generalized to support tomographic reconstruction using double-tilt geometry and incorporate the objective lens contrast transfer function (e.g. defocus, astigmatism, Volta phase shift) into its forward image formation model during its iterative reconstruction process.
Supplementary Material
Fig. S1. Comparison of the representative central XY-slices. (A) the phantom. (B-E) the tomograms reconstructed by WBP (B), SIRT (C), ICON (D) and MBIR (E) from a dataset simulated with tilt angle range −60° ~ +60°, angular increment=2° and SNR=0.5.
Fig. S2. Comparison of the power spectra of the region corresponding to the missing wedge. (A) the phantom. (B-E) the tomograms reconstructed using WBP (B), SIRT (C), ICON (D) and MBIR (E) using a dataset simulated with tilt angle range −60° ~ +60°, angular increment=2° and SNR=0.5. The figures are contrast-normalized to view the information in the region of interest and ensure the reliability of comparison.
Fig. S3. Comparisons of FSC curves between the missing wedge regions. The FSCs were calculated between the phantom and the tomograms reconstructed by different methods using simulated datasets with different tilt ranges. (A-C) show the comparison of the missing wedge’s FSCs of different methods for a certain tilt range. (D-G) show the comparison of the missing wedge’s FSCs of one method for different tilt ranges. The datasets were simulated with varying tilt ranges (−70°~+70°, −60°~+60°, −50°~+50°, angular interval = 2°, SNR=0.5).
Fig. S4. Comparisons of FSC curves between the phantom and the tomograms reconstructed by different methods using simulated datasets with different tilt ranges. (A-C) show the comparison of FSCs of different methods for a certain tilt range. (D-G) show the comparison of FSCs of one method for different tilt ranges. The datasets were simulated with varying tilt ranges (−70°~+70°, −60°~+60°, −50°~+50°, angular interval = 2°, SNR=0.5).
Fig. S5. Comparison of 0° tilt image from tilt series simulated at varying noise levels. The dataset was simulated with tilt range −60°~+60°, angular interval = 2°.
Fig. S6. Comparisons of FSC curves between the phantom and the tomograms reconstructed by different methods using simulated datasets at different noise levels. (A-C) show the comparison of FSCs of different methods at a certain noise level. (D-G) show the comparison of FSCs of one method at different noise levels. The datasets were simulated with varying noise levels (SNR=0.5, 0.25, 0.125 tilt range is −60°~+60°, angular interval = 2°).
Fig. S7. Comparisons of FSC curves between the phantom and the tomograms reconstructed by different methods using simulated datasets with different angular increments. (A-C) show the comparison of FSCs of different methods at a certain angular increment. (D-G) show the comparison of FSCs of one method at different angular increments. The datasets were simulated with varying angular increments (1°, 2°, 4°, tilt range is −60°~+60°, SNR=0.5).
Fig. S8. Observations of aliasing issue in the central XZ-slice power spectra of cryo-ET tomograms downloaded from EMDB. The EMDB ID is marked at the bottom of each image.
Fig. S9. Comparison of the central XZ-slice power spectra from the tomograms reconstructed by different reconstruction techniques. Each row shows the power spectra of central XZ-slices from the same dataset using different methods. Each column shows the power spectra from the same method applied to different datasets. The data type and EMPIAR ID are denoted at the right side of each row.
Fig. S10. Comparison of reprojections at 0° when the tomograms are generated using different reconstruction techniques without the corresponding tilt. Each row shows the reprojections from the same dataset using different methods. Each column shows the reprojections from the same method applied to different datasets. The data type and EMPIAR ID are denoted at the right side of each row. In each image, the gold marker indicted by a white arrow is displayed with corresponding zoomed-in view.
Fig. S11. Comparison of reprojections at 45° when the tomograms are generated using different reconstruction techniques without the corresponding tilt. The details are the same as described in Fig. S10.
Table S1. A summary of datasets used in this study.
Table S2. Computational speeds of different reconstruction techniques. The input data size is 400 pixels × 400 pixels × 61 tilts and the output tomogram size is 400 pixels × 400 pixels × 128 pixels. The CPU model is Intel(R) Core(TM) i7-6900K @ 3.20GHz. The GPU model is NVIDIA GeForce GTX 1080.
Highlights:
MBIR can significantly boost contrast of tomograms of cryo specimens.
MBIR can significantly reduce missing wedge artifacts and retain sharp features.
MBIR can partially restore the missing information in the unsampled angular region.
MBIR can improve the resolution of subtomogram averages.
Acknowledgements
This work was supported in part by Showalter Faculty Scholar grant. We thank Ms. Brenda Gonzalez for her assistance in preparation of the manuscript.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Competing Interests
The authors declare no competing financial interests.
References
- Albert S, Schaffer M, Beck F, Mosalaganti S, Asano S, Thomas HF, Plitzko JM, Beck M, Baumeister W, Engel BD, 2017. Proteasomes tether to two distinct sites at the nuclear pore complex. Proc. Natl. Acad. Sci. U. S. A 114, 13726–13731. 10.1073/pnas.1716305114 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bharat TAM, Russo CJ, Löwe J, Passmore LA, Scheres SHW, 2015. Advances in Single-Particle Electron Cryomicroscopy Structure Determination applied to Sub-tomogram Averaging. Structure 23, 1743–1753. 10.1016/j.str.2015.06.026 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bharat TAM, Scheres SHW, 2016. Resolving macromolecular structures from electron cryo-tomography data using subtomogram averaging in RELION. Nat. Protoc 11, 2054–2065. 10.1038/nprot.2016.124 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bykov YS, Schaffer M, Dodonova SO, Albert S, Plitzko JM, Baumeister W, Engel BD, Briggs JA, 2017. The structure of the COPI coat determined within the cell. Elife 6 10.7554/eLife.32493 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cardone G, Grünewald K, Steven AC, 2005. A resolution criterion for electron tomography based on cross-validation. J. Struct. Biol 151, 117–129. 10.1016/jjsb.2005.04.006 [DOI] [PubMed] [Google Scholar]
- Chang Y-W, Kjasr A, Ortega DR, Kovacikova G, Sutherland JA, Rettberg LA, Taylor RK, Jensen GJ, 2017. Architecture of the Vibrio cholerae toxin-coregulated pilus machine revealed by electron cryotomography. Nat Microbiol 2, 16269 10.1038/nmicrobiol.2016.269 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen Y, Forster F, 2014. Iterative reconstruction of cryo-electron tomograms using nonuniform fast Fourier transforms. J. Struct. Biol 185, 309–316. 10.1016/jjsb.2013.12.001 [DOI] [PubMed] [Google Scholar]
- Chen Y, Zhang Y, Zhang K, Deng Y, Wang S, Zhang F, Sun F, 2016. FIRT: Filtered iterative reconstruction technique with information restoration. J. Struct. Biol 195, 49–61. 10.1016/jjsb.2016.04.015 [DOI] [PubMed] [Google Scholar]
- Deng Y, Chen Y, Zhang Y, Wang S, Zhang F, Sun F, 2016. ICON: 3D reconstruction with “missing-information” restoration in biological electron tomography. J. Struct. Biol 195, 100–112. 10.1016/jjsb.2016.04.004 [DOI] [PubMed] [Google Scholar]
- Fessler JA, Sutton BP, 2003. Nonuniform fast fourier transforms using min-max interpolation. IEEE Trans. Signal Process 51, 560–574. 10.1109/tsp.2002.807005 [DOI] [Google Scholar]
- Gilbert P, 1972. Iterative methods for the three-dimensional reconstruction of an object from projections. J. Theor. Biol 36, 105–117. 10.1016/0022-5193(72)90180-4 [DOI] [PubMed] [Google Scholar]
- Gordon R, Bender R, Herman GT, 1970. Algebraic reconstruction techniques (ART) for three-dimensional electron microscopy and x-ray photography. J. Theor. Biol 29, 471–481. [DOI] [PubMed] [Google Scholar]
- Goris B, Van den Broek W, Batenburg KJ, Heidari Mezerji H, Bals S, 2012. Electron tomography based on a total variation minimization reconstruction technique. Ultramicroscopy 120–130. 10.1016/j.ultramic.2011.11.004 [DOI] [Google Scholar]
- Gregson J, Krimerman M, Hullin MB, Heidrich W, 2012. Stochastic tomography and its applications in 3D imaging of mixing fluids. ACM Trans. Graph 31, 1–10. 10.1145/2185520.2185548 [DOI] [Google Scholar]
- Grigorieff N, 1998. Three-dimensional structure of bovine NADH:ubiquinone oxidoreductase (complex I) at 22 A in ice. J. Mol. Biol 277, 1033–1046. 10.1006/jmbi.1998.1668 [DOI] [PubMed] [Google Scholar]
- Guay MD, Czaja W, Aronova MA, Leapman RD, 2016. Compressed Sensing Electron Tomography for Determining Biological Structure. Sci. Rep 6, 27614 10.1038/srep27614 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Herman GT, 2009. Fundamentals of Computerized Tomography: Image Reconstruction from Projections. Springer. [Google Scholar]
- Himes BA, Zhang P, 2018. emClarity: software for high-resolution cryo-electron tomography and subtomogram averaging. Nat. Methods, 10.1038/s41592-018-0167-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- Himes B, Zhang P, 2017. High resolution in situ structural determination of heterogeneous specimen, 10.1101/231605 [DOI] [Google Scholar]
- Iudin A, Korir PK, Salavert-Torres J, Kleywegt GJ, Patwardhan A, 2016. EMPIAR: a public archive forraw electron microscopy image data. Nat. Methods 13, 387–388. 10.1038/nmeth.3806 [DOI] [PubMed] [Google Scholar]
- Khoshouei M, Pfeffer S, Baumeister W, Förster F, Danev R, 2017. Subtomogram analysis using the Volta phase plate. J. Struct. Biol 197, 94–101. 10.1016/jjsb.2016.05.009 [DOI] [PubMed] [Google Scholar]
- Knopp T, Kunis S, Potts D, 2007. A note on the iterative MRI reconstruction from nonuniform k-space data. Int. J. Biomed. Imaging 2007, 24727 10.1155/2007/24727 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kremer JR, Mastronarde DN, McIntosh JR, 1996. Computer visualization of three-dimensional image data using IMOD. J. Struct. Biol 116, 71–76. 10.1006/jsbi.1996.0013 [DOI] [PubMed] [Google Scholar]
- Kunz M, Frangakis AS, 2014. Super-sampling SART with ordered subsets. J. Struct. Biol 188, 107–115. 10.1016/jjsb.2014.09.010 [DOI] [PubMed] [Google Scholar]
- Lawson CL, Baker ML, Best C, Bi C, Dougherty M, Feng P, van Ginkel G, Devkota B, Lagerstedt L, Ludtke SJ, Newman RH, Oldfield TJ, Rees L, Sahni G, Sala R, Velankar S, Warren J, Westbrook JD, Henrick K, Kleywegt GJ, Berman HM, Chiu W, 2011. EMDataBank.org: unified data resource for CryoEM. Nucleic Acids Res. 39, D456–64. 10.1093/nar/gkq880 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leary R, Saghi Z, Midgley PA, Holland DJ, 2013. Compressed sensing electron tomography. Ultramicroscopy 131, 70–91. 10.1016/j.ultramic.2013.03.019 [DOI] [PubMed] [Google Scholar]
- Lučić V, Förster F, Baumeister W, 2005. STRUCTURAL STUDIES BY ELECTRON TOMOGRAPHY: From Cells to Molecules. Annu. Rev. Biochem 74, 833–865. 10.1146/annurev.biochem.73.011303.074112 [DOI] [PubMed] [Google Scholar]
- Marabini R, Herman GT, Carazo JM, 1998. 3D reconstruction in electron microscopy using ART with smooth spherically symmetric volume elements (blobs). Ultramicroscopy 72, 53–65. [DOI] [PubMed] [Google Scholar]
- Matej S, Fessler JA, Kazantsev IG, 2004. Iterative tomographic image reconstruction using Fourier-based forward and back-projectors. IEEE Trans. Med. Imaging 23, 401–412. 10.1109/TMI.2004.824233 [DOI] [PubMed] [Google Scholar]
- Orlova EV, Saibil HR, 2011. Structural Analysis of Macromolecular Assemblies by Electron Microscopy. Chem. Rev 111, 7710–7748. 10.1021/crl00353t [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paavolainen L, Acar E, Tuna U, Peltonen S, Moriya T, Soonsawad P, Marjomäki V, Cheng RH, Ruotsalainen U, 2014. Compensation of missing wedge effects with sequential statisticalreconstruction in electron tomography. PLoS One 9, e108978 10.1371/joumal.pone.0108978 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Penczek PA, Renka R, Schomberg H, 2004. Gridding-based direct Fourier inversion of the three-dimensional ray transform. J. Opt. Soc. Am. A Opt. Image Sci. Vis 21, 499–509. [DOI] [PubMed] [Google Scholar]
- Penczek P, Marko M, Buttle K, Frank J, 1995. Double-tilt electron tomography. Ultramicroscopy 60, 393–410. [DOI] [PubMed] [Google Scholar]
- Penczek P, Radermacher M, Frank J, 2018. Three-dimensional reconstruction of single particles embedded in ice, in: Series in Structural Biology,pp.175–195. 10.1142/9789813234864_0015 [DOI] [PubMed] [Google Scholar]
- Perona P, Malik J, 1990. Scale-space and edge detection using anisotropic diffusion. IEEE Trans. Pattern Anal. Mach. Intell 12, 629–639. 10.1109/34.56205 [DOI] [Google Scholar]
- Pilhofer M, Ladinsky MS, McDowall AW, Jensen GJ, 2010. Bacterial TEM: new insights from cryo-microscopy. Methods Cell Biol. 96, 21–45. 10.1016/S0091-679X(10)96002-0 [DOI] [PubMed] [Google Scholar]
- Radermacher M, 1992. Weighted Back-Projection Methods, in: Electron Tomography, pp. 91–115. 10.1007/978-1-4757-2163-8_5 [DOI] [Google Scholar]
- Sandberg K, Mastronarde DN, Beylkin G, 2003. A fast reconstruction algorithm for electron microscope tomography. J. Struct. Biol 144, 61–72. [DOI] [PubMed] [Google Scholar]
- Schur FKM, Dick RA, Hagen WJH, Vogt VM, Briggs JAG, 2015. The Structure of Immature Virus-Like Rous Sarcoma Virus Gag Particles Reveals a Structural Role for the p10 Domain in Assembly. J. Virol 89, 10294–10302. 10.1128/JVI.01502-15 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shahmoradian SH, Galiano MR, Wu C, Chen S, Rasband MN, Mobley WC, Chiu W, 2014. Preparation of Primary Neurons for Visualizing Neurites in a Frozen-hydrated State Using Cryo-Electron Tomography. Journal of Visualized Experiments, 10.3791/50783 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tang G, Peng L, Baldwin PR, Mann DS, Jiang W, Rees I, Ludtke SJ, 2007. EMAN2: an extensible image processing suite for electron microscopy. J. Struct. Biol 157, 38–46. 10.1016/jjsb.2006.05.009 [DOI] [PubMed] [Google Scholar]
- Turoňová B, Marsalek L, Davidovič T, Slusallek P, 2015. Progressive Stochastic Reconstruction Technique (PSRT) for cryo electron tomography. J. Struct. Biol 189, 195–206. 10.1016/j.jsb.2015.01.011 [DOI] [PubMed] [Google Scholar]
- Vanhecke D, Asano S, Kochovski Z, Femandez-Busnadiego R, Schrod N, Baumeister W, Lucic V, 2011. Cryo-electron tomography: methodology, developments and biological applications. J. Microsc 242, 221–227. https://doi.org/10.1111/j.1365-2818.2010.03478.x [DOI] [PubMed] [Google Scholar]
- Venkatakrishnan SV, Drummy LF, Jackson MA, De Graef M, Simmons J, Bouman CA, 2013. A model based iterative reconstruction algorithm for high angle annular dark field-scanning transmission electron microscope (HAADF-STEM) tomography. IEEE Trans. Image Process 22, 4532–4544. 10.1109/TIP.2013.2277784 [DOI] [PubMed] [Google Scholar]
- Venkatakrishnan SV, Drummy LF, Jackson M, De Graef M, Simmons J, Bouman CA, 2015. Model-Based Iterative Reconstruction for Bright-Field Electron Tomography. IEEE Transactions on Computational Imaging 1, 1–15. 10.1109/tci.2014.2371751 [DOI] [Google Scholar]
- Wang X, Sabne A, Sakdhnagool P, Kisner SJ, Bouman CA, Midkiff SP, 2017. Massively parallel 3D image reconstruction, in: Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis on - SC ’17. 10.1145/3126908.3126911 [DOI] [Google Scholar]
- Wan X, Zhang F, Chu Q, Zhang K, Sun F, Yuan B, Liu Z, 2011. Three-dimensional reconstruction using an adaptive simultaneous algebraic reconstruction technique in electron tomography. J. Struct. Biol 175, 277–287. 10.1016/jjsb.2011.06.002 [DOI] [PubMed] [Google Scholar]
- Wei Y, Wang G, Hsieh J, 2005. An intuitive discussion on the ideal ramp filter in computed tomography (I). Comput. Math. Appl 49, 731–740. 10.1016/j.camwa.2004.10.034 [DOI] [Google Scholar]
- Zhang W, Kimmel M, Spahn CMT, Penczek PA, 2008. Heterogeneity of large macromolecular complexes revealed by 3D cryo-EM variance analysis. Structure 16, 1770–1776. 10.1016/j.str.2008.10.011 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Fig. S1. Comparison of the representative central XY-slices. (A) the phantom. (B-E) the tomograms reconstructed by WBP (B), SIRT (C), ICON (D) and MBIR (E) from a dataset simulated with tilt angle range −60° ~ +60°, angular increment=2° and SNR=0.5.
Fig. S2. Comparison of the power spectra of the region corresponding to the missing wedge. (A) the phantom. (B-E) the tomograms reconstructed using WBP (B), SIRT (C), ICON (D) and MBIR (E) using a dataset simulated with tilt angle range −60° ~ +60°, angular increment=2° and SNR=0.5. The figures are contrast-normalized to view the information in the region of interest and ensure the reliability of comparison.
Fig. S3. Comparisons of FSC curves between the missing wedge regions. The FSCs were calculated between the phantom and the tomograms reconstructed by different methods using simulated datasets with different tilt ranges. (A-C) show the comparison of the missing wedge’s FSCs of different methods for a certain tilt range. (D-G) show the comparison of the missing wedge’s FSCs of one method for different tilt ranges. The datasets were simulated with varying tilt ranges (−70°~+70°, −60°~+60°, −50°~+50°, angular interval = 2°, SNR=0.5).
Fig. S4. Comparisons of FSC curves between the phantom and the tomograms reconstructed by different methods using simulated datasets with different tilt ranges. (A-C) show the comparison of FSCs of different methods for a certain tilt range. (D-G) show the comparison of FSCs of one method for different tilt ranges. The datasets were simulated with varying tilt ranges (−70°~+70°, −60°~+60°, −50°~+50°, angular interval = 2°, SNR=0.5).
Fig. S5. Comparison of 0° tilt image from tilt series simulated at varying noise levels. The dataset was simulated with tilt range −60°~+60°, angular interval = 2°.
Fig. S6. Comparisons of FSC curves between the phantom and the tomograms reconstructed by different methods using simulated datasets at different noise levels. (A-C) show the comparison of FSCs of different methods at a certain noise level. (D-G) show the comparison of FSCs of one method at different noise levels. The datasets were simulated with varying noise levels (SNR=0.5, 0.25, 0.125 tilt range is −60°~+60°, angular interval = 2°).
Fig. S7. Comparisons of FSC curves between the phantom and the tomograms reconstructed by different methods using simulated datasets with different angular increments. (A-C) show the comparison of FSCs of different methods at a certain angular increment. (D-G) show the comparison of FSCs of one method at different angular increments. The datasets were simulated with varying angular increments (1°, 2°, 4°, tilt range is −60°~+60°, SNR=0.5).
Fig. S8. Observations of aliasing issue in the central XZ-slice power spectra of cryo-ET tomograms downloaded from EMDB. The EMDB ID is marked at the bottom of each image.
Fig. S9. Comparison of the central XZ-slice power spectra from the tomograms reconstructed by different reconstruction techniques. Each row shows the power spectra of central XZ-slices from the same dataset using different methods. Each column shows the power spectra from the same method applied to different datasets. The data type and EMPIAR ID are denoted at the right side of each row.
Fig. S10. Comparison of reprojections at 0° when the tomograms are generated using different reconstruction techniques without the corresponding tilt. Each row shows the reprojections from the same dataset using different methods. Each column shows the reprojections from the same method applied to different datasets. The data type and EMPIAR ID are denoted at the right side of each row. In each image, the gold marker indicted by a white arrow is displayed with corresponding zoomed-in view.
Fig. S11. Comparison of reprojections at 45° when the tomograms are generated using different reconstruction techniques without the corresponding tilt. The details are the same as described in Fig. S10.
Table S1. A summary of datasets used in this study.
Table S2. Computational speeds of different reconstruction techniques. The input data size is 400 pixels × 400 pixels × 61 tilts and the output tomogram size is 400 pixels × 400 pixels × 128 pixels. The CPU model is Intel(R) Core(TM) i7-6900K @ 3.20GHz. The GPU model is NVIDIA GeForce GTX 1080.


