Self-organization, entropy and allostery

Abstract

Allostery is a fundamental regulatory mechanism in biology. Although generally accepted that it is a dynamics-driven process, the exact molecular mechanism of allosteric signal transmission is hotly debated. We argue that allostery is as a part of a bigger picture that also includes fractal-like properties of protein interior, hierarchical protein folding and entropy-driven molecular recognition. Although so far all these phenomena were studied separately, they stem from the same common root: self-organization of polypeptide chains and, thus, has to be studied collectively. This merge will allow the cross-referencing of a broad spectrum of multi-disciplinary data facilitating progress in all these fields.

Introduction

Allostery is a process that regulates the activity of enzymes via binding a modulator at a distal site, sterically different from the chemically active site. It is now well recognized that allostery is a fundamental property of biological macromolecules that regulates most, if not all, biological processes and serves as a foundation for the phenomenon of life [1–3]. It has been intensively studied since the early 1960s when the term was introduced by Jacques Monod and François Jacob [4,5]. These efforts are fueled not only by interest in the fundamental principles of biology but also by the very pragmatic motives as allosteric drugs are viewed as promising therapeutic agents [6,7]. Significant progress has been made in understanding the molecular mechanism of allostery, but the exact nature of the signal transmission between the ligand-binding site and the active site remains a hot topic. Although the first phenomenological models of allostery included mandatory changes in protein structures [8–11], ca. 20 years after the concept of allostery was introduced, Cooper and Dryden [12] pointed out that allosteric regulation can be achieved with no structural changes. They demonstrated that a simple variation in thermal vibration frequency can underlie the long distance signaling. This was an important conceptual breakthrough that completed the thermodynamic portrait of allostery. While changes in protein structure can be directly associated with the enthalpic part of the free energy changes, modulation of thermal vibrations represents the free energy entropic share. It took another 20 years to prove that entropy-driven allostery is real and can be observed, in particular, in catabolite-activating protein (CAP) [13,14] and PDZ domains [15]. There is, however, a significant problem in studying any entropy-related phenomena, as entropy, due to its combinatorial nature, is an elusive concept. Entropic forces emerge from stochastic interactions between a large number of elements and studying them requires a complete picture of the interactions inside the object in question. Our goal is to alleviate this problem by putting entropy-driven allostery into a wider context of protein physics. We over-view the current understanding of the dynamics and interactions inside proteins in an attempt to piece together several areas of knowledge that often remain disconnected. Our purpose is to present an argument that allostery is not a peculiar, protein-specific signaling mechanism, but it is a universal feature that has analogs in numerous self-organizing phenomena that can be observed throughout the universe. Practical implications of these observations are also discussed.

Fractal characteristics of protein interior

Although recursive self-similar objects, that these days we would call fractals, were known in mathematics for several centuries, natural fractal-like objects were first introduced by Benoit Mandelbrot in his seminal paper in 1967 [16], with the term ‘fractal’ soon to follow [17]. By definition, fractal-like objects are self-similar, or, in other words, scale-invariant, i.e. a portion of the object is a reduced copy of the whole object (Figure 1). First observations on the fractal form of protein interior were made in 1980 by Stapleton et al. [18]. They studied electron spin relaxation in several proteins and found that temperature dependence of the relaxation did not follow a well-established formula for solid 3D crystals. Rather, it manifested an unusual non-integer power law. The authors were, apparently, aware of the Mandelbrot’s book that was translated to English just a few years earlier [19] and came to a conclusion that at least three different heme proteins have fractal distribution of atoms with the fractional dimensionality close to the theoretical value for 3D ‘self-avoiding walk’ systems. Almost at the same time, several groups pointed out that protein surface also has fractal dimensionality, a feature that Mandelbrot termed ‘roughness’ [20–22]. These findings, however, did not produce any significant impact in the field as, at that time, the major dispute about protein interior was whether it is a tightly packed crystalline state [23,24] or more like a liquid oil drop [25] with the former model becoming an apparent winner [26]. Nevertheless, in 2001, Liang and Dill [27] published an extended study of the packing in proteins and confirmed that protein packing follows neither the liquid nor the crystal-line models completely. They found that proteins contain multiple voids of varying sizes with few large voids, a larger number of medium-sized voids and numerous small voids, a distribution typical for certain type of fractals (Figure 1B). Such distribution was in agreement with the earlier analysis from Janet Thornton’s group that studied internal cavities and buried waters in 75 proteins and found that 58% of buried water molecules were isolated, 22% belonged to clusters containing only two water molecules and 20% waters were in larger clusters [28]. Analyzing 636 proteins from different folds, Liang and Dill [27] showed that packing follows a typical fractal power law V ∝ R^D (where V is the protein volume, R is the protein length and D is fractal dimension) with D≈2.47±0.04, a number consistent with the theoretical predictions for random spheres stochastically packed into a fractal cluster [29,30]. More comprehensive analysis by Enright and Leitner found later that average fractal dimension of 200 proteins was close to 2.5 with smaller proteins having D≈2.3 and larger proteins up to 2.7. They also noted that fractal dimension of a single protein was itself an average value over all regions of the protein. Similar values for protein fractal dimensionality were obtained later by multiple authors [31–33]. Even intrinsically disordered proteins have been shown to follow a fractal-like density distribution albeit with smaller dimensionality [34]. Several groups studied fractal dimensionality of protein surfaces, indicating that it can play an important role in molecular recognition [35]. This raises a question — why fractal-like features are so predominant in proteins and what are the consequences of their fractality for their dynamic properties?

Figure 1. Fractals and natural fractal-like objects.

(A) Sierpinski triangle. Each triangle contains three reduced copies of the original. (B) An example of three-dimensional fractal: Menger sponge. (C) Natural fractal-like object: a tree. Each branch contains smaller branches of a similar shape. (D) Self-similar rock formation. Smaller areas of the formation look like reduced copies of the whole object.

Percolation theory and origin of fractal objects

The concept of fractal self-similar objects is tightly bound to the phenomenon of critical percolation point in the percolation theory. The latter is a branch of mathematics that studies connected clusters in random graphs. The term ‘percolation’ was introduced in 1957 by Broadbent and Hammersley [36] in their pioneering work where they analyzed diffusion of liquids in porous materials. Since then, this field has experienced an explosion of applications in areas from microbiology to sociology and astrophysics [37]. The main reason for the percolation theory popularity is that it studies the behavior of complex systems where a large number of elements randomly interact with each other forming distinctive groups or clusters. Not surprisingly, a topic of such generality covers an infinitely diverse set of phenomena linking percolation to nonlinear dynamics, chaos theory and self-organized criticality [38]. The central point of the percolation theory is the so-called critical threshold: a point in a complex system development when the size of an average cluster that was growing steadily and slowly before the critical zone (Figure 2A–C) undergoes explosion with an exponentially fast appearance of a so-called giant (Figure 2E), a cluster with the size close to the size of the whole system. A remarkable feature of the ‘giant’ is that it is always a self-similar, fractal object. If the graph continues to grow beyond the critical point, it loses its self-similarity (Figure 2F). According to the percolation theory, natural fractal objects are so ubiquitous because, in many systems, at the moment when the ‘giant’ appears, the system undergoes a transformation that changes the very nature of the object. The fractal-like appearance of the new object is, thus, a ‘snapshot’ of its stochastic origin, a birthmark. It can be, for example, a fracture of a metal piece, or a lightning strike, or formation of a watercourse. In these cases, after the ‘giant’ formation, a piece of metal breaks into two parts, electric potential difference in the atmosphere discharges and water in the river starts running toward the ocean. In other cases, a critical point is passed quickly without obvious changes and the system moves toward a nonfractal, post-critical, state: water percolates through a porous object and fills in all the pores, spins in a ferromagnetic become all ordered etc. Clearly, proteins belong to the first class of systems as they are fractal objects. It is also clear that the only source of the fractal-like packing can be the protein folding process. So what is the connection between the percolation theory and protein folding?

Figure 2. Origin of a fractal-like graph in a process of random geometric graph growth.

(A) The process starts with dropping points randomly on the plane (gray). If two points are closer than a particular threshold distance, they get connected. A few small (2–3 points) clusters are formed (dark blue). (B) Medium size clusters of 8–10 points evenly spread over the plane (dark red). (C) Medium clusters merge into three larger clusters highlighted by magenta color. (D) The system approaches percolation critical point. Three separate clusters fill in the plane but are still disconnected. (E) Critical point: the ‘giant’ graph reaches the size of the whole plane. It has a characteristic tree-like fractal structure. (F) Post-critical state of the graph: the plane is covered with a uniform graph that lacks fractal features. Pictures are adapted from educational video provided by EPFL, Switzerland (Course: Networks out of Control) (https://youtu.be/NUisb1-INIE).

Protein folding and percolation

In 1968, Levinthal [39] noted that proteins should have a particular path for folding since due to their enormous number of degrees of freedom, a completely random process of folding would be unrealistically slow [40]. A few years later, Wetlaufer [41] suggested that rapid protein folding is possible only if it progresses through a nucleation step, when small regions of the polypeptide sequence form relatively stable intermediates that serve as nucleation centers for the folding process. In 1995, Englander and coauthors used the hydrogen exchange method to show that cytochrome c does undergo an unfolding process through discrete partially unfolded states, confirming the idea of protein folding intermediates [42]. Soon after that, Peter Wolynes’ group introduced a concept of ‘foldons’, elementary folding units that randomly occur at the early stage of protein folding [43]. And, although several authors raised concerns about the universality of foldon-driven folding, pointing out that certain small proteins fold with two-state kinetics [44], later development of experimental techniques confirmed the driving role of foldons [45,46]. A common theoretical view on protein folding, currently, is described as a process of sliding down a rugged funnel in a free energy space — the so-called ‘energy landscape’ concept [47] introduced by Onuchic and Wolynes in a set of influential papers [48–50]. Foldons, from the energy landscape point of view, correspond to the rugged parts of the funnel slope representing metastable states of the system, which are moving stochastically down toward the native fold of the protein at the bottom of the funnel. Although this model is widely accepted and has proved to be very helpful, it cannot (despite the fractal-like term ‘roughness’ for the funnel surface) explain why all the proteins are fractals as it is equally applicable to folding of both 3D objects and objects with fractal dimension. To understand the origin of protein fractality, one has to look at protein folding from the percolation theory point of view.

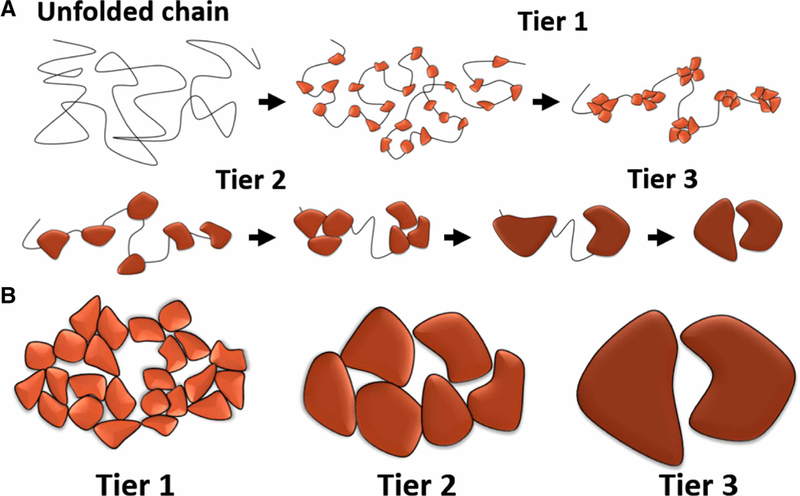
In percolation theory terms, protein folding can be viewed as a graph with spontaneously growing connectivity where vertices correspond to the protein residues and edges to the noncovalent contacts between them. Using an analogy with the formation of the fractal-like graph presented in Figure 2, we can suggest that protein folding occurs hierarchically, that is, similar to tree branches, there should be building blocks of several tiers (Figure 3A). In the early stage of the folding process, blocks of the first tier should appear along the unfolded polypeptide sequence. These blocks should be the most stable with the most dense packing. Most probably, native contacts play the most important role at this stage as they were shown to determine folding of small proteins [51,52]. As the folding progresses, the role of non-native contacts may increase [53] as the first tier blocks should interact with each other and form blocks of the second tier and so on. Finally, when the last, the largest, building blocks interact, the process of folding stops leaving the ‘giant’ fractal-like cluster that has the size of the whole system. Presumably, the increasing size of building blocks should lead to less dense packing between them with larger voids in their interfaces that produce the observed fractal distribution of voids in proteins [27] (Figure 3B). The idea of hierarchical folding, however, is not a new one as, in general terms, it was proposed by George Rose back in 1979 [54], long before the concept of foldons had been introduced. Simply analyzing the geometry of 22 globular proteins, he came to the conclusion that they can be (unlike ‘a ball of yarn’) divided into domains defined as ‘separable, continuous chain regions of the polypeptide chain’. He showed that these domains can be iteratively decomposed into subdomains, with them also being decomposable, and so forth. These ideas developed further and, for example, were successfully used in protein structure prediction [55]. A similar concept was presented by Karplus and Weaver [56] in their ‘diffusion-collision model’ of folding. According to this model, proteins fold via formation of small ‘microdomains’ that through a diffusion process collide and form larger folded blocks.

Figure 3. Hierarchical protein folding.

(A) Progression of a protein folding through three distinctive tiers. (B) Different tiers of folding result in different size of voids between the folded blocks. Tier 3 creates the largest void and tier 1 has the tightest packing.

Although not being derived from the percolation theory, the concepts of ‘foldons’, ‘energy landscape’, ‘hierarchical folding’ and the ‘diffusion-collision model of folding’ all are consistent with the percolation-driven folding process (Figure 3), which can serve as an integrating foundation for the different folding models. As we pointed out earlier, many percolating systems do not stop their development at the critical point and proceed further to form uniform, nonfractal objects (Figure 2F). One can pose a question: why do proteins stop at the percolation critical point, or at least, as it was demonstrated recently by Weber and Pande [57], very close to it? Why did proteins not evolve as tightly packed 3D objects? An interesting observation was made by David Baker’s group who designed a new technique for massive synthesis of de novo proteins. They synthesized 2500 small proteins under a selective pressure of protease treatment in order to generate folds with maximal stability. Comparison of the newly generated proteins with the similar naturally occurring proteins showed that they were significantly more stable [58]. It is unclear if the de novo synthesized proteins were further away from the critical percolation point, but their increased stability is consistent with the idea that natural proteins did not evolve to be maximally stable [59]. A possible explanation of protein packing criticality is that the fine balance between stability and flexibility is important for protein function because intrinsic motions in enzymes are viewed as an important factor for their activity [60,61]. Another explanation can be gleaned from the previous report that criticality can be a universal feature of all self-organizing systems that evolve in an environment that changes in an unpredictable way [62]. According to this paper, criticality is the most beneficial state for the maximal adaptability of any evolving species and can be an essential feature of all living systems.

Two conclusions can be drawn thus far: (1) fractal-like distribution of mass in proteins that, initially, looked like a peculiar oddity is a natural reflection of their self-organizing origin. (2) Because proteins are close to the percolation critical point, their interior is capable of significant fluctuations. Furthermore, we will illustrate how these fluctuations can serve as a foundation for the dynamics-driven allostery.

Fractal interior of proteins and allosteric signaling

Allosteric pathway is a widely used concept in the field that usually suggests a set of neighboring residues that form a continuous path that connects the allosteric and the active sites of the enzyme [2,63–66]. Conceptually, it can be traced back to the ‘Induced fit’ model of Koshland and coauthors [Koshland, Némethy, Filmer (KNF) model] [8] that suggests a cascade of steric interactions propagating through the protein molecule. The competing ‘Conformational selection’ model proposed by Monod, Wyman and Changeux (MWC model) [9] does not require these kinds of sequential interactions. It, instead, relies on the dynamic behavior of the protein, which undergoes a perpetual interchange between two different states driven by thermal energy. A classic example of the allosteric pathway is described by Lockless and Ranganathan [67] in their highly cited 1999 paper where they define a set of evolutionarily coupled residues that connect the allosteric and the active sites in PDZ domains. Despite the initial enthusiasm generated by this publication, the evolutionary approach did not result in significant progress in allostery studies. Besides general criticism of the method [68–70], it was pointed out that the general idea that allosteric pathways can be conserved in the whole family of proteins is rather debatable as protein structures and their dynamics are highly sensitive to small perturbations, regardless of whether it is a mutation or a small molecule binding [71]. It is, thus, hard to expect that signaling pathways can be the same in proteins with significantly different sequences.

An alternative approach, branded as the ‘new view’ of allostery [10], was introduced by several groups in the early, mid-2000s [72–75]. It can be viewed as a development of the MWC model as it is based on the intrinsic protein dynamics. A simple interchange between two conformations in the MWC model is replaced in the ‘new view’ of allostery by a more general process: a population shift in a continuous conformational ensemble. Definition of the conformational ensemble is very broad and can be associated with changes of protein tertiary structure, protein folding/unfolding [75] or even thermal motions of side chains opening the door to the entropy-driven allostery described by Cooper and Dryden [12]. The subsequent accumulation of data made domination of the dynamics-driven allostery model rather evident [76–80], but nevertheless, many authors still attempt to discover allosteric pathways within protein structures as they believe that there should be a certain energetic pathway that connects the allosteric and the active sites [63,81,82]. As the statistical coupling analysis was not very successful in finding these pathways, several attempts were made to detect less straightforward signal transmitters including anisotropic thermal diffusion [83] and streams of entropy [84]. As we mentioned in the Introduction, it is difficult to grasp entropy-related phenomena and the intentions to find a simple mechanistic explanation for allosteric signaling are justifiable.

To make the dynamics-driven allostery more comprehensible, we have recently proposed a ‘violin’ model of allostery that provides a macro-scale analogy for allosteric signal transmission that does not require a certain communication pathway [85]. It is well known that, in case of a violin, bow movement generates characteristic patterns, known as ‘Chladni figures’, that differ for different violin pitches. Obviously, information about the position of the violinist fingers on the fingerboard can be registered throughout the violin body with no particular communication pathways as the vibration mode of the whole instrument is changing. It is easy to draw an analogy between the violin vibrations and vibrations in proteins. The violin bow movement corresponds to thermal motions of the solution that surrounds protein. The movement of residues in proteins corresponds to motion of elementary violin-oscillating units known in acoustics studies as ‘finite elements’ [86]. Interaction between oscillating elements in a violin leads to the formation of standing waves with certain regions of the violin plate moving as distinct groups that can be visualized as the ‘Chladni figures’. Similar to that, thermal motions in proteins do not occur in an evenly distributed, uniform, way as oscillating residues interact with each other and form characteristic clusters of residues that move as semi-rigid objects. They were first observed in 2009 by the Luthey-Shulten group who analyzed molecular dynamics (MD) simulation of a large tRNA:aminoacyl-tRNA synthetase complex [87]. They found that the size and the content of the semi-rigid communities formed by residues and nucleotides were remarkably sensitive to minor modifications of the complex. A single glutamate group transfer from AMP to 2′ -O of tRNA led to a dramatic rearrangement of the community network in the complex. Later, similar dynamic patterns were found by multiple groups in a diverse set of proteins [85,88–96].

The origin of these semi-rigid clusters is easy to understand considering that moving residues can be viewed as a large set of coupled oscillators. At first glance, this suggestion may look too simplistic as it disregards the fact that proteins are chains of covalently bound residues folded into certain secondary structures, and that residues are restricted in their torsional motion. However, as Tirion [97] demonstrated in her 1996 groundbreaking paper, such simplification is rather adequate. A simple ball-and-spring model allowed her to calculate major normal modes of protein motions opening the door to the new area of structural biology — elastic network modeling [98]. The disadvantage of normal mode analysis, however, is that while providing a general view of global motions in the protein, it does not give a detailed picture of local residue mobility that is the key feature of the dynamics-driven allostery. Arrays of coupled oscillators, however, are a very common phenomenon studied by numerous disciplines from nuclear physics to behavioral biology. It is now well recognized that interactions between coupled oscillators can lead to the formation of patterns due to their self-organized synchronization (the most recent overview of the field can be found in ref. [99]). Although self-organization principles are still to be applied to protein dynamics (a few recent works could be mentioned here [33,57,100,101]), emergence of large clusters in an array of coupled oscillators is a common feature of different complex networks. This would be consistent with the observed formation of semi-rigid communities of residues.

The final link that connects self-organized nature of proteins and allostery is the answer to the question: how can variations of the dynamic patterns in a protein regulate its chemical activity? The answer can be found in a series of comprehensive studies performed by the Joshua Wand laboratory [102–105]. They demonstrated that changes in side chain mobility can play a critical role in protein–ligand interactions due to changes in the entropic part of ligand-binding free energy. It is logical to suggest that conformational mobility of the side chains inside the semi-rigid clusters should be different compared with their mobility in the more ‘fluid’ border regions between different clusters, serving as a source of different entropic behavior of the binding site in question.

Conclusions and practical implications

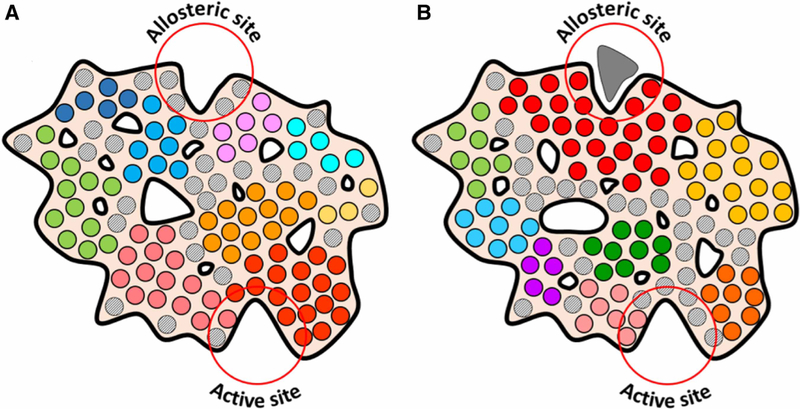
A summary of the entropy-driven allostery mechanism is presented in Figure 4. The general outline of the protein is shown unaltered to emphasize the concept that allosteric signal transmission does not require any structural changes. It does not mean, however, that structural changes are not possible after the ligand binding. Furthermore, we emphasize that the proposed mechanism does not substitute the traditional, well-studied cases of allostery based on large structural rearrangements [106] or association/dissociation of homo-oligomeric ensembles [107,108]. Instead, it attempts to shed light on the physics behind the signal transmission inside allosteric proteins that is based solely on entropic processes. Our argument is that such transmission occurs not because of a domino-like sequential set of steric interactions, but as a result of emergent behavior of self-synchronized oscillators that form semi-rigid communities (domains/clusters) in the protein interior. It means that understanding of allosteric mechanism requires analysis of the protein in its entirety. The most straightfor-ward approach would be MD simulation of the protein in question. Community analysis can be used to dissect protein interior into semi-rigid communities and to estimate the level of communication between them. The Girvan–Newman algorithm is the most popular method used by most authors [109]. The major problem of this approach is that it assigns each residue to a particular community not leaving any residues that would belong to the intermediate, ‘soft’, not rigid, areas that, according to our model (gray circles in Figure 4), play an important role as entropic binders described by the Wand group [105]. This problem can be solved by using alternative algorithms for community analysis that allows communities to overlap [110], or combining Girvan–Newman community analysis with methods other than community analysis. Two recent publications can be recommended for that matter: First, a work of the Hamelberg group that analyzes residue–residue contacts that do not persist through the whole MD simulation but form and brake in a dynamic way [111]. They discovered that the distribution of such ‘dynamic contacts’ reflected propagation of long distant allosteric effects of single mutations and substrate binding in Cyclophilin A. Second, a work by Sala et al. [112] that looked at dynamic behavior of pockets on the surface of three different proteins and demonstrated that these pockets were very dynamic on a nano-second timescale. Communication between different pockets was implicated in propagation of allosteric signals in the proteins. Unfortunately, this approach was restricted to surface-exposed pockets only and did not include isolated voids inside the protein interior that, according to our analysis, should be a part of the overall dynamic landscape of the protein and reflect formation of semi-rigid communities (irregular contours in Figure 4). We predict that both methods will be able to detect the intermediate regions inside proteins and, thus, complete the dynamic portrait of the protein interior.

Figure 4. Entropy/dynamics-driven allostery model.

Communities of residues that move coherently as semi-rigid bodies are coded with different colors. Intermediate residues that are not associated with a particular community are shown as gray circles. (A) Apo-form of the protein. Note the difference between the distribution and size of communities and not associated residues around the Allosteric and the Active sites. The Allosteric site is surrounded by small communities and flexible non-associated residues. Active site is formed mostly by a large semi-rigid community (red circles). (B) Ligand-bound form. Ligand binding causes solidification of the Allosteric site neighborhood. This leads to a redistribution of fractal-like distributed voids inside the protein interior (white contours of irregular shape) and breakup of the large community at the Active site. The latter is now mostly formed by flexible not associated residues changing the entropy-driven affinity of the Active site.

Back in 2004, Nussinov and coauthors asked a thought-provoking question: ‘Is allostery an intrinsic property of all dynamic proteins?’ [74]. In that paper, they had already defined the major features of the dynamics-driven allostery mechanism: a non-homogeneous distribution of contacts and a lack of a defined allosteric pathway. Here, we presented a set of arguments that put this mechanism into a much more general context and showed that its credibility can be drawn from one of the most fundamental principles of nature — self-organization. Several previously disjoined pieces of knowledge: fractality of protein interior, stochastic protein folding, long distance allosteric signaling and entropy-driven molecular recognition, all fall into place revealing a complex and harmonic mosaic of life on the molecular scale.

Abbreviations

MD

molecular dynamics

MWC

Monod, Wyman, Changeux

PDZ domains

a family of small binding proteins

[The abbreviation is derived from the three proteins in which the domain was first detected:]

PSD-95

Post-synaptic density protein 95

Dlg1

Drosophila disc large tumor suppressor

ZO-1

Zona occludens 1