Multisensory control of orientation in tethered flying Drosophila

Summary

A longstanding goal of systems neuroscience is to quantitatively describe how the brain integrates sensory cues over time. Here we develop a closed-loop orienting paradigm in Drosophila to study the algorithms by which cues from two modalities are integrated during ongoing behavior. We find that flies exhibit two behaviors when presented simultaneously with an attractive visual stripe and aversive wind cue. First, flies perform a turn sequence where they initially turn away from the wind and but later turn back toward the stripe, suggesting dynamic sensory processing. Second, turns toward the stripe are slowed by the presence of competing wind, suggesting summation of turning drives. We develop a model in which signals each modality are filtered in space and time to generate turn commands, then summed to produce ongoing orienting behavior. This computational framework correctly predicts behavioral dynamics for a range of stimulus intensities and spatial arrangements.

In Brief

Currier and Nagel use a closed-loop orienting paradigm to continuously monitor the neural integration of multisensory information in tethered Drosophila. The sensorimotor transformations that guide dynamic turning behavior in a range of multisensory contexts can be described as a sum of spatiotemporally filtered signals from each modality.

Graphical Abstract

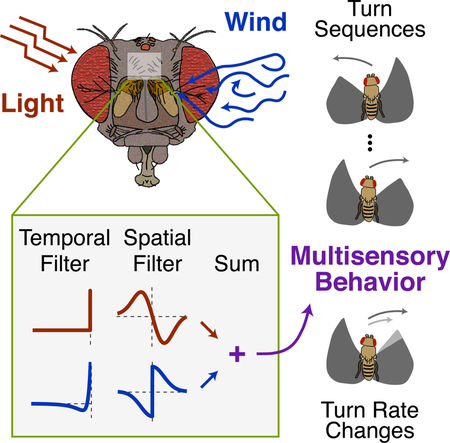
Introduction

A basic function of the nervous system is to combine information across sensory modalities to guide behavior. Sensory data often support similar conclusions about the state of the world [1]. However, conflicting cues must also be integrated by the brain [2,3]. The algorithms used by the nervous system to integrate synergistic and conflicting stimuli across modalities are an active area of investigation [4–9].

The effects of multiple stimuli can be readily seen in stimulus-guided navigation, a behavior undertaken by diverse species, from nematodes [10] and insects [11–15] to fish [16], birds [17] and mammals [18]. The stimuli that guide navigation often span many sensory modalities. When faced with competing navigation cues, the nervous system must select a single movement trajectory. An advantage of using navigation to study multisensory integration is that ongoing locomotion can provide a continuous read-out out of how the brain processes and combines stimuli over time [7,19,20]. In contrast, many studies of multisensory integration have focused on behavioral outcomes that are localized in time, such as two-alternative forced choice paradigms [4–6] and analyses of navigational end-points [12,15].

Here we develop a closed-loop paradigm in tethered flying Drosophila that allows us to examine flies’ responses to an aversive wind (airflow) cue and an attractive visual stripe. Analysis of individual orientation time courses revealed multiple time-varying behaviors. First, flies faced with competing orientation cues can exhibit sequential responses, in which they first turn away from the stimuli and then a turn back toward them. Second, the presence of the aversive mechanosensory cue causes flies to turn more slowly toward the attractive visual target, suggesting summation of opposing turn commands.

Based on these observations, we develop a model in which stimuli from each modality are differentially filtered in space and time to generate turn commands, then summed to update orientation. We find that this model can produce both sequential turning and changes in turn kinetics. The model correctly predicts that turn sequences and turn slowing grow nonlinearly with wind intensity, and that wind can speed or slow turns toward the stripe depending on its angular position. Finally, we develop a pulsatile wind stimulus that allows us to directly observe spatial and temporal filtering of wind input during closed-loop behavior. Our data suggest that orienting behavior in a variety of contexts can be described by summation of spatiotemporally filtered sensory signals.

Results

An orienting paradigm that elicits opposing responses to visual and mechanosensory stimuli.

To generate competing orienting drives in flies, we modified a classical tethered flight paradigm [21] so that two stimuli of different modalities could be delivered alone or together. We monitored a tethered fly’s wingbeats in real time and used the difference in wingbeat angles, a measure of intended turning behavior, to rotate a stimulus arena around the fly in closed-loop (Methods). A high-contrast vertical stripe served as an attractive visual stimulus, while an airflow source (“wind”) at the same location (0°) provided an aversive mechanosensory cue (Figure 1A). Wind and light had rapid onset dynamics (Figure 1B), and windspeed was similar across orientations (Figure 1C). We presented tethered flies (N = 120) with four stimulus conditions: wind only (in the dark, 45 cm/s), vision only (0.15 µW/cm² arena illumination), wind and vision together, or no stimulus. Each condition was presented once from each of 8 starting orientations, randomly interleaved.

Figure 1. An orienting paradigm that elicits opposing responses to visual and mechanosensory stimuli.

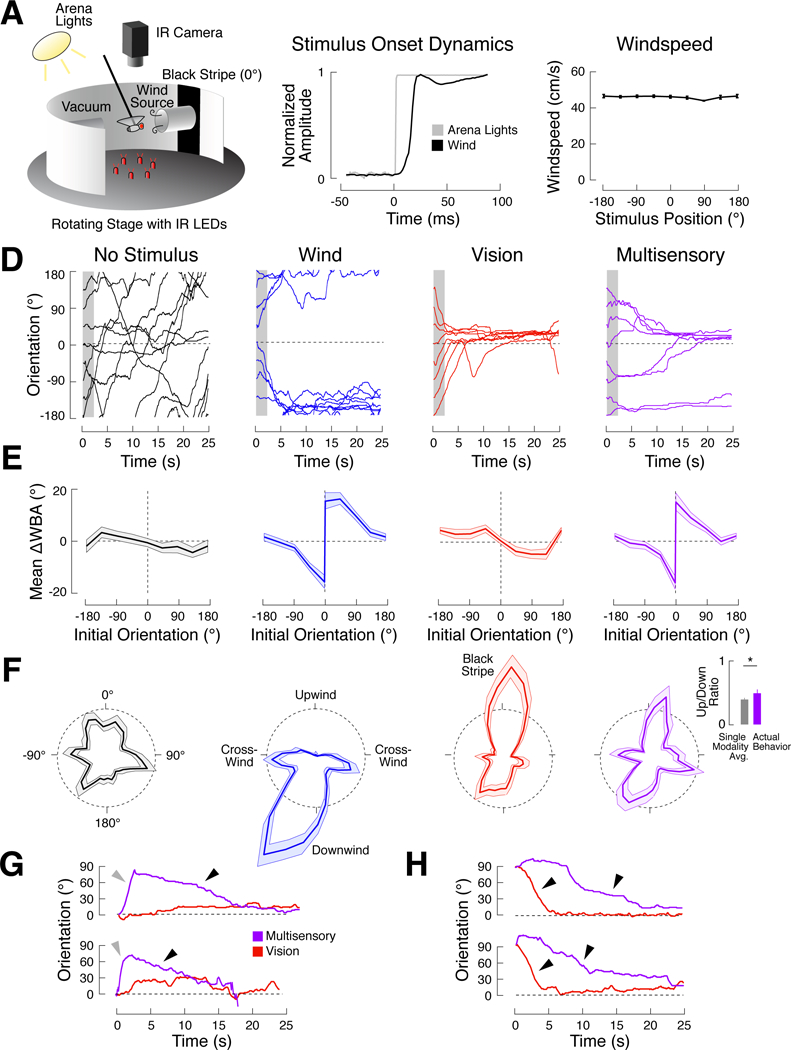
(A) Schematic of our behavioral apparatus (not to scale). A rigidly tethered fly was held between wind and vacuum tubes. A vertical stripe was centered on the upwind tube. Attempted turning behavior was captured as the difference in wing angles (∆WBA) with a camera and IR illumination, and was used to drive a stepper motor that rotated the arena about the fly. Photographs of the actual arena are shown in Figure S2A.

(B) Onset kinetics for arena lights (gray) and wind (black). Stimuli were switched on at time 0.

(C) Mean windspeed +/− SEM for 8 different arena positions. Windspeed is consistent across orientations (one-way ANOVA; p = 0.11).

(D-F) Turning and orienting behavior in this paradigm. Flies turn and orient downwind on wind trials (blue), but turn and orient toward the stripe on vision trials (red). Multisensory behavior (purple) is a combination of these responses. No orientation biases exist when no stimulus is present (black). See also Figures S1 and S2.

(D) Example behavior of a single fly for all stimulus conditions. Each line represents a single trial. Stimulus onset at time 0. Visual stripe and wind source at 0° (dashed black lines). Data from the first 2 seconds of each trial (gray boxes) were used to calculate turn rate as a function of orientation in (E).

(E) Early trial turning behavior for each condition. Mean turn rate (∆WBA) +/− 95% CI over the first two seconds of each trial across all flies (N = 120), as a function of initial orientation. Note that data for the wind and multisensory conditions is split by turn direction at 0° to emphasize that flies’ largest turns were generated near 0° in these conditions (Figure S2D). Visual data was not split.

(F) Late trial orientation for each condition. Polar histograms (bin width = 10° ) showing mean normalized orientation occupancy +/− 95% CI across starting orientations for the final 15 seconds of all trials. Black dashed circles represent a probability density of 0.005 per degree. Orienting behavior is slightly skewed because the wind vector was not perfectly perpendicular to the edge of the arena. In the multisensory condition, the ratio of upwind to downwind orienting (inset) is higher than expected from the mean of single modality histograms (paired t-test, p < 0.05).

(G) Single trial evidence of “turn sequences.” Each panel shows a multisensory trial (purple) overlaid on a vision trial (red) from the same fly starting at the same initial orientation. On multisensory trials, flies first turn away from 0° (gray arrows) before turning back to 0° (black arrows) later in the trial.

(H) Single trial evidence for “turn slowing.” Multi sensory trials are overlaid on vision trials for single flies. Turns toward 0° are slower in the mul tisensory condition than in the vision condition (compare slopes at black arrows).

To characterize flies’ responses to our stimuli, we first plotted orientation as a function of time for each fly (Figure 1D). Flies typically made large turns during the first few seconds after stimulus onset, then maintained a fairly stable orientation over the remainder of the trial. To quantify behavior across flies, we plotted mean turn rates during the first 2 s (as the difference in wingbeat angles) as a function of initial orientation relative to the stimuli (Figure 1E), and orientation histograms over the last 15 s (Figure 1F).

When no stimulus was present, flies had no preferred orientation, and tended to make long, slow turns. In the “wind” condition, flies turned away from the wind source, then maintained down- or cross-wind orientations for the remainder of the trial. The magnitude of this aversive response grew with windspeed (Figure S1) and wind onset rate (Figure S2). Downwind turning was abolished by stabilizing the antennae (Figure S1), as previously shown for other wind-evoked behaviors [15,22,23]. In the “vision” condition, flies turned toward the stripe at stimulus onset and spent most of the trial oriented toward this stimulus. Wind and vision thus drive opposing orientations in our paradigm.

In the multisensory condition, early turning resembled the wind condition, with turns away from the wind/stripe (Figure 1E). Many flies turned back toward the stripe later in the trial, although these turns were slower and more delayed than those in the vision condition. Late-trial orientation appeared to be a combination of wind and vision behavior, with orientation up-, down-, and cross-wind (Figure 1F). However, flies oriented upwind more than would be expected from an average of the vision and wind orientation histograms (Figure 1F inset; p < 0.05). These data suggest that flies respond to conflicting orientation cues with diverse behaviors, including “turn sequences”, in which flies first turn away from the wind, then back toward the stripe, and “turn slowing,” in which turns towards the stripe are slowed in the presence of wind. To examine responses to multimodal stimuli in greater detail, we next compared vision and multisensory trials in single flies that began at the same orientation. Turn sequences were prevalent in multisensory trials starting at 0° (Figure 1G), while in vision trials flies fixated 0° continuously. Conversely, turn slowing w as most apparent when flies started at 90° (Figure 1H). These observations suggest that multimodal behavior depends on a fly’s initial orientation.

Turn sequences and turn slowing arise from neural integration of dynamic multimodal signals

To ask whether stimuli at 90° and 0° reliably elic it turn slowing and turn sequences, respectively, we presented 11 additional flies with wind, vision, and multisensory trials at these orientations multiple times each (see Methods). We found that turns from 90° toward the stripe were consistently slower in the multisensory condition compared to the vision condition (Figure 2A-B, left). Flies’ latencies to cross 45° was long er on multisensory compared to vision trials (Figure 2C, left; p < 0.01), and turn rates over the second surrounding this crossing was slower (Figure 2C, right; p < 0.05). Individual differences in wind sensitivity were weakly correlated with the latency to turn in the multisensory condition (Figure S3C-D). On trials starting at 0°, flies reliably turned away from the stripe before returning to it (Figure 2D-E, left). Flies’ maximal deviations from 0° over the first ten seconds of ea ch trial were larger on multisensory trials compared to vision trials (Figure 2F; p < 0.001). Turn slowing and sequences were also observed when we ran the experiment with a higher feedback gain (Figure S4). These data indicate that turn slowing and turn sequences are reliably evoked by stimuli appearing at 90° and 0°.

Figure 2. Turn sequences and turn slowing arise from neural integration of dynamic multimodal signals.

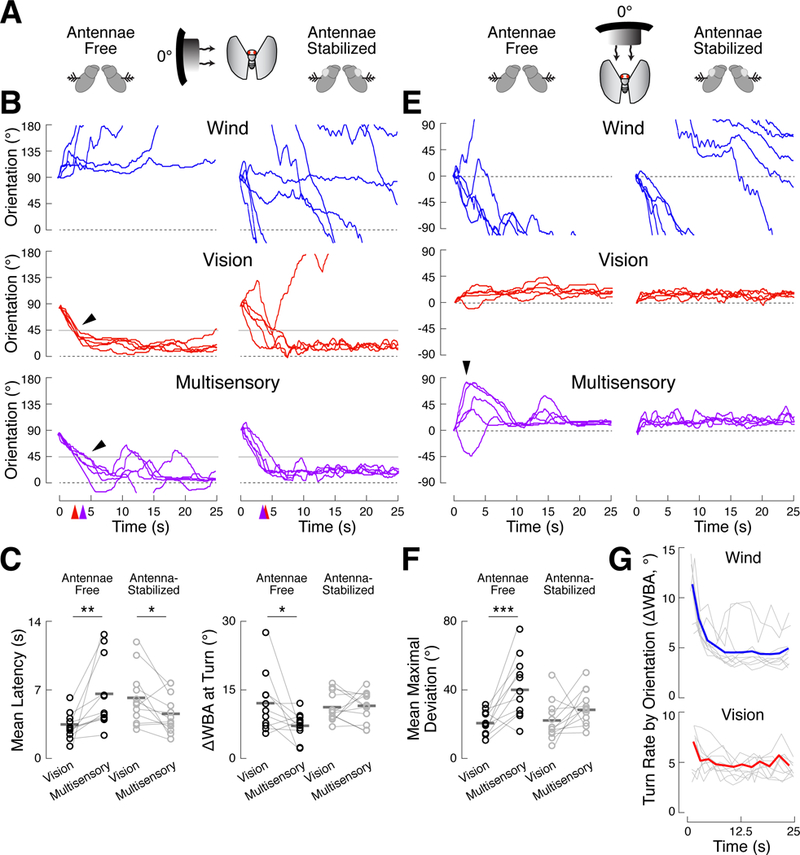
(A-C) Stimuli starting at 90° elicited multisensory turn slowing only when the antennae are free to transduce wind. Eleven control flies and 12 antenna-stabilized flies each received 5 presentations of wind, vision, or both.

(A) Schematic of stimulus presentation (not to scale) and antenna stabilization, which was accomplished via a drop of UV-cured glue at the junction of the second and third antennal segments. See also Figures S1 and S3.

(B) Example behavior of a control fly (left) and an antenna-stabilized fly (right). Orientation axis is truncated for clarity. Turns toward 0° in the mu ltisensory condition are slower than those in the vision condition (black arrows). Thin gray lines indicate the midpoints of vision-guided turns (45°) used to calculate turn latency and speed in ( C). Colored arrows on the time axis show the mean latency to cross 45° for vision (red) and mult isensory (purple) trials in the control fly.

(C) Left: mean latency to cross 45° across 5 stimul us presentations for control (black) and antenna-stabilized (gray) flies in the vision and multisensory conditions. Horizontal bars: means across flies. In control flies, multisensory turns occurred later than vision turns (paired t-test, p < 0.01), while multisensory turns occurred earlier than vision turns in antenna-stabilized flies (p < 0.05). Right: mean turn rate, as ∆WBA, over a 1 s window centered on 45° crossings fo r each fly. Multisensory turns are slower than vision turns in control flies (p < 0.05), but not in antenna-stabilized flies (p = 0.93). See also Figures S4 and S5.

(D-F) Stimuli starting at 0° to the fly elicited ev idence of sequential turning only when the antennae are free to transduce wind.

(E) Example behavior of a control fly (left), showing larger deviations from 0° in the multisensory condition than in the vision condition (black arrows), and an antenna-stabilized fly (right), which does not display a turn sequence.

(F) Mean maximal deviation from 0° for all flies in the vision and multisensory conditions (colors as in (C)). Maximal deviations are the largest absolute orientation attained over the first 10 s of each trial. Control flies turned farther from 0° in the multisensory condition than in the vision condition (p < 0.001), while no such difference was observed in antenna-stabilized flies. See also Figures S4 and S5.

(G) The mean turn rates of 120 flies (from Figure 1), conditioned on orientation, is plotted as a function of time (thin gray lines) for the wind and vision conditions. The orientation conditions are at 30°, 45°, 60°, 75°, 90°, 105°, 120°, 135°, a nd 150°. For wind, turn rate through each orientation decreases as the trial progresses. For vision, some orientations show decreasing turn rate over time, while others show increasing turn rate. Thick colored lines represent the median across orientations.

To further differentiate between wind- and vision-evoked turns, we calculated mean wingbeat angle (WBA), a measure that is correlated with changes in pitch torque [24]. We found that wind-guided turns show a brief drop in WBA, while visual turns have a constant amplitude time course (Figure S5). Multisensory trials also showed this brief drop in WBA, suggesting both that wind-driven turns may possess a pitch component (i.e., a banked turn), and that early turns away from 0º in the multisensory condition are driven by wind.

Do turn sequences and slowing require transduction of wind into neural signals by antennal mechanoreceptors, or do they arise from mechanical forces acting directly on the body or wings? To discriminate between these possibilities, we repeated the above experiment in 12 antenna-stabilized flies. This manipulation abolished downwind orientation in the wind condition (Figure S3A-B). In these flies, turns from 90° tow ard the stripe were not slower in the multisensory compared to the vision condition (Figure 2A-C). Curiously, antenna-stabilized flies executed their turns at shorter latency in the multisensory condition (Figure 2C, left; p < 0.05), perhaps reflecting the contribution of non-antennal wind-sensors (Figure S1). When starting at 0º, antenna-stabilized flies turned no farther from the stripe on multisensory trials compared to vision trials (p = 0.11). These data argue that turn slowing and turn sequences reflect the neural integration of antenna-derived wind signals with visual information.

Why might flies turn away from the wind early in multisensory trials and return to the stripe later? We hypothesized that wind-evoked turning drive might start strong but decay over time so that visual commands dominate by the end of the trial. To test this hypothesis, we asked how turn rates change over time when we control for orientation. Using our first data set, we calculated the average turn rate of flies at the time that they passed through specific orientations (30°, 45°, 60°, 75°, 90°, 105°, 120°, 135°, 150°) o n single modality trials (Figure 2G). In the wind condition, we observed that turn rates decayed strongly at all orientations, each with a similar time course. Turn rates evoked by the visual stimulus changed much less over time than those evoked by wind. This analysis supports the hypothesis that wind commands decay more strongly than visual commands over time.

Summation of spatiotemporally filtered sensory inputs can account for turn slowing and turn sequences.

Our data indicate that flies respond to conflicting orientation drives with either sequential or slower turning, depending on the initial orientation of the stimuli. We wondered if a single computational framework could account for both observations. We therefore developed a simple feedback control model (Figure 3A).

Figure 3. Summation of spatiotemporally filtered sensory inputs can account for turn slowing and turn sequences.

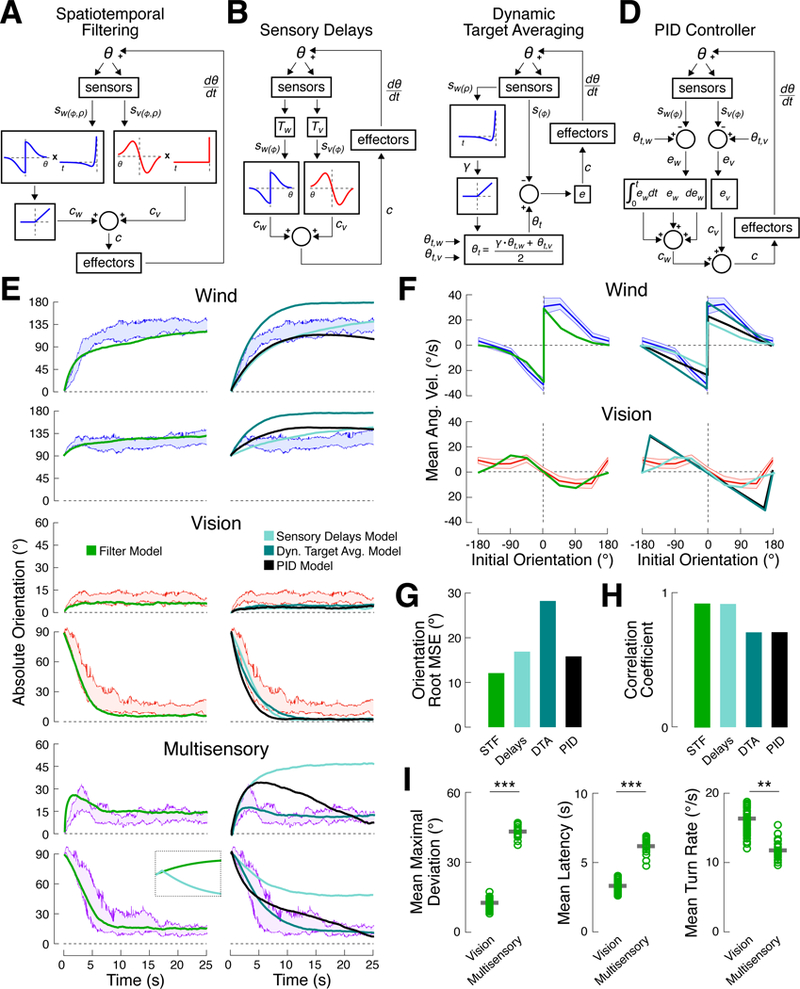
(A) Schematic of the spatiotemporal filtering model. Sensory signals for wind and vision, s_w(φ,ρ) and s_v(φ,ρ), are passed through spatial and temporal filters to generate turn commands, c, for each modality. Turn commands are summed and applied to heading, θ, generating new sensory signals on the next time step.

(B) Sensory delay model. Temporal filters are replaced by fixed processing delays (T) for each modality.

(C) Dynamic target averaging model. The turn command reflects the error, e, between current heading, θ, and target heading, θ_t. Target heading is a weighted average of target headings for vision (0°) and wind (180°). The time course of win d stimulation (s_w(ρ)) is temporally filtered to determine wind target weight.

(D) PID controller model. Sensory signals for each modality are compared to their respective target headings (0° for vision, 180° for wind) to g enerate an error for each modality. Turn commands are computed by summing proportional, integral, and derivative terms for this error. The overall turn command is a sum across modalities.

(E) Best fit simulations for each model compared to empirical data. Colored bands represent 95% confidence intervals for absolute orientation in response to wind (blue), vision (red), and multisensory (purple) conditions for flies starting at 0º and 90º. Left: spatiotemporal model (green, (A)). Right: delay model (light teal, (B)), dynamic target averaging model (dark teal, (C)), PID model (black, (D)). Note the differing y-axis scales. Best-fit parameters for each model are shown in Table 1. Inset shows the first 1 s of a simulation beginning at 60º for the spatiotemporal filtering and sensory delays models, highlighting the rapidity of the turning sequence generated by the latter. Inset vertical axis is 30º.

(F) Simulated turn rate as a function of orientation for each model compared to empirical data. Data (colored bands) is reproduced from Figure 1. Model colors as in (E).

(G) Root mean squared error between the best-fit simulation results, as shown in (E), and the empirical median absolute orientation time course. STF: spatiotemporal filtering model; Delays: sensory delays model; DTA: dynamic target averaging model; PID: PID controller model. Values shown in Table 1. The spatiotemporal filtering model fits the data best. See also Figure S6.

(H) Correlation coefficient between the empirical turn rate functions from (F) and the simulation results is plotted for each model. Correlation coefficient is used in place of RMSE to discount the effect of stimulus intensity. The models that do not include an explicit spatial filter do not fully capture the influence of orientation on turn rate.

(I) Measures of multisensory integration, computed for simulated behavior from the spatiotemporal filtering model. Each plot shows the simulated behavior of 20 “flies” (open circles). Each “fly” is the mean of 5 trials, mimicking the plots in Figure 2. Thick gray bars: mean across “flies.” All metrics are calculated as in Figure 2. Left: simulated flies turn farther from 0º in the multisensory condition compared to the vision condition (rank-sum test, p < 0.0001). Middle and right: simulated turns toward 0º in the multisensory condition occur later (p < 0.0001) and are slower (p < 0.01) than those in the vision condition.

In this model (see Methods), wind direction and the position of the visual landmark are transduced by sensory organs, yielding a pair of sensory vectors, s_w and s_v, that describe the orientation (φ) and magnitude (ρ) of each stimulus in fly-centered coordinates. These sensory signals are fed into a neural controller that computes two single-modality turn commands, c_w and c_v, which are then summed to yield a multisensory turn command. Effector muscles convert this command into a turn, causing a change in the fly’s orientation. This produces a new set of sensory signals, s_w and s_v, that are processed in the same manner at the next time step. The model converts sensory vectors into turn commands by spatially filtering time-varying orientation signals (φ) and temporally filtering time-varying stimulus magnitudes (ρ). Our analysis of turn rate as a function of initial orientation (Figure 1E) suggests distinct spatial filter shapes for each modality. Similarly, our analysis of turn rate as a function of time within the trial (Figure 2G) suggests that wind-evoked turning drive decays over time, while vision-evoked turning drive is relatively constant.

We fit model parameters to the median orientation of flies in the 0º-90º experiment (Figure 2) and found that this model could reproduce key features of the data (Figure 3E-F, left columns) including turn slowing and turn sequences in the multisensory condition (Figure 3I). Sequential turning arises because the wind turn command is initially stronger than vision, then decays. Turn slowing arises because the commands to turn toward the stripe and away from the wind are summed, resulting in a slower turn. These results suggest that a model featuring summation of spatiotemporally filtered sensory signals is sufficient to recapitulate many aspects of our data.

Could another model account for our data equally well? To address this question we built, fit, and tested several alternative models (Figure 3B-D, Table 1). In the first model we asked whether temporal filtering of the wind stimulus could be replaced by simpler differences in sensory processing delays (Figure 3B). Mechanosensation is faster than vision, with estimated delays of 20 ms for mechanosensation and 100 ms for vision [25,26]. A model incorporating these values produced a turn sequence much faster than the one observed in our data (Figure 3E, inset). Furthermore, no sequential response was observed at 0º (Figure 3E, bottom rows). We therefore conclude that known sensorimotor delays are insufficient to account for our data.

Table 1. Best-fit parameters for each considered model.

The corresponding root mean squared error between the empirical median absolute orientation time course and best-fit simulation results are also shown (Figure 3G). Each model has 4 free parameters that were fit via nonlinear regression, except for the sensory delays model which has 2 free parameters. Best-fit parameters for the spatiotemporal filtering model at different wind speeds are also shown (Figures 4 and S7). Permutations over timing parameters are shown in Figure S6 for the PID and spatiotemporal filtering models. All α terms have units of º/s. All τ terms have units of s. All proportionality and integral constants (k_p and k_i) have units of Hz. All k_d and β terms are unitless.

Model	P1	P2	P3	P4	RMSE
Spatiotemporal Filtering	αv 18	αw 54	τw 1.7	βw 0.14	12.1º
High Wind (45 cm/s)	αv 18	αw 70	τw 1.7	βw 0.14	—
Low Wind (10 cm/s)	αv 18	αw 33	τw 1.7	βw 0.14	—
Spatial Filtering w/ Sensory Delays	αv 19	αw 15	—	—	17.1º
Dynamic Target Averaging	kp 0.005	γ 1	τw 1.16	βw 0.14	28.2º
PID Feedback Controller	kp,v 0.007	kp,w 0.002	ki,w −2E−06	kd,w −0.014	15.8º

Next we asked whether a model based on averaging of target headings could account for our data (Figure 3C). Several recent models have proposed that heading is directly controlled during navigation [12,15], potentially by comparing a current heading to an internally stored desired heading [27,28]. In this case, turn rate should depend only on the difference between the current heading and the target heading. We reasoned that a model in which target headings for each modality are fixed could not account for the dynamic multisensory response that we see. We therefore wondered if a model that dynamically weights single modality target orientations (θ_t,v, θ_t,w) could account for our data. This dynamic target averaging (DTA) model does an excellent job reproducing multisensory behavior (Figure 3E, bottom rows), but poorly captures single-modality behavior (Figure 3E, top rows), leading to a worse fit overall (Figure 3G). Because the DTA model generates turns based on the error between current and target orientation, it predicts a linear relationship between stimulus orientation and turn velocity (Figure 3F, right), while we observe a nonlinear relationship, especially for vision. Thus, we favor the model in which integration occurs at the level of turn commands, rather than orientation targets.

Finally, we asked whether a model based on control-theoretic principles (Figure 3D) could outperform the spatiotemporal filtering model. We examined a model in which each stimulus produces a sensory signal (s_w, s_v) that is compared to a target heading (θ_t,w, θ_t,v) to generate an error signal. Terms proportional to the error, to its derivative, and to its integral are summed to generate a turn command (c_w, c_v) for each modality, and these commands are summed. This “PID” model is similar to the spatiotemporal filtering model in that separate commands are generated for each modality and summed. Like that model, it generates sequences and slower turns in the presence of conflicting multimodal stimuli. However, the detailed dynamics of the model differed from our data. Like the DTA model, this model predicts a linear relationship between stimulus orientation and turn velocity (Figure 3F, right). In addition, the spatiotemporal filtering model provides a better fit to the dynamics of responses to multimodal stimuli (Figure 3E, bottom two rows, and Figure S6). Based on these considerations, we conclude that a model based on differential spatiotemporal filtering and summation provides the best overall fit to our data (Figure 3G,H), although other models are also possible.

Turn kinetics vary continuously with stimulus intensity.

We next asked how flies behave when the intensity of the two stimuli is very different. “Winner-take-all” effects have been observed in multisensory decision-making [8,9], while our summation model predicts that the influence of each modality should grow smoothly with intensity. To examine the effects of intensity, we presented real flies with single and multimodal stimuli at higher and lower wind speeds (N = 11, 11, and 12 for wind at 10, 25, and 45 cm/s, respectively), while holding visual stimulus intensity constant.

The orientation time courses of individual flies suggest that winner-take-all strategies do not emerge. Instead, increasing wind intensity resulted in stronger signs of turn slowing and turn sequences. For example, turns toward the stripe from 90° were fast in the vision condition, but became slower as windspeed increased (Figure 4A). Faster wind speeds were associated with progressively slower turn rates (Figure 4C; R² = 0.08, p < 0.05) and longer turn latencies (Figure 4D; R² = 0.22, p < 0.0001). Similarly, flies fixated near the stripe when started at 0° in the vision condition, but made larger turns away from the stripe as windspeed increased (Figure 4B,E; R² 0.29, p < 0.0001). Together, these results argue that both stimuli influence behavior regardless of intensity.

Figure 4. Turn kinetics vary continuously with stimulus intensity.

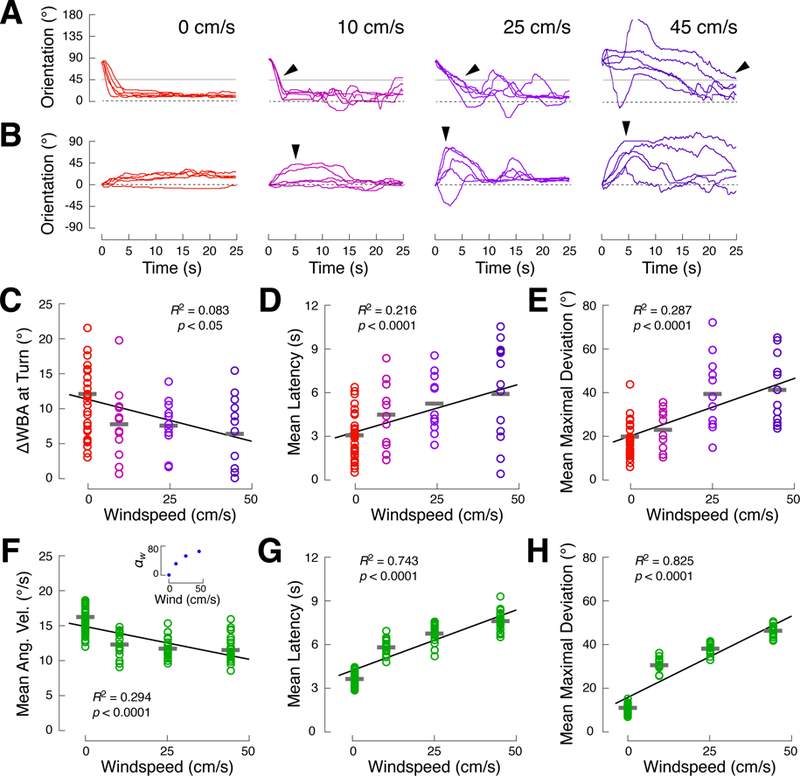
(A) Slowing of visually-guided turns in the presence of a competing wind stimulus increases with windspeed. Each plot shows 5 trials from single flies beginning at 90°. The leftmost plot represents the vision condition (red), while the right hand plots show the multisensory condition at low (10 cm/s, magenta), medium (25 cm/s, purple, reproduced from Figure 2B), and high (45 cm/s, indigo) wind speeds. Arrows highlight the timing of turns through 45° (gray line).

(B) Transient deviations from 0° (arrows) grow with windspeed. Each plot shows 5 trials from single flies beginning at 0°. Third panel is reprod uced from Figure 2B.

(C-E) Behavioral measures evaluated as a function of windspeed. Each fly was presented with the vision stimulus and one of 3 multisensory condition wind speeds yielding (N = 34, 11, 11, and 12 flies for wind at 0, 10, 25, and 45 cm/s, respectively). Circles: single flies; gray bars: mean across flies. Black lines indicate best linear fits, but behavioral parameters generally change nonlinearly with windspeed.

(C) Mean turn rate through 45° on 90° trials (as in Figure 2C) is negatively correlated with windspeed (R² = 0.08, p < 0.05), as shown in (A).

(D) Latency to turn through 45° (as in Figure 2C) i s positively correlated with windspeed (R² = 0.22, p < 0.0001), as shown in (A).

(E) Mean maximal deviation from 0° (as in Figure 2F ) is positively correlated with windspeed (R² = 0.29, p < 0.0001), as shown in (B).

(F-H) Measures of simulated behavior using the spatiotemporal filtering model (Figure 3A). Each stimulus condition contains data from 20 simulated “flies” (the mean of a 5-trial block, as in Figure 3I). The wind intensity parameter (α_w) values corresponding to different wind speeds were found by fitting only this parameter to the wind condition data from the high and low windspeed experiments, above. All other model parameters are unchanged. The inset in panel illustrates the nonlinear relationship between windspeed and the best-fitting α_w. See also Figure S7.

(F) Turn rate (as in (C)) is negatively correlated with wind strength in model simulations (R² = 0.29, p < 0.0001).

(G) Latency to turn (as in (D)) is positively correlated with wind strength in model simulations (R² = 0.74, p < 0.0001).

(H) Mean maximal deviation from 0° (as in (E)) is p ositively correlated with wind strength in model simulations (R² = 0.83, p < 0.0001).

To ask whether the spatiotemporal filtering model could account for these data, we varied a single parameter, α_w, which scales the strength of wind-evoked turning drive, while keeping other parameters fixed (Table 1). We estimated α_w for each intensity by fitting to the median orientation time course in the wind condition (Figure S7). This analysis suggests that wind-evoked turning drive grows nonlinearly with windspeed (Figure 4F, inset). We found that our model reproduced the nonlinear relationship between windspeed and turn rate (Figure 4F; R² = 0.29, p < 0.0001), turn latency (Figure 4G; R² = 0.74, p < 0.0001), and maximal deviation (Figure 4H; R² = 0.83, p < 0.0001), although the model had lower variance than the behavioral data. These results support the notion that a single model can account for behavior across stimulus intensities.

Turn kinetics depend on the relative spatial orientation of stimuli.

Next we asked whether our model could generalize to stimuli with other spatial relationships. For example, can the model predict responses to synergistic as well as conflicting cues? To address this question, we rotated the black stripe in our arena so that it was midway between the upwind and downwind tubes (Figure 5A). In this arrangement, intuition suggests that a fly approaching the stripe while turning downwind will experience synergistic commands, while a fly approaching the stripe turning upwind will experience conflicting signals. Formally, we can use our model to predict turn velocities by circularly shifting the spatial filters for wind and vision (Figure 5B).

Figure 5. Turn kinetics depend on the relative spatial orientation of stimuli.

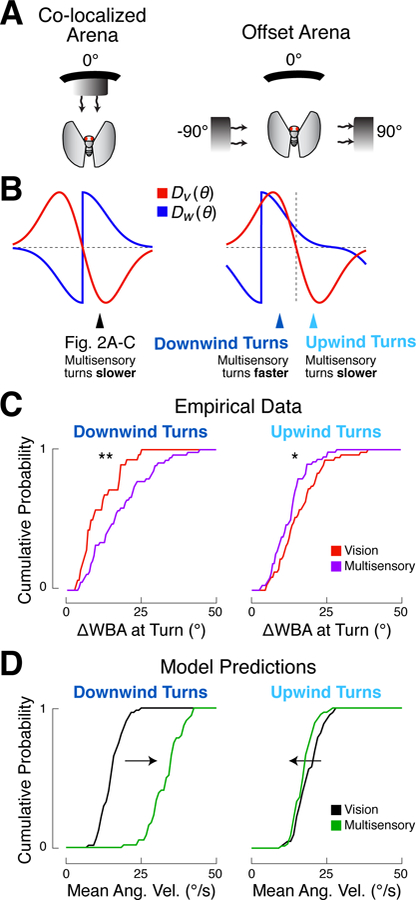
(A) Schematics of co-localized and offset arena configurations (not to scale).

(B) Spatial filters (turn rate as a function of orientation) for each modality in each arena configuration. In the co-localized arena, presentation of both stimuli always produces conflicting (oppositely signed) turn commands. In the offset arena, presentation of both stimuli can be synergistic (same sign) or conflicting (opposite sign), depending on the orientation of the fly.

(C) Distributions of experimentally measured turn rates in the offset arena for vision (red) and multisensory (purple) trials, sorted by turn direction. Flies were started at either −90° or 90° relative to the stripe to produce downwind or upwind turns, respectively. Rates of individual turns toward the stripe were calculated over a 1 s period centered on the time when the fly crossed + or −45°. Downwind turns (left) are faster in the multisensory condition (n = 53) than in the vision condition (n = 28), as seen in the right-shifted multisensory CDF (rank-sum test, p < 0.01). Upwind turns (right) are slower in the multisensory condition (n = 59) compared to the vision condition (n = 54), resulting in a left-shifted multisensory CDF (rank-sum test, p < 0.05).

(D) Predictions of the spatiotemporal filtering model for the offset arena configuration. The wind spatial filter was circularly shifted by −90° to ma tch the arena configuration, as shown in (B). The distribution of turn rates for simulated flies are plotted as CDFs for the vision (black) and multisensory (green) conditions. Rates of individual turns (n = 60 for each direction-condition pair) calculated as in (C). The distribution of multisensory turn rates is right-shifted compared to vision for the downwind direction (left panel), but left-shifted for the upwind direction (right panel).

We found that flies’ behavior matched these predictions (Figure 5C). We collected turn rates for 12 flies orienting in the offset arena, and split the data based on the direction of approach to the visual target (“upwind” or “downwind”) and stimulus condition. We then plotted cumulative density functions (CDFs) for downwind-directed turns toward the stripe in the multisensory (n = 53 turns) and vision (n = 28 turns) conditions (Figure 5C, left). Consistent with our predictions, we observed a significant right-shift in the distribution of turn rates on multisensory versus vision trials (p < 0.01), indicating that multisensory turns were faster. In contrast, the distribution of upwind-directed multisensory turns (n = 59; 54 for vision) was slightly left-shifted, indicating that they were slower (Figure 5C, right; p < 0.05). We evaluated turn rate distributions as independent observations because fewer flies made the expected turn towards the stripe at 0°, perhaps because the tubes that create the wind stimulus act as competing visual targets.

To compare flies’ behavior to the predictions of our model, we used the shifted spatial filters to simulate flies starting at either −90° o r 90°. We then analyzed turns in the same manner as the behavioral data. We found that downwind-directed turns were faster in the multisensory condition than in the visual condition, while upwind-directed turns were slower (Figure 5D). However, predicted downwind turn velocities were faster than those we observed behaviorally, likely because there is a ceiling imposed by our device on how fast a turn can be. Together these data and simulations support the notion that our spatiotemporal filtering model can account for behavior regardless of stimulus orientations, and can predict both slowing and speeding of turns.

A dynamic wind stimulus provides direct evidence for spatial and temporal filtering of turn commands.

Finally, we asked whether we could see direct evidence for spatial and temporal filtering during closed-loop orientation. The DTA and PID models predict a linear relationship between stimulus orientation and turn magnitude, while this function can have an arbitrary shape in the spatiotemporal filtering model. We found that responses to a pulsed wind stimulus supported the notion of spatial and temporal filters on turn rate. In this experiment, we interleaved 2.5 s pulses of wind with 2.5 s of no wind for 50 s. The visual stimulus was on throughout this period. Flies (N = 12) continuously modulated their turn rate, turning away from 0º when the wind was on and turning toward 0º when the wind was off (Figure 6A).

Figure 6. A dynamic wind stimulus provides direct evidence for spatial and temporal filtering of turn commands.

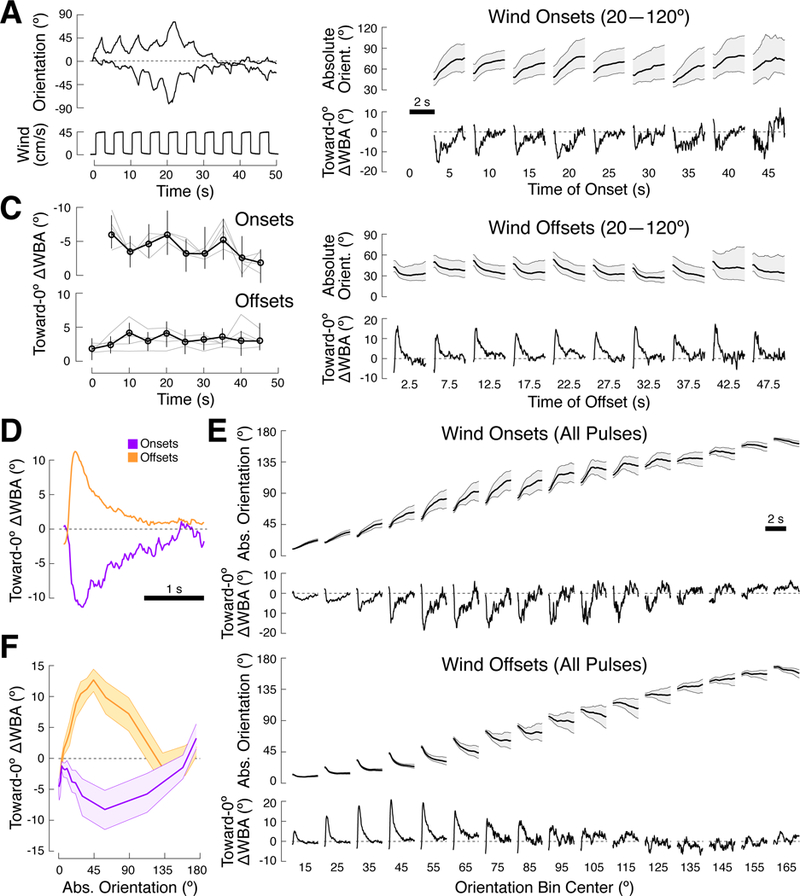
(A) Example behavior of 2 flies orienting in closed-loop to a constant visual stimulus and a pulsing wind stimulus. Each 50 s trial consisted of 10 repetitions of 2.5 s of wind followed by 2.5 s of no wind (bottom panel). Between trials, closed-loop orienting continued without any wind for 30 sec. Flies turned toward 0º when no wind was present, and away from 0º when the wind was on.

(B) Mean behavior as a function of pulse number. Absolute orientation +/− 95% CI and mean toward-0º turn rate (Methods) are plotted as a function of time for each pulse’s onset (top) and offset (bottom). To minimize spatial influences, we only included data from flies that were oriented between 20º and 120º at the time of wind o nset or offset. Data for the first onset is excluded, as all flies began at 0°. The shape and m agnitude of flies’ turning responses are distinct for onset and offset but do not vary systematically with pulse number.

(C) Mean toward-0º turn rate (black) +/− 95% CI as a function of wind pulse timing for wind onsets (top) and offsets (bottom). Data is for flies oriented between 20º and 120º at the time of onset or offset (black). The onset y-axis is inverted for clarity. Thin gray lines represent the mean toward-0º turn rate for smaller orientation ranges: 40º-120º, 30º-100º, 30º-80º, and 20º-60º for onsets; 20º-70º, 40º-70º, 20º-50º, and 10º-40º for offsets.

(D) Mean toward-0º turn rate +/− 95% CI as a function of time within a pulse, averaged across pulses, for wind onsets (purple) and offsets (orange). Data is for flies oriented between 20º and 120º at the time of onset or offset. Both responses decay, but at different rates.

(E) Mean behavior as a function of orientation. Mean absolute orientation +/− 95% CI and mean toward-0º turn rate are plotted as a function of time for all wind onsets (top) and offsets (bottom). Data were binned based on the flies’ orientations at the time of onset or offset (overlapping 30º bins, every 10º). The magnitude of flies’ turning responses to wind onsets or offsets vary with orientation. Spatial tuning is distinct for onsets and offsets.

(F) Mean toward-0º turn rate +/− 95% CI as a function of the absolute orientation at wind onset (purple) or offset (orange). Data was split into 15 equally-sampled spatial bins (each turn is counted only once). The spatial filter on wind onset is broad and peaks near 60º, while the spatial filter on wind offset is narrower and peaks near 45º.

To ask whether turn behavior changed as a function of time, we plotted mean absolute orientation and mean toward-0º turn rate following each wind onset (Figure 6B, top, see Methods). To control for orientation, we analyzed only turns that started between 20° and 120° (smaller ranges produced similar but noisier results — see Figure 6C). The first pulse, which started at 0°, was omitted. We observed that flies initiated strong turns away from the wind during each pulse. Turn magnitude decayed over the duration of each pulse (Figure 6D). However, the amplitude and decay rate of turns did not change dramatically across pulses (Figure 6C). Turns toward 0º following wind offset also exhibited a decay (Figure 6B, bottom), but with a distinct time course (Figure 6D).

To ask whether turn rates depended on orientation, we binned turns by flies’ orientations at the time of wind onset or offset. We then plotted the mean absolute orientation and toward-0º turn rate across all pulses for each spatial bin (Figure 6E). We found that the amplitude of turns strongly depended on orientation, with distinct shapes for wind onset and offset (Figure 6F). Notably, these spatial filters were distinct from those elicited by a single prolonged pulse (Figure 1E). Nevertheless, these data provide direct evidence that the magnitude of turns evoked by wind onset and offset depends on the orientation of the fly with respect to the wind, and are inconsistent with models where turns are driven by the error between current and target orientation. These data provide direct evidence that a fly’s turning rate results from the filtering of sensory signals in space and time.

Discussion

A paradigm for studying continuous integration of multimodal signals in the fly brain

The question of how the nervous system integrates, represents, and utilizes multisensory data has interested neuroscientists for decades. The paradigm described here, like other navigation paradigms [7,19,20], provides a means to directly measure ongoing integration of signals from different sensory modalities. Across stimulus intensities and spatial configurations, we found that turn dynamics reflected both mechanosensory and visual input; antennal stabilization experiments argue that these signals are integrated within the brain. Although integration of both modalities was visible in nearly every stimulus configuration we tested, unexpected turns also occurred in many of our experiments, suggesting that the integrative process on which we have focused must coexist with mechanisms to generate stochastic turns [7,29,30].

In this study we found wind to be aversive. This is surprising, as previous studies using similar airflow delivery systems have found that wind is attractive [15,22], at least in the presence of an attractive odor [22,23]. We explored a wide range of airflow rates (10–45cm/s), onset kinetics, and tube configurations, and were unable to find a regime in which airflow was attractive (Figure S2B-C). We were also unable to alter the valence of airflow by adding an attractive odor (apple cider vinegar, data not shown). We therefore think it is unlikely that our results arise from differences in airflow. In these other studies [15,22,23], flies were tethered to a pin that allowed them to rotate freely in yaw. In that configuration, airflow was found to passively rotate dead flies upwind [15]. Free-yaw tethered flies can also make rapid saccadic movements [31] not possible in our paradigm. Tethering differences might therefore alter the apparent valence of wind, although differences in airflow odor could also contribute.

A critical point in interpreting tethered flight studies is that neither the “wind” presented in this work, nor that presented to free-yaw tethered flies [15,22,23], fully recapitulates what a fly experiences during free flight. This is because wind displaces flying flies, which creates optic flow [32] and may transiently activate antennal mechanoreceptors [26]. Both of these stimuli are altered during tethered flight. Normal forward flight generates a headwind, expanding optic flow, and front-to-back motion on the ground, but each of these stimuli are aversive to rigidly tethered flies [33]. Similar to what we observe with airflow, rigidly tethered flies and mosquitoes orient such that optic flow is back-to-front, as if they were flying backwards [32,33]. We therefore view our paradigm primarily as a means to investigate continuous multisensory integration in a preparation that is compatible with simultaneous electrophysiology and imaging.

Modeling multisensory integration.

How are wind and vision integrated to drive orienting behavior? Based on our behavioral observations, we propose that inputs from each modality are independently filtered in space and time to generate turn commands, and that these commands are then summed to produce overall turning behavior. We found that this model could account for many aspects of our data, including turn sequences, orientation-dependent slowing and speeding of turns, and the nonlinear growth of these phenomena with increasing windspeed. The model performed better than two others with the same number of free parameters and one with two free parameters. Our results do not rule out the possibility that some other model could provide a better fit to the data, but do suggest that summation of spatiotemporally filtered sensory signals is a simple and parsimonious explanation for the data.

Multiple experiments support the idea that wind visual signals are differentially filtered in space. In our initial experiments, the strength of vision- and wind-evoked turns were functions of flies’ starting orientations, with the strongest turns for each modality falling at distinct orientations. Similarly, turns that followed wind onsets and offsets in the pulse experiment were nonlinear functions of stimulus orientation — consi stent with a model based on spatial filtering, but not with a model based on orientation error [15,27,28]. Several observations also support differential temporal filtering of wind and visual cues. We found that turn magnitudes through a fixed orientation decayed consistently over time in the wind condition but not the vision condition. The time constant of this decay was similar to the value we obtained by fitting our model. Summation of cues from different modalities has been proposed previously to explain stabilization reflexes [34,35] and forward velocity control [26,36,37] in flies and fish. Summation of visual and odor information has been observed in turning behavior of tethered flies [38], and in the turn probability of freely moving larvae [7]. Thus, each element of our model is well supported by experimental data and previous work.

Neural circuits supporting multisensory control of orientation.

What neural circuits might support the multisensory integration described here? Wind signals are transduced by antennal mechanoreceptors [39,40] and conveyed to a number of higher-order mechanosensory neurons that exhibit diverse temporal responses and direction tuning [41–44]. The observed decay in wind-evoked turning drive might reflect adaptation occurring in these mechanosensory pathways [43,44]. Visual signals are transduced by photoreceptors and relayed to circuits processing both motion [45,46] and positional signals [47,48].

In order to jointly control orientation, signals from both modalities must converge. Several regions are candidate sites for this integration. The central complex, a region implicated in navigation and turning control [14,49,50], is known to receive both ipsilaterally-tuned input from visual interneurons [48,51] and directional mechanosensory signals [52]. Alternatively, visual and mechanosensory information could converge directly onto descending neurons that target the ventral nerve cord [53], as occurs in neurons that drive escape behavior [54,55]. Finally, it is also possible that visual and mechanosensory signals converge within the ventral nerve cord itself. Future recording experiments and genetic manipulations during behavior will help to unravel the neural circuits underlying multisensory control of orientation.

STAR Methods

Contact for reagent and resource sharing

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Katherine Nagel (Katherine.nagel@nyumc.org).

Experimental model and subject details

Flies

Unless otherwise specified, all flies were raised at 25°C on a cornmeal-agar-based medium under a 12 h light/dark cycle. All experiments were performed on adult female flies 3–5 days post-eclosion. With the exception of the first experiment (Figure 1), all flies were Canton-S (CS) wild-type. Data for that experiment came from control flies in a genetic silencing screen. These flies were raised at 18°C and were of the fol lowing genotypes (number in parenthesis is the number of flies used for that corresponding genotype):

(8) w- CS; UAS-TNTe/+; R12D12-Gal4/tubp-Gal80^ts

(8) w- CS; UAS-TNTe/+; R14C07-Gal4/tubp-Gal80^ts

(6) w- CS; UAS-TNTe/+; R24C07-Gal4/tubp-Gal80^ts

(7) w- CS; UAS-TNTe/+; R24E05-Gal4/tubp-Gal80^ts

(7) w- CS; UAS-TNTe/+; R28D01-Gal4/tubp-Gal80^ts

(8) w- CS; UAS-TNTe/+; R29A11-Gal4/tubp-Gal80^ts

(8) w- CS; UAS-TNTe/+; R34F06-Gal4/tubp-Gal80^ts

(6) w- CS; UAS-TNTe/+; R38B06-Gal4/tubp-Gal80^ts

(7) w- CS; UAS-TNTe/+; R38H02-Gal4/tubp-Gal80^ts

(7) w- CS; UAS-TNTe/+; R43D09-Gal4/tubp-Gal80^ts

(5) w- CS; UAS-TNTe/+; R46G06-Gal4/tubp-Gal80^ts

(7) w- CS; UAS-TNTe/+; R60D05-Gal4/tubp-Gal80^ts

(7) w- CS; UAS-TNTe/+; R65C03-Gal4/tubp-Gal80^ts

(5) w- CS; UAS-TNTe/+; R67B06-Gal4/tubp-Gal80^ts

(8) w- CS; UAS-TNTe/+; R73A06-Gal4/tubp-Gal80^ts

(8) w- CS; UAS-TNTe/+; R84C10-Gal4/tubp-Gal80^ts

(8) w- CS; UAS-TNTe/+; tubp-Gal80^ts/+

Because these flies were raised at 18°C, expression of gal4 was restricted by gal80. We therefore treated these flies as near-wild-type controls for the purposes of this paper, and pooled data from all genotypes. Note that observations in non-CS flies were later confirmed in CS wild type animals.

All flies were cold anesthetized on ice for approximately 5 minutes during tethering. A drop of UV-cured glue (KOA 30, Kemxert) was used to tether the notum of anesthetized flies to the end of a tungsten pin (A-M Systems, # 716000). Tethered flies’ heads were therefore free to move. For antennal stabilization experiments, a small drop of the same UV-cured glue was then placed between the second and third segments of the fly’s antennae, as depicted in Figure 2A. Flies were then allowed to recover from anesthesia for 30–45 minutes in a humidified chamber at 25°C before behavioral testing. All experiments were performed at 25°C.

Method Details

Behavioral apparatus

The behavioral apparatus and the software that controlled it were both custom made. The stimulus arena consisted of a circular piece of rigid plastic (31.75 mm dia, 31.75 mm high) lined on the inside with white copy paper. On opposing faces of the arena, holes were drilled 12.7 mm from the top of the arena to accommodate two teflon tubes (ID 4.76 mm, OD 6.35 mm, Cole-Parmer, # 06605–32) that delivered the wind stimulus. The “upwind” tube was packed with smaller 18 gauge stainless steel tubes (Monoject, # 8881–250016) to laminarize flow at the fly. For all experiments except the one in Figure 5, a 7.62 mm wide strip of black tape (Pro-Gaff) was vertically oriented behind the upwind tube, as shown in Figure 1A. For the stimulus offset experiment (Figure 5), the strip of tape was positioned 90° from the upwind tube. Both tubes extended 12.7 mm into the arena, leaving a 6.35 mm gap where the fly would sit. A 3D-printed tube holder stabilized the tubing and the arena to maintain a rigid position during rotation. Six IR LEDs (870 nm, Vishay, # TSFF5210) provided illumination for wing imaging. They were arranged in a circular pattern on the floor of the arena and were each aimed toward the fly.

A combination rotary union / electrical slip ring system (Dynamic Sealing Technologies, LT-2141-OF-ES12-F1-F2-C2) converted stationary electrical and pressurized air inputs outside the arena into rotating electrical and pressurized air connections inside it, facilitating stimulus delivery. The rotary union was coupled to the stimulus arena and tube holder with a flanged adapter (NEMA23 mount, Servocity). Tygon tubing of various diameters (ID 1.59 – 7.94 mm, Fisher) sequentially carried house air through a regulator (Cole-Parmer, # MIR2NA), a charcoal filter (Dri-Rite, VWR, # 26800), a mass flow controller (Aalborg, # GFC17), a three-way solenoid valve (Lee, # LHDA1233115HA), and the rotary union before air was delivered to the fly. The downwind tube was connected to house vacuum through the rotary union, a second identical solenoid valve and a flowmeter (Cole-Parmer, # PMK1–010608). Flow of house air and vacuum were always switched on and off together.

Each tethered fly was held in place with a pin holder (Siskiyou) which was lowered into the stimulus arena. Tethered flies were positioned directly between the upwind and downwind tubes, approximately 2.5 mm from the wind source, and were held at a pitch angle of approximately 30º with respect to the horizon, near their natural flight posture. Behavioral imaging was performed by a camera (Allied, # GPF 031B) and VZM 100i zoom lens lens (Edmund Optics, # 59–805) equipped with an IR filter (Edmund Optics, # BP850–22.5) that was positioned 45.5 cm above the fly. Strobing of the IR LEDs below the fly was coordinated with the camera frame rate (50 Hz) via a microcontroller (TeensyDuino, PJRC.com), ensuring that IR illumination did not heat the fly over the course of an experiment. Images of behaving flies were digitally processed by a custom LabVIEW (National Instruments) script to produce a nearly binarized white fly on black background. This image was used to extract the angle of each fly’s wings with respect to its long body axis. The difference between wing angles was multiplied by a static gain (0.04) and converted into an angular velocity on each sample. This gain was selected through a set of pilot experiments, where this setting was found to allow flies to fixate a stripe without orientation “ringing.” A static offset was manually selected at the beginning of each experiment to correct for subtle yaw rotations (less than 5°) relative to the camera. The angle of each wing was tracked over time was saved for later analysis. All communication between LabVIEW and arena components was mediated by a NIDAQ board (National Instruments, # PCIe-6321).

The angular velocity signal calculated in LabVIEW was sent to a stepper motor controller (Oriental, # CVD524-K) that converted this information into stepping commands. These commands drove a stepper motor (Oriental, # PKP566FMN24A) by an appropriate amount on each imaging sample. The motor stepped at 500 Hz, and was capable of driving rotations of the arena up to 162 °/s. We used the built-in smooth dr ive and command filter functionality of the motor controller to smooth the drive and reduce vibrations. The motor drive was transferred to the stimulus arena with a pair of gears (Servocity, # 615238), closing the loop back to the fly. Although rapid body saccades could not be reproduced by this motor/gain combination [31], slower course adjustments are well captured. We were restricted in possible rotational velocities by the competing demands of reasonable behavior, minimal vibration, and the high torque required to rotate the pressurized rotary union. The behavioral gain and maximal rotational velocity chosen represent a balance between these considerations. We also found that our core behavioral observations were preserved at higher closed-loop gain (Figure S4). Detailed plans, with images, of the entire stimulus delivery and flight simulator apparatus are available on Github.

Stimulus design

The visual stimulus, as described above, occupied approximately 30° of visual angle. We controlled ambient illumination of the stripe by placing the entire rig in a foam-core (ULINE, S-12859) box that was then draped with a black curtain (Fabric.com), rendering the arena light-tight. A set of warm white LED strips (HitLights, # LS3528_WW600, 36 SMDs) along the roof of the box were powered by a combination driver/dimmer (Luxdrive 2100mA Buckblock, LED Dynamics) and controlled via a microcontroller. Illumination of the stripe was measured with a power meter (Thor, # PM100D). Light levels used in these experiments were 0.1, 0.25, and 15 µW/cm², measured at a wavelength of 488 nm.

The wind stimulus, as described, was manipulated via a mass flow controller and a solenoid valve. Charcoal-filtered house air was pushed out of the upwind tube while vacuum was pulled through the downwind tube. Our custom LabView script regulated the flow through the MFC, and the valves were used to create rapid onset/offset kinetics (see Figures 1B, 6A, and S2). Flow at the fly, regulated by the MFC, was calibrated with an anemometer (a Dantec MiniCTA with split fiber film probe, # 55R55) that had previously been calibrated under similar conditions. Windspeeds of 0, 10, 25 and 45 cm/s were used in our experiments. We also used the anemometer to verify that wind intensity was constant across orientations of the stimulus arena as it rotated (Figure 1C). For the pulsing (Figure 6A) and ramping (Figure S2) wind stimuli, we took anemometer recordings at an arena orientation of 0º before testing flies. After initial calibrations, we re-checked the wind stimulus every 3–4 months to ensure stimulus consistency over time.

Experimental design

All experiments were controlled via custom LabVIEW scripts running on a desktop computer. In the experiments shown in Figure 1, each fly underwent 32 trials that were each a pseudorandomized combination of stimulus condition and initial orientation. There were four stimulus conditions (wind only, light only, both together, or no stimulus) and eight starting orientations (one every 45°). For these first exper iments, wind speed was set to 45 cm/s and light intensity was set to either 0.1 or 0.25 µW/cm². At the start of each trial, the stepper motor rotated the arena to the initial orientation selected by the LabView script, and the selected stimulus/stimuli were switched on. The fly was then given 25 seconds of control over the orientation of the arena. At the end of each trial, all stimuli were switched off, and the arena ceased to rotate. The next set of starting conditions were then selected, and the subsequent trial would begin. The inter-trial interval (ITI) was dictated primarily by the amount of time it took the motor to position the arena at the next starting orientation. The ITIs were therefore variable, but all fell within the range of 50–500 ms. We retained and analyzed data from flies that maintained flight through all 32 trials (45% of all flies tethered, 91% of flies that flew for at least 10 trials).

In the experiments shown in Figure S1, the sequence of events that comprised each trial were identical to the first experiment, but the four stimulus conditions were changed. For this experiment, our LabView script selected among four wind speeds (0, 10, 25 or 45 cm/s), meaning three possible stimulus selections were wind-only conditions, and one possible stimulus selection was a no-stimulus condition. There were still 8 starting positions, and therefore still 32 total trials. A command signal from the LabView script to the MFC altered the windspeed during the ITI, and the solenoid valve was opened at the start of the trial. This allowed us to vary wind intensity while maintaining rapid onset/offset kinetics.

In the experiments shown in Figure 2, we retained the trial design but altered both the initial orientations set and the stimulus conditions set. Here we used only two initial orientations (0° or 90°) and three stimulus conditions (wind onl y, light only, or both together), for a total of 6 possible stimuli. Each stimulus was forced-selected 5 times per fly, but the order of stimulus presentation was random. A full experimental session was therefore comprised of 30 trials. In this experiment, we used a windspeed of 25 cm/s and a stronger arena illumination intensity of 15 µW/cm².

The experiments shown in Figure 4 were identical to the those in Figure 2, but with altered wind speeds. Any given fly experienced wind of either 10 or 45 cm/s in the wind-only and multisensory conditions. Light intensity was unchanged across the third experiment (15 µW/cm²).

The experiment shown in Figure 5 was identical to the third experiment with the exception that the stimulus arena was spatially rearranged and the initial orientations were altered to compensate for this re-arrangement. The white copy paper and black tape that comprised the high-contrast visual stimulus (see above) were replaced such that the black bar was now oriented 90° away from the wind source (Figure 5A). The stripe remained at 0°, the upwind tube was positioned at −90°, and the downwin d tube at 90°. The possible initial orientations used were −90° or 90°. Wind intensity was 45 cm/s, and ambient illumination at the fly was 15 µW/cm².

For the experiment shown in Figure 6, each trial consisted of 50 seconds of constant visual stimulus intensity (15 µW/cm²) and pulsatile wind (45 cm/s). Each trial contained 10 pulses of 2.5 sec each, with a 2.5 sec period of no wind following each pulse. Flies began each trial oriented at 0º, then were given closed-loop control of their orientation relative to the stripe and wind source for 80 sec. The 30 sec of post-wind orienting was meant to allow any wind-based adaptation mechanisms to fully recover. Each fly completed 12 trials (50 sec each) and 11 inter-stimulus recovery periods (30 sec each).

Analysis of behavioral data

All analyses were performed using Matlab (Mathworks, Natick, MA). Turn magnitudes were expressed as the difference in wingbeat angles (WBA), and were low-pass filtered at 2Hz with a Butterworth filter, unless otherwise indicated (a key exception is comparisons between model simulations and data, where both measures must be in the same units — º/s). Orientations were taken from the online-integrated estimate.

Turn magnitude as a function of initial orientation (Figure 1E) was computed for the first 2s of each trial. Data for the wind and multisensory conditions were split at 0° and separate means were computed for mean-positive and mean-negative ΔWBA to emphasize the fact that turns away from the wind were strongest in the vicinity of 0° (Figure S2D). Orientation histograms (Figure 1F, S2C, and S3A-B) were calculated as the mean normalized occupancy across flies for each of 72 heading bins (each 5° w ide, with the first bin centered on 0°) over the last 15 seconds of each trial. Quadrant preference measures (Figure S1) were calculated as the mean normalized occupancy across flies for each of 4 heading bins (90° wide, with the first bin centered on 0°) over the last 15 seconds of each trial.

Turn latency (Figures 2–4) was computed as the latency to cross 45° (for visual and multisensory trials) or 135° (for wind trials, Figure S3). Trials that did not cross this threshold were excluded. Circles represent the mean for each fly. We discarded flies that produced fewer than 3 threshold crossings. WBA at turn (Figures 2–4) was computed over a 1 s window centered on the threshold crossing. Maximal deviation (Figures 2–4) was the maximum orientation reached over the first 10s of each trial. Turn rate through fixed orientations (Figure 2G) was measured by pooling data from all flies (N = 120) in the first experiment (Figure 1), and splitting each time course into 12 evenly sampled temporal bins. For each bin, we computed the mean turn rate through each of the following orientations: 30°, 45°, 60°, 75°, 90°, 105°, 120°, 135°, and 150°. Summary line represents the median across orientations.

Turn CDFs in Figure 5 were computed by first classifying turns as upwind or downwind directed visual turns. An upwind visual turn had negative ΔWBA while crossing 45°; a downwind visual turn had positive ΔWBA while crossing −45°. For each type of turn we c omputed the mean ΔWBA over a 1 s window centered on the threshold crossing.

Absolute orientations and turn rates as a function of time in Figure 6 were computed for each wind pulse and each interval between pulses. To control for effects of starting orientation, we analyzed only turns that originated at absolute orientations between 20º and 120º. To analyze behavior as a function of orientation, we split the data into bins 30º wide and positioned every 10º (such that there was substantial overlap between bins). Data from all times within the trial were included. Toward-0° ΔWBA represents turning toward the stripe/wind source at 0º, and is differentiated absolute orientation.

Models of multisensory orienting

The spatiotemporal filtering model shown in Figure 3A converts wind and visual signals (s_w, s_v) into turn commands (c_w, c_v) that sum to update the model fly’s orientation (θ) at each time step. This model operates in closed loop, as the wind and visual signals depend on the orientation of the fly. Turn commands are computed by applying spatial and temporal filters to the vectors s_w and s_v, with spatial filters applied to the angle (φ) time course, and temporal filters applied to the amplitude (ρ) time course. Filters are assumed to be separable.

Based on our data (Figure 1E) showing turn magnitude as a function of orientation, we modeled the spatial filters for wind and vision as normalized Gaussian functions with a standard deviation of 50° and a mean of 0°, multiplied by a step function (for wind) or a line of slope 1 (for vision). This produced a spatial filter in which the largest wind-evoked turns were generated for orientations just off 0°, while the largest visuall y-evoked turns were generated at 45°.

$${\mathrm{D}}_{\mathrm{w}}\left({\mathrm{s}}_{\mathrm{w}\left(\varphi \right)}\right)=\mathrm{s}\mathrm{g}\mathrm{n}\left({\mathrm{s}}_{\mathrm{w}\left(\varphi \right)}\right)\cdot {\mathrm{e}}^{-\frac{1}{2}{\left(\frac{s_w\left(\varphi \right)}{50}\right)}^2}$$ (1)

$${\mathrm{D}}_{\mathrm{v}}\left({\mathrm{s}}_{\mathrm{v}\left(\varphi \right)}\right)=-{\mathrm{s}}_{\mathrm{v}\left(\varphi \right)}\cdot {\mathrm{e}}^{-\frac{1}{2}{\left(\frac{s_v\left(\varphi \right)}{50}\right)}^2}$$ (2)

The temporal filter for wind was assumed to be the current wind amplitude minus an exponentially filtered history; the filter was parameterized by a decay rate (τ_w), and a steady-state response (β_w):

$$F_{\text{w}}(t)={\text{s}}_{\text{w(}\rho \text{)}}(t)-\frac{1-{\beta }_{\text{w}}}{{\tau }_{\text{w}}}{\int }_0^{\text{t}}{\text{e}}^{\frac{-\text{x}}{{\tau }_{\text{w}}}}{\text{s}}_{\text{w(}\rho \text{)}}(\text{t}-\text{x)dx}$$ (3)

The temporal filter for vision was assumed to be a delta-function, that is no temporal filtering occurred on the visual stimulus.

$$F_v=1$$ (4)

The overall multisensory turn command was then computed as:

$$\text{c(t)=}{\alpha }_{\text{w}}{\text{F}}_{\text{w}}(t)D_{\text{w}}({\text{s}}_{\text{w(}\varphi \text{)}})+{\alpha }_{\text{v}}{\text{F}}_{\text{v}}(t)D_v({\text{s}}_{\text{v(}\varphi \text{)}})$$ (5)

where the coefficients α_w and α_v determine the overall strength of wind- or visually-guided turns.

For the simulations shown in Figure 3E (left), we used the model to simulate flies’ turning response to single or multimodal stimuli presented at 0º or 90º (as in Figure 2). We fit the four free parameters of the model (α_v, α_w, τ_w, β_w) by using nonlinear regression to minimize the difference between the simulated orientation time course and the empirical median absolute orientation data for all six stimuli (Table 1). For display, we then added noise to the turn command with the same power spectrum as ΔWBA in the no stimulus condition. Briefly, we calculated the power spectrum of this signal and applied it to white noise in the frequency domain to obtain a noise signal with a matched power spectrum. We ran 1000 trials of simulation with unique noise traces for each. The mean of these simulations is shown in Figure 3E. Maximal deviation, latency, and turn rate were computed on the resulting orientation traces, as described above. All simulations were performed in Matlab with a time step of 20 ms.

For simulations with varied windspeed (Figure 4), we kept the best fit parameters from Figure 3 but varied α_w for each intensity. We estimated α_w by fitting this parameter only to the wind condition absolute orientation for each intensity (Figure S7). We ran 20 simulations with different turn noise for each intensity (computed as above). In this case, each simulation was a block of 5 trials each, to mimic a real “fly” in the 0º-90º paradigm (Figure 2). For the simulations with spatially offset wind and stripe (Figure 5), we circularly shifted the spatial filter for wind while keeping the spatial filter for vision unchanged. We used the “high wind” α_w parameter in these simulations to match the higher windspeed used in the experiment. We simulated 60 trials, again with different turn noise on each trial.

For the delay model (Figure 4A, second panel), we replaced the exponential filter for wind with delays of 20 ms for wind (T_w) and 100 ms for vision (T_v), based on previous work (Rohrseitz & Fry, 2011; Fueller et al., 2014):

$$\text{c(t)=}{\alpha }_{\text{w}}\cdot {\text{D}}_{\text{w}}({\text{s}}_{\text{w(}\varphi \text{)}}(\text{t}-{\text{T}}_{\text{w}}))+{\alpha }_{\text{v}}\cdot {\text{D}}_{\text{v}}({\text{s}}_{\text{v(}\varphi \text{)}}(\text{t}-{\text{T}}_{\text{v}}))$$ (6)

In the dynamic target averaging model (Figure 3C), the command to turn is an error between the current heading (θ) and a target heading (θ_t). The target heading is a weighted average of the target heading for vision (assumed to be 0°), and the target heading for wind (assumed to be 180°). We applied a differentiating filter, similar to the one used in the spatiotemporal filtering model (Eq. 3), to the time course of wind (i.e., s_w(ρ)), which allowed the weight for wind to decay exponentially. Note that the filter parameters (τ_w, β_w) were fit independently for each model.

$${\theta }_{\text{t}}(t)=\frac{\gamma \cdot {\text{F}}_{\text{w}}(t)\cdot {\theta }_{t,\text{w}}+{\theta }_{t,\text{v}}}{2}$$ (7)

The ratio of wind influence to vision influence is represented by γ. The resulting multisensory target orientation is then compared to current orientation to drive turning, with k_p as a proportionality constant that relates error to turn rate.

$${\text{c(t)=k}}_{\text{p}}\cdot ({\theta }_{\text{t}}(\text{t})-\theta (\text{t}))$$ (8)

For the proportional-integral-derivative (PID) controller model (Figure 3D), each sensory signal (s_w, s_v) was delayed (20 ms for wind, 100 ms for vision), and compared to a static target orientation (0° for vision, 180° for wind). The res ulting error was used to compute turn commands for each modality:

$${\text{e}}_{\text{m}}(\text{t})={\theta }_{\text{t},\text{m}}-{\text{s}}_{\text{m(}\varphi \text{)}}(\text{t}-{\text{T}}_{\text{m}})$$ (9)

Integrated error, differentiated error, and momentary error were each multiplied by a coefficient, then summed to yield the overall command, c_m, for that modality:

$${\text{c}}_{\text{m}}(\text{t})=k_{\text{m},\text{i}}\left({\int }_0^{\text{t}}{\text{e}}_{\text{m}}\text{dt}\right)+{\text{k}}_{\text{m,d}}({\text{de}}_{\text{m}})+{\text{k}}_{\text{m,p}}({\text{e}}_{\text{m}}(t))$$ (10)

The free parameters of the PID model are the three coefficients, k, for each modality. Based on our experimental data, and to maintain similarity with the spatio-temporal filtering model, we set the integral and derivative weights for vision to 0, while retaining all weights for wind (Figure 2C):

$${\text{c(t)=k}}_{\text{w,i}}\left({\int }_0^{\text{t}}{\text{e}}_{\text{w}}\text{dt}\right)+{\text{k}}_{\text{w,d}}(\text{d}{\text{e}}_w)+{\text{k}}_{\text{w,p}}({\text{e}}_{\text{w}}(\text{t}))+{\text{k}}_{\text{v,p}}({\text{e}}_{\text{v}}(\text{t}))$$ (11)

The vision-evoked turning drive is thus proportional to the error between current heading and 0° (i.e. it is spatially tuned but has no temporal dependence), while the wind-evoked turning drive depends on both spatial and temporal features of the stimulus. Moreover, each model has the same number of free parameters: two controlling the strength of turns driven by vision or wind (α_v, α_w vs k_v,p, k_w,p) and two controlling the temporal dynamics of the wind command (τ_w, β_w vs k_w,d, k_w,i).

Quantification and statistical analysis

Unless otherwise indicated, for all behavioral measures we computed the mean for each fly first and plots show mean +/− 95% CI across flies. Anemometer data and the correlation analysis in Figure S3C,D are the only exceptions. For those measures, data is reported as the mean +/− SEM. All correlations were tested for significance using a permutation test on Pearson’s R, all comparisons between stimulus conditions in single flies used paired t-tests and all comparisons across flies used the Wilcoxon rank-sum test. Information about each individual statistical test can be found in Figure Legends.

To compare our computational models quantitatively, we first used nonlinear regression to fit the four free parameters of each model (two free parameters for the sensory delays model) to the absolute orientation data for three stimulus conditions (wind, vision, multisensory) and two starting orientations (0º and 90º). Table 1 contain s the best-fit parameters for each model. We calculated the root mean squared error between the median empirical orientation data across these stimulus conditions and the simulation results from each model. We then performed a permutation analysis on the timing parameters (τ_w, β_w and k_w,d, k_w,i) of the spatiotemporal filtering and PID models while holding other parameters constant (Figure S6). In Figure 3F, we used the best fit parameters for each model to simulate responses to 8 starting orientations. We then computed the mean turn rate over the first two seconds of each simulation.

Highlights.

• Closed-loop behavior provides a continuous readout of multisensory neural integration

• Flies produce opposing orientations to a visual and a mechanosensory cue

• Flies respond to multisensory conflict with turn sequences or turn slowing

• Behavior is predicted by a sum of spatiotemporally filtered single-modality signals