Model selection for spatiotemporal modeling of early childhood sub-cortical development

Abstract

Spatiotemporal shape models capture the dynamics of shape change over time and are an essential tool for monitoring and measuring anatomical growth or degeneration. In this paper we evaluate non-parametric shape regression on the challenging problem of modeling early childhood sub-cortical development starting from birth. Due to the flexibility of the model, it can be challenging to choose parameters which lead to a good model fit yet does not over fit. We systematically test a variety of parameter settings to evaluate model fit as well as the sensitivity of the method to specific parameters, and we explore the impact of missing data on model estimation.

1. INTRODUCTION

Monitoring and measuring change over time is essential in medical research as well as in routine clinical practice. However, observations are often sparsely distributed in time due to factors including time commitment and cost, amongst others. Without dense measurements in time, we instead rely on statistical models to infer between observations, and to inform predictions about the future. Shape regression is a common statistical method to characterize change over time when observations are shapes.^1–4 Ambient space shape regression models have shown great promise and practicality, as deformations in the ambient space naturally act on all embedded objects. Therefore multi-object complexes consisting of a variety of geometry (either point sets, curves, or surfaces in 2D or 3D) can be directly included in model estimation, utilizing geometric information as well the spatial relationship between neighboring structures. Ambient space parametric models include piecewise geodesic⁵ and geodesic shape regression.⁶

Parametric models are powerful and convenient as a statistical representation, but do not offer the flexibility for modeling cyclical motion, such as the beating heart. Furthermore, parametric shape models are arguably poorly suited for capturing childhood development starting from birth, which is characterized by accelerated early growth which quickly saturates. In these cases, non-parametric models may be better suited to capture dynamic changes. One such non-parametric method, based on smooth anatomical growth by controlled acceleration⁷ has recently been included in the open source shape analysis software SlicerSALT (http://salt.slicer.org). However, the transition from methodology to adoption as a software tool requires systematic validation of the methodology. Of particular importance is the impact of parameter settings. Parameters are selected by users of the software who are often not intimately familiar with the underlying methodology. In this paper, we provide a systematic evaluation of model estimation under a variety of parameter settings on the challenging problem of spatiotemporal modeling of sub-cortical development starting from birth.

2. METHODS

We consider the time varying diffeomorphism ɸ_t which belongs to a regular group of deformations. Let a(x, t) be an acceleration field defined at spatial locations x and time t as

$$a(x,t)=\sum _{i=1}^N{K}^V(x,x_i(t)){\alpha }_i(t)$$ (1)

with impulse vectors α_i(t) at spatial coordinates x_i(t) and K^V a Gaussian kernel defined by standard deviation σ_V The time-varying impulse vectors α_i(t) define the spatiotemporal trajectory of a point x through the 2nd order differential equation

$${\ddot{\varphi }}_t(x(t))=\frac{d^{2}x(t)}{d{t}^2}=a(x(t),t),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}x(0)=x_0\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{and}\hspace{0.17em}\hspace{0.17em}\dot{x}(0)={\dot{x}}_0.$$ (2)

Given a collection of observed shapes O_ti at time t_i ([t₀, T]), model estimation consists in minimizing the cost

$$E(\dot{x}(0),\alpha \text{(t))=}\sum _{t_i}{\Vert {\varphi }_{t_i}({\mathbf{o}}_{t_0})-{\mathbf{o}}_{t_i}\Vert }_{W*}^2+{\gamma }_R{\int }_{t_0}^T{\Vert \text{a}(t)\Vert }_V^{2}dt,$$ (3)

where ‖ ‖_W*k_W is the norm on currents⁸ and regularity is defined in matrix notation as ${\Vert \text{a}(t)\Vert }_V^2=\alpha (t)K^V(\text{x(}t\text{),x(}t\text{))}\alpha \text{(}t\text{)}$ The initial positions x(0) are assumed to be located at the vertices of the shape at the earliest time point (x(0) = O_t0 ), and initial velocity is assumed to be zero (ẋ(0) = 0).

2.1. Model Parameters:

There are three parameters which in fluence model estimation:

• σ_V is the size of the kernel that defines the deformation. It is the distance at which neighboring points move in correlation. Higher values result in mostly rigid deformation, while lower values allow points a greater degree of independent movement.

• σ_W is the size of the kernel that defines the metric on currents. For multi-object complexes, one can choose a value of σ_W for each individual shape. This parameter allows tuning of the metric properties of the space of currents to suit the application. Intuitively, this parameter is the scale at which shape differences are considered noise. For matching very detailed shape features, choose a small value. For noisy observations with spurious features, set this value larger than the size of the features. However, too large of values essentially ignore shape di erences altogether.

• γ_R is the trade-off between data-matching and regularity. Since the model is non-parametric, this parameter may have a large impact on estimated models. A low weight on regularity results in models which closely match observed data, tending towards interpolation (rather than regression) as γ_R goes to zero. The value of γ_R must be selected carefully to avoid overfitting.

3. RESULTS

3.1. Model Selection

We focus our parameter evaluation on a longitudinal sequence of a healthy child, with image acquisition at birth (30 days old), and successive follow-ups at 1, 2, 4, 6, and 8 years of age. Sub-cortical structures were segmented with a multi-atlas segmentation method,⁹ including left and right caudate, thalamus, hippocampus, and amygdala. The early accelerated growth of the brain structures can be seen in Figure 1. A grid search is conducted over a range of parameter values: deformation kernel σ_V = [35; 20; 10; 5] mm, shape matching kernel σ_W = [20; 12; 8; 4; 2] mm, and regularity weight γ_R = [10; 1; 0:1; 0:01; 0:001; 0:00001]. A model is estimated for every parameter combination, resulting in 120 realized models. Surface errors are computed using MeshValmet,¹⁰ by measuring surface reconstruction error between the observations and the estimated model at corresponding time points.

Figure 1.

Longitudinal sequence of extracted sub-cortical structures.

First we investigate the impact of the deformation kernel σ_V, summarized in Figure 2 for a variety of values of σ_W and γ_R. Generally, lower values of the deformation kernel σ_V lead to greater data-matching accuracy. There is considerable improvement in data-matching by decreasing σ_V from 20 mm to 10 mm, though only a minor improvement by further decreasing to 5 mm. The smallest extent of the amygdala is 12:4 mm, which leads to a reasonable heuristic for choosing σ_V = 10 as ~ 80% the size of the smallest shape. The impact of the shape matching kernel σ_W follows the same pattern as the deformation kernel, with lower values of σ_W resulting in better data-matching. However, very low values of σ_W may lead to matching noisy local features which are not relevant. In the worst case, a value σ_W which is too low may lead to divergence in shape matching.¹¹ The shape matching kernel may be chosen for each structure as ~ 50% the size of the shape, or explicitly specified based on the application. Surface errors at 4 years old is shown in the top Figure 4 for three estimated models.

Figure 2.

The impact of the deformation kernel σ_V on reconstruction error for a variety of values of σ_W and γ_R.

Figure 4.

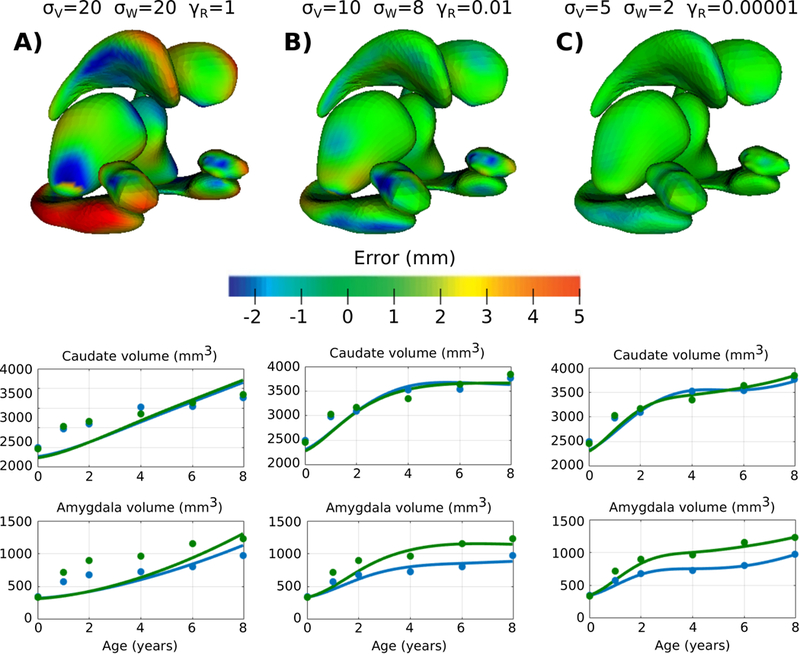
Top) Surface matching errors at 4 years old for models A, B, and C. Bottom) For each model A, B, and C, continuous trajectory of volume extracted from spatiotemporal models (lines) and volume of the observations (circles) shown for left (green) and right (blue) caudate and amygdala.

The regularity weight γ_R plays a more nuanced role in model estimation, and unlike the other parameters, does not relate to physical units for intuitive selection. Figure 3 summarizes the impact of γ_R for two combinations of deformation and shape matching kernels. We observe the general trend of better model t as regularity weight is decreased. We investigate possible overfitting by comparing observed shape volume with volume extracted continuously from the spatiotemporal models, shown in Figure 4 for the left and right caudate and amygdala. As model parameters are chosen to favor more accurate matching, each individual shape observation has a larger impact on model estimation. Model B provides a reasonable balance between data-matching and regularity, with a trajectory that follows the overall trend. Model C on the other hand has the best data-matching, but more closely resembles interpolation, particularly in the trajectory of the amygdala, demonstrating that model estimation is more influenced by individual observations. While there is no clear way to select γ_R, Figure 4 shows there is a large range (3 orders of magnitude) for γ_R (0.1, 0.01, 0.001, 0.0001) which result in similar data-matching, albeit with slightly different shape trajectories.

Figure 3.

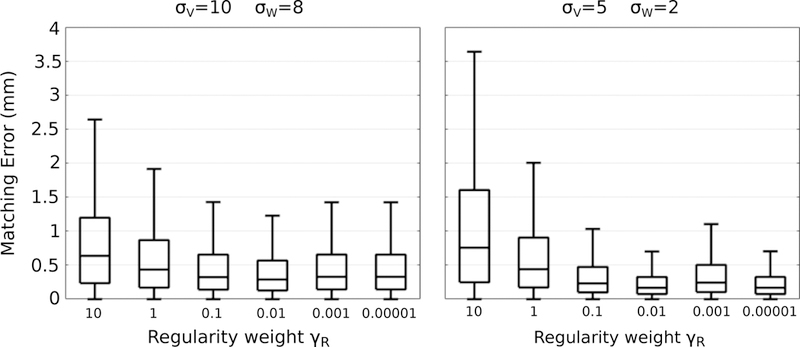
The impact of the regularity weight γ_R on reconstruction error for two sets of values of σ_V and γ_W

3.2. Impact of Missing Data

The previous section demonstrates that parameter settings play a large role in non-parametric model estimation. In fact, if one chooses parameter settings which favor data-matching, the method tends towards interpolation rather than regression. In this case, the inclusion or exclusion of a single observation (perhaps noisy) can greatly alter the resulting model. It is therefore natural to ask the question, how well does the model t when limited observations are available? To explore the impact of missing data, we utilize the following leave-several-out (leave-n-out) experimental design. Of the six available observations, we always include the first and last observations in order to span the entire time interval. We then estimate several models in each category:

• Leave-1-out: Models with a single observation left out during estimation. There are a total of 4 models in this category.

• Leave-2-out: Models with 2 observations left out during estimation. There are a total of 6 models in this category.

• Leave-3-out: Models with 3 observations left out during estimation. There are a total of 4 models in this category.

This experimental design results in 14 realized models, which are all estimated using identical parameter settings. Values were informed by the previous section, in order to strike a reasonable balance between data-matching and regularity, with σ_V = 10 mm, σ_W = 8 mm, and γ_R = 0:01. We do not estimate a model for the case of only 2 observations (leave-4-out), which is more akin to registration than regression. We do not advocate the use of this model in the case of 2 observations, as the geodesic model is much more suitable for registration.

To evaluate goodness of t, we again use MeshValmet to measure surface matching errors between observed and estimated shapes. For each model, we measure surface matching errors for all 6 observations separately, and concatenate the errors into an overall distribution of matching error. To summarize the leave-n-out categories, we also concatenate distributions in each category into an overall error distribution for that category (n =1, 2, and 3). Figure 5 shows the distribution of surface matching errors for the leave-n-out experiments, as well as summary statistics of surface matching errors. Surface matching error increases as the number of observations used for model estimation decreases. However, mean error is similar across leave-n-out categories, and the error distribution is heavily skewed towards zero, which suggests that the majority of surface points are well characterized by the estimated models.

Figure 5.

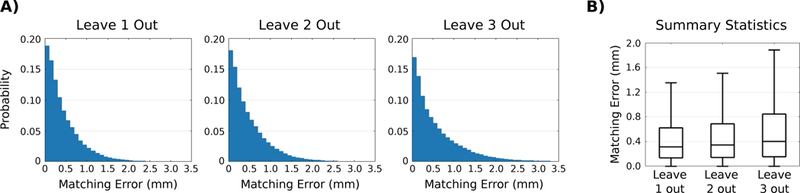
A) Normalized histograms showing the distribution of surface matching errors for all the models in the leave-n-out categories. B) Summary statistics show that surface matching errors increase as fewer observations are used in model estimation. While the mean surface error is comparable across the n categories, the decrease in model fit is clearly illustrated by the third quartile and maximum error. Note that outliers have been omitted, and that the maximum surface error is approximately 5:6 mm for all n categories.

Figure 6 shows the surface matching errors for a leave-2-out experiment where the 1 and 6 year observations were left out during model estimation. It is therefore somewhat expected that the largest surface errors appear at time points corresponding to missing data, at 1 and 6 years old. The error is especially large at 1 year old, where the true growth trajectory is highly accelerated and cannot be readily inferred without the additional information provided by the 1 year old observation, or alternatively, guided by a strong biological prior to inform growth between observations.

Figure 6.

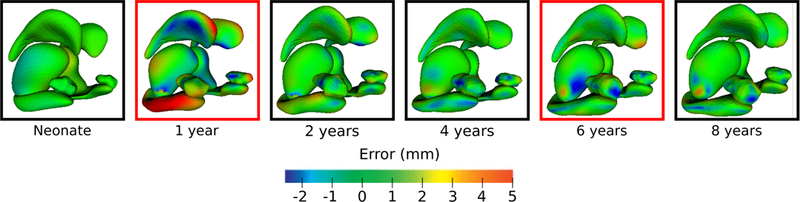
Surface matching errors between shape observations and estimated shapes for a leave-2-out experiment. Shapes bordered in red (1 and 6 years) were left out during model estimation and therefore show the largest magnitude of surface matching errors in the estimated shape trajectory.

4. CONCLUSIONS

The rapid non-linear development of sub-cortical structures starting from birth presents a unique challenge in spatiotemporal shape modeling, motivating the choice of a flexible non-parametric regression scheme. However, model selection is non-trivial, as model estimation can be very sensitive to parameter settings. The model is completely flexible to match arbitrary shape trajectories, and therefore parameters must be chosen carefully to avoid overfitting. Using longitudinal shape observations of 8 individual structures from birth to 8 years, we presented systematic testing over a wide range of model parameters. Results suggest parameters may be initially chosen by simple heuristics, or set by application specific criteria. Further validation will be carried out in future work, including a large scale longitudinal study of early childhood development. Such a study will investigate whether a fixed set of parameters which are suitable for a given individual can adequately capture the variability of a population.