Abstract
In vivo mapping of the neurite density with diffusion MRI (dMRI) is a high but challenging aim. First, it is unknown whether all neurites exhibit completely anisotropic (“stick‐like”) diffusion. Second, the “density” of tissue components may be confounded by non‐diffusion properties such as T2 relaxation. Third, the domain of validity for the estimated parameters to serve as indices of neurite density is incompletely explored. We investigated these challenges by acquiring data with “b‐tensor encoding” and multiple echo times in brain regions with low orientation coherence and in white matter lesions. Results showed that microscopic anisotropy from b‐tensor data is associated with myelinated axons but not with dendrites. Furthermore, b‐tensor data together with data acquired for multiple echo times showed that unbiased density estimates in white matter lesions require data‐driven estimates of compartment‐specific T2 values. Finally, the “stick” fractions of different biophysical models could generally not serve as neurite density indices across the healthy brain and white matter lesions, where outcomes of comparisons depended on the choice of constraints. In particular, constraining compartment‐specific T2 values was ambiguous in the healthy brain and had a large impact on estimated values. In summary, estimating neurite density generally requires accounting for different diffusion and/or T2 properties between axons and dendrites. Constrained “index” parameters could be valid within limited domains that should be delineated by future studies.
Keywords: anisotropy, axons, dendrites, diffusion MRI, myelin, neurites
1. INTRODUCTION
Diffusion MRI (dMRI) makes use of the micrometer scale displacement of water molecules to detect microstructural alterations in the brain due to disease (Chenevert et al., 2000; Horsfield & Jones, 2002; Moseley et al., 1990; Surova et al., 2013; Van Cauter et al., 2012; Werring et al., 2000) as well as normal processes such as learning (Sagi et al., 2012; Scholz, Klein, Behrens, & Johansen‐Berg, 2009) and maturation (Lebel, Walker, Leemans, Phillips, & Beaulieu, 2008; Löbel et al., 2009). However, dMRI does not yield tissue quantities directly. For example, the fractional anisotropy (FA) parameter of diffusion tensor imaging (DTI) (Basser, Mattiello, & LeBihan, 1994) cannot be directly associated to the density of anisotropic structures such as axons since it is sensitive to other factors such as their orientation coherence (Douaud et al., 2011; Pierpaoli, Jezzard, Basser, Barnett, & Di Chiro, 1996).
Biophysical models seek to increase the specificity of dMRI by dividing the signal between “compartments” to estimate tissue quantities (Alexander, Dyrby, Nilsson, & Zhang, 2017; Kiselev, 2017; Nilsson, van Westen, Ståhlberg, Sundgren, & Lätt, 2013; Novikov, Jespersen, Kiselev, & Fieremans, 2016; Novikov, Kiselev, & Jespersen, 2018). The target quantity of early approaches was the axonal volume fraction in coherent white matter, characterized by diffusion in highly anisotropic structures such as “cylinders” with a small but non‐zero (apparent) radial diffusivity (Assaf & Basser, 2005), or “sticks” with an (apparent) radial diffusivity of zero (Behrens et al., 2003). Further developments extended models to non‐coherent white matter by incorporating an orientation distribution function (Jespersen, Kroenke, Østergaard, Ackerman, & Yablonskiy, 2007; Kaden, Knösche, & Anwander, 2007; Sotiropoulos, Behrens, & Jbabdi, 2012; Tariq, Schneider, Alexander, Wheeler‐Kingshott, & Zhang, 2016; Zhang, Hubbard, Parker, & Alexander, 2011; Zhang, Schneider, Wheeler‐Kingshott, & Alexander, 2012) or by mimicking complete orientation dispersion through so‐called powder averaging (Kroenke, Ackerman, & Yablonskiy, 2004). Several contemporary approaches aspire to encompass also gray matter and to capture the combined volume fractions of axons and dendrites (neurites) in a single “neurite density” parameter (Jespersen et al., 2007; Kaden, Kelm, Carson, Does, & Alexander, 2016; White, Leergaard, D'Arceuil, Bjaalie, & Dale, 2013; Zhang et al., 2012). However, estimating a specific tissue quantity such as neurite density from clinical dMRI data necessitates simplifying assumptions whose accuracy and generality are unknown. This work focuses on three challenges for scientists using biophysical models to estimate the neurite density.
The first challenge is that mapping neurites requires a correct model for diffusion in both axons and dendrites. Biophysical models typically use the “neurite assumption” to represent both these structures in a single “stick” compartment with fully anisotropic (one dimensional) diffusion. The rationale is that axons and dendrites should exhibit a radial diffusivity of approximately zero (Behrens et al., 2003; Kroenke et al., 2004) due to their approximately cylindrical shape with diameters that are smaller than the resolution limit (Nilsson, Lasič, Drobnjak, Topgaard, & Westin, 2017). Studies have confirmed this property for axons (McKinnon, Jensen, Glenn, & Helpern, 2017; Veraart, Fieremans, & Novikov, 2017) but the evidence is less conclusive for dendrites. Although “stick‐like” diffusion has been demonstrated in cortical gray matter (Novikov, Jensen, Helpern, & Fieremans, 2014), this could merely reflect the presence of myelinated axons, as suggested by the study on fixed tissue using histology by Jespersen et al. (2010). Furthermore, the low levels of microscopic anisotropy observed in gray matter compared to white matter (Lampinen et al., 2017; Lawrenz & Finsterbusch, 2018; Novikov, Veraart, Jelescu, & Fieremans, 2018) may indicate that the radial diffusivity of dendrites is actually non‐zero.
The second challenge is that mapping densities (volume fractions) from signal fractions requires accounting for potential differences in T2 relaxation between tissue components. Since T2 values cannot be estimated from dMRI data acquired with a single echo time (TE), contemporary approaches implicitly assume T2 values to be equal between “neurite” and “non‐neurite” tissue. We refer to this as the “density assumption.” In white matter, such T2 differences may indeed be small, seeing that intra‐ and extra‐axonal water pools are not clearly distinguishable based on multi‐exponential T2 relaxation (Mackay et al., 1994; Whittall et al., 1997). Although components with different relaxation and diffusion properties have been demonstrated in peripheral nerve (Peled, Cory, Raymond, & Kirschner, 1999), near negligible effects on diffusion have been observed from varying the TE in human white matter (Clark & Le Bihan, 2000; Tax, Rudrapatna, Witzel, & Jones, 2017), as well as in rat brain (Does & Gore, 2000) and in cranial nerves of the garfish (Beaulieu, Fenrich, & Allen, 1998). However, more recent white matter studies indicate that the T2 value of intra‐axonal water may be longer than that of extra‐axonal water (De Santis, Assaf, & Jones, 2016; Veraart, Novikov, & Fieremans, 2017). In gray matter, corresponding issues are not well investigated. In pathologies, the compartment‐specific T2 values could be perturbed, for example, by enlargement of the extracellular space in ischemic degeneration (Englund & Brun, 1990) or by vascular edemas in conditions with blood–brain barrier damage such as tumors and acute MS lesions (Ballabh, Braun, & Nedergaard, 2004).
The third challenge is to find the range of conditions, or “domain of validity,” where the specific interpretations of biophysical model parameters are accurate. This domain may be both small and difficult to delineate for a parameter that is interpreted as the actual physical neurite density (fractional voxel volume occupied by neurites). The domain may be widened, however, if the parameter is interpreted as an “index” for neurite density (Kaden et al., 2016; Zhang et al., 2012), since this acknowledges a multifactorial origin and only claims the “ordinal accuracy” to rank observations. Even for neurite density indices, however, the domain of validity must be delineated to avoid conditions where factors such as T2 relaxation are sufficiently large to “break” the index property and confound the outcome of comparisons.
This work investigates the three above challenges through a “multidimensional” diffusion acquisition using the novel “b‐tensor encoding” approach (Eriksson, Lasič, Nilsson, Westin, & Topgaard, 2015; Eriksson, Lasic, & Topgaard, 2013; Lasič, Szczepankiewicz, Eriksson, Nilsson, & Topgaard, 2014) as well as multiple TE (de Almeida Martins and Topgaard, 2018). First, we examined whether mapping neurites based on the property of microscopic diffusion anisotropy is supported by data. Using the high specificity of b‐tensor encoding and knowledge from histology, we compared the anisotropy between multiple healthy brain regions that are substantially different with respect to axonal density but similar with respect to the combined axonal and dendritic (thus neurite) density. This tests a prediction of the neurite assumption (that microscopic anisotropy should reflect neurite density) against the alternative hypothesis that this property is mainly due to axons. Second, we explored whether T2 relaxation is likely to confound density estimates in healthy white and gray matter as well as in white matter lesions. Using the combined b‐tensor and multiple TE data, we attempted independent estimation of the “stick” fraction and compartment‐specific T2 values in a minimally constrained biophysical model. This tests the feasibility of disentangling density from T2 relaxation and addresses the validity of the density assumption. Age‐related white matter lesions, thought to be typically of ischemic origin (Pantoni & Garcia, 1997), are a suitable material in this context since they may exhibit changes to both diffusion anisotropy, through demyelination (Swieten et al., 1991) and axonal loss (Englund & Brun, 1990), and to T2 relaxation (Englund, Brun, & Persson, 1987). Third, we tested whether the domain of validity for neurite density indices encompass healthy white and gray matter as well as white matter lesions. Using biophysical models that are prevalent in the literature, we compared the resulting rankings of a range of brain regions with respect to the “stick” fraction. Since there can be only one true ranking with respect to a quantity such as neurite density, disagreement between models signifies a domain of validity violation. The results have impact on the standard interpretation of dMRI data, which is elaborated on in the discussion.
2. THEORY
The techniques for data analysis described in this section were employed after arithmetic averaging of the signal across diffusion‐encoding directions, so‐called “powder averaging” (Callaghan, Jolley, & Lelievre, 1979; Jespersen, Lundell, Sønderby, & Dyrby, 2013; Lasič et al., 2014). Provided data is acquired with a sufficient number of directions (Szczepankiewicz, Westin, Ståhlberg, Lätt, & Nilsson, 2016), powder averaging yields a signal whose orientation‐invariant aspects of diffusion are preserved but with an orientation distribution that mimics complete dispersion of anisotropic structures.
2.1. Representation‐based analysis
We represent the powder‐averaged b‐tensor data with a cumulant expansion in b‐values, according to
| (1) |
assuming cylinder‐symmetric b‐tensors. Four parameters represent the signal: the non‐diffusion weighted signal (S 0), the mean diffusivity (MD), the “isotropic kurtosis” (MKI), and the “anisotropic kurtosis” (MKA). Two parameters describe the experiment: the “size” (b) and “shape” (b Δ) parameters of the b‐tensor, where the former is the conventional b‐value (Le Bihan et al., 1986) and the latter ranges from −0.5 (planar) through zero (spherical) to unity (linear) (Eriksson et al., 2015; Topgaard, 2016; Topgaard, 2017). Under the assumption that the diffusion process can be described by a set of non‐exchanging compartments with approximately Gaussian diffusion, the MKI parameter represents variance in isotropic diffusivities (“isotropic heterogeneity”) and the MKA parameter represents microscopic diffusion anisotropy (Szczepankiewicz et al., 2016; Topgaard, 2017; Westin et al., 2016). These properties cannot be separated with data acquired with a single shape of the b‐tensor (Mitra, 1995; Topgaard, 2017). For example, using only the linear tensor encoding (LTE, b Δ = 1) of conventional multi‐shell dMRI yields the (powder‐averaged) signal equation of diffusion kurtosis imaging (DKI; Jensen, Helpern, Ramani, Lu, & Kaczynski, 2005; Yablonskiy, Bretthorst, & Ackerman, 2003) and three parameters: S 0, MD, and MK, where MK = MKI + MKA, as a special case. On the other hand, data acquired with two or more b‐tensor shapes, such as the combination of LTE and spherical tensor encoding (STE; b Δ = 0; Lasič et al., 2014; Szczepankiewicz et al., 2015; Szczepankiewicz, van Westen, et al., 2016) or LTE and planar tensor encoding (PTE; b Δ = −½; Jespersen et al., 2013; Lawrenz & Finsterbusch, 2013), allows estimation of four parameters and disambiguating the source for kurtosis.
2.2. Model‐based analysis
Biophysical models express the signal as the sum of signals from different compartments, according to
| (2) |
where, for the k:th compartment, f k is the fraction (Σf k = 1), S PD;k is the proton density‐weighted signal, A T1;k and A T2;k are the attenuations due to T1 and T2 relaxation, respectively, and A D;k is the attenuation due to diffusion. For the powder‐averaged signal, the diffusion attenuation is solely a function of orientation‐invariant aspects of the diffusion and the encoding. We represent compartment diffusion with an axisymmetric diffusion tensor described by its “size” (isotropic diffusivity), D I = 1/3 · D || + 2/3 · D ⊥ and “shape” (anisotropy), D Δ = (D || – D ⊥) / (D || + 2 · D ⊥) ∈ [−½ 1], where D || and D ⊥ are the axial and radial diffusivities, respectively. As we similarly represent diffusion encoding by an axisymmetric b‐tensor, parameterized by b and b Δ, the compartment diffusion attenuation is a function of four scalar parameters, according to (Eriksson et al., 2015; Topgaard, 2016; Topgaard, 2017)
| (3) |
where
| (4) |
and erf(·) is the error function (Callaghan et al., 1979).
We define a minimally constrained biophysical model based on Equation (2) using three compartments: a “ball” (B), a “stick” (S), and cerebrospinal fluid (CSF; C). By design, the “ball” and CSF compartments feature isotropic diffusion (D Δ;B = 0, D Δ;C = 0) while the “stick” compartment features completely anisotropic diffusion (D Δ;S = 1). While proton densities and T1 relaxation times are assumed to be equal for all compartments, the T2 values are free for “balls” (T2B) and “sticks” (T2S). The T2 value of CSF was fixed as T2C = 1,400 ms, motivated by results from Hopkins, Yeung, and Bratton (1986) and Weigel and Hennig (2006). Finally, the isotropic diffusivities of “balls” (D I;B) and “sticks” (D I;S) are free parameters, while the isotropic diffusivity of CSF is fixed as D I;C = 3 μm2/ms. In total, the model features seven free parameters, summarized in Table 1: S 0, f S (the “stick” fraction), f C (the CSF fraction), T2B, T2S, D I;B and D I;S. Together with the experimental parameters, b, b Δ, and TE, these combine to form the full signal equation, according to
| (5) |
Table 1.
Parameters and sets of constraints for the model‐based analysis
| Constraint set | n par | S 0 | f S | f C | T2B | T2S | D I;B | D I;S |
|---|---|---|---|---|---|---|---|---|
| C0 (minimally constrained) | 7 | ‐ | ‐ | ‐ | ‐ | ‐ | ‐ | ‐ |
| C0 iterated non‐cortex | 5 | ‐ | Iterateda | 0 | ‐ | ‐ | ‐ | ‐ |
| C0 iterated cortex | 6 | ‐ | Iterateda | ‐ | ‐ | ‐ | ‐ | ‐ |
| C1 (SMTb , c) | 5 | ‐ | ‐ | 0 | ‐ | ‐ | Equation (10) | ‐ |
| C2 (Ball and stick/racketsd , e) | 5 | ‐ | ‐ | 0 | ‐ | T2B | ‐ | ‐ |
| C3 (SMTc) | 4 | ‐ | ‐ | 0 | ‐ | T2B | Equation (10) | ‐ |
| C4 (CODIVIDE) | 5 | ‐ | ‐ | ‐ | ‐ | T2B | ‐ | D I;B |
| C5 (NODDIc , e) | 4 | ‐ | ‐ | ‐ | ‐ | T2B | Equation (10) | 0.57 |
| C6 (Ball and stick/racketsd , e , f) | 5 | ‐ | ‐ | 0 | ‐ | 70 | ‐ | ‐ |
Relaxation times are in ms and diffusivities are in μm2/ms; The“‐” denote free parameters.
f S ∈ [0, 0.0125, 0.0375, …, 0.9875].
Featuring two free T2 parameters.
With a “ball‐shaped” (D Δ = 0) “non‐stick” compartment.
Featuring two free isotropic diffusivity parameters.
Powder‐averaged.
Using a different T2 constraint.
where the attenuations are given by
| (6) |
| (7) |
| (8) |
using g(·) from Equation (4). This model thus resembles the “standard model” for white matter (Novikov et al., 2016; Novikov, Veraart, et al., 2018) but extended to gray matter (by the CSF fraction) and to feature T2 relaxation. Unlike the standard model, however, we employ the “ball” constraint of isotropic diffusion outside of “stick‐like” structures. The choice was made to improve feasibility of model fitting, but limited the subsequent data analysis to regions with a low orientation coherence, where this constraint should be valid.
A compartment‐based model (Equation (2)) can attain any capacity, using the word as defined in Goodfellow, Bengio, and Courville (2016), but it is generally necessary to constrain both the number of compartments and the compartment properties to match the degrees of freedom of data and avoid degeneracy in parameter estimation, such as demonstrated in Jelescu, Veraart, Fieremans, and Novikov (2016). We here investigate six sets of constraints on top of the minimally constrained model (set C0; Table 1), yielding six nested “submodels” that represent different contemporary approaches to obtain “stick” fractions.
Set C1 yields an approximation of the spherical mean technique (SMT) model (Kaden et al., 2016), but extended to feature two free compartment T2 values. It comprises a CSF constraint, given by
| (9) |
and a constraint that calculates the “ball” isotropic diffusivity from the “stick” isotropic diffusivity and the “stick” fraction, according to
| (10) |
Set C2 yields a powder‐averaged equivalent of the Ball and stick (Behrens et al., 2003) and Ball and rackets (Sotiropoulos et al., 2012) models, but extended to feature free compartment diffusivities. It comprises a T2 constraint, given by
| (11) |
and the CSF constraint (Equation (9)). Set C3 yields an approximation of the SMT model and comprises all the above constraints (Equations (9), (10), (11)). Set C4 yields the CODIVIDE model (Lampinen et al., 2017) and comprises the T2 constraint (Equation (11)) and a diffusivity constraint, given by
| (12) |
Set C5 approximates the powder‐averaged NODDI model (Lampinen et al., 2017; Zhang et al., 2012) and comprises the relation between isotropic diffusivities and the “stick” fraction in Equation (10), the T2 constraint (Equation (11)), and a fixed “stick” isotropic diffusivity, given by
| (13) |
Set C6 equals set C2 but uses a T2 constraint different than Equation (11), given by
| (14) |
a choice inspired by previous estimates of the voxel T2 value in white matter at 3 T (Wansapura, Holland, Dunn, & Ball Jr, 1999; Whittall et al., 1997) and results in white matter lesions obtained in this work. Note that compared to SMT and NODDI, sets C3 and C5 use the “ball” constraint (D Δ = 0) for the “non‐stick” compartment rather than defining its shape from a tortuosity relation (Szafer, Zhong, Anderson, & Gore, 1995). The difference was negligible in the investigated regions herein (see Supporting information). Finally, the original NODDI model employs a slight rearrangement of the “stick” and CSF fractions (Zhang et al., 2012).
The motivations for the different constraints are related to the data for which the corresponding models are intended. One type of constraint concerns compartment relaxation times (and proton densities), which cannot be estimated unless the acquisition features encoding dimensions sensitive to these properties. Most biophysical models are not designed for variable relaxation weighting and typically use the density assumption, given by
| (15) |
as in sets C2–C5 (with a different T2 for CSF). The dMRI data obtained for multiple TE used here, however, allow the constraint of equal “ball” and “stick” T2 values (Equation (11)) to be tentatively relaxed in the minimally constrained model. Our multiple TE data were acquired for b ≤ 0.5 ms/μm2, thus probing the TE dependence of the first cumulant of the diffusion attenuation (the mean diffusivity, MD) and yielding the following relation
| (16) |
where f S ′ = [S S/S]b = 0 is the relaxation‐weighted “stick” signal fraction before diffusion attenuation. For simplicity, Equation (16) assumes f C = 0. Together with an estimate of the voxel T2 value, this relation may allow estimation of both T2B and T2S. However, the gained precision depends on the difference between “ball” and “stick” isotropic diffusivities, which is clear when considering that the change in MD with respect to TE,
| (17) |
approaches zero as D I;S approaches D I;B.
Another type of constraint concerns diffusion properties. Aside from parameters related to variation across orientations, conventional multi‐shell dMRI only allows the estimation of two diffusion parameters (Kiselev & Il'yasov, 2007), extended to three if multiple shapes of the b‐tensor are used (Lasič et al., 2014; Lampinen et al., 2017). The minimally constrained model (set C0) features four diffusion parameters (f S, f C, D I;B, and D I;S), and thus the sets of constraints designed for conventional multi‐shell dMRI (C3 and C5) use two diffusion constraints and leave two parameters free. Conversely, the sets of constraints designed for b‐tensor encoding (C2, C4 and C6) use one diffusion constraint and leave three parameters free. Finally, set C1 was designed for b‐tensor encoding but still uses two diffusion constraints. Instead of estimating a third diffusion parameter, set C1 relates diffusion to relaxation through the relations in Equations (10) and (16).
3. METHODS
3.1. Subjects, acquisition and postprocessing
Data were acquired on a Siemens MAGNETOM Prisma 3T system (Siemens Healthcare, Erlangen, Germany) in three subject groups: A (n = 5; age = 32 ± 4 years; all male), B (n = 20; age = 25 ± 4 years; male/female = 11/9), and C (n = 10; age = 70 ± 10 years; male/female = 5/5). Subjects in groups A and B were healthy volunteers, who were either scanned specifically for this study (group A) or for a previous study (group B; Lampinen et al., 2017). The elderly subjects in group C were scanned for a larger study that included both patients with Parkinson's disease and controls. These subjects were included to study age‐related white matter lesions regardless of their disease status, wherefore we randomly selected five subjects with lesions (patients/controls = 3/2) and five subjects without lesions (patients/controls = 4/1).
We performed dMRI with b‐tensor encoding using a prototype echo‐planar diffusion sequence (Szczepankiewicz, Sjölund, Ståhlberg, Lätt, & Nilsson, 2016) with encoding gradient waveforms optimized for minimal TE (Sjölund et al., 2015). Data were acquired with both LTE and STE. To obtain diffusion‐relaxation correlation data, Groups A and C were additionally scanned with LTE sequences that repeated the same set of low b‐values and directions for different TE. T1‐weighted MPRAGE images were acquired for segmentation purposes. The experiments were approved by the regional ethical review board in Lund, and all subjects gave informed consent. Sequence parameters for all diffusion acquisitions are shown in Table 2.
Table 2.
Diffusion sequences used in the study
| B‐tensor encoding (LTE + STE) | Multiple TE (LTE) | ||||
|---|---|---|---|---|---|
| Group A | Group B | Group C | Group A | Group C | |
| TR (ms) | 7,000 | 4,000 | 5,200 | 7,000 | 6,900 |
| TE (ms) | 100 | 106 | 106 | 50,90,120,150 | 50,85,120,155 |
| Matrix size | 110 × 110 | 128 × 128 | 128 × 128 | 110 × 110 | 128 × 128 |
| Number of slices | 30 | 27 | 35 | 30 | 35 |
| Resolution (mm2) | 2 × 2 | 2 × 2 | 2 × 2 | 2 × 2 | 2 × 2 |
| Slice thickness (mm) | 2 | 4 | 4 | 2 | 4 |
| PI factora | 2 | 2 | 2 | 2 | 2 |
| Partial Fourier | 0.75 | 0.75 | 0.75 | 0.75 | 0.75 |
| b‐values (ms/μm2) | 0.1,0.5,1.0,1.5,2.0b | 0.1,0.5,1.0,1.5,2.0b | 0.1,0.5,1.0,1.5,2.0b | 0.1, 0.5c | 0, 0.5c |
| b Δ‐values | 1 and 0 | 1 and 0 | 1 and 0 | 1 | 1 |
| # directions/b‐value | 6, 10, 12, 16, 20 | 6, 6, 10, 16, 30 | 6, 6, 10, 16, 30 | 6, 6 | 1, 6 |
| Number of samples | 128 | 136 | 136 | 12 | 12 |
| Scan time (min) | 15.5 | 9 | 12 | 7 | 4.5 |
| Maxwell compensationd | Yes | No | No | Yes | No |
| Head coil array | 64 ch | 20 ch | 20 ch | 64 ch | 20 ch |
| Data prev. published | No | Yese | No | No | No |
The dMRI data were corrected for eddy‐currents and subject motion using ElastiX (Klein, Staring, Murphy, Viergever, & Pluim, 2010) with extrapolated target volumes (Nilsson, Szczepankiewicz, van Westen, & Hansson, 2015). Before model fitting, data were arithmetically averaged across diffusion‐encoding directions (powder‐averaged) for each b‐value and each b‐tensor shape. For the purpose of ROI definition and image registration, we performed a DTI analysis of LTE data at b ≤ 1 ms/μm2. All processing was performed using software available in the multidimensional dMRI toolbox (https://github.com/markus-nilsson/md-dmri)) (Nilsson et al., 2018).
3.2. Regions of interest
The study used data from 11 bilateral regions of interest (ROIs; Figure 1), including one white matter region, with or without lesions, together with two deep gray matter regions, and eight cortical gray matter regions. This selection of ROIs is motivated below.
Figure 1.
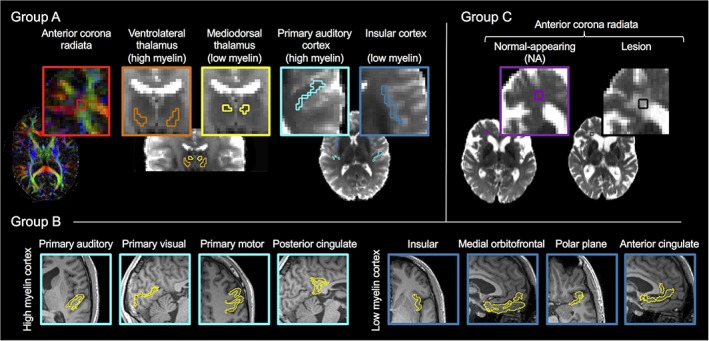
Regions of interest (ROIs). The study used 11 bilateral ROIs, representing white matter with or without lesions, together with deep and cortical gray matter with high or low myelin content. In group A (n = 5), we manually defined five ROIs: white matter (anterior corona radiata), deep gray matter with high myelin (ventrolateral thalamus) and low myelin (mediodorsal thalamus), and cortical gray matter with high myelin (primary auditory cortex) and low myelin (insular cortex). In group B (n = 20), we used the Desikan‐Killany and Destrieux parcellations of Freesurfer to define eight cortical ROIs: four with high myelin (primary auditory cortex, primary visual cortex, primary motor cortex, and posterior cingulate cortex) and four with low myelin (insular cortex, medial orbitofrontal cortex, the polar plane and anterior cingulate cortex). In group C (n = 10), we defined the anterior corona radiata as in group A but classified it as either “normal‐appearing” (NA; n = 5) or “lesion” (n = 5). All ROIs were bilateral. The anterior corona radiata of group A is shown on a DEC map from DTI and the remaining group A and C ROIs are shown on top of DTI S 0 images. The group B ROIs are shown on top of MPRAGE images [Color figure can be viewed at http://wileyonlinelibrary.com]
To investigate the variation in microscopic anisotropy against the variation in axonal content, the gray matter ROIs were selected to feature either a high or a low myelin content. Myelin content was used as a proxy for axonal content, since histology literature provides little information on the latter in gray matter. Deep gray matter was represented by the high myelin ventrolateral thalamus and the low myelin mediodorsal thalamus (Danos et al., 2003). Cortical gray matter with low myelin was represented by the primary auditory cortex (Bock, Kocharyan, Liu, & Silva, 2009; Hopf, 1955), primary visual cortex (Bock et al., 2009), primary motor cortex (Hopf, 1956) and posterior cingulate cortex (Morris, Paxinos, & Petrides, 2000), and low myelin cortical gray matter was represented by the insular cortex (Öngür, Ferry, & Price, 2003), medial orbitofrontal cortex (Hopf, 1956), polar plane (Hopf, 1955), and anterior cingulate cortex (Öngür et al., 2003).
To investigate whether T2 relaxation is likely to confound density estimates, the ROIs were selected to represent the main categories of healthy brain tissue—white matter, deep gray matter, and cortical gray matter—together with an example pathology in the form of white matter lesions. The anterior corona radiata was chosen to represent white matter, both because it is a typical site for white matter lesions and because it has a low orientation coherence (Mollink et al., 2017), which simplified our biophysical modeling.
The ROIs were defined manually for groups A and C, using the S 0 and directionally encoded color (DEC) maps from DTI, and automatically for group B, using the Desikan‐Killany and Destrieux parcellations of Freesurfer. The automatic procedure involved registering the S 0 image from DTI to the MPRAGE using rigid‐body registration implemented in ElastiX. A visual inspection assessed that the registrations yielded proper alignments and that the resulting ROIs were located within the cortex and minimally affected by EPI distortions. DTI parameters were used to make final adjustments of these ROIs: to reduce contamination with CSF and white matter, we excluded voxels with high mean diffusivity (MD > 1.1 μm2/ms) and high orientation coherence (FA > 0.5). For all ROIs, the signal was averaged across voxels before further analysis.
3.3. Brain patterns of microscopic anisotropy from b‐tensor encoding
The level of microscopic anisotropy was assessed for all ROIs (Figure 1) by the MKA parameter obtained from the b‐tensor encoded data (Table 2) in the representation‐based analysis using Equation (1). MKA values were compared using paired two‐tailed t‐tests between the high myelin ventrolateral thalamus and the low myelin mediodorsal thalamus and between the low and high myelin cortical ROIs. To enable detection of smaller effect sizes, the latter comparison used data from the larger group B, and the signal from each subject was averaged across the voxels of all four ROIs representing either high or low myelin. In addition, we compared the contrast of the MKA maps with a myelin‐stained coronal brain section obtained from a subject outside of the imaged group. A 6 μm thick section was cut at the level of the anterior thalamus and stained for myelin using Luxol fast blue together with Cresyl violet counter staining of nuclear structures.
3.4. Biophysical modeling with compartment‐specific T2 values
We first assessed the minimally constrained model's (Equation (5)) precision to estimate the “stick” fraction from the b‐tensor and multiple TE data (Table 2) from the group A and C ROIs (Figure 1). The precision was assessed by plotting a metric of goodness of fit against different values of the “stick” fraction, fixed prior to the fitting in 40 steps between zero and one. If data determine all model parameters, the plot should exhibit a clear minimum for some “stick” fraction. If data are insufficient, however, multiple “stick” fractions should yield a similarly good fit and result in a flatter plot. The CSF fraction was fixed to zero in the non‐cortical regions. The CSF fraction was free in the cortex, reducing the precision, but the procedure still yielded a good representation of the range of data‐compatible “stick” fractions (see Supporting Information).
Goodness of fit was defined as the normalized residual variance (NRV) obtained by dividing the residual variance (σR 2) by the signal variance due to noise (σ2 noise), according to
| (18) |
where n pa;i is the number of powder‐averaged directions for the i:th combination of measurement parameters (b, b Δ, and TE), S i and S' i are the powder‐averaged signals obtained from the measurement and predicted by the fit, respectively, n is the total number of samples (Table 2) and k is the number of parameters that were free to vary in the fitting (Table 1). The value of σ2 noise was estimated, for each ROI, as the voxel and b‐value average of the STE signal variance across the multiple repetitions.
For group C, the model was extended to feature the tissue T1 value (T1B/S = T1) and the constraint T1C = 5,700 ms to account for the repetition time differences between the b‐tensor data and the multiple TE data (Table 2). The precision in the estimated tissue T1 value was likely low given the rather long repetition times used in both sequences, but it was included as a nuisance parameter.
3.5. Brain region rankings by the “stick” fractions of constrained biophysical models
The six constrained “submodels” of the minimally constrained model (Table 1) were fitted to the b‐tensor and multiple TE data (Table 2) from the group A and C ROIs (Figure 1). First, we ensured that the constrained models yielded precise solutions by plotting the goodness of fit (Equation (18)) against fixed values of the “stick” fraction. Second, we tested whether there was a statistically significant disagreement between how the models ranked these regions with respect to the “stick” fraction. A metric for disagreement between rankings was defined according to
| (19) |
where I = 7 and J = 6 are the numbers of regions and models, respectively, r ij is the i:th region's ranking from the j:th model, and 〈r i〉 is the i:th region's average ranking. To test the statistical significance for potential ranking differences between models, we compared the observed value for m against a probability distribution simulated under the null hypothesis of equal rankings. The simulation created 105 sets of rankings by noising a set of “stick” fractions that equaled those observed but were pre‐sorted to agree between models. The added noise was distributed as ε ∈ N(0, σ/n s), where σ is the standard deviation across subjects (n s = 5). Code for performing this procedure is available on https://github.com/belampinen/ranking_test together with example data. Third, we assessed whether the different sets of constraints were compatible with data. To this end, the models were compared with respect to the fit quality obtained in different regions, defined as the sum of squared residuals (SSR) pooled from the combined fits in all subjects.
4. RESULTS
4.1. Brain patterns of microscopic anisotropy from b‐tensor encoding
The representation‐based analysis (Equation (1)) produced high‐quality maps of the level of microscopic anisotropy (MKA; Figure 2a). A strong contrast in anisotropy was observed between white and gray matter, with high levels in white matter and low levels in gray matter in general and in the cortex in particular. The level of isotropic heterogeneity (MKI) was generally low, except in regions with substantial partial volume effects between tissue and CSF. The contrast in mean diffusivity (MD) was flat across the brain tissue with similar levels in white and gray matter.
Figure 2.
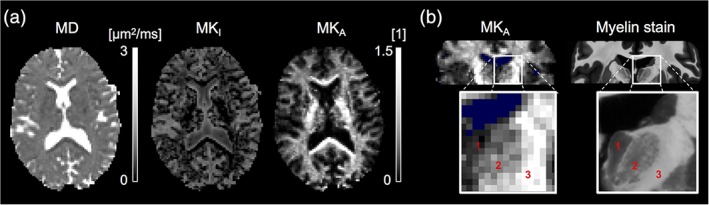
Parameter maps from the representation‐based analysis (Equation (1)) of b‐tensor data. (a) The mean diffusivity (MD) contrast was similar between white and gray matter. The level of isotropic heterogeneity (MKI) was generally low but higher in regions with partial volume effects from CSF. The level of microscopic anisotropy (MKA) was high in white matter and low in gray matter such as the cortex. (b) The level of microscopic anisotropy reflected the level of myelination seen in a coronal myelin‐stained histology slice (obtained from a different subject). From left to right: (1) the myelin‐poor mediodorsal thalamus, (2) the myelin‐rich ventrolateral thalamus, and (3) the internal capsule. Voxels with MD ≥ 2 μm2/ms are colored blue. The shown example is from group A [Color figure can be viewed at http://wileyonlinelibrary.com]
The MKA values were higher in ROIs expected to feature a higher myelin content (Figure 3, Table 3). Pure white matter (the anterior corona radiata) featured the highest values of MKA, the thalamus featured intermediate values and the cortex featured the lowest values. Within the thalamus, the MKA values were significantly higher in the myelin‐rich ventrolateral thalamus compared to in the myelin‐poor mediodorsal thalamus (mean ± SD; 0.71 ± 0.08 vs. 0.42 ± 0.05; t(4) = 19, p < 0.001). Within the cortex, the MKA values were significantly higher in the four combined high myelin regions compared to in the four combined low myelin regions (0.37 ± 0.04 vs. 0.20 ± 0.02; t(19) = 31, p < 0.001). Finally, when featuring a lesion, the anterior corona radiata exhibited decreased MKA values and increased values of MKI and MD, compared to normal‐appearing white matter.
Figure 3.
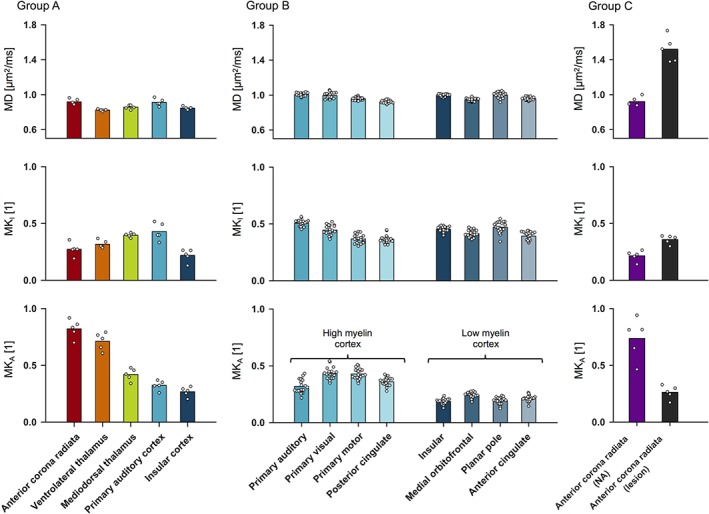
Parameter values from the representation‐based analysis (Equation (1)) of b‐tensor data. The parameter representing microscopic anisotropy (MKA) yielded the overall strongest contrast between regions, and the MKA values were higher in regions expected to feature a higher myelin content. In general, the MKA values were highest in white matter, intermediate in the thalamus and lowest in the cortex. In particular, the MKA was significantly higher in the myelin‐rich ventrolateral thalamus compared to in the more myelin‐poor mediodorsal thalamus (p < 0.001; group A) and in the combined high myelin cortical regions compared to in the combined low myelin cortical regions in (p < 0.001; group B). Meanwhile, no clear trend was observed in the parameters representing the mean diffusivity (MD) and the isotropic kurtosis (MKI). White matter featuring a lesion (the anterior corona radiata; group C) exhibited reduced MKA values and increased MKI and MD values compared to normal‐appearing (NA) white matter [Color figure can be viewed at http://wileyonlinelibrary.com]
Table 3.
Parameter values from the representation‐based analysis (Equation (1)) of b‐tensor data (Figure 1 ROIs), with means and inter‐subject standard deviations
| MD (μm2/ms) | MKI (1) | MKA (1) | |
| Group A | |||
| Anterior corona radiata | 0.92 (0.03) | 0.27 (0.06) | 0.82 (0.08) |
| Ventrolateral thalamus | 0.82 (0.01) | 0.32 (0.03) | 0.71 (0.08) |
| Mediodorsal thalamus | 0.86 (0.02) | 0.40 (0.02) | 0.42 (0.05) |
| Primary auditory cortex | 0.91 (0.04) | 0.43 (0.08) | 0.32 (0.04) |
| Insular cortex | 0.85 (0.02) | 0.22 (0.05) | 0.27 (0.04) |
| Group B (cortex) | |||
| Primary auditory | 1.01 (0.02) | 0.51 (0.03) | 0.32 (0.06) |
| Primary visual | 0.99 (0.03) | 0.45 (0.04) | 0.43 (0.05) |
| Primary motor | 0.96 (0.02) | 0.38 (0.04) | 0.43 (0.05) |
| Posterior cingulate | 0.92 (0.02) | 0.37 (0.03) | 0.36 (0.04) |
| Insular | 1.00 (0.01) | 0.45 (0.02) | 0.19 (0.02) |
| Medial orbitofrontal | 0.95 (0.02) | 0.41 (0.03) | 0.24 (0.03) |
| Polar plane | 1.00 (0.03) | 0.47 (0.05) | 0.19 (0.03) |
| Anterior cingulate | 0.96 (0.02) | 0.39 (0.03) | 0.21 (0.03) |
| Group C (anterior corona radiata) | |||
| Normal‐appearing | 0.92 (0.05) | 0.22 (0.05) | 0.74 (0.18) |
| White matter lesion | 1.52 (0.15) | 0.36 (0.04) | 0.26 (0.06) |
There was a correspondence in contrast between the maps of microscopic anisotropy and the myelin‐stained histology slice (Figure 2b). Both the MKA maps and the myelin‐stain were bright in white matter and dark in cortical gray matter. The correspondence was seen also between substructures, for example, in the intensity gradient between the myelin‐poor mediodorsal thalamus and the myelin‐rich ventrolateral thalamus. The MKA map was comparatively hyperintense in some white matter regions, including the internal capsule and the corpus callous, possibly reflecting a high orientation coherence and anisotropic diffusion in the extracellular space.
4.2. Biophysical modeling with compartment‐specific T2 values
Precise estimation of compartment‐specific T2 values was not possible in the brain (Figure 4a), which precluded accurate estimation of the “stick” fraction. The first row shows powder‐averaged signal curves in different brain regions (presented by column) with multi‐echo signal curves in inset plots. The second row shows how well the minimally constrained model could explain the signal for different fixed “stick” fractions in terms of the NRV (Equation (18)). The flat “valleys” in the residual variance corresponded to acceptable “stick” fractions between, for example, 0.3 and 0.7 in the anterior corona radiata and between 0.0 and 0.7 in the primary auditory cortex. The cause for the low precision is seen in the signal data. While there was a large effect of varying the b‐tensor shape (difference between LTE versus STE reveals microscopic anisotropy), the multi‐echo data did not reveal any obvious TE dependence of the mean diffusivity (change in slope of signal with TE, Equation (16)). As a result, the data did not support estimation of all parameters of the high‐capacity C0 model, and thus wide ranges of “stick” fractions could explain data equally well in all regions.
Figure 4.
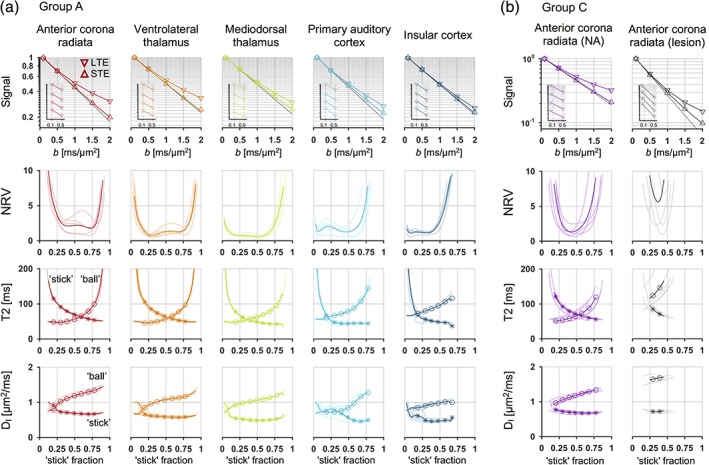
Compartment densities could be estimated independently from T2 relaxation in white matter lesions, but not in the healthy brain. (a) In the healthy brain, different regions (sorted by column) exhibited rather different levels of microscopic anisotropy, as seen by the difference between the powder‐averaged LTE and STE signal curves (first row). The slopes of the signal curves for different TE (inset plots) revealed no clear echo‐time dependence of mean diffusivity (Equation (16)), however, and the regions were not clearly separable by the “stick” fraction of the minimally constrained model (Equation (5)). The goodness of fit plot (second row; Equation (18)) showed wide ranges of data‐compatible (fixed) “stick” fraction values, reflecting wide ranges of data‐compatible compartment‐specific T2 values (third row). For most “stick” fractions, however, the isotropic diffusivity was higher in the “ball” compartment compared to in the “stick” compartment (fourth row). (b) In white matter (anterior corona radiata) with a lesion, precise estimation of the “stick” fraction together with compartment‐specific T2 values was possible. The “ball” compartment featured a longer T2 value and a considerably higher isotropic diffusivity compared to the “stick” compartment, resulting in a sufficient echo‐time dependence of diffusion to yield a narrow range of data‐compatible “stick” fractions. The plots use shaded lines for individual subjects and thick lines for group‐averages [Color figure can be viewed at http://wileyonlinelibrary.com]
The flat “valleys” were related to wide ranges of acceptable compartment‐specific T2 values and diffusivities, as shown by the third and fourth rows of Figure 4a. For example, acceptable T2 values for the “stick” compartment ranged between 57 and 93 ms in the anterior corona radiata and between 44 and 118 ms in the primary auditory cortex. Although the isotropic diffusivity was generally higher in the “ball” compared to the “stick” compartment, the difference was apparently insufficient to yield precise compartment‐specific T2 values (Equation (17)).
Results from white matter lesions stood in contrast to those from the healthy brain. In the lesions, data did allow precise estimation of the “stick” fraction, and the ranges of data‐compatible “stick” fractions were narrow (Figure 4b, second row). The signal exhibited a TE dependence (first row) and the “ball” compartment featured a longer T2 value (third row) and higher isotropic diffusivity (fourth row) compared to the “stick” compartment. These results would be expected for lesions of the ischemic type, where histological findings have shown a loss of tissue integrity that enlarges the extracellular space (Englund & Brun, 1990).
Table 4 shows parameter values from all five lesions. The “stick” fraction exhibited a considerable variation, between approximately 0.25 and 0.45, consistent with white matter lesions lying on a spectrum of tissue changes with varying severity (Gouw et al., 2010). Despite this apparent heterogeneity, the diffusion and relaxation properties of “sticks” were similar across lesions, and the estimated values were similar to values previously reported in healthy white matter. The “stick” T2 values were between 60 and 80 ms, similar to those reported for this region in Veraart, Novikov, and Fieremans (2017), and the isotropic diffusivities were approximately 0.7 μm2/ms, similar to in Veraart, Novikov, and Fieremans (2017) and Dhital, Reisert, Kellner, and Kiselev (2017 1712). A possible interpretation of this finding is that the remaining axons inside white matter lesions retain properties close to those in normal tissue.
Table 4.
Best‐fitting solutions for the minimally constrained model in the five white matter lesion ROIs (Figure 4b)
| f S | T2B | T2S | D I;B | D I;S |
|---|---|---|---|---|
| 0.46 | 173 | 63 | 1.73 | 0.71 |
| 0.43 | 137 | 67 | 1.72 | 0.71 |
| 0.43 | 123 | 70 | 1.63 | 0.67 |
| 0.35 | 110 | 84 | 1.56 | 0.74 |
| 0.24 | 169 | 83 | 1.78 | 0.75 |
Relaxation times are in ms and diffusivities are in μm2/ms.
4.3. Brain region rankings by the “stick” fractions of constrained biophysical models
As expected, all constrained models (Table 1) obtained precise solutions when fit to the combined b‐tensor and multiple TE data. Figure 5a exemplifies how the ranges of “stick” fractions that fit data well (low NRV, Equation (18)) were narrow (solid lines) compared to for the minimally constrained model (C0; dashed line). It also shows that the different constraints tended to “prefer” different values of the “stick” fraction (location of curve minima).
Figure 5.
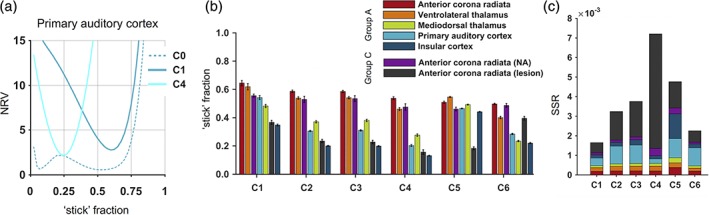
Using different constraints yielded different rankings with respect to the “stick” fraction. (a) The constrained models (solid lines, here C1 and C4; Table 1) yielded precise estimates of the “stick” fraction, seen by the narrow ranges of (fixed) values that yielded a high goodness of fit (Equation (18)) compared to for the minimally constrained model (dashed line, C0). (b) the six constrained models yielded rather different “stick” fraction patterns, and produced significantly different rankings (p = 0.025). Thus, this set of “stick” fractions lacks ordinal accuracy across the domain represented by the healthy brain and white matter lesions, and using these models to index the neurite density may yield constraint‐dependent results. For example, while constraint set C1 would indicate a higher “neurite density” in the mediodorsal thalamus compared to in white matter lesions, set C6 would indicate the opposite. The error bars indicate standard errors. (c) The quality of fit (in terms of a low sum of squared residuals, SSR) was generally high in white matter and in the thalamus, but not always in the cortex or in white matter lesions. In the cortex, only set C4, which featured a CSF compartment, obtained a good fit. In white matter lesions, only sets allowing different compartment T2 values (C1 and C6) obtained a good fit. Note that quality of fit is not enough to rule out poor constraints. For example, using sets C1 and C6, comparing the mediodorsal thalamus with white matter lesions yielded similar fit qualities but different results, while using sets C3 and C4 yielded the opposite [Color figure can be viewed at http://wileyonlinelibrary.com]
Comparing seven regions using the six constrained models yielded rather different patterns of “stick” fractions (Figure 5b), with significantly different rankings (p = 0.025, rank‐based permutation test). As an example of the difference in rankings we use sets C1 and C6, which achieved the overall best fits (Figure 5c), and compare the “stick” fractions in the mediodorsal thalamus and in white matter lesions. Set C1 indicated significantly higher fractions in the former compared with the latter (0.48 ± 0.06 vs. 0.37 ± 0.07, t[5] = 3, p < 0.028), while set C6 indicated the opposite (0.23 ± 0.02 vs. 0.40 ± 0.06, t[5] = −4, p = 0.007), using paired two‐tailed t‐tests. Qualitatively, four different ranking patterns could be observed with respect to the “stick” fraction. The ranking obtained with constraint set C1 (as arbitrary reference) was contradicted by a switching of the primary auditory cortex and the mediodorsal thalamus (using C2–C4) and by comparatively high “stick” fractions in gray matter (using C5) and in white matter lesions (using C6).
No constrained model obtained a good fit both in healthy brain and in white matter lesions (Figure 5c). All models obtained similar fit qualities in white matter and in the thalamus. In the cortex, however, an overall good fit was only obtained using set C4, which features a CSF compartment. In general, fits were poorer in the primary auditory cortex, compared to in the insular cortex, possibly reflecting differences in partial volume effects with CSF. Using set C5 (as in NODDI), however, yielded a poor fit in both cortical regions despite its CSF compartment, likely due to relating microscopic anisotropy to mean diffusivity (Lampinen et al., 2017). In white matter lesions, models using the assumption of equal compartment T2 values (Equation (11); present in C2–C5) yielded comparatively poor fits, consistent with the substantial T2 differences demonstrated in Table 4. The fit within lesions was particularly poor using set C4, likely due to the invalid assumption of equal compartment diffusivities (Table 4).
5. DISCUSSION
Mapping neurite density requires a correct model for diffusion in both axons and dendrites. The conventional neurite assumption is that these structures exhibit highly anisotropic (“stick‐like”) diffusion. If this is the case, their respective prevalence should contribute similarly to microscopic diffusion anisotropy in the brain, and we would expect a contrast in MKA that bears similarity to the contrast in neurite density. In cortical gray matter, histology studies in mice have reported a rather even split between axons and dendrites and a neurite volume fraction of approximately 60% (Braitenberg & Schüz, 1998; Chklovskii, Schikorski, & Stevens, 2002; Ikari & Hayashi, 1981). In white matter, histology studies have reported a neurite density (intra‐axonal volume fraction) of 30–50% in the corpus callosum of macaque (Stikov et al., 2015) and mice (Jelescu et al., 2016) and in the rat spinal cord (Xu et al., 2014). Together with a 20–50% volume fraction of myelin water (Jelescu, Zurek, et al., 2016; Stikov et al., 2015; Xu et al., 2014) with fast T2 relaxation (Mackay et al., 1994) that renders it MR‐invisible at our relatively long echo times, an axonal volume fraction of 30–50% corresponds to an MR‐visible neurite signal fraction, v axons/(1 − v myelin), in the vicinity of the approximate 60% reported for the cortex. Thus, histology suggests that the signal fraction of neurites as observed with dMRI should be similar between gray and white matter, wherefore, by the neurite assumption, their respective levels of microscopic diffusion anisotropy should be similar. In contrast, however, we found that microscopic anisotropy differs substantially between gray and white matter (Figure 2, 3, Table 3). Furthermore, regional differences in microscopic anisotropy were associated with myelin content, and thus axons, both qualitatively (Figure 2b) and quantitatively (Figure 3, Table 3), consistent with previous observations in fixed tissue by Jespersen et al. (2010). These observations contradict the neurite assumption and suggests that highly anisotropic diffusion is a feature of axons but not dendrites. A non‐zero radial diffusivity in dendrites could be due to, for example, fast exchange with the extracellular space or between short dendritic segments with different orientations. A low axial diffusivity in dendrites is not a sufficient cause, however, since it would have manifested in a higher MKI, and constraints that allow an independent “stick” diffusivity (such as C2) should have yielded an “adjusted” “stick” fraction (Table 1; Figure 5b). Our observations could potentially be explained, however, by a low T2 value in dendrites compared to in axons, since that would confound a T2‐weighted metric such as the MKA. Lipid composition differs substantially between white and gray matter (O'Brien & Sampson, 1965), wherefore different degrees of wall relaxation from proton exchange could be one possible factor. Notably, such T2 differences would also confound volume fraction estimates under the density assumption, leading to the second part of our investigation.
Mapping compartment densities using dMRI with a single TE requires that T2 values are approximately equal across tissue components. In white matter lesions, our analysis of b‐tensor and multi‐echo data found that water with isotropic diffusivity exhibited a longer T2 value compared to water exhibiting “stick‐like” diffusion (Figure 4b, Table 4). In the healthy brain, however, compartment‐specific T2 values could not be estimated (Figure 4a) and potential confounding effects on the “stick” fraction could not be determined. This lack of precision also prevented us from directly assessing whether a low T2 value of neurites may explain the low levels of microscopic anisotropy in gray matter. However, the results did indicate the approximate ranges of compartment T2 values and diffusivities for which data are compatible with this hypothesis. Table 5 shows group‐averaged parameter values for the solutions in the flat “valleys” from Figure 4a. In short, the “stick” fraction could assume values in a vicinity of the expected neurite density (0.5–0.7; area in bold) if the T2 value difference between “neurite” and “non‐neurite” tissue was small in white matter but large in gray matter. For example, ballpark figures would indicate similar T2 values for neurite and non‐neurite tissue (60–80 ms) in the anterior corona radiata, but much lower T2 values for neurites (40–50 ms) compared to non‐neurite tissue (80–120 ms) in the cortex. The solutions would also imply a higher axial diffusivity of neurites in white matter (approximately 2.1 μm2/ms in the anterior corona radiata) compared to in gray matter (approximately 1.5 μm2/ms in the cortex). Thus, estimating neurite density may require correcting for such differences, which is a difficult task even using multi‐shell multi‐b‐tensor and multi‐echo data (Figure 4a). Note that application of the density assumption of equal compartment T2 values yields the heterogenous anisotropy observed in the representation‐based analysis (Figures 2 and 3; Table 3), and an interpretation that is in apparent conflict with histology. These results suggest that estimating neurite density from conventional single‐echo dMRI has low accuracy. Whether such parameters could still be indices for neurite density was explored in the third part of our investigation.
Table 5.
Data‐compatible “stick” fractions (f S) for the minimally constrained model in the healthy brain (Figure 4a), with corresponding parameters
| f S | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Anterior corona radiata | ||||||||||
| T2B | − | − | 47 | 51 | 56 | 65 | 80 | − | − | |
| T2S | − | − | 92 | 78 | 69 | 62 | 57 | − | − | |
| D I;B | − | − | 1.02 | 1.12 | 1.19 | 1.25 | 1.30 | − | − | |
| D I;S | − | − | 0.73 | 0.70 | 0.69 | 0.67 | 0.66 | − | − | |
| Ventrolateral thalamus | ||||||||||
| T2B | − | 47 | 47 | 51 | 57 | 66 | 80 | 105 | − | |
| T2S | − | 104 | 84 | 72 | 63 | 57 | 52 | 50 | − | |
| D I;B | − | 0.83 | 0.96 | 1.03 | 1.08 | 1.11 | 1.13 | 1.18 | − | |
| D I;S | − | 0.71 | 0.62 | 0.60 | 0.59 | 0.58 | 0.57 | 0.59 | − | |
| Mediodorsal thalamus | ||||||||||
| T2B | 48 | 49 | 53 | 57 | 63 | 70 | 81 | − | − | |
| T2S | 111 | 76 | 61 | 53 | 48 | 45 | 43 | − | − | |
| D I;B | 0.82 | 0.93 | 0.98 | 1.02 | 1.05 | 1.09 | 1.14 | − | − | |
| D I;S | 0.63 | 0.54 | 0.51 | 0.49 | 0.49 | 0.49 | 0.51 | − | − | |
| Primary auditory cortex | ||||||||||
| T2B | 56 | 62 | 67 | 72 | 80 | 92 | 115 | − | − | |
| T2S | 108 | 60 | 47 | 44 | 44 | 45 | 45 | − | − | |
| D I;B | 0.72 | 0.72 | 0.72 | 0.77 | 0.86 | 1.02 | 1.20 | − | − | |
| D I;S | 0.77 | 0.78 | 0.78 | 0.68 | 0.56 | 0.47 | 0.46 | − | − | |
| Insular cortex | ||||||||||
| T2B | 67 | 74 | 80 | 87.5 | 97 | − | − | − | − | |
| T2S | 114 | 64 | 55 | 50.7 | 48 | − | − | − | − | |
| D I;B | 0.84 | 0.85 | 0.90 | 0.95 | 0.98 | − | − | − | − | |
| D I;S | 0.58 | 0.61 | 0.49 | 0.46 | 0.47 | − | − | − | − |
Shown values are group‐averages from the flat “valleys” of (best fitting) solutions in Figure 4a, with remaining values replaced with ‘‐’. Values associated with “stick” fractions that are similar to approximate neurite density estimates from histology (0.5–0.7) are written in bold. Relaxation times are in ms and diffusivities are in μm2/ms.
An index with sensitivity to a physical quantity could be useful even if lacking absolute accuracy, for example, by having the ordinal accuracy to allow comparisons between regions, conditions, or time points. When confounding effects grow large compared to the effect of interest, however, results become increasingly dependent on the choice of model constraints. Here, when ranking seven regions with respect to the “stick” fraction, using six different sets of constraints yielded significantly different rankings (Figure 5b). From this observation, we draw two conclusions concerning the range of conditions represented by the healthy brain and white matter lesions. First, as there can only be one true ranking with respect to a given quantity, such as neurite density, this range of conditions violates the domain of validity for this set of “stick” fractions. Second, this range of conditions likely features important confounding factors. We suspect compartmental T2 differences to be one such factor, both because of its strong impact on estimated volume fractions (Figure 4), and because three different patterns were observed when constraining it in three different ways (C1: Equation (10); C2–C5: Equation (11); C6: Equation (14)). Another such factor may be isotropic heterogeneity, a confounder for microscopic anisotropy (Mitra, 1995) that is misrepresented by NODDI (Lampinen et al., 2017), seeing that set C5 yielded a strikingly different pattern compared to the other sets using the density assumption (C2–C4; Equation (11)). Note that disagreement in ranking was not always related to difference in quality of fit, so fit quality is not enough to rule out invalid constraints. For example, when comparing the mediodorsal thalamus with white matter lesions, sets C1 and C6 yielded very different results for similar fit qualities, while sets C3 and C4 yielded similar results for very different fit qualities. Although this experiment was discouraging for the prospect of finding a widely applicable neurite density index, overcoming some of these issues should be possible through more extensive acquisitions and/or additional validation work.
Our investigation indicates that accurate estimation of the neurite density requires accounting for different diffusion and/or T2 properties between axons and dendrites. As a consequence, true neurite density estimation may not be feasible with moderate b‐values and limited ranges of TE. Obtaining indices of the neurite (or axonal) density may be possible, although their usefulness is limited to conditions where confounding factors are small or can be reliably constrained. One such condition could be healthy white matter, where the effects of T2 relaxation (Clark & Le Bihan, 2000; Tax et al., 2017) and isotropic heterogeneity (Dhital, Kellner, Reisert, & Kiselev, 2015; Szczepankiewicz et al., 2015) appear to be small, and where excellent (ex‐vivo) correlations have been demonstrated between the “stick” fraction and histological metrics of axonal density (Jespersen et al., 2010). Thus, in healthy white matter, existing methods such as WMTI (Fieremans, Jensen, & Helpern, 2011), NODDI or SMT may be able to capture the relative variation of axonal density. However, the often used “neurite” label suggests a domain of validity that also encompasses gray matter, where neurites may exhibit different diffusion and/or relaxation properties (Table 5) and their disentangling may be further complicated by CSF contamination. Extending a neurite density index to examine pathology entails additional challenges, including new tissue components in tumors (Wen et al., 2015), exchange between tissue components in stroke (Lätt et al., 2009), and perturbing effects on T2 relaxation (Figure 4b) in demyelination and/or degenerative conditions, where the former could mimic axonal loss simply by expanding the pool of MR‐visible water with low diffusion anisotropy. In forthcoming searches for the neurite density with dMRI, studies should attempt to elucidate the contribution of dendrites to microscopic anisotropy, to inform constraints by exploring relations between diffusion and non‐diffusion properties, using, for example, correlation techniques such as those presented by Benjamini and Basser (2018) or by de Almeida Martins and Topgaard (2018), and to delineate the domains of validity for prospective index parameters. The current state of evidence suggests that reporting results in terms of the “stick” signal fraction, or possibly the axonal density index in healthy white matter, would promote the most useful interpretations of clinical studies using biophysical models.
We note several limitations with the present study. First, the waveforms used to produce linear and spherical tensor encoding had slightly different timing properties. Lundell et al. (2017) demonstrated in ex vivo monkey brain that using waveforms with different “spectral content” may confuse time‐dependent diffusion for microscopic anisotropy. We investigated this by comparing LTE obtained using waveforms that have either “tuned” or “detuned” encoding spectra (e.g., similar or different timing properties) with respect to the waveform used for STE (see Supporting Information). No systematic effects of diffusion time were observed, which is in line with multiple studies showing negligible time dependence in living brain tissue for clinically relevant diffusion times, both in humans (Clark, Hedehus, & Moseley, 2001; Clark & Le Bihan, 2000; Nilsson et al., 2009) and animals (Niendorf, Dijkhuizen, Norris, van Lookeren Campagne, & Nicolay, 1996; Ronen, Moeller, Ugurbil, & Kim, 2006). Second, the waveforms used for groups B and C were not optimized for negligible concomitant fields, which may induce a positive bias in microscopic anisotropy (Szczepankiewicz & Nilsson, 2018). From assessing the data for characteristic gross signal errors, however, we do not believe that the effect was large for the waveforms used in this study. Furthermore, such bias should have no systematic impact on the intercortical comparisons performed with the group B ROIs; and the group C data was only extracted from relatively deep parts of the brain (the corona radiata) where the effects of concomitant fields should be small (Szczepankiewicz & Nilsson, 2018). Third, due to the SNR penalty from studying deep gray matter while using small voxels, we acquired multi‐echo data for a maximum b‐value of 0.5 ms/μm2. Accordingly, we could only rely on a TE dependence of the mean diffusivity to separate compartment T2 values (Equation (16)), an effect that has previously been demonstrated to be small in the healthy brain (Clark & Le Bihan, 2000; Qin et al., 2009; Tax et al., 2017; Veraart, Novikov, & Fieremans, 2017). Acquiring multi‐echo data for higher b‐values may be a promising way forward (Veraart, Novikov, & Fieremans, 2017). Simulations presented in the supporting information indicate that extending our dataset with multiple TE to higher b‐values could yield sufficient precision. However, the strong attenuation associated with such data may necessitate dealing with the Rician noise floor (Veraart, Novikov, & Fieremans, 2017) and also complicate motion correction (Nilsson et al., 2015). Fourth, our data had some heterogeneity due to being acquired under different conditions. For example, group B lacked data for multiple TE and group C contained subjects both with and without Parkinson's disease. We do not believe this an issue, however, seeing that the relatively large group B allowed comparisons of the (T2‐weighted) microscopic anisotropy across healthy cortical regions (Figure 3), and that Parkinson's disease seems to have a subtle impact on diffusion (Surova et al., 2016) compared with the effects of white matter lesions studied in group C. Fifth, part of the data analyzed in the cortex were acquired with lower resolution (2 × 2 × 4 mm3; group B) and likely suffered partial volume effects with white matter and CSF. The impact on results from CSF was likely small, however. While the MKA was almost twice as high in high myelin cortex compared to in low myelin cortex, the MKI—a measure of isotropic heterogeneity and indirectly of partial volume effects with CSF (Figure 2a)—was similar (Figure 3; Table 3). With that said, future studies could benefit from CSF nulling by the use of an inversion pulse. Sixth, our minimally constrained model featured the “ball” constraint, thus assuming isotropic diffusion outside of “stick‐like” structures, which may be inaccurate in regions with high orientation coherence (Fieremans et al., 2011; Novikov, Veraart, et al., 2018; Reisert, Kellner, Dhital, Hennig, & Kiselev, 2017). As a consequence, our white matter investigation was limited to the low‐coherence anterior corona radiata. Seventh, our minimally constrained model assumed T1 relaxation and proton density to be equal across compartments. Although we believe that these effects may be important and should be considered in future studies, they were outside the scope of the current work. Finally, we point out a limitation intrinsic to most biophysical models that describe complex tissue with a few parameters: bias due to simplification. For example, the neurite interpretation could be biased if the “stick” compartment captures water in the tree‐like processes of protoplasmic astrocytes that are closely associated with gray matter dendrites, or water in the long processes of fibrous astrocytes that accompany white matter axons (Sun & Jakobs, 2012). Although we believe water diffusion not to appear “stick‐like” in astrocytes due their fast aquaporin‐facilitated exchange (Badaut et al., 2011), we acknowledge that more work is needed in this arena.
6. CONCLUSIONS
This work investigated three challenges associated with estimating the neurite density with dMRI. Analysis of data from brain regions with low orientation coherence and white matter lesions suggested that neurite density estimation requires accounting for different diffusion and/or T2 properties between axons and dendrites, which is not feasible with conventional multi‐shell dMRI acquired with a single echo time. Obtaining parameters that index the neurite (or axonal) density may be possible, but confounding factors may prevent their use in particular outside healthy white matter. Finding a reliable neurite density index in gray matter or pathology likely requires finding correlations between diffusion and non‐diffusion properties as well as an improved understanding of diffusion in dendrites.
CONFLICT OF INTEREST
Markus Nilsson declares research support from Random Walk Imaging, and patent applications in Sweden (1250453‐6 and 1250452‐8), USA (61/642 594 and 61/642 589), and PCT (SE2013/050492 and SE2013/050493). Remaining authors declare no conflict of interest.
Supporting information
Appendix S1: Supporting information
ACKNOWLEDGMENTS
The authors acknowledge the Swedish Research Council (grant no. 2016‐03443), the Swedish Foundation for Strategic Research (grant no. AM13‐0090), Random Walk Imaging (grant no MN15), National Institutes of Health grants R01MH074794, P41EB015902, P41EB015898. The Linnaeus Environment Thinking in Time: Cognition, Communication and Learning, financed by the Swedish Research Council (349‐2007‐869). The authors thank Siemens Healthineers for providing access to the pulse sequence programming environment.
Lampinen B, Szczepankiewicz F, Novén M, et al. Searching for the neurite density with diffusion MRI: Challenges for biophysical modeling. Hum Brain Mapp. 2019;40:2529–2545. 10.1002/hbm.24542
Funding information Stiftelsen för Strategisk Forskning, Grant/Award Number: AM13‐0090; Vetenskapsrådet, Grant/Award Numbers: 2016‐03443, 349‐2007‐869; National Institutes of Health, Grant/Award Numbers: P41EB015898, P41EB015902, R01MH074794; Random Walk Imaging, Grant/Award Number: MN15
REFERENCES
- Alexander, D. C. , Dyrby, T. B. , Nilsson, M. , & Zhang, H. (2017). Imaging brain microstructure with diffusion MRI: Practicality and applications. NMR in Biomedicine. 10.1002/nbm.3841 [DOI] [PubMed] [Google Scholar]
- Assaf, Y. , & Basser, P. J. (2005). Composite hindered and restricted model of diffusion (CHARMED) MR imaging of the human brain. NeuroImage, 27(1), 48–58. [DOI] [PubMed] [Google Scholar]
- Badaut, J. , Ashwal, S. , Adami, A. , Tone, B. , Recker, R. , Spagnoli, D. , … Obenaus, A. (2011). Brain water mobility decreases after astrocytic aquaporin‐4 inhibition using RNA interference. Journal of Cerebral Blood Flow and Metabolism, 31(3), 819–831. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ballabh, P. , Braun, A. , & Nedergaard, M. J. N. o. d. (2004). The blood–brain barrier: An overview: Structure, regulation, and clinical implications, 16(1), 1–13. [DOI] [PubMed] [Google Scholar]
- Basser, P. J. , Mattiello, J. , & LeBihan, D. (1994). MR diffusion tensor spectroscopy and imaging. Biophysical Journal, 66(1), 259–267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beaulieu, C. , Fenrich, F. R. , & Allen, P. S. (1998). Multicomponent water proton transverse relaxation and T2‐discriminated water diffusion in myelinated and nonmyelinated nerve. Magnetic Resonance Imaging, 16(10), 1201–1210. [DOI] [PubMed] [Google Scholar]
- Behrens, T. E. , Woolrich, M. W. , Jenkinson, M. , Johansen‐Berg, H. , Nunes, R. G. , Clare, S. , … Smith, S. M. (2003). Characterization and propagation of uncertainty in diffusion‐weighted MR imaging. Magnetic Resonance in Medicine, 50(5), 1077–1088. [DOI] [PubMed] [Google Scholar]
- Benjamini, D. , Basser P. J. J. M. and Materials M. (2018). Towards clinically feasible relaxation‐diffusion correlation MRI using MADCO. Microporous and Mesoporous Materials, 269, 93–96. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bock, N. A. , Kocharyan, A. , Liu, J. V. , & Silva, A. C. (2009). Visualizing the entire cortical myelination pattern in marmosets with magnetic resonance imaging. Journal of Neuroscience Methods, 185(1), 15–22. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Braitenberg, V. , & Schüz, A. (1998). Cortex: Statistics and geometry of neuronal connectivity. Springer, Berlin. [Google Scholar]
- Callaghan, P. , Jolley, K. , & Lelievre, J. (1979). Diffusion of water in the endosperm tissue of wheat grains as studied by pulsed field gradient nuclear magnetic resonance. Biophysical Journal, 28(1), 133–141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chenevert, T. L. , Stegman, L. D. , Taylor, J. M. , Robertson, P. L. , Greenberg, H. S. , Rehemtulla, A. , & Ross, B. D. (2000). Diffusion magnetic resonance imaging: An early surrogate marker of therapeutic efficacy in brain tumors. Journal of the National Cancer Institute, 92(24), 2029–2036. [DOI] [PubMed] [Google Scholar]
- Chklovskii, D. B. , Schikorski, T. , & Stevens, C. F. (2002). Wiring optimization in cortical circuits. Neuron, 34(3), 341–347. [DOI] [PubMed] [Google Scholar]
- Clark, C. A. , Hedehus, M. , & Moseley, M. E. (2001). Diffusion time dependence of the apparent diffusion tensor in healthy human brain and white matter disease. Magnetic Resonance in Medicine, 45(6), 1126–1129. [DOI] [PubMed] [Google Scholar]
- Clark, C. A. , & Le Bihan, D. (2000). Water diffusion compartmentation and anisotropy at high b values in the human brain. Magnetic Resonance in Medicine, 44(6), 852–859. [DOI] [PubMed] [Google Scholar]
- Danos, P. , Baumann, B. , Krämer, A. , Bernstein, H.‐G. , Stauch, R. , Krell, D. , … Bogerts, B. (2003). Volumes of association thalamic nuclei in schizophrenia: A postmortem study. Schizophrenia Research, 60(2), 141–155. [DOI] [PubMed] [Google Scholar]
- de Almeida Martins, J. P. , & Topgaard, D. (2018). Multidimensional correlation of nuclear relaxation rates and diffusion tensors for model‐free investigations of heterogeneous anisotropic porous materials. Scientific Reports, 8(1), 2488. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Santis, S. , Assaf, Y. , Jones, D (2016). The influence of t2 relaxation in measuring the restricted volume fraction in diffusion MRI. In: Proceedings of the 24th Scientific Meeting, International Society for Magnetic Resonance in Medicine, Singapore, No. 1998.
- Dhital, B. , Kellner E., Reisert M. and Kiselev V. G. (2015). Isotropic diffusion weighting provides insight on diffusion compartments in human brain white matter in vivo. In: Proceedings of the 23rd Annual Meeting of ISMRM, Toronto, Canada, 2015. p. 2788.
- Dhital, B. , Reisert M., Kellner E. and Kiselev V. G. (2017). "Intra‐axonal Diffusivity in Brain White Matter." arXiv preprint arXiv:171204565. [DOI] [PubMed]
- Does, M. D. and Gore J. C. J. M. r. i. m. (2000). "Compartmental study of diffusion and relaxation measured in vivo in normal and ischemic rat brain and trigeminal nerve." 43(6): 837–844. [DOI] [PubMed] [Google Scholar]
- Douaud, G. , Jbabdi, S. , Behrens, T. E. , Menke, R. A. , Gass, A. , Monsch, A. U. , … Matthews, P. M. (2011). DTI measures in crossing‐fibre areas: Increased diffusion anisotropy reveals early white matter alteration in MCI and mild Alzheimer's disease. NeuroImage, 55(3), 880–890. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Englund, E. , & Brun, A. (1990). White matter changes in dementia of Alzheimer's type: The difference in vulnerability between cell compartments. Histopathology, 16(5), 433–439. [DOI] [PubMed] [Google Scholar]
- Englund, E. , Brun, A. , & Persson, B. (1987). Correlations between histopathologic white matter changes and proton MR relaxation times in dementia. Alzheimer Disease and Associated Disorders, 1(3), 156–170. [DOI] [PubMed] [Google Scholar]
- Eriksson, S. , Lasič, S. , Nilsson, M. , Westin, C.‐F. , & Topgaard, D. (2015). NMR diffusion‐encoding with axial symmetry and variable anisotropy: Distinguishing between prolate and oblate microscopic diffusion tensors with unknown orientation distribution. The Journal of Chemical Physics, 142(10), 104201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eriksson, S. , Lasic, S. , & Topgaard, D. (2013). Isotropic diffusion weighting in PGSE NMR by magic‐angle spinning of the q‐vector. Journal of Magnetic Resonance, 226, 13–18. [DOI] [PubMed] [Google Scholar]
- Fieremans, E. , Jensen, J. H. , & Helpern, J. A. (2011). White matter characterization with diffusional kurtosis imaging. NeuroImage, 58(1), 177–188. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goodfellow, I. , Bengio, Y. , & Courville, A. (2016). Deep learning. Cambridge, Boston: MIT Press; http://www.deeplearningbook.com [Google Scholar]
- Gouw, A. A. , Seewann, A. , Van Der Flier, W. M. , Barkhof, F. , Rozemuller, A. M. , Scheltens, P. , & Geurts, J. J. (2010). Heterogeneity of small vessel disease: A systematic review of MRI and histopathology correlations. Journal of Neurology, Neurosurgery & Psychiatry, 204685, 2009. [DOI] [PubMed] [Google Scholar]
- Hopf, A. (1955). Über die Verteilung myeloarchitektonischer Merkmale in der isokortikalen Schläfenlappenrinde beim Menschen. Journal für Hirnforschung, 2(1), 36–54. [Google Scholar]
- Hopf, A. (1956). Über die Verteilung myeloarchitektonischer Merkmale in der Stirnhirnrinde beim Menschen. Journal für Hirnforschung, 2(4), 311–333. [PubMed] [Google Scholar]
- Hopkins, A. , Yeung, H. , & Bratton, C. (1986). Multiple field strength in vivo T1 and T2 for cerebrospinal fluid protons. Magnetic Resonance in Medicine, 3(2), 303–311. [DOI] [PubMed] [Google Scholar]
- Horsfield, M. A. , & Jones, D. K. (2002). Applications of diffusion‐weighted and diffusion tensor MRI to white matter diseases–a review. NMR in Biomedicine, 15(7–8), 570–577. [DOI] [PubMed] [Google Scholar]
- Ikari, K. , & Hayashi, M. (1981). Aging in the Neuropil of cerebral cortex–a quantitative Ultrastructural study. Psychiatry and Clinical Neurosciences, 35(4), 477–486. [DOI] [PubMed] [Google Scholar]
- Jelescu, I. O. , Veraart, J. , Fieremans, E. , & Novikov, D. S. (2016). Degeneracy in model parameter estimation for multi‐compartmental diffusion in neuronal tissue. NMR in Biomedicine, 29(1), 33–47. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jelescu, I. O. , Zurek, M. , Winters, K. V. , Veraart, J. , Rajaratnam, A. , Kim, N. S. , … Kim, S. G. (2016). In vivo quantification of demyelination and recovery using compartment‐specific diffusion MRI metrics validated by electron microscopy. NeuroImage, 132, 104–114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jensen, J. H. , Helpern, J. A. , Ramani, A. , Lu, H. , & Kaczynski, K. (2005). Diffusional kurtosis imaging: The quantification of non‐gaussian water diffusion by means of magnetic resonance imaging. Magnetic Resonance in Medicine, 53(6), 1432–1440. [DOI] [PubMed] [Google Scholar]
- Jespersen, S. N. , Bjarkam, C. R. , Nyengaard, J. R. , Chakravarty, M. M. , Hansen, B. , Vosegaard, T. , … Vestergaard‐Poulsen, P. (2010). Neurite density from magnetic resonance diffusion measurements at ultrahigh field: Comparison with light microscopy and electron microscopy. NeuroImage, 49(1), 205–216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jespersen, S. N. , Kroenke, C. D. , Østergaard, L. , Ackerman, J. J. , & Yablonskiy, D. A. (2007). Modeling dendrite density from magnetic resonance diffusion measurements. NeuroImage, 34(4), 1473–1486. [DOI] [PubMed] [Google Scholar]
- Jespersen, S. N. , Lundell, H. , Sønderby, C. K. , & Dyrby, T. B. (2013). Orientationally invariant metrics of apparent compartment eccentricity from double pulsed field gradient diffusion experiments. NMR in Biomedicine, 26(12), 1647–1662. [DOI] [PubMed] [Google Scholar]
- Kaden, E. , Kelm, N. D. , Carson, R. P. , Does, M. D. , & Alexander, D. C. (2016). Multi‐compartment microscopic diffusion imaging. NeuroImage, 139, 346–359. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaden, E. , Knösche T. R. and Anwander A. J. N. (2007). "Parametric spherical deconvolution: inferring anatomical connectivity using diffusion MR imaging." 37(2): 474–488. [DOI] [PubMed] [Google Scholar]
- Kiselev, V. G. (2017). Fundamentals of diffusion MRI physics. NMR in Biomedicine, 30(3), e3602. [DOI] [PubMed] [Google Scholar]
- Kiselev, V. G. , & Il'yasov, K. A. (2007). Is the “biexponential diffusion” biexponential? Magnetic Resonance in Medicine, 57(3), 464–469. [DOI] [PubMed] [Google Scholar]
- Klein, S. , Staring M., Murphy K., Viergever M. and Pluim J. P. (2010). "Elastix: a toolbox for intensity‐based medical image registration." Medical Imaging, IEEE Transactions on 29(1): 196–205. [DOI] [PubMed] [Google Scholar]
- Kroenke, C. D. , Ackerman, J. J. , & Yablonskiy, D. A. (2004). On the nature of the NAA diffusion attenuated MR signal in the central nervous system. Magnetic Resonance in Medicine, 52(5), 1052–1059. [DOI] [PubMed] [Google Scholar]
- Lampinen, B. , Szczepankiewicz, F. , Mårtensson, J. , van Westen, D. , Sundgren, P. C. , & Nilsson, M. (2017). Neurite density imaging versus imaging of microscopic anisotropy in diffusion MRI: A model comparison using spherical tensor encoding. NeuroImage, 147, 517–531. [DOI] [PubMed] [Google Scholar]
- Lasič, S. , Szczepankiewicz, F. , Eriksson, S. , Nilsson, M. , & Topgaard, D. (2014). Microanisotropy imaging: Quantification of microscopic diffusion anisotropy and orientational order parameter by diffusion MRI with magic‐angle spinning of the q‐vector. Frontiers in Physics, 2, 11. [Google Scholar]
- Lätt, J. , Nilsson, M. , van Westen, D. , Wirestam, R. , Ståhlberg, F. , & Brockstedt, S. (2009). Diffusion‐weighted MRI measurements on stroke patients reveal water‐exchange mechanisms in sub‐acute ischaemic lesions. NMR in Biomedicine, 22(6), 619–628. [DOI] [PubMed] [Google Scholar]
- Lawrenz, M. , & Finsterbusch, J. (2013). Double‐wave‐vector diffusion‐weighted imaging reveals microscopic diffusion anisotropy in the living human brain. Magnetic Resonance in Medicine, 69(4), 1072–1082. [DOI] [PubMed] [Google Scholar]
- Lawrenz, M. and Finsterbusch J. (2018). Detection of microscopic diffusion anisotropy in human cortical gray matter in vivo with double diffusion encoding. [DOI] [PubMed]
- Le Bihan, D. , Breton, E. , Lallemand, D. , Grenier, P. , Cabanis, E. , & Laval‐Jeantet, M. (1986). MR imaging of intravoxel incoherent motions: Application to diffusion and perfusion in neurologic disorders. Radiology, 161(2), 401–407. [DOI] [PubMed] [Google Scholar]
- Lebel, C. , Walker, L. , Leemans, A. , Phillips, L. , & Beaulieu, C. (2008). Microstructural maturation of the human brain from childhood to adulthood. NeuroImage, 40(3), 1044–1055. [DOI] [PubMed] [Google Scholar]
- Löbel, U. , Sedlacik, J. , Güllmar, D. , Kaiser, W. A. , Reichenbach, J. R. , & Mentzel, H.‐J. (2009). Diffusion tensor imaging: The normal evolution of ADC, RA, FA, and eigenvalues studied in multiple anatomical regions of the brain. Neuroradiology, 51(4), 253–263. [DOI] [PubMed] [Google Scholar]
- Lundell, H. , Nilsson M., Dyrby T. B., Parker G. J., Cristinacce P. L. H., Zhou F., Topgaard D. and Lasic S. (2017). "Microscopic anisotropy with spectrally modulated q‐space trajectory encoding. In proceedings for the 25th Annual Meeting of ISMRM, Honolulu, Hawaii, USA, 2017. p. 1086.".
- Mackay, A. , Whittall, K. , Adler, J. , Li, D. , Paty, D. , & Graeb, D. (1994). In vivo visualization of myelin water in brain by magnetic resonance. Magnetic Resonance in Medicine, 31(6), 673–677. [DOI] [PubMed] [Google Scholar]
- McKinnon, E. T. , Jensen J. H., Glenn G. R. and Helpern J. A. J. M. r. i. (2017). "Dependence on b‐value of the direction‐averaged diffusion‐weighted imaging signal in brain." 36: 121–127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mitra, P. P. (1995). Multiple wave‐vector extensions of the NMR pulsed‐field‐gradient spin‐echo diffusion measurement. Physical Review B, 51(21), 15074–15078. [DOI] [PubMed] [Google Scholar]
- Mollink, J. , Kleinnijenhuis, M. , van Walsum, A.‐M. v. C. , Sotiropoulos, S. N. , Cottaar, M. , Mirfin, C. , … Ansorge, O. (2017). Evaluating fibre orientation dispersion in white matter: Comparison of diffusion MRI, histology and polarized light imaging. Neuroimage, 157, 561–574. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morris, R. , Paxinos, G. , & Petrides, M. (2000). Architectonic analysis of the human retrosplenial cortex. Journal of Comparative Neurology, 421(1), 14–28. [DOI] [PubMed] [Google Scholar]
- Moseley, M. , Cohen, Y. , Mintorovitch, J. , Chileuitt, L. , Shimizu, H. , Kucharczyk, J. , … Weinstein, P. (1990). Early detection of regional cerebral ischemia in cats: Comparison of diffusion‐and T2‐weighted MRI and spectroscopy. Magnetic Resonance in Medicine, 14(2), 330–346. [DOI] [PubMed] [Google Scholar]
- Niendorf, T. , Dijkhuizen, R. M. , Norris, D. G. , van Lookeren Campagne, M. , & Nicolay, K. (1996). Biexponential diffusion attenuation in various states of brain tissue: Implications for diffusion‐weighted imaging. Magnetic Resonance in Medicine, 36(6), 847–857. [DOI] [PubMed] [Google Scholar]
- Nilsson, M. , Lasič, S. , Drobnjak, I. , Topgaard, D. , & Westin, C. F. (2017). Resolution limit of cylinder diameter estimation by diffusion MRI: The impact of gradient waveform and orientation dispersion. NMR in Biomedicine, 30, e3711. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nilsson, M. , Lätt, J. , Nordh, E. , Wirestam, R. , Ståhlberg, F. , & Brockstedt, S. (2009). On the effects of a varied diffusion time in vivo: Is the diffusion in white matter restricted? Magnetic Resonance Imaging, 27(2), 176–187. [DOI] [PubMed] [Google Scholar]
- Nilsson, M. , Szczepankiewicz F., Ahlgren A., Martins J. D. A., Lasic S., Westin C.‐F. and Topgaard D. (2018). "An open‐source framework for analysis of multidimensional diffusion MRI data implemented in MATLAB. In Proceedings of the 26th Annual Meeting of ISMRM, Paris, France, 2018. p. 5355.".
- Nilsson, M. , Szczepankiewicz, F. , van Westen, D. , & Hansson, O. (2015). Extrapolation‐based references improve motion and Eddy‐current correction of high B‐value DWI data: Application in Parkinson's disease dementia. PLoS One, 10(11), e0141825. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nilsson, M. , van Westen, D. , Ståhlberg, F. , Sundgren, P. C. , & Lätt, J. (2013). The role of tissue microstructure and water exchange in biophysical modelling of diffusion in white matter. Magma, 26(4), 345–370. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Novikov, D. S. , Jensen, J. H. , Helpern, J. A. , & Fieremans, E. (2014). Revealing mesoscopic structural universality with diffusion. Proceedings of the National Academy of Sciences, 111(14), 5088–5093. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Novikov, D. S. , Jespersen S. N., Kiselev V. G. and Fieremans E. (2016). "Quantifying brain microstructure with diffusion MRI: Theory and parameter estimation." arXiv preprint arXiv:1612.02059. [DOI] [PMC free article] [PubMed]
- Novikov, D. S. , Kiselev, V. G. , & Jespersen, S. N. (2018). On modeling. Magnetic Resonance in Medicine, 79, 3172–3193. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Novikov, D. S. , Veraart J., Jelescu I. O. and Fieremans E. J. N. (2018). "Rotationally‐invariant mapping of scalar and orientational metrics of neuronal microstructure with diffusion MRI." 174: 518–538. [DOI] [PMC free article] [PubMed] [Google Scholar]
- O'Brien, J. S. , & Sampson, E. L. (1965). Lipid composition of the normal human brain: Gray matter, white matter, and myelin. Journal of Lipid Research, 6(4), 537–544. [PubMed] [Google Scholar]
- Öngür, D. , Ferry, A. T. , & Price, J. L. (2003). Architectonic subdivision of the human orbital and medial prefrontal cortex. Journal of Comparative Neurology, 460(3), 425–449. [DOI] [PubMed] [Google Scholar]
- Pantoni, L. and Garcia J. H. J. S. (1997). "Pathogenesis of leukoaraiosis: a review." 28(3): 652–659. [DOI] [PubMed] [Google Scholar]
- Peled, S. , Cory, D. G. , Raymond, S. A. , & Kirschner, D. A. (1999). Water diffusion, T2, and compartmentation in frog sciatic nerve, 42(5), 911–918. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pierpaoli, C. , Jezzard, P. , Basser, P. J. , Barnett, A. , & Di Chiro, G. (1996). Diffusion tensor MR imaging of the human brain. Radiology, 201(3), 637–648. [DOI] [PubMed] [Google Scholar]
- Qin, W. , Shui Yu, C. , Zhang, F. , Du, X. Y. , Jiang, H. , Xia Yan, Y. , & Cheng Li, K. (2009). Effects of echo time on diffusion quantification of brain white matter at 1.5 T and 3.0 T. Magnetic Resonance in Medicine, 61(4), 755–760. [DOI] [PubMed] [Google Scholar]
- Reisert, M. , Kellner E., Dhital B., Hennig J. and Kiselev V. G. J. N. (2017). "Disentangling micro from mesostructure by diffusion MRI: A Bayesian approach." 147: 964–975. [DOI] [PubMed] [Google Scholar]
- Ronen, I. , Moeller, S. , Ugurbil, K. , & Kim, D.‐S. (2006). Analysis of the distribution of diffusion coefficients in cat brain at 9.4 T using the inverse Laplace transformation. Magnetic Resonance Imaging, 24(1), 61–68. [DOI] [PubMed] [Google Scholar]
- Sagi, Y. , Tavor, I. , Hofstetter, S. , Tzur‐Moryosef, S. , Blumenfeld‐Katzir, T. , & Assaf, Y. (2012). Learning in the fast lane: New insights into neuroplasticity. Neuron, 73(6), 1195–1203. [DOI] [PubMed] [Google Scholar]
- Scholz, J. , Klein, M. C. , Behrens, T. E. , & Johansen‐Berg, H. (2009). Training induces changes in white‐matter architecture. Nature Neuroscience, 12(11), 1370–1371. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sjölund, J. , Szczepankiewicz, F. , Nilsson, M. , Topgaard, D. , Westin, C.‐F. , & Knutsson, H. (2015). Constrained optimization of gradient waveforms for generalized diffusion encoding. Journal of Magnetic Resonance, 261, 157–168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sotiropoulos, S. N. , Behrens, T. E. , & Jbabdi, S. (2012). Ball and rackets: Inferring fiber fanning from diffusion‐weighted MRI. NeuroImage, 60(2), 1412–1425. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stikov, N. , Campbell, J. S. , Stroh, T. , Lavelée, M. , Frey, S. , Novek, J. , … Dougherty, R. F. (2015). In vivo histology of the myelin g‐ratio with magnetic resonance imaging. NeuroImage, 118, 397–405. [DOI] [PubMed] [Google Scholar]
- Sun, D. and Jakobs T. C. J. T. N. (2012). "Structural remodeling of astrocytes in the injured CNS." 18(6): 567–588. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Surova, Y. , Lampinen B., Nilsson M., Lätt J., Hall S., Widner H., Van Westen D. and Hansson O. J. P. o. (2016). "Alterations of diffusion kurtosis and neurite density measures in deep grey matter and white matter in Parkinson's disease." 11(6): e0157755. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Surova, Y. , Szczepankiewicz, F. , Lätt, J. , Nilsson, M. , Eriksson, B. , Leemans, A. , … Nilsson, C. (2013). Assessment of global and regional diffusion changes along white matter tracts in parkinsonian disorders by MR tractography. PLoS One, 8(6), e66022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Swieten, J. v. , HOUT, J. V. D. , KETEL, B. V. , Hijdra, A. , Wokke, J. , & Gijn, J. v. (1991). Periventricular lesions in the white matter on magnetic resonance imaging in the elderly: A morphometric correlation with arteriolosclerosis and dilated perivascular spaces. Brain, 114(2), 761–774. [DOI] [PubMed] [Google Scholar]
- Szafer, A. , Zhong, J. , Anderson, A. W. , & Gore, J. C. (1995). Diffusion‐weighted imaging in tissues: Theoretical models. NMR in Biomedicine, 8(7), 289–296. [DOI] [PubMed] [Google Scholar]
- Szczepankiewicz, F. , Lasič, S. , van Westen, D. , Sundgren, P. C. , Englund, E. , Westin, C.‐F. , … Nilsson, M. (2015). Quantification of microscopic diffusion anisotropy disentangles effects of orientation dispersion from microstructure: Applications in healthy volunteers and in brain tumors. NeuroImage, 104, 241–252. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Szczepankiewicz, F. and Nilsson M. (2018). "Maxwell‐compensated waveform design for asymmetric diffusion encoding. Accepted for the 24th Annual Meeting of ISMRM, Paris, France, 2018.."
- Szczepankiewicz, F. , Sjölund J., Ståhlberg F., Lätt J. and Nilsson M. (2016). “Whole‐brain diffusional variance decomposition (DIVIDE): Demonstration of technical feasibility at clinical MRI systems.” arXiv preprint arXiv:1612.06741. [DOI] [PMC free article] [PubMed]
- Szczepankiewicz, F. , van Westen, D. , Englund, E. , Westin, C.‐F. , Ståhlberg, F. , Lätt, J. , … Nilsson, M. (2016). The link between diffusion MRI and tumor heterogeneity: Mapping cell eccentricity and density by diffusional variance decomposition (DIVIDE). NeuroImage, 142, 522–532. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Szczepankiewicz, F. , Westin C.‐F., Ståhlberg F., Lätt J. and Nilsson M. (2016). "Minimum Number of Diffusion Encoding Directions Required to Yield a Rotationally Invariant Powder Average Signal in Single and Double Diffusion Encoding. In Proceedings of the 24th Annual Meeting of ISMRM, Singapore, 2016. p. 2065.".
- Tariq, M. , Schneider, T. , Alexander, D. C. , Wheeler‐Kingshott, C. A. G. , & Zhang, H. (2016). Bingham–NODDI: Mapping anisotropic orientation dispersion of neurites using diffusion MRI. NeuroImage, 133, 207–223. [DOI] [PubMed] [Google Scholar]
- Tax, C. M. , Rudrapatna U. S., Witzel T. and Jones D. K. (2017). "Disentangling in two dimensions in the living human brain: Feasibility of relaxometry‐diffusometry using ultra‐strong gradients. In Proceedings of the 25th Annual Meeting of ISMRM, Honolulu, Hawaii, 2017. p. 838.".
- Topgaard, D. (2016). NMR methods for studying microscopic diffusion anisotropy In Diffusion NMR in confined systems: fluid transport in porous solids and heterogeneous materials. UK: Royal Society of Chemistry Cambridge. [Google Scholar]
- Topgaard, D. (2017). Multidimensional diffusion MRI. Journal of Magnetic Resonance, 275, 98–113. [DOI] [PubMed] [Google Scholar]
- Van Cauter, S. , Veraart, J. , Sijbers, J. , Peeters, R. R. , Himmelreich, U. , De Keyzer, F. , … Van Hecke, W. (2012). Gliomas: diffusion kurtosis MR imaging in grading. Radiology, 263(2), 492–501. [DOI] [PubMed] [Google Scholar]
- Veraart, J. , Fieremans E. and Novikov D. (2017). "Universal Power‐Law Scaling of Water Diffusion in Human Brain Defines What We See with Diffusion MRI. In Proceedings of the 25th Annual Meeting of ISMRM, Honolulu, HI, USA, 2017. p. 282.".
- Veraart, J. , Novikov, D. S. , & Fieremans, E. (2017). TE dependent diffusion imaging (TEdDI) distinguishes between compartmental T2 relaxation times. NeuroImage, 182, 360–369. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wansapura, J. P. , Holland, S. K. , Dunn, R. S. , & Ball, W. S., Jr. (1999). NMR relaxation times in the human brain at 3.0 tesla. Journal of Magnetic Resonance Imaging: An Official Journal of the International Society for Magnetic Resonance in Medicine, 9(4), 531–538. [DOI] [PubMed] [Google Scholar]
- Weigel, M. , & Hennig, J. (2006). Contrast behavior and relaxation effects of conventional and hyperecho‐turbo spin echo sequences at 1.5 and 3 T. Magnetic Resonance in Medicine, 55(4), 826–835. [DOI] [PubMed] [Google Scholar]
- Wen, Q. , Kelley, D. A. , Banerjee, S. , Lupo, J. M. , Chang, S. M. , Xu, D. , … Nelson, S. J. (2015). Clinically feasible NODDI characterization of glioma using multiband EPI at 7 T. NeuroImage: Clinical, 9, 291–299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Werring, D. , Brassat, D. , Droogan, A. , Clark, C. , Symms, M. , Barker, G. , … Miller, D. (2000). The pathogenesis of lesions and normal‐appearing white matter changes in multiple sclerosis: A serial diffusion MRI study. Brain, 123(8), 1667–1676. [DOI] [PubMed] [Google Scholar]
- Westin, C.‐F. , Knutsson, H. , Pasternak, O. , Szczepankiewicz, F. , Özarslan, E. , van Westen, D. , … Kubicki, M. (2016). Q‐space trajectory imaging for multidimensional diffusion MRI of the human brain. NeuroImage, 135, 345–362. [DOI] [PMC free article] [PubMed] [Google Scholar]
- White, N. S. , Leergaard, T. B. , D'Arceuil, H. , Bjaalie, J. G. , & Dale, A. M. (2013). Probing tissue microstructure with restriction spectrum imaging: Histological and theoretical validation. Human Brain Mapping, 34(2), 327–346. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Whittall, K. P. , Mackay, A. L. , Graeb, D. A. , Nugent, R. A. , Li, D. K. , & Paty, D. W. (1997). In vivo measurement of T2 distributions and water contents in normal human brain. Magnetic Resonance in Medicine, 37(1), 34–43. [DOI] [PubMed] [Google Scholar]
- Xu, J. , Li, H. , Harkins, K. D. , Jiang, X. , Xie, J. , Kang, H. , … Gore, J. C. (2014). Mapping mean axon diameter and axonal volume fraction by MRI using temporal diffusion spectroscopy. NeuroImage, 103, 10–19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yablonskiy, D. A. , Bretthorst, G. L. , & Ackerman, J. J. (2003). Statistical model for diffusion attenuated MR signal. Magnetic Resonance in Medicine, 50(4), 664–669. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang, H. , Hubbard P. L., Parker G. J. and Alexander D. C. J. N. (2011). "Axon diameter mapping in the presence of orientation dispersion with diffusion MRI." 56(3): 1301–1315. [DOI] [PubMed] [Google Scholar]
- Zhang, H. , Schneider, T. , Wheeler‐Kingshott, C. A. , & Alexander, D. C. (2012). NODDI: Practical in vivo neurite orientation dispersion and density imaging of the human brain. NeuroImage, 61(4), 1000–1016. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Appendix S1: Supporting information


