Automated dynamic motion correction using normalized gradient fields for ⁸²rubidium PET myocardial blood flow quantification

Abstract

Background.

Patient motion can lead to misalignment of left ventricular (LV) volumes-of-interest (VOIs) and subsequently inaccurate quantification of myocardial blood flow (MBF) and flow reserve (MFR) from dynamic PET myocardial perfusion images. We aimed to develop an image-based 3D-automated motion-correction algorithm that corrects the full dynamic sequence for translational motion, especially in the early blood phase frames (~ first minute) where the injected tracer activity is transitioning from the blood pool to the myocardium and where conventional image registration algorithms have had limited success.

Methods.

We studied 225 consecutive patients who underwent dynamic rest/stress rubidium-82 chloride (⁸²Rb) PET imaging. Dynamic image series consisting of 30 frames were reconstructed with frame durations ranging from 5 to 80 seconds. An automated algorithm localized the RV and LV blood pools in space and time and then registered each frame to a tissue reference image volume using normalized gradient fields with a modification of a signed distance function. The computed shifts and their global and regional flow estimates were compared to those of reference shifts that were assessed by three physician readers.

Results.

The automated motion-correction shifts were within 5 mm of the manual motion-correction shifts across the entire sequence. The automated and manual motion-correction global MBF values had excellent linear agreement (R = 0.99, y = 0.97x + 0.06). Uncorrected flows outside of the limits of agreement with the manual motion-corrected flows were brought into agreement in 90% of the cases for global MBF and in 87% of the cases for global MFR. The limits of agreement for stress MBF were also reduced twofold globally and by fourfold in the RCA territory.

Conclusions.

An image-based, automated motion-correction algorithm for dynamic PET across the entire dynamic sequence using normalized gradient fields matched the results of manual motion correction in reducing bias and variance in MBF and MFR, particularly in the RCA territory. (J Nucl Cardiol 2018)

INTRODUCTION

PET myocardial perfusion imaging has demonstrated increased accuracy for the detection of coronary artery disease (CAD) compared to other noninvasive imaging modalities.¹ Recent data have also shown that quantification of perfusion as myocardial blood flow (MBF) and myocardial flow reserve (MFR) improves detection of CAD^2,3 and risk stratification for adverse cardiac outcomes.^4,5

Misalignment between dynamic images due to respiratory and patient motions can induce errors in estimated MBF and MFR. Uncorrected motion in the left ventricle (LV) blood pool images can lead to artifactually increased blood-to-tissue spillover and overestimated MBF estimates, particularly in the inferior wall.⁶ Because blood pool motion is on average greater during stress than at rest, the MFR values can also be significantly overestimated.⁶ Currently available clinical software with automated motion-correction capabilities only correct the later uptake frames.⁷ Other systems with manual motion-correction options require labor-intensive correction of 28 or more frames per rubidium-82 chloride (⁸²Rb) PET rest/stress study.⁸

Prior studies have corrected cardiac and respiratory motion in gated images.⁹ Other studies have corrected dynamic images from measured respiratory motion using tracking markers or sensors,^10-12 from higher spatial and temporal resolution MR or CT images from hybrid PET/MR and PET/CT systems,^11,13,14 or during reconstruction requiring access to list-mode data.^10-13,15 Data-driven approaches which only utilize single-modality reconstructed images have the advantages of being fast, inexpensive, and robust.¹⁶ However, these motion-correction studies have largely focused on the later tissue-phase frames where periodic respiratory motion is averaged out in longer duration frames,¹⁷ or they did not establish a baseline standard for comparison.¹⁸

We previously demonstrated that motion in the blood pool images was highly prevalent and associated with clinically meaningful overestimates of MBF.⁶ In this study, we sought to develop an image-based, automated motion-correction algorithm for dynamic ⁸²Rb PET myocardial perfusion images across the entire dynamic sequence including the blood pool phase. Our method incorporates image gradients in the form of normalized gradient fields¹⁹ instead of image intensities, combined with dynamic spatiotemporal phase information to account for rapid tracer kinetics during the blood pool phase. The objectives of this study were to compare our automated motion-correction algorithm with manual motion correction by expert physician readers, and to investigate the effects of this motion correction on MBF and MFR estimates.

MATERIALS AND METHODS

PET Imaging

All subjects were instructed to avoid caffeine and methylxanthine intake for 24 hours and to fast overnight prior to PET imaging. ⁸²Rb was administered using a weight-adjusted protocol of 12 MBq/kg (0.32 mCi/kg) using the same activity (481–1665 MBq [13–45 mCi]) for both rest and stress. ⁸²Rb was directly eluted from a generator and infused into a brachial vein at 50 mL/ minute over 5–25 seconds using the Cardiogen-82 infusion system (Bracco Diagnostics, Monroe Township, NJ). Dynamic PET scans were acquired in 3D list mode over 7 minutes from the point of radiotracer injection on a Biograph mCT whole-body PET/CT scanner (Siemens Healthcare USA, Malvern, PA). Pharmacological stress was performed using a bolus injection of 0.4 mg of intravenous regadenoson over 10 seconds followed by a 10-mL flush over 5–10 seconds. Then 30 seconds after the start of the regadenoson injection, the stress ⁸²Rb infusion was administered and the second dynamic PET scan was acquired with the same scan length.

Image Processing

Dynamic ⁸²Rb emission images were reconstructed using iterative 3D ordered-subset expectation-maximization iterative reconstruction or 3D-OSEM with 21 subsets and 3 iterations with point-spread-function (PSF) and time-of-flight (TOF) modeling, standard corrections (randoms, attenuation, scatter, prompt gamma, deadtime, decay), and without post-filtering.²⁰ Images were reconstructed to a matrix size of 128 × 128 and pixel size of 3.18 × 3.18 mm, with a slice thickness of 3 mm. A 30-frame dynamic reconstruction was performed over 6 min and 40 s²¹ after an initial 20-second delay with the following time sampling: 16 × 5, 6 × 10, 3 × 20, 4 × 30, and 1 × 80 seconds, respectively.

Minimal 3D spatial smoothing was applied to the image volume using a “1–12-1” kernel in each of the 3-coordinate axes. Transverse images were resampled into short-axis (SA) images with 3.18 mm isotropic voxels. LV myocardial surfaces were automatically determined using the Corridor4DM software (INVIA, Ann Arbor, MI) that utilized a myocardial image volume summed from the data acquired from 2 to 6 minutes and 40 seconds.²² The LV myocardial tissue activity were estimated midwall, midway between the endocardial and epicardial surfaces.

Blood Pool and Tissue Isolation

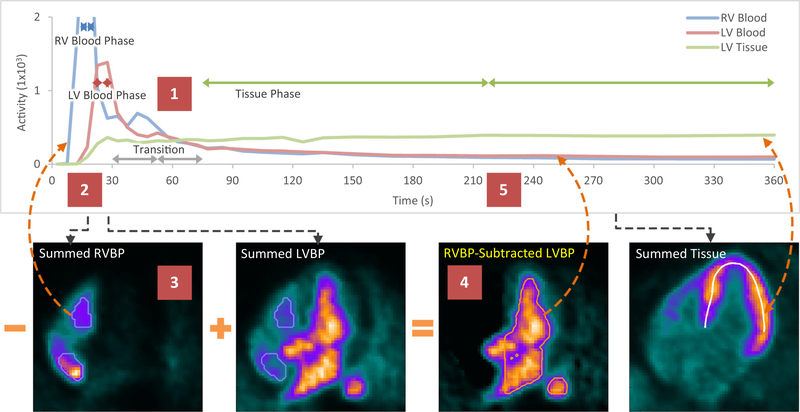
The general strategy of dynamic motion correction is to compare each dynamic frame, also known as a moving frame, to the myocardial image volume, which is referred to as the fixed or reference image volume. The myocardial image volume is summed from the dynamic frames between the estimated tissue-phase start time and the end of acquisition time. While the later tissue-phase moving frames have similar tracer distribution as the reference image volume, the early blood-phase moving frames do not, as the tracer is in the RV and LV cavities and has not yet reached the myocardium. Therefore, the activity in the right ventricular blood pool (RVBP), the left ventricular blood pool (LVBP) and the myocardial tissue were iteratively isolated in both time and space to apply tailored matching criteria for each moving frame in the later motion estimation step. Figure 1 illustrates this first step on an example stress dataset.

Figure 1.

Blood pool and tissue isolation example illustrating (Step 1) temporal phase identification of the time–activity curves (TAC), (Steps 2–4) spatial volumes-of-interest (VOIs) of the blood pools shown in horizontal long-axis (HLA) views for the RVBP (blue outline) and the RVBP-subtracted LVBP (orange outline), and (Step 5) the updating of the TACs for the next iteration. LV tissue midsurface (white contour) and TAC remain unchanged. LV, left ventricle; RV, right ventricle; LVBP, left ventricular blood pool; RVBP, right ventricular blood pool.

Temporal phase identification.

The RVBP-phase, LVBP-phase and tissue-phase start and stop times were updated over four iterations as their respective VOIs were alternatively updated (described below) to allow convergence of the phase times. The RVBP-phase, LVBP-phase and tissue-phase start and stop times were initialized to the start of acquisition to the total count peak time, the total count peak time to 2 minutes, and 2 minutes to the end of the acquisition, respectively. The 2 minute time point was the empirical transition from blood phase to tissue phase.²³ In the subsequent iterations, the RVBP, LVBP, and tissue TACs were sampled from their respective RVBP VOI, LVBP VOI, and midwall myocardium.

RVBP-phase identification.

The RVBP-phase start and stop times were determined where the RVBP TAC was greater than 80% of its maximum and where the RVBP TAC was greater than 25% of the sum of the RVBP TAC and LVBP TAC values, limited to at most 2 frames. The RVBP phase limit of 2 frames were defined due to an observed narrower RVBP TAC peak than the LVBP TAC peak.

LVBP-phase identification.

The LVBP-phase start and stop times were determined where the LVBP TAC was greater than 80% of its maximum, after the RVBP-phase stop frame index, and limited to at most 3 frames. The LVBP-phase was limited to 3 frames since the majority of the full-widths at half-maximum of the LVBP TAC peaks were less than 15 seconds or 3 frames.²³

Tissue-phase identification.

Lastly the tissue-phase start and stop times were determined where the LVBP TAC was less than 67% of the tissue TAC after the LVBP-phase stop time, to the end of acquisition.

Spatial volume-of-interest identification.

The summed RVBP, LVBP and tissue image volumes were averaged from frames between their respective phase start and stop times with relative weights determined by frame activity and frame duration. All summed image volumes were smoothed using a 3D plus-sign-shaped 3 × 3 × 3 kernel. After four iterations of alternating temporal phase and spatial VOI identifications, the final weighted-average RVBP, LVBP, and tissue image volumes were passed onto the motion-correction step.

RVBP VOI identification.

The RVBP VOI was created by thresholding the RVBP image volume to 50% of its maximum count and limited to the RV side of the septal wall, as determined by the LV myocardial surfaces.

LVBP VOI identification.

The isolated LVBP image volume was created by subtracting the RVBP image volume scaled by the average RVBP VOI in the LVBP image volume divided by the average RVBP VOI in the RVBP image volume. Next the LVBP VOI was created by thresholding the isolated LVBP image volume to 50% of its maximum count and limited to LV side of the septal wall.

Tissue VOI identification.

While the summed tissue image volume was iteratively updated, the tissue TAC was not since the tissue midsurface used for sampling the tissue TAC remained fixed.

Automated Motion Correction

Normalized gradient fields.

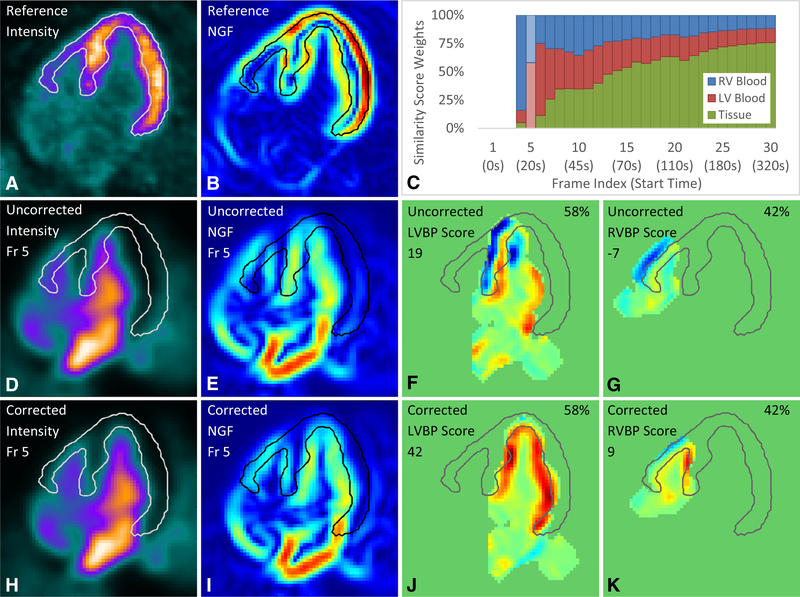
Normalized gradient fields (NGF) generate a simple, intensity-independent distance or similarity measure between two image volumes to be registered.¹⁹ Generally, two image volumes were considered similar if the normalized gradient directions were aligned at a given position. Three-dimensional gradients in the image volume were approximated using a 1D kernel in each of the 3-coordinate axes. Then the gradient in each direction was divided by the magnitude at each voxel to generate the normalized gradient field. Regularization was applied in the normalization step for robustness and noise suppression. Each voxel location of a NGF has three values which form a unit vector in the direction of the gradient. The reference NGF and each moving NGF are displayed with the magnitude of the normalized gradient components in the direction of the HLA plane (Figure 2B, E, I).

Figure 2.

Automated motion correction example in the (D-K) blood phase with (A-B) reference image volume and (C) similarity score weights. Similarity scores vary from high (red) to low (blue). The frame selected is highlighted (lighter shade) in the similarity score weights plot (C). NGF indicates normalized gradient field; Fr, frame; LV, left ventricle; RV, right ventricle; LVBP, left ventricular blood pool; RVBP, right ventricular blood pool.

Second-order gradient edge surfaces.

Robust endocardial and epicardial surfaces of both the LV tissue and the weaker signal RV tissue were estimated using 2nd-order gradients or the curvature information in the image volume. The image volume was first smoothed with a 3D cube-shaped kernel of size 5 × 5 × 5 before its 2nd-order NGFs were computed. The 2nd-order NGFs were computed similarly to the regular 1st-order or regular NGF but using a 1D kernel in each of the 3-coordinate axes. Then each of the 3-axis components of the 2nd-order NGF were summed and thresholded for only negative values which leaves a 3D mask with concave intensity values. To suppress noisy gradients, the voxels of the concave 3D mask with intensity values greater than 25% of the maximum intensity value are kept. Lastly to fill in holes left by convex regions of the 3D mask that typically reside in the relatively flat regions of the image volume, voxels with intensities above a higher threshold of 50% of the maximum intensity are added back in. The final 3D mask has edges that closely correspond with the greatest changes in activity in the myocardium as shown as myocardial contours in Figure 2.

Tissue similarity score.

The tissue similarity map at each shift search location was computed as the dot product of the reference NGF and the moving NGF within a masked region. Masking was applied to reduce the influence of extra-cardiac activity. The tissue mask was generated from a bullet-shaped region loosely bounding the myocardium surfaces (light green region shown in Supplemental Figure 1O). A positive dot product signified agreement between gradients in the same direction. The tissue similarity score was defined to be a summation of all values in the masked tissue similarity map, which is a departure from the conventional sum of squared dot products used in previously described normalized gradient field image registration.^19,24

Blood pool similarity scores.

Two blood pool similarity maps were created. The blood pool similarity maps at each shift search location computed the negative dot product of the reference NGF and the moving NGF within masked regions, to reduce the influence of extra-ventricular activity. The RVBP mask was generated by finding the peak smoothed gradient boundaries, then dilating the binary mask, and limiting to the RV side of the septal wall and above the basal valve plane (example shown in Figure 2K). The LVBP mask was generated in the same manner but limiting to the LV side of the septal wall (example shown in Figure 2J). A negative dot product signified agreement between gradients in opposite directions. The RVBP and LVBP similarity scores are summations of all values in their respective masked similarity maps.

Weighted similarity score.

For each moving frame a weighted-average approach was used in combining the RVBP, LVBP and tissue similarity scores. The time-dependent weights were based on the RVBP, LVBP, and tissue TACs sampled using their respective RVBP, LVBP, and tissue edge surface VOIs where the sum at each dynamic frame was normalized to one (Figure 2C).

Automated motion-correction process.

Automated translational motion estimation and correction was performed across the entire dynamic sequence, except for any initial frames with mean counts in a RVBP and LVBP merged VOI, below 20% of its maximum. The weighted-average tissue image volume from the prior step was set as the reference image volume and was smoothed with a 3D cube-shaped kernel of size 3 × 3 × 3. Each dynamic frame or moving frame was first smoothed with a 3D cube-shaped kernel of size 5 × 5 × 5 because it was noisier than the reference image volume. Bounding masks derived from the weighted-average RVBP, LVBP and tissue image volumes were applied to the moving frame to compute similarity scores to all three regions (RVBP, LVBP, and tissue). Tighter edge surface VOIs using 2nd-order gradient edge surfaces were generated from the peak gradient boundaries of each weighted-average RVBP, LVBP, and tissue normalized gradient fields. The three similarity scores were combined depending on the relative activity in the RVBP, LVBP, and tissue edge surface VOIs at the time of the moving frame. Then each moving frame was shifted in voxel increments (3.2 mm) in each of the 3-coordinates axes in short-axis coordinates (basal-apical, septal-lateral, and inferior-anterior) using an iterative local grid search algorithm to maximize the combined similarity score with respect to the fixed reference image volume. The motion shift with the maximum combined similarity score was further refined to one-tenth of a voxel (0.32 mm) using separable triquadratic interpolation on a 3 × 3 × 3 neighborhood of the combined similarity scores. The interpolated motion estimate was then used to motion correct each eligible frame. Motion estimates for the early ineligible low-count frames were recorded as zero shifts. All motion estimates were recorded as three-dimensional translational motion vectors for each frame.

Manual Motion-Correction Comparison

Manual motion correction was performed on each set of dynamic frames by one of three physician readers as described in a prior study utilizing the same datasets.⁶ These manual motion estimates were recorded as three-dimensional translational motion vectors for each frame and served as the reference for estimating the bias and variance of no motion correction and the automated motion correction.

VOI Definition and TAC Generation

For blood flow estimation, the VOI sampling methodology used a 3D rectangular VOI that was centered at the mitral valve plane in parallel to the long-axis of the LV to automatically extract a unique LV blood pool time-activity curve. The size of the VOI was 2 × 2 pixels wide (6.4 mm) to minimize spillover from the myocardium and spanned in the direction of the long-axis to include activity in both the LV and left atrium (6.4 × 6.4 × 28.6 mm). The myocardial tissue time-activity curves were estimated from the midwall tracer activity for each of the three vascular territories of the left anterior descending (LAD), left circumflex (LCX), and right coronary artery (RCA), and the whole left ventricle (global). Blood pool and tissue activities were sampled both with no motion correction, manual motion correction, and automated motion correction for comparison of blood flow estimation.

Blood Flow Estimation

Both the LV blood pool input function and LV tissue TACs were fit to a 1-tissue compartment model to obtain estimates for uptake rate K₁, washout rate k₂, and LV blood pool to myocardium spillover f_V. Myocardial blood flow was computed from the estimated K₁ using a previously validated K₁-MBF relationship for ⁸²Rb.²⁵ All temporal frames were duration weighted in the kinetic fitting. Global and vascular territory MBF and MFR values were computed with no motion correction, manual motion correction, and automated motion correction. The MBF and MFR values from the manually corrected dynamic sequences were the reference values for computing relative flow differences. The differences were computed for uncorrected and automatically corrected dynamic sequences. Vascular flow differences were computed to observe the regional impact of motion compared to the effect on the global flow.

Statistical Analysis

Statistical significance was assessed with the Wilcoxon signed rank test for paired differences and with the Wilcox-Morgan-Pitman test for comparing variances of two dependent variables with Holm adjustment for multiple comparisons.²⁶ Two-sided values of P < 05 were considered significant. Substantive significance was assessed with effect size using difference of means and Cohen’s d, where d > 0.8 were considered large. All statistical analyses were performed with R 3.3.1 (The R Foundation for Statistical Computing) and Python 2.7.5 (Python Software Foundation).

RESULTS

Study Population

Characteristics of patients evaluated are given in Table 1. The cohort consisted of 130 men and 95 women, age 64 ± 12 years with a high prevalence of coronary risk factors.

Table 1.

Subject characteristics

Characteristic	Patients (n = 225)
Age (year)	65 [57–73]
Weight (kg)	95 [74–116]
Height (m)	1.7 [1.6–1.8]
BMI (kg.m−2)	32 [27–40]
BMI ≥ 30 kg.m−2	138 (61)
Male	130 (58)
Hypertension	183 (81)
Dyslipidemia	159 (71)
Diabetes	103 (46)
Any prior CAD	71 (32)
Stress LVEF (%)	65 [55–72]
Rest LVEF (%)	62 [53–68]
Summed stress score	0.0 [0.0–8.0]
Summed rest score	0.0 [0.0–3.0]
Summed difference score	0.0 [0.0–3.0]
Global MFR	2.0 [1.5–2.4]
Stress global MBF (mL.min−1.g−1)	2.1 [1.6–2.7]
Rest global MBF (mL.min−1.g−1)	1.0 [0.8–1.3]

MFR and MBF values are motion corrected. Continuous variables are presented as median [interquartile range]. Dichotomous variables are presented as number (%). BMI indicates body mass index; CAD, coronary artery disease; LVEF, left ventricular ejection fraction; MFR, myocardial flow reserve; and MBF, myocardial blood flow

Automated Motion-Correction Case Study

Figure 1 illustrates the blood pool and tissue isolation in time and space. In Step 1, the RVBP phase, LVBP phase, and tissue-phase frames are identified at times where their TAC amplitudes are significantly greater than the other two. For example, at 30 seconds the LVBP activity is greater than both the RVBP and tissue activities. In Step 2, the “Summed” image volumes are weighted averages of their most significant frames. In Step 3, the RVBP image volume is then thresholded to create the RVBP VOI. The RVBP image volume is subtracted from the LVBP image volume by a scaled amount determined by a ratio of the RVBP VOI means in the LVBP image volume to the RVBP image volume. In Step 4, the resulting RVBP-subtracted LVBP image volume is thresholded to create the LVBP VOI. In Step 5, the RVBP VOI and LVBP VOI sample the entire dynamic sequence to generate updated TACs. This process is iterated to converge to the final weighted-average RVBP, LVBP, and tissue image volumes.

Figure 2 illustrates the automated motion-correction process for a representative blood-phase dynamic frame (frame 5) using the same example stress dataset, where each row is grouped by the same frame index. The left most two columns show the HLA slice of the intensity image volumes and their respective normalized gradient fields and the right most two columns show two of the three similarity maps per frame. The reference image volume is shown in Figure 2A with an overlaid tissue edge surface (white, black or gray outline), again generated from the peak gradient boundaries from the reference normalized gradient field (Figure 2B). The tissue edge surface is also used for visual comparison of the alignment of the peak gradients between the reference image volume and the moving frames (Figure 2D, H). The similarity maps (Figure 2F-G, J-K) show two edges matched in red, no edge matched in light green, and two edges incorrectly matched and subsequently penalized in blue. Out-of-bounds regions are shown in darker green. The weighted similarity scores are scaled by 1 × 10³ (left) and the time-dependent similarity score weights (Figure 2C) are shown as percentages (upper right corner of Figure 2F-G, J-K).

In further detail, the uncorrected frame 5 which starts at 20 seconds had a moderate motion of 14 mm in the septal direction (Figure 2D) shown with its respective shifted normalized gradient field (Figure 2E). The uncorrected frame had a weighted similarity score of 8: 42% of RVBP score of −7 (Figure 2F), 58% of the LVBP score of 19 (Figure 2G), and 0% of the tissue score of −3 (not shown). The corrected frame and its NGF (Figure 2H, I) that best aligned with the reference and its NGF (Figure 2A, B) had a higher weighted similarity score of 28: 42% of RVBP score of 9 (Figure 2K), 58% of the LVBP score of 42 (Figure 2J), and 0% of the tissue score of −49 (not shown). The lower scores in the uncorrected similarity maps are reflected by the blue penalty regions whereas the higher scores in the corrected similarity maps are reflected by the larger red matching regions with minimal blue penalty regions.

Supplemental Figure 1 illustrates the automated motion-correction process for two other representative dynamic frames with one in the transition phase and another in the tissue phase (frames 8 and 26) using the same example stress dataset. The Supplemental Results explains the motion correction algorithm for additional representative frames in more detail. Supplemental Figure 2 illustrates the spatiotemporal localization and correction of the blood pool isolation and automated motion-correction algorithms across the entire dynamic sequence using the same example stress dataset.

Automated Motion-Correction Shift Bias and Variance

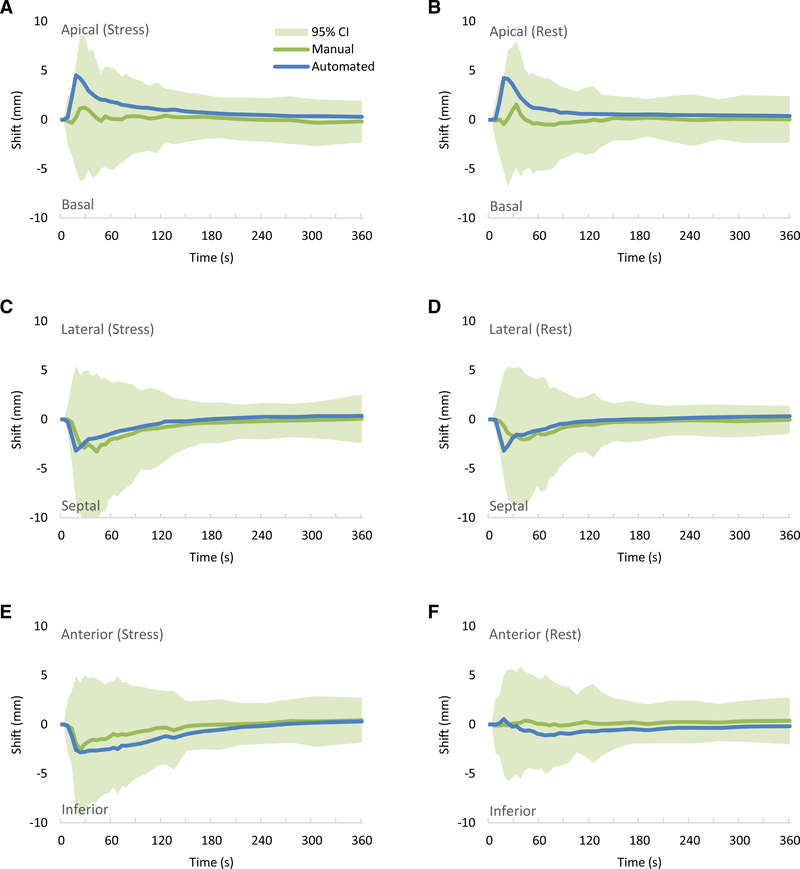
Figure 3 shows the comparison of the automated and the manual motion shift estimates per frame for rest and stress by direction of motion. The mean shift estimates for both automated and manual correction were all in the same directions in the first 2 minutes and within ±2.0 mm beyond 2 minutes. The mean automated motion shifts were all within the limits of agreement (95% confidence interval) of the manual motion shifts. Early mean differences of up to 5.0 mm (less than two voxel lengths) were mostly in the RV blood pool frames as the mean time of peak RVBP activity was 18 seconds and the mean time of the peak LVBP activity was 28 seconds. Table 2 summarizes the automated motion shifts compared to the expert manual motion shifts for each direction, series, and frame or phase.

Figure 3.

Estimated mean patient motion shifts per time across stress datasets in the (A) basal-apical, (C) septal-lateral and (E) inferior-anterior directions, and across rest datasets in the (B) basal-apical, (D) septal-lateral and (F) inferior-anterior directions. Line indicates mean and shaded region (only shown for the manual motion-correction shifts) indicates values within the 95% confidence intervals. Green line indicates manual motion-correction shifts and blue line indicates automated motion-correction shifts.

Table 2.

Motion shifts

			Shift mean (mm)
Phase	Direction	Series	Manual correction	Automated correction	Difference	RMSD (mm)
Blood	Apical	Stress	0.3 [−4.7, 5.3]	2.0 [−2.5, 6.5]	1.7 [−4.0, 7.4]	3.4
		Rest	−0.1 [−4.9, 4.8]	1.6 [−2.9, 6.0]	1.6 [−4.1, 7.4]	3.4
	Septal	Stress	1.7 [−4.4, 7.8]	1.4 [−3.3, 6.1]	−0.3 [−5.2, 4.6]	2.5
		Rest	1.1 [−4.2, 6.5]	1.1 [−3.4, 5.7]	0.0 [−4.6, 4.6]	2.3
	Inferior	Stress	1.1 [−4.4, 6.7]	2.1 [−3.0, 7.1]	0.9 [−3.2, 5.0]	2.3
		Rest	−0.1 [−4.5, 4.4]	0.5 [−3.7, 4.8]	0.6 [−3.4, 4.6]	2.1
Tissue	Apical	Stress	0.1 [−2.3, 2.5]	0.6 [−0.7, 2.0]	0.5 [−1.9, 2.9]	1.3
		Rest	0.1 [−2.4, 2.5]	0.5 [−0.5, 1.5]	0.4 [−2.1, 3.0]	1.4
	Septal	Stress	0.3 [−2.0, 2.7]	−0.1 [−1.4, 1.2]	−0.4 [−2.5, 1.7]	1.1
		Rest	0.2 [−1.8, 2.2]	−0.1 [−1.3, 1.1]	−0.3 [−2.3, 1.6]	1.0
	Inferior	Stress	0.0 [−2.8, 2.8]	0.5 [−1.9, 2,8]	0.5 [−2.1, 3.0]	1.4
		Rest	−0.2 [−2.7, 2.4]	0.4 [−1.4, 2.3]	0.6 [−1.7, 3.0]	1.4

Motion shifts in mean [95% confidence interval]. Difference is Automated-Manual. RMSD is the root mean squared difference. Blood-phase motion is averaged across frames ≤ 2 minutes. Tissue-phase motion is averaged across frames > 2 minutes

Automated Motion-Correction Effects on MBF, MFR, and Spillover

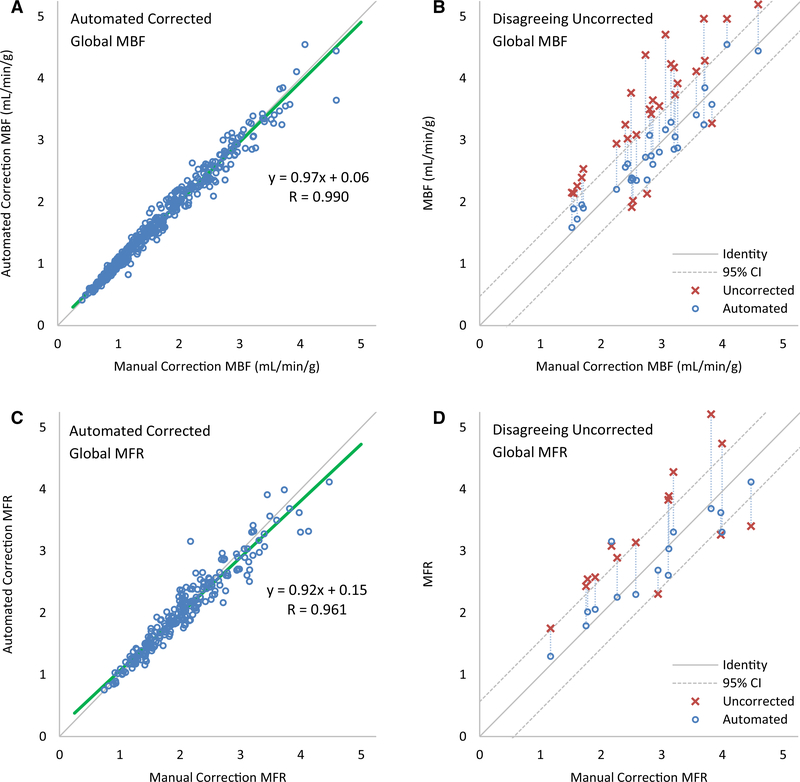
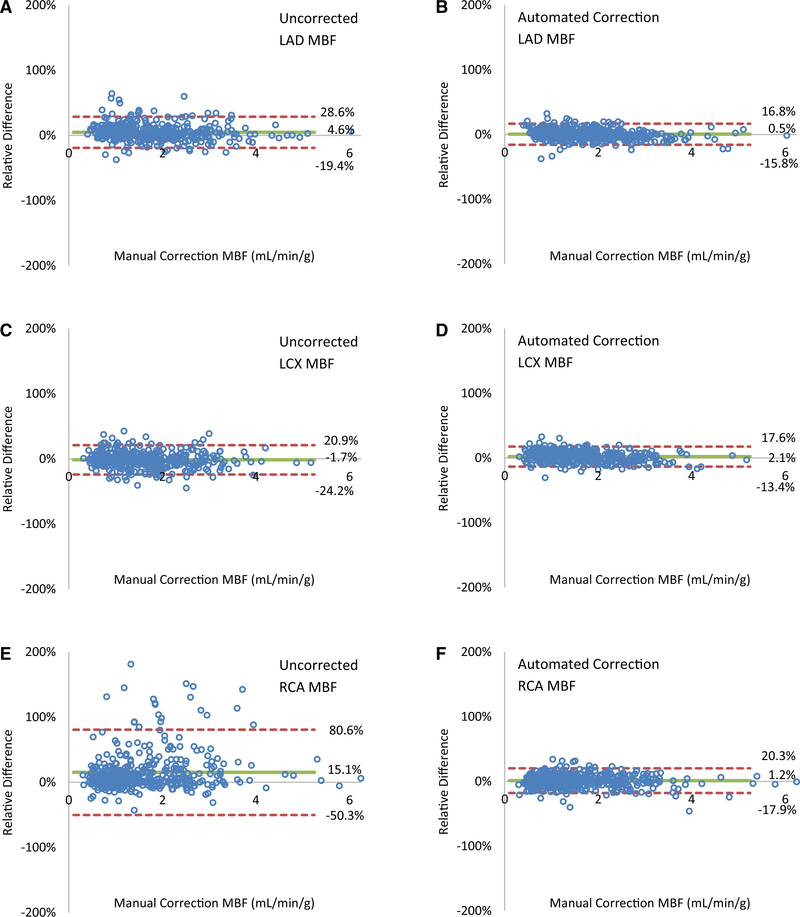
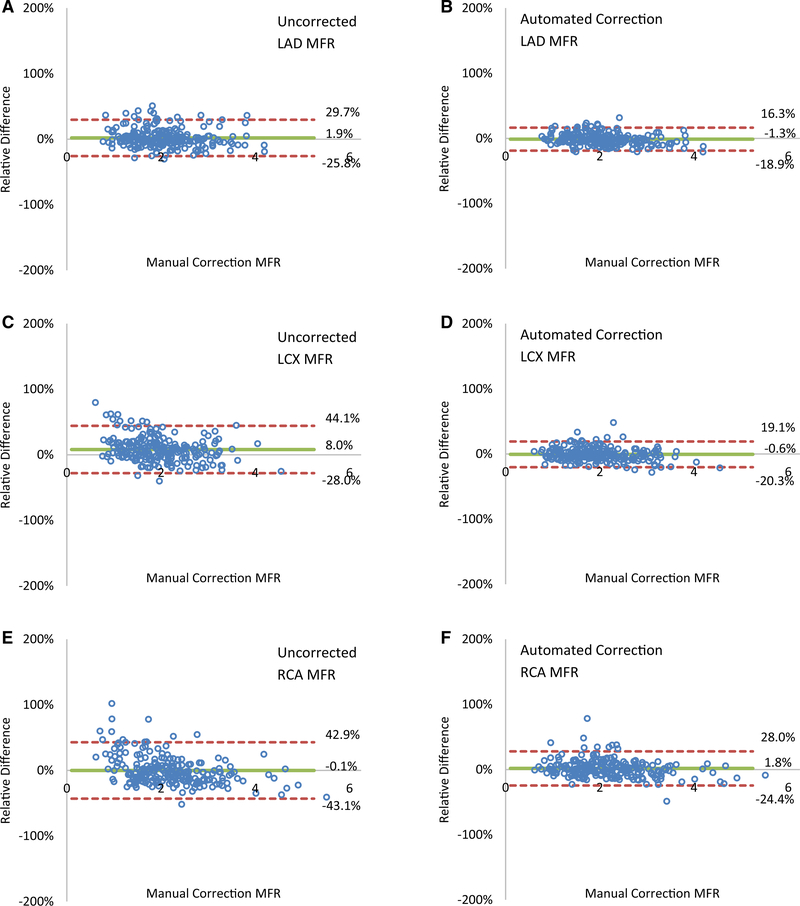
In Figure 4A, C, scatter plots show excellent agreement between automated motion correction compared to manual motion correction for global MBF (Pearson R = 0.99, y = 0.97x + 0.06) and for global MFR (Pearson R = 0.96, y = 0.92x + 0.15). The apparent greater absolute MBF variability above 1.5 mL·min⁻¹·g⁻¹ attributed to stress MBF compared to below 1.5 mL·min⁻¹·g⁻¹ attributed to rest MBF is neither actually greater in terms of relative MBF variability as shown in Figure 6 and Table 3, nor are they statistically different as shown in Table 4. In Figure 4B, a partial scatter plot shows 33 cases of disagreement between uncorrected MBF and manually corrected MBF, out of 450 total values (7%). Disagreeing values are characterized as those with differences with the manually corrected flows outside of the limits of agreement. All but 1 (97%) fall into agreement after automated motion correction, as indicated by the vertical connecting lines. In Figure 4C, a partial scatter plot shows 15 cases of disagreement between uncorrected MFR values and manually corrected MFR, out of 225 total values (7%) of which all but 2 (87%) fall into agreement after automated motion correction. Supplemental Figures 3 and 4 show partial scatter plots of cases of disagreement and their correction for regional MBF and MFR in the vascular territories, with the greatest disagreement and correction in the RCA.

Figure 4.

Automated motion-correction effects on global (A, B) MBF and (C, D) MFR. (A, C) Automated vs manual corrected flows. (A) Four high flow values above 5 mL·min⁻¹·g⁻¹ are not shown. (B, D) Uncorrected flows with differences outside of the limits of agreement (95% confidence intervals) with manual-correction flows improve after automated correction, as indicated by the connecting vertical lines, falling within the same limits of agreement in all but one case for MBF and two cases for MFR.

Figure 6.

Automated motion-correction effects on regional MBF in the (A, B) LAD, (C, D) LCX, and (E, F) RCA vascular territories. (A, C, E) Uncorrected motion vs manual-correction flows and (B, D, F) automated-correction vs manual-correction flows. (E) Two outliers with 306% and 223% uncorrected MBF differences at 1.51 and 1.93 mL·min⁻¹·g⁻¹ manual correction MBF values, respectively, are not shown.

Table 3.

Flow and spillover results

Quantity	Region	Uncorrected	Manual correction	Automated correction	Auto. vs uncorrected difference (%)	Auto. vs manual difference (%)
Stress MBF	Global	2.32 ± 1.00	2.21 ± 0.90	2.21 ± 0.88	4.6 ± 13.4	0.7 ± 6.5
	LAD	2.36 ± 0.99	2.30 ± 0.92	2.27 ± 0.87	3.6 ± 13.1	−0.3 ± 8.4
	LCX	2.05 ± 0.91	2.09 ± 0.91	2.10 ± 0.88	−2.8 ± 12.0	1.5 ± 7.9
	RCA	2.59 ± 1.46	2.09 ± 0.96	2.11 ± 0.95	22.6 ± 41.9	1.7 ± 10.3
Rest MBF	Global	1.15 ± 0.40	1.11 ± 0.40	1.13 ± 0.39	1.9 ± 7.2	1.6 ± 6.3
	LAD	1.23 ± 0.44	1.16 ± 0.41	1.16 ± 0.39	5.1 ± 9.5	1.3 ± 8.2
	LCX	1.08 ± 0.40	1.10 ± 0.42	1.13 ± 0.41	−4.2 ± 8.7	2.7 ± 7.9
	RCA	1.06 ± 0.44	1.00 ± 0.44	1.01 ± 0.39	6.2 ± 19.0	0.7 ± 9.1
MFR	Global	2.09 ± 0.74	2.06 ± 0.70	2.03 ± 0.66	2.9 ± 13.0	−0.6 ± 8.7
	LAD	1.99 ± 0.68	2.06 ± 0.69	2.02 ± 0.65	3.7 ± 14.8	−1.3 ± 9.0
	LCX	1.96 ± 0.66	1.97 ± 0.69	1.94 ± 0.66	9.3 ± 18.9	−0.6 ± 10.1
	RCA	2.55 ± 1.33	2.17 ± 0.84	2.18 ± 0.80	−1.4 ± 19.5	1.8 ± 13.4
Spillover	Global	0.32 ± 0.08	0.31 ± 0.07	0.29 ± 0.06	10.6 ± 12.8	−4.5 ± 7.9
	LAD	0.34 ± 0.08	0.32 ± 0.07	0.30 ± 0.06	12.3 ± 16.4	−5.9 ± 11.8
	LCX	0.24 ± 0.08	0.27 ± 0.08	0.26 ± 0.06	−8.3 ± 22.8	−1.1 ± 15.9
	RCA	0.34 ± 0.15	0.28 ± 0.10	0.27 ± 0.09	26.6 ± 45.8	−2.6 ± 18.1

MBF, myocardial blood flow is in mL.min⁻¹.g⁻¹; and MFR, myocardial flow reserve is unitless. Spillover includes stress and rest. Values are presented as mean ± SD

Table 4.

Flow and spillover statistical analysis

		Test of mean difference		Test of variance
		Automated vs manual correction		Uncorrected vs automated	Uncorrected vs manual	Automated vs manual
Quantity	Region	P	Effect size	P	P	P
Stress MBF	Global	.35	0.00	<.0001*	<.0001*	.33
	LAD	.13	−0.03	<.0001*	.047*	1.00
	LCX	.072	0.01	1.00	1.00	1.00
	RCA	.0056*	0.02	<.0001*	<.0001*	1.00
Rest MBF	Global	.00036*	0.01	1.00	1.00	1.00
	LAD	.035*	0.01	.00046*	.51	1.00
	LCX	<.0001*	0.02	.54	.48	1.00
	RCA	.086	0.01	.29	.00094*	1.00
MFR	Global	.054	−0.02	.51	1.00	.54
	LAD	.0011*	−0.04	1.00	1.00	1.00
	LCX	.044*	−0.03	1.00	1.00	1.00
	RCA	.30	0.01	<.0001*	<.0001*	1.00
Spillover	Global	<.0001*	−0.02	<.0001*	<.0001*	<.0001*
	LAD	<.0001*	−0.02	<.0001*	.40	.00010*
	LCX	<.0001*	−0.01	<.0001*	.04*	<.0001*
	RCA	<.0001*	−0.01	<.0001*	<.0001*	.00033*

MBF, myocardial blood flow is in mL.min⁻¹.g⁻¹; and MFR, myocardial flow reserve is unitless. Spillover includes stress and rest. Effect size is the difference of means.

^*indicates statistical significance of P-values < .05.

^†indicates substantive significance of a large effect size using an alternate Cohen’s d > 0.8 which is unitless

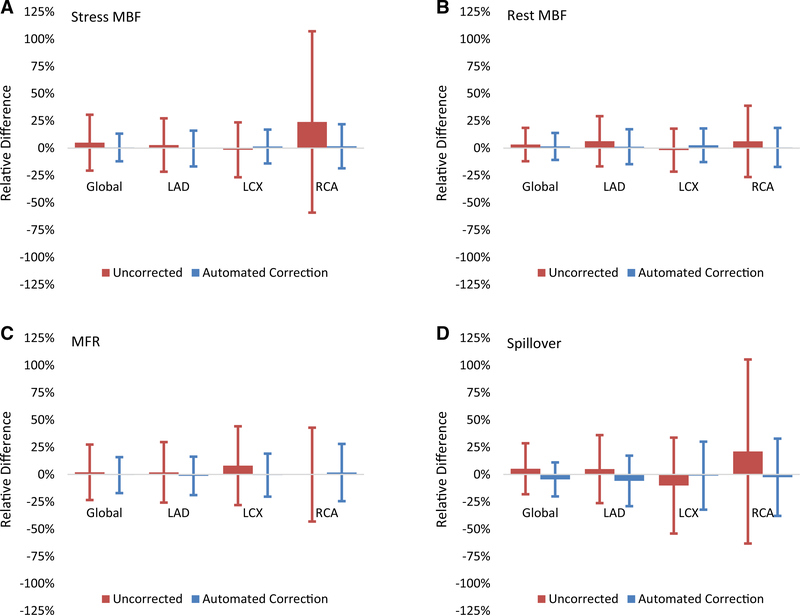
In Figure 5, the reduction in variance (narrower confidence intervals after automated motion correction) shows that the automated correction stress MBF, rest MBF, MFR, and spillover estimates globally and regionally were all closer to the manual correction estimates than with no motion correction. This is most evident in the nearly fourfold reduction in the RCA stress MBF limits of agreement. All global and regional flow and spillover estimates for uncorrected, manual correction, and automated correction with differences between automated correction and manual correction are summarized in Table 3.

Figure 5.

Automated motion-correction effects on (A) stress MBF, (B) rest MBF, (C) MFR, and (D) spillover vs uncorrected values. Manual motion-correction values are the reference. Vertical lines indicate 95% confidence intervals.

Although several differences between automated and manual motion-correction MBF values were statistically different (P ≤ .035), the effects sizes were small (mean differences ≤ 0.02 mL·min⁻¹·g⁻¹; Cohen’s d ≤ 0.05) as shown in Table 4. Similarly, the differences between automated and manual motion-correction MFR values that were statistically different (P ≤ .044) had small effects sizes (mean difference ≤ 0.0 unitless; Cohen’s d ≤ 0.0). All regional and global variances for automated and manual motion-correction MBF and MFR values did not have statistically significant differences (P ≥ .33). While the variances for automated and manual motion correction spillover fractions were statistically different (P ≤ .00033), differences were small in magnitude (standard deviation differences ≤ 0.02 unitless). Lastly, a reduction in variance from the uncorrected to automated motion-correction flows in the RCA territory were confirmed to be statistically significant for stress MBF (P < 0001; standard deviation difference = 0.51 mL·min⁻¹·g⁻¹) and MFR (P < 0001; standard deviation difference = 0.53 unitless) as shown in Tables 3 and 4.

In Figure 6, Bland-Altman plots compare regional effects in the vascular territories of uncorrected and automated motion correction relative to the manual motion correction on the MBF. Automated motion correction reduced the limits of agreement range from 48% to 33% for LAD MBF, 45% to 31% for LCX MBF, and 131% to 38% for RCA MBF.

In Figure 7, Bland-Altman plots compare regional effects in the vascular territories of uncorrected and automated motion correction relative to the manual-motion correction on the MFR. Automated motion correction reduced the limits of agreement range from 55% to 35% for LAD MFR, 72% to 40% for LCX MFR, and 86% to 52% for RCA MFR.

Figure 7.

Automated motion-correction effects on regional MFR in the (A, B) LAD, (C, D) LCX and (E, F) RCA vascular territories. (A, C, E) Uncorrected motion vs manual-correction reserve values and (B, D, F) automated-correction vs manual-correction reserve values.

DISCUSSION

We have developed an automated motion-correction algorithm which matches manual expert corrections in both the blood and tissue phases using an approach of normalized gradient fields which heretofore has not been applied to dynamic PET or cardiac imaging. The accuracy of the automated motion-correction algorithm is most evident in its effectiveness in reducing the large differences of the uncorrected flows to the manually motion-corrected flows, and thus drastically reducing the variability of the flow estimates both globally and regionally.

Normalized Gradient Fields and Modification

Although image-based dynamic motion correction has been previously reported in a few studies, nearly all were not suitable for use in both blood and tissue phases, which can be recast as multi-model images.^17,18 While mutual information is a well-known method for multimodal image registration, normalized gradient fields are similarly powerful yet simpler to implement and more intuitive to understand.^19,27–30 To date only one prior study has used similar methodology, applying normalized gradient fields to dynamic contrast enhanced MRI of the kidney, where an intense blood pool phase is not similarly challenging as in the heart.²⁴ For the motion estimation algorithm to perform accurately, dynamic spatiotemporal phase information was incorporated by automatically identifying the RV and LV blood pool regions. We defined multiple similarity measures customized to each phase of the dynamic sequence and adjusted the similarity measure to retain the direction of two matching edges encoded in the sign of the gradient. Further discussion of the automated motion-correction algorithm and comparison to alternative image registration algorithms is in the Supplemental Discussion.

Expected Motion-Correction Differences

While the manual motion shifts can be confidently estimated in the tissue phase, the transition frames in between the LV blood phase and the tissue phase are not so reliable due to the activity being in both places as it clears the blood pool and enters the myocardium. Therefore, the endocardial surface is no longer clearly delineated and it proves difficult even for experts to confidently estimate motion. The automated algorithm handles this problem by estimating the blood pool and the tissue separately in the transition frames then summing their similarity scores. The weighting between the two based on their respective activity allows a smooth transition between the two phases.

Another difficult phase to estimate motion is in the RV blood phase where the RV myocardium is faint and therefore the RV blood pool tends to align itself with the apical-septal epicardial surface if not properly modeled. Unfortunately, in this study the RV frames were not corrected for most of the cases by the experts, so the automated motion correction of the RV blood phase could not be fully validated. The impact of any discrepancy in the RV blood frame motion correction is minimal since the 1-compartment model in the kinetic analysis employed in this study does not estimate the RV spillover.³¹

Clinical Implementation and Impact

The use of automated motion correction still requires ensuring the input image volumes and their time-activity curves are of high quality.²⁰ While the temporal phase identification algorithm has quality control checks to limit long durations between the phase start and stop times, datasets must be checked for wide boluses, double peaks in the LVBP TAC caused by a delayed saline flush or pooling of tracer in vessels in the axilla,³² and other artifacts of low quality infusion. After the algorithm estimates the motion vectors they should be reviewed for nonspurious or outlier motions, and then be corrected. When performing quality control for motion estimations along the long-axis in the blood phase using LV surface contours with a constant thickness as a proxy for the reference, the tissue uptake image volume may induce a perceived bias of the algorithm over-shifting the blood pool into the apex. Some spillover of the blood pool into the apical myocardium is expected due to blurred cardiac motion and partial volume effects at the apex.

The impact of automated motion correction is significant time savings (<15 seconds per case) compared to manual frame-by-frame motion correction (up to 10 minutes per case). It also has the potential to reduce both intrauser and interuser variability which can lead to increased consistency. This is particularly important for serial monitoring for the progression of CAD and cases such as chronic rejection in heart transplantation.³³

LIMITATIONS

First, this study lacked an absolute truth for the motion vectors as physician reader motion vectors were used as the reference. Second, interuser variability testing of the manual motion shifts between the three readers was not performed on the study population. Third, uncorrected tissue-phase summed images affected by interframe motion will be blurrier and may be an inaccurate motion reference image. This could potentially be improved by iterating the algorithm, at the cost of additional computation time. Fourth, due to a lack of strong RV tissue information in the reference image, motion shifts in the RV blood pool images were not estimated by the expert readers and were cause of difference with the automated motion-correction algorithm. This should, however, have limited impact on resulting flow values as the kinetic model only uses tissue and LVBP activity. Fifth, intraframe motion including cardiac motion and respiratory motion in the longer duration frames were not corrected. Sixth, rotational and nonrigid motions were also not corrected because of a lack of manual correction baselines for these more complicated corrections due to limited image resolution and the presence of image noise in ⁸²Rb PET studies. However, the automated motion-correction algorithm employs a generalizable framework to incorporate rotational and nonrigid motion corrections in the future. Seventh, CT-based attenuation correction (CTAC) misalignment effects were not accounted for, as only post-reconstruction corrections were performed. Misalignments between PET and CT for attenuation correction during the dynamic sequence require varying registrations, which were not performed in this study because it was not available on the Biograph mCT PETCT system. Eighth, variations in other methodological factors such as scatter correction, prompt gamma correction, temporal sampling, image reconstruction and postfiltering, and tracer kinetic modeling could also affect the results.

NEW KNOWLEDGE GAINED

This new image-based, automated, motion-correction algorithm applied to dynamic ⁸²Rb PET studies reduces global magnitude differences with manual motion-correction values, on average, from 12% to 6% in MBF and from 13% to 8% in MFR. It performs particularly well for regional MBF and MFR, as it reduces the limits of agreement for stress MBF fourfold in the RCA territory.

CONCLUSIONS

An image-based, automated, motion-correction algorithm for dynamic PET, using normalized gradient fields with a modified similarity measure, applied across the entire dynamic sequence, reduced bias, and variance in MBF and MFR. The flows from the automated motion correction matched the results from the manual-motion correction by expert physician readers, particularly in the RCA territory. Implications of automated motion correction are better-quality clinical results with reduced user effort.

Abbreviations

MBF

Myocardial blood flow

MFR

Myocardial flow reserve

PET

Positron emission tomography

LVBP

Left ventricular blood pool

RVBP

Right ventricular blood pool

VOI

Volume-of-interest

TAC

Time-activity curve

HLA

Horizontal long-axis

NGF

Normalized gradient field

LAD

Left anterior descending artery

LCX

Left circumflex

RCA

Right coronary artery