Mortality and volume of cases in paediatric cardiac surgery: retrospective study based on routinely collected data

Abstract

Objectives

To determine whether mortality between 1991 and 1995 in hospitals in England carrying out surgery for congenital heart disease in children was associated with the annual volume of cases and to estimate the extent to which an association could explain the apparent divergent mortality at Bristol Royal Infirmary.

Design

Retrospective analysis of data from two sources, a register of returns by surgeons to their professional society and an administrative database.

Setting

12 hospitals in England carrying out surgery for congenital heart disease over the period April 1991 to March 1995.

Main outcome measure

30 day mortality.

Results

For open heart operations in children under 1 year old, and in particular for arterial switches and repair of atrioventricular septal defect, there is strong and consistent evidence of an inverse association between mortality and volume of cases (not taking into account any data from Bristol). A hospital carrying out 120 open operations per year in 1991-5 on children aged under 1 year would be expected to have a mortality 25% lower than that in a hospital carrying out 40 operations. If the children in the hospitals had the same mix of operations, this reduction is 34%. Stratifying for types of operation or including the results from Bristol strengthens this association. It was also estimated that less than a fifth of the excess mortality at Bristol Royal Infirmary in open operations in children less than 1 year old was due to the hospital's lower volume of surgery.

Conclusions

Using appropriate methods, this study showed that mortality in paediatric cardiac surgery was inversely related to the volume of surgery. Considerable caution is needed in interpreting these results, and it does not necessarily follow that concentrating resources in fewer centres would reduce mortality.

What is already known on this topic

Mortality in children undergoing heart operations has been shown to be lower in hospitals with a high volume of such operations

Studies showing a relation between volume of cases and mortality have a range of methodological inadequacies, in particular the choice of a threshold defining high and low volume after the analysis to increase the significance of the results

What this study adds

Disregarding data from Bristol, there is strong and consistent evidence that in England in 1991-5 hospitals performing a higher number of open heart operations in children aged under 1 year tended to have lower mortality

This association explains only a small proportion (less than a fifth) of the excess mortality seen at the Bristol Royal Infirmary over this period

Introduction

As part of its remit to investigate the adequacy of Bristol Royal Infirmary's surgical services for children with heart disease, the Bristol Royal Infirmary Inquiry commissioned a range of statistical work to investigate outcomes of paediatric cardiac surgery and compare Bristol with other centres.¹ This statistical analysis identified a high mortality at Bristol that is highly unlikely to be due to chance, particularly for open heart operations conducted between 1991 and March 1995.² That Bristol was one of the smaller centres performing paediatric cardiac surgery leads to two further questions: whether the outcome of such surgery is associated with the volume of cases; and, if so, to what extent the high mortality in Bristol can be explained by the hospital's lower volume of cases.

Many studies have investigated the relation between clinical outcome and the volume of cases treated by an institution or person.³ A recent review identified 72 studies (covering 40 interventions), most of which showed that centres with higher case volumes have better outcomes.⁴ Nine of 11 studies of cardiac surgery in adults showed a significant association, although a large recent study that examined 97 137 cardiac operations in New York state between 1990 and 1995 found no significant relation between volume and outcomes, after adjustment for clinical risk factors.⁵ This result contrasts with an earlier study on patients in New York and may reflect increasing concordance among institutions, resulting from the intensive quality assurance programme in New York state.⁶

Three published studies on paediatric cardiac surgery found a relation between case volume and outcome, but all have weaknesses in their methods. Jenkins et al studied 2833 children who underwent cardiac surgery in 37 centres in California in 1988 and Massachusetts in 1989 and found that the adjusted mortality in the hospital group with the highest case volume was significantly lower than in other groups, but this group contained only two large centres.⁷ Hannan et al estimated risk adjusted mortality in 16 centres in New York state between 1992 and 1995, but these researchers retrospectively set a cut-off level between “low” and “high” volume hospitals at 100 patients per year, chosen to maximise the significance of the association.⁸ They also took no account of “clustering”—that is, patients treated in the same institution tend to have outcomes that correlate, because of common institutional factors unrelated to volume. Finally, Sollano et al covered essentially the same population as that in Hannan et al's study but used a different source of data and had a better statistical analysis.⁵,⁸ They found a significant association between higher volumes of cases and improved outcomes in children aged under 1 year. However, the figures accompanying the analysis suggest that one large hospital had a substantial influence on the results. Stark et al found no relation between surgical case volume and mortality, but their analysis was based on very small numbers.⁹

Materials and methods

Sources of data

The cardiac surgical register comprises voluntary returns made by surgeons to their professional society and uses diagnostic categories. The hospital episode statistics for 1991-5 comprise four years of administrative data entered by clinical coders. Data are available from 12 centres in England. In each source, operations are primarily treated as either “open” or “closed” and are further subdivided into 13 “procedure groups.”² For this analysis children were grouped by age at time of operation (less than 1 year old and 1 year or older). Neither source of data had any systematic quality control, and the limitations of these sources have been described elsewhere, although the hospital episode statistics have been found to record mortality reasonably accurately.¹⁰,¹¹ Each data source was analysed separately and attention was focused only on results that were consistent across the sources.

The role of Bristol Royal Infirmary

This study was generated by the high mortality in children who underwent heart operations at Bristol Royal Infirmary, a centre with a low volume of cases, and hence it is likely that Bristol would be very influential in any analysis. It is inappropriate to test hypotheses on the same data as those that generated the hypothesis. Thus the primary analysis excluded results from Bristol. This also provided an unbiased assessment of the extent to which any excess mortality in Bristol can be explained by its lower volume of cases. The results from Bristol were included in a separate analysis and in the plots of raw data.

Statistical analysis

Studies of volume and outcome present a number of potential statistical problems. Firstly, results should ideally be adjusted for type of cases (case mix), to avoid some centres seeming to perform poorly because they carry out more complex surgery. Each of the 13 procedure groups was individually analysed, although there are acknowledged difficulties in the coding at this level of detail—a particular difficulty in the cardiac surgical register is distinguishing switch operations for transposition of the great arteries from Mustard or Senning repairs. The primary analysis was therefore based on pooled open operations and was stratified for procedure group. This stratification estimated a common association within procedure groups and should be more robust with respect to errors in allocation to procedure groups.

Secondly, low and high volume should be defined before the analysis. Recently, authors in the United States were accused of deliberately selecting volume thresholds after the analysis of survival rates in liver transplantation to justify their institution remaining the sole provider of the operation in the state.¹²,¹³ Selecting thresholds to maximise significance renders the claimed level of significance uninterpretable, and information is lost by grouping institutions into categories.⁸ No threshold was chosen in the present analysis, and volume was defined as the number of patients treated in each age group. Logistic regression was used to estimate the odds ratio of a specific change in volume; this odds ratio was assumed to be constant across the volume range unless there was strong evidence of a threshold. A degree of stratification for risk was achieved by including procedure group as a factor in the logistic regression. The odds ratio can be transformed to the relative change (r) in odds of death (expressed as a percentage) per additional patient per year—for example, an odds ratio of 0.98 per additional patient per year corresponds to a value of r of −100×(1−0.98)=−2%. This would mean that for each additional operation of the type carried out, the estimated risk for each patient (expressed as odds of death) is reduced by 2%.

Thirdly, general conclusions should not be made from the very good or bad performance of just one or two centres.⁵,⁷ Plots show whether individual centres are having undue influence.

Finally, it should be recognised that the unit of analysis is the hospital, rather than the individual patient, and so estimated standard errors should be adjusted appropriately (see appendix 1).

The relative change in risk for all open operations was estimated in each age group, with and without the inclusion of the data from Bristol and with and without stratification for case mix, for both data sources for the period 1991-5. This analysis was repeated for all closed operations in each age group, with and without Bristol. When there was an association between risk and volume, the impact on absolute mortality and the extent to which the association explains the apparent excess mortality in Bristol was estimated.

Reports detailing the statistical analysis carried out for the Bristol Royal Infirmary Inquiry, including a fuller version of this paper, may be found on the inquiry's website.¹⁴

Results

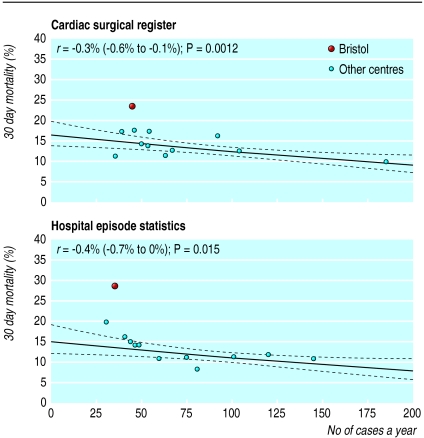
In all open operations in children aged less than 1 year there was a significant association in both data sources between mortality and volume (table 1). Both data sources showed a consistent relation (excluding data from Bristol), despite disagreement in the data (fig 1). As figure 1 implies, including the data from Bristol increases the association and its significance.

Table 1.

Percentage change in odds of death (95% CI; P value) for each extra patient per year in 12 centres in England, including and excluding data for Bristol, according to data for 1991-5 from two data sources

Type of operation	Excluding Bristol data			Including Bristol data
	Hospital episode statistics	Cardiac surgical register		Hospital episode statistics	Cardiac surgical register
All open operations
Children aged <1	−0.38 (−0.71 to −0.04; 0.015)	−0.34 (−0.56 to −0.12; 0.001)		−0.58 (−1.04 to −0.09; 0.01)	−0.42 (−0.69 to −0.13; 0.002)
Children aged ⩾1	−0.20 (−0.81 to 0.46; 0.27)	−0.45 (−1.22 to 0.39; 0.14)		−0.24 (−0.81 to 0.37; 0.22)	−0.47 (−1.20 to 0.31; 0.11)
Open operations (stratified by type of procedure)
Children aged <1	−0.56 (−0.92 to −0.20; 0.0015)	−0.61 (−0.90 to −0.31; <0.0001)		−0.83 (−1.20 to −0.44; <0.0001)	−0.67 (−0.97 to −0.37; <0.0001)
Children aged ⩾1	−0.22 (−0.60 to 0.18; 0.14)	−0.7 (−1.17 to −0.23; 0.002)		−0.25 (−0.61 to 0.13; 0.10)	−0.74 (−1.19 to −0.26; 0.001)
All closed operations
Children aged <1	−0.28 (−1.60 to 1.24; 0.35)	−1.44 (−2.62 to −0.07; 0.02)		−0.28 (−1.68 to 1.36; 0.36)	−1.43 (−2.57 to −0.12; 0.02)
Children aged ⩾1	−9.01 (−9.82 to −4.65; 0.004)	−3.07 (−7.08 to 6.43; 0.2)		−9.17 (−9.84 to −5.61; 0.002)	−2.99 (−6.87 to 5.70; 0.19)

Figure 1.

Relation between mortality and volume of cases in all open heart operations on children aged <1 year, 1991-5. r=estimated change (excluding data from Bristol) in odds of death for each extra case per year; p values are for a two sided test of the hypothesis of no association. Solid line shows the relation fitted by logistic regression, dashed lines show 95% confidence intervals (see appendix 2 for reasons for curved lines)

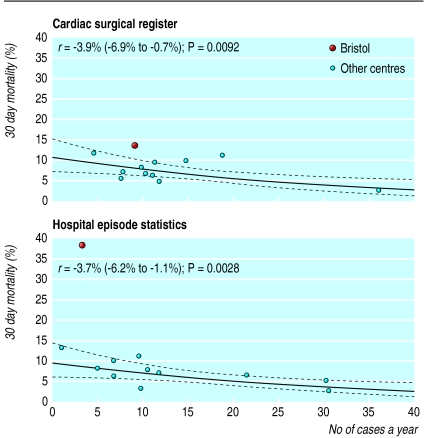
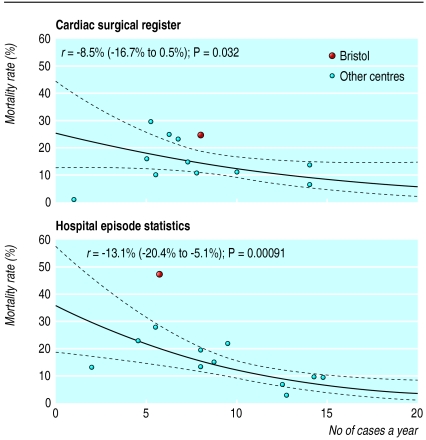
Stratifying the data by procedure group increased the estimated association between mortality and volume (table 1). This result might be expected if larger centres carried out a greater proportion of more complex operations. Again, inclusion of the data from Bristol strengthened this finding. The procedure groups that contributed most to the association are corrective operations for transposition of the great arteries (“switch” operations in the health episode statistics) and repair of atrioventricular septal defect (figs 2 and 3). Much of the relation shown in the data from the cardiac surgical register in figure 2 comes from one large centre.

Figure 2.

Relation between mortality and volume of cases in corrective surgery for transposition of the great arteries in children aged <1 year, 1991-5 (hospital episode statistics show switch operations; the cardiac surgical register includes other types). r=estimated change (excluding data from Bristol) in odds of death for each extra case per year; p values are for a two sided test of the hypothesis of no association. Solid line shows the relation fitted by logistic regression, dashed lines show 95% confidence intervals (see appendix 2 for reasons for curved lines)

For closed operations, no consistent pattern occurred in either data source (table 1). The significant relation seen in children less than 1 year old in the data from the cardiac surgical register is not shown in the hospital episode statistics, and the strong association seen in the older children in the hospital episode statistics was primarily due to one centre. Including the data from Bristol had negligible influence on the relation in closed operations.

When both sets of data shown in table 1 were used, r is around –0.4% without adjustment for operation mix and around –0.6% with adjustment. Table 2 shows the expected difference in mortality in open operations in children less than 1 year old in a hypothetical hospital treating a baseline volume of 40 patients per year (corresponding to a “low” volume) and with a mortality of 15% and hospitals treating 80 and 120 patients per year. Thus a hospital carrying out 120 open operations per year on children less than 1 year old in 1991-5 would be expected to have a mortality that is 25% lower (11.3% v 15.0%) than that in a hospital carrying out only 40 such operations. If the hospitals had exactly the same mix of operations, this relative reduction is 34% (9.9% v 15.0%).

Table 2.

Estimated effect of case volume on annual mortality from open heart operations in children aged <1 year, based on data from the hospital episode statistics and the cardiac surgical register

Adjustment for type of operation (excluding influence of Bristol)	Estimated change (%) in risk for each additional patient	Baseline mortality (%) in a hospital treating 40 children	Predicted mortality (%)
			80 children	120 children
No adjustment	−0.4	15.0	13.0	11.3
Adjustment	−0.6	15.0	12.2	9.9

A change in risk of −0.6% means that each additional patient a year is expected to change the odds of death by a factor of 0.994; hence 40 extra patients reduces the odds of death by a factor of (0.994)⁴⁰ = 0.79. 

Table 3 shows that only an estimated 12% (hospital episode statistics) or 17% (cardiac surgical register) of the excess mortality at Bristol can be explained by Bristol's low volume of cases.

Table 3.

Death rate in children aged <1 year who underwent open heart operations in 1991-5 in 12 English hospitals, showing the extent to which the apparent excess mortality at Bristol Royal Infirmary can be explained by its volume of surgery.

Data source	Mortality (%) in Bristol (A)	Mortality (%) in other centres (B)	Excess mortality in Bristol, not adjusted for volume (C=A−B)	Expected mortality in Bristol, adjusted for volume* (D)	Excess mortality in Bristol, adjusted for volume (E=A−D)	% of excess mortality explained by effect of volume 100(1−E/C)
Hospital episode statistics	28.7 (41/143)	11.2	17.5	13.3	15.4	12.0
Cardiac surgical register	23.7 (43/181)	12.5	11.2	14.4	9.3	17.0

^*Estimated from the fitted line in fig 1, under the assumption that the mortality at Bristol did not differ from the other centres. 

Discussion

Mortality in children aged less than 1 year old who underwent open heart surgery in 1991-5 is significantly related to the volume of cases, even when data from Bristol are excluded. This effect was consistent across both data sources and became more pronounced when the data were stratified according to the mix of operations. This finding is not due to the disproportionate influence of just one or two centres. The data sources were consistent in showing that only a small proportion of the excess mortality at Bristol Royal Infirmary can be attributed to its having a low volume.

Caution is needed in interpreting these findings. The data sources are not of high quality, they have different coding schemes, and they share inadequacies in reporting of data. The conclusions in terms of policy that can be drawn from the study are unclear. For example, for the data from the hospital episode statistics shown in figure 1, it is tempting to recommend a minimum volume of around 50 operations per year, or one a week. Mortality in children aged <1 year in centres with a lower volume was 14.7% (not including Bristol) or 16.7% (including Bristol), whereas the mortality in centres with a higher volume was 10%. Dudley et al take the bold step of using such data to predict the number of “potentially avoidable deaths”—based on the assumption that patients treated at “low” volume centres could have been treated at “high” volume centres, resulting in lower mortality—but this seems to be a quite unwarranted extrapolation.⁴

It is possible that concentrating certain types of operation in fewer centres will lead directly to benefits in outcome—for example, through increased opportunities for surgical learning. However, Posnett warns that such “economies of scale” cannot be guaranteed.¹⁵ Rather than indicating causality, an association between volume and better outcome might be due to a common underlying factor, such as a hospital's longer history, better associated services (such as intensive care), its ability to attract and retain skilled staff, or its ability to attract more patients because of its reputation. None of these factors would necessarily be obtained by, say, merging the caseloads of two centres. It is also important not to extrapolate beyond the available data; further increases in the case volume in larger centres may even lead to poorer outcomes, if communication in the hospital were to start to decline. Finally, it is possible that the concordance between centres might have increased since 1995, because experience with operations such as the arterial switch has been gained.

Figure 3.

Relation between mortality and volume of cases in surgery for repair of atrioventricular septal defect in children aged <1 year, 1991-5. r=estimated change (excluding data from Bristol) in odds of death for each extra case per year; p values are for a two sided test of the hypothesis of no association. Solid line shows the relation fitted by logistic regression, dashed lines show 95% confidence intervals (see appendix 2 for reasons for curved lines)

Appendix

Statistical methods should take into account institutional effects that may induce a correlation among patients in a single hospital. This means it is inappropriate to carry out a simple logistic regression as though all patients were independent, because the estimate of any association would be over-precise and is essentially identical to the need to adjust the analysis in a clinical trial in which patients have been randomised in “clusters” (for example, by their general practice). I used a quasi-likelihood adjustment for over-dispersed binomial data, which provides a single over-dispersion factor by which all standard errors are multiplied.¹⁶

Appendix

The solid line in each figure is obtained from a logistic regression and is therefore linear when mortality is measured on a log (odds) scale. As the figures are plotted on a natural scale, this induces a slight curvature in the fitted line. The dashed lines represent confidence intervals and have additional curvature, as one can be more confident about the mortality at an “average” volume than at the extremes.