Interstitial hydrogen atoms in face-centered cubic iron in the Earth’s core

Abstract

Hydrogen is likely one of the light elements in the Earth’s core. Despite its importance, no direct observation has been made of hydrogen in an iron lattice at high pressure. We made the first direct determination of site occupancy and volume of interstitial hydrogen in a face-centered cubic (fcc) iron lattice up to 12 GPa and 1200 K using the in situ neutron diffraction method. The transition temperatures from the body-centered cubic and the double-hexagonal close-packed phases to the fcc phase were higher than reported previously. At pressures <5 GPa, the hydrogen content in the fcc iron hydride lattice (x) was small at x < 0.3, but increased to x > 0.8 with increasing pressure. Hydrogen atoms occupy both octahedral (O) and tetrahedral (T) sites; typically 0.870(±0.047) in O-sites and 0.057(±0.035) in T-sites at 12 GPa and 1200 K. The fcc lattice expanded approximately linearly at a rate of 2.22(±0.36) ų per hydrogen atom, which is higher than previously estimated (1.9 ų/H). The lattice expansion by hydrogen dissolution was negligibly dependent on pressure. The large lattice expansion by interstitial hydrogen reduced the estimated hydrogen content in the Earth’s core that accounted for the density deficit of the core. The revised analyses indicate that whole core may contain hydrogen of 80(±31) times of the ocean mass with 79(±30) and 0.8(±0.3) ocean mass for the outer and inner cores, respectively.

Introduction

The Earth’s core has supposed to be constituted by iron with ~10% nickel and some light elements. Hydrogen is one of the most probable candidates among the light elements in the Earth’s core. In order to estimate the hydrogen contents in the inner and outer cores, previous studies have determined phase relations, equations of state, magnetic properties, and the sound velocity of iron hydride FeH_x by using synchrotron X-ray^1–7 and theoretical works⁸. Despite intensive studies of iron hydride by X-ray diffraction, precise in situ direct determination of the volume expansion by interstitial hydrogen in metallic iron has not yet been conducted using in situ high pressure and high temperature neutron diffraction studies, except the neutron diffraction of recovered iron hydrides at 90 K and ambient pressure⁹. Therefore, we need to use the volume of hydrogen estimated empirically from many metal hydride compounds¹⁰. To date, neutron diffraction experiments at high pressures have been conducted for deuterides^11,12, but not for hydrides. However, the experimental results for deuterium (D) compounds cannot be directly applied to discuss the behaviors of hydrogen compounds in the lower mantle and core because physical and thermodynamic properties of deuterium and hydrogen compounds differ with each other.

In this study, we directly determined the crystallographic positions of hydrogen atoms and their effects on cell volumes for a high-pressure polymorph, fcc iron hydride, using neutron powder diffraction measurements. This technique provided a precise determination of the hydrogen content in the samples used in previous studies on the phase relations and equation of state of iron hydride. Thus, we can estimate precisely the hydrogen content in the core by comparison with the seismic model of the Earth’s core.

Results

We determined the volume expansion by interstitial hydrogen atoms in the fcc iron hydride lattice by neutron diffraction at various pressures and temperatures for the first time. The phase transition and hydrogenation of iron were observed in both the fcc FeH_x and the double-hexagonal close-packed (dhcp) FeH_x phases. We conducted four separate runs from 3.5 to 12 GPa and in the temperature range from the ambient to 1200 K by using the cubic press (ATSUHIME)¹³ installed at high-pressure neutron beamline PLANET¹⁴ in J-PARC. The phase diagram determined by the present in situ neutron diffraction experiments and the pressure-temperature paths of our experiments are shown in Fig. 1. The phase boundaries of FeH_x compounds determined in this study were significantly different from those estimated previously by using electrical resistivity change due to the phase transitions^15,16; that is, the transition temperature from body-centered cubic (bcc) to fcc was higher than that previously reported in the Fe-H system (Fig. 1). This discrepancy in the phase boundary might be caused by the reaction kinetics of the fcc-bcc-dhcp reactions in FeH_x. We conducted time studies at the conditions of the phase boundaries (Fig. 2). We also observed through the neutron diffraction patterns the phase transitions of forward and reverse reactions in situ by increasing and decreasing the temperature at a constant press load condition (Figs 1 and 2). Therefore, our phase boundaries determined by forward and reverse reactions were more reliable than those reported previously which were obtained indirectly by one-way reaction.

Figure 1.

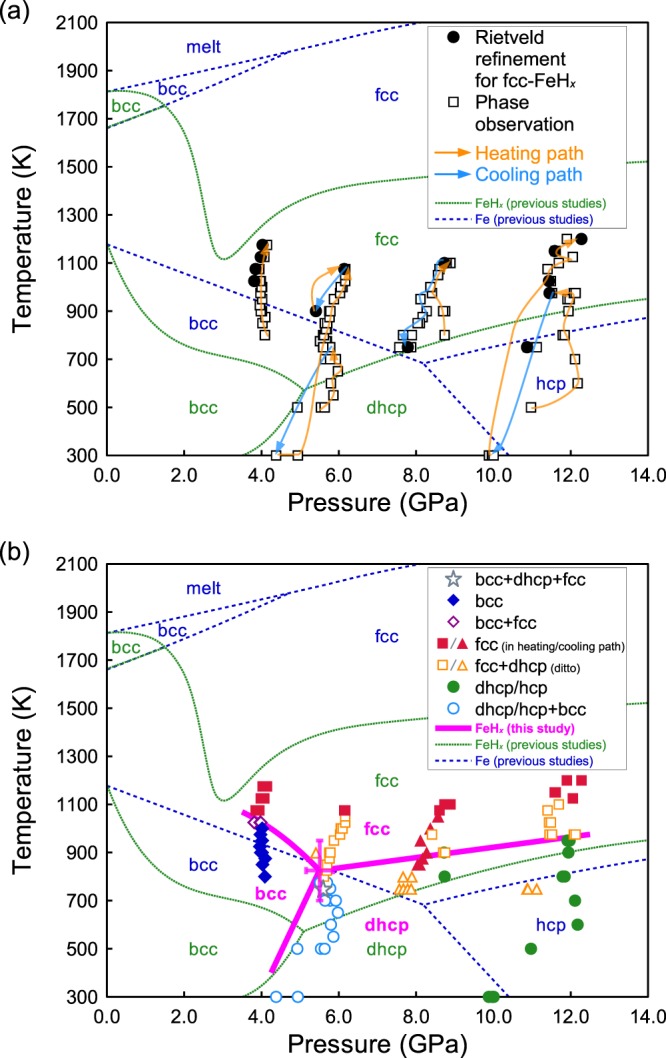
The experimental pressure and temperature conditions and observed phase(s) of FeH_x in this study. (a) The solid circles and open squares represent the experimental conditions of Rietveld refinement for fcc FeH_x and phase observation, respectively. The yellow and blue arrows indicate the heating and cooling paths, respectively. (b) The observed phase(s) in all experimental conditions. The uncertainties in temperature are estimated to be ±50 K. The overall uncertainties in pressure are estimated to be <0.5 GPa; this includes the differences in pressure of 0.2–0.3 GPa before and after neutron diffraction measurement and experimental errors of ~0.1 GPa. Colored symbols show the observed phase(s). Gray star: bcc + dhcp + fcc, blue solid diamonds: bcc, magenta open diamonds: bcc + fcc, red solid squares/triangles: fcc (in heating/cooling paths, respectively), yellow open squares/triangles: fcc + dhcp (in heating/cooling paths, respectively), green solid circles: dhcp/hcp, light blue open circles: dhcp/hcp + bcc. The hcp phase was observed under low temperature conditions where no hydrogen was released from the hydrogen source, NH₃BH₃. The magenta bold line represents the phase boundary of FeH_x phases obtained in this study. The green dotted line and the blue dashed line represent the phase boundaries of FeH_x and Fe as reproduced from previous studies, respectively^15,16,26.

Figure 2.

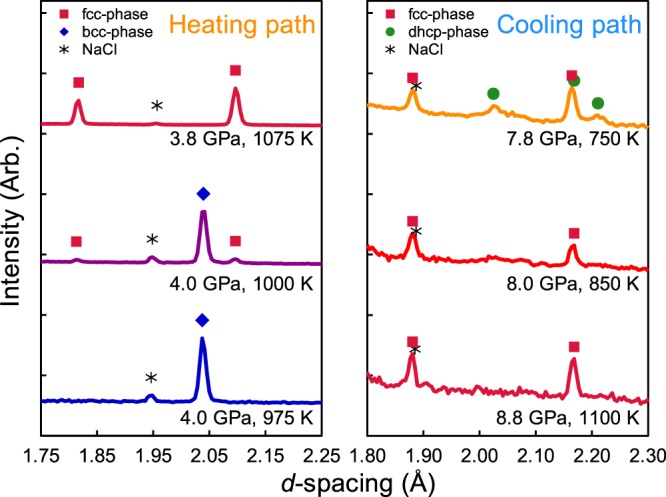
Typical examples of the phase transition for FeH_x in the heating and the cooling paths. Colored symbols indicate the characteristic peaks of each observed phase (red squares: fcc FeH_x, green circles: dhcp FeH_x, blue diamonds: bcc Fe, black asterisks: NaCl). The left column shows a typical example of the phase transition in the heating path from a single bcc Fe phase through the two phases of bcc Fe and fcc FeH_x, and to single fcc FeH_x. The single bcc Fe phase was observed up to 4.0 GPa, 975 K. The fcc FeH_x phase appeared at 4.0 GPa, 1000 K with bcc Fe phase, and the bcc Fe disappeared at 3.8 GPa, 1075 K. The right column shows a typical example of phase transition in the cooling path from the single fcc FeH_x phase to the two phases of fcc FeH_x and dhcp FeH_x. The single fcc FeH_x phase at 8.8 GPa, 1100 K was gradually cooled to 750 K, as shown in Fig. 1. The single fcc FeH_x phase was observed up to 8.0 GPa, 850 K and dhcp FeH_x clearly appeared at 7.8 GPa, 750 K. The neutron diffraction patterns for phase observation were obtained in each P-T condition by 5–10 min keeping time and 5–10 min exposure time after increasing or decreasing the temperature.

The fcc iron lattice has two interstitial sites available for accommodating hydrogen atoms, one octahedral (O) and one tetrahedral (T). In transition metals with an fcc lattice, dissolved hydrogen atoms preferentially occupy the O-site with a free space larger than that of the T-site¹⁷. T-site occupation has been reported for fcc PdD_x¹⁸ and FeD_x¹¹.

This is the first report for site occupancy of hydrogen in both O- and T-sites in the fcc iron hydride lattice. Figure 3 shows examples of a powder neutron diffraction pattern taken at 3.8 GPa, 1025 K and 12.3 GPa, 1200 K with those Rietveld refinements. To estimate the hydrogen content precisely, we performed Rietveld refinement by three different structural models of the fcc iron lattice reported by Machida et al.¹¹: (A) the fcc iron lattice without hydrogen, (B) the fcc iron lattice with hydrogen in only O-sites and (C) the fcc iron lattice with hydrogen in both O- and T-sites. Better refinements have been obtained by using the hydride models B and C instead of the non-hydride model A in all powder neutron diffraction patterns. Especially in some powder neutron diffraction patterns, the best refinements are obtained by the hydride model C. As one of the examples for best refinement, the weighted reliability factor of Rietveld refinement of the non-hydride model A, and the hydride models B and C are 7.42%, 5.71%, and 4.70%, respectively and reduced chi-square are 1.47, 1,31, and 1.23, respectively at 3.8 GPa, 1025 K as shown in Supplementary Fig. S1. Although high background considered as contribution by incoherent scattering from hydrogen was observed in large contents of the hydrogen as shown in Fig. 3b, the intensities were sufficient to conduct Rietveld refinement. The results of the Rietveld refinement for fcc FeH_x in the present experiments are given in Supplementary Table 1. The present analysis showed that hydrogen atoms enter both O- and T-sites. The site occupancy of the hydrogen atoms is also given in Supplementary Table 1. The amounts of hydrogen in T-sites depend on pressure and temperature. Hydrogen atoms occupy both O- and T-sites >1025 K; however, below that temperature, diffraction patterns can be fitted by O-site occupancy for all hydrogen atoms without T-sites. At pressures <5 GPa, the hydrogen content is relatively low at x < 0.3, and it increases to x > 0.3 at higher pressure. The site occupancy is 0.870(±0.047) for O-sites and 0.057(±0.035) for T-sites at 12 GPa and 1200 K, and at 4 GPa and 1175 K, the occupancy is 0.140(±0.009) for O-sites and 0.018(±0.005) for T-sites. The site occupancies of hydrogen in O- and T-sites are similar to those reported by Machida et al.¹¹ for deuterium: 0.532(±0.009) for O-sites and 0.056(±0.005) in T-sites, giving a deuterium content (x) of 0.64(±0.01) at 6.3 GPa and 988 K.

Figure 3.

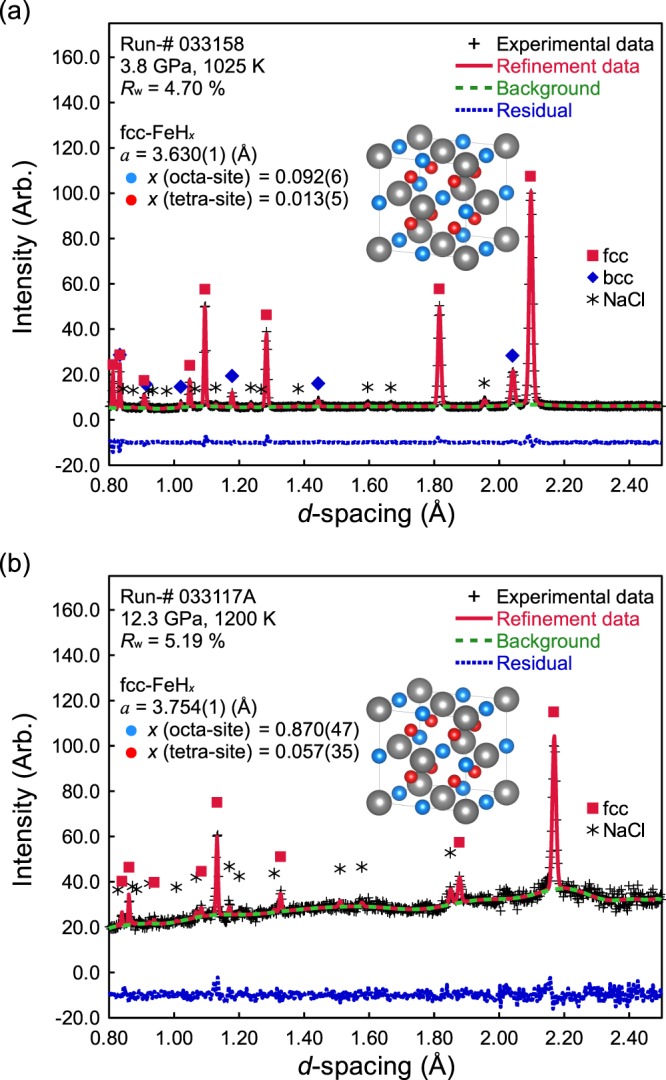
Typical experimental profiles and fitting results of Rietveld refinement for fcc FeH_x. The black + signs represent the neutron diffraction profile obtained experimentally. The red solid line represents refined profiles calculated from Rietveld refinement for fcc FeH_x (and bcc Fe) with NaCl capsule. The green dashed line represents the background of neutron diffraction profile obtained experimentally. The blue dotted line represents the differences between experimental and refined profiles by an offset of −10 in the vertical axis for clarity. Colored symbols indicate the characteristic peaks of each observed phase (red squares: fcc FeH_x, blue diamonds: bcc Fe, black asterisks: NaCl). The inset figure shows the crystal structure of fcc FeH_x (the crystal symmetry is cubic (Fm-3m, Z = 4)) and the atomic sites of Fe are 4a (0, 0, 0), O-sites of fcc FeH_x are 4b (1/2, 1/2, 1/2), and T-sites of fcc FeH_x are 8c (1/4, 1/4, 1/4). Gray balls represent the Fe atom, light blue balls represent an O-site, and light red balls represent a T-site. The experimental conditions and fitting parameters of Rietveld refinement are given in the figures.

Hydrogen atoms generally occupy interstitial O-sites of the iron lattice with a small number of T-sites, therefore the iron lattice expands by hydrogenation. The volume expansion of the iron lattice can be calculated from following formula:

$$\mathit{\Delta }V(\mathrm{H})=[V({\mathrm{F}\mathrm{e}\mathrm{H}}_x)-V(\mathrm{F}\mathrm{e})]/x,$$

where x, V(FeH_x), V(Fe), and ΔV(H) are the hydrogen concentration, atomic volumes of iron hydride and pure iron, and the volume expansion per hydrogen atom, respectively¹⁹. We used the equation of state of fcc iron reported by Tsujino et al.²⁰ for V(Fe). Here, V(FeH_x) and the hydrogen concentration (x) at each pressure and temperature were directly determined by powder neutron diffraction combined with Rietveld refinement, and we could determine the volume expansion per hydrogen atom, ΔV(H), in this study. To date, there have been a limited number of experiments on the determination of ΔV(H) in the fcc lattice of metals, such as the neutron diffraction study of the quenched iron-rich hydride alloy, Fe_0.65Mn_0.29Ni_0.06H_0.95, synthesized by Antonov et al.²¹ at 7 GPa, and recovered to atmospheric pressure at liquid N₂ temperature. They determined the hydrogen concentration by degassing after recovery. The ΔV(H) value of 1.9 ų that they obtained is consistent with that of other 3d transition-metal hydrides with fcc crystal structure (e.g., γ-MnD_0.45: 1.85 ų, γ-CoH: 1.9 ų)¹⁷. The present measurement of a volume increase by a hydrogen atom, ΔV(H), can be compared with this value and is discussed later.

The pressure dependence of the volume increase in the fcc iron lattice by hydrogen dissolution, V(FeH_x) − V(Fe), and its hydrogen content, x, are shown in Fig. 4. As can be observed, both V(FeH_x) − V(Fe) and x increase with increasing pressure; V(FeH_x) − V(Fe) depends very weakly on temperature, whereas x decreases with increasing temperature.

Figure 4.

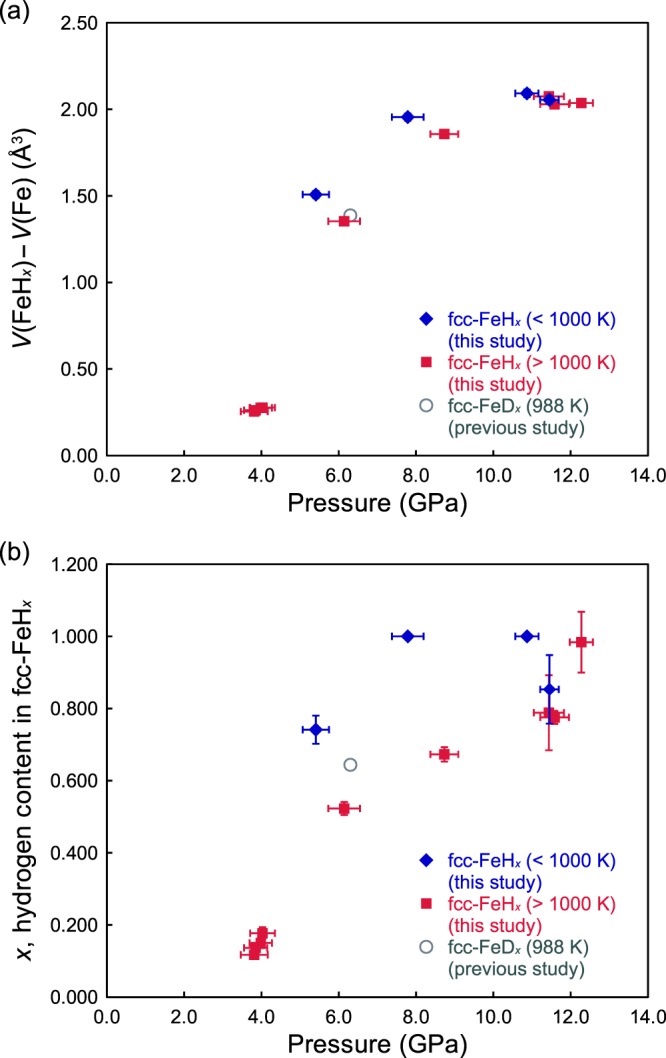
(a) Pressure dependence of the volume expansion [=V(FeH_x) − V(Fe)] from fcc Fe to fcc FeH_x due to hydrogen dissolution. (b) Pressure dependence of the hydrogen content x in fcc FeH_x. The blue diamonds represent the temperature conditions <1000 K and the red squares represent the temperature conditions >1000 K. A gray circle represents the result of iron deuteride (FeD_x) at 6.3 GPa and 988 K¹¹. The errors in pressure are defined in Fig. 1. Other error bars represent the 1σ uncertainty.

Figure 5a shows the magnitude of the volume expansion V(FeH_x) − V(Fe) for the fcc iron lattice increases with increasing the hydrogen content, x. The volume expansion V(FeH_x) − V(Fe) of the lattice seems to increase linearly up to x ~0.8, at a rate of ΔV(H) of ~2.22(±0.36) ų at high temperatures, which is comparable with that of deuterium (ΔV(D) ~2.21 ų) determined at 988 K and 6.3 GPa by Machida et al.¹¹. Figure 5b shows the pressure dependence of the volume increase of the fcc lattice as a result of hydrogen dissolution for one hydrogen atom, ΔV(H). The figure indicates that ΔV(H) is almost independent of pressure at least up to 12 GPa.

Figure 5.

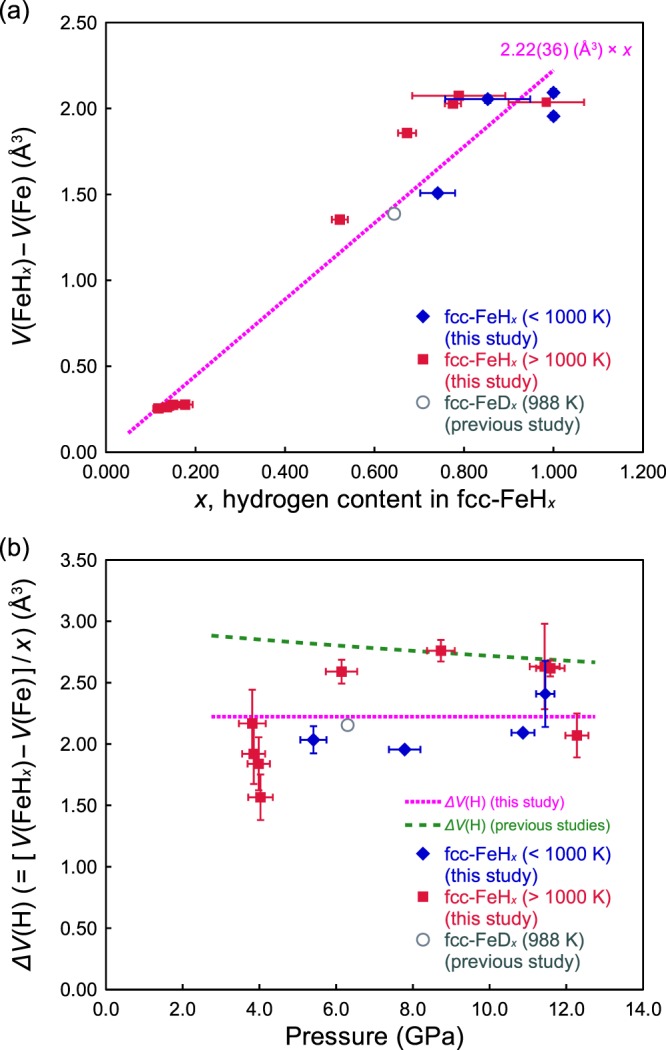
(a) Compositional dependence of the volume expansion of the Fe lattice per Fe atom [=V(FeH_x) − V(Fe)] due to hydrogen dissolution. The volume expansion due to dissolution of one hydrogen atom ΔV(H) {=[V(FeH_x) − V(Fe)]/x} is 2.22(±0.36) ų shown as a magenta dotted line. (b) Pressure dependence of the volume expansion of the fcc lattice due to dissolution of one hydrogen atom, ΔV(H). The pressure dependence calculated theoretically^4,11 is shown as a green dashed line. The abbreviations of symbols and the errors are the same as those in Fig. 4.

Discussion

Several high pressure polymorphs of iron hydride and superhydride phases were reported by using in situ X-ray diffraction method. Hirao et al.⁵ observed dhcp FeH_x phases up to 80 GPa and 300 K. Peppin et al.^6,7 observed iron hydride, FeH₂ and FeH₃ at around 60–80 GPa, and iron superhydride phase, FeH₅ toward to 130–160 GPa after temperature quenching at room temperature. In theoretical work, the presence of further superhydride phase FeH₆ has been suggested⁸. However, these studies were conducted only at room temperature conditions, and had not observed the behavior of hydrogen and its volume in situ. Therefore, our data provide important information for evaluation of the effect of hydrogen dissolution on the compression behavior of the fcc iron lattice that is a high pressure and high temperature phase of FeH_x, and for reliable estimation of the hydrogen content in the Earth’s core by comparison with the density of the PREM (Preliminary Reference Earth Model) Earth’s core²². Chakravarty et al.²³ made ab initio calculations for hydrogen in the iron lattice and showed the pressure effect on the volume of interstitial hydrogen at high pressure. The interstitial volume ΔV(H)²³ fitted using the Vinet equation of state by Fukai¹⁹ (Fig. 5b) was very weakly dependent on pressure, which is consistent with the present work.

The volume increase per hydrogen atom, ΔV(H), in fcc FeH_x has not been determined previously, and the value of ΔV(H) = 1.9 ų per hydrogen atom that is conventionally used for fcc FeH_x was estimated by the neutron diffraction of fcc (Fe_0.65Mn_0.29Ni_0.06)H_0.95 cooled to ~220 K and recovered under ambient pressure²¹. Sakamaki et al.¹ used this value of volume expansion and reported that fcc FeH_x approaches superstoichiometric composition with x = 1.0–1.2 immediately below the melting temperature at 11.5–20 GPa. The present results of lattice expansion per hydrogen atom, ΔV(H) = 2.22(±0.36) ų, at high temperature modify the above arguments; that is, the hydrogen content in fcc FeH_x in the experiments reported by Sakamaki et al.¹ should be x = 0.86–1.03, which is not superstoichiometric but is close to the stoichiometric composition, FeH.

Narygina et al.² synthesized fcc FeH_x at 30 GPa and >1600 K and determined the equation of state of this phase. Based on its compression curve, they estimated the hydrogen content of their synthesized sample to be x = 0.9–1.3 using the volume expansion per hydrogen atom, ΔV(H) = 1.9 ų, and concluded that the amount of hydrogen required to match the density of the Earth’s core would be 0.5–1 wt.% in the outer core and 0.08–0.16 wt.% in the inner core. Thompson et al.³ also studied the hydrogen content in the core based on the equation of state and nuclear resonant inelastic X-ray scattering studies of fcc FeH_x; by using the conventional ΔV(H) value of 1.9 ų, they estimated that the outer core contains 0.8–1.1 wt.% hydrogen, whereas the inner core contains 0.2–0.3 wt.% hydrogen. The hydrogen content in the core estimated in these studies^2,3, that is, 0.5–1.1 wt.% for the outer core and 0.08–0.2 wt.% for the inner core, was overestimated and can be recalculated to 0.65(±0.25) wt.% in the outer core and 0.12(±0.05) wt.% in the inner core by using ΔV(H) = 2.22(±0.36) ų determined in this study. The revised analyses indicate that whole core may contain hydrogen of 80(±31) times of the ocean mass with 79(±30) and 0.8(±0.3) ocean mass for the outer and inner cores, respectively.

Methods

The high-pressure and high-temperature neutron diffraction experiments were conducted at the high-pressure PLANET beamline (BL11) at the Material and Life Science Experimental Facility (MLF) in J-PARC¹⁴. The PLANET beamline has the capability to obtain low background including incoherent scattering from hydrogen due to the excellent collimation of the incident beam and scattered neutron with narrow incident and receiving collimators¹⁴. A six-axis multi-anvil high-pressure apparatus (ATSUHIME)¹³ installed at this beamline was used for high-pressure generation. An iron disc specimen was placed in the center of a hydrogen-sealing capsule made of NaCl with internal hydrogen sources of NH₃BH₃ pellets above and below²⁴. To seal hydrogen, the NaCl capsule was inserted in a cylindrical graphite heater^1,16 and embedded in a pressure-transmitting medium made of Cr-doped MgO [a 10.5 mm edge cube for the anvil with a 7 mm truncated edge length (TEL), and a 15 mm edge cube for the anvil with a 10 mm TEL]. Neutron diffraction data were collected at high pressure and high temperature. The generated pressure was determined by the neutron powder diffraction profile of the capsule material of NaCl. The NaCl-B1 pressure scale used in this experiment was based on Brown²⁵. The experimental temperature was evaluated based on the heating power using a power-temperature calibration curve which was determined by the separate runs with a Pt-Pt 13% Rh thermocouple¹¹. The accuracy of the temperature calibration curve was confirmed by the bcc-fcc transition of iron²⁶. The uncertainty of the temperature determination was ± 50 K. Neutron diffraction profiles were collected during increasing and decreasing temperatures for 5 min. The temporal evolution of the diffraction profile was monitored at several fixed temperatures near the phase boundaries above the decomposition temperature of NH₃BH₃²⁴ which is considered to be <500 K as examples shown in Fig. 2. In addition, no unknown phases were observed except Fe, FeH_x, and NaCl in both heating/cooling paths (Figs 2 and 3). This indicates that the reaction had been occurred only by iron and hydrogen, and there was no contamination of iron hydride sample by boron or nitrogen from the hydrogen sources. The composition and site occupancy of hydrogen atoms in the fcc lattice of FeH_x were determined for the equilibrium state of fcc FeH_x at a fixed pressure based on Rietveld analysis of the diffraction profiles. The temperature was kept constant and the temporal evolution of the diffraction profile was monitored to confirm that FeH_x reached equilibrium with the surrounding H₂ fluid. High-pressure and high-temperature neutron diffraction experiments were conducted at pressures in the range 3–12 GPa and at temperatures in the range 900–1200 K. Two runs (Runs 1 and 4) were conducted in the pressure range 3.5–6 GPa using cubic anvils with a 10 mm truncated edge. The other two runs (Runs 2 and 3) were conducted at pressures in the range 8–12 GPa using anvils with a 7 mm truncated edge. The schematic diagram of the multianvil apparatus with the high-pressure and high-temperature cell assembly and the neutron scattering geometry is given in Machida et al.¹¹. The diffraction intensity of the sample was corrected using the data obtained for a vanadium pellet and an empty cell of a dimension similar to that used in sample data collection. The detailed cell assembly of the present cubic apparatus is given in Supplementary Fig. 2.

Author Contributions

E.O. devised the project. A.S.-F. and T.H. developed the new in situ neutron powder diffraction system at the PLANET Beamline in J-PARC. All authors participated in the experiments. D.I. analyzed the data. All authors discussed the results. D.I. and E.O. wrote the paper with input from all authors.

Data Availability

All data supporting the findings of this study are available within the paper, Methods and Supplementary Information. The crystallographic data are available from the corresponding authors upon request.

Competing Interests

The authors declare no competing interests.

Supplementary information

Supplementary information accompanies this paper at 10.1038/s41598-019-43601-z.