Adaptation of Cochlear Amplification to Low Endocochlear Potential

Abstract

Endocochlear potential (EP) is essential for cochlear amplification by providing the voltage source needed to drive outer hair cell (OHC) transducer current, which leads to OHC electromechanical force. An early study using furosemide to reversibly reduce EP showed that distortion product otoacoustic emissions (DPOAEs) recovered before EP. This indicated that cochlear amplification may be able to adjust to a new, lower EP. To investigate the mechanism of this adjustment, the extracellular OHC voltage, which we term local cochlear microphonic (LCM), was measured simultaneously with DPOAE and EP while using intraperitoneal (IP) and intravenous injection of furosemide to reversibly reduce EP. With IP injection, the DPOAEs recovered fully, whereas the EP was reduced, but LCM showed a similar time course as EP. The DPOAEs failed to accurately report the variation of cochlear amplification. With intravenous injection, for which both reduction and recovery of EP are known to occur relatively quickly compared to IP, the cochlear amplification observed in LCM could attain nearly full or even full recovery with reduced EP. This showed the cochlea has an ability to adjust to diminished operating condition. Furthermore, the cochlear amplifier and EP recovered with different time courses: cochlear amplification just started to recover after the EP was nearly fully recovered and stabilized. Using a Boltzmann model and the second harmonic of the LCM to estimate the mechanoelectric transducer channel operating point, we found that the recovery of cochlear amplification occurred with recentering of the operating point.

Introduction

In the mammalian cochlea, with the positive feedback provided by outer hair cell (OHC) electromechanical force, cochlear amplification locally enhances the basilar membrane (BM) vibration in the best frequency (BF) region to boost the frequency selectivity and sensitivity of the cochlea. Endocochlear potential (EP), the approximately +80 mV scala media (SM) potential, is essential for cochlear amplification (1). It provides part of the voltage source needed to drive OHC transducer current, which leads to OHC electromechanical force. Animal models showed significant decline in hearing function under low EP, including linearization of BM velocity responses and decrease in auditory nerve (AN), compound action potential (CAP), cochlear microphonic (CM), and distortion product otoacoustic emission (DPOAE) responses (2, 3, 4, 5, 6). EP reduction will also reduce the silent current flowing through the cochlea. Quasistatic current across the organ of Corti can modify BM motion (7, 8) and even geometry (3). Thus, EP reduction might affect cochlear amplification in several ways beyond simply reducing the driving force for hair cell (HC) current.

EP is generated in the stria vascularis by active transport of multiple ions (9). Age-related strial degeneration and subsequent EP decline is a common cause of presbycusis (10, 11, 12), resulting in loss of cochlear amplification. Furosemide is a loop diuretic that has ototoxic effects, primarily on the stria vascularis (13, 14), and reversibly decreases EP (4, 5, 15, 16, 17). The recovery takes minutes to hours, depends on the dosage and method of delivery, and gives us a tool to trace the variation in cochlear function with varying EP. In 1991, Ruggero et al. used IV injection of furosemide to change EP and observed the abolishment and recovery of cochlear amplification by measuring the BM velocity at frequencies around the local BF after the injection (2). However, lacking a measurement of EP, it is unclear whether the EP and BM velocity nonlinearity recovered simultaneously. In 1993, DPOAE and EP were measured simultaneously by Mills et al., with DPOAE used to noninvasively probe active cochlear mechanics and amplification (4). With an intraperitoneal (IP) injection of furosemide that reversibly reduced the EP, they found that DPOAEs recovered before EP. This indicated that cochlear amplification may be able to adjust to a new, lower EP. This finding seems at odds with the findings of Sewell et al. (5), in which the EP and AN responses recovered in step with each other. However, AN responses depend on both IHCs and OHCs, and OHC activity might be able to adjust to a change of EP while AN responses are still low. The homeostatic system of cochlear amplification might be relatively robust.

DPOAE represents OHC nonlinearity and is an indirect measure of cochlear amplification, and thus the recovery of amplification with reduced EP hypothesized by Mills et al. (4) needs to be shown to be compelling. In addition, the mechanism for the recovery needs exploration. For example, reduced EP could alter the geometry of the OHC because of electromotility, leading to a static operating point (OP) change of the mechanoelectrical transduction (MET) channels (14, 18). Our results could be analyzed within this OP framework, so we briefly review the basic concepts here: MET channel opening is modeled as a sigmoidal input/output (IO) function, like a Boltzmann function (19). To maximize the IO slope and thus output amplitude, the OP on the Boltzmann function should be centered. For OHCs, which act primarily as alternating current (AC) effectors, one would therefore expect the OP to be approximately centered, and intracellular recordings from OHCs show responses that are reasonably, but not precisely, centered. For inner hair cells (IHCs), for which a direct current (DC) response is important for transmitter release, the MET channel is expected to be uncentered, and that expectation has been born out experimentally (20, 21, 22). It is possible that a recovery of cochlear amplification with low EP could occur by the OHC optimizing its OP to a more centered point on the IO function, compensating for the decreased EP. This centering process may not occur simultaneously with the EP recovery. With sinusoidal input, OP variations can be explored with harmonic analysis of the output. This analysis is guided by previous work by other groups, for example, Kirk et al. (23) and Sirjani et al. (14).

In this study, furosemide was used to reversibly reduce EP, which was continuously monitored. The extracellular OHC voltage at the BM, which represents OHC current and is termed local cochlear microphonic (LCM), was directly measured simultaneously with EP and DPOAE to investigate the adjustment process of cochlear amplification under reduced and recovering EP. The LCM exhibits traveling wave delay, sharp tuning at low and low-moderate stimulus levels, and nonlinearity in the peak region (Fig. 1 D) that is similar to that of BM motion and pressure at the BM (24, 25, 26). Thus, it serves as an appropriate measure of local cochlear amplification. Harmonics of LCM were measured to find OP variations. Our main findings were as follows. 1) With IP injection of furosemide, we confirmed the Mills et al. result: DPOAEs (in the frequency range they studied) recovered fully, whereas the EP was reduced. 2) The EP-dependent changes of LCM (representing cochlear amplification) and DPOAE were different, and thus DPOAE failed to accurately report the variation of cochlear amplification. 3) With intravenous (IV) injection of furosemide, cochlear amplification recovered over a different time course than EP and was related to adjustment of the OP.

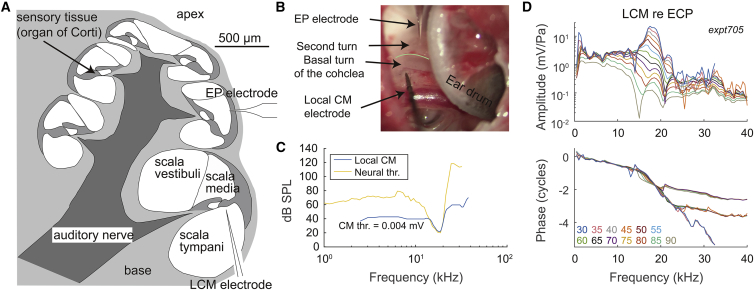
Figure 1.

(A) Cross-sectional view of the cochlea, showing the placement of sensors. The LCM electrode was placed near the BM via a hole in the basal turn of ST. The EP electrode was placed to access the second turn of SM. (B) Experimental photo is shown. The green line shows division of basal and second turn of the cochlea. (C) Comparison of frequency tuning of LCM and AN fiber with BF = 18 kHz (AN data from (27)) is shown. The threshold of LCM was 0.004 mV. (D) Frequency response example of LCM fundamental with stimulus levels ranges from 30 to 90 dB SPL in 5 dB steps (expt705). At the BF of the preparation (18 kHz), the amplitudes show a nonlinearity factor of ∼250. The rapidly accumulating phase at 14–20 kHz shows traveling wave delay, affirming that the measurement was from local OHCs. To see this figure in color, go online.

Materials and Methods

Animal preparation

Animal procedures were approved by the Institutional Animal Care and Use Committee of Columbia University. Adult gerbils with normal CAP response were used in the experiments. Animals were sedated with ketamine and anesthetized with pentobarbital, with supplemental dosing throughout the experiment. 0.5 mL of warm saline was administered every 2 h, and buprenorphine was given every 6 h as an analgesic. Body temperature was monitored and maintained around 37°C by a thermostatically controlled heating pad. After the pinna was removed, the animal was placed in a supine position and a tracheotomy was performed to maintain a clear airway. The bulla was then opened to expose the cochlea.

Furosemide (Salix Injection 5%, Madison, NJ) was administrated via either IP or IV injection. To repeat the Mills et al. study (4), 120 mg/kg furosemide was IP injected. IV injection was performed via the femoral vein of the left leg, at a dose of 100 mg/kg. The injections were performed at t = 0 min in the reported results.

Acoustic stimulus

Sound stimulation was generated by a Tucker-Davis Technologies (Alachua, FL) system driving a Radio Shack dynamic speaker, connected in a closed-field configuration to the ear canal (EC). The calibration of sound was performed within the EC using a Sokolich ultrasonic probe microphone (Newport Beach, CA). Responses were measured for ∼1 s and averaged. Two types of stimuli were applied: single-tone and two-tone. These two types of stimuli were applied alternatively to measure LCM, DPOAE, and distortion products (DPs). Each of the submeasurements took ∼4 min, for 8 min total. The microphone output goes positive for negative pressure, and this 180° offset was corrected in the presented data.

Single-tone stimuli were swept in steps of 0.5 or 1 kHz between 1 and 40 kHz. Multiple stimulus levels were applied (30, 45, 65, and 85 dB sound pressure level [SPL]), to evaluate the nonlinearity of LCM. In one experiment (expt705), after an initial multifrequency, multilevel run, a series of runs were made with just two frequencies (BF and BF/2) at multiple levels (30–90 dB SPL in steps of 5 dB) to achieve finer time and level resolution.

For the two-tone experiments, two pure tones (f1 and f2) with equal levels of 55 and 65 dB SPLs and fixed frequency ratio f2/f1 = 1.25 were applied. f2 frequencies were swept in steps of 0.5 or 1 kHz between 1 and 40 kHz.

Measurement of cochlear potentials

EP

EP was measured via a ∼10 μm diameter hole in the SM of the second turn of the cochlea (Fig. 1, A and B). The reference electrode was placed on the muscle of the right leg, and the animal body was grounded. For both working and reference electrodes, microelectrode holders (World Precision Instruments, Sarasota, FL) with an Ag-Ag/Cl pellet were used. For the working electrode, a pulled-glass micropipette with ∼10 μm tip was connected to the pellet, filled with 0.5 M KCl as a fluid bridge. In the reference electrode, saline was used as a fluid bridge. The EP electrodes had a resistance of 3–8 MΩ when measured in saline. Just before inserting the EP electrode, and again when removing it at the end of the experiment, we measured the voltage at the bony shell of the cochlea to give the 0 mV reference. The difference between these values, the reference drift, usually was less than 3 mV. If the drift exceeded 3 mV, we corrected the EP by a value found by assuming that the reference voltage had drifted linearly with time. After a preamp with a gain of 10, the measured DC voltage was continuously collected every second with a DATAQ DI-710 Data Acquisition & Logger device (DATAQ, Akron, OH) and sent to the computer.

LCM

LCM was measured using a tungsten microelectrode with ∼1 μm tip diameter (FHC, Bowdoin, ME). The electrodes showed a resistance of 0.3–1 MΩ measured in saline with a 500 Hz stimulus and had a flat frequency response over the frequency range of the measurement (change within 0.8 dB up to 80 kHz). The electrode was advanced into the cochlea via a ∼100 μm diameter hole in the scala tympani (ST) of the basal turn of the cochlea, where the BF is 15–20 kHz (Fig. 1, A and B). The electrodes were connected to an AC preamp (PARC EG&G, San Diego, CA) with gain of 1000 and pass band of 0.3–300 kHz, and the data were collected by the Tucker-Davis Technologies system. To measure the local OHC response, the electrode was slowly advanced to be close to the BM until the measured LCM was comparable to that observed in Dong and Olson (24), in which the LCM was measured ∼10 μm away from BM. At this point, traveling wave delay was present in the phase, and the amplitude was sharply tuned at low SPL (Fig. 1 D). In healthy preparations, the LCM showed a high degree of nonlinearity in the peak region, and at low SPL, there was a sharp peak at what was by definition the BF. The LCM phase relative to EC at the BF was ∼1 cycle. In less healthy cochleae, the peak was less prominent, and to be consistent, the BFs of the measurements were determined by the frequency for which phase accumulated over ∼1 cycle. We compared the frequency tuning curve of an AN fiber (27) and LCM, and the sharpness of tuning was similar in the tip region (Fig. 1 C). These observations support the expectation that LCM was generated primarily by local OHCs. Notches do occur, particularly at relatively high SPL, that are likely due to phase cancellation. This cancellation could be between local and nonlocal sources (24, 28) or between local fast and slow mode responses (29). LCM was usually measured every 8 min and was measured every 2 min in the experiment devised for finer time resolution that probed only two frequencies. The time points are defined when 65 dB SPL BF responses were measured, unless noted.

DPOAE

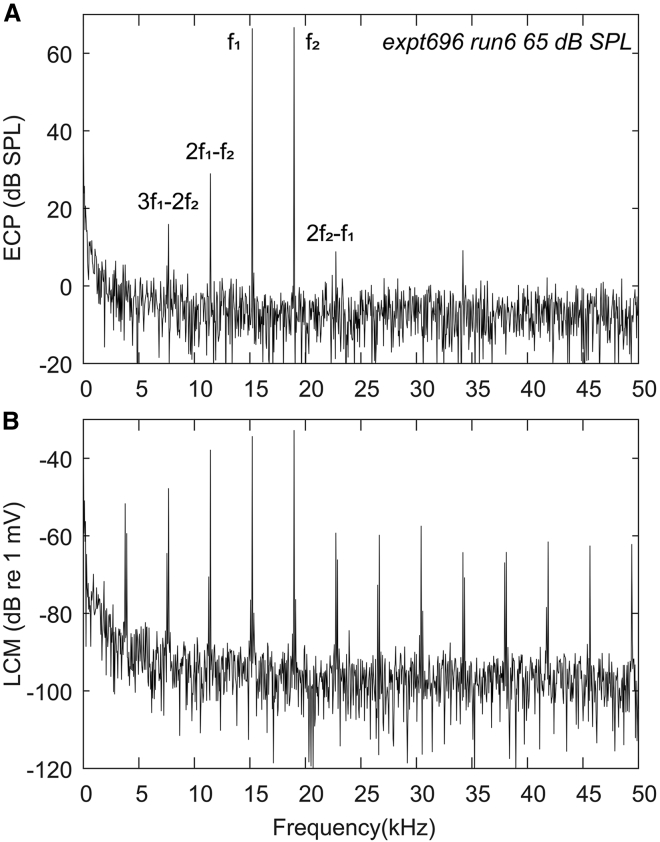
DPOAE was measured in the EC every 8 min. A two-tone stimulus with fixed frequency ratio f2/f1 = 1.25 and equal stimulus levels (55 and 65 dB SPLs) was applied as in our previous studies (25, 30). The amplitude of the cubic distortion tone (2f1 − f2) DPOAE was calculated using the fast Fourier transform of the EC pressure measurement. LCM DP was measured simultaneously via the LCM electrode. The time points were defined when the 65 dB SPL BF response was measured unless noted otherwise. Fig. 2 shows an example of EC pressure (ECP) and LCM spectra with a two-tone stimulus (65 dB SPL).

Figure 2.

Example spectra with 65 dB SPL two-tone stimulus (expt696). (A) ECP spectra are shown. (B) LCM spectra are shown.

CAP

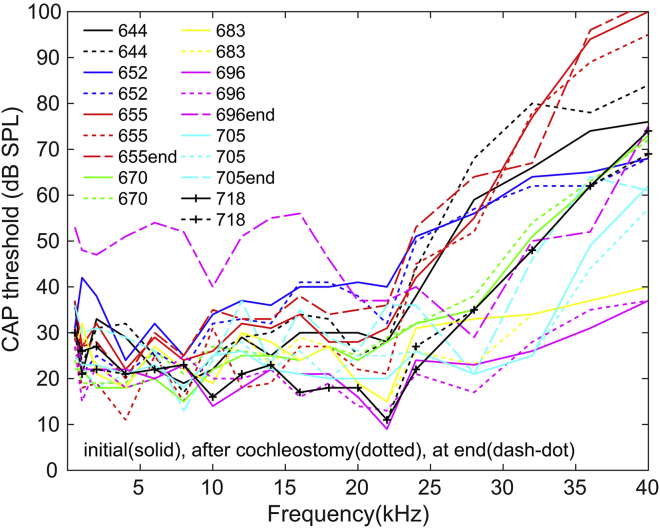
To measure the CAP response, a silver wire electrode was placed on the bony round window (RW) opening. The reference electrode was inserted into the muscle of the jaw, and the gerbil body was grounded. An AC amplifier with a first-order high-pass filter and a second-order low-pass filter, with a pass band of 0.2–4 kHz, was used to measure the CAP response. The CAP stimulus was composed of a 3 ms tone pip of variable frequency presented every 12 ms, with alternating polarity to eliminate the linear component of the CM from the responses. CAP responses were collected for 16 frequencies ranging from 0.5 to 40 kHz. Thresholds were determined by eye as ∼3 μV peak-to-peak responses. CAP thresholds were measured before and after the ST cochleostomy to ensure a healthy starting cochlea (Fig. 3). In three animals, we measured CAP near the end of the experiment. Because EP did not fully recover after furosemide administration, the final CAP thresholds are expected to be elevated somewhat. Two of them (expt655 and expt705) had only a small threshold change, and in general, the change correlated with the final EP, as will be discussed later.

Figure 3.

CAP thresholds measured before (solid) and after cochleostomy (dotted) (n = 8) and at the end of the experiment (dash-dot) (n = 3). The CAP threshold elevations after cochleostomy were less than 5 dB. At the end of the experiment, two of three animals (expt655 and expt705) showed small threshold changes. Because EP did not fully recover, some elevation is expected. To see this figure in color, go online.

Results

DPOAEs could recover fully, whereas EP and LCM remained subnormal after furosemide IP injection

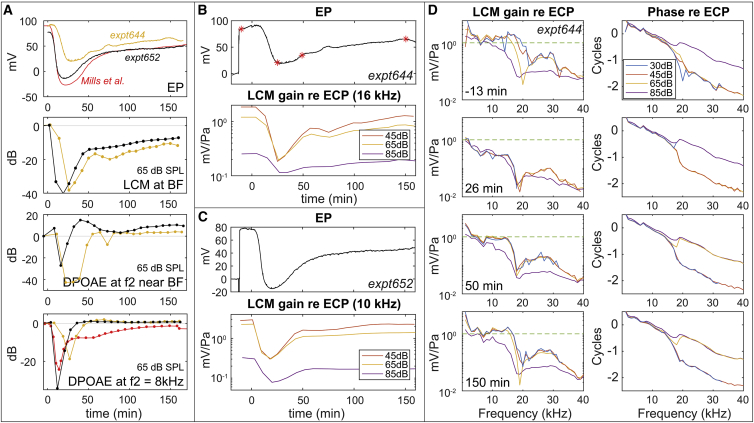
In the first set of experiments, 120 mg/kg furosemide was administrated IP. Fig. 4 A (n = 2, shown in two different colors) compares the time variations of the simultaneously measured EP, LCM (65 dB SPL), and 2f1 − f2 DPOAE (65 dB). As shown in the top of Fig. 4 A, after IP furosemide was administered, EP decreased quickly, reached its minimum within 20–30 min, rapidly recovered between 30 and 50 min, and slowly recovered over ∼150 min. The time course varied somewhat between animals. The EP has not fully recovered in our preparations, and lack of full EP recovery after furosemide injection is common in the literature (4, 16, 17). Fig. 4 A, bottom shows DPOAE variations at two frequencies: near the BF (while avoiding DPOAE notches that might be due to the interference from multiple distortion sources (31)) and at 8 kHz to repeat the Mills et al. study (4). The DPOAE fully recovered at 30–50 min, whereas EP remained subnormal. The DPOAE sometimes even overshot the initial values. These findings were similar to those of Mills et al., which are included in Fig. 4 A (red curves in EP and DPOAE variations). LCM variations are shown in the middle of Fig. 4 A. Unlike DPOAE, the LCM variations were more similar to EP: they did not reach a full recovery. Thus, the recovery of DPOAE failed to reflect a true recovery of cochlear function.

Figure 4.

Cochlear responses after 120 mg/kg furosemide IP injection at 0 min. LCM amplitudes of the fundamental frequency are shown. (A) Variations of EP, LCM at BF (expt644: 16 kHz, expt652: 10 kHz were shown instead of BF = 13 kHz to avoid a notch that might be due to phase cancellation (24, 28)), and 2f1 − f2 DPOAE near f2 = BF (expt644: f2 = 16 kHz, expt652: f2 = 14 kHz) and at f2 = 8 kHz are shown. LCM and DPOAE are in dB referenced to their initial values (see Fig. 5 for fuller DPOAE frequencies). Red lines are results from Mills et al. (4) applying 100 mg/kg IP injection in gerbils. (B and C) EP and LCM (at BF) variations of two animals (B: expt644 and C: expt652) are shown. LCM with 45, 65, and 85 dB SPL stimulus levels are shown. Red stars in (B) indicate the corresponding times for the frequency responses in (D). LCM gain was normalized by ECP. (D) LCM frequency responses from one expt644 at −13, 26, 50, and 150 min after furosemide injection are shown. The green dashed line at 1 is a guide for the eye to compare the magnitude at the different times. LCM gain and phase were normalized by ECP. To see this figure in color, go online.

Fig. 4 D (expt644) shows the detailed frequency response of LCM measured −13, 26, 50, and 150 min after furosemide injection. The corresponding EP time course is in Fig. 4 B, and the superimposed red stars indicate the measurement times of Fig. 4 D. At −13 min, before the furosemide injection, the LCM showed cochlear amplification tuned at the BF of ∼16 kHz. The rapid phase accumulation observed at 15–20 kHz indicates that we were detecting traveling wave responses, which shows that our LCM measurement is dominated by the responses of local OHCs. Along with the EP drop after furosemide injection, the amplitude of LCM at 26 min decreased significantly, and nonlinear compression was absent from 30 to 65 dB SPL. The 85 dB SPL response retained nonlinearity after furosemide injection, likely because the OHC transduction mechanism was approximately saturated—this can be considered “passive nonlinearity.” After that, EP and LCM slowly recovered and stabilized at ∼150 min. The bottom panel of Fig. 4 D at 150 min shows the frequency response when the EP had stabilized. The LCM shows substantial recovery but has not returned fully to its initial condition.

Fig. 4 B (expt644) and Fig. 4 C (expt652) show the time course of normalized LCM with the BF stimulus at 45, 65, and 85 dB SPL. In the EP recovery phase, a two-stage recovery of the LCM response was observed. In the first stage (∼25–40 min), the LCM amplitude increased significantly, but the nonlinear compression was still small, except for the “passive nonlinearity” at 85 dB SPL. In the second stage (∼40–60 min), the recovery of response amplitudes slowed, but the mid-SPL “active” nonlinear compression recovered significantly—the orange and yellow lines in the lower panels of Fig. 4, B and C diverged from each other. The two-stage recovery can also be seen in Fig. 4 D, in which at 26 min, all the SPL curves have dropped well beneath the 1 mV/Pa line, at 50 min, they are back up at the line, and at 150 min, the mid-SPL responses have begun separating, sharpening the lower SPL responses.

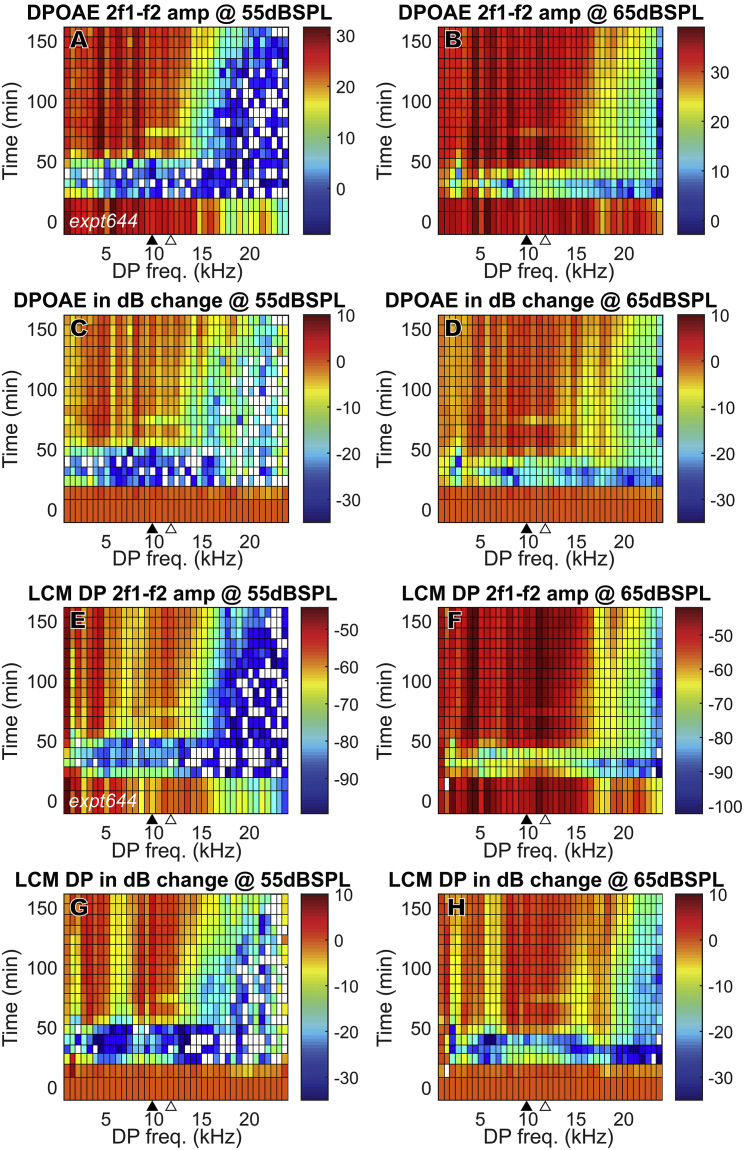
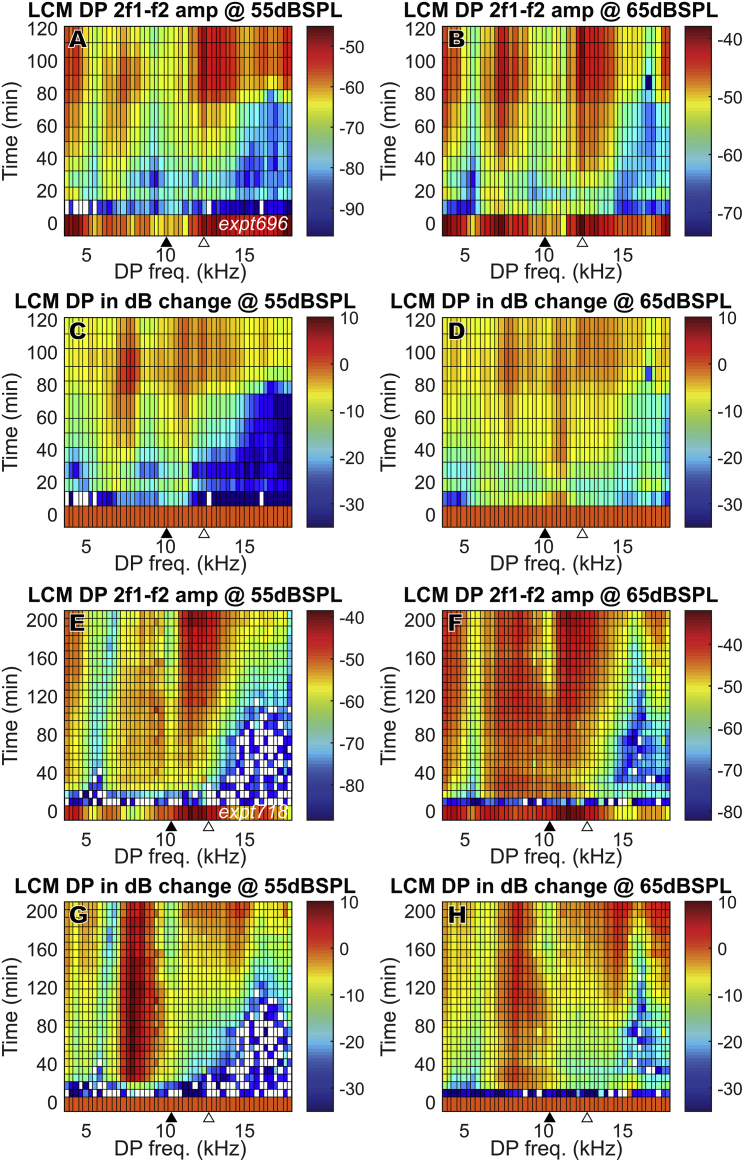
The mesh plots in Fig. 5 show how the 2f1 − f2 DPOAE and DP changed in time after furosemide injection through the full frequency range (f2 = 1–40 kHz, in 1 kHz steps). This figure illustrates the wide frequency range for which DPOAEs and DPs fully recovered and, in some cases, even overshot initial values in the absence of full EP recovery (Fig. 4 A, top). Fig. 4, A–D show DPOAEs, and Fig. 4, E–H show the LCM DPs. Results from one experiment are shown (expt644) for clarity; results from other experiments were similar. Each horizontal row represents DPOAE or LCM DP amplitudes at a specific time after the furosemide injection. The amplitudes are color-coded in dB SPL or dB volts (Fig. 5, A, B, E, and F) and also in dB change relative to their initial values (Fig. 5, C, D, G, and H). Before the furosemide injection, all DPOAE amplitudes started at a healthily high level throughout the frequency range. With the gradual recovery of EP, DPOAE amplitudes almost fully recovered for 2f1 − f2 ≤ 17 kHz, which is equivalent to f1 ≤ 23 kHz and f2 ≤ 28 kHz. At some frequencies, DPOAE overshot its original values (change >0 dB). High frequencies recovered more slowly and did not attain their initial levels. The LCM DP shows a similar time variation as the DPOAE and also shows overshooting compared to initial values.

Figure 5.

DPOAE (2f1 − f2) and LCM DP (2f1 − f2) change in full frequency range after 120 mg/kg furosemide IP injection at 0 min. Sound stimuli were 55 and 65 dB SPL (expt644). DPOAE and LCM DP fully recovered at ∼50 min and could overshoot initial values. (A)–(D): DPOAE, (E)–(H): LCM DP (BF = 16,000, DP = 9600). Amplitudes are in dB SPL for DPOAE and dB volts for DP. dB changes (C, D, G, and H) were referenced to their values before furosemide injection. The closed triangles indicate the DPOAE frequency that corresponds to f2 = LCM measurement BF, and the open triangles indicate the frequency that corresponds to f1 = LCM measurement BF. To see this figure in color, go online.

Changes with IV injection of furosemide

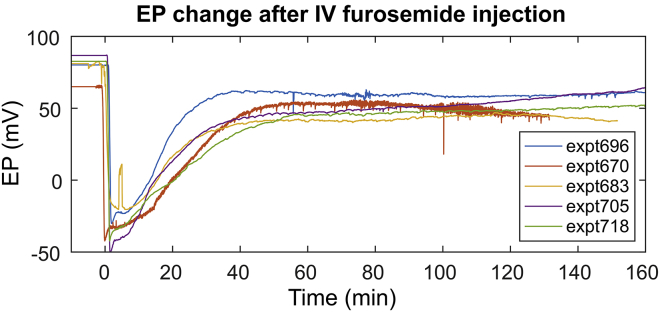
To attain a fuller EP recovery, furosemide was administered via IV injection (100 mg/kg), for which both reduction and recovery of EP are known to occur relatively quickly compared to IP injection (4, 16, 17, 32). Fig. 6 shows the summary of EP change after IV furosemide injection. The EP dropped below 0 mV within just a few minutes and stabilized ∼50 min after furosemide was administered. In most of the animals, EP recovered to 50–60 mV in 50 min. Among all the experiments, expt696 showed the fullest recovery, and thus the full set of data will be shown with this animal, accompanied with data from several other animals to demonstrate repeatability.

Figure 6.

EP change after 100 mg/kg IV furosemide injection (n = 5). Faster decrease and recovery in EP were observed compare to IP injection (Fig. 4A). To see this figure in color, go online.

DPOAE variation after IV furosemide injection

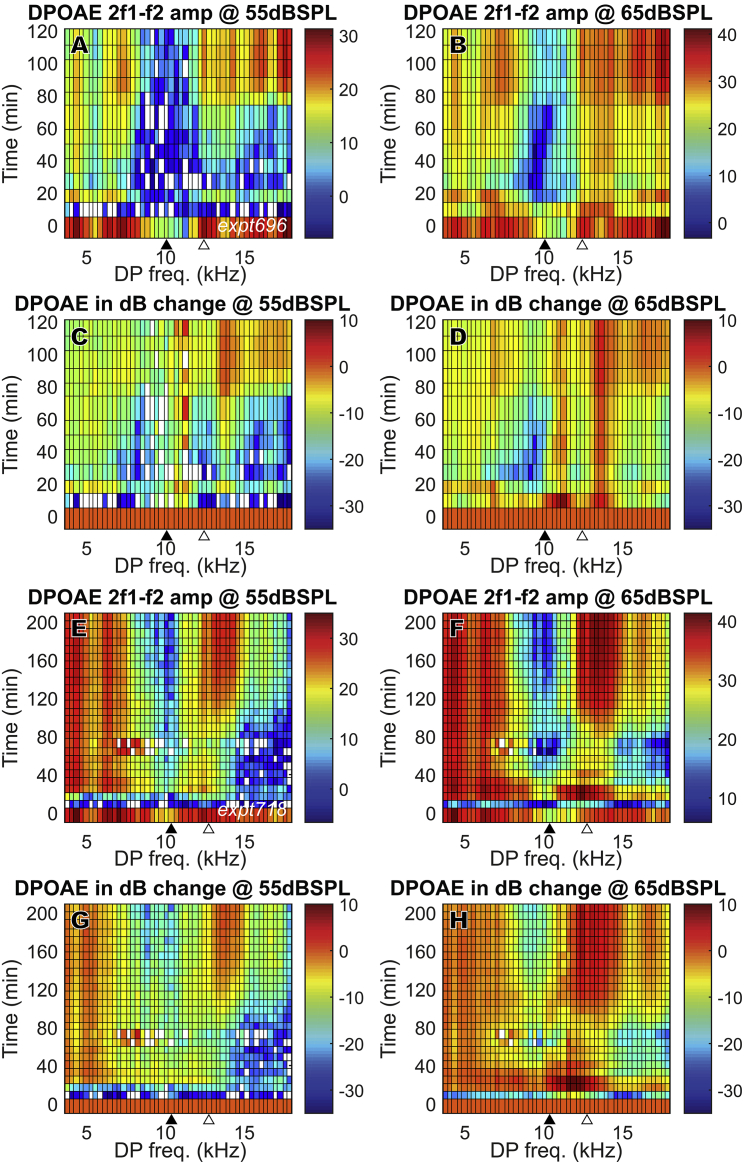
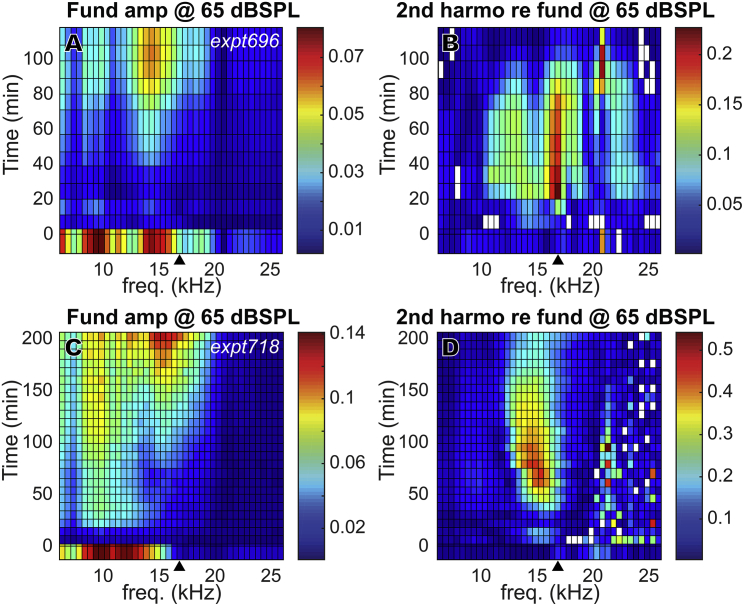
The mesh plots in Fig. 7 show the change of the 2f1 − f2 DPOAEs in time across a wide frequency range. Results from two animals (Fig. 7, A–D: expt696, Fig. 7, E–H: expt718) are shown, with 55 and 65 dB SPL stimuli. Similar to Fig. 5, the amplitude variations are shown in dB SPL (Fig. 5, A, B, E, and F) and in dB change relative to their initial values (Fig. 5, C, D, G, and H). Both preparations show a DPOAE decrease just after furosemide injection and a rapid partial recovery at ∼20 min that was sometimes transient, with a more robust recovery starting at ∼80 min. Expt718 showed a fuller recovery, with nearly full recovery at low frequencies (2f1 − f2 < 8 kHz). But unlike with IP injection, in which the DPOAE fully recovered and even overshot at 2f1 − f2 < 17 kHz, in general, DPOAE did not recover fully with IV injection. Some of the DPOAE results observed at 10–13 kHz in Fig. 7 are likely due to disturbance caused by the proximity of the LCM electrode to the BM. This proximity apparently caused reductions in the initial DPOAE, especially when f2 was approximately the local BF (indicated by filled triangles at bottom of plots). This disturbance was not observed in experiments with IP injection (Fig. 5), possibly because the electrode was further from the BM during the IP experiments. Closer proximity to the BM in the IV experiments is supported by the larger LCM (Fig. 8, H–J) compared with the IP experiments (Fig. 4 D). The disturbance is unlikely to be due to damage because the measured LCM showed a healthy amplitude and degree of nonlinearity, and the cochlear amplifier was functioning before IV furosemide injection and recovered. Furthermore, the initial DPOAE reductions observed at 10–13 kHz were not observed in the LCM DP responses, as will be shown later (Fig. 14). In contrast, in a previous study of DPOAEs and local ST pressure after localized damage, a significant reduction of DPOAEs, local DPs, and cochlear amplification occurred when the BM was damaged by ∼10 μm mechanical indentation (33).

Figure 7.

DPOAE (2f1 − f2) change in full frequency range for two animals (A–D: expt696, E–H: expt718) after 100 mg/kg furosemide IV injection at 0 min. Unlike with IP injection, with IV injection, in general, DPOAE did not recover fully. Amplitudes are in dB SPL. dB changes (C, D, G, and H) were referenced to their initial values before furosemide injection. The closed triangles indicate the DPOAE frequency corresponding to f2 = LCM measurement BF, and the open triangles indicate f1 = LCM measurement BF. To see this figure in color, go online.

Figure 8.

EP and LCM variation after 100 mg/kg furosemide IV injection in three animals. LCM amplitudes of the fundamental frequency are shown. (A–C) EP variation is shown. Red stars show the times that frequency responses (H–J) were measured. (D–F) LCM variation in response to 30, 45, 65, and 85 dB SPL stimuli at the local BF is shown. (SPL key is in H). Amplitude, normalized by ECP, is shown. The BFs are noted on the right bottom corner of (D)–(F). (H–J) The amplitude and phase of LCM relative to ECP, measured before and multiple times after the furosemide injection, are shown. The green dashed line at 1 is a guide for the eye to compare the magnitude at different times. Furosemide was injected at 0 min. See (H) for the color legend. Data lower than noise level (∼1 × 10⁻⁴ mV = −80 dBV (Fig. 2) were excluded. To see this figure in color, go online.

Figure 14.

DP (2f1 − f2) after 100 mg/kg furosemide IV injection at 0 min (same preparations as in Fig. 7; A–D expt696, E–H expt718). Amplitudes are in dB volts (A, B, E, and F). dB changes in (C), (D), (G), and (H) were referenced to their initial values before furosemide injection. The closed triangles indicate the DP frequency that corresponds to f2 = LCM measurement BF, and the open triangles indicate f1 = LCM measurement BF. To see this figure in color, go online.

Cochlear amplification recovered more slowly than EP

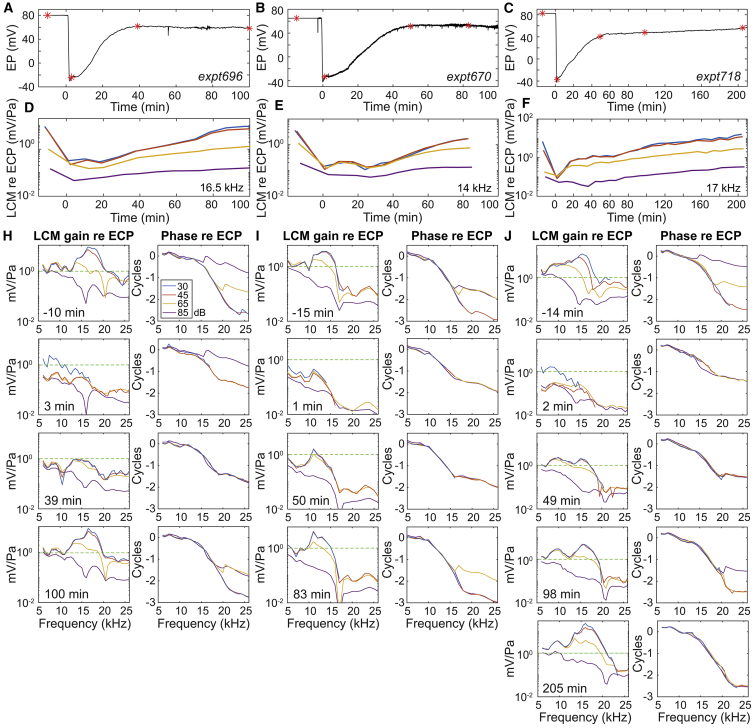
Fig. 8 shows EP and LCM variations for three animals (Fig. 8, A, D, and H: expt696; Fig. 8, B, E, and I: expt670; Fig. 8, C, F, and J: expt718). Fig. 8, A–C show EP variation with furosemide IV injection at 0 min. Fig. 8, D–F show LCM amplitude variation in time at the BF, with stimulus levels of 30, 45, 65, and 85 dB SPL. Fig. 8, H–J show the LCM frequency responses at different time points (labeled as red stars in Fig. 8, A–C) before or after furosemide IV injection. Before furosemide injection, all three animals showed a significant degree of nonlinearity at their BF and rapid phase accumulation around BF frequencies (Fig. 8, H–J, first row). Similar to with IP injection (Fig. 4 D), after furosemide was IV injected, the EP dropped, the amplitude of the LCM decreased, and nonlinear compression disappeared except at the highest SPL (Fig. 8, H–J, second row). The 30 dB SPL response showed a higher gain at lower frequencies (3 and 2 min points in expt696 and expt718) because the data were being collected during the time EP was rapidly dropping. The LCM and EP recovered with different time courses. At ∼40 min, EP had recovered substantially, and the LCM amplitude had recovered to some degree, but nonlinear compression for low-mid SPL remained low (Fig. 8, H–J, third row). At this time, EP stabilized, but LCM continued to recover (Fig. 8, D–F). At ∼100 min, the nonlinear compression and, perhaps more importantly, tuning at low SPL were substantially or even fully recovered (Fig. 8, H–J, fourth row). The LCM of expt718 took a longer time to recover (205 min). Its recovered amplitude was higher than its initial value. The phase excursion at high SPL was greater in the recovered preparation than initially, signifying that the traveling wave mode was being amplified, and thus exceeded the fast mode through a wider frequency and SPL range (29). This latter observation applies to expt696 as well. We acknowledge the possibility that the electrode, starting very close to the BM, could come a few micrometers closer during the experiment, which could account for the observed suprarecovery of the LCM. The observation that cochlear amplification recovered later than the major but incomplete EP recovery indicates the cochlear amplification recovery was not directly due to EP recovery. The LCM almost fully or even fully recovered even when EP was ∼20 mV lower than its initial value.

Simulation of harmonic behavior with sigmoidal OHC MET channel

Because of the electromotility of OHCs, reduced EP can alter the resting state of the OHC. Reduced EP will also affect the ionic composition of cochlear fluids and OHCs. MET channel mechanics are particularly sensitive to OHC [Ca²⁺] (19). Any of these could lead to a static OP change of the MET channels and affect the harmonics of OHC transduction current and LCM. Harmonic analysis can be used to explore a shift in OHC transducer OP. In this section, we use a Boltzmann model to simulate the relationship between harmonics and OP change before showing the experimental harmonic analysis.

The nonlinearity of the forward transduction of OHC MET channels is accepted to be the dominant source of cochlear nonlinearity (34). The LCM can be assumed to be proportional to the local MET channel receptor current, and its relationship with the input stimulus to follow a two-state Boltzmann function (14, 18, 35):

$$CM=V_{off}-V_{sat}+\left(\frac{2V_{sat}}{1+\exp \left(z\times \left(input+OP\right)\right)}\right).$$ (1)

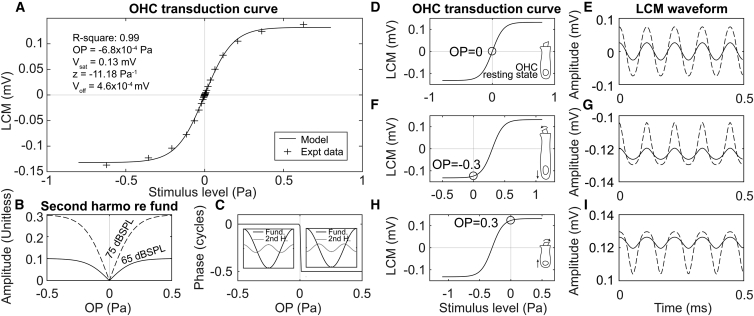
V_off represents the vertical offset, V_sat represents the saturating voltage, and z is a sensitivity factor. OP is the operating point of this OHC transduction curve. This forms a sigmoid shape as in Fig. 9 A (solid line): transduction is approximately linear at low stimulus levels and saturates at high stimulus levels. The source of the data points in Fig. 9 A and the process used to find the Boltzmann parameters will be described in the Discussion.

Figure 9.

Modeled LCM changes driven by OHC transduction OP change. (A) OHC transduction curve based on two-state Boltzmann model is shown. Experimental data were from expt705 in response to 10–90 dB SPL 9 kHz stimuli 8 min after furosemide injection (data shown in Fig. 11 below). (B) Model-predicted second harmonics of LCM (referenced to fundamental amplitude) versus OP change are shown. The amplitude change shows a V-shape that is steeper at higher stimulus levels (solid line: 65 dB SPL; dashed line: 75 dB SPL). (C) Model-predicted phase of second harmonic relative to fundamental versus OP is shown. Phase is right-angled line, and large insets illustrate the meaning. The second harmonic and the fundamental are either in phase (left side, phase difference of zero) or out of phase (right side, phase difference of π = 1/2 cycle) depending on whether the OP is negative or positive. (D–I) OHC transduction curve (D, F, and H) and modeled LCM waveform with pure tone stimuli (E, G, and I; solid line: 65 dB SPL; dashed line: 75 dB SPL) in three different OP cases (0, −0.3, and 0.3 Pa) are shown. At the stimulus level used for this illustration, the LCM is approximately sinusoid when OP = 0 (E) and is distorted when OP moves away from 0 (G and I).

With a centered OP, the MET channel would operate in a relatively linear region of the transduction curve (Fig. 9 D). Then, with a sinusoidal input that is not too large, the output will be nearly sinusoidal (Fig. 9 E). If the OP is shifted (Fig. 9, F and H), the LCM waveform will become asymetrically distorted (Fig. 9, G and I). Because the distortion is asymmetric, it is an even-order distortion, and even harmonics will emerge in the spectrum of the LCM waveform (14, 23, 36, 37). When normalized by the fundamental, the second harmonic amplitude plotted versus OP is V-shaped (Fig. 9 B): the normalized second harmonic is smallest when the OP is centered at 0 and larger when the OP moves away from zero. The phase difference between the second harmonic and the fundamental is either zero or half a cycle (Fig. 9 C). At negative OP, the phase difference is zero, showing that the fundamental and second harmonic are in phase. At positive OP, the phase difference is a half cycle. These relationships have been previously described and supported experimentally in low-frequency CM measurements at the cochlear base (14, 18).

Second harmonic overshoot

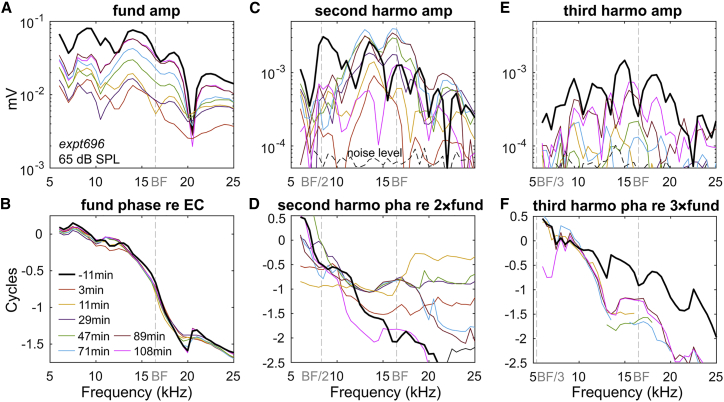
Here, we describe the harmonics of the experimentally measured LCM. Fig. 10 shows the 65 dB SPL LCM frequency response and its harmonics from expt696 with IV furosemide injection. Each color represents a measurement at a different time after furosemide injection. The phase of the fundamental (Fig. 10 B) changed little after furosemide injection, and the plateau region that is dominated by a fast mode started above the BF, at ∼20 kHz. Fig. 10 C shows the second harmonic amplitude. Before furosemide injection, a peak of the second harmonic was apparent at a frequency close to BF/2. This peak might be due to “amplified distortion” that does not originate from the measurement location (38). This distortion is generated basal to the point of measurement and then amplified by the cochlear amplifier as it travels to its own best place. After furosemide injection, the amplified distortion greatly diminished and had still not recovered at 108 min (pink line). The lack of nonlocal distortion is important to the harmonic analysis, which assumes that the harmonics are primarily due to local nonlinearity. Further support for the locality of responses is from the response phase. The second harmonic phase is plotted referenced to two times the phase of the fundamental (Fig. 10 D). At frequencies below the plateau frequency but above the BF (∼20 kHz), the second harmonic phase was generally half or full cycle relative to the fundamental, i.e., either in phase or out of phase, and was composed of approximately flat regions at those values, separated by sloping regions that occur along with local minima in the amplitude. As noted in Fig. 9 C, half or full cycle is the expected harmonic phase for harmonics generated by a nonlinear IO function, and variations from that behavior could indicate travel of the harmonic within the cochlea after generation. The observed amplitude and phase behavior give us confidence that the harmonic responses we measure are mainly locally generated.

Figure 10.

Fundamental (A and B), second harmonics (C and D), and third harmonics (E and F) of LCM frequency responses before and after IV 100 mg/kg furosemide injection. Their amplitudes and phases are plotted against the fundamental frequency, with BF, BF/2, and BF/3 labeled (expt696). To see this figure in color, go online.

In Fig. 10 C, at fundamental frequencies ranging from ∼10 to 20 kHz, second harmonic overshoot (taking values larger than the prefurosemide values) was observed in the period of 47–89 min, whereas by 108 min, the second harmonic had decreased. From the analysis of Fig. 9 B, this indicates that the OP of the MET transduction curve was first moving away from the center of the IO function, and then recentering. At the same time, the fundamental and third harmonic first decreased and then substantially recovered, which is also as expected with a decentering and then recentering of the OP (Fig. 10 E) (18).

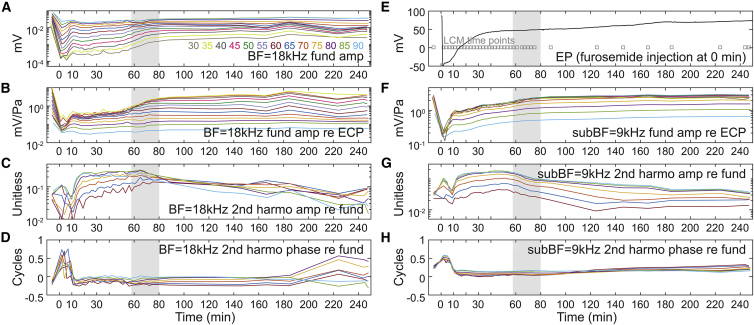
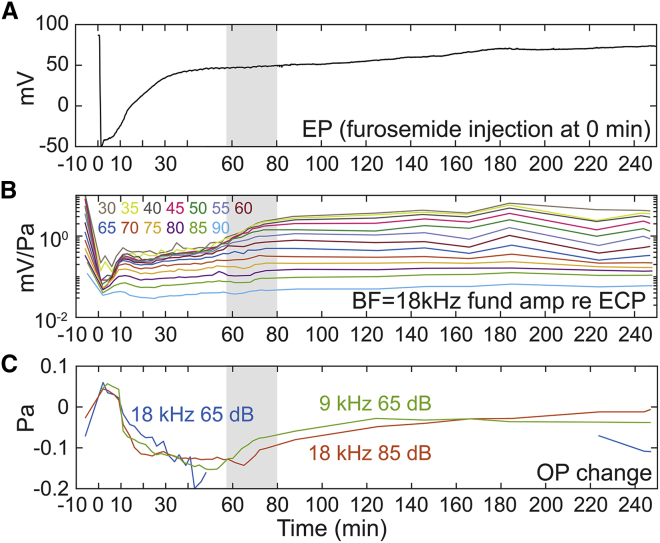
In expt705, with the purpose of exploring the time variation of the LCM nonlinearity in more detail, LCM was measured from 30 to 90 dB SPL in 5 dB steps. To attain a fine time resolution, only single-tone LCM was measured, and responses were measured at only two stimulus frequencies: the 18 kHz BF to show the cochlear amplification variation and 9 kHz as a sub-BF frequency to measure MET channel nonlinearity relatively independent of cochlear amplification. With this protocol, a full set of LCM data could be collected as often as once every 2 min. LCM measurement time points are indicated in the gray boxes included with the EP data of Fig. 11 E. Fig. 11, A–D show the LCM variation at 18 kHz, and Fig. 11, F–H show the variation at 9 kHz. Because the decreasing driving voltage leads to a decrease in the amplitude of both fundamental and harmonics of the LCM, the second harmonic amplitudes are shown normalized to the fundamental (Fig. 11, C and G).

Figure 11.

LCM variation after IV furosemide injection in response to 30–90 dB SPL tones (expt705) with fine time resolution (measurement time points shown in E as gray squares). EP variation is shown in (E). LCM response is shown at two frequencies, BF = 18 kHz (A–D) and sub-BF = 9 kHz (F–H). See Fig. 1 for this preparation’s full frequency response before furosemide injection. At 58–80 min (gray-shaded areas), the cochlear amplification and second harmonic of LCM recovered without a corresponding EP change. To see this figure in color, go online.

After furosemide injection, second harmonic overshoot was observed starting at 12 min at both 9 and 18 kHz. From our harmonic simulation (Fig. 9 B), this indicates that the OP of the MET transduction curve was moving away from the center of the IO function. The LCM fundamental frequency amplitudes at both frequencies showed an immediate decrease followed by a recovery (similar to Fig. 8), and the fundamental amplitudes were stabilized at ∼10 min. From 10 to 58 min, the LCM amplitude at the BF (18 kHz) remained unchanged, and at the sub-BF frequency (9 kHz) mildly increased. At 58–60 min (gray-shaded area in Fig. 11), the cochlear nonlinearity at the BF (Fig. 11 B), which up to this point was only apparent at high SPL (passive nonlinearity), emerged at 30–60 dB SPL, and thus active nonlinearity recovered significantly in this period. In contrast, there was no noticeable EP change in this period (similar to Fig. 8). Instead, the second harmonic amplitude response at both stimulus frequencies (Fig. 11, C and G) decreased, indicating that the OP was recentering at the time (recall Fig. 9 B). Thus, the recovery of cochlear amplification during the gray-shaded time period was not due to a recovery in driving voltage but instead likely resulted from a shift in the MET OP. We expect that the driving voltage was already sufficiently recovered to generate cochlear amplification as early as the 30 min time point, but because at that time the MET OP was substantially off center, the transduction current was too small to generate active nonlinearity. As a final note, the phases of the second harmonics at the time were approximately flat and ∼zero or 1/2 cycle (Fig. 11, D and H), supporting that the measured harmonics were generated from local LCM distortion.

Fig. 12 shows how the fundamental and normalized second harmonic changed in time in two additional preparations, in which the full frequency range was probed. Both of the animals showed second harmonic overshoot through frequencies below their BF. This overshoot was maximum at frequencies near the BF (bright spot in Fig. 10, B and D). That the BF region shows the maximal overshoot of second harmonic/fundamental is in part due to the greater loss of the BF fundamental, which exaggerates the increase of second harmonic when normalized by the fundamental. However, normalization is not the sole reason for the overshoot; recall that Fig. 10 C showed that the second harmonic overshoot occurs in absolute terms, not only in relative terms.

Figure 12.

Fundamental and second harmonic change in full frequency range for two animals (A and B: expt696, C and D: expt718) after 100 mg/kg furosemide IV injection at 0 min, plotted versus fundamental frequency and time of measurement. (A) and (C) show fundamental amplitudes in dB SPL; (B) and (D) show second harmonic amplitudes relative to fundamental amplitudes (unit less). The closed triangles indicate the BF. To see this figure in color, go online.

Discussion

Based on their findings of recovery of DPOAE with low EP (after IP furosemide injection), Mills et al. hypothesized that cochlear amplification could recover with reduced EP (4). This hypothesis is related to the fundamental question of how the cochlea maintains operating conditions so that transduction and cochlear amplification can function properly. The cochlear amplification of the basal region of the cochlea is remarkable, with peak-region motion gain factors of many hundreds in the healthiest preparations (38, 39, 40). The high-frequency region of the cochlea is also remarkably fragile, which makes probing this region in experimental animals challenging for scientists and impacts the high-frequency hearing of aging humans. This fragility suggests that minor perturbations in operating conditions can have serious detrimental effects. The primary objective of this study was to better understand the recovery, and therefore maintenance, of cochlear operating conditions. We explored this primarily through the LCM, measured close to the BM, and simultaneous measurements of EP. The LCM represents the transducer current through local OHCs (24, 41) and shows the tuned response and compressive nonlinearity in the peak of the response curve that is the hallmark of cochlear amplification (Fig. 1). In the LCM, nonlinearity extended through the low-frequency region at SPLs greater than ∼75 dB SPL, and this saturating nonlinearity is expected because of the saturation of transducer current when the channels are approaching their fully open and closed states.

The maintenance and recovery of cochlear operating condition has been studied by others, and a commonly analyzed aspect of operating condition is the OP of the MET channel. The channel operates over a range of less than 0.2 μm (42), which is easy to imagine being perturbed by small static changes in the 10- to 100-μm-sized cells and tissues of the cochlea. Small shifts in OP are likely to lead to substantial changes in cochlear amplification because OHC electromotility and electroforcing are driven by OHC-current-induced voltage (43, 44, 45, 46, 47). To give examples of this previous work, Kirk et al. (35) followed low-frequency CM and f2 − f1 DPOAEs during and after delivery of a high SPL low-frequency tone and hypothesized that a quasistatic mechanical shift gave rise to the known bounce of sensitivity. They modeled their results with a Boltzmann function representing the transducer input-output (I-O) curve. Salt and colleagues (14) measured low-frequency CM and DPOAEs to follow OP changes after several perturbations, including endolymphatic injections and furosemide administration. One of the objectives of their studies was to explore the use of cochlear distortion as an indicator for endolymphatic hydrops. Changes in cochlear responses with low-frequency bias tones have been studied, with the responses following predictable patterns of saturation (48, 49, 50, 51). Our analysis below also traces OP changes after perturbation, and goes beyond previous studies by monitoring changes in LCM at multiple SPLs and many frequencies, including the local BF, simultaneously with EP. These measurements allowed us to directly monitor cochlear amplification and its variation with low EP. Our measurements of DPs and DPOAEs added to the study, but the LCM was the central measurement used for analysis.

Cochlear amplification recovered simultaneously with OP recentering

We found the LCM harmonics changed after furosemide injection, indicating the MET channel OP shifted during the measurement. The delayed recovery of the OP compared to EP recovery likely resulted in the delayed recovery of cochlear amplification. Here, we quantify this notion, using the second harmonic variation and the OHC MET Boltzmann model introduced in result 4 (Eq. 1; Fig. 9) to calculate the time variation of the OP.

The parameters of the Boltzmann model were determined by fitting the expt705 data (experiment from Fig. 11 A). LCM response waveforms to a 9 kHz tone were used for the fit in Fig. 9 A. The 9 kHz stimulus varied over a wide range of SPLs. To remove noise, the response waveforms were reconstructed using the fundamental and second and third harmonics. The maximal and minimal value of the reconstructed waveforms were found and plotted versus their stimulus levels to generate the transduction curve in Fig. 9 A (plus signs). With 10–90 dB SPL stimuli in 5 dB SPL step, 34 pairs of data were generated. The solid line in Fig. 9 A shows the Boltzmann model fit to the data using a least-square fit. This method follows that of Fig. 1 in (20). The response at 8 min after furosemide injection was chosen to generate the Boltzmann model as explained here: 1) at 8 min, the cochlear amplification was approximately inactive. Our objective was to generate and then use the MET curve, in which, strictly speaking, input is stereocilia deflection and output is transducer current. Our measured input is SPL. However, when the cochlear amplifier is inactive, sound pressure and stereocilia deflection likely scale approximately linearly. 2) 8 min after furosemide injection, the amplitude of the normalized second harmonic reached its minimum, which means the transduction curve was the most symmetric at the time. Therefore, the constructed IO curve was not much affected by the fact that our metal-electrode measurement of LCM was AC-coupled. (Truly, even with a DC-coupled electrode, measuring OHC-based DC responses (termed summating potential) would not have been possible because the DC response could have a substantial contribution from IHCs (52).)

Once the Boltzmann curve was known (Fig. 9 A), we determined where the OP was on the curve at subsequent time points using the LCM second harmonic response, normalized by the fundamental response at these time points, by the scheme of Fig. 9, B and C. OP time variations were found for three separate frequency/SPL combinations to check consistency. These three were the responses at 9 kHz, 65 dB and 18 kHz, 65 and 85 dB SPL stimuli (recall the BF = 18 kHz). In Fig. 13, the time course of the OP is in Fig. 13 C, compared with the EP (Fig. 13 A) and normalized fundamental LCM, representing cochlear amplification, in Fig. 13 B. Fig. 11, D and H show that the second harmonic phase referenced to the fundamental was either 0.5 or 1 cycle from 0 to 90 min, as predicted for a locally generated nonlinearity, which our analysis assumes (Fig. 9 C). However, before the furosemide administration and after ∼100 min, the phase values could diverge from these two values, indicating that at these times, some of the second harmonic response likely was generated nonlocally and traveled to the measurement location (38).

Figure 13.

Expt705. See Figs. 1D and 11 for more information. Furosemide was injected via IV at 0 min. Color map is shown in (B). (A) EP variation is shown. (B) Normalized LCM at BF = 18 kHz is shown. (C) OP change is shown estimated from the second harmonic response of BF at 65 dB SPL (blue), 85 dB SPL (red), and sub-BF 9 kHz 65 dB SPL (green), by the Boltzmann model shown in Fig. 9, B and C. During the cochlear amplification recovery from 58 to 80 min (gray shade), no significant EP change was observed, but the OP showed a significant recovery/recentering. To see this figure in color, go online.

Fig. 13 C shows that the three OP estimates resulted in similar OPs, which supports the validity of the OP estimate. (The 18 kHz, 65 dB SPL OP estimation could not be found beyond ∼40 min, likely because the return of amplification prevented the linear proportionality between stereocilia deflection and sound pressure.) An OP change in the negative direction corresponds to MET channel closure (Fig. 9, F and G) so that the OHC is operating in a more hyperpolarized state. This is expected to occur for a static position shift of the BM toward ST. Similarly, a positive OP change corresponds to a relatively depolarized OHC, which is expected for a static position shift of the BM toward scala vestibuli (SV) (Fig. 9, H and I). To describe the time course of the OP variation and speculate on its basis, the OP started at +0.06 Pa after the furosemide injection. At 11 min, the OP passed 0 and jumped to −0.071 Pa, then shifted slightly more negative slowly, reaching its minimum at ∼50 min. The minimal OP change was ∼−0.15 Pa, which is ∼20% of the extent of the Boltzmann curve in Fig. 9 A. In Peng et al. (42), Fig. 2, 20% of the input-output function is ∼10 nm of stereocilia tip displacement, and we can approximate the OP point shift as corresponding to a BM position shift of this magnitude. In this scenario, the OP change was induced by the decreased driving voltage hyperpolarizing the OHC soma, causing the OHC to lengthen and shift the position of the stereocilia. However, the mechanism for OP shift is not revealed by this study.

At 58–80 min (shaded area in Fig. 13), the OP was significantly recentered. This recovery was simultaneous with cochlear amplification recovery, evinced by the recovery of nonlinearity in the LCM at low SPL (Fig. 13 B). This simultaneous recovery indicates that recovery of cochlear amplification was due to OP recentering and was not directly tied to EP recovery (Fig. 13 A). With the OP substantially recentered, the MET transduction operates in a more linear region with larger MET currents and thus greater OHC electromotile forcing. Additional changes that facilitate amplification could occur along with OP recentering.

There are several time points at which the OP affected the LCM. At 10 min, the phase of the second harmonic shifted by a half cycle (Fig. 11), indicating that the OP jumped from positive to negative (Fig. 13 C). At this time point, the amplitude of BF and sub-BF fundamental responses showed a moderate peak, and the second harmonic amplitude showed a valley (Fig. 11). These changes were also observed in other preparations (Figs. 8, D and E and 12 at ∼10 min, Fig. 4 at ∼50 min instead of 10 min because of IP injection). In our earlier work (53), we compared the timecourse of the experimental LCM with the expected “ohmic” LCM change due to the change in driving voltage, using the Davis model (1). The higher SPL data (85 dB) was better predicted by the simple ohmic prediction than the lower SPL data (30, 45, and 65 dB), likely because of the smaller contribution of cochlear amplification at 85 dB SPL. Nevertheless, the ohmic prediction and experimental LCM still differed at 85 dB SPL. This previous finding is consistent with the finding from this analysis that in addition to reducing the driving voltage, the furosemide injection changed the OHC transducer OP, diminishing the sound-induced conductance change of MET channels.

Sirjani et al. (14) administered IV furosemide at 100 or 50 mg/kg in guinea pigs, monitored second harmonics in CM in response to 500 Hz tones measured near the RW, and estimated OP shifts. Responses were followed for 32 min. Despite the experimental differences (frequency and location of CM measurement), the observed variations (Fig. 9 in Sirjani et al. (14)) mostly agree with our results in Figs. 11 and 13. In their results, the second harmonic showed an initial rapid increase, then decreased to a local minimum at 10 min (still larger than the original), and then stabilized or increased slightly. The calculated OP shifted toward SV immediately after the injection and slowly moved toward ST, passing 0 at ∼15 min. Sirjani et al. did not observe full recovery of the OP, but they only observed for 32 min, whereas in our result, the OP was approximately fully recovered at ∼240 min. Their measurement of DPOAE 2f1 − f2 emissions showed a decline followed by an increase, which was also similar to our observation (Fig. 7).

Variation of odd harmonics support the proposed OP change

Theoretically, with OP change, odd order distortions such as third harmonics and 2f1 − f2 DP will show a “W” shape, with a local maximum with the OP at zero, a decrease with OP shift in either direction away from zero, and finally an increase at larger OP shifts (18). Using our Boltzmann simulation with 65 dB SPL stimulation, third harmonics are expected to decrease as OP moves away from zero for OP shifts that are <0.2 Pa. During experiments, the third harmonic was often nearly beneath the noise level because of its small amplitude. Nevertheless, it showed a significant decrease after furosemide injection and a recovery afterward (Fig. 10 E). Fig. 14 shows the DP variation with IV injection through a frequency range of f2 = 5–30 kHz, for two preparations. The amplitude variations are shown in dB volts (Fig. 14, A, B, E, and F) and in dB change relative to their initial values (Fig. 14, C, D, G, and H). Both preparations showed a decrease in DP after furosemide injection, followed by recovery. These variations of odd order distortion support the OP variation predicted with the second harmonic analysis.

Basis for the OP shift under EP change

The OP shift at 10–50 min in our Fig. 13 might be due to the mechanical effects of reduced EP. Reduced EP would decrease OHC transmembrane potential and thus hyperpolarize the OHC, which would increase its static length because of electromotility. As noted above, the OP shift corresponded to ∼10 nm of stereocilia displacement. OHC static length change is ∼2–15 nm/mV in isolated OHCs (45), but in the more constrained in vivo state, OHC static length change is expected to be reduced. However, in an in vitro preparation of the whole cochlea, Jacob et al. (3) found that positive current injection into SM caused position shifts of up to 200 nm, and thus the ∼10 nm shift we estimate is reasonable. EP changes induced by hypoxia have been correlated with OP shifts in past work (18): using a Boltzmann-based analysis, 40 mV of brief (∼5 min) EP decrease caused a <0.1 Pa shift corresponding to displacement toward SV, followed by a 0.3 Pa shift corresponding to displacement toward ST. The OP reached its maximum (toward ST) at the same time EP reached its minimum. The displacement toward ST is as expected if the main effect of reduced EP was to hyperpolarize the OHC. The mechanism and time course of EP reduction in the above study (18) are different than in our study, and the specifics of the OP responses are different, but in both studies, the responses can be thought of in terms of static position shifts brought on by OHC electromotility.

Furosemide may result in an OP change through mechanisms other than reduced EP. Santo-Sacchi et al. (54) showed that furosemide can affect nonlinear capacitance in isolated OHCs. Sirjani et al. (14) found that the OP variation caused by RW perfusion with furosemide was different than that caused with IV injection, indicating that furosemide might affect different pathways in the cochlea. However, in Rybak et al.’s results (55), perilymph concentrations of furosemide with IV injection reached only low micromolar concentrations (∼15 μM), which was >6 times smaller than the amount that was able to alter nonlinear capacitance in the isolated OHC (>0.1 mM). Furthermore, the perilymph concentrations of furosemide required to alter cochlear function with perilymphatic injection (10⁻⁴–10⁻³ M (56)) are 1000 times greater than with the EP-reducing IV injection (1.5 × 10⁻⁶ M (55)) (2). These observations indicate the primary cochlear site of action of furosemide is at the stria vascularis and not the HCs or other cells of the organ of Corti. OHC degeneration has been observed as a result of primary strial dysfunction (57), but only in relatively long-term studies (6, 57, 58).

Furosemide blocks Na, K-ATPase, or the Na-K-Cl cotransporter channel in the marginal cells of stria vascularis (and other cells) (13, 14) and alters the ionic composition of cochlear fluids as well (specifically K⁺ and Cl⁻ (14, 15, 32)). In Rybak and Morizono (32), the IV injection of furosemide reversibly decreased the endolymph K⁺ concentration (termed Ke⁺), and its recovery (starting at ∼25 min) tended to lag behind the EP recovery. This time course of Ke⁺ could affect LCM because potassium acts as the primary cation for OHC transduction current. Rybak and Whitworth (15) showed endolymph Cl⁻ concentration decreased by 16 mM in 30 min when they IV injected 100 mg/kg furosemide, and [Cl⁻] recovery lagged the EP recovery. Chloride is essential to the electromotility of the OHC motor protein prestin (59, 60). Decrease of extracellular and intracellular Cl⁻ had been shown to decrease the peak capacitance and the operating voltage of prestin (60, 61, 62, 63), which leads to a reduction in cochlear amplification. On the other hand, the reduction of those ions may be accompanied by water movement leaving endolymph, osmotic changes that could affect OP (14, 64). Finally, the OHC MET channel is sensitive to intracellular [Ca²⁺], and the reduced voltage drive for this divalent cation might have led to reduced Ca²⁺ flow into OHCs, affecting stereocilia position and OP (19, 65). In summary, our experimental results show that recovery occurs simultaneously with recentering of the OP of OHC MET channels. However, recovery might also hinge on the recovery of proper ionic concentrations and OHC resting potential, required for prestin to return to a functional state (61, 66, 67).

EP reduction has been shown to be a primary factor of metabolic presbycusis (6). In aged gerbils with low EP, CM measured at the RW was comparable to or even larger than in young gerbils (68). These data were explained by a “dead battery” model, in which the strial battery source resistance was increased in aged animals (69). However, in acute application (such as furosemide application or current injection to SM), CM has been positively correlated with EP (7, 70), and our experimental data are in keeping with this. Our study was of acute changes in EP, and the observations are not expected to be similar to those of studies of the long-term reduction of EP that occurs in aging. Certainly, it would be interesting and beneficial if OP adjustment could reduce the deleterious effects of metabolic presbycusis, but this study does not address that question.

BM motion and neural response with reduced EP

In experiments with IV furosemide administration in chinchillas, the BM velocity at BF recovered over a similar timescale as our LCM: the BM velocity nonlinearity was not recovered at 45 min and was recovered at 118 min (2). However, EP was not measured in those experiments.

In experiments with IV furosemide administration in cats, AN response and EP were measured and recovered simultaneously, which is different from the delayed recovery of LCM in our results (5). This difference might be related to the much smaller dose of furosemide (7.5 mg/kg) in the experiment in cats, which only decreased EP to 10 mV, with nearly full recovery within 10 min.

CAP threshold is an indicator of cochlear sensitivity based on AN signals. It is an indicator of low-SPL responses and thus depends strongly on cochlear amplification. In experiments in cats, the relationship between EP change and CAP threshold was found to have a slope close to −1.0 dB/mV (5, 6, 7). In our experiments, comparing initial CAP threshold to that at the end of the experiment, our results are consistent with this value (Fig. 3) in that a final EP decrease of ∼10 mV caused CAP threshold to be elevated ∼10 dB in two animals. In one animal, the final EP was decreased by 20 mV, and CAP threshold was elevated by 20–30 dB. We did not monitor CAP at intermediate time points. When EP was reduced by methods other than furosemide, for example, mutant mice or noise exposure, the relationship between CAP threshold and EP was closer to −0.5 dB/mV (71). However, with these methods, factors other than EP likely contribute to the threshold elevation.

Conclusions

With IP furosemide injection, we reproduced the result by Mills et al. (4), in which, after an initial reduction, the DPOAE recovered before the EP. Because DPOAE is a noninvasive measure of cochlear status, Mills et al. hypothesized that the earlier DPOAE recovery indicated that cochlear amplification recovered before EP. With IP furosemide, our findings with direct measurement of cochlear amplification did not support this hypothesis: cochlear amplification, as measured via LCM, began its recovery with a similar time course as EP. Compressive nonlinearity in the peak region recovered in stages, at the highest SPL first and the lowest SPL last, and with IP furosemide, the recovery of peak-region compression was incomplete in the presence of stabilized but not fully recovered EP. Our interpretation of the full recovery of DPOAE and incomplete recovery of cochlear amplification as measured in LCM is that DPOAE is a relatively simple indicator of cochlear sensitivity. DPOAEs represent distortion, which relies on cochlear nonlinearity, but DPOAEs are not necessarily monotonically related to cochlear amplification. As another example, an earlier experiment showed 2f1 − f2 DPOAE did not change significantly when CM amplitude was reduced by 10% and CAP threshold was elevated by ∼6 dB (23).

With IV injection of furosemide, several aspects of the results were similar to those with IP injection, namely, reduction in DPOAE, LCM, and EP, followed by recovery. However, many aspects of the results were different. Most significantly, the cochlear amplification observed in LCM could attain nearly full or even full recovery with ∼20 mV reduced EP (as shown in Fig. 8). Thus, as Mills et al. hypothesized, the cochlea has an ability to adjust to diminished operating condition. Furthermore, the cochlear amplifier and EP recovered with different time courses: cochlear amplification just started to recover after the EP was nearly fully recovered and stabilized. Using a Boltzmann model and the second harmonic of the LCM to estimate the transducer OP, we showed that this nonsimultaneous recovery of cochlear amplification happened along with a shift in the OP. These observations suggest that cochlear amplification is capable of adjusting to lower EP by optimizing the OP of the MET transducer current.

Author Contributions

Y.W. and E.F. conducted the experiments. Y.W. analyzed single-tone data and developed the model. E.F. analyzed two-tone data. E.S.O. designed the research and supervised the project. Y.W. applied mathematical tools, performed the research, and drafted the manuscript. All authors read and approved the final manuscript.

Editor: Sean Sun.