Abstract
Avibactam is a non-β-lactam β-lactamase inhibitor for treating complicated urinary tract and respiratory infections caused by multidrug-resistant bacterial pathogens, a serious public health threat. Despite its importance, the release mechanism of avibactam from the enzyme-inhibitor complex has been scarcely studied from first principles, considering the total protein environment. This information at the molecular level is essential for the rational design of new antibiotics and inhibitors. In this article, we addressed the release of avibactam from the complex CTX-M-15 by means of molecular dynamics simulations and quantum mechanics/molecular mechanics calculations. This study provides molecular information not available earlier, including exploration of the potential energy surfaces, characterization of the observed intermediate, and their critical points, as well. Our results show that unlike that observed in the acylation reaction, the residues Glu166 and Lys73 would be in their neutral forms. Release of avibactam follows a stepwise mechanism in which the first stage corresponds to the formation of a tetrahedral intermediate, whereas the second stage corresponds to the cleavage of the Ser70-C7 bond, mediated by Lys73, either directly or through Ser130.
Introduction
β-lactam antibiotics represent the most widely used class of antibacterial agents because of their good tolerability profiles and their high level of activity, especially in Gram-negative infections. These drugs act by inhibiting bacterial cell wall biosynthesis by targeting penicillin-binding proteins. To face these antimicrobials, bacteria have evolved to produce enzymes that break the amide bond within the β-lactam ring via a general base hydrolysis mechanism. The production of β-lactamase enzymes is the leading mode of bacterial resistance to β-lactam antibiotics. A successful strategy to face the resistance mechanisms has been to combine a β-lactam antibiotic with a β-lactamase inhibitor (1, 2, 3). This finding has led to the clinical introduction of inhibitors such as tazobactam, sulbactam, and clavulanic acid (4, 5, 6). These compounds form a stable acyl-enzyme intermediate with the catalytic serine, incapacitating the enzyme to react with the antibiotic, and in this way, it avoids its inactivation by the hydrolysis of the amide bond of the β-lactam ring. However, the emergence of inhibitor-resistant β-lactamases in the clinic has motivated the search for new β-lactamase inhibitors.
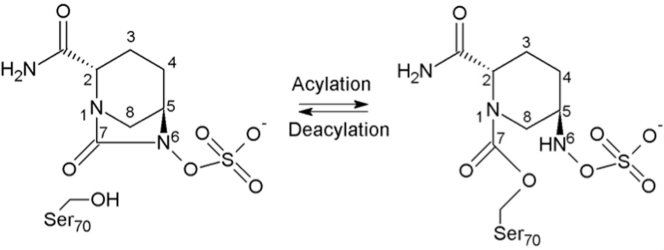
Avibactam is a diazabicyclooctane, non-β-lactam-based inhibitor, which inhibits class A, C, and some class D β-lactamases (7, 8, 9). Its structure has a bicycle consisting of a cyclic urea that was developed to enable efficient acylation by means of interactions with the residues in the active site. In 2015, the combination of avibactam and ceftazidime was approved by the Food and Drug Administration (9). A remarkable feature of avibactam is its unusual covalent reversible mechanism of inhibition with β-lactamases (Fig. 1). This mechanism is quite different from that of clinically used β-lactam-based β-lactamase inhibitors, with which the acyl-enzyme complex formation is practically irreversible, and the acyl-enzyme intermediate can decompose through hydrolysis resulting in the loss of the inhibitory molecule. In contrast, avibactam can be released from the enzyme via deacylation and ring closure, resulting in intact avibactam molecules that can now again acylate others or the same β-lactamases. One possible explanation is that the acyl-enzyme complex is resistant to attack by deacylation water, which could be due to having a nitrogen atom bonded to the carbonyl carbon altering its local environment.
Figure 1.
Scheme of avibactam-mediated reversible inhibition mechanism.
In a previous article (10), we reported the results of a theoretical study, including MD simulations and QM/MM calculations, on the inhibition of the class A β-lactamase CTX-M-15 by avibactam (i.e., acylation stage in the above scheme).
In contrast to the number of articles on the acylation of avibactam, only a few studies on the release of the acylated avibactam have been reported in the literature. In one of them, King et al. (11) addressed the underlying molecular details of avibactam inhibition performed by a kinetic and mutagenesis study on the class A enzyme CTX-M-15. On the other hand, Lahiri et al. (12) by means of ultra-high-resolution structure analysis provided insights into the mechanism of avibactam recyclization. Both studies postulate that Lys73 may potentially be the base responsible for the Ser130 activation, which afterward may deprotonate the N6 atom to allow the intramolecular attack on the C7 carbonyl carbon and the subsequent reforming of the N6-C7 bond.
However, despite the important contributions from the above references in the understanding of the avibactam recyclization mechanism, the chemical reaction from first principles has not been addressed so far. Therefore, there are certain issues that remain unclear and are a matter of discussion (13), namely, the way in which the reaction occurs (i.e., concerted or stepwise) and the role of the residues Ser130 and Lys73 in the protonation of the Ser70 O-γ and subsequent cleavage of the Ser70-C7 bond. To fill this gap of information, quantum chemical calculations that consider the total protein environment are required.
In this article, to shed light on the molecular events involved in the release (deacylation) of avibactam from the acyl-enzyme complex, we report the results of a combined molecular dynamics (MD) and hybrid quantum mechanics/molecular mechanics (QM/MM) study on the class A enzyme CTX-M-15. The approach allows having a clear picture of the reaction pathway from the analysis of the potential energy surface (PES), characterization of the critical points observed on it, and evaluation of the activation barriers, as well. To the best of our knowledge, this issue has not been addressed previously from a theoretical point of view in which authors consider the total protein ambient.
Methods
The methodology used has been reported in a previous article on the acylation of avibactam by CTX-M-15 (14, 15). Briefly, the initial structure of the complex enzyme inhibitor used for the exploration of the PES was taken at 65 ns from a 100-ns molecular dynamics (MD) simulation of the crystal structure of CTX-M-15 in complex with avibactam, determined at 1.1 Å (Protein Data Bank [PDB]: 4HBU) (12). The resulting structure from the simulation was solvated with a cubic box (80 × 90 × 90 Å3) of water molecules centered at the geometrical center of the protein-inhibitor complex. The final system contained 48,432 atoms, of which 44,460 atoms correspond to waters and the rest to protein, avibactam, and ion atoms. The MD simulations were performed with the NAMD program (16) using the CHARMM36 force field (17) and the TIP3P water model (18). Force field parameters were obtained from the CHARMM General Force Field utility.
The simulations were carried without constraints using the NPT ensemble with a time step of 2 fs, and periodic boundary conditions were applied. The temperature and pressure (1 atm) were maintained using NAMD Nosé-Hoover implementations (19). Long-range electrostatic effects were taken into account by the particle mesh Ewald summation method (20), whereas short-range interactions were calculated directly within a cutoff of 12 Å. A switch function starting at 10 Å and turning off at 12 Å was used for van der Waals interactions. Energy minimization of 400 steps was carried out using the conjugate gradients algorithm. Thereafter, MD simulations of 1 ns with 2-fs time steps at 300 K were performed to equilibrate the system. Production MD simulations of 100 ns and 2-fs time steps at 300 K were carried out without harmonic restrictions. During the simulation, all intramolecular motions involving hydrogen atoms were frozen using the SHAKE algorithm with a tolerance of 10−8. Snapshots were saved every 2 ps for a total of 50,000 structures. The VMD (21) was used for the trajectory analysis. The final MD structure was taken at 65 ns as a single representative configuration to model the reaction pathway.
The starting configuration was trimmed to a sphere of 30 Å, centered at the carbonyl carbon of avibactam, consisting of a mobile part of 25 Å (active site and surroundings), a buffer zone of 2 Å, and a reservoir of 3 Å. The system was partitioned into a QM region consisting of avibactam, Ser70, Glu166, Lys73, and Ser130 side chains using the link atom approach to the boundary atoms, whereas the MM region consisted of the rest of the system. Computations were carried out at B3LYP-D3/6-31+G(d,p) level of theory with the Q-Chem/CHARMM interface (22). The PES was explored in terms of the reaction coordinates defined in the next section, with steps of 0.1 Å.
The Q-Chem program was employed to carry out the PES exploration by a series of geometry optimizations of the mobile part of the system in the presence of harmonic restrains applied (RESDmodule) on the reaction coordinates defined in the next section. Each energy minimization was carried out with a gradient tolerance of 0.001 kcal/mol by the ABNR algorithm (23).
The QM subsystem was described at B3LYP-D3/6-31+G(d,p) (24) level of theory, whereas the CHARMM36 force field was used for the MM region, and the electrostatic embedding scheme was applied in the QM/MM treatment. Grimme corrections (25) were incorporated to include the effect of dispersive forces deficiently described by the density functional theory.
The transition state (TS) search was performed on a clusterized model including the inhibitor and the active-site residues. The level of theory is the same mentioned above, and the respective characterization was done with Jaguar (26). It uses a simple quasi-Newton method that searches for the TS nearest to the initial geometry. The method maximizes the energy along the lowest-frequency eigenvector of the Hessian and minimizes along all other coordinates. The procedure is well defined and straightforward when the Hessian has exactly one imaginary frequency, indicating that the structure is near a saddle point (26). Afterward, to check if the TS is the expected TS for the reaction of interest, intrinsic reaction coordinate (IRC) calculations were performed. IRC calculations start at a TS and move downhill in energy along the reaction path toward a minimum of the PES, calculating a series of points in which all geometric variables orthogonal to the path are optimized (26). Natural bond orbital (NBO) analysis was performed using NBO6 (27) as implemented in Jaguar. Metadynamics simulations were carried out with Desmond 5.5 (28).
Results and Discussion
MD simulations were performed considering two forms of the complex enzyme inhibitor, namely, the charged and neutral forms. The first one considers the Glu166 and Lys73 residues in their ionic forms, whereas the other one considers these residues in their neutral form. This procedure is necessary because the protonation states of these residues have not been clearly established; thus, different protonation states have been proposed in the literature (11, 29).
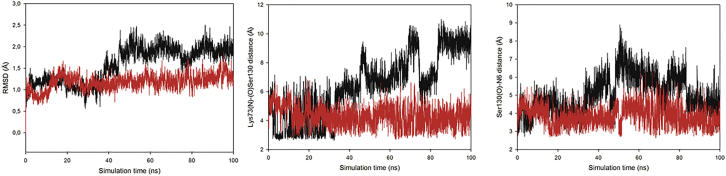
The obtained plot of root mean-square deviation (RMSD) for the active site is shown in Fig. 2. The plot shows a very stable behavior along the simulation for the neutral form compared to that observed for the ionic form. The higher values of the RMSD values for the ionic form is explained by the fact that under this form, Lys73 interacts preferentially with Glu166 by means of the formation of an ionic pair in detriment to the interaction with Ser130. This entails higher conformational freedom for Ser130 which in turn explains the observed trend in the RMSD values. This finding is in agreement with neutron and x-ray crystallography results (12, 13, 30) showing that the conformation of Lys73 appears to be coupled to the protonation state of Glu166. When Glu166 is charged, Lys73 is also charged and interacts mainly with Glu166 and Ser70; when Glu166 is protonated, Lys73 is in its neutral form and moves away from Glu166, favoring the interaction by hydrogen bonding with Ser130 and locating it more firmly at the right distance to abstract the proton from the N6 atom of avibactam. The protonation states of other residues are considered in their standard form; thus, for example, the histidine tautomers are considered in the HID form.
Figure 2.
RMSD plot for the active site (left). Plot of distance between Lys73 and Ser130 (center; black: residues Glu166 and Ly73 in their ionic form; red: residues in their neutral form). Plot of distance between Ser130 and the N6 atom (right; black: ionic form; red: neutral form). To see this figure in color, go online.
The interaction between avibactam and the residues Lys73 and Ser130 has been reported to play an important role in the recyclization of avibactam (11, 29). In consequence, we monitored the distances between them and between Ser130 and the N6 atom of avibactam (Fig. 2). A very stable behavior is observed for the neutral form of the complex compared to that of the ionic form. In consequence, we postulate that for the recyclization of avibactam to occur, these two residues should be in their neutral form.
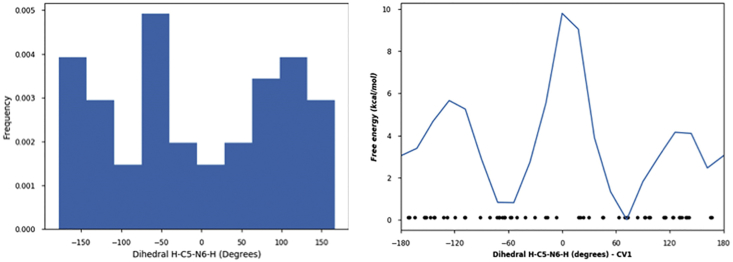
During the dynamics, the orientation of the N6 hydrogen bond oscillates among different possible directions according to the value of the dihedral angle H-C5-N6-H (Fig. 3). When this angle takes positive values (∼80% of the time), the N6-H points to outside of the active site. This orientation does not lead to any reaction. On the other hand, when the dihedral takes negative values (∼20% of the time), the N6 hydrogen bond points inside the active site, allowing interaction with the key residue Ser130 and, in this way, favors the deprotonation of the N6 atom via the proton shuttle toward Lys73 through Ser130. For some molecules, such as proteins, there could be many minima on the energy surface as a result of conformational transitions (31), and the global minimal energy conformation may not be the active conformation. Moreover, the minimal energy states could be separated by high potential barriers. In situations like this, standard MD may not be able to cross the barrier between the conformations sufficiently often to ensure that each conformation is sampled according to the correct statistical weight. In metadynamics, a history-dependent potential encourages the system to explore new values of the collective variables, and the accumulation of potential allows the system to cross potential barriers much more quickly than would occur in standard dynamics (32). For this reason, metadynamics simulations, using the NPT ensemble, were carried out to evaluate the torsional free-energy barrier separating both conformations. In the simulation, we defined the dihedral angle H-C5-N6-H as a collective variable, and a repulsive Gaussian potential with a height of 0.03 kcal/mol and width of 5.0° was used. The result shows that the minimal energy conformations are separated by a relatively high torsional barrier of ∼9.8 kcal/mol (Fig. 3).
Figure 3.
Histogram of the dihedral angle H-C5-N6-H along the 100-ns MD simulation (left). Calculated torsional free-energy barrier for interconversion between the minimal energy state conformations, with those having positive values and negative values of the dihedral angle H-C5-N6-H (right). To see this figure in color, go online.
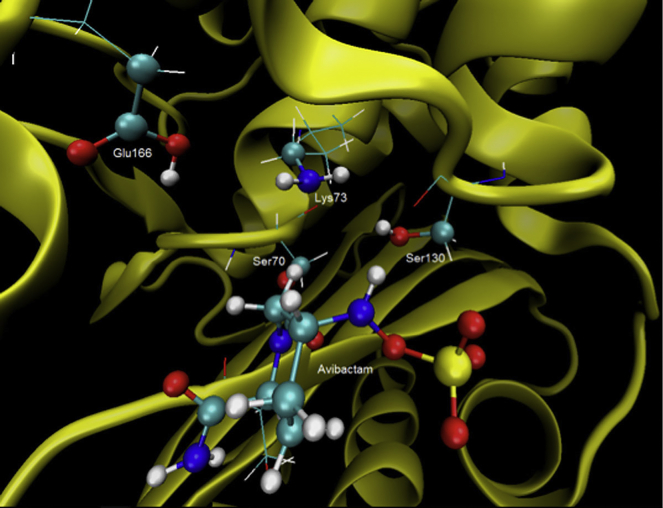
For the exploration PES we took a structure with the right orientation for the expected reaction (i.e., 65 ns). The structure of the active site at this time is shown in Fig. 4. We considered only the neutral form of the complex enzyme-avibactam in light of the MD results and empirical-evidence-based neutron and high-resolution x-ray crystallography showing that during the acylation, the residues Glu166 and Lys73 should be in their ionic form in contrast to that observed during the deacylation stage in which these residues should be in their neutral form (12, 13, 30). Alternative mechanisms for the deacylation of avibactam, considering a charged Glu166 as the base to deprotonate a conserved water molecule, were not considered in light of the results of King et al. (11) for CTX-M-15 in which they report that the E166Q decarbamylation rate is virtually identical to the wild-type rate, suggesting that E166 is not required for Ser70 protonation.
Figure 4.
Structure of the active site at 65 ns. To see this figure in color, go online.
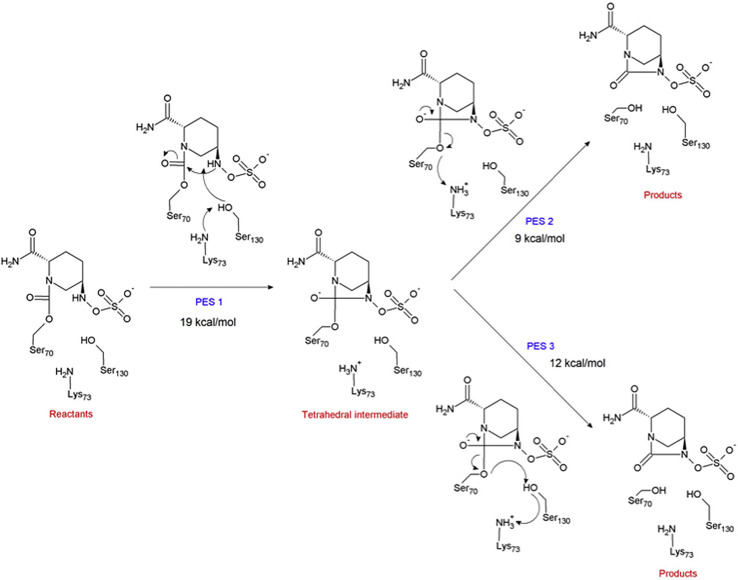
Moreover, the simulations suggest (in base of the positions of Lys73, Ser130, Ser70, and avibactam, the respective distances among them, and the acid-base properties of the residues) that the mechanism of release of avibactam (recyclization) follows a two-stage mechanism in which the first stage corresponds to the formation of a tetrahedral intermediate, whereas the second stage corresponds to the cleavage of the Ser70-C7 bond, mediated by Lys73, either directly or through Ser130.
The first stage is studied by exploring the PES, PES-1, accounting for the deprotonation of the N6 atom by a proton shuttle toward Lys73 through Ser130 and the concomitant nucleophilic attack of the N6 atom on the C7 carbon. Conversely, the second stage is studied by means of the exploration of two PESs, PES-2 and PES-3, accounting for the release of intact avibactam and recovery of the enzyme.
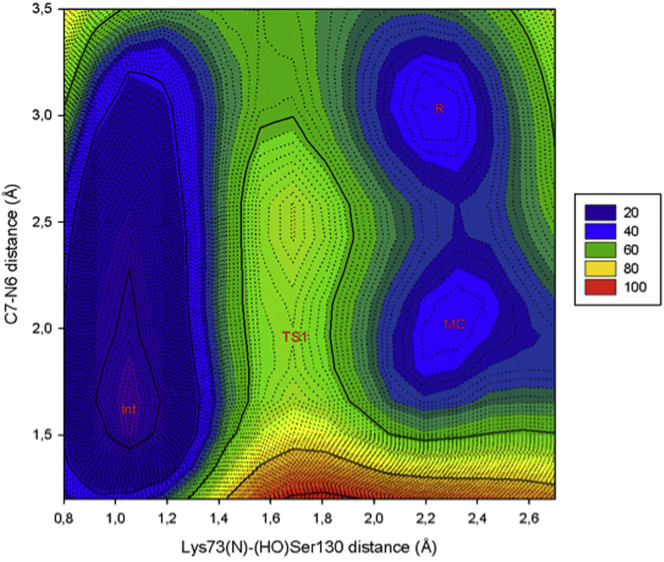
The reaction coordinates used to explore the PES-1 are as follows: R1 is defined as the distance between the hydroxyl proton of Ser130 and the nitrogen atom of Lys73, whereas R2 is defined as the distance between the atom N6 and the C7 atom of avibactam.
The obtained PES-1 (Fig. 5) shows four critical points corresponding to the reactant state (R), Michaelis complex (MC), transition state (TS1), and the tetrahedral intermediate. The topology of the PES suggests the following succession of events along the reaction path: the R by means of a conformational rearrangement reaches the MC. This rearrangement involves the inversion of the pyramidal structure of the N6 atom to dispose the lone pair of the N6 atom pointing to the carbonyl carbon in an angle N6-C7-H of 104.8°, which is in agreement with the Bürgi-Dunitz angle for nucleophilic attacks on a carbonyl carbon. The inversion barrier observed in the PES is 3 kcal/mol, which is in agreement with the inversion barrier of ammonia of ∼5 kcal/mol (33). From the MC, the reaction continues with the proton abstraction from the N6 atom by means of a proton shuttle mechanism to Lys73 (via Ser130) to reach a TS. To characterize the TS, corresponding to the saddle point observed in the PES-1, and to show that it leads to the expected tetrahedral intermediate, we took a representative structure of the saddle point zone considering only the residues in the QM region. Then, a TS search was carried out according to the methodology implemented in Jaguar by using the Poisson-Boltzmann solvation method and B3LYP-D3/6-31+G(d,p) level of theory.
Figure 5.
Two-dimensional view of the PES-1. To see this figure in color, go online.
To save computational time, serines were replaced by methanol, lysine by methylammonium, and water molecules were not considered. The search led to the TS1, whose structure is shown in Fig. S1. This TS was characterized by frequency calculations and IRC calculations; the results show one imaginary frequency (ν = 1095 cm−1; intensity = 4466) corresponding to the stretching of the hydrogen bonds involved in the proton shuttle mentioned above and also corresponding to the stretching of the N6-C7 distance. Animations of the imaginary frequency and the IRC calculations are recorded in Videos S1 and S2. The calculated activation barrier for this event is 19 kcal/mol.
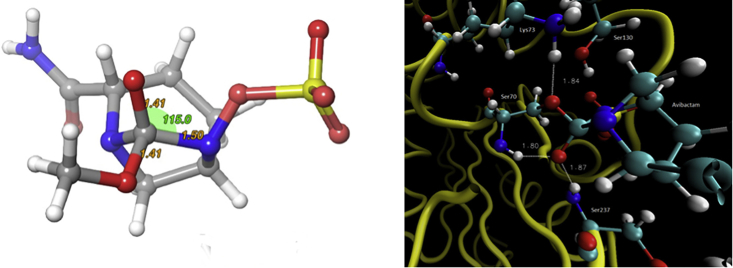
From the TS, the reaction continues until the proton shuttle toward Lys73 is completed (i.e., the N6 atom is deprotonated and Lys73 takes its ionic form). As a result of the event, the tetrahedral intermediate formed (Fig. 6) was stabilized in 24-kcal/mol respect to the R. The stability of the intermediate can be explained by the two hydrogen bonds it forms with the backbone amide groups of Ser237 and Ser70, which is in agreement with literature (34, 35). In this study, the N-H amide group of Ser237, located at 1.8 Å, and the N-H amide group of Ser70, located at 1.9 Å, interact with the oxyanion (Figs. 6 and S2), stabilizing the negative charge on the oxygen atom.
Figure 6.
Structure of the tetrahedral intermediate (left). Structure of the tetrahedral intermediate in the active site and main distances (right). To see this figure in color, go online.
The intermediate was characterized with NBO calculations; the results are summarized in Tables 1 and 2. The values of the atomic charge and bond order confirm the formation of a tetrahedral intermediate; thus, the carbonyl oxygen OC shows an atomic charge of −0.98, which is coherent with the formation of an oxyanion; accordingly, the value of the bond order of 1.26 is consistent with an elongated double C-O bond. Moreover, a rather weak bond order between hydroxyl oxygen of Ser70 and the C7 atom is also observed. All the calculated frequencies of the intermediate have real values, with the exception of some spurious imaginary frequencies, which is a consequence of the clusterized model used for the frequency calculation (Table S1).
Table 1.
Wiberg Bond Index on Key Atoms of the Tetrahedral Intermediate
| Atom | OC | C7 | N6 | OS |
|---|---|---|---|---|
| OC | – | 1.26 | – | – |
| C7 | 1.26 | – | 0.88 | 0.78 |
| N6 | – | 0.88 | – | – |
| OS | – | 0.78 | – | – |
Table 2.
NBO Atomic Charges on Key Atoms
| Atom | NBO Atomic Charge |
|---|---|
| OC | −0.98 |
| C7 | 0.87 |
| N6 | −0.27 |
| OS | −0.68 |
Once the tetrahedral intermediate is formed, the reaction continues with the protonation of the hydroxyl oxygen of Ser70, entailing the cleavage of the Ser70-C7 bond and the release of the intact avibactam. There are two possible residues able to play the role of acid species. On one hand, the residue Lys73 that is in its ionic form (as a consequence of the tetrahedral intermediate formation) may protonate directly the hydroxyl oxygen of Ser70. In the second alternative, Lys73 carries out the protonation through Ser130 via a proton shuttle. We investigate both possibilities by the exploration of the respective PESs.
For the first case, PES-2, we define the following symmetrical reaction coordinates. The coordinate R1, defined as the distance between the hydroxyl oxygen of Ser70 and the C7 carbonyl carbon, accounts for the cleavage of the Ser70–C7 bond, whereas the second coordinate R2 is defined as the distance between the hydroxyl oxygen of Ser70 and the proton of the ammonium group of Lys73. For the second case, PES-3, the reaction coordinates are R3, which is defined in the same way that R1 of the former case was, and the other reaction coordinate, R4, is defined as the distance between the oxygen of Ser70 and the hydroxyl proton of Ser130. This coordinate accounts for the proton shuttle from Lys73 toward Ser70 through Ser130.
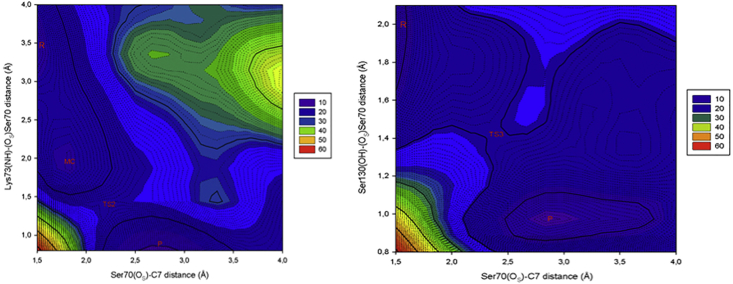
PES-2 (Fig. 7) shows that the event follows a synchronous concerted mechanism in which both reaction coordinates vary almost symmetrically, starting from the R (corresponding to the tetrahedral intermediate), which is located at coordinates R1 ≈ 1.5 Å and R2 ≈ 3.0 Å. From this point, approaching between Lys73 and the Ser70 O-γ is observed, leading to the reactive complex located at coordinates R1 ≈ 2.0 Å and R2 ≈ 2.0 Å. From here, the reaction continues with the elongation of the Ser70-C7 bond (as a consequence of the protonation of the Ser70 O-γ in progress) until the liberation of avibactam is completed at coordinates R1 ≈ 2.7 Å and R2 ≈ 0.9 Å. These values account for the protonation of hydroxyl oxygen of Ser70 by Lys73 and the release of avibactam from the complex enzyme inhibitor. In the course of the reaction, a saddle point at coordinates R1 ≈ 2.2 Å and R2 ≈ 1.6 Å was observed. The respective transition state, TS2, is characterized with only one imaginary frequency (ν = 1452 cm−1; intensity = 3524) corresponding to the stretching of the bond N-H of Lys 73. The corresponding activation barrier is ∼9 kcal/mol. The structure of the transition is shown in Fig. S3. Animations of the imaginary frequency and the IRC calculations are recorded in Videos S3 and S4.
Figure 7.
Two-dimensional view of PES-2 (left). Two-dimensional view of PES-3 (right). To see this figure in color, go online.
On the other hand, PES-3 shows three critical points corresponding to the R located at R1 ≈ 1.5 Å and R2 ≈ 1.8 Å, a TS at R1 ≈ 2.4 Å and R2 ≈ 1.4 Å, and the product at R1 ≈ 3.0 Å and R2 ≈ 0.9 Å (Fig. 7). The activation barrier for this alternative reaction path is ∼12 kcal/mol. The observed transition state, TS3, is characterized with only one imaginary frequency (ν = 1528 cm−1; intensity = 4113) corresponding to the symmetric bond stretching of Ser130 (O-H) and Lys73(N-H) bonds, accounting for the protonation of the Ser70 O-γ and the cleavage of the Ser70-C7 bond. The structure of this TS is shown in Fig. S4. Animations of the imaginary frequency and the IRC calculations are recorded in Videos S5 and S6.
In closing, a reaction mechanism scheme for the release (deacylation) of avibactam from the class A CTX-M-15 enzyme is shown in Fig. 8. This mechanism is in agreement with that proposed by King et al. (11) from a kinetic study of key active-site mutants. The formation of the tetrahedral intermediate is the rate-limiting stage with an activation barrier of 19 (kcal/mol). This value is in agreement with the value of 22.6 kcal/mol, calculated by the TS theory from the experimental value of the rate constant of 1.5 × 10−4 s−1 (11).
Figure 8.
Reaction scheme for the release of avibactam from the class A CTX-M-15 β-lactamase. To see this figure in color, go online.
Conclusions
The results of this study allow us to conclude that the release (deacylation) of avibactam from the enzyme-inhibitor complex requires the residues Glu166 and Lys73 to be in their neutral form, which is in contrast to that observed in the mechanism of acylation of avibactam (Fig. 1) for which these residues should be in their ionic form, which is in agreement with the results reported by Lahiri et al. (12). The release of avibactam follows a stepwise mechanism in which the first stage corresponds to the formation of a tetrahedral intermediate, whereas the second stage corresponds to the cleavage of the Ser70-C7 bond, mediated by Lys73, either directly or through Ser130. The formation of the tetrahedral intermediate is a consequence of the N6 deprotonation by a proton shuttle toward Lys73 through Ser130, as well as the concomitant nucleophilic attack of the N6 atom on the C7 carbon. The activation barrier calculated for the first stage is 19 kcal/mol, corresponding to the rate-limiting stage. The final step, cleavage of the Ser70-C7 bond, is triggered by the protonation of the hydroxyl oxygen of Ser70 by Lys73, either directly or through Ser130. The calculated activation barriers for both cases are 9 and 12 kcal/mol, respectively. Once avibactam is released, Glu166 and Lys73 are in close proximity, making possible the proton transfer between them to acquire their ionic form, closing in this way the acylation/deacylation cycle of avibactam. The results reported herein would be of interest for the development of novel antibiotics or inhibitors.
Author Contributions
I.L. performed the MD simulations, QM/MM calculations, and result analysis. E.J.D. performed the IRC characterization of the TSs and analysis result, as well as wrote the manuscript.
Acknowledgments
The authors acknowledge Fondecyt for financial support (grant 1170091). I.L. acknowledges Conicyt for doctoral fellowship 21180377.
Editor: Alan Grossfield.
Footnotes
Supporting Material can be found online at https://doi.org/10.1016/j.bpj.2019.03.027.
Supporting Material
References
- 1.Aminov R.I. A brief history of the antibiotic era: lessons learned and challenges for the future. Front. Microbiol. 2010;1:134. doi: 10.3389/fmicb.2010.00134. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Bachovchin D.A., Cravatt B.F. The pharmacological landscape and therapeutic potential of serine hydrolases. Nat. Rev. Drug Discov. 2012;11:52–68. doi: 10.1038/nrd3620. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Bebrone C., Lassaux P., Galleni M. Current challenges in antimicrobial chemotherapy: focus on ß-lactamase inhibition. Drugs. 2010;70:651–679. doi: 10.2165/11318430-000000000-00000. [DOI] [PubMed] [Google Scholar]
- 4.Reading C., Cole M. Clavulanic acid: a beta-lactamase-inhiting beta-lactam from Streptomyces clavuligerus. Antimicrob. Agents Chemother. 1977;11:852–857. doi: 10.1128/aac.11.5.852. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Bonomo R.A., Rudin S.A., Shlaes D.M. Tazobactam is a potent inactivator of selected inhibitor-resistant class A β-lactamases. FEMS Microbiol. Lett. 1997;148:59–62. doi: 10.1111/j.1574-6968.1997.tb10267.x. [DOI] [PubMed] [Google Scholar]
- 6.Akova M. Sulbactam-containing β-lactamase inhibitor combinations. Clin. Microbiol. Infect. 2008;14(Suppl 1):185–188. doi: 10.1111/j.1469-0691.2007.01847.x. [DOI] [PubMed] [Google Scholar]
- 7.Ehmann D.E., Jahić H., Fisher S.L. Avibactam is a covalent, reversible, non-β-lactam β-lactamase inhibitor. Proc. Natl. Acad. Sci. USA. 2012;109:11663–11668. doi: 10.1073/pnas.1205073109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Winkler M.L., Papp-Wallace K.M., Bonomo R.A. Avibactam and inhibitor-resistant SHV β-lactamases. Antimicrob. Agents Chemother. 2015;59:3700–3709. doi: 10.1128/AAC.04405-14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Krishnan N.P., Nguyen N.Q., van den Akker F. Inhibition of Klebsiella β-lactamases (SHV-1 and KPC-2) by avibactam: a structural study. PLoS One. 2015;10:e0136813. doi: 10.1371/journal.pone.0136813. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Lizana I., Delgado E.J. Theoretical insights on the inhibition mechanism of a class A serine hydrolase by avibactam. J. Comput. Chem. 2018;39:1943–1948. doi: 10.1002/jcc.25340. [DOI] [PubMed] [Google Scholar]
- 11.King D.T., King A.M., Strynadka N.C. Molecular mechanism of avibactam-mediated β-lactamase inhibition. ACS Infect. Dis. 2015;1:175–184. doi: 10.1021/acsinfecdis.5b00007. [DOI] [PubMed] [Google Scholar]
- 12.Lahiri S.D., Mangani S., Docquier J.D. Structural insight into potent broad-spectrum inhibition with reversible recyclization mechanism: avibactam in complex with CTX-M-15 and Pseudomonas aeruginosa AmpC β-lactamases. Antimicrob. Agents Chemother. 2013;57:2496–2505. doi: 10.1128/AAC.02247-12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Vandavasi V.G., Langan P.S., Coates L. Active-site protonation states in an acyl-enzyme intermediate of a class A β-lactamase with a monobactam substrate. Antimicrob. Agents Chemother. 2016;61 doi: 10.1128/AAC.01636-16. e01636-16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Lizana I., Delgado E.J. Theoretical insights on the inhibition mechanism of a class A serine hydrolase by avibactam. J. Comput. Chem. 2018;39:1943–1948. doi: 10.1002/jcc.25340. [DOI] [PubMed] [Google Scholar]
- 15.Lizana I., Delgado E.J. A QM/MM study on the enzymatic inactivation of cefotaxime. J. Mol. Model. 2017;23:209. doi: 10.1007/s00894-017-3379-8. [DOI] [PubMed] [Google Scholar]
- 16.Phillips J.C., Braun R., Schulten K. Scalable molecular dynamics with NAMD. J. Comput. Chem. 2005;26:1781–1802. doi: 10.1002/jcc.20289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Best R.B., Zhu X., Mackerell A.D., Jr. Optimization of the additive CHARMM all-atom protein force field targeting improved sampling of the backbone φ, ψ and side-chain χ(1) and χ(2) dihedral angles. J. Chem. Theory Comput. 2012;8:3257–3273. doi: 10.1021/ct300400x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Jorgensen W.L., Chandrasekhar J., Klein M.L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983;79:926–935. [Google Scholar]
- 19.Nosé S. A unified formulation of the constant temperature molecular dynamics methods. J. Chem. Phys. 1984;81:511–519. [Google Scholar]
- 20.Darden T., York D., Pedersen L. Particle mesh Ewald: an N⋅log(N) method for Ewald sums in large systems. J. Chem. Phys. 1993;98:10089–10092. [Google Scholar]
- 21.Humphrey W., Dalke A., Schulten K. VMD: visual molecular dynamics. J. Mol. Graph. 1996;14:33–38, 27–28.. doi: 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]
- 22.Shao Y., Gan Z., Head-Gordon M. Advances in molecular quantum chemistry contained in the Q-Chem 4 program package. Mol. Phys. 2015;113:184–215. [Google Scholar]
- 23.Brooks B.R., Bruccoleri R.E., Karplus M. CHARMM: a program for macromolecular energy, minimization, and dynamics calculations. J. Comput. Chem. 1983;4:187–217. [Google Scholar]
- 24.Becke A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993;98:5648–5652. [Google Scholar]
- 25.Grimme S., Ehrlich S., Goerigk L. Effect of the damping function in dispersion corrected density functional theory. J. Comput. Chem. 2011;32:1456–1465. doi: 10.1002/jcc.21759. [DOI] [PubMed] [Google Scholar]
- 26.Bochevarov A.D., Harder E., Friesner R.A. Jaguar: a high-performance quantum chemistry software program with strengths in life and materials sciences. Int. J. Quantum Chem. 2013;113:2110–2142. [Google Scholar]
- 27.Glendening E.D., Landis C.R., Weinhold F. NBO 6.0: natural bond orbital analysis program. J. Comput. Chem. 2013;34:1429–1437. doi: 10.1002/jcc.23266. [DOI] [PubMed] [Google Scholar]
- 28.Bowers K.J., Chow E., Shaw D.E. ACM; 2006. Scalable algorithms for molecular dynamics simulations on commodity clusters. In Proceedings of the 2006 ACM/IEEE Conference on Supercomputing; p. 746. [Google Scholar]
- 29.Choi H., Paton R.S., Schofield C.J. Investigations on recyclisation and hydrolysis in avibactam mediated serine β-lactamase inhibition. Org. Biomol. Chem. 2016;14:4116–4128. doi: 10.1039/c6ob00353b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Vandavasi V.G., Weiss K.L., Coates L. Exploring the mechanism of β-lactam ring protonation in the class A β-lactamase acylation mechanism using neutron and X-ray crystallography. J. Med. Chem. 2016;59:474–479. doi: 10.1021/acs.jmedchem.5b01215. [DOI] [PubMed] [Google Scholar]
- 31.Singharoy A., Chipot C. Methodology for the simulation of molecular motors at different scales. J. Phys. Chem. B. 2017;121:3502–3514. doi: 10.1021/acs.jpcb.6b09350. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Leach A.R. Second Edition. Pearson; London, United Kingdom: 2001. Molecular Modelling, Principles and Applications; p. 458. [Google Scholar]
- 33.Rauk A., Allen L.C., Clementi E. Electronic structure and inversion barrier of ammonia. J. Chem. Phys. 1970;52:4133–4144. [Google Scholar]
- 34.Topf M., Várnai P., Richards W.G. Ab initio QM/MM dynamics simulation of the tetrahedral intermediate of serine proteases: insights into the active site hydrogen-bonding network. J. Am. Chem. Soc. 2002;124:14780–14788. doi: 10.1021/ja026219q. [DOI] [PubMed] [Google Scholar]
- 35.Howe N., Rogers L., Malthouse J.P. Oxyanion and tetrahedral intermediate stabilisation by subtilisin: detection of a new tetrahedral adduct. Biochim. Biophys. Acta. 2009;1794:1251–1258. doi: 10.1016/j.bbapap.2009.04.007. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.