Abstract
Advancements in item response theory (IRT) have led to models for dual dependence, which control for cluster and method effects during a psychometric analysis. Currently, however, this class of models does not include one that controls for when the method effects stem from two method sources in which one source functions differently across the aspects of another source (i.e., a nested method–source interaction). For this study, then, a Bayesian IRT model is proposed, one that accounts for such interaction among method sources while controlling for the clustering of individuals within the sample. The proposed model accomplishes these tasks by specifying a multilevel trifactor structure for the latent trait space. Details of simulations are also reported. These simulations demonstrate that this model can identify when item response data represent a multilevel trifactor structure, and it does so in data from samples as small as 250 cases nested within 50 clusters. Additionally, the simulations show that misleading estimates for the item discriminations could arise when the trifactor structure reflected in the data is not correctly accounted for. The utility of the model is also illustrated through the analysis of empirical data.
Keywords: Bayesian IRT, multilevel IRT, multidimensional IRT, trifactor structure, nested method–source interaction
Educational and psychological studies are often conducted on a smaller scale (e.g., samples consisting of fewer than 500 individuals). Yet these studies often employ sampling and measurement processes that could lead to local dependence in the data if these processes are ignored during an item response analysis. More specifically, the sampling process often entails selecting individuals nested within clusters, leading to cluster effects, and if these effects are discounted, issues related to local person dependence could arise. The measurement process often includes multiple method sources (e.g., subsets of items sharing common characteristics), and if these sources are ignored, issues related to local item dependence could arise. To complicate matters, these method sources could have a dependency in which one method source functions differently across the various aspects of another method source.
Establishing the psychometric properties of data gathered under these conditions could pose a challenge because the sources that lead to both forms of local dependence must be accounted for during an analysis. Such data gathering conditions were why item response theory (IRT) models that simultaneously account for these sources have emerged (e.g., De Jong, Steenkamp, & Fox, 2007; Fujimoto, 2018; Jiao, Kamata, & Xie, 2016; Jiao, Kamata, Wang, & Jin, 2012), which have been referred to as models for dual dependence (Jiao et al., 2012). These models take a multilevel multidimensional approach to account for factors that are related to both forms of local dependence, with the multilevel aspect accounting for the clustering of individuals within the sample and the multidimensional aspect accounting for the method sources. Most of these dual-dependent IRT models, however, have not been demonstrated through simulations to be suitable for sample sizes smaller than 500. Additionally, other than the multilevel cross-classified model (Jiao et al., 2012), these models only account for one method source. Although the cross-classified model accounts for two method sources, it does so by assuming that the effect of one method source is independent of the other method source. When multiple method sources are present, with the effect of one method source dependent on another method source, the multidimensional component of the structure reflected in the data may have a trifactor form (Rijmen, 2011; Segall, 2001).
Currently, the ways in which the estimates for the psychometric properties of the data are affected when dependent method sources are treated as independent have not been investigated. The ramifications of ignoring method sources in general, however, are well known. Research has shown that ignoring method sources could lead to inaccurate person and item parameter estimates and inflated measurement reliabilities (W.-H. Chen & Thissen, 1997; Jiao et al., 2012; Jiao, Wang, & Kamata, 2005; Jiao & Zhang, 2015; Wainer, Bradlow, & Wang, 2007; Wilson & Adams, 1995). It is possible, then, that incorrectly accounting for dependent method sources could also have an impact on the estimates of the psychometric properties. In addition to these consequences, incorrectly accounting for dependent method sources could have ramifications on the validity in the use and interpretation of the dimensional estimates (or scores), and more specifically, the internal structural aspect of construct validity as outlined in Standards for Educational and Psychological Testing (American Educational Research Association, American Psychological Association, & National Council on Measurement in Education, 2014). When the dimensional structure of the latent trait space is more accurately depicted, the substantively relevant and irrelevant variances represented in the item responses are more effectively separated (F. F. Chen, West, & Sousa, 2006). This separation would, in turn, mean that the estimates for the individuals’ positions on the dimensions of substantive interest represent only what they are intended to represent, leading to more valid estimates.
An IRT model that assumes a trifactor dimensional structure for the latent trait space has been proposed outside of the dual-dependent modeling context (Segall, 2001), which could be appropriate for data reflecting dependent method sources. This model, however, does not include a multilevel component and thus does not control for cluster effects. One drawback of ignoring cluster effects during a psychometric analysis is that doing so could also lead to inaccurate parameter estimates and inflated measurement reliability, in addition to overstating the precision in the parameter estimates (Cochran, 1977; Jiao et al., 2012; Raudenbush & Bryk, 2002). Another drawback of ignoring cluster effects is that the amount of variance that exists at the cluster level is not assessed. This amount could be of interest because the proportion of variance at the cluster level could determine whether to pursue investigating factors that predict the cluster units’ role in the item responses (e.g., Fox, 2005; Fox & Glas, 2001; Kamata, 2001; Raudenbush, Johnson, & Sampson, 2003). In addition to not controlling for cluster effects, this model has only been shown to work with sample sizes of at least 3,000 and was devised for dichotomously scored data.
As reviewed, ignoring the cluster and method effects during an item response analysis has ramifications on the estimates for the psychometric properties of the data, and these consequences occur regardless of the sample size and the type of data (i.e., dichotomously or polytomously scored). A more flexible trifactor IRT model, then, is desirable, which is the main focus of this article. The proposed model is one that can simultaneously control for cluster effects and dependent method effects and is suitable for different types and sizes of data. Before proceeding to the presentation of this model, an empirical example is provided to show when such a model could be needed. This empirical example is also used to review possible competing multidimensional structures that could be used to account for multiple method sources.
Empirical Context
The sampling and measurement processes used to gather the acculturative family distancing (AFD) data (Hwang, Wood, & Fujimoto, 2010) provide a context for when an IRT model based on a multilevel trifactor structure could be needed. The subset of the data used in this article are the responses to the 16 rating items in the AFD instrument that measure communication breakdown (CB) among immigrant parents and their U.S.-born children because of differential rate of acculturation. The measurement process that contributes to the trifactor component of the data structure is described first. Then the sampling process that leads to the multilevel component of the data structure is described.
The measurement process used to gather the AFD data included two method sources, which were embedded in the rating instrument. One method source was the polarity in the wording of the items (i.e., the polarity method source), with 10 items phrased in the positive (e.g., “I am able to communicate . . .”) and the remaining items phrased in the negative (e.g., “Although I can get my basic points across, it is hard for me to talk . . .”). The other method source was whether the respondents or the respondents’ family members were the subjects of the items (i.e., the subject-focus method source). In the above items that served as examples for the polarity method source, the respondents (i.e., “I”) were the subjects of the items. Another set of items focused on the respondents’ family members (e.g., “My parents can communicate . . .” when the respondents were the children).
At first glance, these method sources appear to be fully crossed. That is, the items appear to fall into one of the method–source combinations because every item reflects one aspect of each method source. It may be the case, however, that the subject-focus method source functions differently depending on whether the items are positively or negatively phrased. This can occur because of self-attribution bias, which suggests that people are more likely to attribute success to themselves and failures to other factors (Zuckerman, 1979). From this perspective, the “I” aspect of the subject-focus method source could have a different conceptualization depending on the polarity of the items. The positively phrased “I” items should be more favorable to the respondents because these items inquire about their role in promoting communication in their families (which could be viewed as a success). The negatively worded “I” items, conversely, should be less favorable to the respondents because these items focus on the respondents’ role that lead to a breakdown in communication among family members (which could be viewed as a failure). The conceptualization of the “My” aspect of the subject-focus method source should also have a dependency on the polarity of the items. If the subject-focus method source is being processed differently as a function of whether the items are positively or negatively worded, then there should be two separate conceptualizations of this method source, one specific to each polarity. This, in turn, would suggest that the subject-focus method source is nested within the polarity method source.
The nesting of these two method sources could be accounted for by specifying a trifactor structure for the dimensions within the person level of the latent trait space (where for this study, the item responses [Level 1] are viewed as nested within persons [Level 2], which are further nested within cluster units [Level 3]). More specifically, a trifactor structure is composed of three tiers of nested dimensions at Level 2, with all dimensions orthogonal to each other (see Figure 1a for a trifactor representation of the AFD data, with the Level 3 portion of the data structure omitted for ease of viewing). The dimension in the first tier is the primary dimension (the largest circle in the figure) and is usually the dimension of substantive interest. In the AFD data, this dimension represents CB and all items discriminate on it. The dimensions in the second tier represent the polarity method source (with these secondary dimensions located immediately above the items in the figure), and each item discriminates on only one of these secondary dimensions. The third tier of the trifactor structure is composed of four dimensions (with the tertiary dimensions displayed below the items in the figure). Each pair of tertiary dimensions nested within a secondary dimension represents the “I” and “My” aspects of the subject-focus method source that are specific to the polarity of the items that the secondary dimension represents. Because of this nesting, each item can only discriminate on one of the pair of tertiary dimensions nested under the secondary dimension on which the item discriminates. Although the dimensions representing the method sources are assumed to be orthogonal to each other, the nesting of tertiary dimensions indicates that a dependency exists between the method sources. That is, the nesting signifies that the subject-focus method source functions differently depending on the polarity of the items, which is a type of interaction. Thus, this nesting of method sources is referred to hereafter as a nested method–source interaction.
Figure 1.
Three possible structures for the Level 2 portion of the latent trait space to represent the acculturative family distancing (AFD) data: (a) a trifactor structure, which includes three tiers of nested dimensions; (b) a cross-classified structure, which includes two tiers of nested dimensions; and (c) a bifactor structure, which also includes two tiers of nested dimensions. “Dim” represents dimension. “Primary” represents a primary dimension. “Secondary” represents a secondary dimension. “Tertiary” represents a tertiary dimension. “Pos” and “Neg” represent the positive and negative aspects of the polarity method source. “I” and “My” represent the two aspects of the subject-focus method source. The items displayed in the figure have been rearranged for presentation purposes and these items are not ordered as they appear in the AFD rating scale. The Level 3 dimension that represents the family effect in the Level 2 primary dimension is not included in each structure.
Regarding the multilevel component of the data structure, the 317 respondents who contributed to the data were nested within 123 families. Thus, the Level 3 portion of the latent trait space includes one dimension that accounts for the cluster effect (or family effect) in the Level 2 primary dimension, and all items additionally discriminate on this Level 3 dimension. Only one dimension is assumed at this level because dual-dependent IRT models usually assess the cluster effect in only the Level 2 dimension that is of substantive interest (e.g., Jiao et al., 2012).
If a nested method–source interaction is not taking place, then the method sources could be represented by two other multidimensional structures. One alternative structure is the cross-classified structure (Jiao et al., 2016; Zhan, Wang, Wang, & Li, 2014), which can be viewed within Cai’s (2010) two-tier framework (see Figure 1b for a visual representation of a cross-classified structure without the Level 3 portion). In this structure, the first tier includes the primary dimension that represents CB, which is similar to the trifactor structure. The second tier includes four dimensions, with one pair of secondary dimensions representing the polarity method source (located immediately above the items in the figure) and the other pair of secondary dimensions representing the subject-focus method source (located immediately below the items in the figure). Although pairs of dimensions are located above and below the items in the figure, they all belong to the same tier because the subject-focus dimensions are not nested within the polarity dimensions. That is, whether the items that discriminate on the “I” dimension does not depend on the polarity of the items because positively and negatively phrased versions of “I” items (e.g., Items 1 and 11, respectively) discriminate on this dimension. Likewise, all of the “My” items discriminate on the same “My” dimension. In other words, the conceptualization of “I” and “My” remains the same across the aspects of the polarity method source and thus only one pair of dimensions is needed to represent the subject-focus method source.
A multilevel bifactor structure (De Jong et al., 2007; Jiao et al., 2012) could be another way to represent the multiple method sources reflected in the AFD data (see Figure 1c for a visual representation of this structure without the Level 3 portion). A bifactor structure can also be viewed as having two tiers of nested dimensions, with all dimensions assumed to be orthogonal to each other. The issue of accounting for positively and negatively worded items has been investigated by using the bifactor structure within a two-level context (W.-C. Wang, Chen, & Jin, 2015) and a three-level setting (Y. Wang, Kim, Dedrick, Ferron, & Tan, 2018). Those studies, however, only had to address a polarity method source and thus only needed two dimensions in the second tier (one for each polarity) to go along with the dimension in the first tier. In the AFD example, two method sources are present. Thus, one primary dimension along with four secondary dimensions are needed, where each of the secondary dimensions represents one of the joint combination of the crossing of the method sources, with each item discriminating on the primary dimension and one of the secondary dimensions. Because each secondary dimension simultaneously represents aspects from both method sources, these sources are not assumed to be distinctly separate under this structure. This assumption can easily be violated when the method sources have different effects on the response process, which would then require a cross-classified structure or a trifactor structure.
One study involving the AFD data used a structure similar to the multilevel bifactor structure to represent the CB portion of the data and found that the orthogonal assumption was violated, which possibly indicated that the dimensional structure was misspecified (Fujimoto, 2018). That study, however, did not indicate in what way the structure for the secondary dimensions was misspecified or attempt to identify a more appropriate structure for those dimensions. Given the design of the AFD instrument, the multilevel trifactor structure appears most suited to represent the AFD data. The specifications for a model that can account for such a structure in data gathered from smaller samples—the Bayesian multilevel trifactor IRT model—are provided next. Following the specifications of the model are details of a simulation study establishing the model’s performance and demonstrating the consequences of incorrectly accounting for the dependency among the method sources. Then the model’s utility is illustrated through the analysis of the AFD data. This article ends with a discussion and concluding remarks.
The Bayesian Multilevel Trifactor IRT Model
In this section, the Bayesian multilevel trifactor IRT model based on adjacent category probabilities (e.g., the generalized partial credit model; Muraki, 1992) is presented, with the following indices used for its presentation. The persons are indexed using (the th person in cluster ), where (with representing the number of persons in cluster ) and (with representing the number of Level 3 clusters). The items are indexed using k, where (with K representing the total number of items). The category scores are indexed using c, where (with representing the highest score category for the block of items to which item k belongs; details as to why the items are blocked are provided below). The dimensions at Level 2 are indexed using , where (with representing the total number of Level 2 dimensions).
Based on these indices, the proposed model arrives at the probability of a response of to item by person given a set of parameters through
where the systematic component is
| (1) |
that has the constraint
In this systematic component, and represent the Level 2 and Level 3 portions of the model, respectively; represents the overall item intercept; and represents the relative intercept for category c. The following subsections include further details about these parts of the systematic component.
Level 2 Portion of the Model
In terms of the Level 2 portion of the model (i.e., the person level, which is represented by in Equation 1), is a vector of item k’s discriminations on the dimensions at this level, that is, . Following the dimensional layout for the AFD data as presented in Figure 1a, is the item’s discrimination on the dimension in the first tier (i.e., the CB dimension) and is estimated to be greater than 0 for all k. The second tier is represented by and , with only one of these two estimated to be greater than 0 and the other fixed to 0 depending on which polarity dimension item k discriminates. The third tier of the structure is represented by through . If item discriminates on Dimension 2 (i.e., is a positively phrased item), then either or is estimated to be greater than 0 and all remaining discriminations related to tertiary dimensions are fixed to 0. If item discriminates on Dimension 3, then either or is estimated to be greater than 0 and all remaining discriminations related to tertiary dimensions are fixed to 0.
The prior assigned on the estimated discriminations is a lognormal distribution parameterized by a mean and standard deviation (SD), that is,
| (2) |
Because the goal is to produce a model that is suitable for data gathered from smaller samples, the SD is set to 0.50 for each (i.e., for ). To offset the small SD, the mean of the distribution for the discriminations related to dimension is freely estimated and thus assigned a hyperprior of a normal distribution parameterized by a mean and SD, that is,
The values for and depend on which dimension the represents. Using nested dimensional structures (e.g., bifactor, cross-classified, and trifactor structures) to represent the data is reasonable when the primary dimension is assumed to be the dominant one. Thus, the items on the whole should discriminate more strongly on the dimension in the first tier than on the dimensions in the lower tiers. When d represents the primary dimension, then, the hyper-mean and hyper-SD are 0 and 0.20, respectively (i.e., and ). For all other dimensions, the hyper-mean and hyper-SD are set to and 0.20, respectively (i.e., and for all ), where sets the expected value of the lognormal distribution to approximately 0.75 given the SD of the lognormal distribution is 0.50. This expected value, however, is only a starting point and the mean of the lognormal distribution is allowed to vary, which, in turn, allows the items as a set to be more strongly or weakly discriminating on dimension .
Regarding the other parameter associated with the Level 2 portion of the model, is a vector of Level 2 latent trait dimensional positions for person in cluster , where . The prior distribution assigned on is a -variate normal distribution with a mean vector of 0s and an identity matrix () for its variance–covariance matrix, that is,
for all and .
Level 3 Portion of the Model
Regarding the Level 3 portion of the model (i.e., the cluster level, which is represented by in Equation 1), represents cluster j’s position on the dimension at Level 3 and is item k’s discrimination on this dimension. The subscript of 1 in both of these parameters is included to note that this Level 3 dimension corresponds to the primary dimension at Level 2. The prior distributions assigned on the Level 3 parameters depend on the form of the cluster effect being assessed.
Within IRT, traditionally, the cluster effect is assumed to be the same across all items (e.g., Fox & Glas, 2001; Kamata, 2001; Maier, 2001), which is incorporated into the model by constraining the items’ Level 3 discriminations to be equal to their corresponding Level 2 discriminations, that is,
| (3) |
for all k. Because the Level 3 discriminations are not freely estimated under this form of a cluster effect, a prior is not assigned on these parameters. The cluster effect, instead, is assessed through the SD of the normal distribution assigned as the prior for the Level 3 dimensional positions, that is,
| (4) |
for all j, with the SD further assigned a hyperprior of a halt-t distribution parameterized by a mean, SD, and degrees of freedom, that is,
| (5) |
The choice of a half-t distribution was because research has suggested that this distribution leads to a better behaving Markov chain for the SD when the SD is near 0, compared to when an inverse-gamma distribution is assigned on the variance (Gelman, 2006). Better behavior near 0 could be beneficial in ensuring that the presence of a cluster effect is correctly detected, given that the effect is the same across the items.
It is possible, however, that the cluster effect varies across the items. When this is the case, the constraint in Equation 3 could result in inaccurate estimates for the item discriminations and misleading conclusions could be formed about the cluster effect represented in the data (Lee & Cho, 2017). A cluster effect that varies across the items has been more commonly discussed in the multilevel factor analytic literature (e.g., Mehta & Neale, 2005; Muthén, 1991, 1994; Rabe-Hesketh, Skrondal, & Pickles, 2004), though this discussion has recently appeared in unidimensional and multidimensional IRT contexts (Fujimoto, 2018; Lee & Cho, 2017). To allow the cluster effect to vary across the items in the proposed model, separate sets of item discriminations are estimated for Levels 2 and 3 (i.e., unconstraining the item discriminations across levels). In this variation of the model, the Level 3 item discriminations are estimated parameters and thus assigned a lognormal prior distribution, that is,
| (6) |
for all k, with and assigned a hyperprior of
When the Level 3 discriminations are unconstrained, the SD of the prior distribution assigned on the Level 3 dimensional positions is set to 1 (i.e., in Equation 4), which then makes the hyperprior assigned on the SD (i.e., Equation 5) no longer applicable for this variation of the model. To determine the extent of the variability in the cluster effect across the items, the error-free intraclass correlation (ICC) for each item is calculated using
(Lee & Cho, 2017; Muthén, 1991). This type of cluster effect is different from the type in which the cluster effect is the same across the items. For an in-depth discussion about these two forms of cluster effects, see Lee and Cho (2017).
Overall and Relative Category Intercepts
In the proposed model, the item intercepts are decomposed into overall intercepts () and relative category intercepts (). By parameterizing the model in this manner, the items can be blocked into subsets, where the items within a block share a common set of relative category intercepts (e.g., Muraki, 1992). Blocking items in this manner may be necessarily for rating data when the sample sizes are smaller because some items may have categories that are never used (i.e., null categories) or infrequently used, which would lead to difficulties in estimating the relative category intercepts if the model were parameterized to where each item was assigned its own set of these intercepts. When a trifactor structure is specified for the data, the items could be blocked by tertiary dimensions, where the items assigned to the same tertiary dimension share a common set of relative intercepts.
The first relative intercepts (where and is the total number of item blocks) are assumed to be multivariate normally distributed, that is,
for all . The last intercept in each block is constrained to be the negative of the sum of all prior relative intercepts, that is, The overall intercepts are assumed to be univariate normally distributed, that is,
for all , with the mean of the distribution assigned a hyperprior of
In cases where each item is described by its own set of relative category intercepts, which becomes more possible as the sample size increases, the notation for the relative category intercepts can be simplified to
Simulation Study
A simulation study with a fully crossed design (Level 2 sample size by type of item discrimination constraint) was conducted to investigate how well the Bayesian trifactor IRT model functioned across a range of conditions. The sample sizes explored in this study were 250, 300, 500, and 1,500 Level 2 cases that were nested within 50, 60, 100, and 300 Level 3 clusters, respectively (where the number of Level 2 cases in each cluster was set to 5 in all sample size conditions). The smaller sample sizes were included because one of the goals of this study was to produce a multilevel trifactor IRT model that was suitable for smaller data sets. The largest sample size was included to examine whether the informative prior distributions incorporated in the proposed model were still appropriate for larger samples. The specifics of the data generating process, analytic strategies, and other technical details are described in the following subsections.
Data Generation
Twenty-five data sets were simulated for each study condition, with each data set resembling responses to 28 items scored on a 4-point scale. The data were generated with the multilevel trifactor model that was presented earlier, with the item discriminations constrained or unconstrained depending on the study condition. The multilevel trifactor structure specified in the data generating model was similar to the structure that was hypothesized for the AFD data (see Figure 1a). The dimensional structure for the simulations represented a situation in which Method Source B functioned differently across the aspects of Method Source A, where Method Sources A and B correspond to the polarity and subject-focus method sources, respectively, in the AFD example. In total, then, seven dimensions were specified at Level 2. All items discriminated on the dimension in the first tier (Dimension 1). The items further discriminated on one of the two dimensions in the second tier (Dimensions 2 and 3), with the items evenly distributed between these dimensions. The items further discriminated on one of the pair of tertiary dimensions nested within the secondary dimension on which the items discriminated, with the items evenly distributed between the two tertiary dimensions (leading to seven items per tertiary dimension). All items further discriminated on the dimension at Level 3.
The Data Generating Values
The following describes how the values for the parameters of the data generating model were obtained, starting with the unconstrained discrimination condition (where the cluster effect varied across the items). The values for the Level 2 latent trait dimensional positions () were randomly drawn from , and the Level 3 latent trait dimensional positions () were randomly drawn from .
Regarding the discriminations, each item discriminated on four dimensions (one dimension at Level 3 and three dimensions at Level 2). Thus, for each item, four values were randomly drawn from a uniform distribution with a lower bound and an upper bound of 0.5 and 1.5, respectively, . In order to control the overall magnitude of the method and cluster effects, the drawn values within a dimension were rescaled using scaling factors of 1.50, 1.20, 1.20, 1.00, 0.50, 0.50, and 1.00 for Dimensions 1 through 7, respectively, within Level 2, and a scaling factor of 0.75 for the dimension within Level 3. The rescaling was performed using
In this equation, is the rescaled value that was used as the generating value for item k’s discrimination on dimension d; is the drawn value from ; is the target scaling factor for dimension d; is an indicator function that returns 1 when item k discriminates on dimension and 0 otherwise; and is the number of items discriminating on dimension d. The drawn values for the Level 3 discriminations were rescaled in the same way that the values for the Level 2 discriminations were rescaled.
This rescaling was performed so that, among all the dimensions (at both levels), the items as a set most strongly discriminated on the Level 2 primary dimension, and the items as a set had a stronger discrimination on the secondary dimensions relative to the tertiary dimensions within Level 2. The scaling factors for the tertiary dimensions were varied to see whether the priors used in the proposed model could adapt to different strengths of discriminations. Rescaling the discrimination values did not artificially limit their range. The Level 2 item discriminations ranged from 0.31 to 2.31 (across all tiers); the Level 3 item discriminations ranged from 0.53 to 1.22; and the item-level ICCs ranged from .05 to .69 (the data generating values for these item parameters are in Supplemental Material A; all supplementary materials are available in the online version of the article).
The generating values for the overall item intercepts () and the relative category intercepts () were obtained by first drawing values for the direct intercepts (i.e., ) and then transforming them to obtain the values for and . This approach was taken to ensure that the final values for were those in which each subsequent relative intercept advanced in a sufficient manner so that issues of null categories did not arise in any of the generated data sets. The values for the direct category intercepts were obtained in the following manner. The values for the first direct category intercepts () were randomly drawn from for all Next, temporary relative intercepts for Categories 2 and 3 (denoted using and , respectively) were drawn from for each , where b = 1, 2, 3, or and each block included the items assigned to the same tertiary dimension. The direct intercepts for Categories 2 and 3 were obtained by adding the temporary relative intercepts to the first direct intercept. That is, for item , the second direct intercept was and the third direct intercept was . The generating value for item k’s overall intercept, then, was the mean of the direct category intercepts, that is, . The generating values for the relative category intercepts for the items in block b were obtained by subtracting the direct intercepts from the overall intercepts, that is, , where could be any one of the items that belonged to block .
In the constrained discrimination condition (where the cluster effect was the same across the items), the same values as those in the unconstrained discrimination condition were used, except in the following two instances. The Level 3 discriminations were set equal to their corresponding Level 2 discrimination values (i.e., for all ), and because of this constraint, the Level 3 dimensional positions were multiplied by 0.50 (i.e., ), leading to an overall ICC of .20, which also meant that the ICC for each item was .20 (i.e., ICCk1 = .20 for all k).
Analytic Strategy
The models used to analyze the data, the manner in which the models were compared, and how the recovery of the generating values was assessed are described in this subsection.
Models Used in the Study
Ten models were used to analyze each generated data set, with the models belonging to one of two subclasses. The first subclass was composed of models in which the item discriminations were unconstrained across Levels 2 and 3, allowing the cluster effect to vary across the items (Models 1 through 5). Of these models, Model 1 was the multilevel trifactor model as presented earlier. Models 2 and 3 were the multilevel cross-classified and bifactor models, respectively, and Model 4 was the multilevel unidimensional model (i.e., one dimension at Level 2 and another at Level 3). Model 5 was a variation of the main trifactor model (Model 1) in that it included less informative prior distributions being assigned on all freely estimated item discriminations at Levels 2 and 3 (i.e., lognormal distributions with fixed means of 0s and SDs of 1s instead of the priors represented in Equations 2 and 6). This model was included to investigate whether the stronger priors used in the main trifactor model (Model 1) were advantageous with smaller samples and yet were still appropriate to use with larger samples.
The reasoning for this is that, when less informative priors are used, the posterior distribution should be primarily a reflection of the data. In smaller sample sizes, however, the information contained in the data may not be sufficient enough to lead to a posterior distribution that is representative of the true distribution and thus stronger priors could be helpful in obtaining a more accurate posterior distribution. If this is the case, then the trifactor model with stronger priors (Model 1) should produce more accurate estimates than the model with less informative priors (Model 5). In larger samples, the data should contain enough information to obtain an accurate posterior distribution. In the largest sample size condition, then, if the estimates from Model 1 and Model 5 are similar, that would suggest that the impact of the strong priors on the posterior is negligible because the data are dominating, which in turn would indicate that the strong priors can still be used with larger sample sizes.
Models 6 through 10 formed the constrained discrimination subclass of models and were the counterparts to Models 1 through 5, respectively, but with the Level 3 item discriminations set equal to their corresponding Level 2 item discriminations and the SD of the prior distribution assigned on the Level 3 latent trait dimensional positions freely estimated. The models within this subclass, then, assumed that the cluster effect was the same across the items. All comparison models (other than Models 5 and 10) used the same priors as the main trifactor model.
Model Comparisons
The Bayes factor (BF) was used to determine the extent to which the data supported one model (Model A) over another (Model B). The difference between two models’ log-predicted marginal likelihoods (LPMLs) were used to approximate the BF on a 2 × the log scale, that is,
(Gelfand, 1996). Values of 0 to 2, 2 to 6, 6 to 10, and units were interpreted as the data providing no, positive (or slight), strong, and very strong support, respectively, for Model A over Model B (Kass & Raftery, 1995). Because each simulation condition consisted of 25 data sets, the reported LPMLs and BFs are the averages across the data sets within a condition, and all BFs hereafter are assumed to be on a 2 × the log scale.
Recovery of the Model Parameters
How well the models recovered the generating item discriminations related to the primary dimensions at Levels 2 and 3 was assessed by determining the extent of the bias exhibited in the posterior means for these discriminations, where the posterior means served as the estimates for these parameters. The bias was calculated using
where is the parameter of interest; is the generating value; is the posterior mean for that parameter that was produced during the analysis of the zth generated data set within a study condition; and 25 is the total number of generated data sets in each condition. The reason for looking at the bias was because this index reflects when an estimate is under- or over-representing the true value and thus would reveal in what manner the item discrimination estimates are affected when the dimensional structure is misspecified and when less informative priors are used with smaller samples. In certain cases, the root mean square error (RMSE) is reported to highlight the difference between the trifactor models with more informative and less informative priors. The RMSE was calculated using
The recovery of the remaining parameters based on the estimates from the proposed model was also assessed, with these remaining parameters including the Level 2 discriminations related to the dimensions in the second and third tiers, the item intercepts, and the item-level ICCs.
Technical Details
The Markov chain Monte Carlo (MCMC) algorithm used to estimate the posterior distributions for the parameters of all models used in this study was written in C++, though comparable JAGS code for the multilevel trifactor IRT model with unconstrained discriminations is in Supplemental Material B. The algorithm consisted of 255,000 sampling iterations. The first 30,000 of these samples were discarded and then every 15th sample thereafter was saved, leading to a total of 15,000 saved samples. Post-processing was performed on these saved samples before they were summarized. The reason for this post-processing was because, as presented in the previous section, the proposed model was identified in the conventional way that is commonly done in Bayesian IRT models, which includes setting the means and the SDs of the prior distributions for the Level 2 and Level 3 dimensional positions to 0s and 1s, respectively. Jackman (2009) refers to this form of model identification as soft identification, which may not be sufficient enough for more complex models. Thus, post-processing was performed to obtain samples from the posterior where the metric was strongly set (Gelman, Carlin, Stern, & Rubin, 2013). This post-processing included rescaling the values at the sth stage of the MCMC sampling process by standardizing the values for the latent trait positions within each dimension and transforming all remaining sampled values as needed to preserve the likelihood (see Supplemental Material C for the technical details of this post-processing). Batch means, MCMC 95% halfwidth intervals, and traceplots were examined to determine whether the Markov chains stabilized (Geyer, 2011), and no irregularities appeared from any of the models.
Simulation Results
Model Comparisons
Table 1 includes the averaged LPMLs (with higher values indicating better predictive performance of the data) and BFs used to determine which model was favored. Each reported BF indicates the extent to which the data supported the generating model (indicated by the lack of BF) over the model where the BF appears.
Table 1.
The Log-Predicted Marginal Likelihoods (LPMLs) and the Bayes Factors (BFs) on a 2 × the Log Scale in Parentheses From the Simulation Study and the Analysis of the Acculturative Family Distancing (AFD) Data.
| Simulations | Empirical data | |||||
|---|---|---|---|---|---|---|
| Model | Description | AFD | ||||
| Unconstrained discrimination condition | ||||||
| Unconstrained discrimination subclass | ||||||
| 1 | Main trifactor | −6,268 | −7,458 | −12,369 | −37,095 | −6,379 |
| 2 | Cross-classified | −6,297 (58.0) | −7,497 (77.2) | −12,412 (85.6) | −37,190 (>100) | −6,407 (56.4) |
| 3 | Bifactor | −6,340 (>100) | −7,549 (>100) | −12,529 (>100) | −37,599 (>100) | −6,504 (>100) |
| 4 | Unidimensional | −7,242 (>100) | −8,580 (>100) | −14,364 (>100) | −43,009 (>100) | −7,112 (>100) |
| 5 | Trifactor variationa | −6,276 (16.3) | −7,465 (14.1) | −12,375 (11.6) | −37,098 (4.9) | −6,384 (10.0) |
| Constrained discrimination subclass | ||||||
| 1 | Main trifactor | −6,341 (>100) | −7,549 (>100) | −12,526 (>100) | −37,591 (>100) | −6,397 (35.1) |
| 2 | Cross-classified | −6,369 (>100) | −7,584 (>100) | −12,569 (>100) | −37,672 (>100) | −6,442 (>100) |
| 3 | Bifactor | −6,429 (>100) | −7,656 (>100) | −12,712 (>100) | −38,175 (>100) | −6,512 (>100) |
| 4 | Unidimensional | −7,321 (>100) | −8,767 (>100) | −14,565 (>100) | −43,668 (>100) | −7,246 (>100) |
| 5 | Trifactor variationa | −6,347 (>100) | −7,554 (>100) | −12,528 (>100) | −37,588 (>100) | −6,395 (32.4) |
| Constrained discrimination condition | ||||||
| Unconstrained discrimination subclass | ||||||
| 1 | Main trifactor | −6,250 (13.8) | −7,460 (17.9) | −12,349 (22.2) | −37,025 (27.1) | |
| 2 | Cross-classified | −6,284 (81.7) | −7,501 (>100) | −12,388 (98.7) | −37,097 (>100) | |
| 3 | Bifactor | −6,320 (>100) | −7,551 (>100) | −12,512 (>100) | −37,517 (>100) | |
| 4 | Unidimensional | −7,170 (>100) | −8,502 (>100) | −14,237 (>100) | −42,565 (>100) | |
| 5 | Trifactor variationa | −6,260 (33.7) | −7,469 (36.2) | −12,356 (35.8) | −37,028 (32.1) | |
| Constrained discrimination subclass | ||||||
| 1 | Main trifactor | −6,243 | −7,451 | −12,338 | −37,012 | |
| 2 | Cross-classified | −6,277 (68.6) | −7,492 (83.9) | −12,385 (94.1) | −37,110 (>100) | |
| 3 | Bifactor | −6,315 (>100) | −7,546 (>100) | −12,498 (>100) | −37,507 (>100) | |
| 4 | Unidimensional | −7,250 (>100) | −8,704 (>100) | −14,427 (>100) | −43,265 (>100) | |
| 5 | Trifactor variationa | −6,249 (12.1) | −7,456 (11.9) | −12,342 (8.2) | −37,014 (4.5) | |
Note. The reported LPMLs and BFs are the averages across the 25 generated data sets within a condition for the simulation portion of the study. Each reported BF (in parentheses) indicates the extent to which the data supported Model A over Model B. Model A refers to the data generating models in the simulation columns (indicated by where BFs are not reported) and the main multilevel trifactor IRT model with unconstrained discriminations in the AFD column, and Model B refers to the models where the BFs are reported in all columns.
This variation of the trifactor model assigned less informative prior distributions on the item discriminations.
Unconstrained discrimination condition
In this study condition, each model within the unconstrained discrimination subclass (Models 1 through 5) was very strongly favored over its corresponding model within the constrained discrimination subclass (Models 6 through 10) for all sample sizes. Because this pattern was consistent with this condition’s data generating process and for space reasons, only the comparisons of the models within the unconstrained discrimination subclass are reviewed.
Focusing on the main trifactor, cross-classified, bifactor, and unidimensional models within this subclass (Models 1 through 4, respectively), the results show that accounting for the method sources improved predictive performance of the data, though accounting for the correct structure of the method sources led to the highest predictive performance. More specifically, the bifactor model was strongly favored over the unidimensional model for all sample sizes, showing that accounting for the method sources in some manner was beneficial in terms of predictive performance of the data. The cross-classified model, however, was strongly favored over the bifactor model for all sample sizes, indicating that it was better to treat the two method sources as separate entities. The trifactor model, which was the data generating model, was strongly favored over the cross-classified model for all sample sizes, showing that accounting for the nested method-source interaction further improved predictive performance.
Between the main trifactor model (Model 1) and its variation that incorporated less informative priors (Models 5), the former was strongly favored over the latter for the sample sizes of 250, 300, and 500. For the sample size of 1,500, however, the main trifactor model was only slightly favored over the variation with less informative priors. These findings show that the informative priors incorporated in the main trifactor model is beneficial for smaller sample sizes in that it leads to an improvement in predictive performance. Additionally, this finding confirms that the informative priors in the main trifactor model are applicable for larger sample sizes because these two models displayed similar performances in the largest sample size condition.
Constrained discrimination condition
The pattern among the LPMLs and BFs from the constrained discrimination condition was very similar to the pattern among the indices from the unconstrained discrimination condition, but with the models from the constrained discrimination subclass outperforming their respective models in the other subclass. There was, however, one exception. The unconstrained version of the unidimensional model outperformed its constrained version. This exception could have arisen because a unidimensional structure was a gross mismatch to the data generating dimensional structure, and so the additional parameters in the unconstrained version of this model helped it achieve a better predictive performance than its constrained version. Regardless of this exception, the multilevel trifactor IRT model with constrained discriminations (Model 6), which was the data generating model for this discrimination condition, was very strongly favored over all other models according to the BFs.
Recovery Details
For space reasons and because the pattern of the results across the models was very similar in the unconstrained and constrained discrimination conditions, only the recovery results from the unconstrained discrimination condition are reviewed. The recovery details for the constrained discrimination condition are available upon request from the author. In terms of the item discriminations related to the primary dimensions at Levels 2 and 3 ( and , respectively), the recovery details are presented for the main trifactor model (Model 1), the cross-classified model (Model 2), and the trifactor model with less informative priors (Model 5). These three models show the consequences of when the Level 2 dimensional structure is incorrectly specified (Model 2) and when less informative priors are used even when the dimensional structure is correctly specified (Model 5).
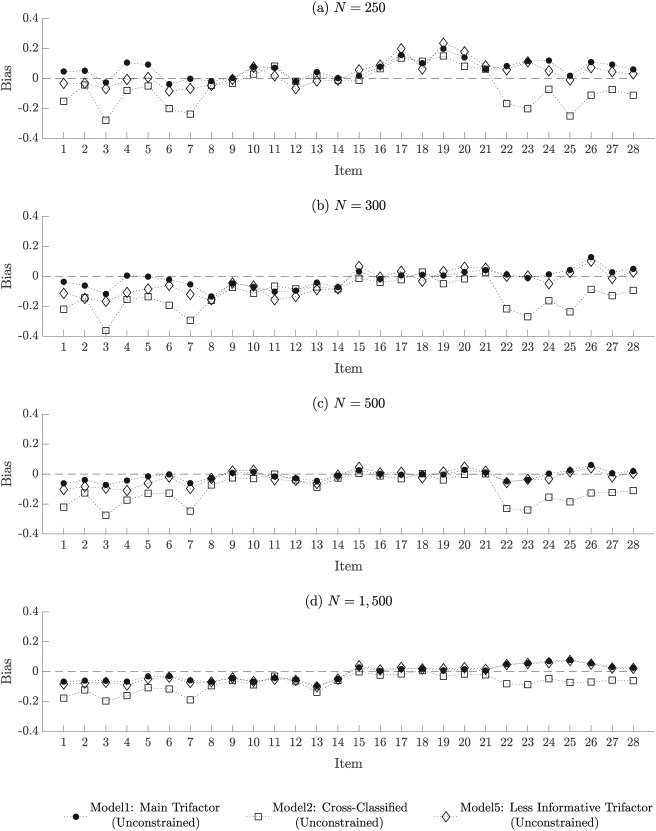
Figure 2 includes the bias plots showing the extent to which the posterior means from the three models were biased estimates for the Level 3 item discriminations (), with each plot representing a sample size. In each plot, the items are ordered along the horizontal line and the vertical line represents the bias, with negative and positive values indicating the estimates were respectively underestimating and overestimating the true values. The main trifactor model (represented by solid circles in the figure; Model 1) and the cross-classified model (represented by squares; Model 2) showed similar patterns of bias across the sample sizes. Many of the estimates from these two models were negatively biased for the sample size of 250, but the bias decreased as the sample size increased. The similarity between these two models was because the data were generated to where only one dimension was specified at Level 3, and both models were specified to match this. The benefit of the informative priors in the main trifactor model becomes apparent when the bias under this model is compared to the bias under the trifactor model with less informative priors (represented by diamonds; Model 5). In general, the trifactor model with less informative priors exhibited greater negative bias than the main trifactor model for the sample sizes of 250, 300, and 500. For the sample size of 1,500, the bias under these two models were nearly identical, providing additional support that the informative priors in the main trifactor model is still suitable for larger sample sizes.
Figure 2.
Bias plots showing the recovery of the items’ discriminations on the Level 3 dimension, from the unconstrained discrimination condition of the simulations. Each plot represents a sample size and three models from the unconstrained discrimination subclass. Model 1 was the main multilevel trifactor model that included assigning informative priors on the item discriminations and Model 5 was also a multilevel trifactor model but assigned less informative priors on the item discriminations. In each subfigure, the items are along the horizontal axis and the vertical axis represents the bias in the estimates.
Figure 3 includes the bias plots showing the recovery of the item discriminations related to the Level 2 primary dimension (), with each plot representing a sample size. Overall, as the sample size increased, the bias decreased under all models. Based on the bias alone, the benefit of the informative priors in the main trifactor model (Model 1) is not as apparent as it was when the recovery of the Level 3 discriminations were reviewed. For the Level 2 discriminations, the benefit of the informative priors appears in the smaller RMSE observed under the the main trifactor model. For the sample size of 250, the RMSE ranged from to (with a mean of and SD of ) and to (with a mean of and SD of ) for Models 1 and 5, respectively. For the sample size of 300, the RMSE ranged from to (with a mean of and SD of ) and to (with a mean of and SD of ) for Models 1 and 5, respectively. For the sample size of 500, the RMSE ranged from to (with a mean of and SD of ) and to (with a mean of and SD of ) for Models 1 and 5, respectively. For the sample size of 1,500, the RMSE was nearly identical under both models.
Figure 3.
Bias plots showing the recovery of the items’ discriminations on the Level 2 primary dimension (i.e., the dimension in the first tier), from the unconstrained discrimination condition of the simulations. Each plot represents a sample size and three models from the unconstrained discrimination subclass. Model 1 was the main multilevel trifactor model that included assigning informative priors on the item discriminations, and Model 5 was also a multilevel trifactor model but assigned less informative priors on the item discriminations. In each subfigure, the items are along the horizontal axis and the vertical axis represents the bias in the estimates.
The impact of misspecifying the Level 2 dimensional structure is revealed when the bias under the cross-classified model (Model 2) and the main trifactor model is compared. Between these two models, the former produced estimates with greater negative bias for Items 1 through 7 and Items 22 through 28, though the bias in these items decreased to a certain degree as the sample size increased.
Figures 4a and 4b are the bias plots detailing the recovery of the discriminations related to the dimensions in the second and third tiers, respectively, under the main trifactor model (Model 1). The discriminations related to the dimensions in the second tier (Figure 4a) were more accurately estimated than the discriminations related to the dimensions in the third tier (Figure 4b), with the bias decreasing in both tiers as the sample size increased. The larger bias observed in the third tier could be because of the data generating condition, which consisted of the items as a set discriminating the weakest on these dimensions relative to the dimensions in the first and second tiers. Because of this, it could be that the data provided the least amount of information for estimating these discriminations. Nevertheless, the estimates for these item discriminations were adequate enough that the estimates of the discriminations related to the dimensions in the other tiers were not affected. Additionally, the estimates were sufficient enough so that a nested method-source interaction was detected when model comparisons were performed.
Figure 4.
Bias plots showing the recovery of: (a) the items’ discriminations on the Level 2 secondary dimensions (i.e., the dimensions in the second tier); (b) the items’ discriminations on the Level 2 tertiary dimensions (i.e., the dimensions in the third tier); (c) the overall item intercepts; and (d) and (e) are the first two relative category intercepts. These plots are from the unconstrained discrimination condition of the simulations based on the estimates produced with the main multilevel trifactor IRT model (Model 1), and within each plot, the lines represent the different sample sizes. In each plot, the items are along the horizontal axis and the vertical axis represents the bias in the estimates.
Figure 4c is the bias plot showing the recovery of the overall item intercepts, and Figures 4d and 4e are the bias plots for the first two relative category intercepts. A bias plot for the last relative category intercept is not provided because the last intercept is a constrained parameter. Thus, any bias in this relative intercept should be reflected in the bias for the first two relative intercepts. As reflected in the plots, the estimates for the overall and relative category intercepts were similar across the sample sizes, with the bias being near zero.
The recovery of the item-level ICCs under the main trifactor model (Model 1) was also assessed, with the estimates for these ICCs and their bias reported in Table 2. The estimates for the items that were generated to have stronger cluster effects exhibited greater negative bias, and this pattern was more noticeable when the sample size was smaller. For instance, the generating ICC for Item 24 was , and the model underestimated this item’s ICC ( with a bias of ) when the sample size was . The estimate improved to (with a bias of ) for the sample size of , which was similar to the estimates for the sample sizes of and (for both sample sizes, with a bias of ).
Table 2.
The Generating and Estimated Item-Level ICCs (With the Bias in the Estimates in Parentheses) From the Unconstrained Discrimination Condition of the Simulations, With the Estimates Produced Using the Main Multilevel Trifactor Item Response Theory Model (Model 1).
| Item | Generating ICC | ||||
|---|---|---|---|---|---|
| 1 | |||||
| 2 | |||||
| 3 | |||||
| 4 | |||||
| 5 | |||||
| 6 | |||||
| 7 | |||||
| 8 | |||||
| 9 | |||||
| 10 | |||||
| 11 | |||||
| 12 | |||||
| 13 | |||||
| 14 | |||||
| 15 | |||||
| 16 | |||||
| 17 | |||||
| 18 | |||||
| 19 | |||||
| 20 | |||||
| 21 | |||||
| 22 | |||||
| 23 | |||||
| 24 | |||||
| 25 | |||||
| 26 | |||||
| 27 | |||||
| 28 |
Note. The bias was calculated before the estimates were rounded to two decimal places.
There were a couple of items in which the bias was more similar between the sample sizes of 250 and 300 than between the samples sizes of 300 and the larger two sample sizes. For instance, the generating ICC for Item 5 was .61, and the estimates for this item were (with a bias of ) and (with a bias of ) for the sample sizes of and , respectively, while the estimates were (with a bias of almost ) and (with a bias of ) for the sample sizes of and , respectively. Even in this instance, however, an item with an ICC of or would be considered to be exhibiting a strong cluster effect. Thus, although the informative priors assigned on the item discriminations of the main trifactor model led to more negatively biased ICC estimates for the items with stronger cluster effects (mainly for the sample size of 250), the correct conclusion about the magnitude of the cluster effect in the items can still be achieved (i.e., whether the effect is strong or weak). The estimates for the ICCs also spanned a range of values in each sample size condition, showing that the informative priors used in the main trifactor model did not restrict their range.
Discussion of the Simulations
Through model comparisons, a nested method source interaction was detected in data from samples consisting of as few as 250 cases at Level 2. If general conclusions are sufficient, a sample size of 250 may be enough, given that the hypothesized structure for the data is similar to the one used in these simulations. However, if inferences are to be made on the item parameter estimates, a sample size of 300 may be more desirable. The reason for this is because, under the main trifactor IRT model, the bias in the estimates of the item-level ICCs and the item discriminations related to the primary dimensions at Levels 2 and 3 was more similar between the sample sizes of 300 and 1,500 than between 250 and 300, where the greatest and least amount of bias was observed for the sample sizes of 250 and 1,500, respectively.
Although not reported, additional simulations were performed to confirm that the LPMLs and BFs were sensitive enough to detect when the effects of the method sources were independent (i.e., could be represented using a cross-classified structure). The data for these additional simulations were generated to conform to a cross-classified structure. In each discrimination condition, the correct cross-classified model with item discriminations specified to match the data generating condition was very strongly favored over all other models (including the multilevel trifactor models) when using LPMLs and BFs. These additional simulations show that these indices can differentiate between data that reflect a multilevel trifactor structure and a multilevel cross-classified structure (results are available from the author upon request).
Empirical Example
The AFD data were analyzed to demonstrate the utility of the Bayesian multilevel trifactor IRT model. For in-depth details about the demographics and recruitment of the sample, see Hwang et al. (2010). In short, 317 Chinese Americans (Level 2; 112 mothers, 85 fathers, and 120 high school–aged children) who were nested within 123 family units (Level 3) provided responses to the 16 items (rated on a 7-point scale) that measured CB. One difference existed between the assignment of the items for the multilevel trifactor structure used in the actual analysis and the hypothesized structure displayed in Figure 1a (without the Level 3 portion represented in the figure). Preliminary analyses revealed that the Markov chain for one of the positively phrased “I” item’s discrimination on a tertiary dimension had difficulty stabilizing. Thus, this discrimination was fixed to 0, which led all chains to stabilize. In the figure, five items are shown to be discriminating on Dimension 4 and this was done for discussion purposes, but for the actual analysis of these data, Item 5’s discrimination on this dimension was set to 0. None of the other models required any adjustments.
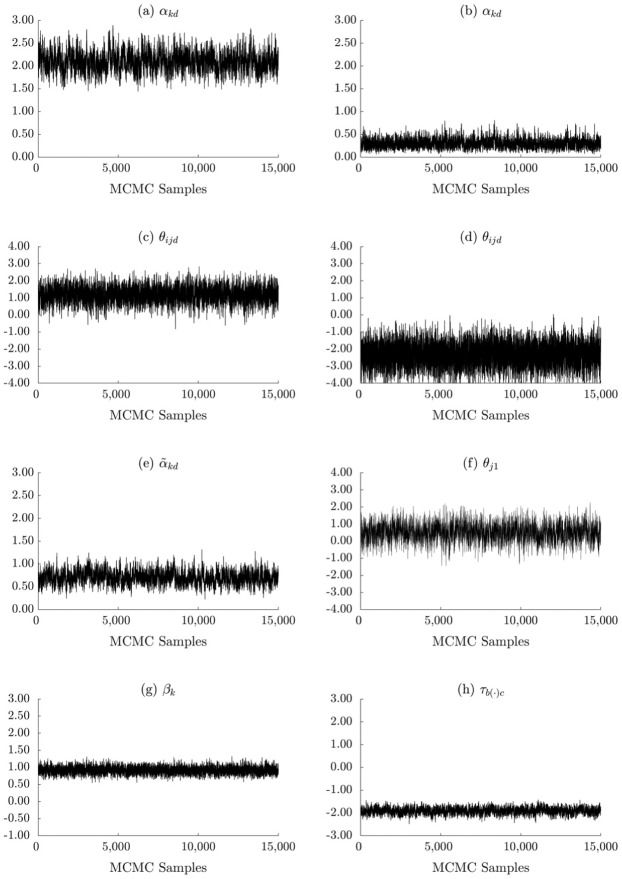
Regarding the analytic strategy, the 10 models used in the simulations were also used to analyze the AFD data. The models were then compared with respect to BF to determine which model was favored the most. The cluster effect exhibited in the item responses was also examined. The total number of MCMC sampling iterations, the number of saved samples, and the thin rate were the same as in the simulations, with post-processing performed on the saved samples. No irregularities appeared in the Markov chains across the models (after fixing Item 5’s discrimination on all tertiary dimensions to 0 for the models based on a trifactor structure). Traceplots for a set of parameters are presented in Figure 5, where these plots represent the values that were sampled under the main multilevel trifactor IRT model with unconstrained discriminations (Model 1) during the analysis of the AFD data. These traceplots provide empirical confirmation that the Markov chains stabilized and sufficient mixing occurred during the sampling process under this model.
Figure 5.
Traceplots of the values sampled under the main multilevel trifactor IRT model (Model 1) during the analysis of the acculturative family distancing data. These plots are for (a) an item’s discrimination on Dimension 1 at Level 2; (b) an item’s discrimination on Dimension 7 at Level 2; (c) an individual’s latent trait position on Dimension 1 at Level 2; (d) an individual’s latent trait position on Dimension 6 at Level 2; (e) an item’s discrimination on Dimension 1 at Level 3; (f) a family’s latent trait position on Dimension 1 at Level 3; (g) an item’s overall intercept; and (h) the cth relative category intercept for a block.
Results
Table 1 (AFD column) includes the LPMLs and BFs from the analysis of the AFD data. Each reported BF indicates the extent to which the data supported the main trifactor model with unconstrained discriminations (Model 1) over the model where the BF appears. Only the key findings are reviewed here because the patterns among the LPMLs and BFs were similar to the patterns observed in the unconstrained discrimination condition of the simulations, with the main trifactor model with unconstrained discriminations (Model 1) very strongly favored over all other models. The main trifactor model (Model 1) was favored over the cross-classified model (Model 2). This finding confirms that the subject-focus method source functioned differently depending on whether the items were positively or negatively worded, which is consistent with the self-attribution bias theory. This nested method–source interaction, then, provides evidence that the method sources were behaving as expected during the measurement process.
The main trifactor model with unconstrained discriminations was also very strongly favored over its counterpart with constrained discriminations (Model 6), suggesting that the cluster effect varied across the items. The item-level ICC estimates from the main trifactor model with unconstrained discriminations ranged from to , with a mean of and an SD of . Constraining the discriminations and thus assuming that the cluster effect was the same across the items, then, would have masked the varying levels of cluster effects that were exhibited across the items.
Discussion
In this article, the Bayesian multilevel trifactor IRT model was presented. This model accounts for cluster effects and nested method–source interactions represented in data, and the prior distributions assigned on the parameters of the model make it suitable for data from smaller and larger samples. Simulations confirmed that this model could detect multilevel trifactor structures in data from samples comprised of as few as 250 Level 2 cases that were nested within 50 Level 3 clusters. The simulations also demonstrated the advantages of the more informative priors that were assigned on the item discriminations, with these advantages more noticeable when the sample sizes were smaller. These advantages included more accurate estimates for the Level 3 discriminations and smaller RMSE in these estimates as well as in the estimates of other parameters. Finally, the simulations showed that treating dependent method sources as independent could lead to inaccurate estimates for the Level 2 item discriminations.
The context for when such a model is needed was also provided in this article. The AFD data were gathered from individuals that belonged to family units, using an instrument that included two method sources. The presented model showed that the item responses reflected both of these data collection processes, with the method sources having a nested interaction structure. Even though these method sources represented substantively irrelevant aspects of the latent trait space, gaining insight into the structure of the method sources served a couple of benefits. One benefit was that a better understanding of how these method sources functioned within the response process was gained. The other benefit was that, by identifying a more appropriate structure for the method sources, the substantively relevant and irrelevant variances were more effectively separated. This latter benefit was supported by the simulations, as the multilevel trifactor model produced the most accurate estimates for the item discriminations.
The primary focus of this study was to contribute to the literature on the modeling of nested dimensional structures by introducing the Bayesian multilevel trifactor IRT model, but other elements of this article also advance the literature. A nested method–source interaction was defined and how to investigate such an interaction using a trifactor structure was outlined. Additionally, a distinction was made between the cross-classified structure and the trifactor structure as applicable to multiple method sources, and this differentiation was made by framing these structures within a tiered system. One reason for using the tiered system was so the different assumptions the structures make were highlighted. That is, the cross-classified structure assumes the effects of the method sources are independent while the trifactor structure allows for a nested method–source interaction. Another reason for using the tiered perspective was because the term “trifactor structure” has been used to refer to two different types of structures. In one context, this term has been used to refer to three tiers of nested dimensions as described in this article (e.g., Rijmen, 2011; Segall, 2001). In another context, this term has been used to refer to a cross-classified structure (e.g., Bauer et al., 2013). By viewing the dimensional structure within tiers, it is easier to distinguish between the different structures with which the term “trifactor structure” has been associated.
Although this study adds to the literature on modeling of nested dimensional structures, limitations are acknowledged with the study. Only one multilevel trifactor structure was explored in the simulations. Whether the informative priors used in the presented model are still applicable in larger dimensional spaces should be investigated. Another limitation of the study was that it included one set of items that were scored on a 4-point scale. A future investigation could examine how well the model functions when the items are scored to represent fewer categories because the amount of information an item contributes decreases as the number of score categories decreases. Last but not least, the posterior distributions were estimated using MCMC, which could be computationally burdensome. The MCMC algorithm written in C++ took approximately 35 and 173 minutes to complete per data set for the Level 2 sample sizes of 300 and 1,500, respectively, running on a computer with a Core-i7 processor based on a Unix operating system.
The Bayesian multilevel trifactor IRT model presented in this article provides the means to determine whether a nested method–source interaction is taking place and whether the cluster effect varies across the items, and this investigation can be carried out on data collected from sample sizes as small as 250. This latter feature is extremely beneficial because many studies conducted in fields like education and psychology do not have the luxury of gathering data from thousands of individuals. If the data from these smaller-scale studies are suspected to represent cluster effects and method effects stemming from nested method sources, this model allows one to account for such effects during an item response analysis rather than settling for a model that incorrectly accounts for one or both of these extraneous effects. By considering the full data structure, one can maximize the psychometric information extracted from the data, information that could be substantively meaningful and useful in establishing the validity in the use and interpretation of the dimensional estimates.
Supplementary Material
Acknowledgments
The author would like to thank two anonymous reviewers for their valuable comments. All errors remain the responsibility of the author.
Footnotes
Declaration of Conflicting Interests: The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
Funding: The author(s) received no financial support for the research, authorship, and/or publication of this article.
Supplemental Material: Supplemental material for this article is available online.
ORCID iD: Ken A. Fujimoto  https://orcid.org/0000-0001-5222-3327
https://orcid.org/0000-0001-5222-3327
References
- American Educational Research Association, American Psychological Association, & National Council on Measurement in Education. (2014). Standards for educational and psychological testing. Washington, DC: American Educational Research Association. [Google Scholar]
- Bauer D. J., Howard A. L., Baldasaro R. E., Curran P. J., Hussong A. M., Chassin L., Zucker R. A. (2013). A trifactor model for integrating ratings across multiple informants. Psychological Methods, 18, 475-493. doi: 10.1037/a0032475 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cai L. (2010). A two-tier full-information item factor analysis model with applications. Psychometrika, 75, 581-612. doi: 10.1007/s11336-010-9178-0 [DOI] [Google Scholar]
- Chen F. F., West S. G., Sousa K. H. (2006). A comparison of bifactor and second-order models of quality of life. Multivariate Behavioral Research, 41, 189-225. doi: 10.1207/s15327906mbr4102_5 [DOI] [PubMed] [Google Scholar]
- Chen W.-H., Thissen D. (1997). Local dependence indexes for item pairs using item response theory. Journal of Educational and Behavioral Statistics, 22, 265-289. doi: 10.3102/10769986022003265 [DOI] [Google Scholar]
- Cochran W. G. (1977). Sampling techniques (3rd ed.). New York, NY: Wiley. [Google Scholar]
- De Jong M. G., Steenkamp J. E., Fox J.-P. (2007). Relaxing measurement invariance in cross-national consumer research using a hierarchical IRT model. Journal of Consumer Research, 34, 260-278. doi: 10.1086/518532 [DOI] [Google Scholar]
- Fox J.-P. (2005). Multilevel IRT using dichotomous and polytomous response data. British Journal of Mathematical and Statistical Psychology, 58, 145-172. doi: 10.1348/000711005X38951 [DOI] [PubMed] [Google Scholar]
- Fox J.-P., Glas C. A. (2001). Bayesian estimation of a multilevel IRT model using Gibbs sampling. Psychometrika, 66, 271-288. doi: 10.1007/BF02294839 [DOI] [Google Scholar]
- Fujimoto K. A. (2018). Bayesian multilevel multidimensional item response theory model for locally dependent data. British Journal of Mathematical and Statistical Psychology, 71, 536–560. doi: 10.1111/bmsp.12133 [DOI] [PubMed] [Google Scholar]
- Gelfand A. E. (1996). Model determination using sampling-based methods. In Gilks W. R., Richardson S., Spiegelhalter D. J. (Eds.), Markov chain Monte Carlo in practice (pp. 145-161). London, England: Chapman & Hall/CRC Press. [Google Scholar]
- Gelman A. (2006). Prior distributions for variance parameters in hierarchical models (comment on article by Browne and Draper). Bayesian Analysis, 1, 515-534. doi: 10.1214/06-BA117A [DOI] [Google Scholar]
- Gelman A., Carlin J. B., Stern H. S., Rubin D. B. (2013). Bayesian data analysis (3rd ed.). Boca Raton, FL: Chapman & Hall/CRC Press. [Google Scholar]
- Geyer C. (2011). Introduction to MCMC. In Brooks S., Gelman A., Jones G., Meng X. (Eds.), Handbook of Markov chain Monte Carlo (pp. 3-48). Boca Raton, FL: Chapman & Hall/CRC Press. [Google Scholar]
- Hwang W.-C., Wood J. J., Fujimoto K. A. (2010). Acculturative family distancing (AFD) and depression in Chinese American families. Journal of Consulting and Clinical Psychology, 78, 655-677. doi: 10.1037/a0020542 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jackman S. (2009). Bayesian analysis for the social sciences. Chichester, England: John Wiley. [Google Scholar]
- Jiao H., Kamata A., Wang S., Jin Y. (2012). A multilevel testlet model for dual local dependence. Journal of Educational Measurement, 49, 82-100. doi: 10.1111/j.1745-3984.2011.00161.x [DOI] [Google Scholar]
- Jiao H., Kamata A., Xie C. (2016). Multilevel cross-classified testlet model for complex item and person clustering in item response data analysis. In Harring J. R., Stapleton L. M., Beretvas S. N. (Eds.), Advances in multilevel modeling for educational research (pp. 139-161). Charlotte, NC: Information Age. [Google Scholar]
- Jiao H., Wang S., Kamata A. (2005). Modeling local item dependence with the hierarchical generalized linear model. Journal of Applied Measurement, 6, 311-321. [PubMed] [Google Scholar]
- Jiao H., Zhang Y. (2015). Polytomous multilevel testlet models for testlet-based assessments with complex sampling designs. British Journal of Mathematical and Statistical Psychology, 68, 65-83. doi: 10.1111/bmsp.12035 [DOI] [PubMed] [Google Scholar]
- Kamata A. (2001). Item analysis by the hierarchical generalized linear model. Journal of Educational Measurement, 38, 79-93. doi: 10.1111/j.1745-3984.2001.tb01117.x [DOI] [Google Scholar]
- Kass R., Raftery A. (1995). Bayes factor and model uncertainty. Journal of the American Statistical Association, 90, 773-795. doi: 10.1080/01621459.1995.10476572 [DOI] [Google Scholar]
- Lee W.-Y., Cho S.-J. (2017). Detecting differential item discrimination (DID) and the consequences of ignoring DID in multilevel item response models. Journal of Educational Measurement, 54, 364-393. doi: 10.1111/jedm.12148 [DOI] [Google Scholar]
- Maier K. S. (2001). A Rasch hierarchical measurement model. Journal of Educational and Behavioral Statistics, 26, 307-330. doi: 10.3102/10769986026003307 [DOI] [Google Scholar]
- Mehta P. D., Neale M. C. (2005). People are variables too: Multilevel structural equations modeling. Psychological Methods, 10, 259-284. doi: 10.1037/1082-989X.10.3.259 [DOI] [PubMed] [Google Scholar]
- Muraki E. (1992). A generalized partial credit model: Application of an EM algorithm. Applied Psychological Measurement, 16, 159-176. doi: 10.1177/014662169201600206 [DOI] [Google Scholar]
- Muthén B. O. (1991). Multilevel factor analysis of class and student achievement components. Journal of Educational Measurement, 28, 338-354. doi:10.1111/j.1745- 3984.1991.tb00363.x [Google Scholar]
- Muthén B. O. (1994). Multilevel covariance structure analysis. Sociological Methods & Research, 22, 376-398. doi: 10.1177/0049124194022003006 [DOI] [Google Scholar]
- Rabe-Hesketh S., Skrondal A., Pickles A. (2004). Generalized multilevel structural equation modeling. Psychometrika, 69, 167-190. doi: 10.1007/BF02295939 [DOI] [Google Scholar]
- Raudenbush S. W., Bryk A. S. (2002). Hierarchical linear models: Applications and data analysis methods. Thousand Oaks, CA: Sage. [Google Scholar]
- Raudenbush S. W., Johnson C., Sampson R. J. (2003). A multivariate, multilevel Rasch model with application to self-reported criminal behavior. Sociological Methodology, 33, 169-211. doi: 10.1111/j.0081-1750.2003.t01-1-00130.x [DOI] [Google Scholar]
- Rijmen F. (2011). Hierarchical factor item response theory models for PIRLS: Capturing clustering effects at multiple levels. IERI Monograph Series: Issues and Methodologies in Large-Scale Assessments, 4, 59-74. [Google Scholar]
- Segall D. O. (2001). General ability measurement: An application of multidimensional item response theory. Psychometrika, 66, 79-97. doi: 10.1007/BF02295734 [DOI] [Google Scholar]
- Wainer H., Bradlow E. T., Wang X. (2007). Testlet response theory and its applications. Cambridge, England: Cambridge University Press. [Google Scholar]
- Wang W.-C., Chen H.-F., Jin K.-Y. (2015). Item response theory models for wording effects in mixed-format scales. Educational and Psychological Measurement, 75, 157-178. doi: 10.1177/0013164414528209 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Y., Kim E. S., Dedrick R. F., Ferron J. M., Tan T. (2018). A multilevel bifactor approach to construct validation of mixed-format scales. Educational and Psychological Measurement, 78, 253-271. doi: 10.1177/0013164417690858 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilson M., Adams R. J. (1995). Rasch models for item bundles. Psychometrika, 60, 181-198. doi: 10.1007/BF02301412 [DOI] [Google Scholar]
- Zhan P., Wang W.-C., Wang L., Li X. (2014). The multidimensional testlet-effect Rasch model. Acta Psychologica Sinica, 46, 1208-1222. doi: 10.3724/SP.J.1041.2014.01218 [DOI] [Google Scholar]
- Zuckerman M. (1979). Attribution of success and failure revisited, or: The motivational bias is alive and well in attribution theory. Journal of Personality, 47, 245-287. doi: 10.1111/1467-6494.ep7594052 [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.