Abstract
Central output of gonadotropin-releasing hormone (GnRH) neurons controls fertility and is sculpted by sex-steroid feedback. A switch of estradiol action from negative to positive feedback initiates a surge of GnRH release, culminating in ovulation. In ovariectomized mice bearing constant-release estradiol implants (OVX+E), GnRH neuron firing is suppressed in the morning (AM) by negative feedback and activated in the afternoon (PM) by positive feedback; no time-of-day-dependent changes occur in OVX mice. In this daily surge model, GnRH neuron intrinsic properties are shifted to favor increased firing during positive feedback. It is unclear whether this shift and the observed concomitant increase in GABAergic transmission, which typically excites GnRH neurons, are independently sufficient for increasing GnRH neuron firing rate during positive feedback or whether both are needed. To test this, we used dynamic clamp to inject selected previously recorded trains of GABAergic postsynaptic conductances (PSgs) collected during the different feedback states of the daily surge model into GnRH neurons from OVX, OVX+E AM, and OVX+E PM mice. PSg trains mimicking positive feedback initiated more action potentials in cells from OVX+E PM mice than negative feedback or OVX (open feedback loop) trains in all three animal models, but the positive-feedback train was most effective when applied to cells during positive feedback. In silico studies of model GnRH neurons in which >1000 PSg trains were tested exhibited the same results. These observations support the hypothesis that GnRH neurons integrate fast-synaptic and intrinsic changes to increase firing rates during positive feedback.
SIGNIFICANCE STATEMENT Infertility affects 15%–20% of couples; failure to ovulate is a common cause. Understanding how the brain controls ovulation is critical for new developments in both infertility treatment and contraception. Ovarian estradiol alters both the intrinsic properties of gonadotropin-releasing hormone (GnRH) neurons and synaptic inputs to these cells coincident with production of sustained GnRH release that ultimately triggers ovulation. We demonstrate here using dynamic clamp and mathematical modeling that estradiol-induced shifts in synaptic transmission alone can increase firing output, but that the intrinsic properties of GnRH neurons during positive feedback further poise these cells for increased response to higher frequency synaptic transmission. These data suggest that GnRH neurons integrate fast-synaptic and intrinsic changes to increase firing rates during the preovulatory GnRH surge.
Keywords: dynamic clamp, estradiol feedback, GABA, GnRH
Introduction
Gonadotropin-releasing hormone (GnRH) neurons form the final common pathway for the central control for reproduction. GnRH initiates the release of luteinizing hormone (LH) and follicle-stimulating hormone from the pituitary. Gonadotropins activate follicle maturation and steroidogenesis in the ovary. For most of the estrous cycle, estradiol negative feedback suppresses GnRH/LH release. At the end of the follicular phase (proestrus in rodents), rising levels of estradiol switch from suppressing GnRH/LH to positive feedback action that induces a continuous surge of release that initiates an LH surge that triggers ovulation (Sarkar et al., 1976; Moenter et al., 1991).
In ovariectomized rodents implanted with estradiol capsules (OVX+E), GnRH/LH surges can be induced on a daily basis (Norman et al., 1973; Legan and Karsch, 1975; Christian et al., 2005). Release of GnRH and LH, as well as GnRH neuron firing rate, are suppressed in the morning (negative feedback) and elevated in the afternoon (positive feedback) (Christian et al., 2005; Glanowska et al., 2012). No time-of-day-dependent shift in GnRH neuron firing rate is observed in OVX mice not treated with estradiol. Work using this daily surge paradigm, other estradiol-induced surge paradigms, and studies during different stages of the natural estrous cycle have identified multiple estradiol and time-of-day-dependent changes to GnRH neuron intrinsic properties and fast-synaptic transmission that may drive an increase in firing rate during positive feedback (Chu and Moenter, 2006; Christian and Moenter, 2007; Zhang et al., 2007, 2009; Christian et al., 2009; Sun et al., 2010; Pielecka-Fortuna et al., 2011; Adams et al., 2018a). Changes to voltage-gated sodium, potassium, and calcium channel properties culminate in an increase in GnRH neuron excitability during positive feedback and may increase both spontaneous firing and responsiveness to fast-synaptic inputs to help drive an increase in GnRH firing rate at this time (Adams et al., 2018b). In addition to these changes in intrinsic properties, GABA postsynaptic current (PSC) frequency and amplitude are suppressed during negative feedback and increased during positive feedback in both the daily surge model and during the estrous cycle (Christian and Moenter, 2007; Adams et al., 2018a); activation of GABAA receptors in these cells can be excitatory (DeFazio et al., 2002).
Whether changes in GABAergic fast-synaptic transmission, intrinsic properties, or both are necessary or sufficient for increasing GnRH neuron firing rate during positive feedback is not known. We hypothesized that time-of-day and estradiol-dependent changes in intrinsic properties render GnRH neurons more responsive to GABA PSCs during positive feedback compared with negative feedback and the open-loop OVX condition. To test our hypothesis, we used the daily surge paradigm to examine GnRH neuron response to trains of GABA postsynaptic conductances (PSgs), and used dynamic clamp to introduce synaptic conductances to evoke postsynaptic potentials (PSPs) and measure membrane response. Trains of conductances were modeled from representative patterns from negative and positive feedback and the open-loop OVX condition (Christian and Moenter, 2007). We also used GnRH neuron models of two feedback conditions to test >1000 previously recorded trains of PSCs in silico.
Materials and Methods
All chemicals were purchased from Sigma-Aldrich, unless noted.
Animals.
All animal work was approved by the Institutional Animal Care and Use Committee of the University of Michigan. Transgenic mice expressing GFP under the control of the GnRH promoter (Tg(Gnrh1-EGFP)51Sumo MGI:6158457) (GnRH-GFP mice) were used (Suter et al., 2000). Mice were housed in a vivarium kept at 21°C–23°C on a 14 h light/10 h dark cycle with lights off at 5:00 P.M. (Eastern Standard Time). Teklad 2916 chow (Envigo) and water were available ad libitum. Adult females 58–170 d of age were randomly selected from our colony. Ovariectomy was performed under isoflurane (VetOne) anesthesia. At the time of OVX, mice were randomized to either receive a Silastic (Dow Corning) capsule containing 0.625 μg 17β-estradiol suspended in sesame oil (OVX+E) or not be treated further (OVX). Bupivacaine (0.25%, APP Pharmaceuticals) was applied to surgical sites to reduce postoperative pain and distress. Electrophysiologic experiments were performed 2–3 d after surgery, and estradiol status was confirmed by measurements of uterine mass (OVX, n = 7, 49.1 ± 3.3 mg; OVX+E, n = 12, 174.1 ± 4.8 mg; two-tailed unpaired Student's t test, t(17) = 18.4, p < 0.001). It is important to point out that this daily surge model does not recapitulate the pattern of estradiol during the cycle. It does, however, effectively induce both negative and positive feedback on LH release in vivo and GnRH neuron activity in the brain slice relative to measurements in OVX mice (Christian et al., 2005). This separates two variables, time of day and circulating estradiol level, known to contribute to the generation of the LH surge in mice and other rodents and which were the targets of the present investigations. Firing rates, GnRH neuron excitability, and GABAergic transmission during the daily estradiol-induced surge are similar to those during the proestrous surge of the estrous cycle (Silveira et al., 2017; Adams et al., 2018a).
Brain slice preparation.
All solutions were bubbled with 95% O2/5% CO2 throughout the experiments and for at least 15 min before exposure to tissue. Brain slices were prepared either from 7.5 to 8.5 h before lights out (AM recordings) or 1–2 h before lights out (PM recordings). The brain was rapidly removed and placed in ice-cold sucrose saline solution containing the following (in mm): 250 sucrose, 3.5 KCl, 26 NaHCO3, 10 d-glucose, 1.25 Na2HPO4, 1.2 MgSO4, and 3.8 MgCl2, at pH 7.6 and 345 mOsm. Coronal (300 μm) slices were cut with a VT1200S Microtome (Leica Biosystems). Slices were incubated in a 1:1 mixture of sucrose saline and ACSF containing the following (in mm): 135 NaCl, 3.5 KCl, 26 NaHCO3, 10 d-glucose, 1.25 Na2HPO4, 1.2 MgSO4, and 2.5 CaCl2, pH 7.4, 305 mOsm, for 30 min at room temperature (21°C-23°C). Slices were then transferred to 100% ACSF at room temperature for 0.5–5 h before recording.
Data acquisition.
During recording, slices through the preoptic area and anterior hypothalamus, which contain the majority of GnRH neuron somata, were placed into a chamber continuously perfused with ACSF at a rate of 2 ml/min with oxygenated ACSF heated to 29.5°C–31.5°C with an inline-heating unit (Warner Instruments). GFP-positive cells were visualized with a combination of infrared differential interference contrast and fluorescence microscopy on an Olympus BX51WI microscope. Recording pipettes were pulled from borosilicate glass capillaries (1.65 mm OD × 1.12 mm ID; World Precision Instruments) using a Flaming/Brown P-97 unit (Sutter Instrument). Pipettes measured 2–4.5 mΩ when filled with the following (in mm): 125 K gluconate, 20 KCl, 10 HEPES, 5 EGTA, 0.1 CaCl2, 4 MgATP, and 0.4 NaGTP, 300 mOsm, pH 7.2, with NaOH. Pipettes were wrapped with Parafilm (Bemis) to reduce capacitive transients; remaining transients were electronically cancelled. Pipettes were placed in contact with a GFP-positive neuron using an MP-285 micromanipulator (Sutter Instrument). All potentials reported were corrected online for a liquid junction potential of −14.2 mV (Barry, 1994). Recordings were made with an EPC-10 dual patch-clamp amplifier (HEKA Elektronik) and a Macintosh computer running Patchmaster software (HEKA Elektronik). Experiments were analyzed offline using custom software (DeFazio and Moenter, 2002; DeFazio et al., 2014) written in IgorPro (Wavemetrics).
Whole-cell patch-clamp.
After achieving a >1 GΩ seal and the whole-cell configuration, membrane potential was held at −60 mV between protocols. Series resistance (Rs), input resistance (Rin), membrane capacitance (Cm), and holding current (Ihold) were measured every 2–3 min using a 5 mV hyperpolarizing step from −60 mV (mean of 20 repeats, 20 ms duration, sampled at 100 kHz). Only recordings with an Rin of >500 mΩ, Ihold of −30 to 25 pA, stable Rs of <20 mΩ, and stable Cm between 10 and 23 pF were used for analysis.
In current clamp, direct current (<35 pA, −9.0 ± 2.1 pA, n = 34) was adjusted to keep cells within 3 mV of −59 mV. Membrane potential was sampled at 20 kHz and filtered at 6.7 kHz. Bridge balance (95%) was used for most cells; for a few cells, bridge balance was not used but results were similar. In all current-clamp and dynamic-clamp recordings, ACSF contained 100 μm picrotoxin, 20 μm d-APV (Tocris), and 20 μm CNQX to block ionotropic GABA and glutamate receptors. To confirm estradiol and diurnal changes in GnRH neuron excitability, cells were injected with current from 0 to 30 pA (500 ms, 10 pA steps). Confirming previous work (Adams et al., 2018b), GnRH neurons from OVX+E PM mice fired more spikes in response to 500 ms current steps from 20 to 30 pA compared with all other groups (p < 0.05, two-way repeated-measures ANOVA/Bonferroni; data not shown).
Dynamic clamp.
Dynamic clamp was implemented using the freely available QuB software (MLab edition; https://milesculabs.biology.missouri.edu/QuB.html) (Milescu et al., 2008) running on a separate computer (Marquis C733-T with dual Intel Xeon E5-2667v2 Ivy Bridge-EP 3.3 GHz, 8-core processors, 8 × 16 Gb DDR3-1866 SDRAM, ASLabs) equipped for data acquisition system (PCIe-6361 Multifunction DAQ card with a BNC interface, National Instruments). The digital outputs of the EPC10 were used to trigger events in the dynamic-clamp system. The input to the dynamic-clamp system is the membrane potential of the cell (Vm), read from the EPC10 patch-clamp amplifier in current-clamp mode; the output of the dynamic clamp is the computed command current (Idc), which drives the current command input of the EPC10. This input–output cycle is repeated at ∼50 kHz.
To implement the synaptic conductance model in dynamic clamp, Idc was calculated from the PSg (gsim) and the linear driving force: Idc = gsim × (Vm − EGABA), where EGABA is the reversal potential for current through the GABAA receptor channel (EGABA = −36.5 mV) (DeFazio et al., 2002). The time course of synaptic conductances was modeled using a single exponential (gsim = gmaxe(−t/τ)), where gmax is the maximum conductance, τ is the decay time constant, and t is the time after a trigger. The decay time constant of GABAergic PSCs depends primarily on the intracellular chloride concentration (Houston et al., 2009) in the membrane potential range used in these studies. It is thus critical to use a physiologic chloride concentration to determine the endogenous conductance time course for use in dynamic-clamp studies. Whole-cell voltage-clamp recordings of endogenous GABA PSCs were obtained using a physiologic 20 mm chloride pipette solution at a holding potential of −70 mV. Recordings were made in the presence of 20 μm d-APV and 20 μm CNQX to block glutamatergic transmission. The decay time constant was estimated using a single exponential fit from 90% of the peak to 10% of the peak of the averaged GABA PSC for each cell. Decay time constant was not different among groups (OVX: n = 6, 8.8 ± 1.2 ms; OVX+E AM: n = 8, 11.0 ± 2.6 ms; OVX+E PM: n = 5, 9.0 ± 1.5; p = 0.94, Kruskal–Wallis/Dunn's). The mean ± SEM was 9.8 ± 1.0 ms; thus, a value of 10 ms was used in dynamic-clamp experiments.
Mathematical modeling.
We used a published model GnRH neuron in which parameter distributions were developed to reproduce GnRH neuron firing and action potential (AP) characteristics during positive feedback, negative feedback, and the open-loop OVX condition (Adams et al., 2018b). Ten representative parameter sets were chosen from each distribution to simulate a neuron for two groups: negative/OVX, which were described by a single distribution of parameters; and positive feedback. Using these model neurons, we measured GnRH neuron model response to PSg trains constructed from >300 cells and 1000 PSC trains recorded from GnRH neurons prepared from the daily surge model. Previous voltage-clamp experiments have isolated IA, IK, IHVA, and ILVA in the daily surge model (Sun et al., 2010; Pielecka-Fortuna et al., 2011). We used these experiments and experiments measuring ILVA from another model of estradiol feedback (Zhang et al., 2009) to estimate parameters for IA, IK, IHVA, and ILVA.
Mathematical equations.
We previously modified a GnRH neuron model developed by Moran and Khadra (Moran et al., 2016) that was itself based upon the original Hodgkin and Huxley GnRH neuron model (LeBeau et al., 2000). In this model, membrane potential is expressed in mV, time is in ms, currents are in pA, and conductances are in nS. The governing equation for membrane potential is described by the following:
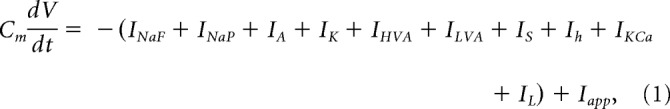 |
where Cm = 20 pF is the cell capacitance (Pielecka-Fortuna et al., 2011), V is the cell membrane potential, and t is the time. INaF and INaP are fast transient and persistent sodium currents, respectively. IA is the A-type transient potassium current, and IK is the delayed-rectifier or sustained potassium current. IHVA and ILVA are high-voltage-activated and low-voltage-activated calcium currents. IS describes a slow inward calcium current. Ih is the hyperpolarization-activated nonspecific cation current. IKCa is a calcium-dependent potassium current, and IL is the leak current. Iapp is the applied current, which was adjusted to hold the cell membrane at −60 mV.
Individual ionic currents were modeled using Ohm's law, I = G(V − E), where G is the conductance, V is the membrane potential, and E is the reversal potential for that ion. V − E describes the driving force across the membrane, and G is equal to the maximum conductance if all channels are open (g) multiplied by the proportion of open channels. For the majority of currents, the proportion of open channels was estimated using the Hodgkin–Huxley formalism as follows:
where m and h indicate activation and inactivation gating variables and p is the number of independent activation gates. The Hodgkin–Huxley formalism was also used for the following currents:
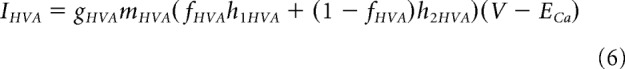 |
In the case of IA, IHVA, and Ih, the inactivation variable is the weighted sum of gating variables hi, which have different voltage-dependent time constants and represent two different populations of inactivating gates present in the cell membrane as follows:
 |
where fA = 0.8, fHVA = 0.2, fh = 0.384 for h1A, h1HVA, and h1h, respectively.
The activation and inactivation gating variables are governed by the following:
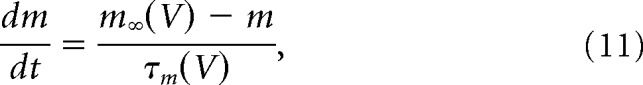 |
 |
where m∞ and h∞ are steady-state activation and inactivation functions and τ is the time constant (which can be voltage-dependent or independent) in milliseconds. Steady-state activation and inactivation functions are of the following form:
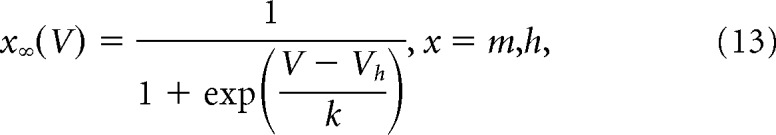 |
V is the membrane potential, Vh is voltage at half-activation or inactivation, and k is the steepness of the steady-state function.
Voltage-dependent time constants were estimated from one of two functions as follows:
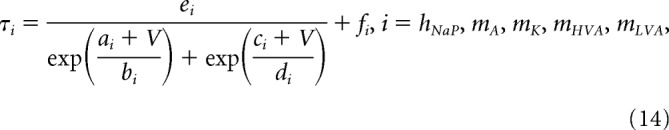 |
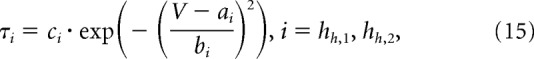 |
where V is the membrane potential and a–e, and f are constants. Parameter estimates for f were close to 0 or 0 for mA, mK, and mLVA.
Fast transient sodium current is described using a Markov model with each of three subunits having three states, open (O), closed (C), and inactivated (I), as in Moran et al. (2016) as follows:
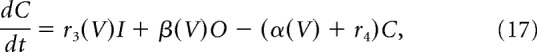 |
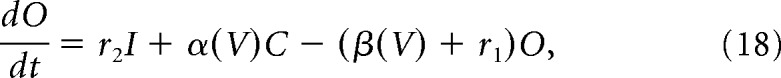 |
V is the membrane potential, r1, r2, and r4 are voltage-independent constants, and r3, α, and β are voltage-dependent constants described by the following:
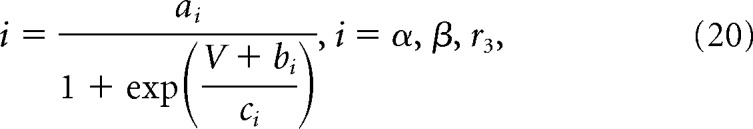 |
where a–c are constants.
Calcium-activated potassium currents were estimated with the current equation as follows:
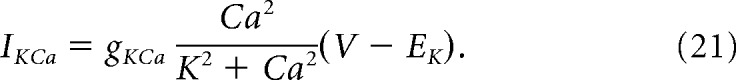 |
Here, K = 1.0 μm, and Ca is the calcium concentration (μm) in the cytosol. Cytosolic calcium increased when calcium entered the cell through voltage-gated channels (ICa) and decreased when it was pumped out of the cytosol through calcium-ATPases. Calcium is governed by the following equations:
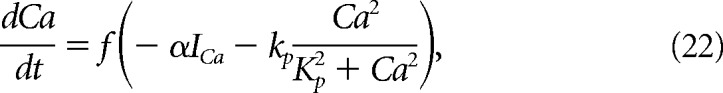 |
where f = 0.0025 is the fraction of unbound calcium in the cytosol, ICa is the total calcium current, kp = 0.265 μm/ms is the maximum pump rate, Kp = 1.2 μm is the concentration of calcium at which half of the pumps are occupied, and α = 0.00185 μm/(pA · ms) is a current to flux conversion factor.
Leak current was estimated with the following function:
GABA conductances were estimated with single exponential decay as described above.
Experiments studying ionic conductances in the daily surge model demonstrated four parameters that differ among cells from OVX, OVX+E AM, and OVX+E PM animals: the maximum conductances (g) of IA, ILVA, and INaP, and the V1/2 inactivation of IA. Our experimental data indicated that GnRH neuron firing and AP characteristics do not differ between OVX and negative feedback despite having different ionic conductance characteristics. A Markov Chain Monte Carlo method estimated probability distributions for the four estradiol and time-of-day-dependent parameters to predict intrinsic properties underlying excitability changes (Adams et al., 2018b). A single identifiable distribution of solutions accounted for similar GnRH neuron excitability in all groups other than positive feedback despite different underlying conductance properties. This was attributable to the interdependence of voltage-gated potassium channel properties: as gA increased, V1/2 became more hyperpolarized, thus maintaining the same AP response to current injection. For the present work, we thus picked 10 parameter sets that traverse the entire distribution range to represent both OVX and negative feedback parameter sets (which do not vary in excitability) in our negative feedback model. Because the Markov Chain Monte Carlo method did not converge to a single, identifiable distribution of solutions in the case of positive feedback (Adams et al., 2018b), 10 representative parameter sets were chosen to produce 10 separate positive feedback neurons.
Maximum conductance values and reversal potentials are in Table 1. Parameter values for the activation and inactivation variables are in Table 2. Parameter values for INaF are in Table 3. Parameters that varied between the negative and positive feedback models are in Table 4.
Table 1.
Parameter values for ionic currents appearing in Equations 2–9a
| E (mV) | g (nS) | |
|---|---|---|
| INaF | 54 | 758 |
| INaP | 54 | Table 4 |
| IA | −101 | Table 4 |
| IK | −101 | 57 |
| ILVA | 82.5 | 0.0679 |
| IHVA | 82.5 | Table 4 |
| IS | 82.5 | 0.18 |
| Ih | −40 | 1 |
| IKCa | −101 | 1.18 |
| IL | −65 | 1 |
aE, Reversal potential; g, maximum conductance. Parameters are from the following: Zhang et al. (2009), Sun et al. (2010), and Pielecka-Fortuna et al. (2011).
Table 2.
Parameter values for the activation and inactivation variables appearing in Equations 13–15a
|
INaP |
IA |
IK |
ILVA |
IHVA |
IS |
Ih |
||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| m | h | m | h1 | h2 | m | m | h | m | h1 | h2 | m | h1 | h2 | |
| Vh (mV) | −41.5 | −47.4 | −29.4 | b | b | −19.7 | −51.4 | −80.1 | −11 | −36.6 | −36.6 | −45 | −77.4 | −77.4 |
| k (mV) | −3.0 | 8.2 | −6.64 | 4.26 | 4.26 | −12.3 | −4.07 | 5.5 | −7 | 14.6 | 14.6 | −12 | 9.2 | 9.2 |
| τ (ms) | 0.4 | Eq. 14 | Eq. 14 | 7.67 | 100 | Eq. 14 | Eq. 14 | 250 | 0.816 | 53.4 | 728 | 1500 | Eq. 15 | Eq. 15 |
| a | — | 67.3 | −2.91 | — | — | 23.8 | 31.3 | — | — | — | — | — | −89.8 | −82.6 |
| b | — | −27.5 | 25.6 | — | — | 18 | 10.1 | — | — | — | — | — | 11.6 | 25.7 |
| c | — | 67.3 | 65.3 | — | — | 23.8 | 31.3 | — | — | — | — | — | 35.8 | 370.9 |
| d | — | 27.5 | −10.6 | — | — | −18 | −10.1 | — | — | — | — | — | 7.6 | 54.1 |
| e | — | 574.5 | 1 | — | — | 10.6 | 109 | — | — | — | — | — | — | — |
| f | — | 62.6 | 0.0527 | — | — | 0 | 0.0391 | — | — | — | — | — | — | — |
aVh and k are the voltage at half-activation or inactivation and the steepness of the steady-state function. τ, Time constant that is voltage independent for mNap, h1A, h2A, hLVA, mHVA, h1HVA, h2HVA, and ms. For hNaP, mA, mK, mLVA, h1h, and h2h, τ is voltage-dependent and governed by Equation 14 (a, b, c, and d are in mV, e and f are in ms) or Equation 15 (a and b are in mV, and c is in ms).
bSee Table 4.
Table 3.
| α(V) | β(V) | r1 | r2 | r3(V) | r4 | |
|---|---|---|---|---|---|---|
| Rate (ms−1) | Eq. 20 | Eq. 20 | 1.0 | 0.2 | Eq. 20 | 0.05 |
| a (ms−1) | 55 | 60 | — | — | 30 | — |
| b (mV) | 6.4 | 32 | — | — | 77.5 | — |
| c (mV) | −15.9 | 10 | — | — | 12 | — |
aα(V) and β(V) describe the transition rates (ms−1) between the closed and open states, r1 and r2 describe the transition rates between the open and inactivated states, and r3(V) and r4 describe the transition rates between the inactivated and closed states. α(V), β(V), and r3(V) are voltage-dependent, whereas r1, r2, and r4 are voltage-independent. Maximum conductance was reestimated to be 758 nS.
Table 4.
Parameter sets for negative feedback and positive feedback GnRH models
| Parameter (figure) | gNaP (nS) | gA (nS) | V1/2 inact (IA, mV) | gHVA (nS) |
|---|---|---|---|---|
| Positive feedback | ||||
| Model 1 (Fig. 5A) | 1.006 | 391.953 | −73.382 | 3.099 |
| Model 2 (Fig. 5B) | 0.741 | 473.829 | −74.577 | 2.989 |
| Model 3 (Fig. 5C) | 0.929 | 467.298 | −74.244 | 3.483 |
| Model 4 (Fig. 5D) | 1.068 | 444.406 | −73.833 | 4.265 |
| Model 5 (Fig. 5E) | 1.598 | 447.050 | −73.019 | 7.348 |
| Model 6 (Fig. 5F) | 1.167 | 394.336 | −72.585 | 6.824 |
| Model 7 (Fig. 5G) | 1.974 | 411.111 | −72.143 | 9.407 |
| Model 8 (Fig. 5H) | 0.781 | 244.552 | −71.273 | 2.342 |
| Model 9 (Fig. 5I) | 0.804 | 230.366 | −70.988 | 2.389 |
| Model 10 (Fig. 5J) | 0.713 | 202.316 | −70.469 | 1.643 |
| Negative feedback | ||||
| Model 11 (Fig. 5K) | 0.389 | 313.792 | −69.785 | 4.815 |
| Model 12 (Fig. 5L) | 0.515 | 291.525 | −69.176 | 6.394 |
| Model 13 (Fig. 5M) | 0.391 | 338.008 | −70.352 | 4.071 |
| Model 14 (Fig. 5N) | 0.284 | 329.019 | −70.220 | 4.000 |
| Model 15 (Fig. 5O) | 0.350 | 328.879 | −70.124 | 4.591 |
| Model 16 (Fig. 5P) | 0.351 | 320.634 | −69.962 | 4.560 |
| Model 17 (Fig. 5Q) | 0.403 | 312.056 | −69.693 | 5.608 |
| Model 18 (Fig. 5R) | 0.361 | 305.658 | −69.591 | 5.592 |
| Model 19 (Fig. 5S) | 0.504 | 305.299 | −69.464 | 6.206 |
| Model 20 (Fig. 5T) | 0.468 | 296.911 | −69.333 | 6.022 |
All simulations were performed in MATLAB (MathWorks; https://www.mathworks.com/). MATLAB scripts are available upon request.
Experimental design.
We measured GnRH neuron response to conductance trains modeled from previously recorded PSC trains (example in Fig. 1). Representative 30 s PSC trains for each group (OVX AM, OVX+E AM, OVX+E PM) were chosen based upon mean isolated spontaneous GABA PSC amplitude and frequency from a published dataset containing voltage-clamp recordings of >300 cells from OVX AM, OVX PM, OVX+E AM, and OVX+E PM mice (Christian and Moenter, 2007). Because OVX AM and OVX PM trains did not differ in mean frequency, interevent interval distribution, or amplitude (Christian and Moenter, 2007), these groups were combined. For each PSC train, conductance of each event was calculated (g = I/(V − EGABA)) (OVX AM: mean gmax = 0.78 ± 0.1 nS, n = 6 events; OVX+E AM: gmax = 0.73 ± 0.2, n = 4 events; OVX+E PM: gmax = 0.9 ± 0.2, n = 18 events; p > 0.6, one-way ANOVA). Peak conductances and event times were used to construct a new PSg train using the physiologic decay time constant determined above (10 ms). Each of the three trains was injected in random order 1–4 times into cells from OVX AM, OVX PM, OVX+E AM, and OVX+E PM animals. Direct current (<30 pA, 1.7 ± 2.5 pA, n = 34) was adjusted to keep cells within 3 mV of −59 mV. A duration of 30 s for PSg trains was chosen because it permitted data collection in response to all three train types within a 7 min period after recording stabilization, a time period during which GnRH neurons do not experience a decrease in excitability (Adams et al., 2018b). Because cells from OVX AM and PM mice did not differ in the number of APs fired in response to conductance trains (n = 8 and n = 6, respectively, p > 0.59, two-tailed Mann–Whitney U test), these groups were combined for analysis.
Figure 1.
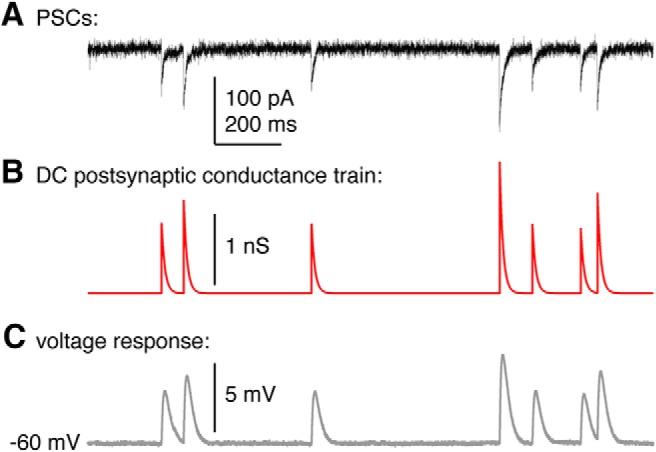
GABA PSCs in voltage clamp were used to construct a PSg train for dynamic-clamp studies. A, GABA PSCs recorded at −70 mV in voltage clamp using a high-chloride pipette solution that slows decay time. B, Simulated dynamic-clamp PSg train constructed from the peak times and amplitudes in A, but using the decay time constant (10 ms) observed with physiological pipette chloride. C, Response by an RC (resistor-capacitor) circuit to the PSg train in B.
Statistical analyses.
Data were analyzed using Prism 7 (GraphPad) or SPSS (IBM) and are reported as the mean ± SEM unless otherwise noted. The number of cells per group is indicated by n. No more than three cells were used per animal with at least 5 animals tested per group (OVX 14 cells from 7 mice; OVX+E AM 10 cells from 6 mice; OVX+E PM 10 cells from 6 mice). Data distribution was tested with Shapiro–Wilk. Data requiring one-way analyses were compared using one-way ANOVA with Fisher's least square difference (LSD) post hoc analysis or Kruskal–Wallis test with Dunn's post hoc analysis as dictated by data distribution. All data requiring two-way or three-way analyses were compared using two-way or three-way ANOVA with Fisher's LSD post hoc analysis, respectively. ANOVA did not assume equal subgroup sizes. Fisher's LSD was selected because of the large number (16–18) of multiple comparisons being examined. Significance was set at p < 0.05, but all p values <0.1 are specified. Slopes and intercepts were fit using linear regression, and ANCOVA were performed to compare slopes and intercepts among groups.
Results
Both PSg frequency and estradiol feedback contribute to increases in GnRH neuron firing rate
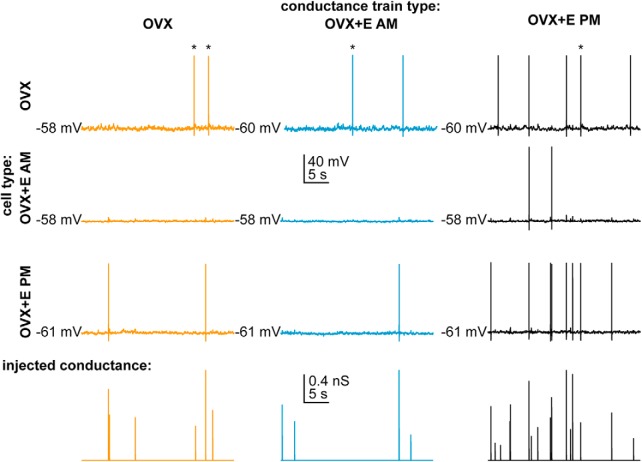
In the daily surge model, estradiol and time-of-day interact to alter GnRH neuron intrinsic properties, resulting in increased spontaneous firing rate and excitability during positive feedback (Christian et al., 2005; Adams et al., 2018b). To investigate whether observed concomitant changes in GABAergic transmission (Christian and Moenter, 2007) play a critical role in increasing GnRH neuron firing, we used dynamic clamp to deliver GABA PSg trains mimicking the input measured during negative feedback, positive feedback, and the open feedback loop condition into cells from OVX+E AM, OVX+E PM, and OVX mice (AM and PM combined). Figure 2 shows representative AP firing from all three animal models in response to all three conductance trains. Spikes were identified as induced by a PSg if they occurred during the resulting postsynaptic potential and before the membrane potential returned to baseline (typically near the PSP peak). In one cell from each of 2 animals in positive feedback, a PSg initiated a burst of APs; all of these events were counted as induced events if the time interval between subsequent events was ≤250 ms and if a continuous increase in Vm between spikes was observed. In some cells, spontaneous spikes (that did not meet the above definition) occurred; these are marked with an asterisk in Figure 2. The number of spontaneous APs was not different between PSg trains or among groups (OVX+E PM: 3.2 ± 0.8 spikes; OVX+E AM: 0.3 ± 0.2 spikes; OVX 2.4 ± 0.6 spikes; p > 0.1, two-way repeated-measures ANOVA). Data quantifying response to trains (Fig. 3) include only spikes that were induced by a PSg.
Figure 2.
Representative recordings of cells from OVX (top), OVX+E AM (middle), and OVX+E PM (bottom) animals in response to conductance trains from OVX (orange), OVX+E AM (blue), and OVX+E PM (black) conditions. *Spontaneous APs that were not induced by a PSg.
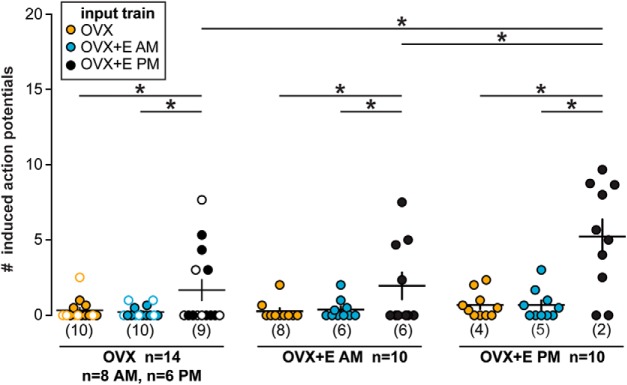
Figure 3.
Positive feedback conductance trains are most effective at initiating spikes, and positive feedback animal models are most responsive. Individual values and mean ± SEM spikes induced during individual PSgs in each train in all three cell types. In the OVX group, open circles represent cells recorded in the PM and closed circles represent cells recorded in the AM. Numbers in parentheses along x axis indicate number of cells not firing any spikes. *p < 0.05, two-way repeated-measures ANOVA/Fisher's LSD test (cell type: F(2,31) = 3.8, p = 0.03; train: F(2,62) = 33.4, p < 0.001; interaction: F(4,62) = 5.3, p = 0.001).
The positive feedback PSg train induced more APs in cells from all three animal models than the negative feedback or open-loop OVX PSg trains (Fig. 3; p < 0.05, two-way repeated-measures ANOVA/Fisher's LSD). In addition to PSg train type, the animal model of the recorded cell influenced the GnRH response. Specifically, positive feedback trains initiated more induced APs in cells during positive feedback (OVX+E PM) than in cells during negative feedback (OVX+E AM) or cells from OVX mice. These changes were not attributable to differences in input resistance, capacitance, or holding current among groups (Table 5). There was no difference in number of APs induced by PSg trains from negative feedback versus the open-loop condition among any of the groups, despite a difference in frequency and amplitude of GABA transmission between these states (Christian and Moenter, 2007).
Table 5.
| Parameter | OVX | OVX + E AM | OVX + E PM |
|---|---|---|---|
| Mean ± SEM of GnRH whole-cell passive properties from Figures 2–4 | |||
| Input resistance (mΩ) | 951 ± 60 | 819 ± 68 | 1040 ± 96 |
| Capacitance (pF) | 16.9 ± 0.9 | 15.4 ± 1.0 | 14.9 ± 0.8 |
| Series resistance(mΩ) | 11.6 ± 0.9 | 11.4 ± 0.8 | 11.6 ± 0.8 |
| Holding current (pA) | 0.7 ± 4.1 | 6.1 ± 3.8 | −8.3 ± 4.5 |
| One-way ANOVA for comparison of GnRH passive properties among groups: cells from diestrous and proestrous mice (Figs. 2–4) | |||
|---|---|---|---|
| Group | |||
| Input resistance (mΩ) | F(2,31) = 2.1 | — | — |
| Capacitance (pF) | KW statistic = 2.3 | — | — |
| Series resistance (mΩ) | KW statistic = 0.6 | — | — |
| Holding current (pA) | KW statistic = 4.8 (p = 0.09) | — | — |
Properties of PSgs associated with successful spike initiation
To assess whether amplitude of the PSg and/or time between these events affected the probability of inducing an AP, PSgs from all trains were combined and sorted according to their peak conductance and preceding interevent interval. Increased peak conductance was correlated with increased probability of initiating an AP in cells from all three animal models (Fig. 4A,B; OVX+E AM: r2 = 0.84, p < 0.001; OVX: r2 = 0.62, p < 0.0001; OVX+E PM: r2 = 0.76, p < 0.0001 by linear regression) and the slopes of the linear regressions differed among these, being greatest in OVX+E PM cells and lowest in OVX cells (OVX+E PM slope = 0.43 ± 0.05; OVX slope = 0.13 ± 0.02; OVX+E AM slope = 0.23 ± 0.02; F = 22.35, p < 0.0001 by linear regression). In contrast, the likelihood of initiating a spike was independent of interevent interval (Fig. 4C,D; p > 0.1, linear regression/ANCOVA). The slopes of the linear regressions of interevent interval did not differ among cells from different animal models, but the overall intercepts did (OVX+E PM = 0.27 ± 0.05; OVX+E AM = 0.076 ± 0.02; OVX = 0.072 ± 0.02; F = 7.6, p < 0.0001), reflecting the increased response to PSg trains during positive feedback relative to all other cell types.
Figure 4.
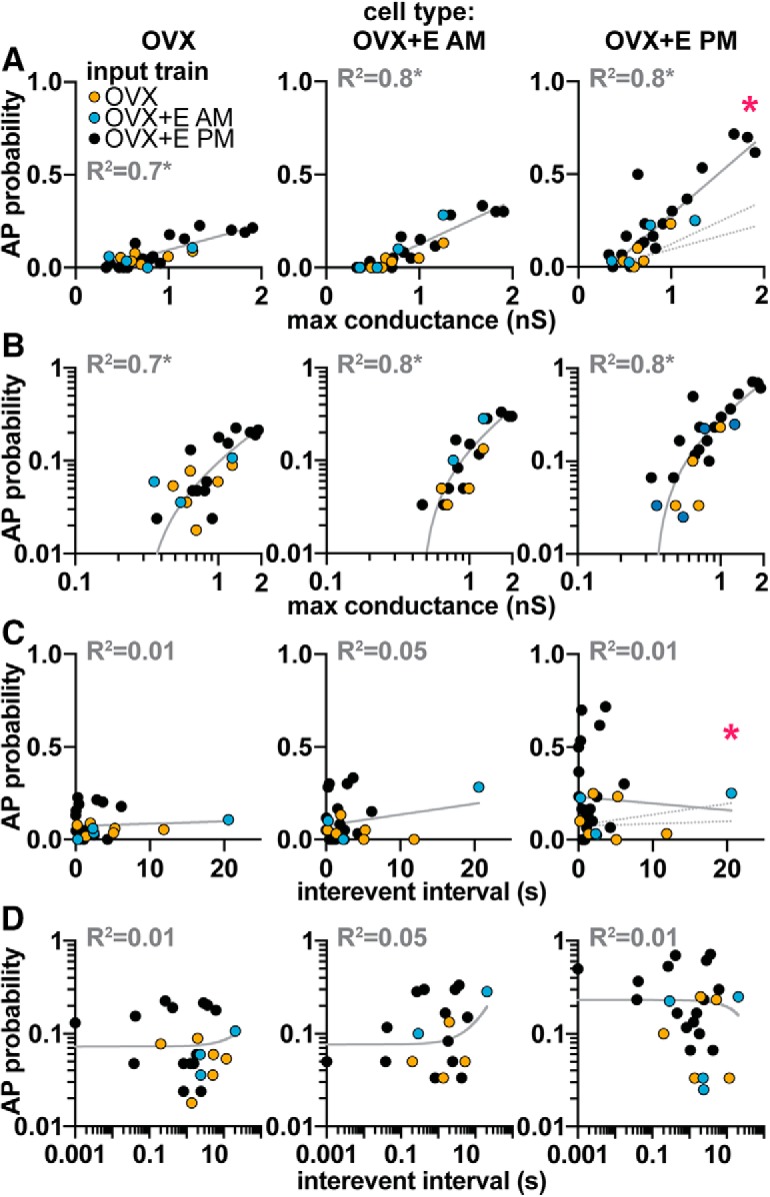
Increasing maximum peak conductance increases the probability of initiating an AP. Mean likelihood of initiating an AP for individual conductances from OVX (orange), OVX+E AM (blue), and OVX+E PM (black) PSg trains in cells from OVX (left column), OVX+E AM (middle column), and OVX+E PM (right column) mice, considering the following: conductance amplitude (A, linear scale; B, log-log scale) or time since previous event (C, linear scale; D, log-log scale). Different number of points between linear and log-log scales is attributable to exclusion of 0 values on the latter. Gray lines in left and middle columns indicate a linear fit to the data. R2 is indicated above each fit. Gray asterisk indicates that the slope of the linear regression is significantly non-zero, suggesting the correlation is significant (p < 0.0001); and the three individual fits (from OVX, OVX+E AM, and OVX+E PM cells) are shown in the right-most column; with red asterisks indicating p < 0.05 ANCOVA (A, slope: F(2,78) = 22.4; C, slope: F(2,78) = 0.5, intercept: F(2,80) = 8.4).
Both PSg frequency and estradiol feedback contribute to increases in firing rate in models of GnRH neurons
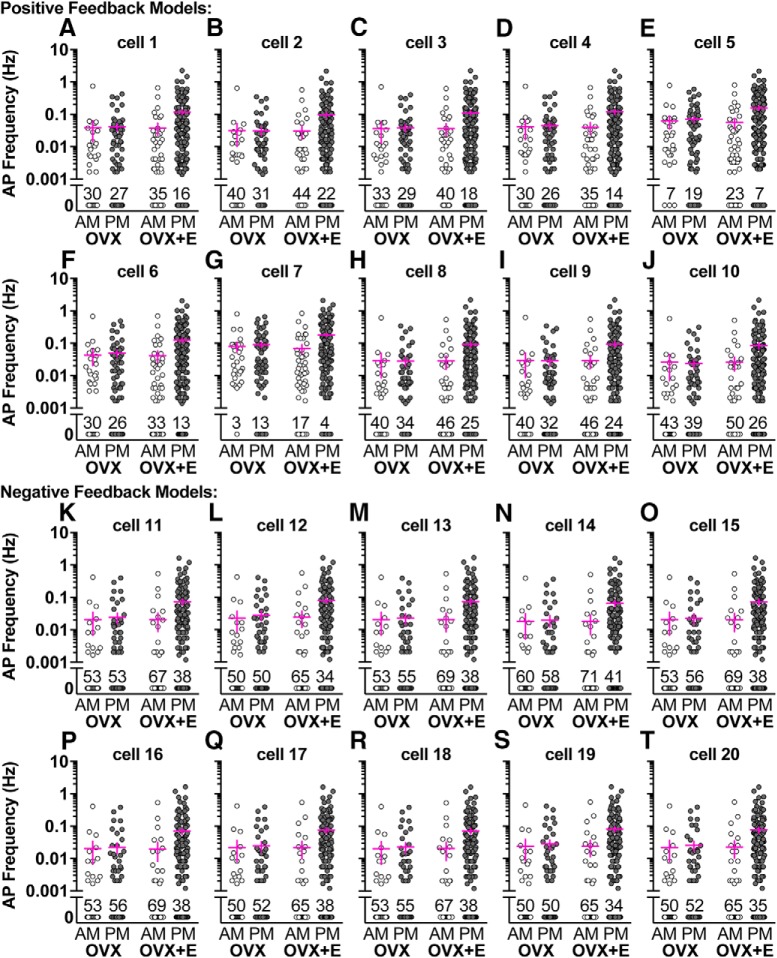
We have demonstrated that both fast-synaptic input and GnRH neuron intrinsic properties contribute to firing rate. Whole-cell patch-clamp recordings of the required stability are limited to 10 to 20 min, however, and our dynamic-clamp dataset was limited to the response to representative 30 s patterns of PSCs selected from a much larger dataset of >1000 two min PSC trains from >300 cells recorded by Christian and Moenter (2007). To measure GnRH response to this entire dataset, we used mathematical models of GnRH neurons during multiple feedback states first developed to predict intrinsic properties underlying excitability changes. One model identified a single, unimodal distribution of solutions (parameter sets) to account for similar GnRH neuron excitability in OVX/negative feedback neurons despite different underlying conductance properties; this was attributable to the interdependence of voltage-gated potassium channel properties. In contrast, there was not a single distribution of solutions to account for the positive feedback model, perhaps indicative of redundant mechanisms for achieving the positive feedback state essential for reproduction.
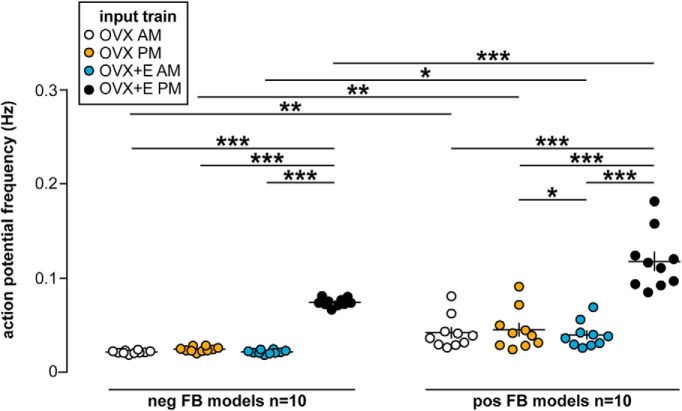
Given this, we chose 10 parameter sets for “negative feedback” cells that traversed the range of parameters expected for both OVX and OVX+E AM cells while also reproducing OVX/OVX+E AM excitability, and 10 positive feedback cells chosen in a similar fashion (Table 4). Each model neuron was exposed to >1000 two min PSg trains from 307 GnRH neurons (30 OVX AM, 62 OVX PM, 48 OVX+E AM, and 167 OVX+E PM) and APs generated by the model were counted. Recording duration varied in Christian and Moenter (2007), so different numbers of PSg trains were available from each recorded cell. Model response to all the PSg trains from a recorded GnRH neuron was averaged to account for variability in recording duration. Firing response of a single model neuron did not differ among PSg train types (two-way ANOVA; Fig. 5; Table 6). In contrast, when mean response to PSg conductance trains was compared among all 20 model neurons, both train type and feedback model contributed to firing frequency (Fig. 6). The positive feedback (OVX+E PM) conductance trains initiated more APs in both negative and positive feedback model neurons (three-way repeated-measures ANOVA/Fisher's LSD, p < 0.001). Further, all four conductance train types initiated more APs in positive feedback model neurons relative to negative feedback model neurons (three-way repeated-measures ANOVA/Fisher's LSD, p < 0.001).
Figure 5.
Positive and negative feedback model response to OVX AM, OVX PM, OVX+E AM, and OVX+E PM conductance trains from cells recorded by Christian and Moenter (2007). A–T, Each graph represents a single-model neuron, and each data point is that model neuron's response to PSg trains from a single GnRH neuron prepared from OVX AM (30 cells), OVX PM (62 cells), OVX+E AM (48 cells), or OVX+E PM (167 cells) mice. In some cases, PSg trains from a single GnRH neuron did not induce AP firing (frequency = 0 Hz); the percentage of cells that did not induce AP firing in the model neurons is indicated above the 0 Hz data points for each group.
Table 6.
Two-way ANOVA parameters for comparison of model GnRH neuron response to OVX AM, OVX PM, OVX + E AM, and OVX + E PM PSg trainsa
| Parameter (figure) | Estradiol | Time-of-day | Interaction |
|---|---|---|---|
| Positive feedback | |||
| Model 1 (Fig. 5A) | F(1,303) = 1.7 | F(1,303) = 2.1 | F(1,303) = 1.8 |
| Model 2 (Fig. 5B) | F(1,303) = 1.6 | F(1,303) = 1.7 | F(1,303) = 1.7 |
| Model 3 (Fig. 5C) | F(1,303) = 1.7 | F(1,303) = 2.0 | F(1,303) = 1.8 |
| Model 4 (Fig. 5D) | F(1,303) = 1.7 | F(1,303) = 2.2 | F(1,303) = 1.9 |
| Model 5 (Fig. 5E) | F(1,303) = 1.7 | F(1,303) = 3.2 (p = 0.07) | F(1,303) = 2.3 |
| Model 6 (Fig. 5F) | F(1,303) = 1.8 | F(1,303) = 2.6 | F(1,303) = 1.9 |
| Model 7 (Fig. 5G) | F(1,303) = 1.6 | F(1,303) = 3.8 (p = 0.05) | F(1,303) = 2.6 |
| Model 8 (Fig. 5H) | F(1,303) = 1.6 | F(1,303) = 1.5 | F(1,303) = 1.6 |
| Model 9 (Fig. 5I) | F(1,303) = 1.6 | F(1,303) = 1.5 | F(1,303) = 1.6 |
| Model 10 (Fig. 5J) | F(1,303) = 1.5 | F(1,303) = 1.3 | F(1,303) = 1.5 |
| Negative feedback | |||
| Model 11 (Fig. 5K) | F(1,303) = 1.4 | F(1,303) = 1.7 | F(1,303) = 1.4 |
| Model 12 (Fig. 5L) | F(1,303) = 1.5 | F(1,303) = 2.0 | F(1,303) = 1.4 |
| Model 13 (Fig. 5M) | F(1,303) = 1.4 | F(1,303) = 1.7 | F(1,303) = 1.4 |
| Model 14 (Fig. 5N) | F(1,303) = 1.3 | F(1,303) = 1.5 | F(1,303) = 1.3 |
| Model 15 (Fig. 5O) | F(1,303) = 1.4 | F(1,303) = 1.6 | F(1,303) = 1.4 |
| Model 16 (Fig. 5P) | F(1,303) = 1.3 | F(1,303) = 1.6 | F(1,303) = 1.4 |
| Model 17 (Fig. 5Q) | F(1,303) = 1.4 | F(1,303) = 1.8 | F(1,303) = 1.4 |
| Model 18 (Fig. 5R) | F(1,303) = 1.4 | F(1,303) = 1.7 | F(1,303) = 1.4 |
| Model 19 (Fig. 5S) | F(1,303) = 1.5 | F(1,303) = 2.0 | F(1,303) = 1.5 |
| Model 20 (Fig. 5T) | F(1,303) = 1.5 | F(1,303) = 1.8 | F(1,303) = 1.4 |
aData from Christian and Moenter (2007).
Figure 6.
Conductance trains from OVX+E PM GnRH neurons are most effective at initiating spikes in model neurons, but the feedback model also affects response. Individual values and mean ± SEM frequency during PSg trains prepared from OVX AM, OVX PM, OVX+E AM, and OVX+E PM mice in negative feedback (neg FB) and positive feedback (pos FB) model neurons. *p < 0.05, **p < 0.01, ***p < 0.0001: three-way repeated-measures ANOVA/Fisher's LSD test (PSg time-of-day: F(1,18) = 395, p < 0.001; PSg estradiol: F(1,18) = 2989, p < 0.001; PSg estradiol × time-of-day: F(1,18) = 910, p < 0.001; PSg time-of-day × feedback model: F(1,18) = 13.8, p = 0.002; PSg estradiol × feedback model: F(1,18) = 85.6, p < 0.001; PSg estradiol × time-of-day × feedback model: F(1,18) = 37.5, p < 0.001).
Discussion
The brain regulates fertility via GnRH release. For most of the mammalian reproductive cycle, GnRH release is pulsatile and estradiol feedback suppresses GnRH and LH release. At the end of the follicular phase, high sustained estradiol levels initiate a surge of continuous GnRH release culminating in ovulation (Sarkar et al., 1976; Moenter et al., 1991). This shift in estradiol feedback is associated with changes in both intrinsic properties of, and synaptic inputs to, these cells. Here we show that, during positive feedback, GnRH neurons integrate changes in their intrinsic properties with changes to fast-synaptic transmission to increase firing rate.
This work supports findings demonstrating increased GABAergic drive to GnRH neurons is correlated with increased firing rate in several animal models (Sullivan and Moenter, 2004, 2005; Christian et al., 2005; Pielecka et al., 2006; Christian and Moenter, 2007; Roland and Moenter, 2011; Adams et al., 2018a). Past conclusions have been limited to speculation regarding the relationship of these parameters measured in independent studies. The present work extends those findings by demonstrating directly increased effectiveness of GABAergic transmission mimicking positive feedback in driving firing of GnRH neurons from all animal models both in dynamic-clamp and modeling studies. It further reveals that the intrinsic changes that occur in GnRH neurons during positive feedback (Chu and Moenter, 2006; Sun et al., 2010; Pielecka-Fortuna et al., 2011; Adams et al., 2018b) are sufficiently robust to poise the cell for increased response to synaptic input.
The dynamic-clamp data were limited for practical reasons to one representative conductance train per feedback state. These data were supported by results using mathematical models of GnRH neurons developed to reproduce GnRH neuron firing response to current injection during positive feedback, and during negative feedback and in the open-loop condition (which exhibit similar excitability). Based on experimental data, five parameters were varied between these feedback state models (those governing IA, INaP, and IHVA) (Chu and Moenter, 2006; Zhang et al., 2007, 2009; Sun et al., 2010; Pielecka-Fortuna et al., 2011). Ten parameter sets traversing the full parameter range were examined for each feedback state. For all model neurons, conductance trains mimicking GABAergic transmission during positive feedback invoked greater firing rates than conductance trains mimicking negative feedback or OVX states. Further, regardless of conductance train type, positive feedback model neurons fired more frequently than negative feedback/OVX neurons. This suggests that IA, INaP, and IHVA likely contribute to the enhanced firing response to fast-synaptic inputs during positive feedback. Of interest in this regard, blocking IHVA decreases GnRH neuron response rate to dynamic-clamp induced GABA PSgs (Hemond et al., 2012).
Spontaneous GnRH neuron firing rate monitored using extracellular recordings in cells from OVX mice is intermediate to that of cells from OVX+E AM and OVX+E PM mice in the daily surge model (Christian et al., 2005). In contrast, no differences were observed in the present study between cells from brain slices prepared during negative feedback versus the open-loop condition in GnRH neuron AP firing in response to any conductance train. Similarly, there was no difference between the negative feedback and open-loop condition in GnRH neuron excitability (Adams et al., 2018b). There are several possible explanations for this difference. First, the present work was done in the whole-cell configuration, which dialyzes many second messenger systems; extracellular recordings are not subject to this limitation. Second, fast synaptic transmission was not inhibited during extracellular recordings; although of very low frequency, glutamatergic inputs may also contribute to differences in firing rate. Third, the GABAergic PSCs used to generate PSg trains were monitored with blockers of glutamatergic transmission and, thus, may underestimate actual values. Fourth, it is possible that 30 s patterns are not sufficient for observing a difference in firing rate between these two cell types, considering that most extracellular recordings determining firing rate were averaged over 30 min to 1 h. This is supported by the finding that differences in firing rate between positive and negative feedback model neurons exposed to longer PSg trains were detected for every train type, and a difference in response to OVX PM and OVX+E AM conductance trains could be detected in positive feedback model neurons.
In many neurons, postsynaptic potentials decay to baseline in a matter of milliseconds (<100 ms), and tens to hundreds of coordinated PSPs are necessary to initiate an AP. Some neurons in the hypothalamus appear unique in that their membrane potentials decay more slowly, permitting fast-synaptic inputs to summate over prolonged timescales. For example, in AGRP, POMC, and PVH neurons, activation of a voltage-gated sodium current slows postsynaptic potential decay times and, consequently, relatively few successive postsynaptic potentials can depolarize the membrane until threshold is reached and a spike is initiated (Branco et al., 2016). Given these observations, we postulated that decreasing time between successive PSgs would increase spiking. We rejected this hypothesis as interevent interval did not influence the probability of initiating a spike over the intervals tested, perhaps because sufficiently short intervals did not occur in the datasets used. In vivo, with all synaptic connections present, it is possible that shorter interevent intervals that are more effective in initiating APs exist. In contrast to the lack of effect of interevent interval, peak conductance amplitude was highly correlated with AP firing. These data suggest that PSg amplitudes and GnRH neuron responsiveness appear to be more important than coordinated or successive GABA release from GnRH afferents, at least within the limitations of brain slices. It is tempting to speculate that shifts in conductance via the GABAA receptor also modulate GnRH neuron activity in vivo. Numerous substances interact with this receptor in an allosteric manner to increase total conductance, including benzodiazepines and the neurosteroid allopregnanolone (Defazio and Hablitz, 1998; Sullivan and Moenter, 2003). It is also possible that the composition of GABAA receptor subunits shifts among feedback conditions (Sim et al., 2000; Burger et al., 2018)
Afferent neurons and the postsynaptic responses they initiate (fast synaptic and neuromodulatory) are likely to play a major role in estradiol feedback as GnRH neurons typically do not express detectable estrogen receptor α (Hrabovszky et al., 2000, 2001; Couse et al., 2003; Wintermantel et al., 2006; Christian et al., 2008). Kisspeptin neurons of anteroventral periventricular (AVPV) nucleus, which use GABA as a cotransmitter and express estrogen receptor α, are one likely relay (Cravo et al., 2011). The neuromodulator kisspeptin acts directly on GnRH neurons to modulate multiple ionic currents, enhance GnRH neuron excitability, and stimulate AP firing (Pielecka-Fortuna et al., 2008, 2011; Zhang et al., 2008, 2013; Adams et al., 2018b). AVPV kisspeptin expression is increased by estradiol treatment (Smith et al., 2005) and on the afternoon of proestrus (positive feedback during the cycle) (Smith et al., 2006), and these cells fire higher frequency APs and more bursts under these conditions (Zhang et al., 2015; Wang et al., 2016). We postulate that kisspeptin release during positive feedback enhances GnRH neuron responsiveness to the concurrent increase in GABAergic fast-synaptic inputs. In this regard, estrogen receptor α KO in GABAergic neurons blocked positive feedback and the LH surge in mice (Cheong et al., 2015) and optical activation of GABAergic neurons in the AVPV-initiated LH surges (Kalil et al., 2016). Countering these observations, work from the same group demonstrated KO of the γ2 subunit of the GABAA receptor in GnRH neurons does not appear to affect fertility (Lee et al., 2010). Because AVPV neurons can communicate using GABA and/or kisspeptin, increased GABA transmission to GnRH neurons might be interpreted as merely a marker for increased cotransmission of the excitatory neuromodulator (Piet et al., 2018). The present work, however, demonstrates that increasing GABA drive to GnRH neurons likely contributes to their increased firing rate during estradiol positive feedback.
Our focus was on the interaction between GABAergic transmission and GnRH neuron properties. Although estradiol increases glutamatergic transmission to GnRH neurons on proestrus in rats, glutamatergic transmission to GnRH neurons in mice is very low frequency, with no AMPA- or NMDA-mediated currents detected in approximately one-third of cells (Christian et al., 2009; Tada et al., 2013; Liu et al., 2017). The minor differences detected among groups at these low frequencies are unlikely to have a substantial impact on firing, despite a more depolarized reversal potential. Kisspeptin neurons may also have an additional role in driving increased GnRH firing rate as kisspeptin also acts indirectly via unspecified afferents to increase GABA PSC frequency and amplitude, and glutamate EPSC frequency (Pielecka-Fortuna et al., 2008).
Multiple factors can influence the switch from negative to positive feedback. In addition to time-of-day and estradiol-dependent signals, other internal and environmental cues may play a role. It remains unclear whether each of these signals is necessary for initiating the GnRH surge or each acts as a redundant mechanism for ensuring ovulation. The present studies suggest that GnRH neurons do not merely relay upstream signals but act to integrate multiple signals to modulate firing rate and to initiate GnRH release.
Footnotes
This work was supported by National Institute of Health/Eunice Kennedy Shriver National Institute of Child Health and Human Development (NICHD) R01 HD41469 to S.M.M., and R01 NS105825 and R03 NS103029 to C.A.C. C.A. was supported by NIH National Institute of General Medical Sciences T32 GM007863, NICHD T32 HD079342, and NICHD F30 HD085721. L.S.M was supported in part by American Heart Association Grant 13SDG16990083. We thank Elizabeth Wagenmaker and Laura Burger for expert technical assistance; and James L. Kenyon (University of Nevada, Reno) for the Excel spreadsheet used to calculate junction potentials.
The authors declare no competing financial interests.
References
- Adams C, Chen X, Moenter SM (2018a) Changes in GABAergic transmission to and intrinsic excitability of gonadotropin-releasing hormone (GnRH) neuron during the estrous cycle in mice. eNeuro 5:ENEURO.0171-18.2018. 10.1523/ENEURO.0171-18.2018 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Adams C, Stroberg W, DeFazio RA, Schnell S, Moenter SM (2018b) Gonadotropin-releasing hormone (GnRH) neuron excitability is regulated by estradiol feedback and kisspeptin. J Neurosci 38:1249–1263. 10.1523/JNEUROSCI.2988-17.2017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barry PH. (1994) JPCalc, a software package for calculating liquid junction potential corrections in patch-clamp, intracellular, epithelial and bilayer measurements and for correcting junction potential measurements. J Neurosci Methods 51:107–116. 10.1016/0165-0270(94)90031-0 [DOI] [PubMed] [Google Scholar]
- Branco T, Tozer A, Magnus CJ, Sugino K, Tanaka S, Lee AK, Wood JN, Sternson SM (2016) Near-perfect synaptic integration by Nav1.7 in hypothalamic neurons regulates body weight. Cell 165:1749–1761. 10.1016/j.cell.2016.05.019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burger LL, Vanacker C, Phumsatitpong C, Wagenmaker ER, Wang L, Olson DP, Moenter SM (2018) Identification of genes enriched in GnRH neurons by translating ribosome affinity purification and RNASeq in mice. Endocrinology 159:1922–1940. 10.1210/en.2018-00001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheong RY, Czieselsky K, Porteous R, Herbison AE (2015) Expression of ESR1 in glutamatergic and GABAergic neurons is essential for normal puberty onset, estrogen feedback, and fertility in female mice. J Neurosci 35:14533–14543. 10.1523/JNEUROSCI.1776-15.2015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Christian CA, Moenter SM (2007) Estradiol induces diurnal shifts in GABA transmission to gonadotropin-releasing hormone neurons to provide a neural signal for ovulation. J Neurosci 27:1913–1921. 10.1523/JNEUROSCI.4738-06.2007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Christian CA, Mobley JL, Moenter SM (2005) Diurnal and estradiol-dependent changes in gonadotropin-releasing hormone neuron firing activity. Proc Natl Acad Sci U S A 102:15682–15687. 10.1073/pnas.0504270102 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Christian CA, Glidewell-Kenney C, Jameson JL, Moenter SM (2008) Classical estrogen receptor alpha signaling mediates negative and positive feedback on gonadotropin-releasing hormone neuron firing. Endocrinology 149:5328–5334. 10.1210/en.2008-0520 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Christian CA, Pielecka-Fortuna J, Moenter SM (2009) Estradiol suppresses glutamatergic transmission to gonadotropin-releasing hormone neurons in a model of negative feedback in mice. Biol Reprod 80:1128–1135. 10.1095/biolreprod.108.075077 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chu Z, Moenter SM (2006) Physiologic regulation of a tetrodotoxin-sensitive sodium influx that mediates a slow afterdepolarization potential in gonadotropin-releasing hormone neurons: possible implications for the central regulation of fertility. J Neurosci 26:11961–11973. 10.1523/JNEUROSCI.3171-06.2006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Couse JF, Yates MM, Walker VR, Korach KS (2003) Characterization of the hypothalamic-pituitary-gonadal axis in estrogen receptor (ER) null mice reveals hypergonadism and endocrine sex reversal in females lacking ERalpha but not ERbeta. Mol Endocrinol 17:1039–1053. 10.1210/me.2002-0398 [DOI] [PubMed] [Google Scholar]
- Cravo RM, Margatho LO, Osborne-Lawrence S, Donato J Jr, Atkin S, Bookout AL, Rovinsky S, Frazão R, Lee CE, Gautron L, Zigman JM, Elias CF (2011) Characterization of Kiss1 neurons using transgenic mouse models. Neuroscience 173:37–56. 10.1016/j.neuroscience.2010.11.022 [DOI] [PMC free article] [PubMed] [Google Scholar]
- DeFazio RA, Moenter SM (2002) Estradiol feedback alters potassium currents and firing properties of gonadotropin-releasing hormone neurons. Mol Endocrinol 16:2255–2265. 10.1210/me.2002-0155 [DOI] [PubMed] [Google Scholar]
- DeFazio RA, Heger S, Ojeda SR, Moenter SM (2002) Activation of A-type gamma-aminobutyric acid receptors excites gonadotropin-releasing hormone neurons. Mol Endocrinol 16:2872–2891. 10.1210/me.2002-0163 [DOI] [PubMed] [Google Scholar]
- DeFazio RA, Elias CF, Moenter SM (2014) GABAergic transmission to kisspeptin neurons is differentially regulated by time of day and estradiol in female mice. J Neurosci 34:16296–16308. 10.1523/JNEUROSCI.3057-14.2014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Defazio T, Hablitz JJ (1998) Zinc and zolpidem modulate mIPSCs in rat neocortical pyramidal neurons. J Neurophysiol 80:1670–1677. 10.1152/jn.1998.80.4.1670 [DOI] [PubMed] [Google Scholar]
- Glanowska KM, Venton BJ, Moenter SM (2012) Fast scan cyclic voltammetry as a novel method for detection of real-time gonadotropin-releasing hormone release in mouse brain slices. J Neurosci 32:14664–14669. 10.1523/JNEUROSCI.1303-12.2012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hemond PJ, O'Boyle MP, Roberts CB, Delgado-Reyes A, Hemond Z, Suter KJ (2012) Simulated GABA synaptic input and L-type calcium channels form functional microdomains in hypothalamic gonadotropin-releasing hormone neurons. J Neurosci 32:8756–8766. 10.1523/JNEUROSCI.4188-11.2012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Houston CM, Bright DP, Sivilotti LG, Beato M, Smart TG (2009) Intracellular chloride ions regulate the time course of GABA-mediated inhibitory synaptic transmission. J Neurosci 29:10416–10423. 10.1523/JNEUROSCI.1670-09.2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hrabovszky E, Shughrue PJ, Merchenthaler I, Hajszán T, Carpenter CD, Liposits Z, Petersen SL (2000) Detection of estrogen receptor-beta messenger ribonucleic acid and 125I-estrogen binding sites in luteinizing hormone-releasing hormone neurons of the rat brain. Endocrinology 141:3506–3509. 10.1210/endo.141.9.7788 [DOI] [PubMed] [Google Scholar]
- Hrabovszky E, Steinhauser A, Barabás K, Shughrue PJ, Petersen SL, Merchenthaler I, Liposits Z (2001) Estrogen receptor-beta immunoreactivity in luteinizing hormone-releasing hormone neurons of the rat brain. Endocrinology 142:3261–3264. 10.1210/endo.142.7.8176 [DOI] [PubMed] [Google Scholar]
- Kalil B, Mcclennan T, Piet R, Herbison A (2016) Role of rostral periventricular area of the third ventricle (RP3V) GABAergic neurons in generating the preovulatory luteinizing hormone surge in female mouse. In: Society for Neuroscience. San Diego: Neuroscience Meeting Planner. [Google Scholar]
- LeBeau AP, Van Goor F, Stojilkovic SS, Sherman A (2000) Modeling of membrane excitability in gonadotropin-releasing hormone-secreting hypothalamic neurons regulated by Ca2+-mobilizing and adenylyl cyclase-coupled receptors. J Neurosci 20:9290–9297. 10.1523/JNEUROSCI.20-24-09290.2000 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee K, Porteous R, Campbell RE, Lüscher B, Herbison AE (2010) Knockdown of GABA(A) receptor signaling in GnRH neurons has minimal effects upon fertility. Endocrinology 151:4428–4436. 10.1210/en.2010-0314 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Legan SJ, Karsch FJ (1975) A daily signal for the LH surge in the rat. Endocrinology 96:57–62. 10.1210/endo-96-1-57 [DOI] [PubMed] [Google Scholar]
- Liu X, Porteous R, Herbison AE (2017) Dynamics of GnRH neuron ionotropic GABA and glutamate synaptic receptors are unchanged during estrogen positive and negative feedback in female mice. eNeuro 4:ENEURO.0259–17.2017. 10.1523/ENEURO.0259-17.2017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Milescu LS, Yamanishi T, Ptak K, Mogri MZ, Smith JC (2008) Real-time kinetic modeling of voltage-gated ion channels using dynamic clamp. Biophys J 95:66–87. 10.1529/biophysj.107.118190 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moenter SM, Caraty A, Locatelli A, Karsch FJ (1991) Pattern of gonadotropin-releasing hormone (GnRH) secretion leading up to ovulation in the ewe: existence of a preovulatory GnRH surge. Endocrinology 129:1175–1182. 10.1210/endo-129-3-1175 [DOI] [PubMed] [Google Scholar]
- Moran S, Moenter SM, Khadra A (2016) A unified model for two modes of bursting in GnRH neurons. J Comput Neurosci 40:297–315. 10.1007/s10827-016-0598-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Norman RL, Blake CA, Sawyer CH (1973) Estrogen-dependent 24-hour periodicity in pituitary LH release in the female hamster. Endocrinology 93:965–970. 10.1210/endo-93-4-965 [DOI] [PubMed] [Google Scholar]
- Pielecka J, Quaynor SD, Moenter SM (2006) Androgens increase gonadotropin-releasing hormone neuron firing activity in females and interfere with progesterone negative feedback. Endocrinology 147:1474–1479. 10.1210/en.2005-1029 [DOI] [PubMed] [Google Scholar]
- Pielecka-Fortuna J, Chu Z, Moenter SM (2008) Kisspeptin acts directly and indirectly to increase gonadotropin-releasing hormone neuron activity and its effects are modulated by estradiol. Endocrinology 149:1979–1986. 10.1210/en.2007-1365 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pielecka-Fortuna J, DeFazio RA, Moenter SM (2011) Voltage-gated potassium currents are targets of diurnal changes in estradiol feedback regulation and kisspeptin action on gonadotropin-releasing hormone neurons in mice. Biol Reprod 85:987–995. 10.1095/biolreprod.111.093492 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Piet R, Kalil B, McLennan T, Porteous R, Czieselsky K, Herbison AE (2018) Dominant neuropeptide cotransmission in kisspeptin-GABA regulation of GnRH neuron firing driving ovulation. J Neurosci 38:6310–6322. 10.1523/JNEUROSCI.0658-18.2018 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roland AV, Moenter SM (2011) Prenatal androgenization of female mice programs an increase in firing activity of gonadotropin-releasing hormone (GnRH) neurons that is reversed by metformin treatment in adulthood. Endocrinology 152:618–628. 10.1210/en.2010-0823 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sarkar DK, Chiappa SA, Fink G, Sherwood NM (1976) Gonadotropin-releasing hormone surge in pro-oestrous rats. Nature 264:461–463. 10.1038/264461a0 [DOI] [PubMed] [Google Scholar]
- Silveira MA, Burger LL, DeFazio RA, Wagenmaker ER, Moenter SM (2017) GnRH neuron activity and pituitary response in estradiol-induced vs proestrous luteinizing hormone surges in female mice. Endocrinology 158:356–366. 10.1210/en.2016-1771 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sim JA, Skynner MJ, Pape JR, Herbison AE (2000) Late postnatal reorganization of GABA(A) recpetor signalling in native GnRH neurons. Eur J Neurosci 12:3497–3504. 10.1046/j.1460-9568.2000.00261.x [DOI] [PubMed] [Google Scholar]
- Smith JT, Cunningham MJ, Rissman EF, Clifton DK, Steiner RA (2005) Regulation of Kiss1 gene expression in the brain of the female mouse. Endocrinology 146:3686–3692. 10.1210/en.2005-0488 [DOI] [PubMed] [Google Scholar]
- Smith JT, Popa SM, Clifton DK, Hoffman GE, Steiner RA (2006) Kiss1 neurons in the forebrain as central processors for generating the preovulatory luteinizing hormone surge. J Neurosci 26:6687–6694. 10.1523/JNEUROSCI.1618-06.2006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sullivan SD, Moenter SM (2003) Neurosteroids alter gamma-aminobutyric acid postsynaptic currents in gonadotropin-releasing hormone neurons: a possible mechanism for direct steroidal control. Endocrinology 144:4366–4375. 10.1210/en.2003-0634 [DOI] [PubMed] [Google Scholar]
- Sullivan SD, Moenter SM (2004) Prenatal androgens alter GABAergic drive to gonadotropin-releasing hormone neurons: implications for a common fertility disorder. Proc Natl Acad Sci U S A 101:7129–7134. 10.1073/pnas.0308058101 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sullivan SD, Moenter SM (2005) GABAergic integration of progesterone and androgen feedback to gonadotropin-releasing hormone neurons. Biol Reprod 72:33–41. 10.1095/biolreprod.104.033126 [DOI] [PubMed] [Google Scholar]
- Sun J, Chu Z, Moenter SM (2010) Diurnal in vivo and rapid in vitro effects of estradiol on voltage-gated calcium channels in gonadotropin-releasing hormone neurons. J Neurosci 30:3912–3923. 10.1523/JNEUROSCI.6256-09.2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Suter KJ, Song WJ, Sampson TL, Wuarin JP, Saunders JT, Dudek FE, Moenter SM (2000) Genetic targeting of green fluorescent protein to gonadotropin-releasing hormone neurons: characterization of whole-cell electrophysiological properties and morphology. Endocrinology 141:412–419. 10.1210/endo.141.1.7279 [DOI] [PubMed] [Google Scholar]
- Tada H, Kuroki Y, Funabashi T, Kamiya Y, Goto T, Suyama K, Sano A, Mitsushima D, Etgen AM, Takahashi T (2013) Phasic synaptic incorporation of GluR2-lacking AMPA receptors at gonadotropin-releasing hormone neurons is involved in the generation of the luteinizing hormone surge in female rats. Neuroscience 248:664–669. 10.1016/j.neuroscience.2013.06.040 [DOI] [PubMed] [Google Scholar]
- Wang L, DeFazio RA, Moenter SM (2016) Excitability and burst generation of AVPV kisspeptin neurons are regulated by the estrous cycle via multiple conductances modulated by estradiol action. eNeuro 3:ENEURO.0094-16.2016. 10.1523/ENEURO.0094-16.2016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wintermantel TM, Campbell RE, Porteous R, Bock D, Gröne HJ, Todman MG, Korach KS, Greiner E, Pérez CA, Schütz G, Herbison AE (2006) Definition of estrogen receptor pathway critical for estrogen positive feedback to gonadotropin-releasing hormone neurons and fertility. Neuron 52:271–280. 10.1016/j.neuron.2006.07.023 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang C, Bosch MA, Levine JE, Rønnekleiv OK, Kelly MJ (2007) Gonadotropin-releasing hormone neurons express K(ATP) channels that are regulated by estrogen and responsive to glucose and metabolic inhibition. J Neurosci 27:10153–10164. 10.1523/JNEUROSCI.1657-07.2007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang C, Roepke TA, Kelly MJ, Rønnekleiv OK (2008) Kisspeptin depolarizes gonadotropin-releasing hormone neurons through activation of TRPC-like cationic channels. J Neurosci 28:4423–4434. 10.1523/JNEUROSCI.5352-07.2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang C, Bosch MA, Rick EA, Kelly MJ, Rønnekleiv OK (2009) 17Beta-estradiol regulation of T-type calcium channels in gonadotropin-releasing hormone neurons. J Neurosci 29:10552–10562. 10.1523/JNEUROSCI.2962-09.2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang C, Rønnekleiv OK, Kelly MJ (2013) Kisspeptin inhibits a slow afterhyperpolarization current via protein kinase C and reduces spike frequency adaptation in GnRH neurons. Am J Physiol Endocrinol Metab 304:E1237–E1244. 10.1152/ajpendo.00058.2013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang C, Bosch MA, Qiu J, Rønnekleiv OK, Kelly MJ (2015) 17β-Estradiol increases persistent Na(+) current and excitability of AVPV/PeN Kiss1 neurons in female mice. Mol Endocrinol 29:518–527. 10.1210/me.2014-1392 [DOI] [PMC free article] [PubMed] [Google Scholar]