Abstract
Previous research has suggested that the conceptual representation of a compound is based on a relational structure linking the compound’s constituents. Existing accounts of the visual recognition of modifier-head or noun-noun compounds posit that the process involves the selection of a relational structure out of a set of competing relational structures associated with the same compound. In this article, we employ the information-theoretic metric of entropy to gauge relational competition and investigate its effect on the visual identification of established English compounds. The data from two lexical decision megastudies indicates that greater entropy (i.e., increased competition) in a set of conceptual relations associated with a compound is associated with longer lexical decision latencies. This finding indicates that there exists a competition between potential meanings associated with the same complex word form. We provide empirical support for conceptual composition during compound word processing in a model that incorporates the effect of the integration of co-activated and competing relational information.
Keywords: word recognition, morphology, entropy, lexical decision, conceptual combination
The internal structure of endocentric compounds provides additional information above and beyond specifying the morphological role of each constituent. To illustrate, consider a compound such as teacup, which is composed of the modifying constituent tea and the head constituent cup. People seem to be able to know more than just that it is a cup that is in some way related to tea. Instead, they posit a particular connection between the constituents; the meaning of teacup can be paraphrased as “a cup for tea”. Although relational structures are not often discussed in current theories of complex words (including compounds), such structures were prominent in earlier linguistic theories. Kay and Zimmer (1976), for example, noted that the semantic structure of nominal compounds is interesting in that “the relation between the two nouns is not explicitly present at any linguistic level, but rather is evoked by the construction itself” (pp. 29). As an example, consider that olive oil is oil derived from olives, but the same relation does not apply to baby oil. In this paper, we investigate whether relational links between constituents, which are not present in the orthography, contribute to compound word recognition.
There have been several attempts to characterize the specific relational link that exists between constituents of compounds (e.g., Downing, 1977; Finin, 1980; Lees, 1966; Levi, 1978; Li, 1971; Warren, 1978). Linguists and psycholinguists have proposed between 10 and 20 common relation categories that capture the majority of semantically transparent compounds (Downing, 1977; Gleitman & Gleitman, 1970; Kay & Zimmer, 1976; Lees, 1960; Levi, 1978; Warren, 1978). Examples of relations include MADE OF (paper bag = bag made of paper), FOR (computer screen = screen for a computer), and HAS (chocolate muffin = muffin that has chocolate). Although the nature of the categories vary, the assumption is that the underlying structure of compounds and modifier-noun phrases provides information about how the constituents are linked and that this structure plays an important role in determining the meaning of the whole compound/phrase. For example, Gleitman and Gleitman (1970) argue that modifier-noun phrases are derived from underlying relative clauses and that these underlying structures are recoverable. Levi (1978) makes a similar proposal, and claims that all complex nominals that are not derived by nominalization processes are derived from underlying semantic structures from which a predicate (e.g., CAUSE, HAVE, MAKE, FOR) has been deleted.
In the psycholinguistic literature, there have been several findings that suggest the language system might attempt to compute meaning whenever morphemic representations become available. For example, Libben, Derwing, and de Almeida (1999) have examined the parsing of novel ambiguous compounds such as clamprod, which can be parsed as either clam prod or clamp rod. They examined whether participants would assign the first possible parse (that is, the parse which is first encountered using a left-to-right parsing strategy). They did this by presenting novel compounds to people and asking them to indicate where they think the compound should be divided. The results failed to show a preference for this left-to-right strategy; parsing preferences were equally divided between the two possible parses. However, the decisions about where to parse the compounds were not arbitrary; participants appeared to be selecting the parse based on the plausibility of the various parses. That is, parsing preference was correlated with the plausibility of the meaning of the various parses. This correlation indicates that the processing of novel compounds involves generating and evaluating multiple representations. This finding is especially interesting because it demonstrates that parsing is affected by the semantic fit between constituents rather than solely by properties of the compound.
More direct evidence for the involvement of relational structures in the processing of noun phrases and compounds has accumulated over the years (see Gagné & Spalding, 2014 for a review). For example, Coolen, van Jaarsveld, and Schreuder (1991) conducted a study in Dutch and found that it took longer to correctly respond to novel compounds that had been rated as being highly interpretable than it did to respond to novel compounds that had been rated as being less interpretable. This suggests that the easier it was to construct a meaning based on the constituents, the more difficult it was for people to reject the novel compound as being an existing word. To further examine this issue, Coolen et al. (1991) asked participants to provide paraphrases for the novel compounds. These paraphrases were then classified according to Levi’s (1978) relations. Whether an item can be classified using Levi’s relation was related to interpretability. High interpretability items were more likely to be paraphrased using one of Levi’s relations than were low interpretability items. This observation led Coolen et al. (1991) to conclude that one aspect of the lexical decision process might rely on the meaning constructions based on a small set of semantic relations.
Subsequent research on novel compounds found that ease of interpretation was affected by the availability of the required relational structure (Gagné, 2000, 2001, 2002; Gagné & Shoben, 1997). Availability is affected by both general usage and recent usage. General usage refers to knowledge about how likely a particular relation is to be used with a constituent. For example, for the modifier mountain, the LOCATED relation is the most likely relation. Gagné and Shoben (1997) created a set of novel compounds and classified them in terms of relational categories. These classifications were used to calculate the frequency with which each modifier and head noun was used for each relation. Novel compounds that required a relation that was most likely for the modifier (e.g., mountain cloud uses the LOCATED relation) were processed more quickly (in a sense-nonsense task) than were novel compounds that required a relation that was not likely for the modifier (e.g., mountain magazine uses the ABOUT relation). Furthermore, recent usage also influences the availability of a relation. Several studies have demonstrated that it takes less time to make a sense-nonsense judgment to a novel compound when it has been preceded by a compound using the same modifier and the same relation than when preceded by a compound using the same modifier and a different relation (Gagné, 2000, 2001; Gagné & Shoben, 2002).
Relational structures also appear to be involved in the processing of established (i.e., familiar) compounds in that relational availability affects ease of processing. For example, Gagné and Spalding (2004; 2009) found evidence of relational priming: lexical decision latencies to a compound were faster when the compound had been preceded by a prime that used the same relation and the same modifier than when preceded by a prime that used a different relation. Other research indicates that both the relation selection and constituent assignment are involved because relational priming only occurs when the repeated constituent is used in the same position for both the prime and the target (Gagné, Spalding, Figueredo, & Mullaly, 2009). For example, responses were faster to fur gloves when preceded by fur blanket than by fur trader. However, there was no difference in response times following either acrylic fur or brown fur. This finding suggests that relational information is accessed/evaluated in the context of a constituent’s morphosyntactic role.
Moreover, evidence also suggests that the nature of the priming effect is primarily competitive. The influence of relational competition demonstrated for novel compounds, for which semantic composition is obligatory (e.g., Gagné & Shoben, 1997; Gagné, 2001; Spalding, Gagné, Mullaly & Ji, 2010) is also found in the processing of lexicalized compounds. Spalding and Gagné (2011) found that having a prime with a different relation (e.g., snowshovel as a prime for the target snowball) slowed responses relative to a modifier-only prime (e.g., snow), whereas the related prime (e.g., snowfort) was equivalent to the modifier-only prime. This finding is suggestive of competition from the different relation prime rather than facilitation from the same relation prime.
In sum, research suggests that processing of both novel and familiar compounds is influenced by the availability of relational structures and this effect is specifically competitive in nature. These effects are predicted by the RICE theory of conceptual combination and its predecessor (the CARIN theory), which both propose that relational structures provide a gist-based representation that captures a simple paraphrase of the compound (Gagné & Shoben, 1997; Spalding et al., 2010). In particular, these theories claim that the interpretation of both novel and familiar compounds proceeds in three (partially overlapping) stages. First, the relations associated with the modifier compete to be selected as a potential interpretation, then relations associated with both modifier and the head are used (along with semantic information associated with both constituents) to select and verify a gist interpretation or paraphrase of the compound, and finally this gist interpretation can be elaborated (as needed) in order to derive fuller meanings of the compounds (see Spalding et al., 2010, for a detailed description and explanation). Thus, a key prediction of the CARIN and RICE theories is that during the interpretation of modifier-noun phrases and compounds, relational structures compete for selection during semantic composition. This specific prediction about the role of competition in compound interpretation has been verified several times, both in the sense that relations associated with a particular constituent compete with each other for selection (as shown by, e.g., Gagné & Shoben, 1997; Spalding & Gagné, 2008, 2011; Spalding et al., 2010), and in the sense that full relational interpretations compete with each other (as shown by, e.g., Gagné & Spalding, 2014; Spalding & Gagné, 2014). That is, it is not simply the case that frequent relations/interpretations are easy to derive, but that relations that are strong relative to other relations/interpretations are easy. In short, increased competition among relational interpretations produces increased processing difficulty.
In the aforementioned experiments conducted by Gagné and colleagues, degree of competition was manipulated by using a prime that had either the same or a different relation, or by manipulating the constituent’s availability as measured by the constituent’s relational distribution. However, another way to evaluate competition – the way we adopt in the present paper – is in terms of the information-theoretic measure of entropy (Shannon, 1948). For the specific case of a paradigm of i semantic relations, each with its own probability of association with a given compound pi, entropy H is defined as H = −∑pi log2 pi. Thus, in the present case of gauging the competition between activated relational links during compound processing, entropy measures the expected amount of information in the probability distribution of semantic relations, and - for a specific compound - estimates the average amount of uncertainty in choosing any of i relations to be associated with the compound’s relational meaning. Entropy increases when more semantic relations are associated with a compound and also when the probabilities of those relations are closer in value to each other. These mathematical properties make entropy a valuable tool for assessing competition between relations, which indeed is expected to be more effortful when more relations are available and none of them has a clear dominance over others.
Prior research has highlighted the utility of entropy and related measures for characterizing competition within morphological paradigms, which we illustrate using only two of many available examples (see Milin, Kuperman, Kostić & Baayen, 2009, and Milin, Durdević, & Moscoso del Prado Martín, 2009, for a more complete survey of applications of information-theoretic tools to morphology). As a first example, Moscoso del Prado Martín, Kostić, and Baayen (2004) calculated entropy based on inflectional information using statistics of the base frequency of an inflectional paradigm (a series of inflected morphologically complex forms sharing the same base morpheme e.g., vote, votes, voted, voting) and the surface frequency of a word. They predicted that inflectional entropy as a metric of competition should be negatively correlated with lexical decision latencies. In addition, they calculated entropy of derivational paradigms (a series of derived morphologically complex forms sharing the same base morpheme, e.g., perform, performance, performer) based on word base frequency and cumulative root frequency. Entropy was higher for morphological paradigms with more members than for paradigms with fewer members. Moscoso del Prado Martín et al. (2004) found morphologically-based entropy effects, in that words with the morphological family that had very few dominant members were processed more quickly than words with morphological family members that had many competing dominant members. That is, the more uncertainty (i.e., the higher the entropy) present in a word’s morphological paradigm, the more difficult it was to process the word. Similarly, Kuperman, Pluymaekers, Ernestus, and Baayen (2007) found that entropy in the morphological family of a compound’s head affected speech production of Dutch compounds with interfixes (-s- in oorlogsverklaring “announcement of war” and -en- in dierenarts “veterinary”). Higher entropy, indicating a larger amount of uncertainty in the head’s morphological family, led to prolonged acoustic durations in the pronunciation of interfixes.
As well as the successful application of information-theoretical tools to psycholinguistic data, the aforementioned studies also offer a crucial theoretical point of connection with our own efforts to model the visual identification of compound words. That is, they provide theoretical insights which are of special interest to the present investigation of conceptual integration during compound processing. Interestingly, Moscoso del Prado Martín et al. (2004) argue that the effect of entropy of family size is driven by semantic similarity existing between competing family members within a derivational morphological paradigm. The idea is that larger and more established families (i.e., sets of compounds sharing constituents) facilitate recognition of family members, arguably by boosting “semantic resonance” via simultaneous activation of multiple, typically semantically related words. This claim is also supported by findings of De Jong (2002) and Moscoso del Prado Martín, Deutsch, Frost, Schreuder, De Jong and Baayen (2005) in Dutch, English and Hebrew. Furthermore, studies investigating the purported effects of inflectional paradigm size on the processing of case-marking inflected forms, such as those in Serbian (Milin et al., 2009b), have also drawn the conclusion that the morphological family size effect is likely to play a role at the semantic level of lexical processing.
Importantly, these and most other applications of entropy to psycholinguistic data are based on the distributional characteristics of ‘visible’ aspects of words, such as the orthographic forms of compound constituents (see however Hahn & Sivley, 2011). As Moscoso del Prado Martín et al. (2004) note, the family size effect is not influenced by individual relations between pairs of words, but rather by the frequency-derived structural relations between morphological paradigms. Therefore, while this stream of research may well be validly capturing the so-called semantic “entanglement” of complex words (Baayen, Milin, Đurđević, Hendrix & Marelli, 2011), the reported effects are based on distributional measures of surface form characteristics, which are only indirectly related to the semantic properties of words. On the other hand, a measure of competition among relational structures of compounds is a variable that is unequivocally semantic in nature. As discussed earlier in the Introduction, relational structures are not explicitly stated in the surface form of the compound, but rather are implied structures. Therefore, detecting an effect of competition between semantic relations during compound word processing, as gauged by entropy, would provide a novel window into the semantic processing of complex words, and would do so without recourse to lexical measures derived from surface form characteristics.
Thus far, the implementation of information-theoretic measures in the study of relation-based competition has been promising. Pham and Baayen (2013) considered a measure which was based on Gagné and Shoben’s (1997) finding that the relative number of conceptual relations within the compound’s modifier family affected compound processing. Pham and Baayen (2013) calculated entropy over the probability distribution of the conceptual relations that exist within a modifier family. In other words, for a given compound (e.g., snowball) they calculated entropy over the distribution of all the conceptual relations associated with the modifier (snow) in the language, including the conceptual relation tied to that specific compound (ball MADE OF snow). This measure affected lexical decision times, such that greater entropy slowed down lexical decision response times. This finding indicates that when reading a compound word, competition exists between the relative strength of the relations associated with a modifier. Moreover, unlike Gagné and Shoben’s (1997) measure, Pham and Baayen’s measure of competition takes into account the probability distribution of all conceptual relations associated with a given modifier, and not just its three most frequent relations. Thus, Pham and Baayen (2013) demonstrated that lexical processing is affected by the divergence of the relation of modifier in a compound from the distribution of relations for the modifier defined over all compounds in that modifier’s family. Crucially, Pham and Baayen (2013) derived their distribution of relations from a corpus in which each compound was coded with a specific semantic relation. However, entropy can also be calculated over distributions of conceptual relations using data generated from a possible relations task, upon which we will now elaborate.
In the possible relations task, participants are presented with a compound consisting of two words and are asked to pretend that they are learning English and know each of the two words, but have never seen the words used together. Their task is to choose the most likely literal meaning for a pair of nouns (e.g., snow ball). The choice is made out of a set of possible relational interpretations that participants are provided with (e.g, ball CAUSES snow, ball CAUSED BY snow, ball HAS snow, ball MAKES snow, ball FROM snow, ball MADE OF snow, ball IS snow, ball USED BY snow, ball USES snow, ball LOCATED snow, snow LOCATED ball, ball FOR snow, ball ABOUT snow, ball DURING snow, and ball BY snow). The set of relations was used in Gagné and Shoben (1997) and was an adaptation of Levi’s (1978) original set of relations. The possible relations task generates a distribution of possible relational interpretations of a compound. Per compound, each relational interpretation is associated with a frequency with which that relational interpretation has been selected.
Until now, two information theoretic measures have been computed using data from a possible relations task (see Gagné & Spalding, 2014). The first is Relational Diversity, defined as the number of distinct relational interpretations given to a compound. Another is Relational Relative Entropy, which measures the degree to which the probability distribution of relations identified for a particular compound differs from the probability distribution of relations estimated across a larger set of compounds. More specifically, the Relational Diversity Ratio is calculated by obtaining, for each item, the number of relations that were attested by ten or more participants (that is, by at least 10% of the participants who judged the item), and dividing that number by the total number of relations chosen by any participant for that item. Relational Relative Entropy for a given item is calculated as the probability of a given relation for that item multiplied by the binary logarithm of the probability of that relation for that item divided by the probability of that relation in the total relational distribution, summed across all 16 relations. Relational Diversity Ratio and Relational Relative Entropy were entered as predictors in a linear mixed effects model fitted to lexical decision latencies. Relational Diversity Ratio interacted with Relational Relative Entropy, and the relationship between the diversity measure and Relational Relative Entropy was different for semantically opaque and transparent compounds. In particular, for opaque compounds, the effect of Relational Diversity Ratio was attenuated when Relational Relative Entropy was low (i.e., when the item’s relational distribution was close to the overall relational distribution). For transparent compounds, when Relational Relative Entropy was low, the effect of diversity was similar to the effect seen with opaque compounds. However, when Relational Relative Entropy was high, the effect of diversity was opposite to the effect seen with opaque compounds. High Relational Diversity and high Relational Relative Entropy were associated with slower response times for transparent compounds, whereas low Relational Diversity and low Relational Relative Entropy were associated with fast response times. These results demonstrate that lexical processing of transparent compounds is facilitated when a compound has a large number of potential relations but only a small number of them are strong candidates. On the other hand, the processing of opaque compounds is attentuated by the combination of high Relational Diversity and low Relational Relative Entropy, which channels lexical access towards a computed meaning which will not be the established meaning of the compound.
The current study
As we have summarized, several studies have shown evidence that both novel and established compounds are affected by availability of conceptual relations and that competition among relations influences ease of processing. Moreover, information-theoretic measures have been successfully used as indices of competition in terms of morphological forms, and, more recently, in terms of semantic relational structures. Thus, there is evidence that lexical processing is affected by both the diversity of the relational distribution of a given compound and its divergence from the relational distribution defined over all compounds in the set. However, this line of inquiry presently lacks one critical test of the competition within a relational distribution for a single compound. Namely, it remains to be tested whether Entropy (rather than Relational Diversity, Relational Relative Entropy or Pham and Baayen’s (2013) measure of entropy) of the relational distribution of the compound itself influences the speed of processing.
It is important to test entropy because this measure differs in several ways from the measures that have already been tested. Relational Relative Entropy used by Spalding and Gagné (2014) gauges how much the probability distribution of relations for a single compound differs from the probability distribution calculated over relations of all compounds. In a similar fashion to Pham and Baayen’s (2013) measure of entropy based on the relative frequency of relations in the compound’s modifier family, Relational Relative Entropy can be broadly construed as a metric of how one’s experience with possible interpretations for all compounds needs to be adjusted for interpretations available for a specific compound under recognition. Unlike entropy, this metric does not quantify how difficult it is to converge on one interpretation for a compound given the available set of relations, each with its own probability.
The distinction between Relational Diversity used by Spalding and Gagné (2014) and entropy can be illustrated by considering two different compounds, floodlight and newsroom. Both compounds have the same Relational Diversity value; they both have 9 relations that were chosen by more than one participant. Yet, for those 9 relations, the compounds’ distributions of how often each relation was chosen tell a very different story. The compound floodlight has a distribution of responses that are apportioned equally among its 9 relations. For example, 3 relations within the distribution of 9 for floodlight (light FROM flood, flood IS light and light DURING flood) are all equiprobable, each with a selection frequency of 4 (i.e., each of these relations was chosen by 4 participants). On the other hand, newsroom has a very clear candidate for a relational interpretation (room FOR news), which has 66 responses (i.e., this relation was chosen by 66 participants). Thus, the FOR relation has the greatest share of responses and does not have an equally frequent competitor relation. Therefore, relative to newsroom, the average uncertainty in choosing any one relation to define the intepretation of floodlight is high and is expressed with a greater entropy value. The entropy of the distribution of conceptual relations can be operationalised in the present study as a precise measure of the competition among relation candidates that are engaged during compound word recognition.
The aim of the current project, then, is to further examine entropy as a measure of relational competition. In doing so, we are able to more directly test for evidence of the influence of relational information and, more specifically, of relational competition in the context of established compounds. Moving from Relational Diversity to entropy ensures that not only the number of distinct interpretations or the most frequent interpretation are accounted for, but also their balance of probabilities. Moreover, shifting focus from Relational Relative Entropy to entropy further gives prominence to the competition effect of item-specific relational structures, rather than an estimation of competition stemming from population-wide distributions of relational structures aggregated across multiple compounds.
As argued above, entropy is the most direct measure of relational competition within a morphological paradigm. Following the predictions of the CARIN and RICE theories of conceptual combination, we anticipate that higher entropy will reflect a stronger competition between available relations and will cause an increased processing effort in visual comprehension tasks. In this study, we test this prediction by using relational distributions for a number of compounds collected in two experiments (Gagné & Spalding, 2014; Spalding & Gagné, 2014), and their behavioral latencies attested in two lexical decision megastudies, English Lexicon Project (Balota, Yap, Hutchison, Cortese, Kessler, Loftis, Neely, Nelson, Simpson & Treiman, 2007) and British Lexicon Project (Keuleers, Lacey, Rastle & Brysbaert, 2012). We will thus test whether entropy can predict compound RTs in two separate lexical decision data sets.
Methods
Materials
The data set we considered was composed of the results of two separate experiments, which each had collected possible relations judgements for a number of compounds. One such source, from Spalding and Gagné (2014), included judgements for a total of 188 existing English compounds from 159 unique participants. The mean number of ratings per compound in this data source was 53 (range 52-54). The other source was a set of 56 existing English compounds, used in Gagné and Spalding (2014), which includes relation judgements to these compounds from a total of 111 unique participants (all participants contributed ratings for all compounds in this data source).
Once we combined both data sets, the resulting data source consisted of 232 unique compound words, each with a separate frequency distribution of possible relations judgements over 16 modifier-head relations. After combining both data sets, we found that 12 items overlapped across both sources. Because these compounds were present in two separate experiments, each of the 12 compounds was attested with a pair of differing judgement distributions. We decided to consider both judgement distributions in our statistical models. Thus, while there were 232 unique compounds, when taking into account the 12 duplicated items, we had a data source consisting of 244 different judgment distributions. Moreover, once the data from both experiments were combined, a total of 270 participants contributed responses and a median of 53 participants provided a judgement per compound. This stimulus data is provided as a supplementary data file. For further details on the procedure and stimuli selection, see Spalding and Gagné (2014), and Gagné and Spalding (2014).
Dependent variables
Trial-level lexical decision latencies were obtained from the English Lexicon Project [ELP] and the British Lexicon Project [BLP]. We only considered reaction times (RTs) of trials for which there was a correct response. We also removed outlier responses by eliminating the top and bottom 1% of the RT distribution for both ELP and BLP samples. This led to a loss of 2.15% of the total data points in ELP and 2.04% of the total data points in BLP samples. In order to attenuate the influence of outliers, we used the inverse transform method to convert response times as indicated by the Box-Cox power transformation (Box & Cox, 1982). The percentage of incorrect responses to our stimuli of interest was too low (ELP: 9.91%, BLP: 16.69%) to warrant a separate investigation of the effect of critical variables on response accuracy. In both the ELP and BLP data sources, the compounds were all presented for lexical decision in a concatenated format (i.e. unspaced). Overall, of the 232 compounds for which we had possible relations judgements, 187 were present in the ELP data source and 143 were present in the BLP data source. A total of 130 items overlapped across the ELP and BLP data source, while 44 items from the original data pool did not occur in either ELP or BLP.
Independent variables
The critical variables of interest are ones related to the judgements of conceptual relations. One measure is Relational Diversity, estimated as the number of relations (out of the set of 16) that had been chosen by more than one participant for a given compound. The lower threshold of more than one participant was chosen to reduce the number of random or accidental (erroneous) responses. Another measure is Entropy calculated over the probability distribution of interpretations of conceptual relations for a given compound. The probability distribution was estimated only for relations that were selected more than once in the judgement task. Entropy is defined as H = −∑pi log2 pi, where pi is the probability of a relation within the respective distribution of possible relations for a given compound. Thus, for the compound lawsuit, the relations are FOR (selected 12 times), FROM (7), MADE OF (7), USES (6), CAUSES (4), USED BY (4), HAS (3), ABOUT (3), CAUSED BY (2) and BY (2). The resulting probability distribution for these relations is 0.24, 0.14, 0.14, 0.12, 0.08, 0.08, 0.06, 0.06, 0.04 and 0.04, which yields an Entropy value of 3.097. For both ELP and BLP data sources, the number of relations that were selected more than once per compound (Relational Diversity) ranged from 3 to 16 and the median number of relations that were selected per compound was 8.
In addition to the relational structure of a compound, a further morpho-semantic component of compound word recogniton is semantic transparency, which is defined as the predictability of the meaning of the compound word given the meaning of its parts (see Amenta & Crepaldi (2012) for a review of the effects of semantic transparency in lexical decision experiments). A highly transparent compound (e.g., flashlight) is composed of constituents with semantic denotations that are semantically similar to the meaning of the whole word (flash and light). An opaque compound (e.g., brainstorm), on the other hand, includes constituents (brain and storm) out of which at least one morpheme bears a meaning that is unrelated to the compound word. In order to control for the potentially confounding effects of semantic transparency we included measures of semantic transparency in our analysis. As a gauge of semantic transparency we employed the computational measure of Latent Semantic Analysis (LSA) (Landauer & Dumais, 1997), which is a statistical technique for analysing and estimating the semantic distance between words, based on the contexts in which the words have co-occurred in a corpus. Following previous research that has employed LSA as a metric of semantic transparency (Pham & Baayen, 2013; Marelli, Dinu, Zamparelli & Baroni, 2014), we collected LSA scores for three types of semantic relationships: the left constituent (modifier) and the whole compound (Modifier-Compound; e.g., flash and flashlight), the right constituent (head) and the whole compound (Head-Compound; e.g., light and flashlight), and the left constituent and the right constituent (Modifier-Head; e.g., flash and light). The term-to-term LSA scores were collected from http://lsa.colorado.edu with the default setting of 300 factors: a higher score implies a greater semantic similarity between the pair of words under comparison. Modifier-Head LSA scores were available for all compounds, while Head-Compound and Modifier-Compound LSA scores were only available for 171 compounds.
Other control variables included measures that were demonstrated in prior research to affect compound processing: compound length (in characters), compound frequency, frequencies of the left and right compound’s constituents, as well as the positional family size of the left and right constituents (defined as the number and summed frequency of compounds that share a constituent with the fixed position of either the left or right constituent of the target compound). Family-based estimates were calculated from the 18 million-token English component of the CELEX lexical database (Baayen, Piepenbrock & Van Rijn, 1995), with the help of its morphological parses. Word frequencies from the 51 million-token SUBTLEX-US corpus (Brysbaert & New, 2009), based on subtitles from US film and media, were obtained for the compounds and their respective constituents that were present in the ELP data source. Likewise, word frequencies from the 201 million-token SUBTLEX-UK corpus (van Heuven, Mandera, Keuleers & Brysbaert, 2014), based on UK television (BBC) subtitles, were obtained for the compounds present in the BLP data source. Frequency-based characteristics all pertain to compounds in their concatenated format. The possible relations experiment of origin for each item was included as a covariate. It did not show either a main effect or an interaction with any of the variables of interest, suggesting that the two data sources are equivalent for the purposes of the present study: we did not consider experiment of origin in further analyses. Distributional characteristics of all variables are reported in Table 1.
Table 1:
Descriptive statistics for the dependent and independent variables: Reported are the range, mean and standard deviations of the original and transformed variables after selection and trimming procedures.
| Variable | Original | Transformed | ||||
|---|---|---|---|---|---|---|
| A. BLP data source | range | mean | sd | range | mean | sd |
| Reaction times (RT) | 311:2019 | 648 | 185 | −3.22:−0.5 | −1.64 | 0.38 |
| Entropy | 1.08:3.65 | 2.52 | 0.56 | −2.37:1.94 | 0 | 1 |
| Relational Diversity | 5:16 | 10.09 | 3.48 | −1.63:3.03 | 0 | 1 |
| Compound Length | 6:11 | 8.5 | 1.87 | −2.06:2.65 | 0 | 1 |
| Compound Frequency (UK frequency) | 2:8808 | 414 | 1065 | −2.93:2.81 | 0 | 1 |
| Left constituent Frequency (UK frequency) | 102:358568 | 20329 | 38895 | −2.73:2.48 | 0 | 1 |
| Right constituent Frequency (UK frequency) | 47:540985 | 34857 | 85612 | −2.89:2.4 | 0 | 1 |
| Left constituent Family Size | 0:42 | 14 | 11 | −0.78:4.01 | 0 | 1 |
| Right constituent Family Size | 0:56 | 17 | 14 | −0.86:4.4 | 0 | 1 |
| Modifier-Head LSA Similarity | −0.02:0.74 | 0.22 | 0.17 | −1.36:4.19 | 0 | 1 |
| Modifier-Compound LSA Similarity | −0.06:0.74 | 0.23 | 0.2 | −1.42:3.41 | 0 | 1 |
| Head-Compound LSA Similarity | −0.06:0.92 | 0.25 | 0.23 | −1.37:4 | 0 | 1 |
| B. ELP data source | Original | Transformed | ||||
| Reaction times (RT) | 207:2956 | 761 | 279 | −4.83:−0.34 | −1.45 | 0.42 |
| Entropy | 1.18:3.65 | 2.54 | 0.54 | −2:2 | 0 | 1 |
| Relational Diversity | 5:16 | 10.5 | 3.61 | −1.66:3.04 | 0 | 1 |
| Compound Length | 6:11 | 8.5 | 1.87 | −2.24:2.17 | 0 | 1 |
| Compound Frequency (US frequency) | 1:1142 | 93 | 146 | −2.52:2.59 | 0 | 1 |
| Left constituent Frequency (US frequency) | 5:102467 | 5249 | 12507 | −3.56:2.56 | 0 | 1 |
| Right constituent Frequency (US frequency) | 9:204428 | 9794 | 26164 | −2.78:2.56 | 0 | 1 |
| Left constituent Family Size | 0:54 | 16 | 14 | −0.73:6.12 | 0 | 1 |
| Right constituent Family Size | 0:155 | 22 | 28 | −0.7:11.1 | 0 | 1 |
| Modifier-Head LSA Similarity | −0.02:0.74 | 0.24 | 0.18 | −1.42:4.14 | 0 | 1 |
| Modifier-Compound LSA Similarity | −0.07:0.74 | 0.25 | 0.21 | −1.49:3.16 | 0 | 1 |
| Head-Compound LSA Similarity | −0.07:0.92 | 0.24 | 0.23 | −1.36:4.37 | 0 | 1 |
Statistical considerations
We fitted linear mixed-effects models to the reaction time latencies from ELP and BLP. We computed models using the lmerTest (Kuznetsova, Brockhoff & Christensen, 2013) package in the R statistical computing software program (R Core Team, 2014). Across all models we used restricted maximum likelihood (REML) estimations. All continuous independent variables were scaled to reduce collinearity. All models included by-item and by-participant random intercepts. We also included by-participant random slopes for trial and Entropy: according to the model comparison likelihood ratio tests, these random slopes did not significantly improve model fit and were therefore excluded from all models. Furthermore, across all analyses, we refitted models after removing outliers from both data sets by excluding standardized residuals exceeding 2.5 standard deviations. Final models are reported in Tables 3 and 4. Collinearity between compound and constituent frequency-based measures was high (multicollinearity condition number > 30): importantly, it had no bearing on model estimates for our critical variable of Entropy. This is because Entropy and frequency-based measures correlated very weakly (all rs < 0.16). A correlation matrix of all independent variables is provided in Table 2.
Table 3:
Fixed effects of the linear mixed-effect model fitted to ELP lexical decision RTs. The R2 of the model is 0.6 and the standard deviation of the residual is 0.25. The standard deviation estimate for the random effect of Compound is 0.26. The standard deviation estimate for the random effect of Participant is 0.11. Number of trials = 5817. Number of trials after trimming = 5727.
| Estimate | Std. Error | t | p | |
|---|---|---|---|---|
| Intercept | −1.437 | 0.013 | −111.478 | 0.000 |
| Entropy | 0.021 | 0.010 | 2.137 | 0.034 |
| Compound Frequency | −0.078 | 0.010 | −8.089 | 0.000 |
| Compound Length | 0.004 | 0.009 | 0.426 | 0.671 |
| Left constituent Frequency | −0.012 | 0.010 | −1.241 | 0.216 |
| Right constituent Frequency | −0.018 | 0.010 | −1.739 | 0.084 |
| Left constituent Family Size | 0.001 | 0.010 | 0.139 | 0.890 |
| Right constituent Family Size | −0.004 | 0.009 | −0.422 | 0.673 |
Table 4:
Fixed effects of the linear mixed-effect model fitted to BLP lexical decision RTs. The R2 of the model is 0.47 and the standard deviation of the residual is 0.27. The standard deviation estimate for the random effect of Compound is 0.105. The standard deviation estimate for the random effect of Participant is 0.211. Number of trials = 4677. Number of trials after trimming = 4624.
| Estimate | Std. Error | t | p | |
|---|---|---|---|---|
| Intercept | −1.627 | 0.026 | −62.759 | 0.000 |
| Entropy | 0.030 | 0.011 | 2.782 | 0.006 |
| Compound Frequency | −0.087 | 0.010 | −8.552 | 0.000 |
| Compound Length | −0.009 | 0.010 | −0.899 | 0.371 |
| Left constituent Frequency | −0.015 | 0.011 | −1.372 | 0.173 |
| Right constituent Frequency | 0.001 | 0.012 | 0.065 | 0.948 |
| Left constituent Family Size | −0.008 | 0.012 | −0.650 | 0.517 |
| Right constituent Family Size | −0.031 | 0.012 | −2.614 | 0.010 |
Table 2:
Correlation matrix of all predictor (independent) variables.
| 1. | 2. | 3. | 4. | 5. | 6. | 7. | 8. | 9. | 10. | 11. | 12. | 13. | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1. Entropy | |||||||||||||
| 2. Relational Diversity | 0.86*** | ||||||||||||
| 3. Compound Length | −0.07 | −0.17** | |||||||||||
| 4. Compound Frequency (UK) | 0.03 | −0.01 | −0.06 | ||||||||||
| 5. Left constituent Frequency (UK) | 0.11 | 0.13* | −0.13* | 0.07 | |||||||||
| 6. Right constituent Frequency (UK) | 0.17** | 0.19** | −0.16* | 0.13 | 0.00 | ||||||||
| 7. Compound Frequency (US) | −0.11 | −0.11 | 0.03 | 0.87*** | 0.07 | −0.01 | |||||||
| 8. Left constituent Frequency (US) | 0.11 | 0.14* | −0.12 | 0.12 | 0.93*** | 0.02 | 0.17* | ||||||
| 9. Right constituent Frequency (US) | 0.15* | 0.16* | −0.12 | 0.09 | 0.00 | 0.95*** | 0.01 | 0.02 | |||||
| 10. Left constituent Family Size | −0.23*** | −0.23*** | −0.16* | 0.20* | 0.24*** | 0.02 | 0.00 | 0.21** | 0.01 | ||||
| 11. Right constituent Family Size | 0.07 | 0.07 | −0.10 | 0.10 | −0.02 | 0.26*** | −0.06 | −0.04 | 0.28*** | 0.04 | |||
| 12. Modifier-Head LSA Similarity | −0.01 | 0.03 | −0.03 | 0.09 | 0.07 | 0.10 | 0.05 | 0.10 | 0.07 | 0.03 | −0.10 | ||
| 13. Modifier-Compound LSA Similarity | −0.14 | −0.12 | 0.10 | −0.02 | −0.01 | 0.01 | −0.02 | 0.03 | 0.00 | 0.11 | −0.11 | 0.21** | |
| 14. Head-Compound LSA Similarity | −0.13 | −0.08 | −0.09 | 0.14 | 0.02 | −0.03 | 0.07 | −0.05 | −0.04 | 0.17* | −0.13 | 0.30*** | 0.12 |
Correlation is significant at the .001 level.
Correlation is significant at the .01 level.
Correlation is significant at the .05 level.
Results and discussion
The initial data pools consisted of 5937 ELP trials and 4747 BLP trials. We removed two compounds (dustpan and tinfoil) with an Entropy value of more than 2.5 standard deviations away from the respective mean of ELP and BLP Entropy distributions. We also removed two compounds with a log frequency of more than 3 standard deviations from the respective mean log frequencies of the the ELP and BLP subset of compounds. These high frequency compounds (ELP: boyfriend and breakfast; BLP: sunday) were all over 1 standard deviation from the next highest frequency compound in each data set. The remaining ELP data pool contained 5817 RTs to 184 unique compounds, and the remaining BLP data pool consisted of 4677 RTs to 141 unique compounds. A total of 815 unique participants contributed RTs in ELP and 78 unique participants contributed to RTs in BLP.
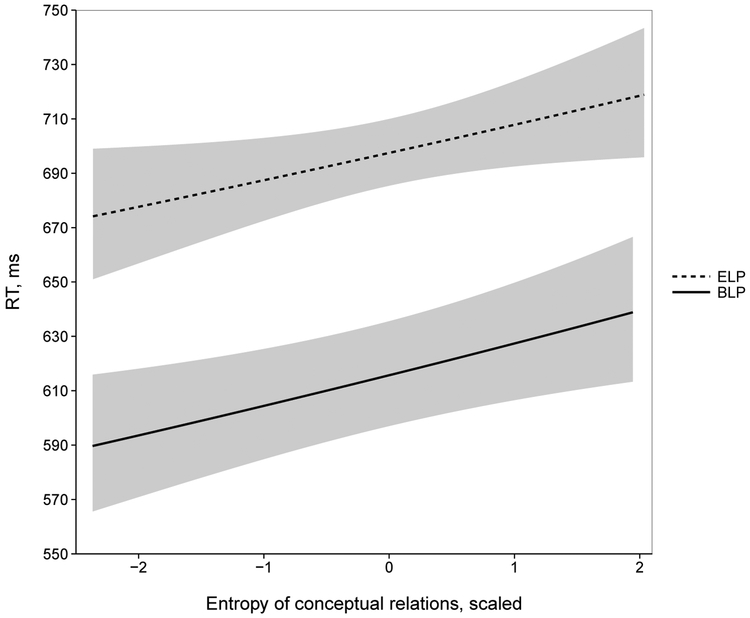
Entropy of the probability distribution of conceptual relations chosen by more than one participant demonstrated an expected inhibitory effect on ELP and BLP response times. The effect indicated that a larger amount of uncertainty regarding the relational interpretation of a given compound led to a larger effort (i.e., longer response times) in responding to the compound in lexical decision (ELP: , SE = 0.01, t = 2.14, p = 0.03; BLP: , SE = 0.01, t = 2.78, p = 0.006). Tables 3 and 4 report the final mixed-effects models fitted to ELP and BLP RTs, respectively. The reported partial effects of Entropy are presented in Figure 1 (plots depict back-transformed values of response times (in ms) to aid interpretability). In addition, we also calculated Entropy over the complete probability distribution (i.e., not just the conceptual relations that were chosen more than once in the possible relations task). We included this Entropy measure in an identical model to those in which significant effects of the original Entropy measure were found. This particular measure did not exert any significant influence on response times in either ELP or BLP. This was likely due to the prevalence of random or accidental choices of irrelevant semantic relations by participants.
Figure 1:
The partial effect of Entropy of relational competition (scaled) on RTs in ELP (English Lexicon Project) and BLP (British Lexicon Project) samples. Slopes represent predicted values of the linear-mixed effects models fitted separately to ELP and BLP samples. Grey bands represent lower and upper limit of 95% confidence interval for each model.
As well as revealing the novel effect of Entropy of conceptual relations, the models described in Tables 3 and 4 also report, for completeness, effects of other lexical characteristics. Mostly, they take the same direction as in prior literature and are small in magnitude, often failing to reach statistical significance. Compounds with larger morphological families were processed faster than words with smaller morphological families (cf. Juhasz & Berkowitz, 2011), especially in the BLP sample. Secondly, more frequent compounds and compounds with more frequent constituent morphemes were processed faster (cf. Andrews, Miller & Rayner, 2004 and Zwitserlood, 1994). These measures may not have reached significance because of high collinearity between the predictors. This collinearity could have been reduced, however the outcome of these variables was not the focus of the current study.
We also found that Entropy of conceptual relations was a more consistent and more robust predictor of lexical decision than Relational Diversity. Relational Diversity, i.e., the number of relations chosen by more than one participant, predicted RTs only in the BLP sample (, SE = 0.01, t = 2.57, p = 0.01). This model indicated that increased diversity of conceptual relations was associated with slower response times. The model explained a negligibly smaller amount of variance (0.02%) than the model fitted to Entropy for the BLP data set. Moreover, the model fitted to Entropy produced a smaller Akaike information criterion (AIC) value when compared to the model including Relational Diversity as a predictor, indicating that the model containing Entropy of conceptual relations as a predictor was a slightly better fit.
Additionally, it was possible that the Entropy of conceptual relations effect was confounded with the semantic transparency of the compound. To investigate this, we tested the influence of the interaction of semantic transparency (we used LSA to gauge transparency, this is outlined in the Methods section) and Entropy (correlations between these variables are reported in Table 2). We first added each of the LSA variables to the fixed effect structure for models pertaining to both the ELP and BLP data samples. We found that none of the LSA variables influenced the regression coefficient or the statistical significance of Entropy (or Relational Diveristy in BLP). This was expected given weak correlations between Entropy and the semantic transparency measures. We then analysed the interaction between all LSA measures and Entropy (with each LSA measure entered as a single multiplicative interaction with Entropy in three separate models, and with all three LSA measures simultaneously interacting with Entropy in one model) for the ELP and BLP data set. In all of these models, semantic transparency did not enter into a significant interaction with Entropy. We also repeated this analytical procedure with Relational Diversity, which also did not produce significant interaction effects. Thus, we conclude that two aspects of compound semantics (captured by the semantic transparency measures and entropy of conceptual relations) are unrelated and do not modulate each other’s impact on compound recognition.
General discussion
Conceptual integration is demonstrably an important factor that codetermines the retrieval of compound word meaning (see Fiorentino & Poppel, 2007; Gagné & Spalding, 2014; Taft, 2003, for reviews). Indeed, prior studies have shown that the integration of visually-presented compounds involves semantic composition, such that, under experimental conditions, the processing of established compound words exhibits sensitivity to the availability of conceptual relations (Gagné & Spalding, 2004; 2009; Pham & Baayen, 2013). Gagné and Spalding (2009) presented evidence that a central component of the visual identification of compound words involves the construction of interpretive gists, whereby the cognitive system draws upon relational information linking compound constituents. Under this hypothesis, candidate relations are generated based on the characterisitics of the modifier and head of the compound, and are then evaluated for plausibility. In addition, Gagné and Spalding (2006; 2014) and Gagné & Shoben (1997) revealed that relational structures compete for selection and that increased competition results in increased processing difficulty. Despite the insights presented in these studies, the precise locus of the effect of relational competition still remained unclear. It was still unknown whether the number of activated competitors or the relative probability of activated conceptual relations was driving the competition effect. The present study addressed this issue by introducing entropy calculated over the distribution of conceptual relations as a direct measure of relative competition.
In the current study we reanalyzed data obtained from a previous set of experiments in which participants were serially presented with a list of noun-noun compounds. For each compound, participants were asked to choose the most likely conceptual relation out of a possible 16 interpretations, which yields a frequency distribution of relational interpretations per compound. Previous research revealed that lexical processing is systematically affected by both the diversity of the relational distribution of a given compound and its divergence from the relational distribution of all compounds. Of particular interest here was to further investigate the influence of relational information on compound processing and also to test for evidence of compound-specific competition between conceptual relations. To test these hypotheses, we employed an information-theoretic measure as an index of competition among relational interpretations during lexical processing. The measure – the entropy of the distribution of responses per compound (Entropy) – thus served as a critical variable in a virtual experiment in which we examined its influence on visual lexical decision latencies obtained from two behavioural megastudies (the English and British Lexicon Projects, Balota et al., 2007; Keuleers et al., 2012).
We found robust evidence, replicated over two separate lexical decision data sources, that increased entropy of relational competition inhibited response times. These results demonstrate, through a more parsimonious measure of relational competition than ones employed earlier, that the relative difficulty of converging on any one interpretation of a compound translates into increased processing effort, i.e., longer response times in ELP and BLP. This difficulty is precisely what entropy calculated over a probability distribution of the compound’s potential relations gauges. Interestingly, two very similar slopes were observed across ELP and BLP samples, indicating very similar effect sizes for the partial effect of entropy (range of predicted values in ELP = 45 ms; range of predicted values in BLP = 49 ms).
Another interesting aspect of this finding is that only a subset of available relations, and their entropy, affect word recognition, and not the entire set of theoretically possible relations. We saw effects of entropy on lexical decision times only when it was defined over relations that were selected for a compound by more than one participant; entropy calculated over a full set of relations (i.e., relations chosen just once or not at all), had no noticeable effect on RTs. In our data set, the number of selections per compound ranged between 4 and 16, out of a total of 16 of Levi’s (1978) relations, which indicates that this is the range of relational interpretations among which semantic competition is possible. This finding might not seem so suprising given the analogous observation made by that information-theoretic measures based on morphological families only affected word recognition behavior when based on relevant family members, i.e., ones that are semantically related to the shared meaning of the entire family (e.g., compare bluebird and jailbird as members of the family sharing bird as the second constituent). This implies that not only are higher-order interpretative processes able to navigate a wealth of semantic information, but also that they exploit only the semantic information that is relevant and has the potential to be selected as the meaning of the word that is being recognized. Thus, taken together with prior findings, our results suggest that there exists a competition between meanings associated with a single compound word. This competition is as real as the well-established neighbourhood competition effects between orthographic forms in word recognition.
In sum, we have shown that for established endocentric compounds, the ease of selecting a compound’s relational interpretation (e.g., a ball made of meat for the compound meatball) out of an available relational set influences the ease with which the meaning of a compound is obtained. The more relational interpretations there are for a compound, and the more similar they are in their probability of being the most plausible interpretation for the compound, the longer it takes to identify the established meaning of that compound. We therefore conclude that semantic composition during the visual identification of exisiting compounds is a competitive process.
Situating our results within a theory of compound processing, our results are both concomitant with and extend the CARIN and RICE theoretical models of semantic integration developed by Gagné and Shoben (1997) and Spalding et al. (2010). In both theories (Gagné & Shoben, 1997; Spalding, et al., 2010), conceptual integration of compound word meaning involves the activation and competition of multiple relational gists. This process is summarized by Spalding and Gagné (2008), who posited that “ruling out any competitor relation likely requires some processing time, and ruling out more competitor relations should presumably require more time” (pp. 1576). In this paper, we have confirmed an extension to this hypothesis by showing that the time it takes to rule relations out is not only sensitive to the number of activated relations, but also to the degree of competition between them.
In addition to contributing to a wealth of evidence which suggests that co-activated conceptual relations affect compound word processing, we have also gauged conceptual competition using an information-theoretic scale that is, in principle, comparable to previous psycholinguistic studies that have provided empirical support for the central role of semantic access during complex word identification (Milin et al., 2009a; Milin et al., 2009b; Moscoso del Prado Martín et al., 2004; Pham & Baayen, 2013). The interpretation of our results - that competition at the conceptual level co-determines the visual identification of compound words - is thus tied to a perspective of complex word recognition that assumes “fast mapping” of form to meaning (Baayen et al. 2011). Under this view, the cost of processing arises when the language system attempts to single out one meaning among the many meanings that are activated by the word form that is under visual inspection. Accordingly, the successful resolution of form-meaning association is determined at the semantic level by higher-level cognitive processes. We believe that conceptual combination during compound word recognition, a process that is captured by the effect entropy of conceptual relations, is an example of one such high-level semantic process.
In summary, the success of deepening our understanding of complex word recognition depends on the ability to tap into the semantic components of complex words that have concrete psychological implications. We believe that entropy of conceptual relations is an important extension to previous work that has sought to understand semantic processing mechanisms underlying complex word recognition. The experimental psycholinguistic community has long relied upon the behavioural activity associated with frequency based measures, such as morpheme frequency or morpheme family size, as an index of meaning retrieval during compound word recognition. Another commonly used measure of compound semantics in psycholinguistics studies is semantic transparency, which is considered as a more direct measure of the conceptual composition of complex word. Similarly, this measure is also based on information that can be gleaned from the orthography of a complex word; transparency requires only the evaluation of the semantic similarity between the meaning denotations of two surface forms. Unlike these measures, entropy of conceptual relations appears to reliably drill down to an implicit source of morpho-semantic information. Thus, by supplementing the study of form with the study of meaning, we bring to bear a further lexical characteristic that meaningfully contributes to the information that a morphologically complex word carries, namely, ‘relational competition’.
Acknowledgements
This work was supported by the Ontario Trillium Award and a Graduate fellowship awarded by the Lewis & Ruth Sherman Centre for Digital Scholarship to the first author. The second author’s contribution was partially supported by the SSHRC Insight Development grant 430-2012-0488, the NSERC Discovery grant 402395-2012, the NIH R01 HD 073288 (PI Julie A. Van Dyke), and the Early Researcher Award from the Ontario Research Fund. The third author’s contribution was supported by the National Sciences and Engineering Research Council of Canada (05100). The fourth author’s contribution was supported by the National Sciences and Engineering Research Council of Canada (250028). Thanks are due to Bryor Snefjella for his valuable comments on earlier drafts of this work. We thank for technical support the Research & High-Performance Computing Support group at McMaster University.
Contributor Information
Daniel Schmidtke, McMaster University, Canada.
Victor Kuperman, McMaster University, Canada.
Christina L. Gagné, University of Alberta, Canada
Thomas L. Spalding, University of Alberta, Canada
References
- Amenta S, & Crepaldi D (2012). Morphological processing as we know it: an analytical review of morphological effects in visual word identification. Frontiers in Psychology, 3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Andrews S, Miller B, & Rayner K (2004). Eye movements and morphological segmentation of compound words: There is a mouse in mousetrap. European Journal of Cognitive Psychology, 16 (1-2), 285–311. [Google Scholar]
- Baayen RH, Milin P, Đurđević DF, Hendrix P, & Marelli M (2011). An amorphous model for morphological processing in visual comprehension based on naive discriminative learning. Psychological Review, 118 (3), 438. [DOI] [PubMed] [Google Scholar]
- Baayen RH, Piepenbrock R, & Van Rijn H (1995). The CELEX database. Nijmegen: Center for Lexical Information, Max Planck Institute for Psycholinguistics, CD-ROM. [Google Scholar]
- Balota DA, Yap MJ, Hutchison KA, Cortese MJ, Kessler B, Loftis B, … Treiman R (2007). The English Lexicon Project. Behavior Research Methods, 39 (3), 445–459. [DOI] [PubMed] [Google Scholar]
- Box G, & Cox D (1982). An analysis of transformations revisited, rebutted. Journal of the American Statistical Association, 77 (377), 209–210. [Google Scholar]
- Brysbaert M, & New B (2009). Moving beyond Kucera and Francis: A critical evaluation of current word frequency norms and the introduction of a new and improved word frequency measure for American English. Behavior Research Methods, 41 (4), 977–990. [DOI] [PubMed] [Google Scholar]
- Coolen R, Van Jaarsveld HJ, & Schreuder R (1991). The interpretation of isolated novel nominal compounds. Memory & Cognition, 19 (4), 341–352. [DOI] [PubMed] [Google Scholar]
- De Jong NH (2002). Morphological families in the mental lexicon (Unpublished doctoral dissertation). University of Nijmegen Nijmegen. [Google Scholar]
- del Prado Martín FM, Deutsch A, Frost R, Schreuder R, De Jong NH, & Baayen RH (2005). Changing places: A cross-language perspective on frequency and family size in dutch and hebrew. Journal of Memory and Language, 53 (4), 496–512. [Google Scholar]
- Downing P (1977). On the creation and use of English compound nouns. Language, 53 (4), 810–842. [Google Scholar]
- Finin TW (1980). The semantic interpretation of compound nominals (Unpublished doctoral dissertation). [Google Scholar]
- Fiorentino R, & Poeppel D (2007). Compound words and structure in the lexicon. Language and Cognitive Processes, 22 (7), 953–1000. [Google Scholar]
- Gagné CL (2000). Relation-based combinations versus property-based combinations: A test of the carin theory and the dual-process theory of conceptual combination. Journal of Memory and Language, 42 (3), 365–389. [Google Scholar]
- Gagné CL (2001). Relation and lexical priming during the interpretation of noun–noun combinations. Journal of Experimental Psychology: Learning, Memory, and Cognition, 27 (1), 236. [PubMed] [Google Scholar]
- Gagné CL (2002). Lexical and relational influences on the processing of novel compounds. Brain and Language, 81 (1), 723–735. [DOI] [PubMed] [Google Scholar]
- Gagné CL, & Shoben EJ (1997). Influence of thematic relations on the comprehension of modifier–noun combinations. Journal of Experimental Psychology: Learning, Memory, and Cognition, 23 (1), 71. [Google Scholar]
- Gagné CL, & Shoben EJ (2002). Priming relations in ambiguous noun–noun combinations. Memory & Cognition, 30 (4), 637–646. [DOI] [PubMed] [Google Scholar]
- Gagné CL, & Spalding TL (2004). Effect of relation availability on the interpretation and access of familiar noun-noun compounds. Brain and Language, 90 (1), 478–486. [DOI] [PubMed] [Google Scholar]
- Gagné CL, & Spalding TL (2006). Conceptual combination: Implications for the mental lexicon In The representation and processing of compound words (pp. 145–168). Oxford University Press, Oxford UK. [Google Scholar]
- Gagné CL, & Spalding TL (2011). Inferential processing and meta-knowledge as the bases for property inclusion in combined concepts. Journal of Memory and Language, 65 (2), 176–192. [Google Scholar]
- Gagné CL, & Spalding TL (2014). Relation diversity and ease of processing for opaque and transparent English compounds. In Morphology and meaning: Selected papers from the 15th International Morphology Meeting, Vienna, February 2012 (Vol. 327, pp. 153–162). [Google Scholar]
- Gagné CL, Spalding TL, Figueredo L, & Mullaly AC (2009). Does snow man prime plastic snow? The effect of constituent position in using relational information during the interpretation of modifier-noun phrases. The Mental Lexicon, 4 (1), 41–76. [Google Scholar]
- Gleitman LR, & Gleitman H (1970). Phrase and paraphrase: Some innovative uses of language. [Google Scholar]
- Hahn LW, & Sivley RM (2011). Entropy, semantic relatedness and proximity. Behavior Research Methods, 43 (3), 746–760. [DOI] [PubMed] [Google Scholar]
- Juhasz BJ, & Berkowitz RN (2011). Effects of morphological families on English compound word recognition: A multitask investigation. Language and Cognitive Processes, 26 (4-6), 653–682. [Google Scholar]
- Kay P, & Zimmer K (1976). On the semantics of compounds and genitives in English. In Sixth California Linguistics Association Proceedings (pp. 29–35). [Google Scholar]
- Keuleers E, Lacey P, Rastle K, & Brysbaert M (2012). The British Lexicon Project: Lexical decision data for 28,730 monosyllabic and disyllabic English words. Behavior Research Methods, 44 (1), 287–304. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuperman V, Pluymaekers M, Ernestus M, & Baayen RH (2007). Morphological predictability and acoustic duration of interfixes in Dutch compounds. The Journal of the Acoustical Society of America, 121 (4), 2261–2271. [DOI] [PubMed] [Google Scholar]
- Kuznetsova A, Brockhoff P, & Christensen R (2013). lmertest: Tests for random and fixed effects for linear mixed effect models (lmer objects of lme4 package). R package version, 2–0. [Google Scholar]
- Landauer TK, & Dumais ST (1997). A solution to plato’s problem: The latent semantic analysis theory of acquisition, induction, and representation of knowledge. Psychological Review, 104 (2), 211. [Google Scholar]
- Lees RB (1966). The grammar of english nominalizations (Unpublished doctoral dissertation). [Google Scholar]
- Levi JN (1978). The syntax and semantics of complex nominals. Academic Press, New York. [Google Scholar]
- Li CN (1971). Semantics and the structure of compounds in chinese (Unpublished doctoral dissertation). University of California, Berkeley. [Google Scholar]
- Libben G, Derwing BL, & de Almeida RG (1999). Ambiguous novel compounds and models of morphological parsing. Brain and Language, 68 (1), 378–386. [DOI] [PubMed] [Google Scholar]
- Marelli M, Dinu G, Zamparelli R, & Baroni M (2014). Picking buttercups and eating butter cups: Spelling alternations, semantic relatedness, and their consequences for compound processing. Applied Psycholinguistics, 1–19. [Google Scholar]
- Milin P, Kuperman V, Kostic A, & Baayen RH (2009a). Paradigms bit by bit: An information theoretic approach to the processing of paradigmatic structure in inflection and derivation. In Analogy in grammar: Form and acquisition (pp. 214–252). Citeseer. [Google Scholar]
- Milin P, Đurđević DF, & del Prado Martín FM (2009b). The simultaneous effects of inflectional paradigms and classes on lexical recognition: Evidence from Serbian. Journal of Memory and Language, 60 (1), 50–64. [Google Scholar]
- Moscoso del Prado Martín F, Kostic A, & Baayen RH (2004). Putting the bits together: An information theoretical perspective on morphological processing. Cognition, 94 (1), 1–18. [DOI] [PubMed] [Google Scholar]
- Pham H, & Baayen RH (2013). Semantic relations and compound transparency: A regression study in carin theory. Psihologija, 46 (4), 455–478. [Google Scholar]
- R Core Team. (2014). R: A language and environment for statistical computing [Computer software manual]. Vienna, Austria: Retrieved from http://www.R-project.org/ [Google Scholar]
- Shannon CE (1948). A mathematical theory of communication. The Bell Technical Journal, 27 (4), 379–423. [Google Scholar]
- Spalding TL, & Gagné CL (2008). Carin theory reanalysis reanalyzed: a comment on Maguire, Devereux, Costello, and Cater (2007). Journal of Experimental Psychology: Learning, Memory, and Cognition, 34 (6), 1573–1578. [DOI] [PubMed] [Google Scholar]
- Spalding TL, & Gagné CL (2011). Relation priming in established compounds: facilitation? Memory & Cognition, 39 (8), 1472–1486. [DOI] [PubMed] [Google Scholar]
- Spalding TL, & Gagné CL (2014). Relational diversity affects ease of processing even for opaque English compounds. The Mental Lexicon, 9 (1), 48–66. [Google Scholar]
- Spalding TL, Gagné CL, Mullaly AC, & Ji H (2010). Relation-based interpretation of noun-noun phrases: A new theoretical approach. Linguistische Berichte Sonderheft, 17, 283–315. [Google Scholar]
- Taft M (2003). Morphological representation as a correlation between form and meaning In Reading complex words (pp. 113–137). Springer. [Google Scholar]
- van Heuven WJ, Mandera P, Keuleers E, & Brysbaert M (2014). SUBTLEX-UK: A new and improved word frequency database for British English. The Quarterly Journal of Experimental Psychology, 67 (6), 1176–1190. [DOI] [PubMed] [Google Scholar]
- Warren B (1978). Semantic patterns of noun-noun compounds. Acta Universitatis Gothoburgensis. Gothenburg Studies in English Goteborg, 41, 1–266. [Google Scholar]
- Zwitserlood P (1994). The role of semantic transparency in the processing and representation of Dutch compounds. Language and Cognitive Processes, 9 (3), 341–368. [Google Scholar]