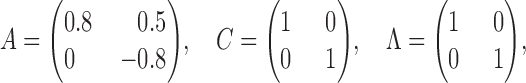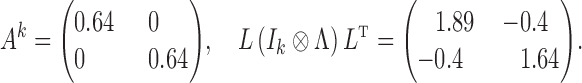Summary
Causal inference in multivariate time series is challenging because the sampling rate may not be as fast as the time scale of the causal interactions, so the observed series is a subsampled version of the desired series. Furthermore, series may be observed at different sampling rates, yielding mixed-frequency series. To determine instantaneous and lagged effects between series at the causal scale, we take a model-based approach that relies on structural vector autoregressive models. We present a unifying framework for parameter identifiability and estimation under subsampling and mixed frequencies when the noise, or shocks, is non-Gaussian. By studying the structural case, we develop identifiability and estimation methods for the causal structure of lagged and instantaneous effects at the desired time scale. We further derive an exact expectation-maximization algorithm for inference in both subsampled and mixed-frequency settings. We validate our approach in simulated scenarios and on a climate and an econometric dataset.
Keywords: Mixed frequency, Non-Gaussian error, Structural vector autoregressive model, Subsampling, Time series
1. Introduction
Classical approaches to multivariate time series and Granger causality assume that all time series are sampled at the same rate. However, due to data integration across heterogeneous sources, many datasets in econometrics, health care, environment monitoring, and neuroscience comprise multiple series sampled at different rates, referred to as mixed-frequency time series. Furthermore, due to the cost or technological challenge of data collection, many series may be sampled at a rate lower than the true causal scale of the underlying physical process. For example, many econometric indicators, such as gross domestic product, GDP, or housing price data, are recorded at quarterly and monthly scales (Moauro & Savio, 2005), though there may be important interactions between these indicators at the weekly or biweekly scale (Boot et al., 1967; Stram & Wei, 1986; Moauro & Savio, 2005). In neuroscience, imaging technologies with high spatial resolution, such as functional magnetic resonance imaging or fluorescent calcium imaging, have relatively low temporal resolutions, but many important neuronal processes and interactions happen at finer time scales (Zhou et al., 2014). A causal analysis rooted at a slower time scale than the true causal time scale may miss true interactions and add spurious ones (Boot et al., 1967; Breitung & Swanson, 2002; Silvestrini & Veredas, 2008; Zhou et al., 2014). A comprehensive approach to Granger causality in multivariate time series should be able to simultaneously accommodate both mixed-frequency and subsampled data.
Recently, causal discovery in subsampled time series has been studied with methods in causal structure learning using graphical models (Danks & Plis, 2013; Plis et al., 2015; Hyttinen et al., 2016). These methods are model-free and automatically infer a sampling rate for causal relations most consistent with the data. We maintain a similar goal, but take a model-based approach and examine the identifiability of structural vector autoregressive models under both subsampling and mixed-frequency settings. Structural models are an important tool in time series analysis (Harvey, 1990; Lütkepohl, 2005) and are a mainstay in econometrics and macro-economic policy analysis. These models combine classical linear autoregressive models with structural equation modelling (Bowen & Guo, 2011) to allow analysis of both instantaneous and lagged causal effects between time series. However, structural models are commonly applied to regularly sampled data, where each series is observed at the same regular intervals; moreover, the time scale of such an analysis is typically restricted to this shared sampling scale.
Gong et al. (2015) recently explored identifiability and estimation of vector autoregressive models under subsampling with independent innovations, i.e., no instantaneous causal effects or error correlations. They showed that with non-Gaussian errors, the transition matrix is identifiable under subsampling, implying that Granger causality estimation is possible. Unfortunately, their results do not cover correlated errors, a common and important aspect of many real-world time series (Lütkepohl, 2005). Interestingly, non-Gaussian errors have also been shown to aid model identifiability in structural autoregressive models with standard sampling assumptions (Hyvärinen et al., 2008; Zhang & Hyvärinen, 2009; Hyvärinen et al., 2010; Peters et al., 2013; Lanne et al., 2017). This line of work applies techniques developed for structural equation modelling with non-Gaussian errors and independent component analysis (Hyvärinen et al., 2004) to the structural time series context. Non-Gaussian errors allow identification of the structural model without other identifying restrictions (Lanne et al., 2017) and also allow identification of the causal ordering of the instantaneous effects if these are known to follow a directed acyclic graph (Hyvärinen et al., 2010). These models have been successfully applied to many non-Gaussian time series in econometrics (Lanne & Lütkepohl, 2010; Lanne et al., 2010; Lanne et al., 2017; Herwartz & Plödt, 2016).
Our approach to subsampling unifies existing approaches to identifiability along two complementary directions. First, our work connects the non-Gaussian subsampled autoregressive model to the independent innovations method (Gong et al., 2015) in the non-Gaussian structural autoregressive framework (Hyvärinen et al., 2008, 2010; Zhang & Hyvärinen, 2009; Peters et al., 2013; Lanne et al., 2017) by proving identifiability of a structural vector autoregressive model of order one under arbitrary subsampling. As a result, we find that one can identify not only the causal structure of lagged effects from subsampled data with correlated errors, but also the directed acyclic graph of the instantaneous effects, without prior knowledge of the causal ordering.
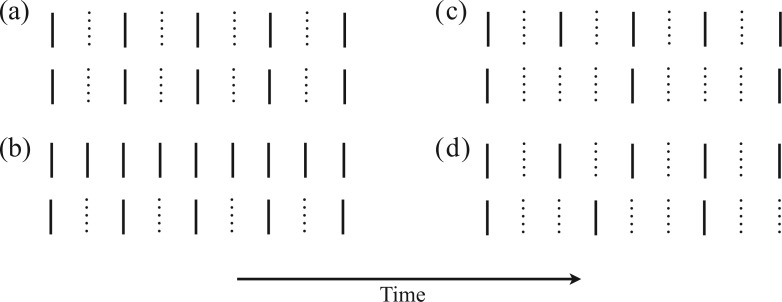
Second, we generalize our results to the mixed-frequency setting with arbitrary subsampling, where the subsampling level may be different for each time series. In doing so, we provide a unified theoretical approach and estimation method for subsampled and mixed-frequency cases. Deriving identifiability conditions on the model parameters in the mixed-frequency case is difficult (Anderson et al., 2016) and has only been studied based on the first two moments of the mixed-frequency process. Our work follows a complementary direction by leveraging higher-order moments and provides the first set of specific model conditions for mixed-frequency structural models needed for identifiability. Furthermore, previous mixed-frequency approaches have assumed a causal ordering, while our results indicate that this may be estimated by leveraging non-Gaussianity. Finally, our approach to identifiability allows us to move beyond the classical mixed-frequency setting, where the time scale is fixed at the most finely sampled series (Anderson et al., 2016); we instead consider identifiability and estimation in more general mixed-frequency cases. The four sampling types covered by our approach are shown in Fig. 1. To simplify the presentation, we first introduce our theoretical results for subsampled series of case (a) in § 3. We then generalize the results to the mixed-frequency cases (b), (c) and (d) in § 4.
Fig. 1.
Four types of structured sampling, where black lines indicate observed data and dotted lines indicate missing data: (a) both series are subsampled; (b) the standard mixed-frequency case, where only the second series is subsampled; (c) a subsampled version of case (b) where each series is subsampled at a different rate; (d) a subsampled mixed-frequency series that has no common factor across sampling rates and thus is not a subsampled version of case (b).
We introduce an exact expectation-maximization algorithm for inference in both subsampled and mixed-frequency cases. Gong et al. (2015) also use such an algorithm, but because they formulate inference directly on the subsampled process by marginalizing the missing data, their approach requires an extra approximation. Our approach instead casts inference as a missing-data problem and uses a Kalman filter to exactly compute the E-step for both subsampled and mixed-frequency cases. We validate our estimation and identifiability results via extensive simulations and apply our method to evaluate causal relations in a subsampled climate dataset and a mixed-frequency econometric dataset. Taken together, we present a unified theoretical analysis and estimation methodology for subsampled and mixed-frequency cases, which have previously been studied separately. A summary of our contributions is presented in Table 1.
Table 1.
Summary of contributions of our work to identifiability and estimation in mixed-frequency sampling for structural autoregressive models: the subsampling types are as in Fig. 1; citations refer to previous work and check marks indicate our contributions
| Sampling type | None | A | B | D | ||
|---|---|---|---|---|---|---|
|
Identifiability | Lut05 | Gong15 | ✓ | ✓ | ✓ |
| Estimation | Lut05 | Gong15 (approx.) ✓ | ✓ | ✓ (ce) | ✓ (ce) | |
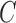 free free |
Identifiability | Hyv08 | ✓ | ✓ | ✓ | ✓ |
| Estimation | Hyv08 | ✓ | ✓ | ✓ (ce) | ✓ (ce) |
(ce), computationally expensive; Hyv08, Hyvärinen et al. (2008); Gong15, Gong et al. (2015); Lut05, Lütkepohl (2005).
2. Background
Let 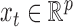
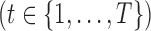 be a
be a 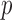 -dimensional multivariate time series generated at a fixed sampling rate. We collect all the
-dimensional multivariate time series generated at a fixed sampling rate. We collect all the 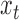 into the matrix
into the matrix 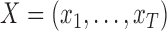 . We assume that the dynamics of
. We assume that the dynamics of 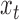 follows a combination of instantaneous effects, autoregressive effects and independent noise:
follows a combination of instantaneous effects, autoregressive effects and independent noise:
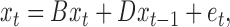 |
(1) |
where 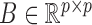 is the structural matrix that determines the instantaneous-time linear effects,
is the structural matrix that determines the instantaneous-time linear effects, 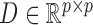 is an autoregressive matrix that specifies the lag-one effects conditional on the instantaneous effects, and
is an autoregressive matrix that specifies the lag-one effects conditional on the instantaneous effects, and 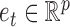 is a white noise process such that
is a white noise process such that 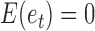 for all
for all 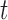 and
and 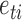 is independent of
is independent of 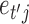 for all
for all 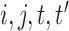 such that
such that 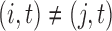 . We assume that
. We assume that 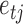 is distributed as
is distributed as 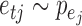 . Solving (1) in terms of
. Solving (1) in terms of 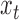 gives the following lag-one structural vector autoregressive process for the evolution of
gives the following lag-one structural vector autoregressive process for the evolution of 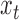 :
:
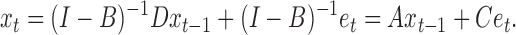 |
(2) |
Under the representation in (2), each element 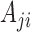 denotes the lag-one linear effect of series
denotes the lag-one linear effect of series 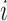 on series
on series 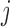 and
and 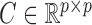 is the structural matrix. The error
is the structural matrix. The error 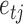 is referred to as the shock to series
is referred to as the shock to series 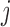 at time
at time 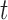 , and the element
, and the element 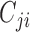 is the linear instantaneous effect of
is the linear instantaneous effect of 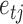 on
on 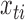 .
.
Conditions on 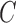 , or equivalently
, or equivalently 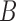 , for model identifiability and estimation have been explored (Harvey, 1990; Kilian & Lütkepohl, 2016). The most typical condition is that
, for model identifiability and estimation have been explored (Harvey, 1990; Kilian & Lütkepohl, 2016). The most typical condition is that 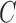 is a lower triangular matrix with ones on the diagonal, implying a known causal ordering of the instantaneous effects. In this case, one may interpret the instantaneous effects as a directed acyclic graph (Lauritzen, 1996), i.e., a graph
is a lower triangular matrix with ones on the diagonal, implying a known causal ordering of the instantaneous effects. In this case, one may interpret the instantaneous effects as a directed acyclic graph (Lauritzen, 1996), i.e., a graph 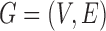 with vertices
with vertices 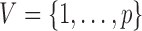 and directed edge set
and directed edge set 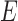 that has no directed cycles. A causal ordering is an ordering of the vertices into a sequence,
that has no directed cycles. A causal ordering is an ordering of the vertices into a sequence, 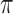 , such that if
, such that if 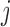 comes before
comes before 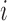 in
in 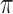 then
then 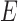 does not contain a path of edges from
does not contain a path of edges from 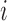 to
to 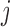 ; see, e.g., Shojaie & Michailidis (2010) for details. In the structural context, for
; see, e.g., Shojaie & Michailidis (2010) for details. In the structural context, for 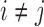 there exists a directed edge
there exists a directed edge 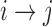 from
from 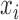 to
to 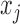 in
in 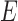 if and only if
if and only if 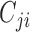 is nonzero. Classical estimation for structural models with known causal ordering typically proceeds by simultaneously fitting
is nonzero. Classical estimation for structural models with known causal ordering typically proceeds by simultaneously fitting 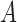 and
and 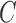 with the identifiability constraint that
with the identifiability constraint that  be lower triangular. When there are no unobserved confounders, as we assume throughout this paper, we may refer to the entries in
be lower triangular. When there are no unobserved confounders, as we assume throughout this paper, we may refer to the entries in 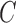 as instantaneous causal effects.
as instantaneous causal effects.
A recent line of work (Zhang & Hyvärinen, 2009; Hyvärinen et al., 2010; Lanne et al., 2017) focuses on estimating 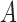 and
and 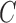 when
when 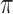 is unknown. When the errors
is unknown. When the errors 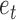 are non-Gaussian, both the causal ordering and the instantaneous effects
are non-Gaussian, both the causal ordering and the instantaneous effects 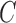 may be inferred directly from the data using techniques from independent component analysis (Hyvärinen et al., 2010). Alternatively, one may dispense with orderings and lower triangular restrictions and directly estimate
may be inferred directly from the data using techniques from independent component analysis (Hyvärinen et al., 2010). Alternatively, one may dispense with orderings and lower triangular restrictions and directly estimate 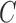 under non-Gaussian errors (Lanne et al., 2017). Our analysis continues along these directions, leveraging non-Gaussianity of the structural model with subsampling or mixed frequencies.
under non-Gaussian errors (Lanne et al., 2017). Our analysis continues along these directions, leveraging non-Gaussianity of the structural model with subsampling or mixed frequencies.
3. Subsampled structural vector autoregressive models
3.1. The subsampled process
Subsampling occurs when, due to low temporal resolution, we only observe 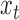 every
every 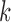 time-steps, as displayed graphically in case (a) of Fig. 1. In this situation, we only have access to observations
time-steps, as displayed graphically in case (a) of Fig. 1. In this situation, we only have access to observations 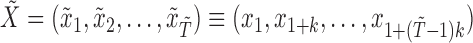 , where
, where 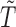 is the number of subsampled observations. By marginalizing out the unobserved
is the number of subsampled observations. By marginalizing out the unobserved 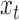 , we obtain the evolution equations
, we obtain the evolution equations
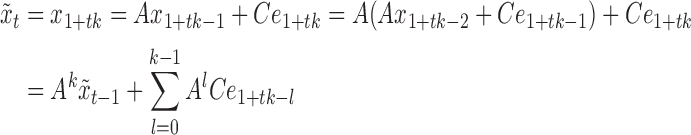 |
(3) |
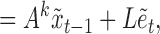 |
(4) |
where 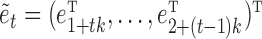 is the stacked vector of errors for time
is the stacked vector of errors for time 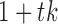 and the unobserved time-points between times
and the unobserved time-points between times 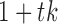 and
and 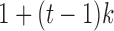 , and
, and 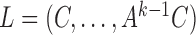 . Equation (3) states that the subsampled process is a linear transformation of the past subsampled observations with transition matrix
. Equation (3) states that the subsampled process is a linear transformation of the past subsampled observations with transition matrix 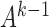 and a weighted sum of the shocks across all unobserved time-points. Each shock is weighted by
and a weighted sum of the shocks across all unobserved time-points. Each shock is weighted by 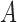 raised to the power of the time lag. We provide an example of (3) in the Supplementary Material.
raised to the power of the time lag. We provide an example of (3) in the Supplementary Material.
Equation (4) appears to take a similar form to the structural process in (1), but now the vector of shocks, 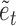 , is of dimension
, is of dimension 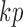 , with special structure on both the structural matrix
, with special structure on both the structural matrix 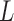 and the distributions of the elements in
and the distributions of the elements in 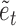 . Unfortunately, this representation does not have the interpretation of instantaneous causal effects described in § 2, as there are now multiple shocks per individual time series. We will refer to the full parameterization of the subsampled structural model in (4) as
. Unfortunately, this representation does not have the interpretation of instantaneous causal effects described in § 2, as there are now multiple shocks per individual time series. We will refer to the full parameterization of the subsampled structural model in (4) as  . Identifiability of this model means that there is a unique pair of matrices
. Identifiability of this model means that there is a unique pair of matrices 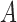 and
and 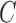 consistent with the joint distribution of
consistent with the joint distribution of 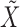 at subsampling rate
at subsampling rate 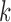 .
.
3.2. Lagged and instantaneous causality confounds of subsampling
A classical analysis based on 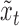 that does not account for subsampling would incorrectly estimate lagged Granger causal effects in
that does not account for subsampling would incorrectly estimate lagged Granger causal effects in 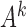 , because
, because 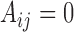 does not imply
does not imply 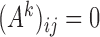 , and vice versa (Gong et al., 2015). Similarly, estimation of structural interactions may also be biased if subsampling is ignored. Classical structural estimation methods that assume a known causal ordering of the instantaneous shocks simply estimate the covariance of the error process,
, and vice versa (Gong et al., 2015). Similarly, estimation of structural interactions may also be biased if subsampling is ignored. Classical structural estimation methods that assume a known causal ordering of the instantaneous shocks simply estimate the covariance of the error process, 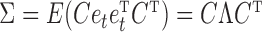 , and let the estimated structural matrix be the Cholesky decomposition of
, and let the estimated structural matrix be the Cholesky decomposition of 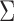 . Under subsampling, the covariance of the error process is
. Under subsampling, the covariance of the error process is
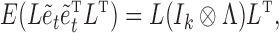 |
(5) |
where 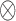 is the Kronecker product and
is the Kronecker product and 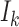 is the identity matrix of size
is the identity matrix of size 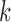 . The causal structure given by zeros in the Cholesky decomposition of (5) need not be the same as that implied by
. The causal structure given by zeros in the Cholesky decomposition of (5) need not be the same as that implied by 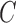 .
.
Example 1.
Consider the process (Gong et al., 2015)
so that
. Then, for a subsampling of
,
This implies no lagged causal effect between
and
but a relatively large instantaneous interaction, contrary to the true data-generating model; see Fig. 2.
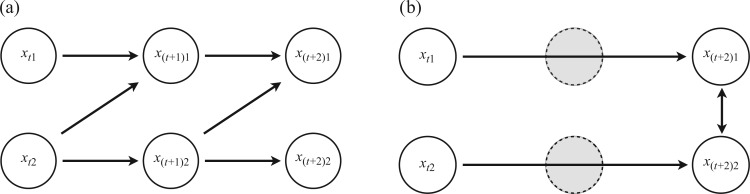
Fig. 2.
Graphical depiction of how subsampling confounds causal analysis of both lagged and instantaneous effects: (a) the true causal diagram for the regularly sampled data; (b) the estimated causal structure of the subsampled process when the effects of subsampling are ignored.
3.3. Identifiability of L under subsampling
While both lagged Granger causality and instantaneous structural interactions are confounded by subsampling, we show here that by accounting for subsampling we may, under some conditions, still estimate the 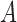 and
and 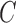 matrices of the underlying process directly from the subsampled data. As a first step towards proving the identifiability of
matrices of the underlying process directly from the subsampled data. As a first step towards proving the identifiability of 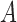 and
and 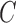 , we show that the matrix
, we show that the matrix 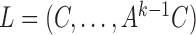 in (4) is identifiable up to permutation and scaling of columns when the
in (4) is identifiable up to permutation and scaling of columns when the  , the distributions of the
, the distributions of the  , are all non-Gaussian.
, are all non-Gaussian.
Proposition 1.
Suppose that all the
are non-Gaussian. Given a known subsampling factor
and subsampled data
generated according to (4),
may be determined up to permutation and scaling of columns.
The proof closely follows that of Proposition 1 in Gong et al. (2015) and depends on the following fundamental result in independent component analysis (Eriksson & Koivunen, 2004).
Lemma 1.
Let
and
be two representations of the
-dimensional random vector
, where
and
are constant matrices of orders
and
, respectively, and
and
are random vectors with independent components.
If the
th column of
is not proportional to any column of
, then
is Gaussian. Moreover, if the
th column of
is proportional to the
th column of
, then the logarithms of the characteristic functions of
and
differ by a polynomial in a neighbourhood of the origin.
This result states that if 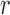 is non-Gaussian with independent elements and if
is non-Gaussian with independent elements and if 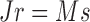 , then
, then 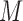 and
and 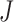 must be equal up to permutation and scaling of columns. This implies that one may estimate
must be equal up to permutation and scaling of columns. This implies that one may estimate 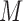 from only observations of
from only observations of 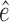 and that the estimate of
and that the estimate of 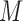 should be equal, up to permutations and scalings, to the true
should be equal, up to permutations and scalings, to the true 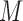 .
.
To prove Proposition 1 using Lemma 1, note that 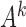 is identifiable by linear regression. Hence, the error component
is identifiable by linear regression. Hence, the error component 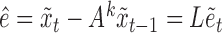 satisfies the conditions of Lemma 1 and
satisfies the conditions of Lemma 1 and 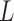 is identifiable up to permutations and scalings since the
is identifiable up to permutations and scalings since the 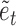 are non-Gaussian.
are non-Gaussian.
3.4. Complete identifiability of the structural autoregressive model when 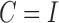
Using the identifiability result for 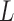 in Proposition 1, we can derive identifiability statements and conditions for
in Proposition 1, we can derive identifiability statements and conditions for 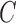 and
and 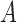 in the subsampled case. We require a few mild assumptions.
in the subsampled case. We require a few mild assumptions.
Assumption 1.
Let
be stationary so that all singular values of
have modulus less than
.
Assumption 2.
The distributions
are distinct for each
after rescaling
by any nonzero scale factor; their characteristic functions are all analytic, or are all nonvanishing, and none of them has an exponent factor with polynomial of degree at least two.
Assumption 3.
All the
are asymmetric.
Assumption 1 is standard in time series modelling (Lütkepohl, 2005), and Assumption 2 is common in independent component analysis. While many of our identifiability results for 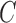 only require that the
only require that the 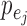 distributions be non-Gaussian, our identifiability results for
distributions be non-Gaussian, our identifiability results for 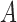 in part (ii) of Theorems 1 and 2 and part (iii) of Theorems 3 and 4 further require Assumption 3, namely that the
in part (ii) of Theorems 1 and 2 and part (iii) of Theorems 3 and 4 further require Assumption 3, namely that the 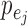 be asymmetric. In practice, assuming fully Gaussian errors may be unrealistic, as aspects of non-Gaussianity, such as asymmetry (Harvey & Siddique, 2000; Walls, 2005; Lanne & Pentti, 2007), heavy tails (Cont, 2001; Rachev, 2003) or stochastic volatility (Justiniano & Primiceri, 2008), are often observed. Not only are non-Gaussian errors empirically appealing but, furthermore, theoretical and modelling approaches that harness the higher-order moments of non-Gaussian distributions aid in identifying model parameters that are unidentifiable from the first two moments alone.
be asymmetric. In practice, assuming fully Gaussian errors may be unrealistic, as aspects of non-Gaussianity, such as asymmetry (Harvey & Siddique, 2000; Walls, 2005; Lanne & Pentti, 2007), heavy tails (Cont, 2001; Rachev, 2003) or stochastic volatility (Justiniano & Primiceri, 2008), are often observed. Not only are non-Gaussian errors empirically appealing but, furthermore, theoretical and modelling approaches that harness the higher-order moments of non-Gaussian distributions aid in identifying model parameters that are unidentifiable from the first two moments alone.
Gong et al. (2015) give identifiability results under Assumptions 1 and 2 for the subsampled autoregression with no error correlations, 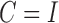 . We restate their result in our framework.
. We restate their result in our framework.
Theorem 1
(Gong et al., 2015) Suppose that
is non-Gaussian for all
and
, and that the data
are generated by (2) with
. Assume that the process admits another representation
. If Assumptions 1 and 2 hold, then we have the following:
(i)
can be represented as
, where
is a diagonal matrix with
or
on the diagonal; if we constrain the self influences to be positive, represented by the diagonal entries, then
.
(ii) If Assumption 3 also holds, then
.
3.5. Complete identifiability of general structural autoregressive models
For identifiability of the full model under subsampling, we require two more assumptions.
Assumption 4.
The variance of each
is equal to
, i.e.,
.
Assumption 5.
The matrix
is of full rank.
Assumption 4 is common in structural modelling and removes the nonidentifiability between scaling the 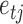 and scaling the columns of
and scaling the columns of 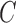 . Assumption 5 is mild, and covers the more restrictive assumption in non-Gaussian structural models that
. Assumption 5 is mild, and covers the more restrictive assumption in non-Gaussian structural models that 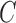 may be row- and column-permuted to a lower triangular matrix (Shimizu et al., 2006). Under these assumptions, we have the following identifiability result for general subsampled structural models.
may be row- and column-permuted to a lower triangular matrix (Shimizu et al., 2006). Under these assumptions, we have the following identifiability result for general subsampled structural models.
Theorem 2.
Suppose that the
are all non-Gaussian and independent, and that the data
are generated by (2) with representation
. Assume that the process also admits another subsampling representation
. If Assumptions 1, 2 and 4 hold, then we have the following:
(i)
is equal to
up to permutation of columns and scaling of columns by
or
; that is,
where
is a scaled permutation matrix with elements being
or
; this implies that
.
(ii) If Assumptions 3 and 5 also hold, then
.
The requirement that 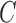 be of full rank stems from the structure of
be of full rank stems from the structure of 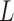 . Since one may identify
. Since one may identify 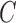 as the first
as the first 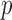 columns of
columns of  , to obtain
, to obtain 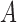 we must premultiply the second set of
we must premultiply the second set of 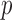 columns of
columns of 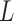 by
by 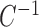 . The asymmetry assumption is needed since the scaling of the columns of
. The asymmetry assumption is needed since the scaling of the columns of 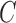 and
and 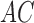 by factors of
by factors of 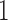 or
or 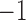 is ambiguous if the distributions are symmetric; the asymmetry assumption ensures that the unit scalings are identifiable; see the Supplementary Material.
is ambiguous if the distributions are symmetric; the asymmetry assumption ensures that the unit scalings are identifiable; see the Supplementary Material.
If the instantaneous causal effects follow a directed acyclic graph, we may identify the structure without any prior information about causal ordering of the variables.
Corollary 1.
Suppose that Assumptions 1, 2 and 4 hold. If the true structural process corresponds to a directed acyclic graph
, i.e., it has a lower triangular structural matrix
with positive diagonals, and if it admits another representation with structural matrix
, then
. Hence the structure of
is identifiable without prior specification of the causal ordering of
.
This result follows because 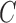 may be identified up to a column permutation. Based on the identifiability results of Shimizu et al. (2006), if
may be identified up to a column permutation. Based on the identifiability results of Shimizu et al. (2006), if 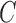 corresponds to an acyclic graph, it may be row- and column-permuted to a unique lower triangular matrix. The row permutations identify the causal ordering, and the nonzero elements below the diagonal identify the edges in
corresponds to an acyclic graph, it may be row- and column-permuted to a unique lower triangular matrix. The row permutations identify the causal ordering, and the nonzero elements below the diagonal identify the edges in 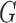 . See Shimizu et al. (2006) for more details on identifiability and estimation of the graph from
. See Shimizu et al. (2006) for more details on identifiability and estimation of the graph from 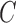 .
.
Taken together, the results of Theorem 2 and Corollary 1 imply that when the shocks 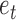 are independent and asymmetric, a complete causal diagram of the lagged effects and the instantaneous effects is fully identifiable from the subsampled time series,
are independent and asymmetric, a complete causal diagram of the lagged effects and the instantaneous effects is fully identifiable from the subsampled time series, 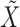 .
.
4. Mixed-frequency structural autoregressive models
4.1. Background and motivation
Estimation and forecasting of mixed-frequency time series are commonly approached using autoregressive models (Schorfheide & Song, 2015). Typically, the model is fitted at the same scale as the fastest sampled time series, which is depicted in Fig. 1(c). The primary motivating example of Fig. 1(c) in the literature is GDP (Anderson et al., 2016). The subsampled structure of Fig. 1(c) simplifies the temporal aggregation of GDP and is used to simplify analysis. Due to costly data collection, especially for macro-economic indicators such as GDP, the scale of the fastest sampled series is generally arbitrary and may not reflect the true causal dynamics, leading to confounded Granger and instantaneous causality judgements (Breitung & Swanson, 2002; Zhou et al., 2014). If the true causal scale, or one of interest to an analyst, is at a lower rate, as in case (d) of Fig. 1, then an analysis at the observed rate will run into the same problems as those for the single-frequency subsampling case discussed in § 3.2. We provide an example at the end of § 4.2.
Finding identifiability conditions for mixed-frequency autoregressive models with no subsampling at the fastest scale, Fig. 1(b), was an open problem for many years (Chen & Zadrozny, 1998). Recently Anderson et al. (2016) showed that the mixed-frequency nonstructural autoregressive model of Fig. 1(b) is generically identifiable from the first two observed moments, so unidentifiable models make up a set of measure zero in the parameter space. Explicit identifiability conditions for the lag-one, bivariate case from the first two moments have also been established (Anderson et al., 2012). However, no explicit identifiability conditions for structural models or models in higher dimensions have been explored.
In this section, we generalize our identifiability results from § 3 to the mixed-frequency case with arbitrary levels of subsampling for each time series. Our analysis indicates that Granger and instantaneous causal effects can be accurately estimated from mixed-frequency time series. Specifically, we use the results from § 3 to provide explicit identifiability conditions for mixed-frequency structural models under arbitrary subsampling, namely cases (b), (c) and (d) in Fig. 1, with non-Gaussian error assumptions. Altogether, our framework provides a unified way of deriving explicit identifiability conditions for both subsampling and mixed-frequency cases. While case (c) in Fig. 1 is a subsampled version of the standard mixed-frequency case, our results also cover mixed-frequency subsampling as in case (d). To the best of our knowledge, these results are the first identifiability results for subsampled mixed-frequency cases like (c) and (d).
4.2. Mixed-frequency structural autoregressive models
We assume that each time series in 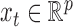 is sampled at one of two sampling rates, a slow subsampling rate
is sampled at one of two sampling rates, a slow subsampling rate 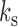 and a fast subsampling rate
and a fast subsampling rate 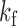 . We write
. We write 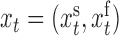 , where
, where 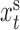 are those series subsampled at
are those series subsampled at 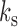 and
and 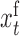 are those subsampled at
are those subsampled at 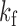 . Let
. Let 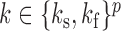 be the list of subsampling rates for each time series. In Fig. 1(b),
be the list of subsampling rates for each time series. In Fig. 1(b), 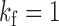 and
and 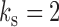 , whereas in Fig. 1(c),
, whereas in Fig. 1(c), 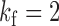 and
and 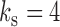 . Analogously to the subsampled case, we refer to a parameterization of a mixed-frequency structural model as
. Analogously to the subsampled case, we refer to a parameterization of a mixed-frequency structural model as 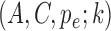 , where
, where 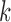 is now a
is now a 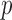 -vector. Let
-vector. Let 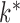 be the smallest multiple of both
be the smallest multiple of both 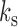 and
and 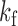 ; for example, in Fig. 1(c) we have
; for example, in Fig. 1(c) we have 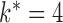 .
.
We may derive a similar representation to (4) for mixed-frequency series. Fix a time-point 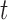 such that all series are observed. Let
such that all series are observed. Let 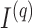 be a modified
be a modified 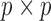 identity matrix where all rows
identity matrix where all rows 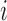 such that
such that 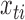 is not observed at time
is not observed at time  are set to zero. Further, let
are set to zero. Further, let 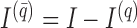 ,
, 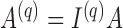 and
and 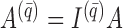 . Then
. Then
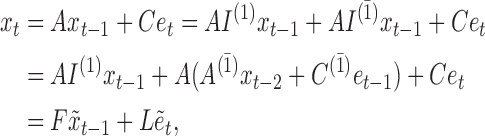 |
(6) |
where
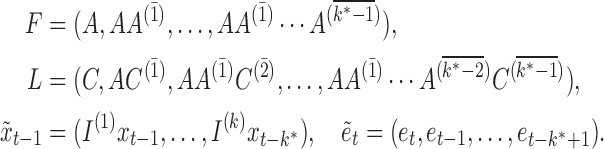 |
Equation (6) has the same form as (4), suggesting that similar identifiability results will hold. We provide an example of (6) for a mixed-frequency series in the Supplementary Material.
In a subsampled mixed-frequency setting where the fastest rate is greater than unity, Fig. 1(c), not accounting for subsampling leads not only to the kind of mistaken inferences discussed in § 3.2 but also to further mistakes unique to the mixed-frequency case.
Example 2.
Consider a subsampled mixed-frequency structural process generated by (6) with the
parameters given by Example 1. Suppose subsampling is not taken into account and that
is analysed instead as a classical mixed-frequency series, case (b), based on the first two moments (Anderson et al., 2016). We consider two cases.
Case 1: the sampling rate is
. In this case, if
is analysed at the rate
using the first two moments, then
and
are not identifiable at this rate since both off-diagonal elements of
are zero (Anderson et al., 2016). Thus, no inference of both the instantaneous correlations and the lagged effects is possible.
Case 2: the sampling rate is
. In this case, if
is analysed at the rate
using the first two moments, the estimated
and covariance
will be the same as in Example 1 (Anderson et al., 2016), leading to an incorrect inference that there is an instantaneous effect but no directed lagged effect.
4.3. Identifiability of mixed-frequency structural autoregressive models
We provide generalizations of Theorems 1 and 2 to the mixed-frequency case.
Theorem 3.
Suppose the
are non-Gaussian and independent for all
and
, and that the data
are generated by (2) with
. Assume that the process also admits another mixed-frequency representation
. If Assumptions 1 and 2 hold, then we have the following:
(i)
can be represented as
, where
is a diagonal matrix with
or
on the diagonal.
(ii) If any multiple of
is
smaller than some multiple of
, then
. If
, this implies
, i.e., the
th columns of
and
are equal,
.
(iii) If Assumption 3 also holds, then
.
Proof.
Statements (i) and (iii) follow since we may further subsample all series in
to a subsampling rate of
. This gives a subsampled
with representation
. Applying Theorem 1 gives the result. Furthermore, if some multiple of
is equal to some multiple of
minus 1, then there exists a set of times
for (6) such that series
is observed at time
and series
is observed at time
. By identifiability of linear regression,
. This resolves the sign ambiguity of the columns in (iii) so that
. □
Theorem 4.
Suppose the
are non-Gaussian and independent for all
and
, and that the data
are generated by (2) with representation
. Assume that the process also admits another mixed-frequency subsampling representation
. If Assumptions 1, 2 and 4 hold, then we have the following:
(i)
is equal to
up to permutation of columns and scaling of columns by
or
, i.e.,
where
is a scaled permutation matrix with elements being
or
; this implies that
.
(ii) If
is lower triangular with positive diagonals, i.e., the instantaneous interactions follow a directed acyclic graph, and if for all
there exists a
such that any multiple of
is
smaller than some multiple of
with
, then
.
(iii) If Assumptions 3 and 5 also hold, then
.
The proofs of statements (i) and (iii) follow the same subsampling argument as in the proof of Theorem 3. The proof of (ii) is given in the Supplementary Material.
Theorems 3 and 4 demonstrate that identifiability of structural models still holds for mixed-frequency series with subsampling under non-Gaussian errors. Statements (i) and (iii) of Theorems 3 and 4 are the same as their subsampled counterparts; statement (ii) in both theorems shows how the mixed-frequency setting provides additional information for resolving parameter ambiguities in the non-Gaussian setting. Specifically, when there is a one-time-step difference between when series 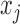 and
and 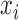 are sampled, then
are sampled, then 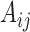 is identifiable. We can then use this information to resolve sign ambiguities in columns of
is identifiable. We can then use this information to resolve sign ambiguities in columns of 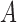 , which leads to statement (ii) in both of Theorems 3 and 4. This result applies directly to the standard mixed-frequency setting (Schorfheide & Song, 2015; Anderson et al., 2016), where one series is observed at every time-step in Fig. 1(b). It also applies to case (d), since there exist certain time-steps where one series is observed one time-step before another series.
, which leads to statement (ii) in both of Theorems 3 and 4. This result applies directly to the standard mixed-frequency setting (Schorfheide & Song, 2015; Anderson et al., 2016), where one series is observed at every time-step in Fig. 1(b). It also applies to case (d), since there exist certain time-steps where one series is observed one time-step before another series.
5. Estimation
5.1. Modelling non-Gaussian errors
We model the non-Gaussian errors as a mixture of Gaussian distributions with 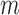 components. This approach has been adopted widely in econometrics and other fields as a flexible and tractable way of modelling non-Gaussian innovations (Gong et al., 2015; Lanne et al., 2017). Formally, we assume that
components. This approach has been adopted widely in econometrics and other fields as a flexible and tractable way of modelling non-Gaussian innovations (Gong et al., 2015; Lanne et al., 2017). Formally, we assume that 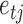 is drawn from the mixture distribution
is drawn from the mixture distribution
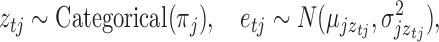 |
where 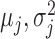 and
and 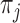 are
are 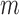 -vectors specifying the mean, variance and mixing weight of each mixture component. The
-vectors specifying the mean, variance and mixing weight of each mixture component. The 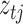 component indicators are auxiliary variables introduced to facilitate inference. The mixture model for the errors implies that conditional on the assignment indicators
component indicators are auxiliary variables introduced to facilitate inference. The mixture model for the errors implies that conditional on the assignment indicators 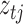 , the mean and variance of the error distribution for each series
, the mean and variance of the error distribution for each series 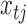 are time-dependent. This mixture model can capture the types of non-Guassianity required for identifiability and also those observed in real-world time series. Asymmetric errors may be formed when the mixture centres are nonzero and the variances or mixture weights are different. A non-Gaussian symmetric distribution with kurtosis greater than 1 may be formed by setting the mixture centres to zero but allowing the mixture variances to have different values. The full set of parameters for the structural model is
are time-dependent. This mixture model can capture the types of non-Guassianity required for identifiability and also those observed in real-world time series. Asymmetric errors may be formed when the mixture centres are nonzero and the variances or mixture weights are different. A non-Gaussian symmetric distribution with kurtosis greater than 1 may be formed by setting the mixture centres to zero but allowing the mixture variances to have different values. The full set of parameters for the structural model is 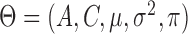 where
where 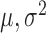 and
and 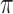 concatenate the mixture parameters of the errors across series. For example,
concatenate the mixture parameters of the errors across series. For example, 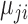 is the mean of the
is the mean of the 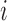 th mixture component for the
th mixture component for the 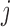 th error distribution, and likewise for
th error distribution, and likewise for 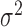 and
and 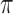 .
.
5.2. Expectation-maximization algorithm
We develop an expectation-maximization algorithm for joint maximum likelihood estimation of the full set of parameters  based only on the observed subsampled and mixed-frequency data
based only on the observed subsampled and mixed-frequency data 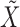 . Unlike the method of Gong et al. (2015), which is tailored to the subsampled case, our method is the same for both types of data. Furthermore, the non-structural-specific, i.e.,
. Unlike the method of Gong et al. (2015), which is tailored to the subsampled case, our method is the same for both types of data. Furthermore, the non-structural-specific, i.e., 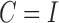 , algorithm of Gong et al. (2015) introduces auxiliary noise terms to facilitate inference, rendering the resulting algorithm inexact, whereas our algorithm introduces no such approximations. Since the loglikelihood is nonconvex, we employ multiple random restarts to avoid poor local optima. For the subsampled case, the local optimum problem is particularly severe due to the nonidentifiability under the first two moments; many values of
, algorithm of Gong et al. (2015) introduces auxiliary noise terms to facilitate inference, rendering the resulting algorithm inexact, whereas our algorithm introduces no such approximations. Since the loglikelihood is nonconvex, we employ multiple random restarts to avoid poor local optima. For the subsampled case, the local optimum problem is particularly severe due to the nonidentifiability under the first two moments; many values of 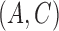 can give a good fit to the data. The basic algorithm also suffers from slow convergence due to the large amount of missing data. To speed up the algorithm, we deploy the adaptive over-relaxed method of Salakhutdinov & Roweis (2003).
can give a good fit to the data. The basic algorithm also suffers from slow convergence due to the large amount of missing data. To speed up the algorithm, we deploy the adaptive over-relaxed method of Salakhutdinov & Roweis (2003).
Let 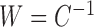 , and let
, and let 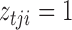 if error
if error 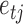 was generated by mixture component
was generated by mixture component 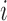 and
and 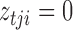 otherwise. The complete loglikelihood,
otherwise. The complete loglikelihood, 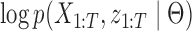 , of our structural model is
, of our structural model is
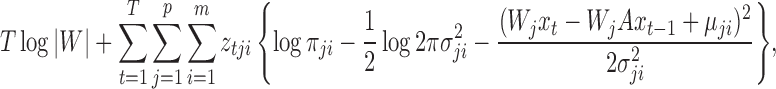 |
where 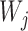 is the
is the 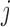 th row vector of
th row vector of 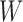 . The algorithm alternates between the E-step, where we compute the conditional expectation
. The algorithm alternates between the E-step, where we compute the conditional expectation 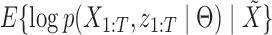 , and the M-step, where that expectation is maximized with respect to the parameters
, and the M-step, where that expectation is maximized with respect to the parameters 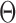 . We first describe the M-step updates, and then explain how the conditional expectations are computed using a Kalman filter.
. We first describe the M-step updates, and then explain how the conditional expectations are computed using a Kalman filter.
5.3. The M-step
In the M-step, we maximize the expected complete loglikelihood conditional on the observed data, 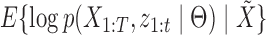 , with respect to
, with respect to 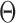 via coordinate ascent, cycling through
via coordinate ascent, cycling through 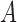 ,
, 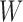 and
and 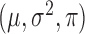 until convergence. The specific updates are as follows.
until convergence. The specific updates are as follows.
Updating 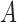 : each row of
: each row of 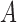 ,
, 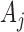 , may be updated independently according to
, may be updated independently according to
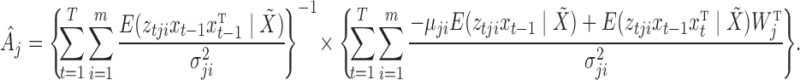 |
Updating 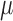 ,
, 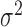 and
and  : these may be optimized jointly in one step using
: these may be optimized jointly in one step using
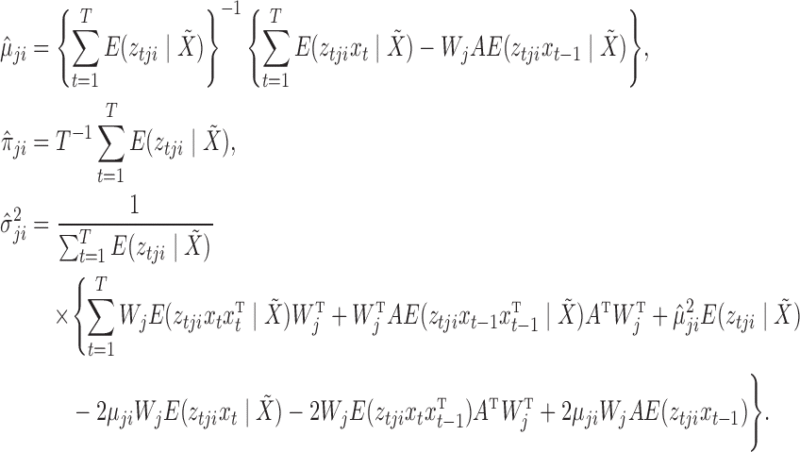 |
Updating 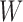 : since the maximization is not given in closed form, we use the Newton-Raphson method. Let
: since the maximization is not given in closed form, we use the Newton-Raphson method. Let 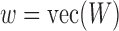 be the
be the 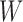 vectorization. At each step, the next
vectorization. At each step, the next 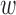 iterate is
iterate is
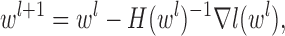 |
where 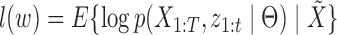 and
and 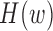 is the Hessian of
is the Hessian of 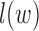 with respect to
with respect to 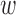 . Expressions for the gradient and Hessian are given in the Supplementary Material.
. Expressions for the gradient and Hessian are given in the Supplementary Material.
5.4. The E-step
All conditional expectations in the M-step above are computed using the Kalman filtering-smoothing algorithm. For simplicity, consider one block of data, so that 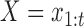 , where
, where 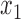 and
and 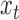 are fully observed but the
are fully observed but the 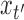 for
for 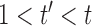 have some missing data and hence are not included in
have some missing data and hence are not included in 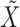 . Any subsampled or mixed-frequency series can be broken into blocks of this type. The conditional expectation
. Any subsampled or mixed-frequency series can be broken into blocks of this type. The conditional expectation 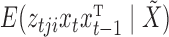 can be computed by noticing that
can be computed by noticing that
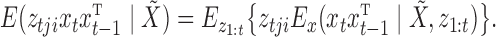 |
For a fixed 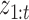 ,
, 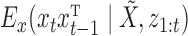 is computed using the Kalman filtering-smoothing algorithm, since for fixed
is computed using the Kalman filtering-smoothing algorithm, since for fixed 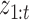 ,
, 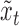 is a linear Gaussian state-space model with latent observations
is a linear Gaussian state-space model with latent observations 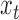 . We compute
. We compute 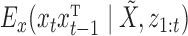 for each
for each 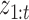 combination and then add these together weighted by
combination and then add these together weighted by 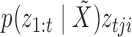 . The probability
. The probability 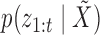 may be computed as
may be computed as
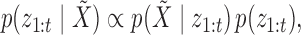 |
where 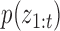 is the set of prior mixture component weights,
is the set of prior mixture component weights, 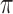 , and
, and 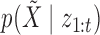 is the likelihood of the observed data, which may also be computed by one Kalman pass. This process is repeated for all expectations in the E-step. The computational complexity of this exact algorithm scales as
is the likelihood of the observed data, which may also be computed by one Kalman pass. This process is repeated for all expectations in the E-step. The computational complexity of this exact algorithm scales as 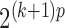 , since the Kalman filter must be run for all combinations of
, since the Kalman filter must be run for all combinations of 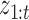 for each block. The approximate algorithm of Gong et al. (2015) has the same complexity. Like Gong et al. (2015), we have explored approximate inference methods based on variational and Markov chain Monte Carlo methods but found their performance to be poor; see § 8.
for each block. The approximate algorithm of Gong et al. (2015) has the same complexity. Like Gong et al. (2015), we have explored approximate inference methods based on variational and Markov chain Monte Carlo methods but found their performance to be poor; see § 8.
6. Simulations
6.1. Estimation dependence on the subsampling factor and number of observations
We first investigate the performance of the expectation-maximization algorithm under subsampling. We simulate data with  time series and
time series and 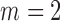 mixture components. The asymmetric error distributions are given by
mixture components. The asymmetric error distributions are given by 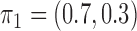 ,
, 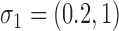 and
and 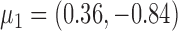 for
for 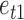 , and
, and 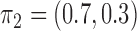 ,
, 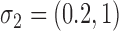 and
and 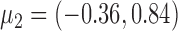 for
for 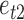 . We consider two cases for
. We consider two cases for 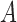 and
and  :
:
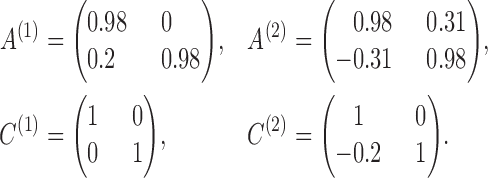 |
Simulations are performed for two subsampling factors, 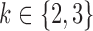 , and three sample sizes,
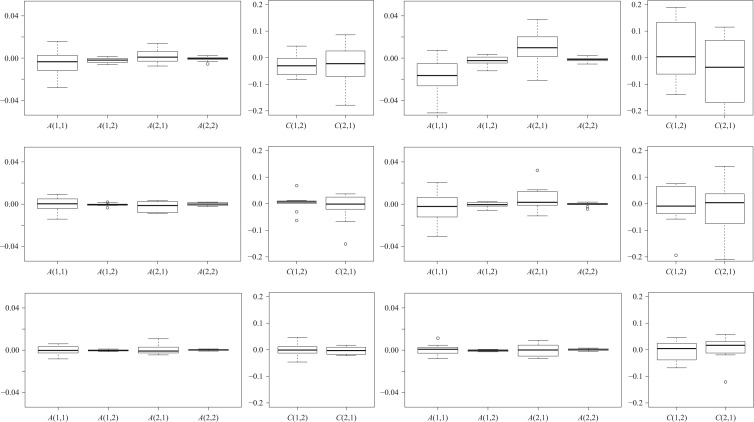
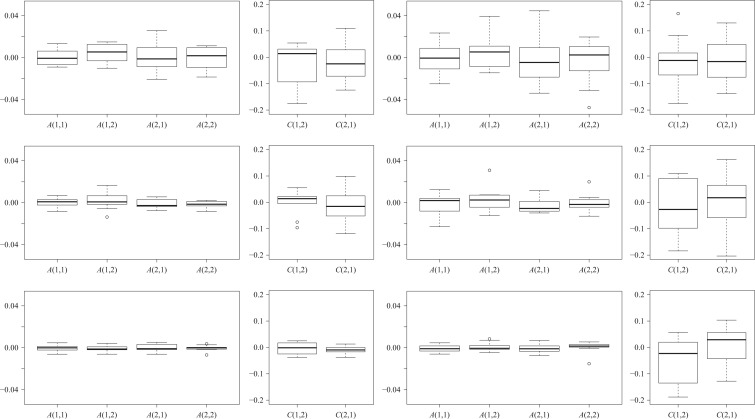
, and three sample sizes, 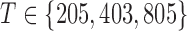 . Due to subsampling, the actual sample sizes are reduced. Data from each parameter configuration are generated 10 times, and the estimation algorithm is run on each realization using 1000 random restarts. Boxplots of the error estimates for two of the scenarios are shown in Figs. 3 and 4; see the Supplementary Material for plots in the other two settings.
. Due to subsampling, the actual sample sizes are reduced. Data from each parameter configuration are generated 10 times, and the estimation algorithm is run on each realization using 1000 random restarts. Boxplots of the error estimates for two of the scenarios are shown in Figs. 3 and 4; see the Supplementary Material for plots in the other two settings.
Fig. 3.
Boxplots of errors in 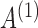 and
and 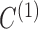 parameter estimates over 10 random data samplings. The original series is of length 203 (top), 403 (middle) or 805 (bottom) and is then subsampled at
parameter estimates over 10 random data samplings. The original series is of length 203 (top), 403 (middle) or 805 (bottom) and is then subsampled at 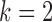 (left) and
(left) and 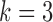 (right).
(right).
Fig. 4.
As Fig. 3 but for 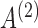 and
and 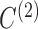 .
.
We perform a similar experiment for 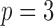 . We simulate data with parameters
. We simulate data with parameters
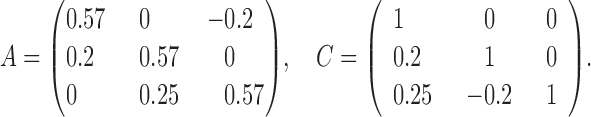 |
The mixture of normal error distributions for 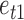 and
and 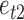 is the same as that for the
is the same as that for the  case. The parameters for
case. The parameters for 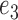 are
are 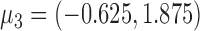 ,
, 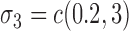 and
and 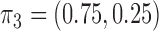 . The average error rates are displayed in Table 2 and indicate increasingly accurate estimation in trivariate structural systems as the sample size increases.
. The average error rates are displayed in Table 2 and indicate increasingly accurate estimation in trivariate structural systems as the sample size increases.
Table 2.
Average log mean squared error of 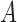 and
and 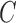 in a
in a 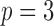 structural system over ten random samples for
structural system over ten random samples for 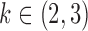 and three sample sizes
and three sample sizes
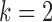
|

|
|||||
|---|---|---|---|---|---|---|
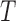
|
203 | 403 | 805 | 203 | 403 | 805 |
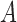
|
 2.4 2.4 |
 7.0 7.0 |
 7.5 7.5 |
 0.9 0.9 |
 1.6 1.6 |
 6.8 6.8 |
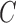
|
 3.6 3.6 |
 4.8 4.8 |
 5.8 5.8 |
 1.8 1.8 |
 1.8 1.8 |
 3.9 3.9 |
6.2. Estimation dependence on the asymmetry of errors
We analyse estimation performance as a function of the skewness of the error distribution, 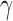 , which is a measure of asymmetry. We simulate data from the same
, which is a measure of asymmetry. We simulate data from the same 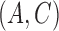 parameter configurations as in § 6.1 for
parameter configurations as in § 6.1 for 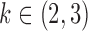 and
and 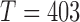 . While keeping the variance fixed, we vary the error distributions across a range of
. While keeping the variance fixed, we vary the error distributions across a range of 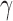 ,
, 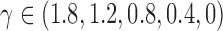 , so that
, so that 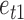 and
and 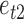 have the same magnitude of skewness but opposite signs. The skewness values are obtained by gradually modifying the
have the same magnitude of skewness but opposite signs. The skewness values are obtained by gradually modifying the 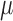 ,
, 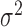 and
and 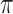 values in a bivariate mixture of normals. See the Supplementary Material for the exact parameter values and plots of the simulated error distributions.
values in a bivariate mixture of normals. See the Supplementary Material for the exact parameter values and plots of the simulated error distributions.
The results for estimation of 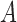 are shown in Table 3. First, for
are shown in Table 3. First, for 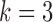 estimation remains accurate across all skewness settings for
estimation remains accurate across all skewness settings for 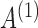 , while for
, while for 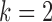 the error stays low for
the error stays low for 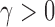 but spikes for
but spikes for  . For
. For 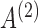 , estimation is stable until
, estimation is stable until 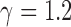 for
for 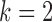 , but for
, but for 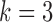 estimation is only stable at
estimation is only stable at 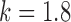 . Taken together, these results suggest that the strength of identifiability depends on a combination of factors,
. Taken together, these results suggest that the strength of identifiability depends on a combination of factors, 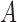 ,
, 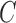 and
and 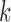 , and the level of asymmetry of the error distributions. Similar results for
, and the level of asymmetry of the error distributions. Similar results for 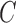 are reported in the Supplementary Material.
are reported in the Supplementary Material.
Table 3.
Average log mean squared error of 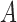 over ten random samplings for both
over ten random samplings for both 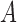 and
and 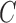 estimates across multiple settings of the parameters, number of observations, and subsampling factors
estimates across multiple settings of the parameters, number of observations, and subsampling factors
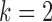
|
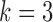
|
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|
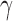
|
1.8 | 1.2 | 0.8 | 0.4 | 0 | 1.8 | 1.2 | 0.8 | 0.4 | 0 |
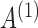
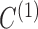
|
 9.0 9.0 |
 7.7 7.7 |
−7.3 | −7.0 | −0.018 | −8.1 | −7.0 | −7.1 | −7.0 | −7.4 |
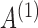
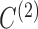
|
 9.0 9.0 |
 7.9 7.9 |
−7.7 | −7.4 | 0.16 | −7.9 | −7.2 | −7.4 | −7.2 | −7.5 |
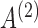
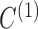
|
 9.1 9.1 |
 7.9 7.9 |
−0.94 | −0.26 | 1.2 | −8.0 | −0.33 | 0.71 | 1.6 | 1.6 |

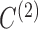
|
 9.1 9.1 |
 8.0 8.0 |
−0.94 | 0.15 | 1.3 | −8.0 | −0.32 | 1.0 | 1.4 | 1.2 |
6.3. Estimation dependence on the signal-to-noise ratio
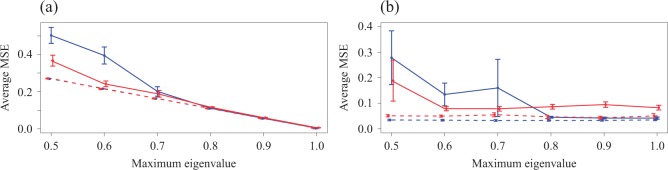
We next investigate estimation performance in subsampling and mixed-frequency sampling as a function of the signal-to-noise ratio. In these experiments we use 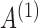 and
and 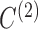 . We scale
. We scale 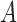 by a factor to set its maximum eigenvalue to the desired level. We perform these experiments both for full subsampling of
by a factor to set its maximum eigenvalue to the desired level. We perform these experiments both for full subsampling of 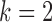 and
and 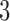 and for mixed-frequency subsampling where one series is observed at every time-point and the other is subsampled. Data from each parameter configuration are generated 40 times. In Fig. 5 we plot the average absolute error for estimating the
and for mixed-frequency subsampling where one series is observed at every time-point and the other is subsampled. Data from each parameter configuration are generated 40 times. In Fig. 5 we plot the average absolute error for estimating the 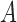 and
and 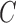 matrices as a function of the maximum eigenvalue of
matrices as a function of the maximum eigenvalue of 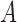 . Estimation under subsampling is stable until the maximum eigenvalue falls to about
. Estimation under subsampling is stable until the maximum eigenvalue falls to about 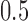 , and thereafter estimation becomes dramatically worse, indicating unstable estimation in this regime. The increasing error in the estimation of
, and thereafter estimation becomes dramatically worse, indicating unstable estimation in this regime. The increasing error in the estimation of 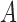 as a function of the signal-to-noise ratio is also observed in the mixed-frequency case. However, the estimation error increases less dramatically than in the subsampled case, partly due to the presence of fewer local optima in the mixed-frequency case. In the mixed-frequency case, the error in
as a function of the signal-to-noise ratio is also observed in the mixed-frequency case. However, the estimation error increases less dramatically than in the subsampled case, partly due to the presence of fewer local optima in the mixed-frequency case. In the mixed-frequency case, the error in 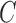 estimation appears to be constant across the maximum eigenvalue range we considered.
estimation appears to be constant across the maximum eigenvalue range we considered.
Fig. 5.
Average mean squared error (MSE) in estimation of (a) 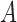 and (b)
and (b) 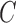 as a function of the maximum eigenvalue of
as a function of the maximum eigenvalue of 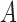 . Results are shown for subsamplings of
. Results are shown for subsamplings of 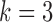 (red solid),
(red solid), 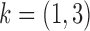 (red dashed),
(red dashed), 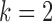 (blue solid), and
(blue solid), and 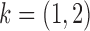 (blue dashed). Error bars indicate one standard error from 40 simulation runs.
(blue dashed). Error bars indicate one standard error from 40 simulation runs.
Unstable estimation arises from a combination of two factors. First, under subsampling, the transition matrix of the subsampled process is 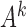 , indicating that the signal strength between observations scales exponentially as a function of
, indicating that the signal strength between observations scales exponentially as a function of 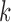 . Furthermore, the likelihood surface is multimodal, such that multiple high probability modes all have approximately the same
. Furthermore, the likelihood surface is multimodal, such that multiple high probability modes all have approximately the same 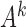 value. As the signal-to-noise ratio falls,
value. As the signal-to-noise ratio falls, 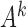 estimation becomes more difficult due to subsampling, and so the multimodal estimation becomes more severe, and modes far from the true
estimation becomes more difficult due to subsampling, and so the multimodal estimation becomes more severe, and modes far from the true 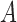 occasionally have higher likelihood. Overall, these simulations indicate that in the subsampling case, there appears to be a threshold on the maximum eigenvalue, below which inference becomes unstable.
occasionally have higher likelihood. Overall, these simulations indicate that in the subsampling case, there appears to be a threshold on the maximum eigenvalue, below which inference becomes unstable.
The simulations cover cases (a) and (b) in Fig. 1. Unfortunately, the complexity of the E-step forbids performing simulations in a reasonable time for cases (c) and (d). Future work will explore tractable inference in these cases; see the discussion at the end of § 7.
7. Real data
7.1. Subsampled ozone data
We use the subsampled structural model to analyse the causal scale and pathways in an ozone and temperature dataset. The temperature-ozone data are the 50th causal effect pair from the website https://webdav.tuebingen.mpg.de/cause-effect/, and were also considered by Gong et al. (2015). The dataset consists of temperature and ozone concentration values, sampled daily. First we standardize each time series to zero mean and unit variance. We fit the subsampled structural model to the pre-processed series for 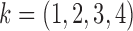 subsampling regimes under both independent errors,
subsampling regimes under both independent errors, 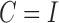 , and structural covariance in the instantaneous errors,
, and structural covariance in the instantaneous errors, 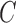 free. To ensure that good optima are found, we perform 30 000 restarts and run the adaptive over-relaxed algorithm until the relative change in loglikelihood is less than
free. To ensure that good optima are found, we perform 30 000 restarts and run the adaptive over-relaxed algorithm until the relative change in loglikelihood is less than 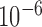 .
.
The estimated 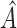 for
for 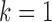 is
is
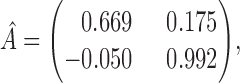 |
with a maximum eigenvalue of 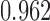 , suggesting that accurate estimation of subsampled parameters is possible. The Bayesian information criterion scores for all models are displayed in Table 4. Across all subsampling rates, the structural model,
, suggesting that accurate estimation of subsampled parameters is possible. The Bayesian information criterion scores for all models are displayed in Table 4. Across all subsampling rates, the structural model, 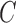 free, has lower score, indicating that the two extra parameters of the structural model, the off-diagonal elements of
free, has lower score, indicating that the two extra parameters of the structural model, the off-diagonal elements of 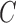 , provide necessary flexibility. Furthermore, the best-performing model is the structural model with subsampling rate
, provide necessary flexibility. Furthermore, the best-performing model is the structural model with subsampling rate 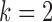 . The estimated transition matrix for
. The estimated transition matrix for 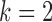 is
is
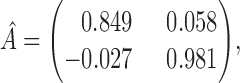 |
similar to that given by Gong et al. (2015) for 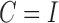 . After normalizing the columns, we obtain
. After normalizing the columns, we obtain
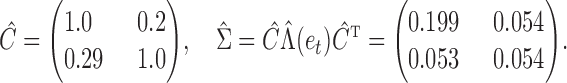 |
Table 4.
Bayesian information criterion scores of subsampling and covariance types on the atmospheric dataset; an asterisk indicates the lowest value
Model / 
|
1 | 2 | 3 | 4 |
|---|---|---|---|---|
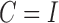
|
901.96 | 791.02 | 839.56 | 797.00 |
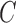 free free |
784.53 | 777.78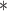
|
790.46 | 791.23 |
These results indicate weak lagged effects at the subsampled scale, but stronger instantaneous effects between temperature and ozone. Furthermore, the temperature series derives most of its power from a strong error variance, while the ozone series is driven more by the autoregressive component. See the Supplementary Material for quantile-quantile plots of the inferred mixture of error distributions.
7.2. Mixed-frequency data: GDP and treasury bonds
We perform a structural autoregressive analysis on the mixed-frequency dataset of quarterly GDP and monthly price of treasury bonds. The dataset has previously been compiled and analysed in the mixed-frequency setting by Schorfheide & Song (2015) and is available in the Supplementary Material. We follow Schorfheide & Song (2015) and compute the logarithm of both series. Furthermore, as is common in mixed-frequency analysis (Chen & Zadrozny, 1998), we compute first differences to remove first-order nonstationarities.
There are multiple approaches to modelling mixed-frequency GDP data in the literature. Recently, many authors have treated GDP as a flow variable and used state-space models to directly model the aggregation over months in a quarter (Schorfheide & Song, 2015; Ghysels, 2016). Others ignore the generative subsampling structure and instead jointly model the high- and low-frequency variables in a quarter using mixed data sampling methods (Ghysels, 2016). We follow another line of work that simplifies the analysis by ignoring aggregation (Chen & Zadrozny, 1998; Seong, 2012; Eraker et al., 2014; Anderson et al., 2016; Zadrozny, 2016), thus treating GDP as a purely subsampled series, and apply our mixed-frequency structural autoregressive model at the monthly rate. Indeed, recent theoretical work on mixed-frequency autoregressive models for GDP also focuses on the purely subsampled, rather than aggregated, case (Anderson et al., 2016). Since our subsampled approach to modelling GDP is a simplifying assumption that ignores aggregation, extending our framework to handle aggregated variables is an important direction of future research.
In the traditional approaches to mixed-frequency analysis, 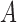 and the instantaneous covariance
and the instantaneous covariance 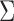 are generically identifiable from the first two moments (Anderson et al., 2016). What sets our non-Gaussian approach apart in this mixed-frequency domain is its ability to uniquely identify the ordering of the instantaneous causal effects in the structural matrix
are generically identifiable from the first two moments (Anderson et al., 2016). What sets our non-Gaussian approach apart in this mixed-frequency domain is its ability to uniquely identify the ordering of the instantaneous causal effects in the structural matrix 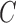 . To highlight this ability, we perform model selection on the zero entries in
. To highlight this ability, we perform model selection on the zero entries in 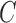 to determine the causal ordering of the instantaneous effects. Specifically, we calculate the Bayesian information criterion for the nested models
to determine the causal ordering of the instantaneous effects. Specifically, we calculate the Bayesian information criterion for the nested models 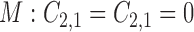 ,
, 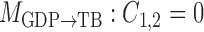 ,
, 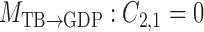 , and
, and 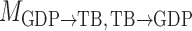 . Models
. Models  ,
, 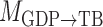 and
and 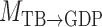 represent acyclic structures on the instantaneous effects, while the unrestricted model
represent acyclic structures on the instantaneous effects, while the unrestricted model 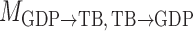 does not. The scores for all models shown in Table 5 indicate that
does not. The scores for all models shown in Table 5 indicate that 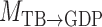 performs best. The estimated matrices of
performs best. The estimated matrices of
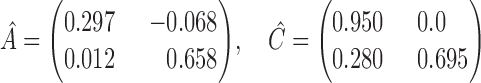 |
suggest a slight negative lagged interaction from GDP to treasury bonds and an instantaneous interaction at the monthly scale from treasury bonds to GDP. See the Supplementary Material for quantile-quantile plots of the inferred mixture of error distributions.
Table 5.
Bayesian information criterion scores of different instantaneous causality structures on the GDP dataset; an asterisk indicates the lowest value
| Model |
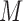
|
|
|
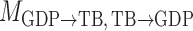
|
|---|---|---|---|---|
| 1984.00 | 1983.41 | 1981.08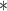
|
1987.55 |
The above analysis fits a structural model at the time scale of months, the same sampling rate as the treasury bond time series. The results from § 4 indicate that we could uniquely identify models at bimonthly, or even more granular, time scales. However, even at the bimonthly rate, the computational complexity of the E-step of our algorithm becomes prohibitive due to the large number of combinations of error mixture components in a data block, as discussed in § 5.4. Since the E-step requires running the forward-backward algorithm many times, a considerable computational speed-up could be achieved from a parallel implementation.
8. Discussion
Our results provide sufficient conditions for identifiability of structural autoregressive models for both subsampled and mixed-frequency series. The causal diagram of both lagged and instantaneous effects is identifiable under arbitrary subsampling and non-Gaussian errors.
We have developed an exact expectation-maximization algorithm for estimation and analysed its performance via simulations. Our algorithm has two drawbacks: high complexity due to a Kalman filter evaluation for all mixture error assignments within a time block; and many local optima due to weak identifiability. Our simulations show that the latter problem is more severe under even subsampling factors and low signal-to-noise regimes.
An ongoing line of work is to develop approximate inference for these models using Markov chain Monte Carlo or variational methods. Unfortunately, we have found that the local optima make sampling difficult. A Gibbs sampler we have explored gets stuck in one local mode and requires the same number of random restarts as our algorithm to find a good solution. Perhaps incorporating recent advances in sampling (Ma et al., 2016) may prove beneficial. We have also found the performance of a variational algorithm to be poor. Similarly, Gong et al. (2015) reported significantly worse results for a variational approach than for their approximate expectation-maximization algorithm. By breaking the dependence between the unobserved, subsampled 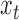 and the auxiliary
and the auxiliary 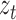 , the variational approach avoids the combinatorial evaluation of a Kalman filter; however, this dependence is critical for correctly evaluating the probable trajectories of the latent
, the variational approach avoids the combinatorial evaluation of a Kalman filter; however, this dependence is critical for correctly evaluating the probable trajectories of the latent 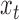 , without which inference of
, without which inference of 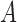 suffers.
suffers.
While our work has focused on point estimation, future research aims to adapt the time series bootstrap to the mixed-frequency and subsampled settings for constructing confidence intervals. It would be interesting to explore method-of-moments estimation for this problem, which may side-step the local optima difficulty and the combinatorial complexity of our algorithm.
Supplementary Material
Acknowledgement
This research was partially funded by the U.S. National Science Foundation, National Institutes of Health, Air Force Office of Scientific Research, and Office of Naval Research. We thank the referees for helpful comments and suggestions.
Supplementary material
Supplementary material available at Biometrika online includes an example of the subsampled and mixed-frequency structural processes, detailed proofs of Theorems 2 and 4, details on the 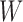 update in the expectation-maximization algorithm, additional simulation results, both of the real datasets that we analysed, and the code for the expectation-maximization algorithm.
update in the expectation-maximization algorithm, additional simulation results, both of the real datasets that we analysed, and the code for the expectation-maximization algorithm.
References
- Anderson, B. D., Deistler, M., Felsenstein, E., Funovits, B., Koelbl, L. & Zamani, M. (2016). Multivariate AR systems and mixed-frequency data: G-identifiability and estimation. Economet. Theory 32, 793–826. [Google Scholar]
- Anderson, B. D., Deistler, M., Felsenstein, E., Funovits, B., Zadrozny, P., Eichler, M., Chen, W. & Zamani, M. (2012). Identifiability of regular and singular multivariate autoregressive models from mixed-frequency data. In 51st IEEE Conference on Decision and Control (CDC 2012). Piscataway, New Jersey: IEEE, pp. 184–9. [Google Scholar]
- Boot, J. C., Feibes, W. & Lisman, J. H. C. (1967). Further methods of derivation of quarterly figures from annual data. Appl. Statist. 16, 65–75. [Google Scholar]
- Bowen, N. K. & Guo, S. (2011). Structural Equation Modeling. Oxford: Oxford University Press. [Google Scholar]
- Breitung, J. & Swanson, N. R. (2002). Temporal aggregation and spurious instantaneous causality in multiple time series models. J. Time Ser. Anal. 23, 651–65. [Google Scholar]
- Chen, B. & Zadrozny, P. A. (1998). An extended Yule-Walker method for estimating a vector autoregressive model with mixed-frequency data. Adv. Economet. 13, 47–74. [Google Scholar]
- Cont, R. (2001). Empirical properties of asset returns: Stylized facts and statistical issues. Quant. Finance 1, 223–36. [Google Scholar]
- Danks, D. & Plis, S. (2013). Learning causal structure from undersampled time series. In NIPS 2013 Workshop on Causality (Lake Tahoe, Nevada, 9December2013). [Google Scholar]
- Eraker, B., Chiu, C. W., Foerster, A. T., Kim, T. B. & Seoane, H. D. (2014). Bayesian mixed-frequency VARs. J. Finan. Economet. 13, 698–721. [Google Scholar]
- Eriksson, J. & Koivunen, V. (2004). Identifiability, separability, and uniqueness of linear ICA models. Sig. Proces. Lett. 11, 601–4. [Google Scholar]
- Ghysels, E. (2016). Macroeconomics and the reality of mixed-frequency data. J. Economet. 193, 294–314. [Google Scholar]
- Gong, M., Zhang, K., Schölkopf, B., Tao, D. & Geiger, P. (2015). Discovering temporal causal relations from subsampled data. In Proceedings of the 32nd International Conference on Machine Learning (Lille, France). New York: Association for Computing Machinery, pp. 1898–906. [Google Scholar]
- Harvey, A. C. (1990). Forecasting, Structural Time Series Models and the Kalman Filter. Cambridge: Cambridge University Press. [Google Scholar]
- Harvey, C. R. & Siddique, A. (2000). Conditional skewness in asset pricing tests. J. Finance 55, 1263–95. [Google Scholar]
- Herwartz, H. & Plödt, M. (2016). The macroeconomic effects of oil price shocks: Evidence from a statistical identification approach. J. Int. Money Finance 61, 30–44. [Google Scholar]
- Hyttinen, A., Plis, S., Järvisalo, M., Eberhardt, F. & Danks, D. (2016). Causal discovery from subsampled time series data by constraint optimization. arXiv: 1602.07970. [PMC free article] [PubMed] [Google Scholar]
- Hyvärinen, A., Karhunen, J. & Oja, E. (2004). Independent Component Analysis. New York: John Wiley & Sons. [Google Scholar]
- Hyvärinen, A., Shimizu, S. & Hoyer, P. O. (2008). Causal modelling combining instantaneous and lagged effects: An identifiable model based on non-Gaussianity. In Proceedings of the 25th International Conference on Machine Learning (Helsinki, Finland). New York: Association for Computing Machinery, pp. 424–31. [Google Scholar]
- Hyvärinen, A., Zhang, K., Shimizu, S. & Hoyer, P. O. (2010). Estimation of a structural vector autoregression model using non-Gaussianity. J. Mach. Learn. Res. 11, 1709–31. [Google Scholar]
- Justiniano, A. & Primiceri, G. E. (2008). The time-varying volatility of macroeconomic fluctuations. Am. Econ. Rev. 98, 604–41. [Google Scholar]
- Kilian, L. & Lütkepohl, H. (2016). Structural Vector Autoregressive Analysis. Cambridge: Cambridge University Press. [Google Scholar]
- Lanne, M. & Lütkepohl, H. (2010). Structural vector autoregressions with non-normal residuals. J. Bus. Econ. Statist. 28, 159–68. [Google Scholar]
- Lanne, M., Lütkepohl, H. & Maciejowska, K. (2010). Structural vector autoregressions with Markov switching. J. Econ. Dynam. Contr. 34, 121–31. [Google Scholar]
- Lanne, M., Meitz, M. & Saikkonen, P. (2017). Identification and estimation of non-Gaussian structural vector autoregressions. J. Economet. 196, 288–304. [Google Scholar]
- Lanne, M. & Pentti, S. (2007). Modeling conditional skewness in stock returns. Eur. J. Finance 13, 691–704. [Google Scholar]
- Lauritzen, S. L. (1996). Graphical Models. Oxford: Oxford University Press. [Google Scholar]
- Lütkepohl, H. (2005). New Introduction to Multiple Time Series Analysis. Berlin: Springer. [Google Scholar]
- Ma, Y.-A., Chen, T., Wu, L. & Fox, E. B. (2016). A unifying framework for devising efficient and irreversible MCMC samplers. arXiv: 1608.05973. [Google Scholar]
- Moauro, F. & Savio, G. (2005). Temporal disaggregation using multivariate structural time series models. Economet. J. 8, 214–34. [Google Scholar]
- Peters, J., Janzing, D. & Schölkopf, B. (2013). Causal inference on time series using restricted structural equation models. In Proceedings of the 26th International Conference on Neural Information Processing Systems (Lake Tahoe, Nevada). New York: Association for Computing Machinery, pp. 154–62. [Google Scholar]
- Plis, S., Danks, D., Freeman, C. & Calhoun, V. (2015). Rate-agnostic (causal) structure learning. In Proceedings of the 28th International Conference on Neural Information Processing Systems (Montreal, Canada). New York: Association for Computing Machinery, pp. 3303–11. [PMC free article] [PubMed] [Google Scholar]
- Rachev, S. T. (2003). Handbook of Heavy Tailed Distributions in Finance, vol. 1 of Handbooks in Finance. Amsterdam: Elsevier. [Google Scholar]
- Salakhutdinov, R. & Roweis, S. T. (2003). Adaptive overrelaxed bound optimization methods. In Proceedings of the 20th International Conference on Machine Learning (Washington, DC). New York: Association for Computing Machinery, pp. 664–71. [Google Scholar]
- Schorfheide, F. & Song, D. (2015). Real-time forecasting with a mixed-frequency VAR. J. Bus. Econ. Statist. 33, 366–80. [Google Scholar]
- Seong, B. (2012). Cointegration analysis with mixed-frequency data of quarterly GDP and monthly coincident indicators. Korean J. Appl. Statist. 25, 925–32. [Google Scholar]
- Shimizu, S., Hoyer, P. O., Hyvärinen, A. & Kerminen, A. (2006). A linear non-Gaussian acyclic model for causal discovery. J. Mach. Learn. Res. 7, 2003–30. [Google Scholar]
- Shojaie, A. & Michailidis, G. (2010). Penalized likelihood methods for estimation of sparse high-dimensional directed acyclic graphs. Biometrika 97, 519–38. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Silvestrini, A. & Veredas, D. (2008). Temporal aggregation of univariate and multivariate time series models: A survey. J. Econ. Surv. 22, 458–97. [Google Scholar]
- Stram, D. O. & Wei, W. W. (1986). A methodological note on the disaggregation of time series totals. J. Time Ser. Anal. 7, 293–302. [Google Scholar]
- Walls, W. D. (2005). Modelling heavy tails and skewness in film returns. Appl. Finan. Econ. 15, 1181–8. [Google Scholar]
- Zadrozny, P. A. (2016). Extended Yule–Walker identification of VARMA models with single or mixed-frequency data. J. Economet. 193, 438–46. [Google Scholar]
- Zhang, K. & Hyvärinen, A. (2009). Causality discovery with additive disturbances: An information-theoretical perspective. In Joint European Conference on Machine Learning and Knowledge Discovery in Databases (Berlin, Germany). Berlin: Springer, pp. 570–85. [Google Scholar]
- Zhou, D., Zhang, Y., Xiao, Y. & Cai, D. (2014). Analysis of sampling artifacts on the Granger causality analysis for topology extraction of neuronal dynamics. Front. Comp. Neurosci. 8, 10.3389/fncom.2014.00075. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.