ULTRA: A Model Based Tool to Detect Tandem Repeats

Abstract

In biological sequences, tandem repeats consist of tens to hundreds of residues of a repeated pattern, such as atgatgatgatgatg (‘atg’ repeated), often the result of replication slippage. Over time, these repeats decay so that the original sharp pattern of repetition is somewhat obscured, but even degenerate repeats pose a problem for sequence annotation: when two sequences both contain shared patterns of similar repetition, the result can be a false signal of sequence homology. We describe an implementation of a new hidden Markov model for detecting tandem repeats that shows substantially improved sensitivity to labeling decayed repetitive regions, presents low and reliable false annotation rates across a wide range of sequence composition, and produces scores that follow a stable distribution. On typical genomic sequence, the time and memory requirements of the resulting tool (ULTRA) are competitive with the most heavily used tool for repeat masking (TRF). ULTRA is released under an open source license and lays the groundwork for inclusion of the model in sequence alignment tools and annotation pipelines.

1. INTRODUCTION

Tandem repeats (TRs) such as catcatcatcatcatcat (a ‘cat’ subunit, repeated six times) make up more than 3% of the human genome and are found in over 25% of human proteins [6]. Identification of TRs is key to characterizing their role in evolution [8, 11, 12], function [2, 3, 13, 14] and disease [22], though the primary motivation for development of TR–detecting software has long been avoidance of false positive matches during sequence annotation [18, 19, 24]. These false matches arise because TRs are widespread and deviate from the random nature assumed in the scoring systems of all sequence alignment software. As a concrete example, consider the ‘cat’ repeat sequence above; in a truly random genome of 3 billion nucleotides, we expect to see zero copies of this sequence, but the current release of the human genome (hg38) contains more than 700 non–overlapping exact copies, and more than 1200 instances with a single mutation from the perfect length–18 repeat pattern. These exact and inexact copies, owing their existence to replication slippage [21] and subsequent mutation, are not homologous to each other, yet would be considered significant matches by typical sequence alignment software such as BLAST [1] and HMMER [7].

A common strategy for avoiding false annotation due to repetitive sequence is to somehow identify repeat regions, then “mask” (hide) them away from sequence alignment tools, for example by changing a masked region in a genome to a sequence of Ns; alignment software assigns no score to alignments in such masked regions. An alternative strategy, soft masking, marks characters so that they will not serve as alignment seeds, but allows them to be used in scoring after seeding is complete. Numerous tools have been developed over the years to detect tandem repeats and mask them in sequence annotation pipelines (for review see [15–17]). Early approaches [19, 25] were superseded at the turn of the century by Tandem Repeats Finder (TRF [4]), which remains the most heavily used DNA repeat detector to date. TRF models repetitive regions as a series of Bernoulli trials, dependent on the identification of pairs of nearby identical length–k runs. TRF is reasonably fast and considered effective at recognizing repetitive regions and can report a repeat’s consensus subunit, but it does not provide estimates of the statistical significance of its annotated repeats and suffers from unstable score distribution on random sequence (see Section 2.3).

A more recent approach in the software TANTAN [9] utilizes a simple hidden Markov model (HMM) to quickly compute the probability that each residue is part of a tandem repeat. The generative model includes a state for non–repetitive sequence, with transitions into states for repeats of various periodicity. While much more sensitive than TRF, TANTAN is prone to either entirely missing repeat regions containing insertions or deletions (indels) or breaking them into small islands, and is designed only for masking (i.e. it does not report a repeat’s consensus subunit).

Though masking with these tools often restricts alignment software from finding a high–scoring alignment to the masked sequence, false matches are still frequently observed in sequences with decayed repeat regions that are missed by repeat–masking software [10]. For example, when annotating the human genome with models of transposable element families, we found many thousands of examples of high–scoring false matches caused by decayed repeats missed by TRF [23]; overcoming these false annotations required significant semi–manual masking of the transposable element family models.

These unmasked repeats are typically the result of insertions and deletions relative to the consensus subunit (e.g. Figure 1, third line), which complicate their detection. It is a straightforward process to identify a repeat consisting of perfect copies of a subunit, however such perfect repeats typically decay over time, due to substitution mutations and short indels. Substitution mutations are relatively straightforward to model: for a subunit of length k, assign some score or probability to the character observed at a position i by comparing that character with the character offset k positions earlier in the sequence, and accumulate these scores/probabilities over a run of positions — repetitive sequence will accumulate higher score/probability than nonrepetitive sequence. Indels pose the more challenging problem. In the case of a single–letter insertion relative to the length–k consensus subunit, each of the following k letters should be compared to the character k+1 positions earlier. The difficulty in identifying decayed repeat regions lies in tracking this sort of offset from the standard frame across various lengths of potential insertion and deletion. The models underlying TRF and TANTAN both focus on core indel–free runs with secondary accommodation of indels. Others have explicitly incorporated indels into their model, most notably the “sunflower” model of Nánási et. al. [20]; this approach, though able to effectively model complex inexact repeat patterns, results in models too large and slow to apply at genomic scale.

Figure 1:

Example of a Tandem Repeat consisting of four perfect CATG copies (first line), degenerated by substitution mutations (second line), then insertions and deletions (third line). All deviations from the perfect repeat are shown in a gray font.

Here, we describe an approach based on an HMM that fills the gap between the simple model of [9] and the highly expressive model of [20]. The result is a new tool that we call ULTRA (‘ULTRA Locates Tandemly Repetitive Areas’) that models repeats of various offset length and includes numerous states for indels at each offset. ULTRA finds degenerate TRs missed by other software, maintains low false annotation rates across a broad range of sequence composition, demonstrates a stable distribution of scores on random sequence, reports contiguous repeat regions, and runs at speed comparable to other TR detection software. Though it does not currently report consensus subunits or P–values, the framework supports such future improvements as relatively straightforward enhancements. While ULTRA is initially released as a standalone tool used to detect and mask TRs, it will eventually be incorporated directly into sequence alignment tools as an improved model of “random” sequence.

In the following sections, we demonstrate ULTRA’s efficacy in labeling approximately repetitive sequence regions of various composition (in terms of both coverage and expected false annotation), discuss labeling overlap among three tools, describe score distributions, and analyze ULTRA’s performance characteristics. We then describe the model, along with implementation strategies used to improve speed and space requirements. We focus our attention on DNA sequence, as this is the most pressing need. We leave as future work a variety of natural extensions: subunit consensus reporting, statistics, incorporation into alignment pipelines, application to proteins, and characterization of repeats made possible by the new model.

Unlike TRF, ULTRA is released under an open source license. This enables incorporation at the source level into other software and analysis pipelines, and provides an opportunity for feature enhancement from the community.

2. RESULTS

Measuring the efficacy of repeat annotation tools is complicated by the fact that there are no reliable “true repeat” benchmarks. Though there exist advanced methods for simulating plausibly complex genomic sequence containing regions of varying sequence bias (isochores) and a distribution of transposable elements (e.g. [5]), modeling of tandem repeats is less advanced — even in these tools, tandem repeats are simply injected into simulated sequence based on the distribution of known tandem repeats. The circularity of testing with such simulated sequence limits utility.

We approach the problem of assessing the efficacy of tandem repeat detecting tools in three ways. First, we assess sensitivity to decayed repeats by considering coverage (the number of residues labeled as repetitive) of real genomic sequence; this includes analysis of sequence with high composition bias. Because increased sensitivity can be achieved simply by parameterizing in a way that increases labeling of non–repetitive sequence, we also test the extent of false labeling using shuffled genomic sequence. Second, we explore the extent to which the tools agree or disagree in their labeling. This includes both quantitative inspection of overlapping coverage and a qualitative consideration of the sort of repeats found by one tool that are missed by others. Finally, because a stable distribution of scores is necessary for reliable incorporation into annotation pipelines, we explore the distribution of scores on non–repetitive sequence.

2.1. Sensitivity of Repeat Labeling

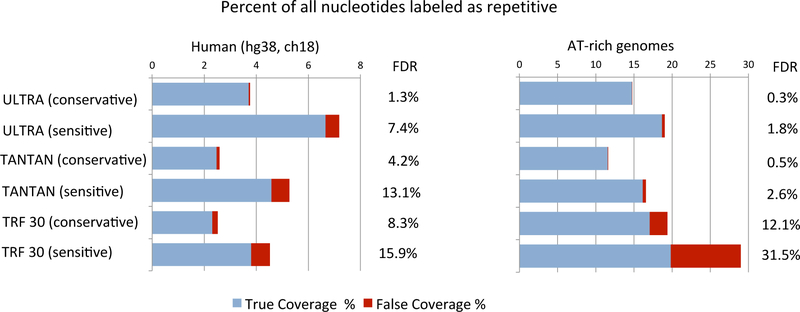
We tested the labeling performance of ULTRA, TANTAN, and TRF. To understand how well each tool labels decayed repetitive regions in genomic sequence, we applied the tools to (i) the human genome (chromosome 18; this has AT content of 60%, representative of the entire human genome), and (ii) two AT–rich genomes (Plasmodium falciparum & Dictyostelium discoideum; results averaged over both genomes, which are each 80% AT). For each tool, we used a pair of parameterizations, one “sensitive” (higher coverage, at the cost of higher rate of false labeling), and one “conservative” (lower false labeling rate, with accompanying lower coverage). Sensitivity was assessed based on the coverage of genomic sequence (the number of nucleotides labeled as being part of a repetitive region), while expected false labeling was determined by using each tool to mask window–shuffled sequence (chromosomal sequence mononucleotide shuffled in blocks of 10Kb, with the goal of preserving the potentially confounding effects of isochore composition variability; see Section 3.4). Figure 2 shows the results of these experiments.

Figure 2:

Repeat labeling of the human genome (chromosome 18, 60% AT–rich) and two AT–rich eukaryotes (Plasmodium falciparum and Dictyostelium discoideum). The length of the bar (blue + red) gives the total percent of the genome that is labeled as repetitive by the corresponding tool/setting. The length of the red bar is an estimate of the extent of expected false labeling. Thus, the blue bar shows the proportion of the labeling that is expected to be correct. For each dataset and each tool, an estimated False Discovery Rate (FDR) is computed as the ration of estimated false coverage to total coverage.

Under both sensitive and conservative settings, and on genomes with both moderate and biased composition, ULTRA labels substantially more genomic sequence as repetitive than TANTAN. This increased coverage does not come at the cost of false annotation: in all cases, ULTRA’s estimated false annotation rate is somewhat lower than that of TANTAN, and its False Discovery Rate (FDR) is much lower.

The picture for TRF is somewhat more complex. On relatively neutral composition (the human genome), ULTRA is clearly much more sensitive, and and less prone to false labeling. On AT-rich genomes, the sensitive parameterization of TRF labels ~10% more of the genome as repetitive than does ULTRA, but nearly all of that increased coverage appears to be the result of false labeling — more than 30% of TRF’s labeled repeats are expected to be false. Similar results are seen with the conservative parameterization of TRF, which compare unfavorably even to the conservative parameterization of ULTRA.

TRF’s high false labeling rate on sequences with highly–biased composition is due to the fact that the model of TRF does not account for sequence composition, and that such biased sequence naturally produces regions that looks vaguely repetitive if the context is ignored. Another concern is the risk of overextension in AT–rich sequence: when a correctly–labeled AT–rich repeat is flanked by more AT–rich non–repetitive sequence, some of that flanking sequence may be incorrectly pulled in as part of the repeat, simply because it slightly helps the scoring of the true repeat. Our false labeling test does not identify this sort of problem, but manual inspection of sensitive TRF’s annotation of AT–rich sequence suggests that this may be a common phenomenon (i.e. is a possible hidden source of additional false labeling).

2.2. Comparing Repeats Labeled by Each Tool

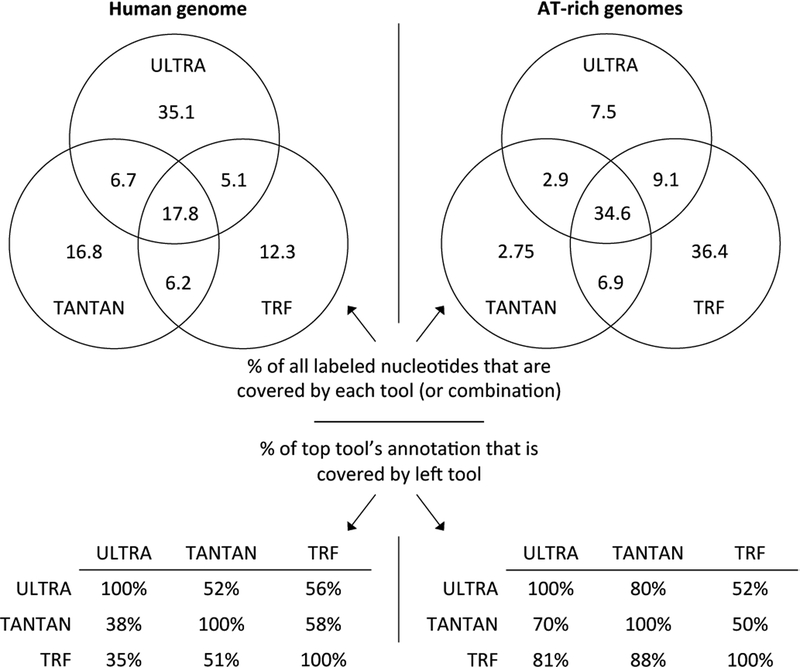
While coverage and false labeling numbers provide summary statistics useful for comparing tools and parameterizations, we have found it enlightening to consider how these tools overlap in coverage. Figure 3 (top) shows, of all nucleotides labeled by at least one tool, the fraction labeled by each collection of tools. It also shows the reciprocal shared coverage of nucleotides (bottom). We find it particularly striking that even though ULTRA demonstrates much greater coverage, each other tool labels a large number of repeats not labeled by ULTRA, much larger than the expected false labeling.

Figure 3:

Overlap between the set of nucleotides labeled by three tools. Each tool was run with sensitive settings. The Venn diagrams show, among all nucleotides labeled as repetitive by at least one tool, the fraction that were labeled by each tool or set of tools. The tables on bottom show what percent of nucleotides called repetitive by the top tool were also called repetitive by the left tool. For example, in the human sequence, ULTRA labels as repetitive 52% of the nucleotides labeled repetitive by TANTAN, while TANTAN labels as repetitive only 38% of the nucleotides labeled repetitive by ULTRA. Target sequences are the same as in Figure 2.

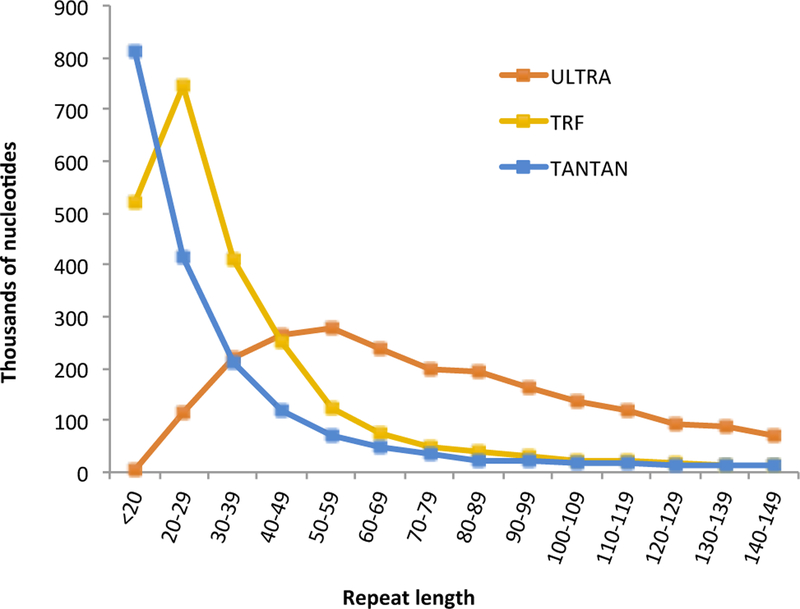
We have manually inspected the collection of tool–unique repeats, and find that when TRF and/or TANTAN label a region that is not labeled by ULTRA, the region is typically fairly short (under 40 nucleotides in length; see Figure 4 for overall length distribution). TANTAN–unique repeats frequently look to us more like low–complexity sequence (high levels of AT or CG, often as bursts of mononucleotide strings) than degenerate repeats (see Figure 6A&B). Meanwhile, regions labeled by ULTRA and not the others are often longer, with more complex patterns of insertion and deletion that, once visualized, suggest the repetitive nature of the sequence (see 6C). While we have tried to present an unbiased sampling of representative unique matches, we make available our datasets so that others may review them and develop their own impression (see Section 4.4).

Figure 4:

Number of nucleotides labeled in repeats, by length. We considered the repeats labeled on human chromosome 18, using each tool at sensitive setting. We counted all nucleotides labeled as repetitive, binned according to the length of the repeat.

Figure 6:

A qualitative survey of repeat regions labeled by one tool but not others. (A) TRF–labeled repeats not found by ULTRA are typically made up 2–3 copies of a modest–length subunit. We have broken the examples into multiple rows to highlight the repeat (implied insertions are selected by hand). (B) TANTAN-labeled repeats not found by ULTRA are usually of the form shown here: frequently short, often composed of degenerate mono- or di-nucleotide repeats. Because of the simplicity of these repeats, they are not broken out across multiple lines. (C) ULTRA–labeled repeats not found by the other tools often match this form: a fairly long period with repeats containing non–trivial insertion or deletion structure. As with TRF repeats, the examples are broken across multiple lines to show the repetitive structure. In the case of the ULTRA “alignment” of repeats, the gap structure matches that used by the model to identify the repeat (i.e. it allows only consecutive insertions or deletions, and has not been optimized).

2.3. Score Distribution

The most common use of tandem repeat detection is to mask a sequence prior to annotation of other elements (e.g. genes or transposable elements) based on sequence alignment score. An alternative is to compete putative alignment matches with putative repeat regions, selecting the annotation with greatest significance. In development of [23] we devised an approach that converts TRF scores to P–values, assuming a mixture of Gumbel distributions. The method enables comparison of matches in the annotation pipeline by comparing P-values for TRF matches to E–values for homology search tool hits, but the choice of fat–tailed distribution is not well supported. This is in part because we don’t know how the distribution decays (we selected the Gumbel for simplicity), but primarily because TRF score frequencies vacillate wildly (Figure 5A — frequently showing a 10-fold difference in counts between two neighboring integer scores). Furthermore, reasonably high–scoring repeats found in non–repetitive sequence are much more likely to be labeled as a high–period repeat than a low–period repeat (e.g. for TRF hits with score >30, the number of period–10 repeats is ~200× larger than the number of period–4 repeats).

Figure 5:

Score distribution on non–repetitive sequence. TRF was used to label 400GB of non–repetitive sequence, and demonstrates dramatic swings in score (e.g. on random sequence, 10× more hits with score 34 than score 33). ULTRA was used to label 144GB of non–repetitive sequence, and produces scores with a more stable distribution.

This instability of score and period distributions was a primary motivator in the development of ULTRA. To understand stability of score distribution, we used TRF and ULTRA to label large volumes of non–repetitive sequence (uniform nucleotide distribution), and captured the frequency of scores. TRF scores are reported as integers, so no additional binning is required. ULTRA scores are floating point; we binned in increments of 0.3 bits to gain granular insight. ULTRA’s score distribution shows a much more stable decay (Figure 5B).

TANTAN was not considered in this analysis, as repeat regions are not scored — the only provided metric is a per–residue measure of TANTAN’s confidence that the labeled residue is part of a repeat. This supports masking, but not a more nuanced comparison of candidate annotations.

2.3.1. Performance.

We measured the computational performance of ULTRA, TRF, and TANTAN on Human and AT rich sequences (Table 1). TRF runs reasonably quickly on sequences with few repeats, but slows with high repeat density. Human centromeres in hg38 contain simulated repetitive sequence, which leads to a dramatic increase in run time for TRF, but not ULTRA or TANTAN. Since labeling simulated sequence is not an appropriate use of TRF, we masked centromeres before this test. TANTAN demonstrates excellent runtime and memory usage across a broad range of sequences. We found that ULTRA runs comparably to TRF in sequences with few repeats, and significantly faster in more repetitive sequences. ULTRA’s memory requirements are modest.

Table 1:

Run time and memory requirements for each tool, using human chromosome 18 (75.0 megabases) and AT rich sequences (47.7 megabases) as described in Figure 2.

	sequence	ULTRA	TANTAN	TRF
Run time	Human chrl8	6m58s	29s	3m43s
	AT-rich	5ml9s	26s	20m31s
Memory (Mb)	Human chrl8	315	486	177
	AT-rich	263	337	1,200

3. METHODS

3.1. A Hidden Markov Model for Random Sequence Including Tandem Repeats

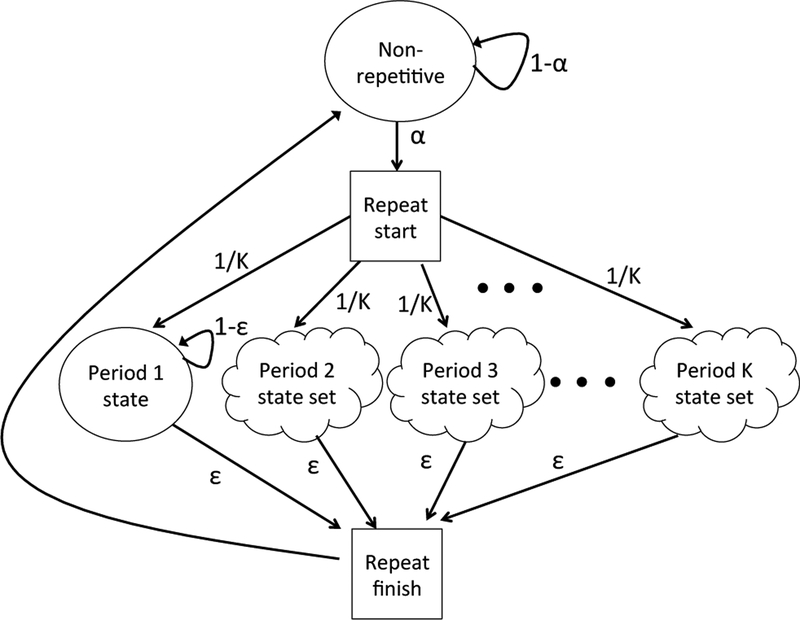
ULTRA is based on a model of repetitive sequence interspersed within a background of non–repetitive sequence. A hidden Markov model (HMM) is a probabilistic model capable of generating sequences that “look like” the modeled sequence, and also of labeling new, unlabeled sequence so that regions may be said to have been generated by one state (e.g. the non–repetitive state) or another (e.g. the period 3 state, meaning that the sequence consists of multiple copies of a three–letter subunit). A high–level representation of the model is shown in Figure 7.

Figure 7:

Hidden Markov model of sequence consisting of mostly non–repetitive sequence (top state), containing repeats of various periodicities (other states). Square states are silent (non–emitting). Cloud shape state sets represent the core state designed to maintain periodic repeats, along with states to allow for deviation due to insertion and deletion (see Figure 8 for expanded description of state sets. Square states are silent. All unlabeled edges have probability 1 (represent mandatory transitions).

3.1.1. A state for non–repetitive sequence.

The central state in ULTRA’s model generates non–repetitive sequence. This is a memoryless 0th order state that repeatedly emits a single character from a fixed distribution without regard for what has been previously emitted. This is effectively the model of background sequence assumed by alignment tools based on both score matrices (e.g. BLAST [1]) and profile HMMs (e.g. HMMER [7]).

3.1.2. States for repetitive sequence.

ULTRA’s model includes state–sets responsible for generating repeats with subunit size (periodicity) of 1 (mono–residue repeats) through an arbitrary cap (default in our experiments is 25). Each repeat–period state set consists of (i) a core state that produces letters based on previously–observed letters, and (ii) a collection of auxiliary states that allow for decay of perfectly periodic repetition resulting from insertions and deletions.

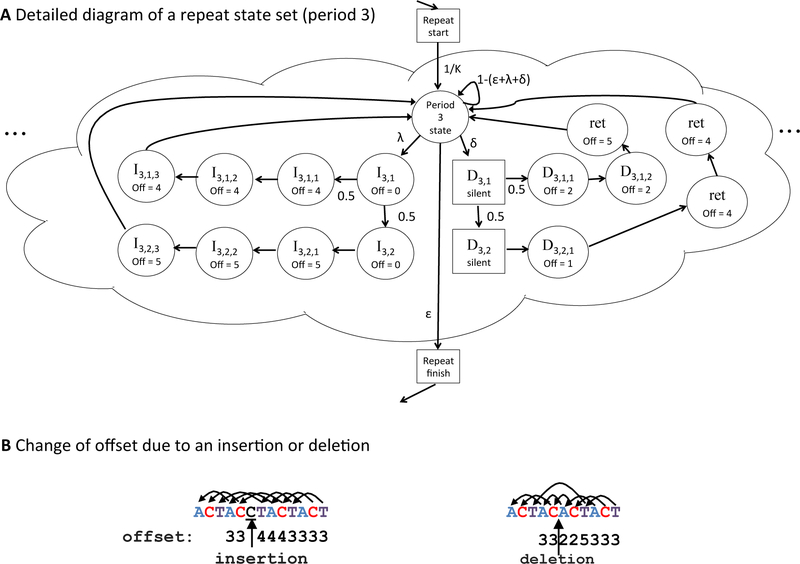
There is one core repeat state for each subunit length. The 1st–order state emits (possibly degenerate) mono–residue runs, the 2nd–order state emits di–residue repeats, and so forth. In a repeat state of order k, the probability of emitting a certain letter at position i, depends on the letter observed at position (i−k). As an example, the letter emission distribution for a 3rd–order−state (for a repeat with period 3) depends on the letter observed three positions earlier. In typical HMMs, a kth–order state has an emission distribution that depends on all k most–recently observed letters; our model simplifies this to consider only the letter found k positions back, allowing even high–order states to have small emission probability tables. The core repeat states are part of the state set pictured in Figure 7, and shown in detail in Figure 8.

Figure 8:

(A) This diagram shows the handling of insertions and deletions within a sample state set (for subunit of size 3). For example, after an insert of length 1 (state I_1,1, which emits a letter from background), there will be three emissions that must look back to an offset of 4, after which the model returns to the default offset of 3. After an insert of length 2 (state I_1,2), the three following letters will depend on an offset of 5. Deletions begin with d ≥ 1 silent states, followed by (3−d) emitted letters at offset (3−d), followed by d letters at an offset of (3*2−d) — comparing to the last appropriate match before the deletion. Square states are silent. All unlabeled edges have probability 1 (represent mandatory transitions).

In addition to the core repeat state, ULTRA’s model contains a collection of states designed to allow insertions or deletions (Figure 8). Ideally, these would allow insertions and deletions at arbitrary locations in the pattern (as in [20]), but for simplicity, the model only allows consecutive insertions or deletions. For example, for a subunit ATCGT, the repeat ATCGTATTCGGTATCGT contains two discontinuous insertions; ULTRA will seek identify two consecutive insertions instead, e.g. ATCGTATTCGGTATCGT, causing a small number of additional offset mismatches. The speed enabled by this simplification appears to be worth the dependency on nonconsecutive insertions. In experiments presented here, we limited the maximum length of consecutive insertion or deletion to 5 (no apparent loss in sensitivity). This limits growth of the number of states in the HMM, which keeps run time at an acceptable level.

3.1.3. Scoring a repeat region depends on a non–repetitive model.

With an HMM, an observed sequence of letters can be explained as having been generated by any sequence of states; the probability of the observed sequence and one particular sequence of responsible states is simply the product of the probabilities of transitioning between those states and the probabilities of the observed sequence being emitted by those states. Given a short sequence S, the ULTRA HMM computes the most–probable state path for S using the Viterbi algorithm, based on emission and transition probabilities from Figures 7 and 8.

The score of a repeat region is computed as the log of the ratio of this probability (due to the repetitive model) and the probability under a simple model of non–repetitive sequence. The non–repetitive model is a single state identical to that described in Section 3.1.1.

3.1.4. Parameterization.

For the current study, we have hand selected apparently–reasonable parameters. In the future, it may prove valuable to train the parameters of our model on trustworthy repeat sequences (though results from [9] suggest that this may not be fruitful). Though the model is general, all tests were performed on DNA only; parameters have thus only been tested for DNA.

The non–repetitive state (and background) emission probabilities are determined from the composition of the sequence to be labeled. To account for composition variability due to isochores, ULTRA considers the composition of a large (default 100Kb) window centered around each labeled residue. By including this background model, ULTRA effectively avoids spurious labeling due to simple sequence composition bias.

Repetitive states have a probability of emitting a letter that matches the previous letter (based on appropriate periodicity). In non–repetitive DNA with uniform letter distribution, the expected probability of matching a previous letter is 25%; that number rises as composition becomes increasingly biased. To offset this background expectation of matching, we employ a simple ad-hoc strategy for setting the expected frequency of emitting a match in a repetitive state: if μ is the expected frequency of a match in non–repetitive sequence, then the repetitive match probability M = min(1.0, 0.1+2μ). This leads to a match probability of 0.61 in human chromosome 18, and 0.78 in 80% AT–rich sequence. The probability of each of the three mismatched letters in repetitive states is simply a uniform division of the remaining probability, (1−M)/3.

The probability of transitioning from non–repetitive) sequence to repetitive sequence (α) was set to 1%. Though higher–period repeats may be less common than lower ones, we adopted a flat prior for these tests: each subunit length was considered equally likely. The probability of beginning an insertion (λ) or deletion (δ) was set to 5%. The probability of extending either was set to 50%. The probability of ending the repeat (ϵ) was set to 4%. We have no reason to expect that these are optimal parameters.

3.2. Traceback and score derivation

Repeats are found in a two pass process. In the first pass, a full dynamic programming Viterbi matrix is filled in for a sequence block of default size 10Kb, using the model and parameters described above. The 10Kb windows are overlapped to ensure traceback quality. In the second pass, the standard Viterbi traceback is performed, starting (at the end of the matrix) from the state with highest score; this recovers the most–probable assignment of all letters in the window to their emitting states. In regions in which the traceback passes through repetitive states, the scores at the beginning and end of the repeat–labeled sequence are captured; this is the score of the repeat region. If that score is greater than reporting threshold, the region is reported as a TR. At present, the distribution of scores is not sufficiently characterized to convert these scores to meaningful E–values.

3.3. Collapsing Calculation on the Insert and Delete Paths

ULTRA’s model consists of numerous insertion and deletion (indel) state paths. These are key to ULTRA’s improved modeling of the indels that are common in degenerate repeat regions, but they also cause a large increase in the state space within which HMM Viterbi calculations are made. Here, we describe an optimization that allows ULTRA to include a large number of state paths without incurring a significant performance penalty.

All states within insertion and deletion paths have a single parent from which they are reached. Additionally, when a length–n insert is found in an order–k repeat state–set, an insertion path will consist of a contiguous block of n 0th order states (the insertions relative to the repeat) followed directly by a contiguous block of k states with the order k +n. (Similarly, in a given deletion path there is a contiguous block of k − n order states followed directly by a contiguous block of 2k − n order states.) These properties enable a significant reduction in required calculations, demonstrated here in the context of an insertion. After having calculated the score for the final state of an insertion path once at position t of the target sequence, we can calculate the score for the final state of an alternate indel path at position t + 1 by reusing redundant calculations shared by the two paths, and computing the small number of non–redundant calculations. This reduction in calculation is analogous to calculating a moving average by only computing values that been removed/added since the last time the moving average was computed.

As an example, let I_k,n,k (t) be the final state in the path coming out of a length n insertion within the repetitive period–k state set, when emitting the nucleotide at position t. Let θ_k (t) represent the kth order emission score for the letter at position(t). Instead of recalculating the entire insertion path, we can perform the following calculation:

$$I_{k,n,k}\left(t+1\right)=\frac{I_{k,n,k}\left(t\right){\theta }_k\left(t-m-n\right){\theta }_0\left(t-m+1\right){\theta }_{k+n}\left(t+1\right)}{{\theta }_k\left(t-m-n-1\right){\theta }_0\left(t-m-n\right){\theta }_{k+n}\left(t-m\right)}$$

Figure 9 demonstrates with a concrete example of this reduction applied to three consecutive insertions within a period–4 repetitive state. The calculation reduction effectively reduces the number of states needed from O(K²) to O(K), where K is the maximum periodicity.

Figure 9:

Example of the relationship between the calculations required for (i) an insertion of length 3 within the order-4 state set ending at position t + 7 of the labeled sequence, and (ii) an insertion of length 3 within the order-4 state set ending at position t + 8. Most calculations are redundant (represented by vertical lines between offset calculations), so the value for I_4,3,4 at t + 8 can be computed by starting with the value for I_4,3,4 at t + 7, subtracting the non-redundant values from the top row (no vertical line), and adding the non-redundant values from the bottom row (no vertical line).

3.4. Sensitivity experiments

Experiments were performed using human chromosome 18 (version hg38), Plasmodium falciparum (EPr1), and Dictyostelium discoideum (2.7). False annotation experiments were performed by block–shuffling: genomic sequence was broken into contiguous 10Kb blocks, and each block was mononucleotide shuffled. This breaks apart all actual repetitive sequence, but preserving the potentially confounding effects of composition variability due to genetic isochores.

TRF version 4.09 was tested with conservative settings (default from TRF documentation: match=2 mismatch=7 indel=7 pm=80 pi=10 minscore=30 maxperiod=25) and sensitive changes to those settings recommended in [9] (mismatch=5 indel=5).

TANTAN version 13 was run on the human genome with default settings, constrained to maximum period of 25 (–w 25). For AT–rich genomes, we used the ATMask matrix provided on the TANTAN website, and increased the probability of starting a repeat as recommended (–r 0.01). TANTAN determines which nucleotides to report as repetitive by computing labeling confidence. In default settings, it reports all nucleotides for which it is at least 50% confident in the annotation — this is the sensitive variant of TANTAN in our experiments. To achieve lower false discovery rate, our conservative variant of TANTAN used a confidence threshold of >85%.

ULTRA was run with default settings: enter–repeat=0.01 exit–repeat=0.04 insertion=0.05 deletion=0.05 maxinsertions=5 maxdeletions=5 rolling–window=100,000. ULTRA score thresholds were selected based on expected false positive levels (chosen to be integer values with false annotation no worse than TANTAN for the corresponding search) — on human sequence the resulting score thresholds were 9 (sensitive) and 13 (conservative); on AT–rich genomes, 12 (sensitive) and 16 (conservative). At time of manuscript submission, these thresholds were set manually, but predicted false labeling from block–shuffled sequence will support automatic thresholds upon software release.

3.5. Complexity and performance

Let K be the maximum periodicity of repeat states, and Φ be the maximum number of allowed contiguous insertions, and Δ be the maximum number of allowed contiguous deletions (both Φ and Δ are set to 5 by default). Then the total number of states in our model, including indel recovery states, is O(K²(Φ+Δ)). The removal of redundant calculations described in Section 3.3, reduces the number of computed values for each labeled letter to be reduced by a factor of K, so that labeling a sequence of length m requires time O(mK(Φ + Δ)).

Testing was performed on a 4.2 GHz Intel Core i7 iMac with 16 GB available RAM running MacOS 10.13.4. Custom python and bash scripts were written to run and analyze experiments.

4. DISCUSSION

We have developed an HMM–based tool, ULTRA, that efficiently detects tandem repeats within a background of non–repetitive sequence. It is effective even in the face of repeats decayed by insertions and deletions relative to the repeat subunit. Due to optimizations in indel state calculations, the speed and memory requirements of ULTRA are competitive with the most used repeat labeling tool, TRF. In both sensitive and conservative modes, ULTRA shows excellent sensitivity and false labeling performance on genomes with a variety of sequence composition.

At present, ULTRA reports score and subunit size (periodicity) for each repeat, but not consensus pattern. Recovering and reporting the consensus will come in the future.

4.1. Parameterization

We acknowkedge that ULTRA utilizes hand-optimized parameters, which may have resulted in an over-fitting of the tool to particular inputs. We have tried to avoid this by testing across a range of input sequences, and depending on FDR to guide score thresholds. More careful consideration of parameterization is called for. In addition, ULTRA has been tested only on DNA; while it uses a general model that should apply in straightforward fashion to protein repeat annotation, additional parameterization will be required.

4.2. Statistics

The score distributions produced by ULTRA are more stable than the score distributions produced by TRF, but statistics of these scores are not yet understood. Reliable statistics will improve the value of repeat annotation — rather than simple masking of sequence, the significance of a repeat annotation can be held in contrast to the significance of a homology search tool hit containing that repeat.

4.3. Non–overlapping Tool Results

The substantial independence of repeat regions labeled by various tools is surprising. Based on experience with false sequence homology annotation due to degenerate repeats, we expect the the repeats unique to ULTRA will prove more valuable for annotation correctness, as current homology tools have reasonably effective ways to deal with simple (non–repetitive) biased composition. Also, the increased abundance of longer and more complex repeats found by ULTRA is important because longer repeats are more likely to supply enough support in sequence homology tools to bring a false hit above annotation threshold for a sequence search tool.

Looking to future applications of the ULTRA model, in which the model is incorporated into homology software, and probability/score of repetitiveness is used to offset the score of a homology hit: the regions labeled exclusively by TRF and TANTAN in these tests aren’t ignored by ULTRA -, their scores simply do not rise above ULTRA’s reporting threshold. In the context of annotation, those sub–threshold values for short sequences will still be useful for offsetting the scores of false homlogy matches.

4.4. Availability

ULTRA is released under the BSD–3–Clause open source license. Software and documentation are available at https://github.com/TravisWheelerLab/ULTRA.

All benchmarks are available at https://wheelerlab.org/publications/Olson18/Olson18.suplement.tar.gz.

CCS CONCEPTS.

• Applied computing → Molecular sequence analysis; Recognition of genes and regulatory elements;

ACM Reference Format:

Daniel Olson and Travis Wheeler. 2018. ULTRA: A Model Based Tool to Detect Tandem Repeats. In ACM-BCB’18: 9th ACM International Conference on Bioinformatics, Computational Biology and Health Informatics, August 29-September 1, 2018, Washington, DC, USA. ACM, New York, NY, USA, 10 pages. https://doi.org/10.1145/3233547.3233604