Prediction Models for 30-Day Mortality and Complications After Total Knee and Hip Arthroplasties for Veteran Health Administration Patients With Osteoarthritis

Abstract

Background

Statistical models to preoperatively predict patients’ risk of death and major complications after total joint arthroplasty (TJA) could improve the quality of preoperative management and informed consent. Although risk models for TJA exist, they have limitations including poor transparency and/or unknown or poor performance. Thus, it is currently impossible to know how well currently available models predict short-term complications after TJA, or if newly developed models are more accurate. We sought to develop and conduct cross-validation of predictive risk models, and report details and performance metrics as benchmarks.

Methods

Over 90 preoperative variables were used as candidate predictors of death and major complications within 30 days for Veterans Health Administration patients with osteoarthritis who underwent TJA. Data were split into 3 samples—for selection of model tuning parameters, model development, and cross-validation. C-indexes (discrimination) and calibration plots were produced.

Results

A total of 70,569 patients diagnosed with osteoarthritis who received primary TJA were included. C-statistics and bootstrapped confidence intervals for the cross-validation of the boosted regression models were highest for cardiac complications (0.75; 0.71–0.79) and 30-day mortality (0.73; 0.66–0.79) and lowest for deep vein thrombosis (0.59; 0.55–0.64) and return to the operating room (0.60; 0.57–0.63).

Conclusions

Moderately accurate predictive models of 30-day mortality and cardiac complications after TJA in Veterans Health Administration patients were developed and internally cross-validated. By reporting model coefficients and performance metrics, other model developers can test these models on new samples and have a procedure and indication-specific benchmark to surpass.

Total joint arthroplasty (TJA) is a common and safe treatment for severe osteoarthritis (OA) of the hip or knee. In the United States, approximately 300,000 primary total hip arthroplasties (THAs) and 700,000 total knee arthroplasties (TKAs) are performed annually [1], and together constitute the largest procedural expenditure for Medicare [2]. Although the short-term risk of mortality and major complications after elective TJA for OA is generally low, studies have identified patient [3–7] and setting characteristics [8] that are associated with higher risk. However, far fewer studies have explicitly set out to develop and validate accurate risk models that might be used to quantify a patient’s risk to inform preoperative management, informed consent, or shared decision-making.

In addition to potential for informing preoperative decision-making, accurate statistical models associating patient factors with outcomes are essential for risk adjusting outcome-based performance measures and reimbursement programs. The Centers for Medicare and Medicaid Services (CMS) have implemented risk-standardized measures of mortality, complications, and readmissions after THA or TKA into their Value-Based Purchasing, Readmission Reduction, and Hospital Compare programs. Clearly, the value and fairness of these measures are heavily dependent on the validity and accuracy of the underlying risk-standardization models. Also, CMS incentivizes clinicians to use a surgical risk calculator during discussions before THA or TKA through its Physician Quality Reporting System [9]. However, incenting the use of calculators with unknown or poor accuracy is unlikely to improve safety or quality.

A recent and informative review of currently available preoperative prediction models for THA and TKA notes that the available risk calculators for postoperative mortality and short-term complications have limitations [10], including the lack of transparency regarding model coefficients and/or poor or unknown performance on cross-validation. Thus, it is currently impossible to know how well current models predict mortality or complications after TJA for OA patients, or if newly developed models are better or worse.

Assessing predictive model performance is complex and multidimensional, but 2 terms are foundational: discrimination and calibration. Discrimination is the ability of a model to distinguish patients who experience the outcome from those who do not. For binary outcomes (eg, 30-day mortality), discrimination is often quantified by the C-index, which represents the probability that a patient who experienced the outcome would have a higher predicted probability than a randomly selected patient without the outcome. In crude terms, C-indexes can be interpreted as excellent (area under the curve 0.9–1), good (0.8–0.89), fair (0.7–0.79), poor (0.6–0.69), or fail/no discriminatory capacity (0.5–0.59) [11,12]. However, because the C-index is based on rank, it has limitations in terms of quantifying model accuracy. Thus, it is important to also assess a model’s calibration, which compares predicted and observed outcomes across the entire range of the data. Calibration is often visually represented and assessed by plotting observed vs predicted outcomes over equally sized deciles of risk.

The American College of Surgeons (ACS) National Surgical Quality Improvement Program (NSQIP) has an online universal surgical risk calculator (http://riskcalculator.facs.org/RiskCalculator/) that inputs Current Procedural Terminology codes and demographic and clinical variables, and returns risk estimates for 11 separate postoperative complications including 30-day mortality. Although this tool has good overall accuracy averaged across procedures [13], studies of its accuracy for specific procedures are limited. One validation study of the ACS-NSQIP model’s performance for elective TJA in a single-site sample of Medicare patients was found to have generally fair to poor C-indexes for mortality and complications [14]. Another single-site study found the ACS-NSQIP model to have fair discrimination for 90-day prosthetic joint infection (C-index 0.71; confidence interval [CI 0.599–0.826]) [15]. Larger validation studies in more varied contexts are needed to better understand and evaluate the performance of the ACS calculator in the context of TJA.

The American Joint Replacement Registry Risk Calculator (https://teamwork.aaos.org/ajrr/SitePages/Risk%20Calculator.aspx), developed with data from large samples of Medicare patients [6], inputs procedure type and demographic and clinical variables, and returns risk estimates for 90-day mortality and 2-year risk of prosthetic joint infection. No model coefficients or accuracy metrics have been reported, nor has the model been validated.

Although developed for risk adjustment of hospital-level outcomes rather than for preoperative decision-making, the CMS risk-standardization models for postoperative mortality, complications, and readmission could be used to produce patient-specific risk estimates. Although these models were rigorously developed, validated, and transparently reported, their overall discrimination is poor (C-indexes ~ 0.65) [16,17].

Other models of short-term complications and mortality have been published, but cannot be used for preoperative decisions because they include intraoperative or index stay characteristics as predictors (eg, lowest intraoperative heart rate) [18–20] and/or have poor-reported performance [19,21]. Another potential limitation of the currently available models is the failure to consider the impact of indication on overall risk or as a modifier of other predictors. TJA is primarily performed in the context of OA, but is also conducted in the contexts of cancer, inflammatory arthritis, and fractures, often related to osteoporosis. Patients receiving TJA for other indications have different comorbidity profiles and overall risk of mortality compared with patients receiving TJA for OA. Therefore, models of risk for TJA should include indication as a predictor, as well as interaction terms with other predictors, or better yet be indication-specific. However, given low rates of most outcomes, a balance must be struck between specificity and having adequate data for modeling purposes [22]. Finally, existing risk models for TJA have used traditional regression approaches, such as logistic regression, rather than more modern, and occasionally more powerful “machine learning” strategies [23–26]. These strategies are becoming the state-of-the-art for prediction problems across domains of science and industry, but have only begun to be applied to predictions within orthopedics [27], and have never been applied to the prediction of TJA complications.

Thus, the need still remains for an accurate, rigorously tested, and transparently reported prediction model for mortality and major complications after TJA among OA patients that can be used to inform preoperative discussions and decisions. The recent Transparent Reporting of a Multivariable Prediction Model for Individual Prognosis or Diagnosis statement and the Consensus Statement on Electronic Health Predictive Analytics describe the methodological and reporting standards for the development of clinical risk calculators [28,29]. Therefore, we sought to use modern regression strategies to develop and conduct internal cross-validation of risk models of 30-day mortality and major complications after TJA in OA patients of the Veterans Affairs (VA), and transparently report model details and performance metrics as a benchmark for other model developers to exceed.

Materials and Methods

Sample

The US Department of Veteran Affairs (VA) Surgical Quality Improvement Program (VASQIP) has nurse abstractors in VA medical centers across the United States who collect preoperative, perioperative, and postoperative data on annual samples of high-volume surgical procedures, including THA and TKA [30]. The VASQIP data are often used as a gold standard in validation studies of methods that rely solely on administrative codes [31]. All primary THA and TKA cases included in VASQIP for 6 years (fiscal year 2008–2015) were included in the initial sample. The sample was then restricted to patients with documented OA in the year before the index procedure.

Candidate Predictors

In addition to the VASQIP data, other clinical and demographic variables were extracted from the VA Corporate Data Warehouse (CDW). VASQIP variable definitions include specific timeframes. Many variables (eg, dyspnea, open wound/wound infection) are determined by patient report and/or clinical impression during the immediate, usually 30-day, preoperative period. Other variables are defined using a previous 6-month observation period (eg, a history of myocardial infarction) or longer (eg, previous cardiac surgery). For many VASQIP variables, especially those targeted to the immediate preoperative period, we also included versions derived from the CDW data with a longer observation period.

Over 120 preoperative demographic, clinical, and laboratory variables from VASQIP and CDW data were initially screened for consideration by conducting separate bivariate logistic regression analyses and excluding candidate predictors with an associated P value >.25 [11]. The remaining 90 variables, presented in Table 1, were retained as candidate predictors for model building.

Table 1.

Candidate Predictor Variables.

Demographics	Comorbidities	Laboratory and Test Values (Closest to Surgery)
Age*	Chronic heart failure***,^,^^
Gender*	Venous insufficiency*,^^	Body mass index**
Race/ethnicity***	CVD*,^^	Alkaline phosphatase**
Homelessness*,^^	COPD***,^^^,^^	BUN**
	Dementia*,^^	Hematocrit**
Medications and treatments and treatment history	Ulcer*,^^	PT-INR**
	Malignancy*,^^
Steroids***,^,^^	Depression*,^^	Serum creatinine**
Dialysis**,^^^^	Schizophrenia*,^^	Total bilirubin**
Hypertension medications**,^^^	Bipolar disorder*,^^	Platelet count**
Chemotherapy for cancer**,^	Hyperglycemia*,^^	PT
Pain medication use*	Hypertension*,^^	Partial thromboplastin time**
Radiotherapy for cancer in previous 90 d**	Alcohol use disorder*,^^	Serum glutamic oxaloacetic transaminase**
	Dyspnea***,^^^,^^	White blood cell count**
	Rheumatoid arthritis*,^^	Sodium**
Angioplasty or revascularization procedure for atherosclerotic PVD**,^^^	Renal disease*,^^	Albumin**
	MI*^^
	Liver disease*,^^
	Diabetes**,^^^
Percutaneous transluminal coronary artery angioplasty or PCI**,^^^	Paralysis*,^^
	Hemiplegia**,^^^
	Pulmonary disease*,^^
	AIDS*,^^
	Current smoker*,^^
Major cardiac surgical procedure**,^^^	Hx TIA**,^^^
	Hx cerebrovascular accident***,^^^,^^
Setting characteristics
VA facility ID**	>10% weight decrease in body weight in the previous 6 months**
Postgraduate year of surgeon**
	Angina**,^
	Obstructive sleep apnea*,^^
	Rest pain/gangrene**,^
	Acute renal failure**,^^^
	Other psychosis*,^^
	Wound infection***,^^^,^^
	Peripheral vascular disease*,^^
	ASA class**

Timing:

^{^}within 30 presurgical days

^{^^}within 12 presurgical months

^{^^^}any history

^{^^^^}currently or within 2 presurgical weeks.

ASA, American Society of Anesthesiologists; BUN, blood urea nitrogen; CDW, Corporate Data Warehouse; COPD, chronic obstructive pulmonary disease; CVD, cardiovascular disease; Hx TIA, history of transient ischemic attack; ID, Station Number; INR, international normalized ratio; MI, myocardial infarction; PCI, percutaneous coronary intervention; PT, prothrombin time; PVD, peripheral vascular disease; TIA, transient ischemic attack; VA, Veteran Affairs; VASQIP, VA Surgical Quality Improvement Program.

Source:

^*VA CDW

^**VASQIP

^***Both.

Outcomes

Several classes of major outcomes occurring within 30 days of TJA were considered and are described in more detail in Table 2—including 30-day mortality, cardiac complications, central nervous system complications, respiratory complications, wound complications (including deep periprosthetic infection), systemic sepsis, return to the operating room, progressive renal insufficiency, and any major complication—all as defined and documented in the VASQIP data.

Table 2.

Definitions and Frequency of Major Outcomes Occurring Within 30 Days in 70,569 TJA Patients.

Outcome	Definition	N(%)
Cardiac complications	Cardiac arrest requiring CPR or myocardial infarction	430 (0.61)
Central nervous system complications	Coma lasting >24 h postoperative or cerebral vascular accident/stroke	213 (o.3o)
Respiratory complications	Failure to wean >48 h or pneumonia or pulmonary embolism or reintubation	952 (1.35)
Wound complications	Wound disruption/dehiscence or organ/space SSI or deep SSI	499 (0.70)
30-d mortality	Same	186 (0.26)
Systemic sepsis	Same	295 (0.42)
Return to OR	Same	1555 (2.20)
Progressive renal insufficiency	Same	1165 (1.65)
DVT/thrombophlebitis	Same	566 (0.80)
Any major complication	At least one of the above	3780 (5.35)

CPR, cardiopulmonary resuscitation; DVT, deep vein thrombosis; OR, operating room; SSI, surgical site infection; TJA, total joint arthroplasty.

Model Building and Statistical Analyses

Two predictive modeling strategies were used and compared: least absolute shrinkage and selection operator (LASSO) [26] and boosted regressions [23]. LASSO regression is a method that performs both variable selection and regularization to improve the final model’s prediction accuracy and interpretability [26]. LASSO regression minimizes the sum of squared errors with a bound on the sum of the absolute values of the coefficients. By contrast, boosted regression is rooted in machine learning in that way it is iterative and adaptive. The model predicts an outcome, then iteratively predicts remaining error by combining large numbers of base models adaptively to optimize predictive performance. Here, we used a 20-knot spline as the base model. Boosted regression models can handle different data types (eg, numeric, categorical, ordered), do not have strict distributional assumptions, automatically handle interactions and higher order associations, and accommodate missing data. The performance of risk models developed with boosted regression often far exceeds their traditional regression counterparts; however, overfitting in the training data needs to be managed and evaluated by cross-validation. For each modeling strategy for each outcome, the sample was randomly split into 3 subsamples: one to select the model tuning parameters, a model development sample, and a cross-validation sample. The number of boosts was chosen to maximize the C-statistic in the test set using 10-fold cross-validation by bootstrapping in the tuning set.

After preliminary analyses developing separate models for THA and TKA, we decided to work with a combined sample with an indicator variable for procedure type (THA vs TKA). This decision was primarily driven by event rate considerations that became problematic as the sample was further split. Also, we initially included all TJA cases regardless of indication (OA, rheumatoid arthritis only, or other), but found significant interactions suggesting that different models for each indication would produce more usable and accurate models.

Missing Data

Demographic and comorbidity data contained almost no missing data. However, many preoperative laboratory values had up to 40% missing data. When data are missing at random, statistical methods such as multiple imputation give less biased and realistic results compared with complete case analysis or single imputation [32]. However, in this context, the ordering of a laboratory test is likely driven by factors that make assumptions underlying multiple imputation untenable. In the absence of a wholly satisfying method to address missing data, the following approach was adopted. For each variable, missing data were imputed with the centered mean, and an indicator variable for missingness was created. Then, both the primary variable and missingness indicator were evaluated in a mixed-effects logistic regression model. In cases where both the primary variable and missingness indicator were both significantly related to mortality, they were both included as candidates for possible selection in the main model. In cases where only the primary variable was significantly related to mortality, only the primary mean imputed variable was considered.

Model Performance

We used several methods to assess model performance: the C-index, calibration plots, and comparison of the distributions of predicted probabilities between those experiencing an outcome vs those not experiencing an outcome. Because of the low number of events for many outcomes, the resulting C-statistics were sensitive to which events were randomly assigned to each of the development and validation sample. Therefore, we conducted 100 bootstrap replicates of this process and reported the mean (95% CI) of the C-statistics. Then, we compared and described the distributions of predicted probabilities for patients experiencing each outcome or for those not experiencing. Finally, we constructed calibration plots to help visualize the congruence between observed event rates across deciles of risk. Owing to the low event rates and skewed distribution of predicted probabilities, we created deciles of predicted probabilities with equal number of patients from the cross-validation (test) sample.

Results

Event rates for all major outcomes are presented in Table 2 and selected characteristics of the final sample are presented in Table 3. Mortality within 30 days was the least frequent outcome (0.26%), progressive renal insufficiency was the most frequent (1.65%), and 5.35% of patients had at least one major negative outcome. The mean (95% Cl) of the bootstrapped C-statistics for both the LASSO and boosted models are presented in Table 4. The highest mean of the bootstrapped C-statistics was achieved for cardiac complications and 30-day mortality. In general, the boosted regression produced C-statistics that were slightly higher than the LASSO models. For most outcomes, however, the mean C-statistics were lower than 0.70 for both methods, which is considered suboptimal for prediction models.

Table 3.

Selected Sample Characteristics and Outcomes in 70,569 TJA Patients.

Preoperative Characteristics	Summary
Hip arthroplasty (vs knee)	31.7%
Male (vs female)	94.0%
Caucasian	76.8%
African American	16.0%
Housing instability	4.2%
Age mean (SD)	63.9 (9.0)
BMI mean (SD)	31.6(14.8)
ASA class
I	0.5%
II	26.3%
III	70.6%
IV	2.7%
Functional status
Independent	97.7%
Partially dependent	2.2%
Totally dependent	0.1%
Dyspnea with exertion	8.0%
Dyspnea at rest	0.3%
Current smoker	25.9%
Any malignancy	9.9%
Dementia	0.2%
Preoperative open wound/wound infection	0.3%
Wound infection in previous 6 mo (CDW)	0.5%
Ulcers	1.4%
History of CVA CDW	1.0
History CVA/stroke with deficit	1.3%
Cerebrovascular disease (CDW)	5.2%
History of myocardial infarction (CDW)	2.2%
Hemiplegia	0.6%
History of angina	0.5%
History of revascularization for PVD	0.9%
Pain medication use	72.1%
Chemotherapy within 30 d	0.1%
Rest pain/gangrene	0.2%
Previous PTCA or PCI	7.5%

ASA, American Society of Anesthesiologists; BMI, body mass index; CDW, Corporate Data Warehouse; CVA, cerebrovascular accident; PCI, percutaneous coronary intervention; PTCA, percutaneous transluminal coronary angioplasty; PVD, peripheral vascular disease; SD, standard deviation; TJA, total joint arthroplasty; VA, Veteran Affairs; VASQIP, VA Surgical Quality Improvement Program.

CDW = data from VA CDW. All other variables sourced from VASQIP data.

Table 4.

C-Statistics for Cross-Validation of Models Predicting Outcomes Within 30 Days of Total Joint Arthroplasty.

Outcome	LASSO	Boosted
Cardiac complications	0.73 (0.70–0.76)	0.75 (0.71–0.79)
30-d mortality	0.69 (0.63–0.76)	0.73 (0.66–0.79)
Progressive renal insufficiency	0.65 (0.62–0.67)	0.69 (0.66–0.72)
Respiratory complications	0.63 (0.60–0.67)	0.66 (0.63–0.69)
Systemic sepsis	0.63 (0.57–0.69)	0.68 (0.62–0.74)
Wound complications	0.62 (0.59–0.66)	0.66 (0.61–0.71)
CNS complications	0.59 (0.53–0.65)	0.62 (0.55–0.69)
Return to OR	0.57 (0.55–0.60)	0.60 (0.57–0.63)
DVT/Thrombophlebitis	0.58 (0.54–0.61)	0.59 (0.55–0.64)
Any complication	0.58 (0.57–0.60)	0.60 (0.57–0.63)

CNS, central nervous system; DVT, deep vein thrombosis; LASSO, least absolute shrinkage and selection operator; OR, operating room.

Focusing on cardiac complications and 30-day mortality where the best discrimination was achieved, LASSO regression model coefficients (which are far simpler to present than the boosted regression models) are presented in Table 5. The LASSO coefficients can be used prospectively to calculate a patient’s risk score by multiplying the patient’s values by the coefficients and summing the products. The risk score can then be translated to a predicted probability of an adverse event with the formula Prob(adverse event) = exp(score)/(l + exp[score]). A simple spreadsheet to make these calculations, including more detailed input definitions, is available from the authors.

Table 5.

Formula for Score and Probability Prediction.

Predictor Variable	Cardiac Complications	30-d Mortality
Age (centered)	0.0561	0.0420
CVA/stroke with deficit	0.0028	0.0109
Cerebrovascular disease	0.0618	–
History of MI	0.0978	–
Pain medication use	−0.2465	–
Chemotherapy within 30 d	1.3760	–
Rest pain/gangrene	0.4938	–
Previous PTCA or PCI	1.0021	0.7915
Dyspnea-minimal exertion	0.1985	0.3394
Dyspnea-rest	–	1.3392
Preoperative BUN	0.0028	–
Preoperative serum albumin	–	−0.3652
Partial thromboplastin time	–	0.0449
Wound infection	–	0.6922
Dementia	–	0.6411
Ulcers	–	0.0085
Any malignancy	–	0.0441
Hemiplegia	–	1.0695
Angina (1 mo)	–	0.7451
Revascularization for PVD	–	0.3934
ASA class 4	–	1.1930
Intercept	−5.1846	−6.4855

ASA, American Society of Anesthesiologists; BUN, blood urea nitrogen; CVA, cerebrovascular accident; MI, myocardial infarction; PCI, percutaneous coronary intervention; PTCA percutaneous transluminal coronary angioplasty; PVD, peripheral vascular disease.

For the patients in the cross-validation sample who experienced a cardiac complication, the mean predicted probability of a cardiac complication within 30 days was 1.1%, significantly higher compared with 0.60% for those who did not experience a cardiac complication (P < .001). For patients in the cross-validation sample who died, the mean predicted probability of death within 30 days was 0.51%, significantly higher compared with 0.27% for those who did not die (P = .009).

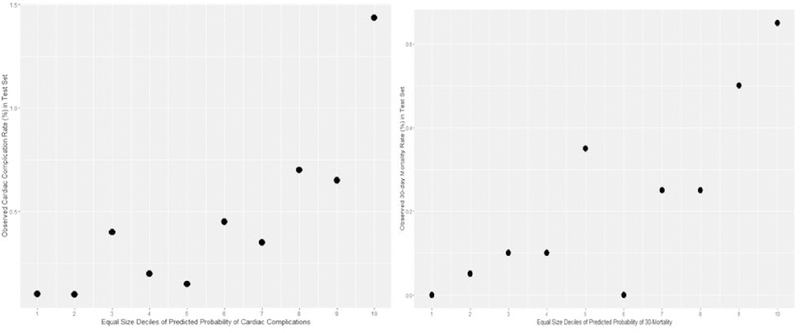
To assess the models’ calibration, we plotted the observed rates of cardiac complications and 30-day mortality against deciles of predicted probability, with equal number of patients in each decile. As presented in Figure 1, rates of both outcomes generally trend upward with the predicted probabilities, with the highest decile having markedly higher event rates.

Fig. 1.

Calibration plots for models of cardiac complications and 30-day mortality.

Discussion

To our knowledge, this study was the first to apply modern regression strategies to the prediction of TJA complications. However, to paraphrase Yogi Berra (paraphrasing others), prediction is hard, especially about the future [33]. Fairly accurate predictive models of cardiac complications and death within 30 days of TJA for VA patients with clinically documented OA were developed and internally cross-validated. The performance of models to predict other outcomes was poor. These results highlight the difficulty of predicting rare outcomes with patient data available at the time of the preoperative evaluation. Models that include interoperative data might produce more accurate predictions of postoperative outcomes, but would not be applicable to preoperative processes such as risk modification, risk stratification, or shared decision-making.

Note that prediction models should not be interpreted as explanatory models, meaning that the inclusion or exclusion of particular variables, or even the sign or magnitude of coefficients for included variables, should not be taken to imply causal relationships or lack thereof. Many candidate variables are intercorrelated, which affords opportunities for better prediction, but makes interpretation of individual variables or coefficients problematic. Many factors that may have associations to outcomes are not included in the models if they do not provide nonoverlapping additional predictive power.

Without model details or comparable performance data on publicly available risk models in the context of TJA, such as those hosted by ACS and American Joint Replacement Registry, it is impossible to know if the models developed here are more or less accurate for this population. The one single-site validation study of the ACS risk calculator in a sample of joint replacement patients produced similar, but generally lower, C-indexes compared with the models tested in the present study, but was based on very low event rates for many outcomes (eg, 4 deaths). Thus, more validation studies of the ACS models for TJA are needed, which would be greatly facilitated if the model details were publicly available or at least made available to researchers. The American Joint Replacement Registry models have never been validated and model details have not been published. However, we are currently attempting to externally cross-validate the American Joint Replacement Registry models using VA data.

Another nuance is worthy of discussion. It is important to note that predictive models of short-term surgical outcomes depend on data from people who underwent surgery. They do not include data from people who did not undergo the procedures because they were deemed to be poor candidates by presurgical screening. Therefore, the models are focused on predictors among patients who have been otherwise cleared for surgery. In other words, the models are trying to screen patients for risk after they have already been screened for risk. Although this makes prediction harder, it is the entire point of the enterprise to give surgeons and patients information that they do not already have.

This research and the models it produced have several limitations. It is unknown how well these results will generalize outside of the VA system. The VA TJA patient population is unlike many other systems (94% men, low socioeconomic status, including housing instability). Also, we used many years of data to have sufficient outcome rates, thus could not track temporal trends in risk or predictors of risk. Another limitation is the potentially incomplete nature of the data on some predictor variables. In some cases, our historical timeframes may have been too short to accurately capture data on relevant comorbidities. Many patients are dual users of other health care systems, making their medical histories as represented in VA data incomplete.

Another factor that may have impacted results is the possibility that some preoperative characteristics may have been discovered postoperatively for patients who experienced complications, but not others. Thus, ascertainment of risk factor information may have been better for patients who experienced complications, making complications “self-predicting.” Although it is unknown if or how often this occurred, the possibility should be entertained. Furthermore, facility-level differences in identifying and documenting comorbidities may exist, which in turn may be related to outcomes. If facilities with less intense screening and documentation of risk factors have worse surgical outcomes, outcomes will be harder to predict. Also, the 30-day window for ascertainment of complications in VASQIP might have missed events that occurred later. The US Centers for Disease Control uses a 90-day window for surveillance of deep surgical site infection after TJA. Finally, we did not focus in this study on predicting other important outcomes such as longer-term functioning and satisfaction, which may be equally important to address in preoperative discussions.

In conclusion, although we were able to develop and internally cross-validate fairly accurate models of 30-day mortality and cardiac complications, other outcomes were even harder to predict. By reporting coefficients and performance metrics, other model developers can test our models on new samples (external cross-validation). It is currently unknown if these or any currently available predictive models provide information that is not already known to surgeons or patients. The real test of the value of a predictive model should not only be discrimination or calibration. The effects of specific applications of predictive models (eg, informed consent, shared decision-making, risk stratification) need to be rigorously evaluated in terms of their impact on patient outcomes and satisfaction [34].