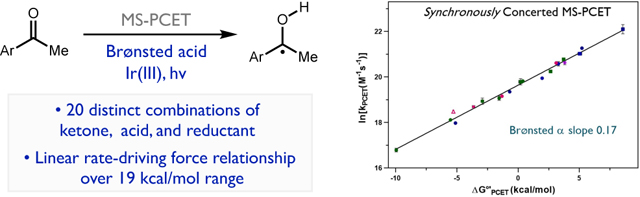
Abstract
Here we present a detailed kinetic study of the multisite proton-coupled electron transfer (MS-PCET) activations of aryl ketones using a variety of Brønsted acids and excited-state Ir(III)- based electron donors. A simple method is described for simultaneously extracting both the hydrogen bonding equilibrium constants and the rate constants for the PCET event from deconvolution of the luminescence quenching data. These experiments confirm that these activations occur in a concerted fashion, wherein the proton and electron are transferred to the ketone substrate in a single elementary step. The rates constants for the PCET events were linearly correlated with their driving forces over a range of nearly 19 kcal/mol. However, the slope of the rate-driving force relationship deviated significantly from expectations based on Marcus theory. A rationalization for this observation is proposed based on the principle of non-perfect synchronization, wherein factors that serve to stabilize the product are only partially realized at the transition state. A discussion of the relevance of these findings to the applications of MS-PCET in organic synthesis is also presented.
Graphical Abstract
Introduction
The applications of multisite proton-coupled electron transfer (MS-PCET) in organic synthesis have expanded considerably in recent years.1–8 These efforts proceed from the premise that MS-PCET can serve as a non-traditional mechanism for homolytic bond activation with orthogonal chemoselectivities and a broader thermodynamic range than traditional hydrogen atom transfer reactions.9 As such, MS-PCET enables the formal addition of H• to (or removal of H• from) a wider range of organic functional groups, providing catalytic access to many useful radical intermediates that can be engaged in further bond-forming or bond-breaking reactions. While these synthetic aspects of MS-PCET continue to advance, detailed mechanistic studies of MS-PCET activations for many non-canonical substrate classes remain rare.10 Accordingly, studies that delineate the key features of these chemistries may offer new avenues and insights into expanding the scope and selectivity of these processes, explicating previous observations, and evaluating the validity of hypotheses underlying the reaction design.
In this context, we became interested in better understanding the MS-PCET activation of aryl ketones. In 2013 we reported a photocatalytic method for intramolecular ketyl-olefin cyclization that proceeds via a neutral ketyl radical intermediate that was proposed to form through a concerted MS-PCET activation of an aryl ketone mediated by a Brønsted acid and one-electron reductant.11,12 During the course of these studies we observed a strong correlation between reaction viability and the thermodynamic driving force for the PCET event, which is jointly determined by the identities of the acid and reductant employed.
By comparing the strength of the new O-H bond formed in the PCET event (O-H bond dissociation free energy (BDFE) ~26 kcal/mol for the acetophenone ketyl in MeCN) to an effective bond strength that can be calculated from the pKa and potential of the acid/reductant combination employed13–15, it was possible to assess the thermodynamic favorability of the exchange. When the identities of the acids and reductants were varied, we observed that catalyst combinations with effective BDFEs similar to or lower than the strength of the nascent ketyl O-H bond were uniformly effective in promoting cyclization of a model substrate, while those with effective BDFEs significantly above this value provided no conversion of the starting material (Scheme 1). Notably, acids that were effective in combination with a strong reductant were found to be ineffective when paired with a less-reducing electron donor. Similarly, reductants that were found to promote cyclization with stronger Brønsted acids ceased to function in combination with weaker proton donors.
Scheme 1.
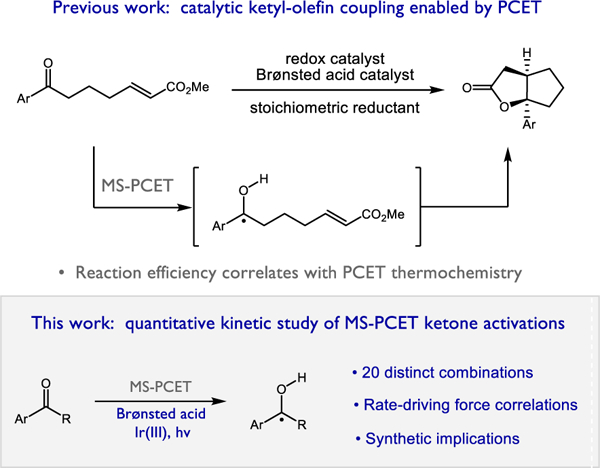
Thermodynamic considerations in PCET-based ketone activations
These preliminary observations suggest that the overall driving force for the MS-PCET event is a key factor in the kinetics of ketyl formation, rather than the identities of the specific reagents employed – a view consistent with previous studies on rate-driving force relationships in MS-PCET.16–22 However, they also raise more fundamental questions about the nature of the rate-driving force relationship for a concerted transfer event. For example, do different acid/reductant pairs with identical effective bond strengths activate a given substrate at identical rates? Does one factor (pKa or potential) have a greater impact on the rate than the other? Under what conditions do the transfers occur in a concerted fashion? The modularity of MS-PCET reactions, wherein the acid, reductant, and substrate can all be varied independently, is well-suited to address these questions. In turn, the answers could have a significant impact in the synthetic applications of PCET, providing a basis for both the rational selection of catalyst pairs to activate a specific functional group in a complex substrate while ensuring compatibility with other potentially reactive sites, and as a means to finely control the kinetics of formation for key radical intermediates. To put this work in context, it is important to note that Fukuzumi previously examined the kinetics of photo-reduction for aryl ketones by Ru(bpy)3Cl2 and the strong Brønsted acid HClO4, though other acids and excited-state reductants were not examined.23–24
In this study, we extend the scope of our earlier qualitative experiments, developing a method to quantify the kinetics of the MS-PCET activation of aryl ketones using excited-state reductants as well as the impact of the driving force on the rates of ketyl formation. To do so we have evaluated MS-PCET activations utilizing combinations of five electronically differentiated aryl ketones (Chart 1, 1–5), four neutral Ir(III)-based excitedstate reductants, (Chart 1, 6–9) and four Brønsted acids of varying strength.25–28 By systematically modulating these three components, we evaluated the rates for 20 distinct combinations that span a wide range of driving forces (~19 kcal/mol). These studies revealed that the rates of MS-PCET activations of ketones are kinetically facile with rate constants on the order of 107 – 109 M−1s−1, and these rates are linearly correlated with the driving force for ketyl formation over the entire range of energies examined. Moreover, the changes in the driving force arising from variation of either the acid or the reductant had an equal impact on the rate constant for the PCET event, providing compelling experimental evidence that these transfer events are synchronously concerted (vide infra). However, we also observe that the slope of the rate-driving force relationship is significantly smaller than would be predicted using a standard Marcus analysis.29–31 An explanation based on the principle of non-perfect synchronization and its attendant impact on the intrinsic barriers for charge transfer is presented to account for these outcomes. Details of these studies and a discussion of their implications in organic synthesis are provided herein.
Chart 1.
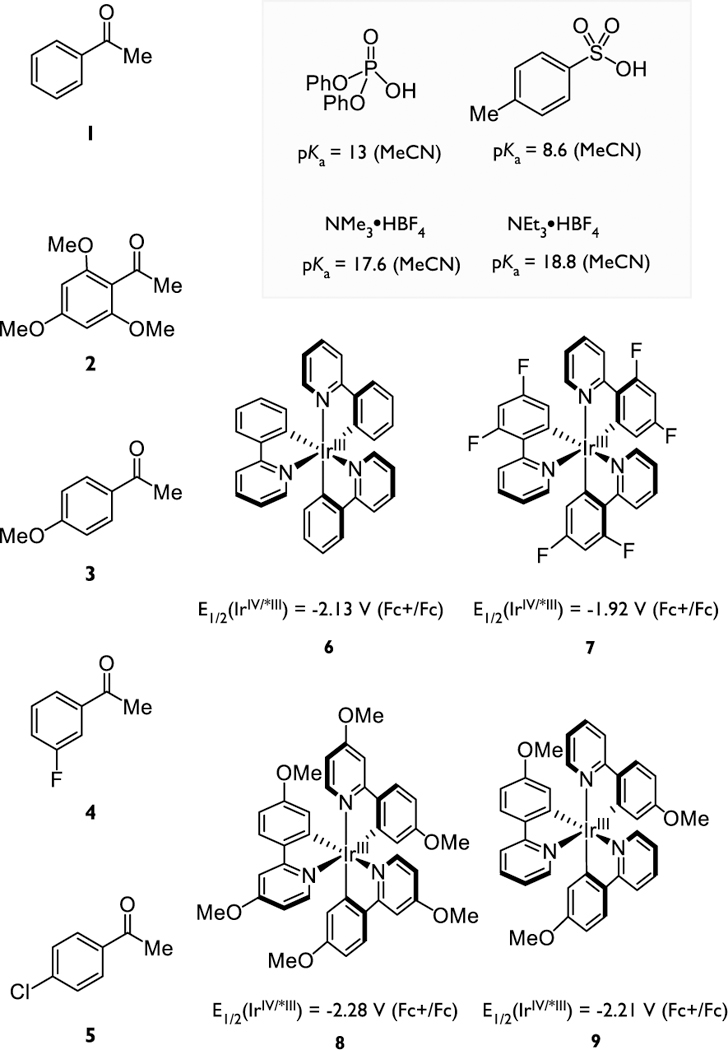
Ketone substrates, excited-state reductants, and Brønsted acids
Methods
The studies outlined above required methods to assess the equilibrium constant for hydrogen bonding between the ketone substrate and the Brønsted acid, the rate constants for the PCET event, and the thermochemistry of the exchange. The impact of each of these energetic features can be generalized in the reaction coordinate diagram depicted in Figure 1. As in previous studies of MS-PCET reactions, we are unable to determine the energetic contributions of post-PCET H-bonding (ΔG°post, Figure 1) to the overall driving force (vide infra). As such we define the driving force for the set of reactions in this study as ΔG°’PCET, which we define as the free energy change from the pre-PCET H-bonded reactant state to the unbound product state (Figure 1).
Figure 1.
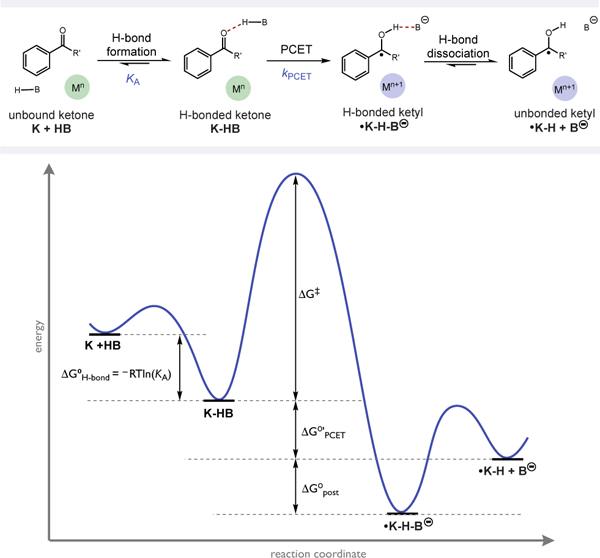
General free energy surface for the MS-PCET activation of ketones described in this study.
Reaction thermochemistry:
In accord with our previous work, the reaction thermochemistry for the PCET activation of ketones was determined by comparing the bond dissociation free energy (BDFE) of the O-H bond formed in the ketyl radical to the effective bond strength (‘BDFE’) of the acid/reductant pair as proposed by Mayer.13–15 This formalism relates the ability of any Brønsted acid and one-electron reductant to function together as a formal H• atom donor. Using a thermochemical cycle similar to the classical Breslow32 and Bordwell33 schemes for the determination of covalent bond strengths to hydrogen, this method defines an effective bond strength, or ‘BDFE’ for a given acid/reductant pair based on the pKa and redox potential of the individual components. These effective BDFE values can be calculated using the following expression (eq. 1):
| (1) |
The activations in this study were carried out in MeCN, and the third term in equation 1 relating to the energetics of proton reduction was taken to equal 54.9 kcal/mol.13 The effective BDFE value can then be compared to the BDFE for the new O-H bond in the neutral ketyl intermediate formed in the PCET reaction to estimate the thermochemistry of the reaction. Ketyl O-H bonds strengths were calculated using density functional theory according to Scheme 2. All calculations were carried out using the unrestricted B3LYP functional with the 6–311G+(d,p) basis set in acetonitrile (CPCM) as implemented in Gaussian 09.34 The computed O-H bond strengths for ketyls derived from ketones 1–5 are presented in Table 2.
Scheme 2.
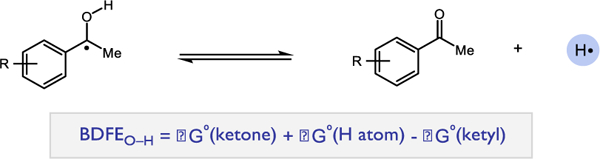
Thermochemistry of BDFEO-H
Table 2.
Kinetic and H-bonding equilibrium data for ketone MS-PCET reactions
| entry | ketone | acid | reductant | BDFEO-H (kcal/mol) |
‘BDFE’–BDFEO-H (kcal/mol) |
KA (M−1) | ΔG°H-bond (kcal/mol) |
ΔG°’PCET (kcal/mol) |
kPCET(M−1s−1) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | (PhO)2P(O)OH | 6 | 27.1 | −3.1 | 6.3 | −1.1 | −2.0 | 4.5 ×108 |
| 2 | 2 | (PhO)2P(O)OH | 6 | 21.5 | 2.4 | 92 | −2.7 | 5.1 | 6.0 ×107 |
| 3 | 3 | (PhO)2P(O)OH | 6 | 24.8 | −0.8 | 17 | −1.5 | 0.7 | 2.5 ×108 |
| 4 | 4 | (PhO)2P(O)OH | 6 | 29.6 | −5.6 | 2.1 | −0.4 | −5.2 | 1.5 ×109 |
| 5 | 5 | (PhO)2P(O)OH | 6 | 28.3 | −4.4 | 6.2 | −1.1 | −3.3 | 8.2 ×108 |
| 6 | 1 | (PhO)2P(O)OH | 9 | 27.1 | −4.9 | 6.3 | −1.1 | −3.8 | 8.6 ×108 |
| 7 | 2 | (PhO)2P(O)OH | 8 | 21.5 | −1.4 | 92 | −2.7 | 1.3 | 2.2 ×108 |
| 8 | 3 | (PhO)2P(O)OH | 8 | 24.8 | −4.6 | 17 | −1.5 | −3.1 | 7.8 ×108 |
| 9 | 1 | (PhO)2P(O)OH | 7 | 27.1 | 1.7 | 6.3 | −l.l | 2.9 | 1.3 ×108 |
| 10 | 2 | (PhO)2P(O)OH | 7 | 21.5 | 7.2 | 92 | −2.7 | 10.2 | 2.0 ×107 |
| 11 | 3 | (PhO)2P(O)OH | 7 | 24.8 | 4.0 | 17 | −1.5 | 5.5 | 6.0 ×107 |
| 12 | 4 | (PhO)2P(O)OH | 7 | 29.6 | −0.8 | 2.1 | −0.4 | −0.3 | 4.0 ×108 |
| 13 | 5 | (PhO)2P(O)OH | 7 | 28.3 | 0.5 | 6.2 | −1.1 | 1.6 | 1.9 ×108 |
| 14 | 3 | NEt3HBF4 | 8 | 24.8 | 3.4 | 17 | −1.7 | 5.3 | 1.1 ×108 |
| 15 | 3 | NMe3HBF4 | 8 | 24.8 | 1.8 | 16 | −1.6 | 3.4 | 1.3 ×108 |
| 16 | 3 | p-TsOH | 7 | 24.8 | −2.0 | 21 | −1.8 | −0.2 | 3.9 ×108 |
| 17 | 5 | p-TsOH | 7 | 28.3 | −5.4 | 15 | −1.6 | −3.7 | 9.4 ×108 |
| 18 | 5 | p-TsOH | 6 | 28.3 | −10.3 | 15 | −1.6 | −8.5 | 2.9 ×109 |
| 19 | 1 | p-TsOH | 7 | 27.1 | −4.2 | 15 | −1.6 | −2.7 | 6.2 ×108 |
| 20 | 3 | p-TsOH | 6 | 24.8 | −6.9 | 21 | −1.8 | −5.1 | 1.3 ×109 |
Determination of hydrogen bonding equilibria and PCET kinetics:
Our previous studies on the MS-PCET reactions of ketones revealed that diphenyl phosphoric acid (PhO)2P(O)OH and the excited state of Ir(ppy)3 (6) can activate acetophenone in acetonitrile at 25° C to reversibly generate neutral ketyl radicals. Stern-Volmer assays revealed that neither the phosphoric acid nor the acetophenone substrate alone quenched the excited state of the Ir(III) complex. However, solutions containing mixtures of both acid and ketone resulted in efficient quenching, which exhibited a first-order kinetic dependence on the concentration of each component. This relationship is summarized in equation 2 where S0 is the initial concentration of ketone substrate and A0 is the initial concentration of the Brønsted acid and kobs τ0 is the gradient of the Stern-Volmer plot.
| (2) |
Here we extend these studies and utilize both steady-state and time-resolved luminescence quenching techniques to evaluate the kinetic features of the PCET event. Unlike traditional quenching studies between an excited-state redox partner and a single substrate, these studies involve electron transfer to a hydrogen-bonded complex between the ketone substrate and the proton donor. A key challenge in defining the energetic features of these MS-PCET reactions is accurately determining the strength of this pre-equilibrium hydrogen-bonding interaction (KA), as the experimentally determined kobs in equation 2 is a composite of both KA and the rate constant for the PCET event (kPCET). However, the H-bonded complexes between aryl ketones and the Brønsted acids used in this study are relatively weak in MeCN and proved difficult to study independently using standard spectroscopic approaches. Accordingly, we formulated a simple method for simultaneously extrapolating both the hydrogen bonding equilibrium constant and the rate constant for the MS-PCET step from analysis of luminescence quenching data assayed over a range of substrate concentrations. The details of this method are described below.
At equilibrium, the concentration of the key H-bonded ketone-acid adduct (x) is given by equation 3a (Figure 2a). This expression can be rearranged to give two alternate forms, 3b and 3c.
Figure 2.
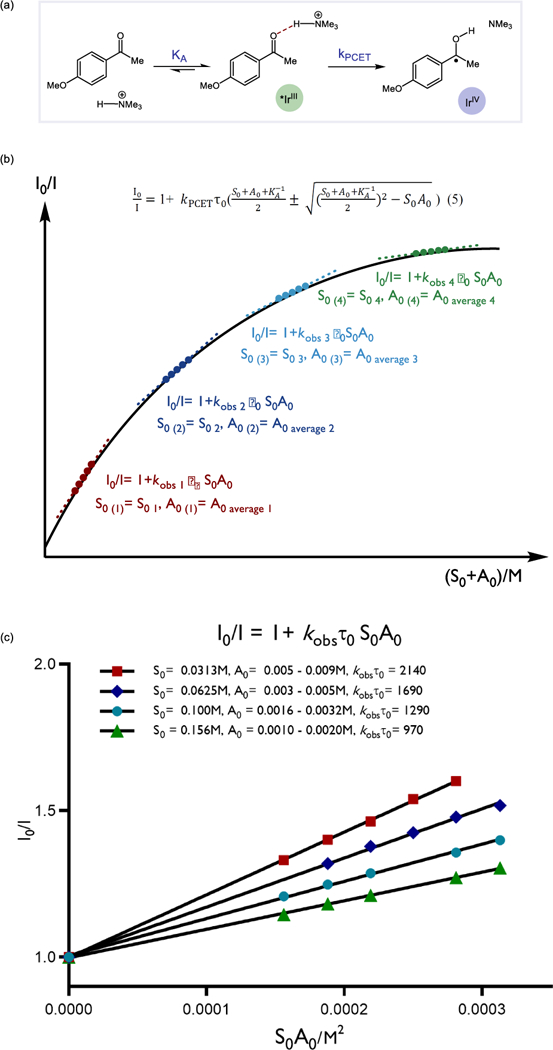
(a) Hydrogen-bonding equilibria between acid and ketone (b) Graphical illustration for the proposed method. The black curve represents non-linear equation 5. Each tangent line represents a distinct set of Stern-Volmer quenching experiments, where the slopes are equal to kobs as described in equation 2. The variation in kobs obtained by variation in S0 and A0 can be used to map the curvature of equation 5 and extract values for kPCET and Ka using equation 8. (c) Quenching data from the model study involving ketone 3 and NMe3•HBF4 acid using reductant 8. In each, the initial concentration of the ketone was held constant (S0), and the initial concentration of the acid was varied. The luminescence intensity I0/I is plotted against the concentration product S0•A0 and the slope gives the corresponding kobs T0 for each set of S0 and A0 values.
| (3a) |
| (3b) |
| (3c) |
Under conditions where neither the Brønsted acid nor the ketone alone quenches the luminescence of the Ir(III) excited state, the concentration of their H-bonded adduct (x) will be linearly correlated with the degree of luminescence quenching by equation 4, in which the slope of the resulting plot is proportional to the rate constant for PCET reaction, kPCET, and the lifetime (τ0) of the *Ir (III) excited state in the absence of any quenching species.
| (4) |
Combining equations 3c and 4 gives equation 5.
| (5) |
This equation reveals that the experimental differential luminescence (I0/I) should be non-linear with respect to the initial concentrations of both the ketone and acid. As such, accurate fitting of equation 5 would require a large number of data points covering a broad range of ketone and acid concentrations. However, we anticipated that sufficiently small variations in the acid or ketone concentrations would result in linear changes in the luminescence intensity. The gradients of these Stern-Volmer plots can be taken as tangent lines to equation 5, enabling equation 2 to serve as a reasonable approximation for equation 4 when the concentration changes are kept appropriately small (Figure 2b). Assuming that KA and kPCET are invariant over the range of concentrations studied, combining equations 2 and 4 furnishes equations 6 and 7.
| (6) |
| (7) |
Equation 7 can be substituted into equation 3b to deliver key equation 8.
| (8) |
By varying the initial concentrations of ketone and acid, equation 8 can be used to determine both the hydrogen-bonding equilibrium constant, KA, and the PCET rate constant, kPCET, from the observed Stern-Volmer quenching constant (kobs τ0). To illustrate this we discuss a model study involving ketone 3 and NMe3•HBF4 using reductant 8. Four distinct luminescence quenching assays were performed. In each assay S0 was held at a constant value while the initial acid concentration A0 was varied over a small range. The slopes of the resulting Stern-Volmer plots provide four distinct values for kobs τ0 according to equation 2 (Figure 2c). The average of the range of A0 values surveyed in each assay was taken to approximate the point of tangency with equation 5, and was used as the value of A0 in equation 8. Substitution of the S0 and average A0 values and the corresponding kobs τ0 values into equation 8 delivers a system of four new equations, each with two unknowns – KA and kPCET. Solving this set of four simultaneous equations provides six values for KA and kPCET, and the average of these six values is reported in Table 1. The consistency of the six values obtained from the four sets of concentration-dependent quenching data suggests that KA and kPCET remain constant over the range of concentrations studied.
Table 1a.
Summary of the Four Luminescence Experiments Shown in Figure 2
| exp | S0 (M) | A0 (M) | S0A0 (M2) |
S0+A0 (M) |
kobs τ0 (M−2) |
|---|---|---|---|---|---|
| 1 | 0.0313 | 0.008 | 0.00025 | 0.039 | 2140 |
| 2 | 0.0625 | 0.004 | 0.00025 | 0.066 | 1690 |
| 3 | 0.100 | 0.0025 | 0.00025 | 0.102 | 1290 |
| 4 | 0.156 | 0.0016 | 0.00025 | 0.158 | 970 |
While the data presented were collected under steady state irradiation conditions, we also confirmed the dynamic nature of the quenching process using time-resolved luminescence experiments (See SI for details). It is important to note that some ketones or acids alone resulted in diminished luminescence intensity of *Ir(III), indicating that competitive non-PCET quenching mechanisms were operative. In these cases, time-resolved luminescence experiments revealed that the non-PCET quenching event was dynamic in nature, allowing it to be factored into a modified form of equation 2 and corrected for (See SI for details). In most instances, we observed that the background quenching was negligible relative to the rates of quenching when both acid and reductant were present (<1%) and thus is not expected to contribute significantly to the observed kinetics.
We sought to validate the accuracy of this method by reproducing literature equilibrium constant values for weak hydrogen bonded complexes in nitrile solvents. Specifically, we focused on a recent report from Wenger and coworkers studying the MS-PCET reactions of pyridine-phenol complexes.21 For the complex formed between 4-chlorophenol and pyridine, Wenger used NMR methods to measure and equilibrium constant of 1.5 ± 0.1 M-1. Using our luminescence quenching method on the same complex under identical conditions in MeCN with [Ir(dF(CF3)ppy)2dtbbpy]PF6 as the excited-state oxidant, we determined the KA value to be 1.4 ± 0.1 M-1. For the complex formed between 4-methylphenol and pyridine, Wenger measured an equilibrium constant of 1.1 ± 0.1 M-1. Under identical conditions in MeCN with [Ir(dF(CF3)ppy)2dtbbpy]PF6 as the excited-state oxidant, our method provided a KA value of 1.1 ± 0.1 M-1. Similarly, Linschitz reported that 4-methylphenol and pyridine form a H-bond adduct with an association constant of 2.6 ± 0.3 M−1 in PhCN.17 Using our luminescence quenching method under identical conditions with [Ir(dF(CF3)ppy)2dtbbpy]PF6 as the excited-state oxidant, we determined the KA value to be 2.6 ± 0.1 M-1. These results provide support for the viability and accuracy of this method. Notably, this method bypasses the need to push binding to saturation, which can be difficult to achieve in systems with small values of KA. As such we are optimistic that it might find use more broadly in the study of weak hydrogen bonded complexes that are not amenable to quantification using traditional spectroscopic methods.
Results and Discussion
Using the method described above, we determined the hydrogen bonding equilibrium constants and the rate constants for excited-state PCET reactions between 20 distinct combinations of five aryl ketones, four Ir(III) photocatalysts, and four Brønsted acids spanning a range of driving forces ~19 kcal/mol (Table 2). In this series of experiments, the equilibrium constant KA varies over a range of 2.3 kcal/mol. When these hydrogenbonding effects on ground state energetics are taken into account, we observed a linear correlation between the rate constants and driving forces for each of the 20 PCET reactions studied (Figure 3).
Figure 3.
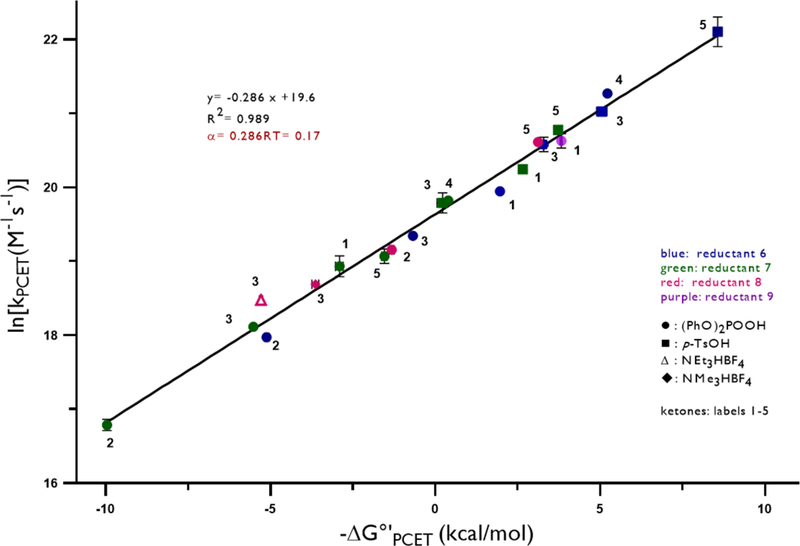
Plot of rate-driving force relationship for the data presented in Table 2. The color of data points represents the reductant: blue- 6, green-7, red- 8, purple- 9. The shapes of data points represent the acid: - (PhO)2POOH, - p-TsOH, - NEt3HBF4, - NMe3HBF4. Numerals next to the data points refer the ketone listed in Chart 1.
These results provide strong evidence that simple thermodynamic considerations are a major determinant in the rates of MS-PCET activations of aryl ketones. Moreover, the correlation suggests that distinct acid/reductant combinations with the same effective BDFE will activate a given ketone substrate at essentially identical rates, irrespective of the identities of the individual proton and electron donors. These outcomes also provide additional support for the view that that effective bond strengths can serve as an effective criterion for catalyst selection in the design of MS-PCET reactions.35–41
A closer inspection of the data in Table 2 and Figure 3 reveals that the rates of PCET respond with equal sensitivity to changes in the driving force resulting from variation of either the proton or the electron transfer event. Stated differently, a specific change in the free energy of the reaction will have an equivalent impact on the rates regardless of whether that specific change arose from varying the pKa of the acid or the potential of the reductant. Mayer has recently proposed that linear rate-driving force relationships for MS-PCET reactions that exhibit equal sensitivity to variation in either the acid or reductant are a useful experimental definition for a synchronously concerted transfer event.22 As such, the data presented here can be taken as evidence that these ketone PCET activations are synchronously concerted.20
Moreover, the magnitude of the measured rate constants discounts the viability of the potentially competitive stepwise electron transfer (ET) or proton transfer (PT) pathways on thermochemical grounds. The 20 measured rate constants all fall between 107–109 M−1s−1, considerably faster than the emissive decay of *Ir (III) excited state (~5 × 105 s−1).42 Considering the pKa difference in MeCN between protonated acetophenone (pKa = –0.1)43 and the strongest acid studied, p-TsOH (pKa = 8.6), the free energy change of proton transfer ΔG°PT is + 11.9 kcal/mol. In turn, this corresponds to a very unfavorable equilibrium for PT, with Keq = 1.8 × 10−9 M-1. Setting this equilibrium constant equal to the ratio of the forward and reverse rate constants for the proton transfer step suggests that the maximum potential value for the rate constant of the forward reaction is achieved when the rate constant for the back reaction is equal to the diffusion limit (2 × 1010 M−1s−1 in MeCN at rt).44 This detailed balance argument suggests that the maximum value for protonation of the ketone (kf) in this system is 36 M−1s−1, much too slow to account for the observed quenching kinetics. While pKa values for the other ketones in this study have not been measured experimentally, it stands to reason that simple substituent effects present in the other ketone substrates would not enable the PT rate constant to increase over a million-fold. Direct electron transfer pathways are more readily discounted by the lack of observable quenching for most ketone in the absence of exogenous acid. In cases where some background quenching is observed, the magnitude of the direct ET rate constant relative to the rate of the MS-PCET reactions is small - less than 1% (see SI for details). Taken together, these data further support that concerted transfer is the dominant mechanism for ketyl formation.
Rigorously, the thermodynamic driving force for the PCET step can be defined as the free energy change associated with converting the pre-PCET ketone-acid complex to the post-PCET H-bonded successor complex.45 In prior work we have presented evidence that the post-PCET H-bonding complexes between neutral ketyls and the phosphate anions are energetically meaningful, and likely strong. Most notably, the use of chiral phosphoric acids in ketone PCET reactions enables highly enantioselective reactions of the resulting ketyl-phosphate complexes.12 In addition, we have observed that numerous acid/reductant combinations are catalytically competent to enable C-C bond-forming reactions even when the PCET event is significantly endergonic (ΔG° ~ +7 kcal/mol).11 The additional driving force associated with a post-PCET hydrogen bonding interaction may make these reactions more favorable than would be suggested through effective bond strength considerations alone. In a similar way, the additional driving force associated with a post-PCET hydrogen bond may also underlie the unexpectedly fast rate constants observed for the most endergonic data points in Figure 3. While we anticipate that post-PCET H-bonding is likely operative in ketone MS-PCET reactions presented in this study, we are currently unable to quantify the magnitude of this interaction. However, the observed rate-driving force correlation is nevertheless strong. This may suggest that the strengths of the post-PCET hydrogen bonds are very similar across the series, or that factors that influence the strength of this hydrogen bond are modestly developed at the transition state (vide infra). We note that all other previous studies of rate-driving force relationships in MS-PCET have also been unable to account for post-PCET hydrogen bonding, and have also defined the overall driving force to reflect a state with full dissociation of the radical and the conjugate acid/base.
Marcus analysis of the reaction
Marcus theory predicts that the Brønsted α value for a series of similar reactions is given by equations 9 and 10.46,47
| (9) |
| (10) |
In the low driving force regime where is predicted to be a constant value of 0.5. In accord with this prediction, most of the previous rate-driving force studies on MS-PCET reactions reported α-values near to 0.5.21,22,48–50 Interestingly, the data presented in Figure 3 reveals a much smaller Brønsted α value of only 0.17.51
A possible interpretation of the modest Brønsted slope can be drawn from Bernasconi’s principle of non-perfect synchronization (NPS), which holds that the development of factors resulting in product stabilization lags behind changes in bonding at the transition state.52 This imbalance serves to moderate the impact of these effects in stabilizing the transition state structure, and thus diminishes the slope of the rate-driving force relationship. 53–55 While these ideas were originally developed in the context of resonance stabilization for polar proton transfer reactions, identical arguments have been constructed for other factors that differentially stabilize starting materials, products, and transition states, including solvation, hyperconjugation, hydrogen bonding, aromaticity, steric effects, and others.56 Accordingly, NPS arguments have been applied successfully in the analysis of a wide variety of reaction types.57–58
We propose that these ideas may also apply to the ketone activations presented in this study. To a greater extent than most elementary steps, MS-PCET reactions involve numerous secondary molecular processes that occur concurrently with the primary proton and electron exchange events (including solvent reorganization, inner sphere geometric distortion, charge stabilization, hydrogen bonding, and resonance contributions) and these processes will have progressed to different extents at the transition state. While the results in Figure 3 suggest that the proton and electron transfers are synchronous, the small α value implies that the TS occurs early on the reaction coordinate when many of the factors that might stabilize the products are not yet fully realized. Accordingly, variation of these factors has a smaller impact on the transition state energetics than would otherwise be expected. The early transition state structures implied by this argument could also serve as a potential explanation for the apparent lack of variation in the energetics of the post-PCET hydrogen-bonded complexes. In this framework, the changes in the hydrogen-bonding interface that serve to stabilize the ketyl intermediate are minimally developed at the transition state, which in turn moderates their ability to modulate the barrier for the PCET process.
To connect these ideas to a Marcus frame of reference, the differential ability of these factors to stabilize the starting materials and products may impact the intrinsic barrier for the PCET process. The expressions in (9) and (10) assume that the parabolic potential functions for the product and reactant states have identical shape and curvature. However, this simplifying assumption is not necessarily true in practice. The curvature of the two parabolas reflects on how all the operative factors - solvation, resonance, hydrogen bonding, vibrational force constants, charge distributions, and others60 – impact the energetic costs associated with displacement of the system from its equilibrium position. If these collective factors serve to differentially stabilize the reactant and product states for the PCET reactions, the potential functions may be desymmetrized, leading to the α-values that deviate from the expected value of 0.5 in the low driving force regime. The impacts of unsymmetrical Marcus parabolas have been discussed by Kresge,61 and non-symmetrical parabolas have been invoked previously in Marcustype rate-driving force analyses, most notably by Compton.62–63
In seeking support for these ideas described above, we elected to study the activations of two additional aryl ketone substrates wherein the key hydrogen bond interface that mediates the PCET event would be sterically perturbed - isopropyl phenyl ketone 10 and tert-butyl phenyl ketone 11. In theoretical models of MS-PCET the internuclear distance between the heavy atoms involved in the pre-equilibrium hydrogen bond contracts at the transition state. 64,65 As pointed out by Mayer in a recent study of TEMPO-H oxidations by MS-PCET, when sterically encumbered reaction partners are employed this contraction demands a greater degree of geometric distortion to obtain the required transition state geometry.22 Ostensibly, the energetic penalties associated with contracting the proton transfer coordinate at a sterically crowded interface can be offset to some extent for later transition states where additional product stabilizing factors will have a greater impact.
Accordingly, we would expect that these more hindered ketone substrates would exhibit higher α values indicative of later transition states than their less hindered methyl ketones congeners. This outcome was observed experimentally. Specifically, 10 and 11 were activated with (PhO)2P(O)OH and a range of different excited-state Ir(III) reductants (6–9) in MeCN at rt. For each ketone, the change in the driving force for ketyl formation is solely a result of the changing potentials of the redox catalysts, while the H-bond equilibrium and ketyl O-H bond strengths remain constant in each case. Using the analysis presented above, the rate constants for PCET were extracted and linear rate driving force relationships were observed, with the isopropyl ketone exhibiting an increased α value of 0.27 and the tert-butyl ketone an α value of 0.44 (Figure 4). These results are consistent with later transition states and suggest that the steric environment of the key hydrogen bonded complex may play a role in modulating the intrinsic barrier for the PCET process. Another possible explanation for the small slope is the involvement of vibrational excited states as proposed by Hammes-Schiffer. This effect was recently suggested to rationalize the small α value observed for a novel C-H bond cleavage reaction via concerted PCET reported by Mayer.51,66 Efforts to more fully delineate these features will be the focus of future work.
Figure 4.
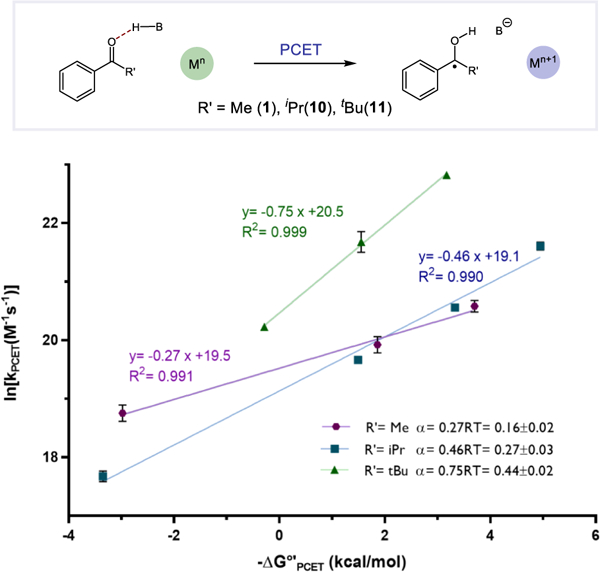
Different Brønsted slopes α for R’= methyl, isopropyl, and tert-butyl substituted ketones.
We have also determined the H/D kinetic isotope effects (KIE) for ketones 1, 10, and 11 using (PhO)2P(O)OH or (PhO)2P(O)OD, and photoreductant 6. In all cases that kH/kD ratio was great that unity, and the magnitude of the KIE increases with the steric bulk of the ketone (kH/kD = 1.2 for 1, 1.3 for 10, and 3.0 for 11).11 These results are consistent with the proposed PCET mechanism where proton motion is associated with the quenching of the Ir excited state.67–71
Implications for MS-PCET in Organic Synthesis
The results above reinforce a number of potential advantages for the use of PCET in organic synthesis. First, ketones are weakly basic (pKa ~ 0 for the protio-oxocarbenium ion derived from acetophenone in MeCN) and their protonation requires very strong Brønsted acids. Similarly, the potentials required for direct one-electron reduction of aryl ketones are strongly negative (E = –2.48 V vs Fc+/Fc in MeCN for acetophenone). However, the reactions studied here demonstrate that neutral ketyls can be accessed using concerted MS-PCET using reagents with pKa and potential values far removed from these values, enabling generation of the reactive intermediate under much milder reaction conditions than would be required to promote direct electron transfer or proton transfer processes. Second, the driving forces for ketone MS-PCET reactions are jointly determined. The correlations in Figure 3 illustrate that while the rates of ketone activation vary linearly with the driving force, they are agnostic to the identities of the reagents employed. A weaker reductant and stronger acid of a given effective BDFE will activate the substrate at an identical rate to a combination of a stronger reductant and weaker acid with the same driving force. This is an unusual and highly advantageous feature, as it suggests that the conditions of the PCET reaction can be varied across a wide range of pKa and potential regimes, allowing one to rationally select the identity of the acid/reductant pair to accommodate the sensitivities of any other basic or redox-active functional groups present in the same substrate. Third, these reactions demonstrate that ketone MS-PCET reactions can proceed at extremely fast rates (up to 109 M−1s−1) even in the low driving force regime, allowing the successful use of excited-state redox partners. Moreover, the modest Brønsted slope in this LFER indicates that the rates of ketone PCET activation diminish very slowly over a wide range of driving forces. Lastly, these studies reinforce the key role of pre-equilibrium H-bonding in the overall kinetics of MS-PCET reactions, and present a foundation for understanding some of the unusual chemoselectivities observed in competitive MS-PCET reactions that have been proposed to arise, at least in part, from differential hydrogen bonding.
Conclusions
The reductive MS-PCET reaction of aryl ketones was studied using a variety of Brønsted acids and excited state electron donors. A simple method for extrapolating both the equilibrium constant for hydrogen bonding and the rate constants for the PCET event was developed based on a simple analysis of steady-state luminescence quenching data. Evidence is presented that these events occur in a concerted fashion, and that the rate constants of these MS-PCET reactions are linearly correlated with their driving forces, which are jointly determined by both acidity of the Brønsted acid and the potential of the excited-state reductant. Importantly, sets of reactions with identical driving forces proceed at identical rates, even if the structures of the acids and reductants employed are different in each case. This suggests it is not the specific identities of the reagents that impact the reaction kinetics, so much as the overall thermodynamic favorability of the PCET process. Interestingly, the slope this LFER deviated significantly from expectations based on Marcus theory. A rationalization for this deviation was presented based on non-perfect synchronization, wherein factors that serve to stabilize the product are only partially realized at the transition state, leading to an unusually shallow dependence of the rate of PCET on the thermodynamic driving force. Future efforts will focus on adopting the framework developed here to other synthetically relevant MS-PCET processes and to the understanding of chemoselectivity in reactions with multiple PCET-active functional groups.
Supplementary Material
Table 1b.
Six Sets of Values of KA and kPCET τ0 Obtained, upon Substituting the Information of Any Two Experiments (as in Table 1a) into Equation 8
| into equation 8 | KA/M−1 | kPCET τ0/M−1 | kPCET /M−1s−1 |
|---|---|---|---|
| 1&2 | 15 | 225 | 1.41 ×108 |
| 1&3 | 16 | 212 | 1.33 ×108 |
| 1&4 | 16 | 212 | 1.33 ×108 |
| 2&3 | 18 | 203 | 1.27 ×108 |
| 2&4 | 17 | 208 | 1.30 ×108 |
| 3&4 | 16 | 210 | 1.31 ×108 |
| average | 16 | 210 | 1.3 ×108 |
(kcal/mol) = -RTInKA= −1.65
ACKNOWLEDGMENT
We gratefully acknowledge the NIH for funding this work (R01 GM113105). We acknowledge Emily Gentry for assistance with preparation of the manuscript.
ABBREVIATIONS
- BDFE
bond dissociation free energy
- ET
electron transfer
- LFER
linear free energy relationship
- MS
multi-site
- NMR
nuclear magnetic resonance
- NPS
non-perfect synchronization
- PCET
proton-coupled electron transfer
- PT
proton transfer
Footnotes
Supporting Information
The Supporting Information is available free of charge on the ACS Publications website.
Experimental procedures, luminescence quenching data, thermochemical calculations (PDF)
The authors declare no competing financial interest.
REFERENCES
- (1).Gentry EC; Knowles RR “Synthetic Applications of Proton Coupled Electron Transfer.” Acc. Chem. Res. 2016, 49,1546. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (2).Shaw MH; Twilton J; MacMillan DWC “Photoredox Catalysis in Organic Chemistry.” J. Org. Chem. 2016, 81,6898. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (3).Miller DC; Tarantino KT; Knowles RR “Proton-Coupled Electron Transfer in Organic Synthesis: Fundamentals, Applications, and Opportunities.” Topics in Current Chemistry 2016, 374. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (4).Hoffmann N “Proton-Coupled Electron Transfer in Photoredox Catalytic Reactions.” Eur. J. Org. Chem. 2017, 2017,1982 [Google Scholar]
- (5).Yayla HG; Wang H; Tarantino KT; Orbe HS; Knowles RR “Catalytic Ring-Opening of Cyclic Alcohols Enabled by PCET Activation of Strong O-H Bonds.” J. Am. Chem. Soc. 2016, 138,10794. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (6).Choi GJ; Zhu Q; Miller DC; Gu CJ; Knowles RR “Catalytic Alkylation of Remote C–H Bonds Enabled by Proton-Coupled Electron Transfer.” Nature 2016, 539,268. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (7).Zhu Q; Graff DE; Knowles RR “Intermolecular Anti-Markovnikov Hydroamination of Unactivated Alkenes with Sulfonamides Enabled by Proton-Coupled Electron Transfer.” J. Am. Chem. Soc, 2018, 140,741. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (8).Gentry EC; Rono LJ; Hale ME; Matsuura R; Knowles RR “Enantioselective Synthesis of Pyrroloindolines via Non-Covalent Stabilization of Indole Radical Cations and Applications to the Synthesis of Alkaloid Natural Products.” J. Am. Chem. Soc. 2018, 140,3394. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (9).Mayer JM “Understanding hydrogen atom transfer: from bond strengths to Marcus theory.” Acc. Chem. Res,2011, 44, 36. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (10).For a recent example, see: Ruccolo S; Qin Y; Schnederman C; Nocera DG “General Strategy for Improving the Quantum Efficiency of Photoredox Hydroamidation Catalysis.” J. Am. Chem. Soc,2018, 140,14926. [DOI] [PubMed] [Google Scholar]
- (11).Tarantino KT; Liu P; Knowles RR “Catalytic Ketyl-Olefin Cyclizations Enabled by Proton-Coupled Electron Transfer.” J. Am. Chem. Soc. 2013, 135,10022. [DOI] [PubMed] [Google Scholar]
- (12).Rono LJ; Yayla HG; Wang DY; Armstrong MF; Knowles RR “Enantioselective Photoredox Catalysis Enabled by Proton-Coupled Electron Transfer: Development of an Asymmetric Aza-Pinacol Cyclization.” J. Am. Chem. Soc. 2013, 135, 17735. [DOI] [PubMed] [Google Scholar]
- (13).Warren JJ; Tronic TA; Mayer JM “Thermochemistry of proton-coupled electron transfer reagents and its implications.” Chem. Rev. 2010, 110,6961. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (14).Waidmann CR; Miller AJM; Ng C-WA; Scheuermann ML; Porter TR; Tronic TA; Mayer JM “Using combinations of oxidants and bases as PCET reactants: thermochemical and practical considerations.” Energy Environ. Sci. 2012, 5, 7771 [Google Scholar]
- (15).Weinberg DR; Gagliardi CJ; Hull JF; Murphy CF; Kent CA; Westlake BC; Paul A; Ess DH; McCafferty DG; Meyer TJ “Proton-coupled electron transfer.” Chem. Rev. 2012, 112,4016. [DOI] [PubMed] [Google Scholar]
- (16).Biczók L; Linschitz H “Concerted electron and proton movement in quenching of triplet C60 and tetracene fluorescence by hydrogen-bonded phenol-base pairs” J. Phys. Chem. 1995, 99, 1843 [Google Scholar]
- (17).Biczók L; Gupta N; Linschitz H “Coupled electron-proton transfer in interactions of triplet C60 with hydrogen-bonded phenols: Effects of solvation, deuteration, and redox potentials” J. Am. Chem. Soc,1997, 119,12601 [Google Scholar]
- (18).Fecenko CJ ; Meyer TJ; Thorp HH “Fecenko CJ, Meyer TJ, Thorp HH Electrocatalytic Oxidation of Tyrosine by Parallel Rate-Limiting Proton Transfer and Multisite Electron– Proton Transfer” J. Am. Chem. Soc,2006, 128,11020. [DOI] [PubMed] [Google Scholar]
- (19).Fecenko CJ; Thorp HH; Meyer TJ “The Role of Free Energy Change in Coupled Electron– Proton Transfer” J. Am. Chem. Soc. 2007,129, 15098. [DOI] [PubMed] [Google Scholar]
- (20).Bourrez M; Steinmetz R; Ott S; Gloaguen F; Hammarström L “Concerted proton-coupled electron transfer from a metal-hydride complex” Nat. Chem. 2015, 7, 140. [DOI] [PubMed] [Google Scholar]
- (21).Nomrowski J; Wenger OS “Photoinduced PCET in ruthenium–phenol systems: thermodynamic equivalence of Uni-and bidirectional reactions” Inorg. Chem. 2015, 54,3680. [DOI] [PubMed] [Google Scholar]
- (22).Morris WD; Mayer JM “Separating Proton and Electron Transfer Effects in Three-Component Concerted Proton-Coupled Electron Transfer Reactions.” J. Am. Chem. Soc,2017, 139,10312. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (23).Fukuzumi S; Ishikawa K; Hironaka K; Tanaka T “Acid catalysis in thermal and photoinduced electron-transfer reactions.” J. Chem. Soc., Perkin Trans. 1987, 2, 751 [Google Scholar]
- (24).Fukuzumi S; Chiba M; Tanaka T “Acid-Catalyzed Reduction of Ketones by an NADH Model Compound and the Relation with Acid-Catalyzed Photoinduced Electron-Transfer Reactions.” Chem. Lett. 1989, 18,31 [Google Scholar]
- (25).The pKa of 13 (MeCN) reported for (PhO2)P(O)OH is an estimated value based on a the pKa of BINOL-P(O)OH. Rueping M; Nachtsheim BJ; Ieawsuwan; Atodiresei I “Modulating the acidity: highly acidic Brønsted acids in asymmetric catalysis.” Agnew. Chem. Int. Ed. 2011, 50, 6706. [DOI] [PubMed] [Google Scholar]
- (26).Kütt A; Leito I; Kaljurand I; Sooväli L; Vlasov VM; Ya-gupolskii LM; Koppel IA “A comprehensive self-consistent spectrophotometric acidity scale of neutral Brønsted acids in acetonitrile.” J. Org. Chem. 2006, 71,2829. [DOI] [PubMed] [Google Scholar]
- (27).Kaljurand I; Lilleorg R; Murumaa A; Mishima M; Burk P; Koppel I; Koppel IA; Leito I “The basicity of substituted N, N-dimethylanilines in solution and in the gas phase.” J. Phys. Org. Chem. 2013, 26, 171 [Google Scholar]
- (28).Kaljurand I; Kütt A; Sooväli L; Rodima T; Mäemets V; Leito I; Koppel IA “Extension of the self-consistent spectrophotometric basicity scale in acetonitrile to a full span of 28 pKa units: unification of different basicity scales.” J. Org. Chem. 2005, 70, 1019. [DOI] [PubMed] [Google Scholar]
- (29).Marcus RA “Marcus RA, J. Chem. Phys. 24, 966 (1956).” J. Chem. Phys. 1956, 24, 966 [Google Scholar]
- (30).Marcus RA “On the theory of oxidation-reduction reactions involving electron transfer. I.” J. Chem. Phys. 1956, 24,979 [Google Scholar]
- (31).Marcus RA; Sutin N “Electron transfers in chemistry and biology.” Biochim. Biophys. Acta, Rev. Bioenerg. 1985, 811,265 [Google Scholar]
- (32).Breslow R; Chu W “Thermodynamic Determination of pKa’s of Weak Hydrocarbon Acids Using Electrochemical Reduction Data.” J. Am. Chem. Soc. 1973, 95, 411 [Google Scholar]
- (33).Bordwell FG; Cheng JP; Harrelson JA “Homolytic bond dissociation energies in solution from equilibrium acidity and electrochemical data.” J. Am. Chem. Soc. 1988, 110,1229 [Google Scholar]
- (34).Gaussian 09, M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski, D. J. Fox, Gaussian, Inc., Wallingford CT, 2009
- (35).Yayla HG; Knowles RR “Proton-Coupled Electron Transfer in Organic Synthesis: Novel Homolytic Bond Activations and Catalytic Asymmetric Reactions with Free Radicals.” Synlett 2014, 25, 2819 [Google Scholar]
- (36).Nguyen LQ; Knowles RR “Catalytic C-N Bond Forming Reactions Enabled by Proton-Coupled Electron Transfer Activation of Amide N-H Bonds.” ACS Catal. 2016, 6, 2894 [Google Scholar]
- (37).Nakajima M; Fava E; Loescher S; Jiang Z; Rueping M “Photoredox-Catalyzed Reductive Coupling of Aldehydes, Ketones, and Imines with Visible Light.” Angew. Chem., Int. Ed. 2015, 54,8828. [DOI] [PubMed] [Google Scholar]
- (38).Choi GJ; Knowles RR “Catalytic Alkene Carboaminations Enabled by Oxidative Proton-Coupled Electron Transfer.” J. Am. Chem. Soc. 2015, 137,9226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (39).Fava E; Millet A; Nakajima M; Loescher S; Rueping M “Reductive Umpolung of Carbonyl Derivatives with Visible-Light Photoredox Catalysis: Direct Access to Vicinal Diamines and Amino Alcohols via α-Amino Radicals and Ketyl Radicals.” Angew. Chem., Int. Ed. 2016, 55, 6776. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (40).Lee KN; Ngai MY “Recent developments in transitionmetal photoredox-catalysed reactions of carbonyl derivatives.” Chem. Commun. 2017, 53,13093. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (41).Lee KN; Lei Z; Ngai M-Y “β-Selective Reductive Coupling of Alkenylpyridines with Aldehydes and Imines via Synergistic Lewis Acid/Photoredox Catalysis.” J. Am. Chem. Soc. 2017, 139,5003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (42).Dixon IM; Collin J; Sauvage J; Flamigni L; Encinas S; Barigelletti F “A family of luminescent coordination compounds: iridium (III) polyimine complexes.” Chem. Soc. Rev. 2000, 29, 385 [Google Scholar]
- (43).Kolthoff IM; Chantooni MK “Protonation constants of very weak uncharged bases in acetonitrile.” J. Am. Chem. Soc. 1973, 95, 8539 [Google Scholar]
- (44).Schrauben JN; Cattaneo M; Day TC; Tenderholt AL; Mayer JM “Multiple-site concerted proton–electron transfer reactions of hydrogen-bonded phenols are nonadiabatic and well described by semiclassical marcus theory.” J. Am. Chem. Soc. 2012, 134,16635. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (45).Mader EA; Mayer JM “The Importance of Precursor and Successor Complex Formation in a Bimolecular Proton– Electron Transfer Reaction.” Inorg. Chem. 2010, 49, 3685. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (46).Dempsey JL; Winkler JR; Gray HB “Proton-coupled electron flow in protein redox machines.” Chem. Rev. 2010, 110,7024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (47).Huynh MHV; Meyer TJ “Proton-coupled electron transfer.” Chem. Rev. 2007, 107,5004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (48).Rhile IJ; Mayer JM “One-electron oxidation of a hydrogen-bonded phenol occurs by concerted proton-coupled electron transfer.” J. Am. Chem. Soc. 2004, 126,12718. [DOI] [PubMed] [Google Scholar]
- (49).Markle TF, Rhile IJ, DiPasquale AG, and Mayer JM “Probing concerted proton–electron transfer in phenol–imidazoles.” Proc. Natl. Acad. Sci. U.S.A. 2008, 105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (50).Markle TF; Tronic TA; DiPasquale AG; Kaminsky W; Mayer JM “Effect of Basic Site Substituents on Concerted Proton–Electron Transfer in Hydrogen-Bonded Pyridyl–Phenols.” J. Phys. Chem. A. 2012, 116, 12249. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (51).However, Mayer reported an example with the C-H bond cleavage via MS-PCET displays a similarly small Brønsted slope α~ 0.20. Markle TF ; Darcy JW; Mayer JM “A new strategy to efficiently cleave and form C–H bonds using proton-coupled electron transfer.” Sci. Adv. 2018: 4: eaat5776 [DOI] [PMC free article] [PubMed] [Google Scholar]
- (52).Bernasconi CF “The principle of imperfect synchronization: I. Ionization of carbon acids.” Tetrahedron. 1985, 41,3219 [Google Scholar]
- (53).Bernasconi CF “Intrinsic barriers of reactions and the principle of nonperfect synchronization.” Acc. Chem. Res. 1987, 20,301 [Google Scholar]
- (54).Bernasconi CF “The principle of nonperfect synchronization: More than a qualitative concept?” Acc. Chem. Res. 1992, 25,9 [Google Scholar]
- (55).Bernasconi CF “The principle of non-perfect synchronization.” Adv. Phys. Org. Chem. 1992, 27,119 [Google Scholar]
- (56).Bernasconi CF “The principle of nonperfect synchronization: recent developments.” Adv. Phys. Org. Chem. 2010, 44, 223 [Google Scholar]
- (57).Richard JP; Amyes TL; Toteva MM “Formation and stability of carbocations and carbanions in water and intrinsic barriers to their reactions.” Acc. Chem. Res. 2001, 34,981. [DOI] [PubMed] [Google Scholar]
- (58).Zhong ZL; Snowden TS; Best MD; Anslyn EV “Rate of enolate formation is not very sensitive to the hydrogen bonding ability of donors to carboxyl oxygen lone pair acceptors; a ramification of the principle of non-perfect synchronization for general-base-catalyzed enolate formation.” J. Am. Chem. Soc. 2004, 126,3488. [DOI] [PubMed] [Google Scholar]
- (59).Liu F; Yang Z; Yu Y; Mei Y; Houk KN “Bimodal Evans–Polanyi Relationships in Dioxirane Oxidations of sp3 C–H: Non-perfect Synchronization in Generation of Delocalized Radical Intermediates.” J. Am. Chem. Soc. 2017, 139,16650. [DOI] [PubMed] [Google Scholar]
- (60).Fletcher SJ “The theory of electron transfer.” Solid State Electrochem,2010, 14,705 [Google Scholar]
- (61).Koeppl GW; Kresge AJ “Marcus rate theory and the relationship between Brønsted exponents and energy of reaction.” J. Chem. Soc, Chem. Commun,1973, 371 [Google Scholar]
- (62).Laborda E; Henstridge MC; Compton RG “Asymmetric Marcus theory: Application to electrode kinetics.” J. Electroanal. Chem,2012, 667, 48 [Google Scholar]
- (63).Laborda E; Henstridge MC; Compton RG “Giving physical insight into the Butler–Volmer model of electrode kinetics: Part 2– Nonlinear solvation effects on the voltammetry of heterogeneous electron transfer processes.” J. Electroanal. Chem,2012, 681,96 [Google Scholar]
- (64).Hammes-Schiffer S; Stuchebrukhov AA “Theory of coupled electron and proton transfer reactions.” Chem. Rev. 2010, 110,6939. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (65).Hatcher E; Soudackov A; Hammes-Schiffer S “Nonadiabatic Proton-Coupled Electron Transfer Reactions: Impact of Donor– Acceptor Vibrations, Reorganization Energies, and Couplings on Dynamics and Rates.” J. Phys. Chem. B 2005, 109,18565. [DOI] [PubMed] [Google Scholar]
- (66).Hammes-Schiffer S; Sayfutyarova ER; Goldsmith ZK “Theoretical Study of C–H Bond Cleavage via Concerted Proton-Coupled Electron Transfer in Fluorenyl-Benzoates.” J. Am. Chem. Soc. 2018,140,15641. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (67).Warren JJ; Menzeleev AR; Kretchmer JS; Miller TF III; Gray HB; Mayer JM Long-Range Proton-Coupled Electron-Transfer Reactions of Bis(imidazole) Iron Tetraphenylporphyrins Linked to Benzoates. J. Phys. Chem. Lett. 2013, 4, 519. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (68).Warren JJ; Mayer JM Proton-Coupled Electron Transfer Reactions at a Heme-Propionate in an Iron-Protoporphyrin-IX Model Compound. J. Am. Chem. Soc. 2011, 133,8544. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (69).Megiatto JD Jr.; Méndez-Hernandez DD; Tejeda-Ferrari ME; Teillout A-L; Llansola-Portolés MJ; Kodis G; Poluektov OG; Rajh T; Mujica V; Groy TL; Gust D; Moore TA; Moore AL A bioinspired redox relay that mimics radical interactions of the Tyr-His pairs of photosystem II. Nat. Chem. 2014, 6, 423. [DOI] [PubMed] [Google Scholar]
- (70).Hammes-Schiffer S; Soudackov AV Proton-Coupled Electron Transfer in Solution, Proteins, and Electrochemistry. J. Phys. Chem. B 2008, 112, 14108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (71).Edwards SJ; Soudackov AV; Hammes-Schiffer S Analysis of Kinetic Isotope Effects for Proton-Coupled Electron Transfer Reactions. J. Phys. Chem. A 2009, 113,2117. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


