Skip to main content
PMC home page
NIST Author Manuscripts logoLink to NIST Author Manuscripts
. Author manuscript; available in PMC: 2019 May 9.
Published in final edited form as: Adv Funct Mater. 2018;28:10.1002/adfm.201706448. doi: 10.1002/adfm.201706448

Spatially Resolved Electric-Field Manipulation of Magnetism for CoFeB Mesoscopic Discs on Ferroelectrics

You Ba 1,2, Yan Liu 3,4,5, Peisen Li 6,7,8, Liang Wu 9, John Unguris 10, Daniel T Pierce 11, Danni Yang 12, Ce Feng 13,14, Yike Zhang 15,16, Hao Wu 17, Dalai Li 18, Yuansi Chang 19, Jinxing Zhang 20, Xiufeng Han 21, Jianwang Cai 22, Ce-Wen Nan 23, Yonggang Zhao 24,25,*
PMCID: PMC6508615  NIHMSID: NIHMS971716  PMID: 31080382

Abstract

Electric-field control of magnetism in ferromagnetic/ferroelectric multiferroic heterostructures is a promising way to realize fast and nonvolatile random-access memory with high density and low-power consumption. An important issue that has not been solved is the magnetic responses to different types of ferroelectric-domain switching. Here, for the first time three types of magnetic responses are reported induced by different types of ferroelectric domain switching with in situ electric fields in the CoFeB mesoscopic discs grown on PMN-PT(001), including type I and type II attributed to 109°, 71°/180° ferroelectric domain switching, respectively, and type III attributed to a combined behavior of multiferroelectric domain switching. Rotation of the magnetic easy axis by 90° induced by 109° ferroelectric domain switching is also found. In addition, the unique variations of effective magnetic anisotropy field with electric field are explained by the different ferroelectric domain switching paths. The spatially resolved study of electric-field control of magnetism on the mesoscale not only enhances the understanding of the distinct magnetic responses to different ferroelectric domain switching and sheds light on the path of ferroelectric domain switching, but is also important for the realization of low-power consumption and high-speed magnetic random-access memory utilizing these materials.

1. Introduction

The rapid development of information storage requires new concepts for fast and nonvolatile random-access memory with high density and low-power consumption, which is a significant and challenging task. One promising way to realize this goal is the electric-field control of magnetism in multiferroic heterostructures composed of ferromagnetic (FM) and ferroelectric (FE) materials.[1–3] Several approaches to realize electric-field control of magnetism via magnetoelectric (ME) coupling have been demonstrated,[4–6] such as manipulations via exchange bias,[7] interface charge carrier,[8] strain,[9] and cooperation of strain and exchange bias effect.[10,11] Among them, the strain-mediated FM/FE multiferroic heterostructures have been widely studied due to the various choices of room temperature ferromagnetic and ferroelectric materials with large magnetoelectric coupling,[5] which makes them promising for applications. There have been many reports of electric-field control of magnetism in the strain-mediated ferromagnetic/ferroelectric multiferroic heterostructures.[6,9–15] Relaxor ferroelectric (1−x)Pb(Mg1/3Nb2/3)O3–xPbTiO3 (PMN–PT) single crystals near the morphotropic phase boundary[16] are especially promising, because of the large piezoelectric response,[17] and have been widely used in the strain-mediated ferromagnetic/ferroelectric multiferroic heterostructures. However, most of the previous reports on electric-field control of magnetism in ferromagnetic/PMN-PT through strain-mediated interaction are volatile with a butterfly-like behavior,[18–20] which is useless for information storage. Recently, we reported a large and nonvolatile loop-like bipolar-electric-field-controlled magnetization at room temperature in Co40Fe40B20(CoFeB)/PMN-PT(001) and it was demonstrated by piezoresponse force microscopy (PFM) and X-ray diffraction reciprocal space mapping that the unusual nonvolatile behavior is related to the 109° ferroelectric domain switching in PMN-PT.[9] This deterministic nonvolatile loop-like bipolar-electric-field-controlled magnetization is in contrast to that observed in the strain-mediated ferromagnetic/PMN-PT(011) heterostructures, in which the nonvolatile electric-field control of magnetism was realized with electric fields in a very specific narrow range,[21] or not fully relaxed local strain[22] and the effects are not deterministic.

For PMN-PT(001) with the rhombohedral (R) phase, there are three types of ferroelectric domain switching under bipolar electric fields along the [001] direction, namely 109°, 71°, and 180° domain switching,[9,23,24] which should result in different behaviors of electric-field control of magnetism in the strain-mediated ferromagnetic/PMN-PT(001) heterostructures. It was proposed that 109° ferroelectric domain switching leads to a 90° rotation of the magnetic easy axis (MEA) due to the 90° rotation of the in-plane strain, while the 71° and 180° ferroelectric domain switching do not result in change of the magnetic easy axis since they do not induce any change of in-plane strain.[24] Therefore, the electric-field control of magnetism is site dependent, since different regions of the ferromagnetic film will show different behaviors depending on the ferroelectric domain switching underneath. To explore the distinct behaviors of electric-field control of magnetism corresponding to the different types of ferroelectric domain switching in the strain-mediated ferromagnetic/PMN-PT(001) heterostructures, techniques with spatial resolution are needed. So far, there is only one report on CoFeB/PMN-PT(001) characterized with scanning Kerr microscopy and scanning electron microscopy with polarization analysis (SEMPA). However, the rotating magneto-optic Kerr effect (ROT-MOKE) investigation did not show evidence of 90° rotation of the magnetic easy axis corresponding to the 109° ferroelectric domain switching. This anomaly was attributed to the use of continuous ferromagnetic films, in which intralayer magnetic interactions hinder the complete response of magnetic domain to the strain induced by 109° ferroelectric domain switching.[25] So, the interactions of different magnetic domains in the continuous ferromagnetic films[25,26] make it difficult to observe the distinct behaviors of electric-field control of magnetism corresponding to the different types of ferroelectric domain switching in the strain-mediated CoFeB/PMN-PT(001) heterostructures. To solve this problem, one needs to pattern the ferromagnetic film into small, noninteracting structures whose size is about the same as the ferroelectric domains. Such mesoscopic structures are essential for observing the distinct behaviors of electric-field control of magnetism corresponding to the different types of ferroelectric domain switching and are also important for applications, such as the realization of low-power consumption and high-speed magnetic random-access memory.[27,28]

In this work, we study the distinct behaviors of electric-field control of magnetism corresponding to the different types of ferroelectric domain switching in CoFeB mesoscopic discs on PMN-PT(001), by using magneto-optic Kerr effect and scanning electron microscopy with polarization analysis with in situ electric fields. Three different behaviors of electric-field control of magnetism were observed; especially a 90° rotation of the magnetic easy axis corresponding to the 109° ferroelectric domain switching. Scanning electron microscopy with polarization analysis, with very high spatial resolution, directly showed the direction of the magnetization in the discs and revealed three types of responses of magnetic moments to electric field. Moreover, for the three different behaviors, the effective magnetic anisotropy fields of CoFeB discs deduced from the rotating magneto-optic Kerr effect data exhibit quite different responses to electric field, especially around the coercive field (Ec) of PMN-PT. These three different behaviors of the effective magnetic anisotropy fields with electric field, which can be understood in terms of the different types of ferroelectric domain switching, also shed light on the path of ferroelectric domain switching. Our work not only reveals the distinct behaviors of electric-field control of magnetism corresponding to the different types of ferroelectric domain switching, but also provides a new way to study electric-field control of magnetism in ferromagnetic/ferroelectric multiferroic heterostructures. It should be significant for understanding the mechanism of electric-field control of magnetism in ferromagnetic/ferroelectric multiferroic heterostructures as well as for applications.

2. Results and Discussion

Samples were prepared by first using magnetron sputtering to grow amorphous ferromagnetic CoFeB films on (001)-oriented PMN-PT single crystals whose edges were along the [100] and [010] directions. An array of isolated CoFeB discs with 10 μm diameters and 300 μm separations was then made using photo lithography combined with Ar ion etching. The sample configuration is schematically shown in Figure S1 (Supporting Information). The size of CoFeB discs was chosen to approximately match the FE domain size of the PMN-PT.

We used PFM with the cantilever along the [110] direction to investigate the FE domain size and domain structures of PMN-PT polarized by electric fields. First, we measured the ferroelectric domain structure of the as-grown state of a PMN-PT substrate as shown in Figure 1a–c. Every row from left to right shows topography, out-of-plane PFM image (OP-PFM) and in-plane PFM image (IP-PFM). The size of the FE domains in the as-grown state, as seen in the IP-PFM image (Figure 1c), ranges from about 1 to 5 μm. There are three types of domain switching (109°/71°/180° switching) for the PFM-tip polarized case as shown in Figure S2 (Supporting Information), which is consistent with the report of Zhang et al.[9] The size of the domains in the polarized FE depends upon the way the electric fields were applied. However, for electric-field control of magnetism in CoFeB/PMN-PT, the PMN-PT was polarized by applying electric fields between the bottom and top thin-film electrodes. In this case, the FE domain size is unknown and it should be different from that when the FE is polarized by a PFM tip. This difference is an unsolved issue for electric-field control of magnetism in FM/PMN-PT. There have been limited reports on the difference for FE domains in the BiFeO3 films polarized by the tip method and top-electrode method,[29,30] where it was shown that the FE domains for the former method had a much smaller size compared to that of the latter. This difference was attributed to the localized switching of the electric polarization by the PFM tip, which nucleated high-energy walls surrounding the domains, and left the switched domains subject to relaxation.[29] The domains switched by the top-electrode method were more stable.[29,30]

Figure 1.

Figure 1

Open in a new tab

PFM images of the as-grown (top), remanent states of the positively (middle), and negatively (bottom) polarized cases, respectively. The electric field was applied using the flexible conductive membrane method. Every row (from left to right) shows a,d,g) topography, b,e,h) OP-PFM images, and c,f,i) IP-PFM images.

To our knowledge, there has been no report on the FE domain structure using PFM after the PMN-PT is polarized by a top electrode since a conductive metal film will prevent retrieval of the PFM contrast. To solve this problem, we use a new method to polarize the PMN-PT single crystal by using a removable conductive membrane as the top electrode to contact closely with PMN-PT without using adhesive, and Au sputtered on the bottom of PMN-PT as the bottom electrode. Detailed information about the new polarization method is presented in Section S3 in the Supporting Information. The PFM results of PMN-PT are shown in Figure 1 where the second and third rows show the remanent states of the positively and negatively polarized cases, respectively. The OP-PFM shows uniform color meaning that the sample was fully polarized and remained in the switched state even when the electric field was reduced to zero (Figure 1e,h). Comparing the IP-PFM of the polarized state (Figure 1f,i) with those of the as-grown state (Figure 1c), it can be seen that the color of the IP-PFM became more uniform after the crystal was polarized, indicating that the FE domains became larger (about 10 μm). As shown by the P–E loops (Figure S3, Supporting Information), the PMN-PT substrate was nearly fully polarized with our new method, while for the case of sputtered Pt as the top electrode as used in the measurement of electric-field control of magnetism, the PMN-PT substrate was fully polarized. Hence, the size of FE domains underneath the FM discs is expected to be larger. Based on these FE domain measurements, a CoFeB disc diameter of 10 μm was chosen. The size is suitable for studying the distinct magnetic responses to different FE domain switching as well as the interesting case that the discs locate on the boundaries between different FE domains. The disc size is also large enough for MOKE measurements.

The magnetic responses of different discs to in situ electric fields were measured using MOKE. We used longitudinal MOKE (L-MOKE) to measure Mr/Ms (remanent magnetization/saturation magnetization) and the coercive field (Hc), and ROT-MOKE[31] of different discs to get the angle ϕ of MEA (ϕ is the angle between the MEA and the [100] direction of PMN-PT) and the effective magnetic anisotropy fields, HK (detailed information can be found in Section S4 in the Supporting Information). These discs exhibited three types of different and unique magnetic responses to electric field as shown in Figure 2 and denoted as type I, type II, and type III, respectively.

Figure 2.

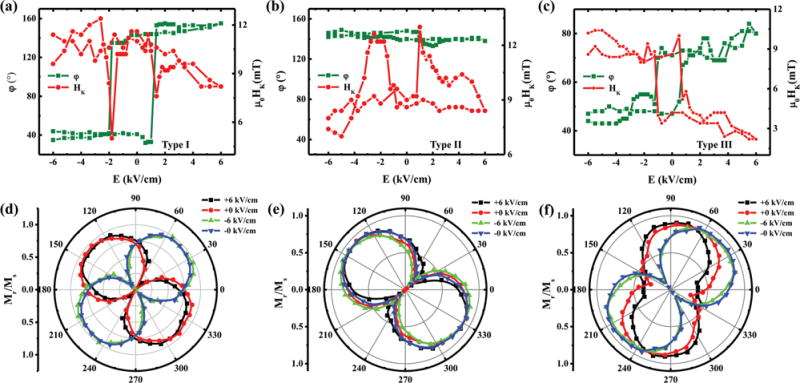
Figure 2

Open in a new tab

The ROT-MOKE results for a) type I, b) type II, and c) type III, respectively. The olive and red curves indicate the variations of the angle of MEA, ϕ and HK with the change of in situ electric field, respectively. The single standard deviation uncertainties, based on repeated measurements, for ϕ and μ0HK measurements were less than 5° and 0.6 mT, respectively. (Error bars not shown for clarity.) The corresponding Mr/Ms curves with different in situ electric fields (+6, +0, −6, −0 kV cm−1) obtained from L-MOKE for d) type I, e) type II, and f) type III, respectively. The angle θ is defined as the angle between the applied magnetic field and the [100] direction of PMN-PT.

  1. For type I, as shown in the ROT-MOKE result of Figure 2a, the MEA is close to the [−110] direction of PMN-PT (ϕ = 140°) under the positive electric fields larger than the switching electric field Es (1.5 kV cm−1) and rotates toward the [110] direction (ϕ = 40°) under the negative electric fields smaller than −Es, resulting in a 80° rotation of the MEA (we take the angle smaller than 90°). The angular dependences of Mr/Ms for the same disc measured by L-MOKE for different electric fields are shown in Figure 2d. After applying a positive electric field, the Mr/Ms data show an obvious MEA with the largest Mr/Ms value along the [−110] direction (130°) of PMN-PT and the smallest Mr/Ms value along the [110] (40°) direction of PMN-PT. Moreover, the MEA rotates by 90° from 130° to 40° after applying a negative electric field. This 90° rotation of the MEA is comparable to that of the ROT-MOKE result (Figure 2a) and is clearly nonvolatile. The minor difference of the rotation angles of MEA deduced from Figure 2a,d (ROT-MOKE and L-MOKE) is acceptable within the limit of experimental error. In addition, HK shows the following distinct behavior. The value of μ0HK (μ0 is the vacuum permeability) is about 8.2 mT at E = +6 kV cm−1 and increases slowly to 10 mT with decreasing electric field, and decreases dramatically to 5 mT at −Es, then returns to 11 mT after being fully polarized by negative electric fields. The same trend was also observed with the electric field changing from −6 to +6 kV cm−1. Moreover, the change of μ0HK is about 3 mT at +Es and 5 mT at −Es. Thus, type I displays a nonvolatile and nearly 90° switching with applied bipolar electric fields.

  2. For type II, a typical result is shown in Figure 2b. The MEA is along the [−110] direction of PMN-PT with ϕ around 140° and does not change with electric field. Similar behavior also occurs for the Mr/Ms as shown in Figure 2e with the MEA around the [−110] direction (about 135°). However HK does show some changes with electric field. The value of μ0HK changes slowly around 8.5 mT when the value of electric field is larger than E (2 kV cm−1) for both the positive and negative electric fields, but it increases abruptly from 8.5 to 12.5 mT around ±Es. The change of 4.0 mT is comparable to that of type I, which shows an abrupt decrease of HK around ±Es in contrast to the increase of HK around ±Es here.

  3. For type III, as shown in Figure 2c,f, both the MEA and HK show loop-like responses to electric field, which is very different from that of type I and type II. Specifically, the MEA rotates from 80° to 45° as the electric field changes from +6 to −6 kV cm−1, and the rotation is nonvolatile with an amplitude of 25° at E = 0 kV cm−1. The μ0HK is 2 mT at +6 kV cm−1 and increases to 9 mT at −6 kV cm−1, with a nonvolatile change of 4.5 mT at 0 kV cm−1, which is comparable to that of type I and type II.

We also measured the angular dependences of the coercive magnetic field for different applied electric fields; the results are shown in Figure S5 (Supporting Information). For discs showing the type I and type II behaviors, the Hc decreases when the direction of magnetic field is away from the MEA and reaches the smallest value for the hard axis. For discs showing the type III behavior, the Hc shows irregular behavior under electric fields. The angular dependence of Hc is closely related to the magnetization reversal mechanism,[32–34] which is further determined by the FM domain structure of the discs. Thus, the different angular dependence behaviors of Hc can be attributed to the different FM domain states within the discs, which will be seen in the SEMPA images below.

Although MOKE can resolve the average FM state of a disc, its resolution is not sufficient to reveal the distribution and change of magnetic moment vector with electric field within a disc. SEMPA has a higher spatial resolution ≈10 nm[35,36] and can directly image the direction of the in-plane magnetization,[37] especially while applying in situ electric fields.[25] We used SEMPA to image the mesoscale variations of the in-plane magnetic moment vector with in situ electric field on the three types of discs mentioned above. The results are shown in Figure 3. The three rows correspond to the three types of discs. The first two columns show the remanent states for the positively polarized case and for the negatively polarized case, respectively. The third column shows the angular distribution of magnetization directions derived from the SEMPA images. More SEMPA images are presented in Figure S6 in the Supporting Information.

Figure 3.

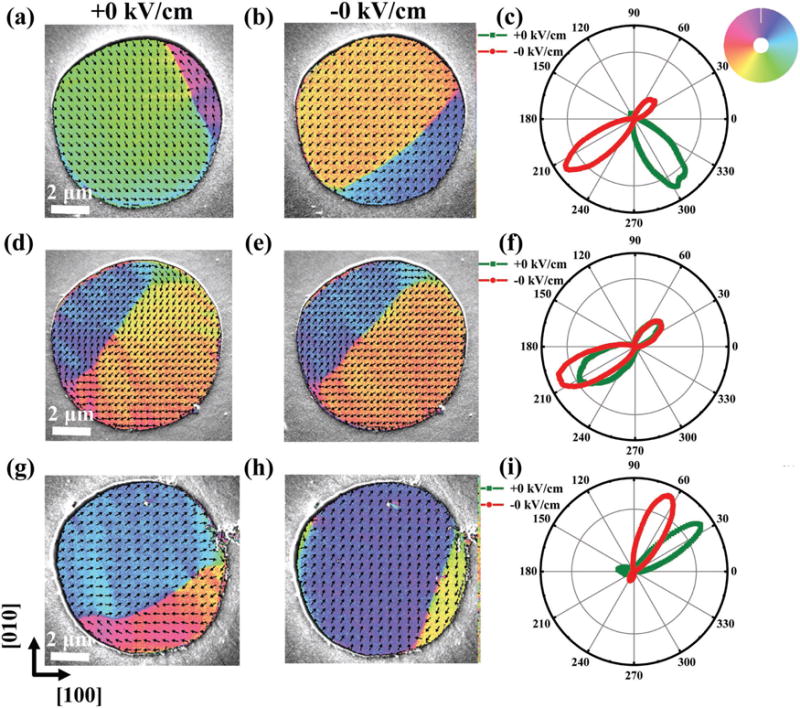
Figure 3

Open in a new tab

SEMPA images of type I (top), type II (middle), and type III (bottom), respectively. a,d,g) The SEMPA images for the remanent states of the positively polarized cases. b,e,h) The SEMPA images for the remanent states of the negatively polarized cases. The magnetization directions in SEMPA images are given by the color wheel. c,f,i) Polar plots showing the distribution of magnetization directions presented in SEMPA images with the olive/red curves indicating the remanent states of the positively/negatively polarized cases.

  1. For a type I disc shown in Figure 3a, it can be seen that after applying a positive electric field, the disc includes two FM domains (two colors) with one along the [1–10] direction of PMN-PT and the other along the [−110] direction of PMN-PT separated by a 180° Neel domain wall,[38] indicating that the MEA is along the [1–10]/[−110] direction. After applying a negative field, the FM domain structures change with the main part of domain along the [−1–10] direction and the other part along the [110] direction of PMN-PT as shown in Figure 3b, indicating that the MEA is now along the [−1–10]/[110] direction. Therefore most of the magnetization within the disc rotates by 90° due to the 90° rotation of the MEA direction, except for some regions near the domain wall and the disc edge. In particular, the magnetostatic energy favors magnetic directions aligned with the edge of the disc near the edge of the disc and hinders the rotation of the magnetic moments located there. The angular distribution of the magnetization as shown in Figure 3c clearly demonstrates an almost 90° rotation of the average magnetic moment vector. This rotation is nonvolatile (more details in Figure S6, Supporting Information), and is consistent with our MOKE observations.

  2. For a type II disc as shown in Figure 3d–f, SEMPA images after positive electric fields show two FM domains along the [110] and [−1–10] directions separated by a 180° Neel domain wall, indicating that the MEA of this disc is along the [110]/[−1–10] direction. In contrast to the type I, however, the disc magnetization shows little change after reversing the electric field, only the relative proportion of the two domains changes a little.

  3. For the type III disc as shown in Figure 3g–i, the MEA rotates by about 30° upon voltage reversal. In the remanent state of the negatively polarized case (Figure 3h), there are mainly two FM domains separated by an 180° Neel domain wall. After reversing the voltage two domains remain, but they are separated by a domain wall that rotates the magnetization less than a full 180° (Figure 3g).

To further study the process of magnetization rotation in the disc, we studied another disc with smaller electric-field intervals and found that the electric-field-induced changes in the magnetization are facilitated by both magnetic moment rotation and domain wall motion. These are shown in more detail in Figure S7 in the Supporting Information. In addition to SEMPA, we also imaged the disc magnetization using magnetic force microscopy (MFM) (Figure S8, Supporting Information). The MFM images show a domain wall similar to that seen in the SEMPA images and also display a clear change of domain wall after reversing electric fields.

Summarizing MOKE and SEMPA results, both measurements show three different magnetic responses to electric field, with the 90° rotation of MEA of particular interest. Furthermore, the magnetization changes always occur at electric fields of 1 to 2 kV cm−1 corresponding to the ferroelectric coercive field (Ec) of the PMN-PT, which indicates that the three unique magnetic behaviors are closely related to the FE domain switching. Thus, these three different magnetic responses can be understood by taking into account the different FE domain switching in PMN-PT. It has been shown that 109° switching leads to the loop-like strain with the direction of the in-plane strain rotating by 90°,[9] while 71°/180° switching results in the butterfly-like strain without a change in the direction of the in-plane strain.[24] These strains affect the magnetic anisotropies in the FM discs due to the inverse magnetostrictive effect. Therefore, in our work, the FE domain underneath the type I discs, which display a nonvolatile 90° MEA rotation, switched by 109° after reversing electric fields. The FE domain underneath the type II discs, which display little MEA change, switched by 71°/180° after electric fields reversals. And the FE structure underneath the type III discs, which display a nonvolatile MEA rotation with angles much smaller than 90°, is likely to consist of an FE multidomain state that exhibits different kinds of FE domain switching with electric fields. A multidomain state is possible since the size of FE domains is similar to that of the FM disc.

To further understand the coupling between FM and FE states, we analyze the mechanism of the change of the effective magnetic anisotropy field HK with electric fields. Because of the amorphous character of the CoFeB film, we assume that the magnetocrystalline anisotropy is negligible. Thus, the magnetic anisotropy of the CoFeB disc away from the disc edge is mainly due to the strain induced magnetoelastic anisotropy. According to the previous reports on strain-induced effective magnetic field,[39,40] the internal effective magnetic anisotropy field (HK) induced by the electric field can be expressed as, HK = 3λ·Y·(ε[110] − ε[−110])/μ0 MS, where HK is the internal effective magnetic anisotropy field induced by the piezostrain, λ is the magnetostriction coefficient, Y is the Young’s modulus, ε[110] and ε[−110] are the electric-field-induced strains along the [110] and [−110] directions, respectively, and MS is the saturation magnetization. Therefore, HK is directly proportional to the net strain induced by electric field. We measured the strain of a similar PMN-PT substrate along the [110] and [−110] directions using a strain gauge. The resultant S–E curves shown in Figure 4a are asymmetric butterfly-like curves, mainly due to the contributions of 71°/180° switching and 109° switching as illustrated in the report of Yang et al.[24] To further clarify the relationship between HK and strain, we need to do some simple processing of the strain curves. First, according to HK = 3 λ·Y·(ε[110] − ε[−110])/μ0 MS, we need to get the net strain by subtracting the strain along the [−110] direction from that along the [110] direction as shown in Figure 4b. The net strain is further separated into antisymmetric loop-like (109° FE domain switching) and symmetric butterfly-like (71°/180°FE domain switching) contributions as shown in Figure 4c (detailed information can be found in Section S9 in the Supporting Information).[24] It should be mentioned that the loop-like and butterfly-like S–E curves of the (001)-cut PMN-PT used in our work are qualitatively different from that of the (011)-cut PMN-PT,[41] as in the latter case the butterfly-like S–E curve results from the twice non-180° domain switching under bipolar electric fields and the loop-like S–E curve stems from the first non-180° domain switching and can only be realized under unipolar electric fields with the critical electric field in a very specific narrow range, which is a disadvantage for applications. To compare to the HK–E curves derived from the ROT-MOKE measurements where only positive values of HK were taken (Figure 2a–c), we only considered the absolute value of HK by taking the absolute value of strain as shown in Figure 4d, which was obtained from Figure 4c. Comparing Figure 4d with the experimental results of HK–E curves (Figure 2a–c), some correlations can be deduced as follows. (i) The magnitude of the strain induced by the loop-like 109° domain switching keeps a high value at electric fields larger than Ec and decreases abruptly at ±Ec (Figure 4d, olive curve), which is consistent with the type I HK–E curve (Figure 2a). (ii) The magnitude of the strain induced by the butterfly-like 71°/180° domain switching shows an abrupt increase around Ec with peaks at ±Ec (Figure 4d, red curve), which is similar to the type II HK–E curve (Figure 2b). (iii) For type III, we assume that the FE domain structure underneath the CoFeB disc is a multidomain state and contains three kinds of FE domain switching. Thus, the type III HK–E curve (Figure 2c) contains the contributions related to different FE domain switching, which is similar to the macroscopic average magnetic result.[42] Therefore, the strains induced by the different types of FE domain switching qualitatively explain the different types of HK–E curve.

Figure 4.

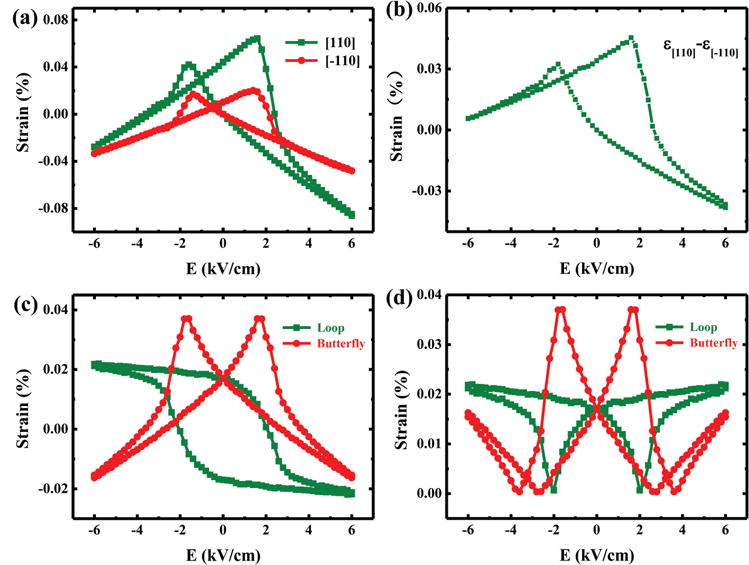
Figure 4

Open in a new tab

a) S–E curves along the [110] (olive) and [−110] (red) directions, respectively. The single standard deviation uncertainty, based on repeated measurements, of the strain measurements is 0.003% (smaller than the plotted point size). b) The net strain obtained by subtracting the strain along the [−110] direction from that along the [110] direction. c) The antisymmetric loop-like strain (olive) and symmetric butterfly-like strain (red) decomposed from (b). d) The absolute value of strain deduced from (c).

Our spatially resolved measurements of HK responses to different types of FE domain switching, which have not been reported in the literature before, also provide some useful new insights into the different FE polarization rotation paths involved in the switching. Different responses of HK to electric field are attributed to the strains induced by different FE switching. Moreover, the strain behaviors originate from the different FE domain rotation paths (or polarization rotation path) for different FE domain switching. There have been some reports on the polarization rotation path for an FE single crystal with the rhombohedral phase under electric fields, and it was claimed that the monoclinic phase (MA, MB, or MC) was induced and mediated the reversal of FE domain of the R phase during electric loading.[43–49] However, there are no consistent conclusions about the specific reversal rotation path because the polarization rotation path is determined by many factors such as FE single crystal orientation, composition, and the value of the electric field (more information can be found in Section S10 in the Supporting Information).[43–49] Therefore, the polarization switching path in PMN-PT used in our work is still unknown. We propose three FE domain switching paths as shown in Figure 5 based on the possible polarization rotation paths mentioned in Section S10 in the Supporting Information to explain the observed different HK responses to different FE domain switching (Figure 2a–c).

Figure 5.

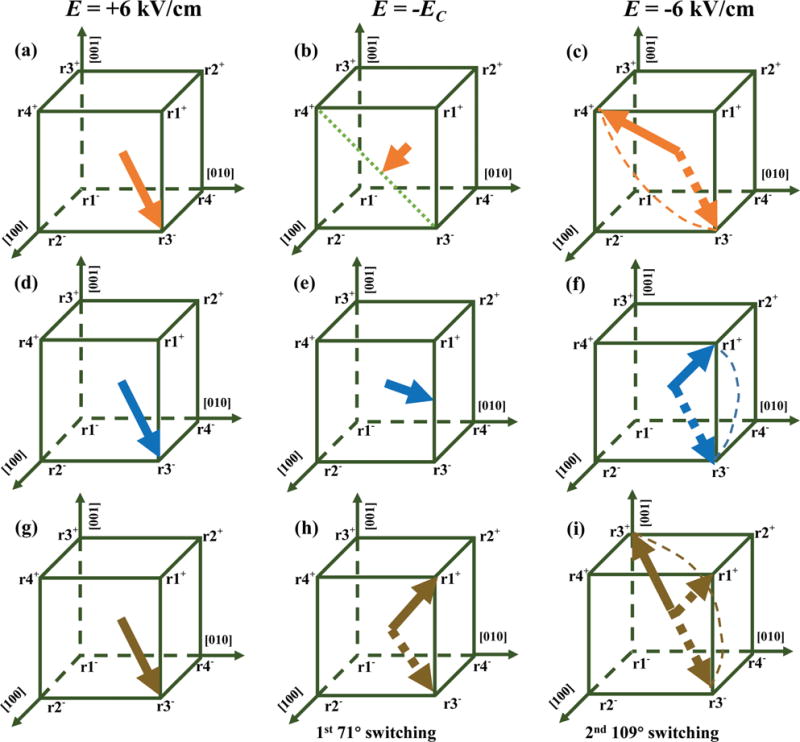
Figure 5

Open in a new tab

The proposed switching paths of three kinds FE domain switching: a–c) 109° switching, d–f) 71° switching, and g–i) 180° switching.

  1. Figure 5a–c shows the 109° switching path. When E = +6 kV cm−1, the polarization is r3−; as the electric field is reduced to −Ec, the polarization rotates along the diagonal from r3− to an intermediate state as shown in Figure 5b; when the electric field is changed to −6 kV cm−1, the polarization rotates to r4+, finishing the 109° switching. Before and after 109° switching, the in-plane strain rotates by 90°, but |ε[110] − ε[−110]| remains unchanged. In the intermediate state (Figure 5b), the projections of polarization along the two in-plane diagonals have the same magnitude so that the net strain |ε[110] − ε[−110]| and hence HK reach the smallest value.

  2. Figure 5d–f shows the 71° switching path. When E = +6 kV cm−1, the polarization is r3−; as the electric field is reduced to −Ec, the polarization rotates along the edge from r3− to an intermediate state as shown in Figure 5e; and when electric field is changed to −6 kV cm−1, the polarization rotates to r1+, finishing the 71° switching. According to the theoretical calculation, the polarization magnitude of the intermediate state (Figure 5e) is comparable to that of the original state (Figure 5d);[17] therefore, the in-plane projection of polarization of the intermediate state can be larger than that of the original state. Thus, the in-plane strain remains unchanged before and after 71° switching, while in the intermediate state, the in-plane projection of polarization increases leading to the increase of the |ε[110] − ε[−110]|

  3. The 180° switching path is more complicated. Studies have shown that the 180° switching is not a one-step but a two-step (71°/109° switching) process,[7,29] shown in Figure 5h,i. On account of this, we suggest that the HK response induced by 180° switching is likely to be different from that of 71° switching, which means we should observe another kind of behavior beyond type I and type II (type III is a combined behavior of multi-FE-domain switching). However, we did not observe a new behavior different from that of type I, type II, and type III after testing more than 30 discs. This may be due the following two reasons. (1) The number of discs we tested is not enough, but the PMN-PT tended to fatigue after repeated electric-field loadings and the CoFeB discs were often broken due to the large strain transferred from the PMN-PT. (2) The 180° switching is actually a rare event (compared with the 71° switching and 109° switching). A study showed that 71° switching is more stable than 180° switching[29] and that there is mainly 71°/109° switching under high electric fields.[50]

3. Conclusion

In summary, three different magnetic responses induced by different ferroelectric domain switching are revealed in the CoFeB mesoscopic discs with in situ electric fields, especially, the first observation of 90° rotation of the magnetic easy axis induced by 109° ferroelectric domain switching. Both MOKE and SEMPA demonstrate three types of magnetic responses to electric fields, with type I and type II attributed to 109°, 71°/180° ferroelectric domain switching, respectively, and type III attributed to a combined behavior of multiferroelectric domain switching. In addition, we explain the unique HK–E behaviors by the proposed different ferroelectric domain switching paths. This work is significant for understanding the distinct magnetic responses to different ferroelectric domain switching and shedding light on the path of ferroelectric domain switching. The spatially resolved study of electric-field control of magnetism on the mesoscale paves the way for further nanoscale research, which is important for the realization of low-power consumption and high-speed magnetic random-access memory utilizing these materials.

4. Experimental Section

Sample Preparation

Samples with Ta (5 nm)/CoFeB (20 nm)/Pt (35 nm)/PMN-PT (0.5 mm) structure were investigated. Pb(Mg1/3Nb2/3)0.7Ti0.3O3 (PMN-PT) substrates were (001)-cut and one-side-polished with a size of 5 mm × 5 mm × 0.5 mm. Co40Fe40B20 soft magnetic films with Pt (35 nm) underlayer and a Ta (5 nm) protective overlayer were deposited in an ultrahigh vacuum magnetron sputtering system with a base pressure of 1 × 10−6 Pa without a magnetic field. Au layers with a thickness of 300 nm were sputtered on the bottom of the structures as electrodes. The 10 μm discs were prepared by using lithography and lift-off techniques. The amorphous property of CoFeB and crystalline property of PMN-PT have been studied with X-ray diffraction and transmission electron microscopy in our previous report.[51]

Magnetic Measurement

Measurements of the spatial distribution of electric-field control of magnetism were performed by using L-MOKE and ROT-MOKE with a diode laser operated at a 660 nm wavelength with in situ electric fields.

SEMPA Measurement

The SEMPA measurement was carried out using a scanning electron microscope that was modified for secondary electron spin polarization analysis. Images were acquired using a 25 keV, 5 nA incident electron beam. The two orthogonal in-plane magnetizations were simultaneously measured and combined into an image of the in-plane magnetization.

PFM Measurement

PFM was carried out with the cantilever along the diagonal of PMN-PT FE substrate.

MFM Measurement

The MFM was carried out in atomic force microscopy using commercial piezoresistive cantilevers (spring constant k: 1 to 5 N m−1, resonant frequency f0: 60 to 100 kHz). MFM images were taken in a constant height mode with a scanning plane ≈50 nm above the sample surface.

Strain-Electric Field Measurement

The strain gauges were pasted on the sample surface with glue along the in-plane [110] and [−110] directions. The electric field was applied perpendicular to the sample surface.

Polarization Versus Electric Field Measurement

The P–E hysteresis loop for PMN-PT was measured by using a commercial precision ferroelectric tester.

Supplementary Material

UngurisAdvancedFunctionalMaterialsSupplement

Acknowledgments

This work was supported by the Science Center of National Science Foundation of China (Grant No. 51788104), the 973 project of the Ministry of Science and Technology of China (Grant No. 2015CB921402), National Science Foundation of China (Grant Nos. 51572150, 11704388, 11604384, 11434014, and 51332001), and State Key Laboratory of Low-Dimensional Quantum Physics (Grant Nos. ZZ201701 and KF201717).

Footnotes

Supporting Information

Supporting Information is available from the author.

Contributor Information

You Ba, Department of Physics and State Key Laboratory of Low-Dimensional Quantum Physics, Tsinghua University, Beijing 100084, China; Collaborative Innovation Center of Quantum Matter, Beijing 100084, China.

Dr. Yan Liu, Department of Physics and State Key Laboratory of Low-Dimensional Quantum Physics, Tsinghua University, Beijing 100084, China Collaborative Innovation Center of Quantum Matter, Beijing 100084, China; Key Laboratory of Space Utilization, Technology and Engineering Center for Space Utilization, Chinese Academy of Sciences, Beijing 100094, China.

Dr. Peisen Li, Department of Physics and State Key Laboratory of Low-Dimensional Quantum Physics, Tsinghua University, Beijing 100084, China Collaborative Innovation Center of Quantum Matter, Beijing 100084, China; College of Mechatronics and Automation, National University of Defense Technology, Changsha 410073, China.

Liang Wu, School of Materials Science and Engineering and State Key Lab of New Ceramics and Fine Processing, Tsinghua University, Beijing 100084, China.

Dr. John Unguris, Center for Nanoscale Science and Technology, National Institute of Standards and Technology, Gaithersburg, MD 20899, USA

Dr. Daniel T. Pierce, Center for Nanoscale Science and Technology, National Institute of Standards and Technology, Gaithersburg, MD 20899, USA

Danni Yang, Department of Physics, Beijing Normal University, Beijing 100875, China.

Ce Feng, Department of Physics and State Key Laboratory of Low-Dimensional Quantum Physics, Tsinghua University, Beijing 100084, China; Collaborative Innovation Center of Quantum Matter, Beijing 100084, China.

Yike Zhang, Department of Physics and State Key Laboratory of Low-Dimensional Quantum Physics, Tsinghua University, Beijing 100084, China; Collaborative Innovation Center of Quantum Matter, Beijing 100084, China.

Dr. Hao Wu, Beijing National Laboratory for Condensed Matter Physics, Institute of Physics, Chinese Academy of Sciences, Beijing 100190, China

Dr. Dalai Li, Beijing National Laboratory for Condensed Matter Physics, Institute of Physics, Chinese Academy of Sciences, Beijing 100190, China

Yuansi Chang, Beijing National Laboratory for Condensed Matter Physics, Institute of Physics, Chinese Academy of Sciences, Beijing 100190, China.

Prof. Jinxing Zhang, Department of Physics, Beijing Normal University, Beijing 100875, China

Prof. Xiufeng Han, Beijing National Laboratory for Condensed Matter Physics, Institute of Physics, Chinese Academy of Sciences, Beijing 100190, China

Prof. Jianwang Cai, Beijing National Laboratory for Condensed Matter Physics, Institute of Physics, Chinese Academy of Sciences, Beijing 100190, China

Prof. Ce-Wen Nan, School of Materials Science and Engineering and State Key Lab of New Ceramics and Fine Processing, Tsinghua University, Beijing 100084, China

Prof. Yonggang Zhao, Department of Physics and State Key Laboratory of Low-Dimensional Quantum Physics, Tsinghua University, Beijing 100084, China; Collaborative Innovation Center of Quantum Matter, Beijing 100084, China.

References

  • 1.Spaldin NA, Fiebig M. Science. 2005;309:391. doi: 10.1126/science.1113357. [DOI] [PubMed] [Google Scholar]
  • 2.Hu JM, Li Z, Chen LQ, Nan CW. Nat Commun. 2011;2:553. doi: 10.1038/ncomms1564. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 3.Li P, Chen A, Li D, Zhao Y, Zhang S, Yang L, Liu Y, Zhu M, Zhang H, Han X. Adv Mater. 2014;26:4320. doi: 10.1002/adma.201400617. [DOI] [PubMed] [Google Scholar]
  • 4.Hu JM, Chen LQ, Nan CW. Adv Mater. 2016;28:15. doi: 10.1002/adma.201502824. [DOI] [PubMed] [Google Scholar]
  • 5.Vaz CA. J Phys: Condens Matter. 2012;24:333201. doi: 10.1088/0953-8984/24/33/333201. [DOI] [PubMed] [Google Scholar]
  • 6.Chen AT, Zhao YG. APL Mater. 2016;4:032303. [Google Scholar]
  • 7.Heron JT, Bosse JL, He Q, Gao Y, Trassin M, Ye L, Clarkson JD, Wang C, Liu J, Salahuddin S, Ralph DC, Schlom DG, Iniguez J, Huey BD, Ramesh R. Nature. 2014;516:370. doi: 10.1038/nature14004. [DOI] [PubMed] [Google Scholar]
  • 8.Molegraaf HJA, Hoffman J, Vaz CAF, Gariglio S, van der Marel D, Ahn CH, Triscone JM. Adv Mater. 2009;21:3470. [Google Scholar]
  • 9.Zhang S, Zhao YG, Li PS, Yang JJ, Rizwan S, Zhang JX, Seidel J, Qu TL, Yang YJ, Luo ZL, He Q, Zou T, Chen QP, Wang JW, Yang LF, Sun Y, Wu YZ, Xiao X, Jin XF, Huang J, Gao C, Han XF, Ramesh R. Phys Rev Lett. 2012;108:137203. doi: 10.1103/PhysRevLett.108.137203. [DOI] [PubMed] [Google Scholar]
  • 10.Chen A, Zhao Y, Li P, Zhang X, Peng R, Huang H, Zou L, Zheng X, Zhang S, Miao P, Lu Y, Cai J, Nan CW. Adv Mater. 2016;28:363. doi: 10.1002/adma.201503176. [DOI] [PubMed] [Google Scholar]
  • 11.Gao Y, Hu JM, Nelson CT, Yang TN, Shen Y, Chen LQ, Ramesh R, Nan CW. Sci Rep. 2016;6:23696. doi: 10.1038/srep23696. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 12.Eerenstein W, Wiora M, Prieto JL, Scott JF, Mathur ND. Nat Mater. 2007;6:348. doi: 10.1038/nmat1886. [DOI] [PubMed] [Google Scholar]
  • 13.Ma J, Hu J, Li Z, Nan CW. Adv Mater. 2011;23:1062. doi: 10.1002/adma.201003636. [DOI] [PubMed] [Google Scholar]
  • 14.Liu M, Zhou Z, Nan T, Howe BM, Brown GJ, Sun NX. Adv Mater. 2013;25:1435. doi: 10.1002/adma.201203792. [DOI] [PubMed] [Google Scholar]
  • 15.Gopman DB, Dennis CL, Chen PJ, Iunin YL, Finkel P, Staruch M, Shull RD. Sci Rep. 2016;6:27774. doi: 10.1038/srep27774. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 16.Park SE, Shrout TR. J Appl Phys. 1997;82:1804. [Google Scholar]
  • 17.Fu H, Cohen RE. Nature. 2000;403:281. doi: 10.1038/35002022. [DOI] [PubMed] [Google Scholar]
  • 18.Thiele C, Dörr K, Bilani O, Rödel J, Schultz L. Phys Rev B. 2007;75:054408. [Google Scholar]
  • 19.Yang J, Zhao Y, Tian H, Luo L, Zhang H, He Y, Luo H. Appl Phys Lett. 2009;94:212504. [Google Scholar]
  • 20.Zhang S, Zhao Y, Xiao X, Wu Y, Rizwan S, Yang L, Li P, Wang J, Zhu M, Zhang H, Jin X, Han X. Sci Rep. 2014;4:3727. doi: 10.1038/srep03727. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 21.Bao M, Bur A, Kim HKD, Mohanchandra KP, Lynch CS, Carman GP. Appl Phys Lett. 2011;99:182903. [Google Scholar]
  • 22.Gao Y, Hu JM, Wu L, Nan CW. J Phys: Condens Matter. 2015;27:504005. doi: 10.1088/0953-8984/27/50/504005. [DOI] [PubMed] [Google Scholar]
  • 23.Zhao T, Scholl A, Zavaliche F, Lee K, Barry M, Doran A, Cruz MP, Chu YH, Ederer C, Spaldin NA, Das RR, Kim DM, Baek SH, Eom CB, Ramesh R. Nat Mater. 2006;5:823. doi: 10.1038/nmat1731. [DOI] [PubMed] [Google Scholar]
  • 24.Yang L, Zhao Y, Zhang S, Li P, Gao Y, Yang Y, Huang H, Miao P, Liu Y, Chen A, Nan CW, Gao C. Sci Rep. 2014;4:4591. doi: 10.1038/srep04591. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 25.Li P, Zhao Y, Zhang S, Chen A, Li D, Ma J, Liu Y, Pierce DT, Unguris J, Piao HG, Zhang H, Zhu M, Zhang X, Han X, Pan M, Nan CW. ACS Appl Mater Interfaces. 2017;9:2642. doi: 10.1021/acsami.6b13620. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 26.Trassin M, Clarkson JD, Bowden SR, Liu J, Heron JT, Paull RJ, Arenholz E, Pierce DT, Unguris J. Phys Rev B. 2013;87:134426. [Google Scholar]
  • 27.Sohn H, Nowakowski ME, Liang CY, Hockel JL, Wetzlar K, Keller S, McLellan BM, Marcus MA, Doran A, Young A. ACS Nano. 2015;9:4814. doi: 10.1021/nn5056332. [DOI] [PubMed] [Google Scholar]
  • 28.Klimov A, Tiercelin N, Dusch Y, Giordano S, Mathurin T, Pernod P, Preobrazhensky V, Churbanov A, Nikitov S. Appl Phys Lett. 2017;110:222401. [Google Scholar]
  • 29.Baek SH, Jang HW, Folkman CM, Li YL, Winchester B, Zhang JX, He Q, Chu YH, Nelson CT, Rzchowski MS, Pan XQ, Ramesh R, Chen LQ, Eom CB. Nat Mater. 2010;9:309. doi: 10.1038/nmat2703. [DOI] [PubMed] [Google Scholar]
  • 30.Cruz MP, Chu YH, Zhang JX, Yang PL, Zavaliche F, He Q, Shafer P, Chen LQ, Ramesh R. Phys Rev Lett. 2007;99:217601. doi: 10.1103/PhysRevLett.99.217601. [DOI] [PubMed] [Google Scholar]
  • 31.Mattheis R, Quednau G. J Magn Magn Mater. 1999;205:143. [Google Scholar]
  • 32.Stoner EC, Wohlfarth E. Philos Trans R Soc, A. 1948;240:599. [Google Scholar]
  • 33.Kondorsky E. J Phys. 1940;2:161. [Google Scholar]
  • 34.Wang J, Zhao Y, Fan C, Sun X, Rizwan S, Zhang S, Li P, Lin Z, Yang Y, Yan W. Appl Phys Lett. 2013;102:102906. [Google Scholar]
  • 35.Unguris J, Bowden SR, Pierce DT, Trassin M, Ramesh R, Cheong SW, Fackler S, Takeuchi I. APL Mater. 2014;2:076109. [Google Scholar]
  • 36.Scheinfein MR, Unguris J, Kelley MH, Pierce DT, Celotta RJ. Rev Sci Instrum. 1990;61:2501. [Google Scholar]
  • 37.Gilbert I, Chavez AC, Pierce DT, Unguris J, Sun WY, Liang CY, Carman GP. Appl Phys Lett. 2016;109:162404. doi: 10.1063/1.4965028. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 38.Cullity BD, Graham CD. Introduction to Magnetic Materials, John Wiley & Sons, New Jersey. 2011 [Google Scholar]
  • 39.Lou J, Liu M, Reed D, Ren Y, Sun NX. Adv Mater. 2009;21:4711. [Google Scholar]
  • 40.Liu M, Obi O, Cai Z, Lou J, Yang G, Ziemer KS, Sun NX. J Appl Phys. 2010;107:073916. [Google Scholar]
  • 41.Zhao P, Bao M, Bur A, Hockel JL, Wong K, Mohanchandra KP, Lynch CS, Carman GP. J Appl Phys. 2011;109:124101. [Google Scholar]
  • 42.Zhang S, Chen Q, Liu Y, Chen A, Yang L, Li P, Ming ZS, Yu Y, Sun W, Zhang X, Zhao Y, Sun Y, Zhao Y. ACS Appl Mater Interfaces. 2017;9:20637. doi: 10.1021/acsami.7b03051. [DOI] [PubMed] [Google Scholar]
  • 43.Cao H, Bai F, Wang N, Li J, Viehland D, Xu G, Shirane G. Phys Rev B. 2005;72:064104. [Google Scholar]
  • 44.Kiat JM, Uesu Y, Dkhil B, Matsuda M, Malibert C, Calvarin G. Phys Rev B. 2002;65:064106. [Google Scholar]
  • 45.Viehland D, Li JF. J Appl Phys. 2002;92:7690. [Google Scholar]
  • 46.Bai F, Wang N, Li J, Viehland D, Gehring PM, Xu G, Shirane G. J Appl Phys. 2004;96:1620. [Google Scholar]
  • 47.Chien RR, Schmidt VH, Tu CS, Hung LW, Luo H. Phys Rev B. 2004;69:172102. [Google Scholar]
  • 48.Liu H, Chen J, Fan L, Ren Y, Pan Z, Lalitha KV, Rodel J, Xing X. Phys Rev Lett. 2017;119:017601. doi: 10.1103/PhysRevLett.119.017601. [DOI] [PubMed] [Google Scholar]
  • 49.Fang F, Luo X, Yang W. Phys Rev B. 2009;79:174118. [Google Scholar]
  • 50.Zavaliche F, Shafer P, Ramesh R, Cruz MP, Das RR, Kim DM, Eom CB. Appl Phys Lett. 2005;87:252902. [Google Scholar]
  • 51.Zhang S. Electric-Field Control of Magnetization and Electronic Transport in Ferromagnetic/Ferroelectric Heterostructures, Springer, Berlin, Heidelberg. 2014 [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

UngurisAdvancedFunctionalMaterialsSupplement
NIHMS971716-supplement-UngurisAdvancedFunctionalMaterialsSupplement.pdf (13.1MB, pdf)

RESOURCES