Bethe-Salpeter equation calculations of core excitation spectra

Abstract

We present a hybrid approach for Bethe-Salpeter equation (BSE) calculations of core excitation spectra, including x-ray absorption (XAS), electron energy loss spectra (EELS), and nonresonant inelastic x-ray scattering (NRIXS). The method is based on ab initio wave functions from the plane-wave pseudopotential code ABINIT; atomic core-level states and projector augmented wave (PAW) transition matrix elements; the NIST core-level BSE solver; and a many-pole self-energy model to account for final-state broadening and self-energy shifts. Multiplet effects are also approximately accounted for. The approach is implemented using an interface dubbed OCEAN (Obtaining Core Excitations using ABINIT and NBSE). To demonstrate the utility of the code we present results for the K edges in LiF as probed by XAS and NRIXS, the K edges of KCl as probed by XAS, the Ti L_2,3 edge in SrTiO₃ as probed by XAS, and the Mg L_2,3 edge in MgO as probed by XAS. These results are compared with experiment and with other theoretical approaches.

I. INTRODUCTION

Recently there has been considerable progress in the theory of optical response beyond the independent-particle approximation.¹ For example, methods based on time-dependent density-functional theory (TDDFT) and the GW/Bethe-Salpeter equation (GW/BSE) approach have been extensively studied.^1–4 While computationally simpler than the BSE, TDDFT is currently limited by approximations to the exchange-correlation functional. On the other hand, the GW/BSE approach includes an explicit treatment of quasiparticle effects within Hedin’s GW self-energy approximation⁵ and particle-hole interactions, both of which are often crucial to a quantitative treatment. In the GW approximation the electron self-energy is related to the product of the one-electron Green’s function and the screened Coulomb interaction, which are respectively denoted by symbols G and W. A number of codes based on these approaches have been developed both for periodic^6–8 and aperiodic systems.^9,10

Calculations of core-level spectra, on the other hand, pose additional theoretical challenges. Core-hole effects, energy-dependent damping, self-energy shifts, and atomic multiplet effects all complicate the theory. Consequently relatively few GW/BSE treatments presently exist.^11–14 To address these challenges, we present here a hybrid GW/BSE approach for periodic systems encompassing x-ray absorption spectra (XAS) and related core-excitation spectra. Quasiparticle damping and self-energy shifts are included in terms of a many-pole self-energy and the quasiboson formalism. Our BSE Hamiltonian also accounts approximately for atomic-multiplet effects in the spectra by explicitly including intra-atomic Coulomb and spin-orbit interactions. Also, in contrast to atomic-multiplet models that rely on crystal-field parameters, our implementation includes self-consistent potentials for an extended system. While multi-electron excitations and correlation effects beyond the quasiparticle approximation can also be treated with the quasiboson formalism, such effects are presently neglected. Also, although our approach is designed for periodic systems, aperiodic systems can be modeled using supercells. However, the method is limited to a range of order 10² eV above a given core threshold due to the limited size of the plane-wave basis sets in practical calculations. Thus the method is complementary to the real-space Green’s function (RSGF) approach for core spectra,^13,15,16 which is applicable over a very broad spectrum of excitation energies up to about 10⁴ eV. Though formally equivalent to the GW/BSE of this work, the RSGF implementation uses finite clusters and spherical scattering potentials which can be inaccurate near threshold.

GW/BSE calculations of core-level spectra rely on a number of theoretical and many-body considerations. A key ingredient is the screened electron-core hole interaction. In the BSE, this interaction is typically treated via linear response, which in itself can be a demanding task. In contrast, many current calculations of core-excitation spectra are based on effective, independent-electron models with various ad hoc treatments of the screening effects.^17–19 For example, a number of implementations use a final-state Hamiltonian with a self-consistently screened core hole,^{7,14,17,19–21} as in the final-state rule. A second important ingredient is a complex, energy-dependent self-energy to account for final-state self-energy shifts and damping. As shown below, such quasiparticle effects are important for a quantitative account of peak positions, heights, and widths in the spectra. Although small near an absorption edge and often neglected, final-state damping becomes particularly important above about 10 eV where interband and plasmon excitations can be important. A third important ingredient is an account of intra-atomic interactions that lead to multiplet effects in the spectra. Finally, the approach should include accurate self-consistent potentials and a basis that encompasses the near edge structure over a range of about 10 eV to 100 eV.

In order to address the above considerations our core-level GW/BSE approach is based on several key elements: (1) Orbitals for occupied and unoccupied Kohn-Sham levels from a self-consistent plane-wave pseudopotential code; (2) atomic core-level states and projector augmented wave (PAW) transition matrix elements; (3) the NIST core-level Bethe-Salpeter equation solver (NBSE); (4) a many-pole GW self-energy model (MPSE) to approximate final-state broadening and self-energy shifts; and finally (5) atomic-multiplet effects are included through the inclusion of core-hole spin-orbit splitting and atomic multipole interactions. In the present implementation ABINIT²² is used for the Kohn-Sham wave functions; however, this is not a strict restriction and the code can be adapted to other plane-wave pseudopotential codes. For the multiplet calculations, the electron/core-hole wave function is expressed in terms of electron PAW/core-hole product states, with the Coulomb interaction matrix elements between these product states calculated using an atomic structure program. Both orbital-and spin-degrees of freedom are included.²³ However, our approach neglects multielectron excitations and interference between intrinsic and extrinsic losses, although such effects can be included, in principle, in terms of an effective spectral function and the quasiboson model. We also neglect the effects of dynamic disorder. Other sources of error in the approach arise from the pseudopotentials, the PAW derived transition matrix elements, and the adiabatic RPA core-hole screening approximation. Thus our approach is not applicable to strongly correlated systems. Moreover, vibrational damping is neglected. While often small in the near-edge regime, such damping is sometimes important, e.g., in the final-state dependent broadening in SrTiO₃,^24,25 and in cases where symmetry breaking effects of disorder are important.

Within the scope of the above approximations, our hybrid GW/BSE approach provides a first-principles method for calculations of near-edge spectra, including x-ray absorption spectra (XAS), electron energy-loss spectra (EELS), and nonresonant inelastic x-ray scattering spectra (NRIXS), also known as x-ray Raman spectra, at finite momentum transfer q. The core-BSE calculations are quite efficient compared to those for optical spectra based, e.g., on AI2NBSE, since the core-level subspace is smaller than the valence band manifold. The approach is implemented using an interface dubbed OCEAN (Obtaining Core Excitations using ABINIT and NBSE), which generates relevant input files for the various modules and serves as a driver for all steps of the calculation. This interface is a generalization to core excitations of AI2NBSE, a recently developed interface for valence excitations.⁶ In the current implementation, the OCEAN package can handle up to about 50 atoms per unit cell and spectra up to about 100 eV above threshold.

The remainder of this paper is as follows. Section II summarizes the theory underlying our approach. Section III presents illustrative results for the K edges in LiF and KCl, the Mg L_2,3 edge in MgO, and the Ti L_2,3 edge in SrTiO₃. Finally, Sec. IV presents a summary and prospects for future development.

II. THEORY

A. BSE for core-level spectra

Core-level x-ray absorption spectra (XAS), electron energy-loss spectra (EELS), and nonresonant inelastic x-ray scattering (NRIXS) are all related to the loss function L(q, ω) = −Im ε⁻¹(q, ω), which is proportional to dynamic structure factor S(q, ω). Here q is the momentum transfer, while ω is the photon energy in XAS and the energy transfer in NRIXS and EELS. (Unless otherwise specified we use Hartree atomic units with e = ħ = m = 1 throughout this paper.) For XAS we have |q| = ω/c, where c ≈ 137.036 is the speed of light. Formally the loss function is given by

$$L(\mathbf{q},\omega )=-\frac{4\pi }{q^2}\text{Im}\langle {\mathrm{\Psi }}_0\mid {\widehat{P}}^{†}{[E_0+\omega -\widehat{H}+i\eta ]}^{-1}\widehat{P}\mid {\mathrm{\Psi }}_0\rangle .$$ (1)

Here P̂ is the operator that couples the many-body ground state |Ψ₀〉 with the probe photon, e.g., e^iq·r for NRIXS. In the case of XAS, a slightly different formula provides the spectrum. This formula involves a different operator, namely (ê · r) + (i/2) (ê · r) (q · r) + ···, where ê is the electric field direction. Ĥ is the particle-hole Hamiltonian including self-energy and lifetime effects as described below, and η is a positive infinitesimal. Our approach for calculating Eq. (1) is adapted from the treatments of the BSE in the quasiparticle approximation of Soininen and Shirley¹⁹ and Shirley,²³ which are summarized below. Satellite effects due to multielectron excitations are neglected, though they can be approximated a posteriori in terms of an effective spectral function in our self-energy approximation.

In order to evaluate the core-loss function in Eq. (1), we make the approximation that the excited states of a system can be described using a basis set of electron-hole states {|Φ_{nk+q, αk}〉}. Each electron-hole state has an electron in band n with crystal momentum k + q, and a core hole denoted by an atomic level α, with the corresponding orbitals in each cell combined using a phased sum to form a Bloch state with crystal momentum k. Our calculations also account for electron and hole spin degrees of freedom, which are not explicitly written in what follows. The Hamiltonian Ĥ is represented by an effective particle-hole Hamiltonian Ĥ_eff

$${\widehat{H}}_{\text{eff}}={\widehat{H}}_e-{\widehat{H}}_h+{\widehat{H}}_{eh}.$$ (2)

Here Ĥ_e/h account for the single-particle energies of the electron and hole states, including the spin-orbit interaction for the core states and self-energy and/or lifetime corrections:

$$\begin{gathered} {\widehat{H}}_e={\widehat{H}}_0+\mathrm{\sum }, \\ {\widehat{H}}_h={\epsilon }_c+i\mathrm{\Gamma }, \end{gathered}$$ (3)

where Ĥ₀ is the noninteracting single-particle Hamiltonian, ε_c is the core level energy, Σ is the final state self-energy and Γ the core-hole lifetime. The electron-hole interaction is given by

$${\widehat{H}}_{eh}={\widehat{V}}_D+{\widehat{V}}_X,$$ (4)

where V̂_D and V̂_X account for the direct and exchange electron-hole interactions, respectively. The highly localized nature of core states allows for division of the screening of the direct term V̂_D into a short-range part calculated using the RPA, and a long-range part treated with a model dielectric function,²⁶ while the exchange term V̂_X is unscreened. In order to treat multiplet effects the shortest range electron-core hole interaction is expressed using a compact multiplet Hamiltonian based on the core atomic orbitals, PAW functions, and the related Slater F and G integrals, following the treatment of Ref. 23.

Inserting a complete set of electron-hole states {|Φ〉}, Eq. (1) becomes

$$Im[{\epsilon }^{-1}(\mathbf{q},\omega )]=-\frac{4\pi }{q^2}\sum _{\mathrm{\Phi },{\mathrm{\Phi }}^{\prime }}Im[\langle {\mathrm{\Psi }}_0\mid {\widehat{P}}^{†}\mid \mathrm{\Phi }\rangle \times \langle \mathrm{\Phi }\mid {[\omega -{\widehat{H}}_{\text{eff}}+i\eta ]}^{-1}\mid {\mathrm{\Phi }}^{\prime }\rangle \langle {\mathrm{\Phi }}^{\prime }\mid \widehat{P}\mid {\mathrm{\Psi }}_0\rangle ].$$ (5)

To obtain the particle-hole states, {|Φ〉}, the band states ϕ_n,k+q(r) are calculated for both occupied and unoccupied levels using the ground-state Kohn-Sham Hamiltonian, while the core states χ_α,k(r) are taken to be Bloch states derived from the atomic core states for a given absorption edge calculated with an atomic Hartree-Fock code. A transition |Ψ₀〉 → |Φ_nk+q,αk〉 has a matrix element of the form

$$\begin{gathered} \langle {\mathrm{\Phi }}_{n,\mathbf{k}+\mathbf{q},\alpha \mathbf{k}}\mid \widehat{P}\mid {\mathrm{\Psi }}_0\rangle =N^{-1}\sum _{\mathbf{R}}{e}^{i\mathbf{k}·\mathbf{R}}\langle {\varphi }_{n,\mathbf{k}+\mathbf{q}}\mid \widehat{P}\mid {\chi }_{\alpha ,\mathbf{R}}\rangle \\ =\langle {\varphi }_{n,\mathbf{k}+\mathbf{q}}\mid \widehat{P}\mid {\chi }_{\alpha ,\mathbf{R}=\mathbf{0}}\rangle . \end{gathered}$$ (6)

Here N is the number of unit cells in the crystal. Making use of an appropriate sum over identical core states located at every lattice site {R}, the particle-hole state is thus constructed to have good crystal momentum q. The resolvent in Eq. (5) is then calculated using a Lanczos algorithm which was found to converge within about 100 iterations.²³

B. PAW transition matrix elements

The transition matrix between the ground state and one-electron excited states in Eq. (6) is then calculated locally by expressing the conduction band states in terms of atomic states centered about the specific core-hole located at position τ within the unit cell using the projector augmented wave (PAW) expansion²⁷

$${\varphi }_{n,\mathbf{k}+\mathbf{q}}(\mathbf{R}+\mathbf{r}+\tau )\approx e^{i(\mathbf{k}+\mathbf{q})·\mathbf{R}}\sum _{\mathit{vlm}}{A}_{\mathit{vlm}}^{n\mathbf{k}+\mathbf{q}}{F}_{vl}^{ps}(r)Y_{lm}(\widehat{\mathbf{r}}),$$ (7)

where { $F_{vl}^{ps}$} are the PAW basis functions with angular quantum numbers l and m. The index ν denotes the use of multiple PAW basis functions per angular momentum to adequately span the space. In terms of these PAW basis functions, transition matrix elements are found easily using an atomic structure program. Further details are given elsewhere.²³

C. Many-pole self-energy

One of the key considerations in calculations of core excitation spectra is the treatment of the final-state self-energy shifts and damping effects observed in experimental spectra. A number of methods for this purpose now exist.²⁸ Because these effects are small near an excitation threshold they are often neglected. However, they become increasingly important when the excitation energy exceeds plasmon and interband energies of order 10 eV, and thus become crucial at high excitation energies. To treat these effects we have implemented the efficient many-pole GW self-energy model (MPSE) of Kas et al.²⁹ This MPSE is a straightforward extension of the Hedin and Lundqvist single plasmon-pole GW self-energy model, and is based on the calculated dielectric response specific to a given material, e.g., as obtained using AI2NBSE.

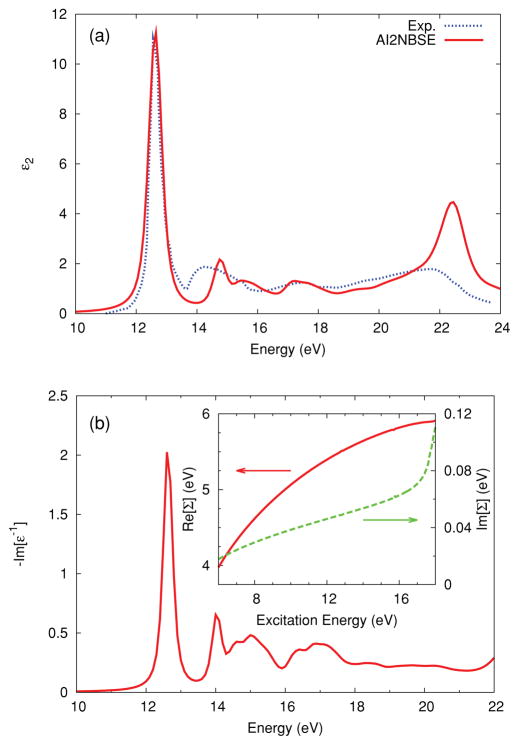
In brief, our implementation of the MPSE is as follows. We first represent the loss function in the optical regime L(ω) = −Im[ε⁻¹(q = 0,ω)] as a weighted sum over closely-spaced δ functions at ω_j with weights w_j = L(ω_j)Δ_j chosen to preserve the loss-function sum rule. The inclusion of many (typically of order 10²) poles allows for smooth, energy dependent broadening and quasiparticle shifts in excitation energies, and accounts for losses in the near-edge region well below the dominant excitations. As an example, Fig. 1 shows a comparison of the imaginary part of the dielectric function ε₂(ω) for LiF as measured experimentally and that calculated by AI2NBSE. The pole representation also permits a straightforward way to extrapolate the long-wavelength limit ε⁻¹(q = 0,ω) to finite momentum transfer. Our MPSE uses the same the dispersion relation as in the original Hedin-Lundqvist plasmon-pole model.²⁹ We then calculate the self-energy Σ = iGW within the GW approximation, where the Green’s function G is taken to be the free propagator of an electron gas and W = ε⁻¹v is calculated using the many-pole model of the dielectric function. Using the same strategy as for the plasmon-pole model, the resulting self-energy can be expressed as a Hartree-Fock exchange term, plus a weighted sum of plasmon-pole-like, dynamically screened exchange terms, each with a different plasma frequency ω_j. Thus the model retains the efficiency of the plasmon-pole model yet yields accurate calculations of the self-energy over a broad energy range from near the Fermi level to of order 10⁴ eV above the Fermi level. A typical calculation can be performed in only a few minutes on a modern single-processor desktop computer once the loss function at zero momentum transfer is known. In order to apply the self-energy [inset of Fig. 1(b)] to calculations of core level XAS, we use an a posteriori convolution of the spectrum with a Lorentzian spectral function built from our calculated quasiparticle self-energy. Multielectron excitations and interference effects leading to satellites can also be included in this convolution,²⁹ but are currently ignored.

FIG. 1.

(a) Imaginary part of the dielectric function (top) ε₂(ω) calculated with AI2NBSE (red, solid line) and experiment³⁰ (blue, dotted line) (data taken from Puschnig and Ambrosch-Draxl³¹); and (b) loss function −Im ε⁻¹(ω) (bottom) with (inset) real and imaginary parts of the self-energy calculated from AI2NBSE. The self-energy is calculated from the loss function using the many-pole self-energy method (see text) and is shown relative to the valence band maximum. This self-energy is applied to the LiF K edges providing energy dependent broadening and energy shifts to correct the single-particle energies from DFT.

Currently the MPSE is calculated only for the unoccupied states, and no attempt is made to determine absolute edge energies. This self-energy is then added, assuming that all transitions occur either from the highest occupied level in the case of the valence response, or from a single localized core level in the case of core response. For core excitations this is a good approximation, while for valence response the approximation is valid only for narrow valence bands and future refinements should take the width of the valence band into account. An example of the resulting XAS is shown for LiF in Fig. 2. Clear improvement can be seen due to the MPSE, which corrects both the peak positions and amplitudes in the spectrum.

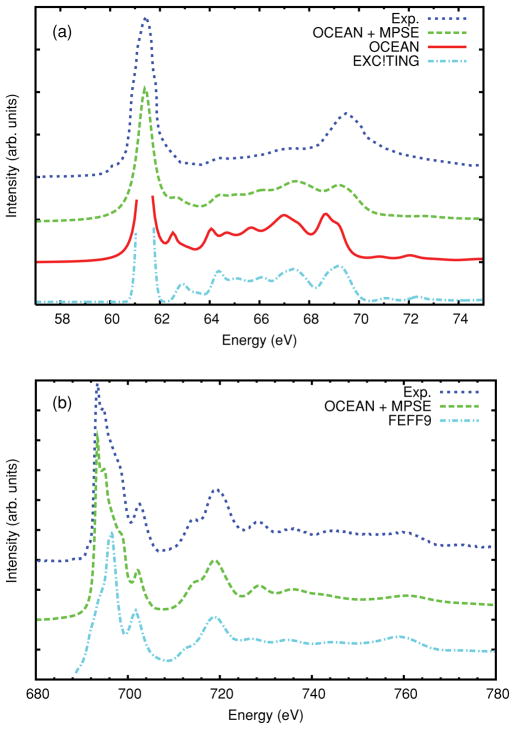
FIG. 2.

(a) The x-ray absorption near-edge structure (XANES) spectra for the Li K edge of LiF (top) and (b) the F K edge (bottom). The BSE spectra (solid, red line) are compared to the same spectra convoluted with the MPSE correction (green, dashed line) and experiment^34,35 (Li data from Olovsson et al.³⁶) (blue, dotted line). In (a) the result of another BSE code,³⁶ (light blue, dashed-dotted line) and in (b) a calculation with the FEFF9 code (light blue, dashed-dotted line) are shown for comparison.

III. CALCULATIONS AND RESULTS

In this section we illustrate our approach with a number of examples. The results are sensitive to the choice of pseudopotentials and PAW projectors, and care must be taken to ensure an adequate treatment. Briefly, our implementation of OCEAN uses ABINIT wave-functions with norm-conserving pseudopotentials generated using the FHI³² or OPIUM³³ codes utilizing the designed nonlocal approach. Our choice of cutoffs is generally larger than in typical ground state calculations to avoid possible convergence issues. Our PAW transition elements from atomic core states utilize from 4 to 10 projectors depending on valence band width; the NIST NBSE solver for core excitations; and the GW MPSE outlined above. Our calculations use separate grids to calculate the wave functions for the final states and for the screening. For all of the materials, calculations of the final states on a 10 × 10 × 10 Brillouin-zone grid with a symmetry breaking shift of (1/80, 2/80, 3/80) were found to be adequate for convergence. The number of final state bands included in the calculation only affects the range of validity of the spectrum above the edge. Depending on the example, between 40 and 70 conduction bands are included.

The screening in the direct interaction V̂_D was calculated using states from a 2 × 2 × 2 Brillouin-zone grid with a similar symmetry breaking shift as the final state calculation. This grid was found to be adequate for convergence. For the screening calculation, a large number of unoccupied states must also be included for convergence. Including bands up to 100 eV above the Fermi level was found to be sufficient for all of our cases. Dielectric screening was calculated in real space as described by Shirley.²⁶

A. LiF

LiF is a wide-gap insulator leading to strongly bound excitonic peaks in the absorption spectra which are highly dependent on the screened direct interaction between the excited electron and hole for their strength and binding energy. LiF has a rock-salt structure with a lattice constant of 4.028 Å,³⁷ and the electronic dielectric constant ε_∞ (i.e., the value for low frequencies well above characteristic vibrational frequencies) is 1.92.³⁸ The first 56 conduction bands were included covering energies up to 100 eV above the Fermi level, and a 100 Ry cutoff was used for the plane-wave basis. The plane-wave cutoffs necessary for our calculations reflect both the need for pseudopotentials to be accurate several Rydbergs above the fermi level and the inclusion of semicore states in heavier elements: Ti, Sr, and K. While LDA calculations often underestimate bandgaps in insulators, the MPSE almost completely corrects the conduction energy levels and bandgap in LiF. This is illustrated in the UV calculation of ε₂ and the loss function −Im ε⁻¹ (Fig. 1).

Results for the Li K-edge XAS of LiF are presented in Fig. 2. Note that the inclusion of final-state broadening and self-energy shifts from our MPSE yields results that agree well with experiment. If these final-state effects are ignored, one obtains sharper, more compressed spectra, in poorer agreement with experiment. However, our calculation fails to account for the strength of the experimental peak near 70 eV, i.e., about 10 eV above the edge. The reasons for this discrepancy are not yet understood. While the use of the Tamm-Dancoff approximation is known to give errors in the optical spectra at high energies,³⁹ we expect such errors to be negligible for core spectra. A comparison is also included with the results from the BSE-based EXC!TING code.³⁶ Although EXC!TING ignores energy dependent GW corrections, we find good agreement in peak positions and spacing between the two codes for this case.

Results for the F K edge of LiF including the final-state corrections from MPSE are shown in Fig. 2(b). As for the Li K edge, the broadening and self-energy shifts from the GW MPSE lead to good agreement with experiment. Overall the F K edge Fig. 2(b) exhibits much better agreement with the experiment than for the Li K edge. A comparison is also included with the FEFF9 code.⁴⁰ While the results are generally in good agreement, our calculation yields better agreement with experiment in the edge region.

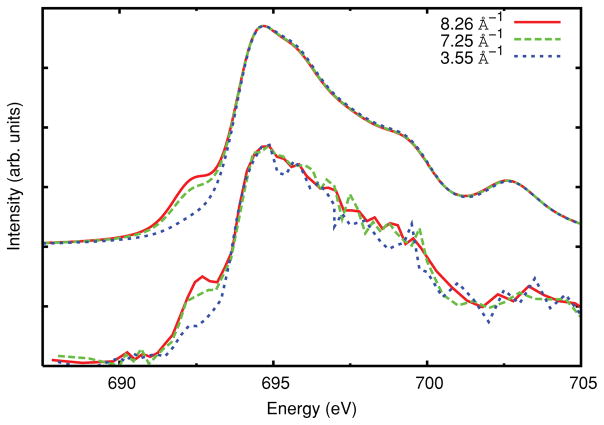
As an illustration of momentum transfer dependent calculations with OCEAN, results for the NRIXS of LiF are shown in Fig. 3 for q =3.55 Å⁻¹, 7.25 Å⁻¹ and 8.26 Å⁻¹. For this predominantly s-p electron system the momentum transfer dependence is strong only in the edge region, and reflects the behavior of an s-type exciton. Our results are found to be in good agreement both with experiment and with previous calculations.

FIG. 3.

The theoretical (above) and experimental⁴¹ (below) NRIXS spectra for LiF for momentum transfer q = 3.55 Å⁻¹, 7.25 Å⁻¹, and 8.26 Å⁻¹ normalized to the height of the main peak. Note that momentum transfer only affects the edge-spectra due to the behavior of the s-type exciton in this system.

B. KCl

As an example of deep core K-edge spectra we present the XAS for both the K and Cl K edges in KCl. KCl has a rock-salt structure with lattice constant 6.29 Å and ε_∞ =2.19.³⁸ A plane-wave cutoff of 160 Ry and 172 conduction bands were used for the screening calculations. Both K edges exhibit very good agreement with experiment both for peak positions and intensities (Fig. 4).

FIG. 4.

(a) The K-edge XAS of potassium (top) and (b) the Cl K edge in KCl calculated with OCEAN (red, solid line) and compared to experimental results⁴² (blue, dotted line).

C. MgO

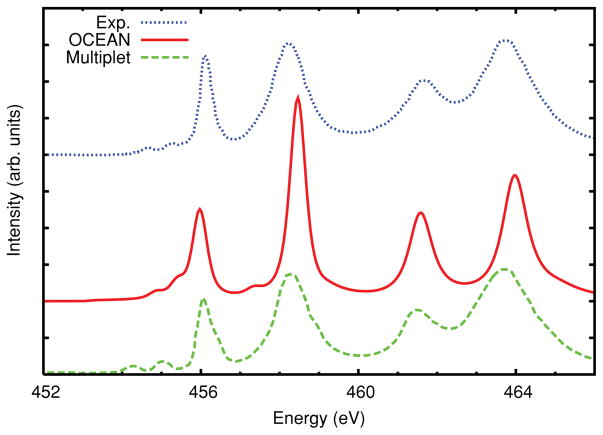
To illustrate a shallow L-edge calculation we show the XAS for the Mg L_2,3 edge in MgO (Fig. 5). MgO also has a rock-salt structure with a lattice constant of 4.212 Å and ε_∞ = 2.95.³⁸ The screening calculation used 196 conduction bands and a plane-wave cutoff of 200 Ry. The splitting between the L₂ and L₃ edges in Mg is only 0.25 eV and is therefore hidden by conduction band widths and experimental broadening. Our XAS calculation of the Mg L_2,3 edge in MgO is particularly sensitive to computational details such as the treatment of core-hole screening. The calculation is in good agreement for peak positions, though not the relative strengths. The calculated spectrum is too weak in the range 60 eV to 70 eV while the peak near 75 eV is too strong and more narrow than that in the experiment. The excitonic peak is also too strong compared to the main edge (Fig. 5). It seems likely that underscreening of the core hole leads to the overestimation of the strength of the excitonic peak.

FIG. 5.

Calculated XANES spectra for the Mg L_2,3 edge of MgO compared with experimental reflection (R^1/2) data.⁴³ The calculated spectra has been broadened and by a Gaussian of 0.9 eV FWHM in addition to the MPSE.

D. SrTiO₃

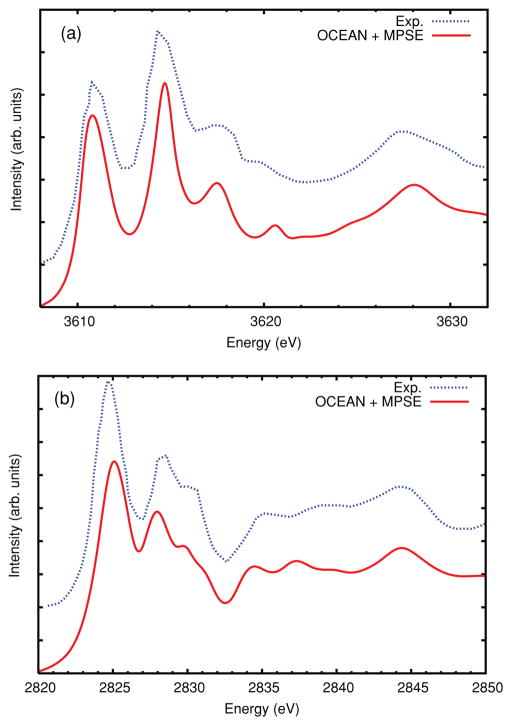
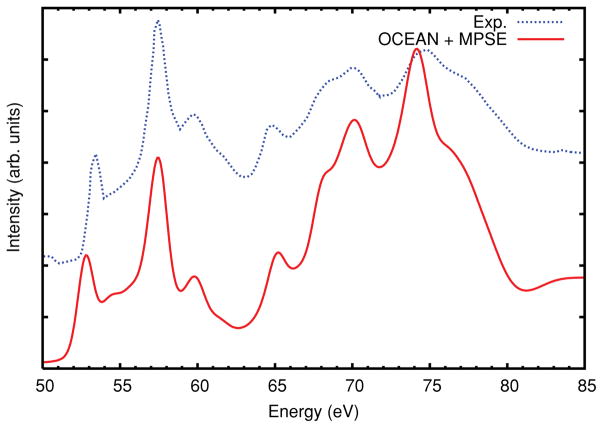
The Ti L_2,3 edge of SrTiO₃ is included here as an example of our treatment of multiplet effects. Cubic perovskite SrTiO₃ has a lattice constant of 3.91 Å ⁴⁵ and ε_∞ =5.82.⁴⁶ A plane-wave cutoff of 220 Ry and 450 conduction bands were used for the screening. Each Ti atom is surrounded by oxygen octahedra leading to a 2.5 eV splitting in the 3d-like Ti final states according to their symmetry.

Transition metal L_2,3 edges exhibit strong multiplet effects due to the competition between intra-atomic Coulomb interactions, spin-orbit coupling, and the scattering potential of the surrounding atoms. This results in a shift in the L₃/L₂ intensity ratio away from the noninteracting ratio of 2: 1. By including the core-level spin-orbit energy splitting and simultaneously treating 2p_1/2 and 2p_3/2 initial states in the BSE Hamiltonian, our approach yields ab initio estimates of shifts in the spectral weight which are comparable to that in the experimental spectra. The Ti L_2,3 edge of SrTiO₃ has also been the subject of recent work using the BSE,⁴⁷ ab initio charge-transfer multiplets in finite clusters,⁴⁸ and multichannel multiple-scattering calculations in finite clusters.⁴⁹ All of these approaches including that of our work account for the observed multiplet splittings in SrTiO3 reasonably well, but tend to underestimate the broadening observed in experiment. This is due in part to the neglect of energy-dependent phonon-broadening effects.^24,25 Additionally the calculated spin-orbit splitting between the L₂ and L₃ edges is found to be 5.7 eV, though the observed splitting in the final calculated spectra is smaller due to other contributions to the BSE Hamiltonian. Also an additional contribution was added to the imaginary part of the self-energy to match the experimentally observed core-hole lifetime difference between the L₂ and L₃ edges. Our calculation gives good agreement for peak positions and produces a ratio between the two edges in reasonable agreement with experiment (Fig. 6). The two pre-edge features below 457 eV in the experiment are also reproduced in the calculation, though they are too close to the leading edge. This error is likely due to our screening approximation.

FIG. 6.

Calculated XANES spectra for the Ti L_2,3 edge of SrTiO₃ (red, solid line) compared to experimental data (blue, dotted line) and a multiplet calculation⁴⁴ (green, dashed line). Due to the close spacing of the edges the full MPSE was not included. Instead, the imaginary part of the self-energy was applied by aligning the onset with respect to each edge and including a core-hole lifetime (0.10 eV and 0.24 eV), shifting between the two at 461.5 eV. This lifetime broadening also neglects solid-state Coster-Kronig and phonon effects.

IV. SUMMARY AND FUTURE PROSPECTS

We have developed a hybrid approach for GW/BSE calculations of core-excitation spectra in periodic materials based on plane-wave pseudopotential wave functions (from ABINIT in this case), PAW constructed matrix elements, the NIST BSE solver, and a many-pole GW self-energy from AI2NBSE. The method takes into account the many-body effects of inelastic losses and core-hole interactions, and can also include multiplet effects. This approach is implemented in the OCEAN package, which is applicable to core level XAS, EELS and related spectra including finite momentum transfer. Moreover, the approach can be applied to many other spectra, and some future extensions include resonant inelastic x-ray scattering (RIXS),¹⁹ relativistic EELS,⁵⁰ and the mixed dynamic form factor (MDFF). The pseudopotential base allows for computationally efficient calculations of fairly large systems (currently up to about 50 atoms) for near-edge spectra within about 10² eV of threshold for arbitrary core levels. Moreover, by combining OCEAN with AI2NBSE and the complementary RSGF code FEFF9, full-spectrum calculations from the UV-VIS to hard x-rays are feasible. Overall the results are found to be in good to excellent agreement with experiment, and can improve on other theoretical approaches. Nevertheless further improvements such as the inclusion of multielectron excitations and vibrational effects are desirable. Additional applications, e.g., to the XAS and NRIXS of water and ice, are described elsewhere.⁵¹