Predicting Efavirenz Concentrations in the Brain Tissue of HIV‐Infected Individuals and Exploring their Relationship to Neurocognitive Impairment

Nithya Srinivas; Sarah Beth Joseph; Kevin Robertson; Laura P Kincer; Prema Menezes; Lourdes Adamson; Amanda P Schauer; Kimberly H Blake; Nicole White; Craig Sykes; Paul Luciw; Joseph J Eron; Alan Forrest; Richard W Price; Serena Spudich; Ronald Swanstrom; Angela DM Kashuba

doi:10.1111/cts.12620

. 2019 Feb 27;12(3):302–311. doi: 10.1111/cts.12620

Predicting Efavirenz Concentrations in the Brain Tissue of HIV‐Infected Individuals and Exploring their Relationship to Neurocognitive Impairment

Nithya Srinivas ^1,⁶, Sarah Beth Joseph ², Kevin Robertson ², Laura P Kincer ², Prema Menezes ², Lourdes Adamson ³, Amanda P Schauer ¹, Kimberly H Blake ¹, Nicole White ¹, Craig Sykes ¹, Paul Luciw ³, Joseph J Eron ², Alan Forrest ^†, Richard W Price ⁴, Serena Spudich ⁵, Ronald Swanstrom ², Angela DM Kashuba ^1,^2,^✉

PMCID: PMC6510381 PMID: 30675981

Abstract

Sparse data exist on the penetration of antiretrovirals into brain tissue. In this work, we present a framework to use efavirenz (EFV) pharmacokinetic (PK) data in plasma, cerebrospinal fluid (CSF), and brain tissue of eight rhesus macaques to predict brain tissue concentrations in HIV‐infected individuals. We then perform exposure‐response analysis with the model‐predicted EFV area under the concentration‐time curve (AUC) and neurocognitive scores collected from a group of 24 HIV‐infected participants. Adult rhesus macaques were dosed daily with 200 mg EFV (as part of a four‐drug regimen) for 10 days. Plasma was collected at 8 time points over 10 days and at necropsy, whereas CSF and brain tissue were collected at necropsy. In the clinical study, data were obtained from one paired plasma and CSF sample of participants prescribed EFV, and neuropsychological test evaluations were administered across 15 domains. PK modeling was performed using ADAPT version 5.0 Biomedical Simulation Resource, Los Angeles, CA) with the iterative two‐stage estimation method. An eight‐compartment model best described EFV distribution across the plasma, CSF, and brain tissue of rhesus macaques and humans. Model‐predicted median brain tissue concentrations in humans were 31 and 8,000 ng/mL, respectively. Model‐predicted brain tissue AUC was highly correlated with plasma AUC (γ = 0.99, P < 0.001) but not CSF AUC (γ = 0.34, P = 0.1) and did not show any relationship with neurocognitive scores (γ < 0.05, P > 0.05). This analysis provides an approach to estimate PK the brain tissue in order to perform PK/pharmacodynamic analyses at the target site.

Study Highlights.

WHAT IS THE CURRENT KNOWLEDGE ON THE TOPIC?

☑ Sparse antiretrovirals (ARV) concentration data are available for human brain tissue. Previous studies have analyzed the relationship between cerebrospinal fluid (CSF) pharmacokinetics (PK) of several classes of ARVs and neurocognitive impairment due to HIV.

WHAT QUESTION DID THIS STUDY ADDRESS?

☑ We present a novel modeling framework using sparse preclinical and clinical data to predict the human brain tissue distribution of efavirenz (EFV) and the relationship between brain tissue exposure and neurocognitive impairment in HIV‐infected individuals.

WHAT DOES THIS STUDY ADD TO OUR KNOWLEDGE?

☑ This study provides novel translational and Bayesian modeling approaches to predict EFV distribution in human brain tissue.

HOW MIGHT THIS CHANGE CLINICAL PHARMACOLOGY OR TRANSLATIONAL SCIENCE?

☑ This study provides important information on the extent of brain tissue distribution of EFV and the use of plasma concentrations as a surrogate measure. The study shows that CSF EFV concentrations are not an appropriate surrogate for brain tissue concentrations. The Bayesian estimation modeling approach presented here can be applied to other classes of drugs to estimate tissue distribution using sparse data.

People living with HIV may face a spectrum of neurocognitive deficits called HIV‐associated neurocognitive disorders (HAND) that remain prevalent despite highly active antiretroviral therapy (HAART). Although the prevalence of HIV‐associated dementia has dramatically declined from 60% in the pre‐HAART era to 5% currently,1 milder forms of HAND remain high at 20–50% prevalence.1

HAND persistence in HAART‐treated individuals may be due to irreversible damage to neurons in the central nervous system (CNS) resulting from uncontrolled HIV replication and inflammation that occurred before initiating antiretroviral (ARV) therapy.2 The extent of ARV penetration into the CNS may also contribute to HAND during HAART. Restricted ARV brain tissue exposure could lead to ongoing viral replication and CNS damage.3 Alternatively, for ARVs that achieve high brain tissue concentrations, potential neurotoxicity may contribute to HAND. Several studies have investigated neurocognitive impairment as a function of ARV cerebrospinal fluid (CSF) pharmacokinetics (PK) but have been inconclusive.4 This may be because neurocognitive impairment was assessed as a function of CSF exposure. With the inability to obtain brain tissue in humans premortem for PK sampling, either CSF concentrations or CNS‐penetration effectiveness (CPE) scores are used as surrogates.5 The CPE scores are derived from clinical observations regarding the ARVs’ ability to control CSF HIV replication, CSF concentrations, and physicochemical properties. Because ARVs act either within or on the surface of HIV target cells (macrophages, microglia, and CD4+ T cells) in the brain, brain tissue is the relevant target for PK assessment.

Modeling and simulation techniques may be useful to predict drug distribution in the brain tissue. Nonlinear mixed effects modeling (NLMEM), frequently applied to “population” PK/pharmacodynamic (PD) analyses, can also provide better estimates at the individual subject level, when population inference is not relevant. Bayesian estimation methods, such as the iterative two‐stage (IT2S) method, are particularly useful to describe individuals with sparse data.6 In such an approach, parameter estimates are initially defined from a prior distribution as in other Bayesian analyses, with an iterative estimation of the parameters to provide refined estimates for each individual. Such an NLMEM method allows data to be leveraged from all study samples to better describe the PK in each study subject.

In this work, we apply NLMEM to develop a model to predict efavirenz (EFV) exposure in human brain tissue based on PK data (plasma, CSF, and brain tissue concentrations), obtained in rhesus macaques, combined with sparse plasma and CSF concentrations, obtained in a clinical trial. EFV is part of a fixed dose combination regimen (Atripla, Gilead Sciences(R), Foster City, California; 600 mg EFV, 200 mg emtricitabine, and 300 mg tenofovir disoproxil fumarate given once daily) that is a part of the World Health Organization's list of essential medicines7 and is used in several developing regions of the world where the HAND prevalence is comparable to, or higher than, rates in the Western world.8 Given the clinical relevance and established link of EFV usage with HAND prevalence,9 we investigated whether a relationship could be established between model‐predicted EFV brain tissue concentrations and neurocognitive impairment.

Methods

ARV dosing in rhesus macaques and preclinical study design

Nine adult rhesus macaques (Macaca mulatta) were dosed for 10 days with tenofovir 30 mg/kg and emtricitabine 16 mg/kg subcutaneously daily, EFV 200 mg orally daily, and raltegravir 100 mg/kg orally twice a day with food. Five animals were first infected with 104.5 TCID50 of RT‐SHIVmac239 intravenously to determine if infection status influences EFV concentrations in the brain. Plasma was sampled at 0, 4, 10, and 24 hours after the first dose, then 24 hours postdose on days 4, 6, 9, and 10 (necropsy). Animals were sedated to collect plasma and CSF followed by euthanasia by barbiturate overdose. Brain tissue from four distinct regions (frontal cortex, parietal cortex, cerebellum, and basal ganglia) were collected, snap‐frozen, and stored at −80°C. All procedures were performed according to locally approved Institutional Animal Care and Use Committee protocols from the University of California Davis (protocol 18345). One simian human immunodeficiency virus (SHIV)‐infected macaque developed liver failure during the course of the study and was excluded from analysis.

Clinical study participants

The Tropism of HIV, Persistence, Inflammation, and Neurocognition in Therapy Initiation Cohort (grant PO1 MH094177) study was conducted in full accordance with the Declaration of Helsinki. The study protocol was institutional review board–approved at all sites, and participants provided informed consent before study enrollment. This large study included several interlinked projects that enrolled HIV‐positive participants into two distinct observational cohorts based on their length of time on ARV therapy. Cohort A was comprised of individuals who were newly diagnosed, naive to treatment, or who were off ARV therapy for at least 3 months. Cohort B was comprised of treatment‐experienced individuals who were on therapy for at least 1 year before study enrollment and virally suppressed in the plasma and CSF. All participants were on drug regimens chosen by their primary care physician. Although these distinct cohorts were enrolled to evaluate two distinct hypotheses, participants from both cohorts provided PK samples for the PK substudy analysis. Methods and results from the PK substudy alone are presented in this paper.

Clinical study design

A longitudinal analysis was conducted for cohort A participants. These subjects were enrolled, initiated on ARVs, and followed for 1 year with four distinct study visits: the study enrollment (baseline) visit, and 2 weeks, 6 months, and 1year postenrollment. At the enrollment, 6‐month, and 1‐year visits, neurocognitive tests were administered under the supervision of a neuropsychologist. At the 2‐week and 1‐year study visits, blood was drawn to measure plasma concentrations, and a lumbar puncture was performed to measure CSF concentrations. Participants were followed for 1 year to track changes in cognitive function over time from high viral load (entry) to no detectable viral replication (1 year). Cognitive tests were performed every 6 months to reduce memory bias. Blood and CSF sampling procedures were scheduled within 2–3 hours of each other, with no preselected sampling time.

A cross‐sectional (single time point) analysis was conducted for cohort B participants; participants enrolled into the study and had one study visit within 2 weeks. At this visit, plasma and CSF were sampled at a single time point, and neuropsychological tests were administered. There were no follow‐up visits for this cohort.

Neuropsychological test evaluations

Neuropsychological performance was assessed in 15 tests across the following domains: premorbid verbal/language, learning, verbal memory, speed of information processing, attention/working memory, fine motor, gross motor, and executive functioning.

For each participant and each individual domain/test, z‐scores were computed from the normative scores that were demographically corrected by adjusting for age, education, gender, and race. This was done by subtracting the raw test score from the corrected score followed by dividing by the normative SD.10 The total z‐score for each participant was calculated by averaging the individual z‐scores across the 15 tests. A score of zero reflected average performance, positive scores denoted better than average performance, and negative scores denoted lower than average performance. The global deficit score (GDS)11 was computed by taking individual test scores across the neuropsychological battery and converting them to deficit scores. The deficit scores ranged from 0 (normal or above normal performances) to five (severe impairment).12 The GDS was determined by averaging the deficit scores.

Quantification of EFV concentration in the fluid and tissue matrices

EFV concentrations in the plasma, CSF, and brain tissue were analyzed by liquid chromatography tandem mass spectroscopy assays.13, 14 The lower limit of quantification (LLOQ) was 50 ng/mL (plasma), 1 ng/mL (CSF), and 0.005 ng/mL (brain homogenate), with intraday and interday precision and accuracy within 15%. If EFV concentration was below the limit of quantification (BLOQ), then the concentration was imputed as half of LLOQ.

Development of the preclinical PK model

EFV concentrations in the plasma, CSF, and brain tissue of the macaques were fit sequentially in ADAPT version 5.0 (Biomedical Simulation Resource, Los Angeles, CA).15 First, plasma concentrations alone were fit in each macaque using the IT2S NLMEM approach.16 Then the individual macaque plasma PK parameter estimates were fixed, and the CSF and brain data were added into the model and fit using a pooled analysis from all macaques to get initial estimates for the CSF and brain parameters. This approach was used because the plasma data were sufficient to obtain macaque‐specific estimates, but the CSF and brain data were limited. The volume of the CSF in macaques (0.015 L) was obtained from the literature17 and fixed due to issues with identifiability. In the final PK analysis, plasma, CSF, and brain tissue exposure data from all eight animals (79 concentrations in all three matrices) were comodeled by IT2S. Table S1 includes detailed modeling methods and total data available at each step. Weighting of data was by the inverse of the estimated observation variance, containing additive and proportional components. Model discrimination was by Akaike's Information Criterion.18 Bias and precision were evaluated based on the objective function, relative standard error (RSE)%, and goodness‐of‐fit diagnostic plots, such as the observation vs. individual model prediction and conditional weighted residuals vs. time.

Development of the clinical PK model

A sequential approach was also used to fit the clinical data. The plasma data were initially fit alone by the IT2S method.6, 19 The structural PK model was the same as for the macaques, and the parameter estimates used to initially describe the study subjects were derived from a previously published population PK model.20 Then the individual plasma PK parameters were fixed in each participant, and the CSF concentrations were added to fit the CSF and brain tissue parameters. CSF volume of distribution (V_CSF) in humans was fixed to a physiologically relevant volume of 0.15 L,21 allometrically scaled from the macaque CSF volume. The initial estimate of brain tissue volume of distribution (V_brain) was allometrically scaled from the macaque model, whereas the initial estimates of distributional rate constants describing movement among the plasma, CSF, and brain tissue were based on the final macaque model. Finally, all parameters other than the V_CSF were re‐estimated using IT2S. Model discrimination and residual variance weighting was as described for the macaque model. The final PK model was used to simulate EFV concentrations at steady state over a 24‐hour dosing interval in the plasma, CSF, and brain tissue in the study volunteers. The model was validated by measuring EFV in brain tissue samples from the National Neuro‐AIDS Tissue Consortium (NNTC) repository. Postmortem brain tissue concentrations from three HIV‐positive participants were overlaid with the final model predictions.

PK/PD correlation analysis

Individual concentration vs. time profiles were simulated from the final model in the plasma, CSF, and brain tissue and the trough concentration (C24h), and the area under the concentration‐time curve over the dosing interval (AUC_0–24 h) were determined in the various matrices. The individual AUC_0–24 h was correlated with the neurocognitive scores.

Statistical analysis

Comparison of EFV concentrations between brain tissue regions, and by gender and infection status in the rhesus macaques was performed by the Kruskal‐Wallis test. Correlation analyses were performed using the Spearman test. PK estimates are presented as geometric means and model‐predicted PK parameters are presented as median (range). Data were analyzed using SigmaPlot version 13.0 (Systat Software, San Jose, CA).

Results

PK model for EFV in rhesus macaques

The EFV concentration was 691 ng/g (280–1,929 ng/g) in the cerebrum, 687 ng/g (232–2,440 ng/g) in the cerebellum, 758 ng/g (213–2,139 ng/g) in the basal ganglia, and 834 ng/g in the parietal cortex (190–1,890 ng/g). Because these concentrations were similar (P = 0.95), median brain tissue concentration was used per animal. There were also no differences in EFV concentrations by infection status (P = 0.1; Figure S1). EFV disposition was best described by an eight‐compartment PK model with log‐normal error model, which included the central and peripheral compartments, one compartment each representing the CSF and brain tissue, and three transit compartments to accommodate delayed EFV absorption (Figure 1). Models without a peripheral compartment were also tested, and the number of transit compartments was determined by adding in these compartments sequentially until the best fit was obtained. The best fit was defined as when the run showed successful minimization (no near singular matrix and low SEs for the parameter estimates) and individual plasma R ² values of > 0.8. In four macaques, plasma C24h measured from day 4 until necropsy were 4‐fold to 40‐fold lower than the C24h after the first dose (Figure S2). We accommodated this interoccasion variability with a multiplicative term (M) on clearance such that the oral clearance (CL/F) after 24 hours was given by the product of clearance and M (if time > 24 hours, then CL/F = CL/F·M). Four macaques had observed EFV concentrations that were BLOQ in the CSF. The BLOQ data were censored by the M5 (BLOQ values imputed as LLOQ/2) method. This simple approach was considered appropriate to censor our data because we used a Bayesian iterative estimation method (inferences are based on assumed prior distribution and are not sensitive to missing values). The parameter estimates from the M5 method were also similar to the M1 (BLOQ values ignored) and the M7 (BLOQ values imputed as 0) methods. In the individual macaque fits, the median RSEs were generally small (< 30%) with moderate RSEs (30–45%) for the peripheral volume of distribution, K _plasma‐CSF, K _CSF‐brain, and K _brain‐CSF. The V_brain (conditioned on V_CSF) was 0.037 L. The parameter estimates are listed in Table 1. The R ² value for the line of individual conditional model predictions vs. observations in the plasma (overall, minimum‐maximum individual value) was 0.96 (0.91–0.99; Figure S3). The overall R ² values for the individual conditional model predictions vs. observations in the CSF and the brain tissue were 0.91 and 0.99, respectively. The overlay between observations and individual model predictions for the eight macaques are shown in Figure 2.

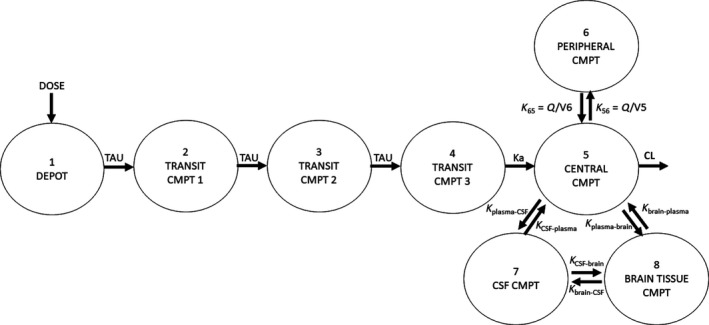
Structure of the pharmacokinetic model for efavirenz (EFV) describing distribution in the plasma, cerebrospinal fluid (CSF), and brain tissue in rhesus macaques and humans. An eight‐compartment model best described EFV disposition in the plasma, CSF, and brain tissue. Three transit compartments were used to describe the delayed peak of EFV in the plasma. In the rhesus macaques, a multiplicative term (M) was incorporated on clearance such that the clearance (CL/F) after 24 hours was given by the product of clearance for the first 24 hours and M (if time > 24 hour, then CL/F = CL/F·M). Plasma distribution was described by two compartments, with first‐order absorption and linear elimination from the central compartment. Drug movement was bidistributional among the plasma, CSF, and the brain tissue and described by rate constants. The CSF volume of distribution was fixed to physiologically relevant values in rhesus macaques and humans (0.015 and 0.15 L) with the brain tissue volume of distribution being conditioned on this value. CMPT, compartment; K_a, absorption rate constant; K_{brain‐plasma}, rate constant for drug movement from brain tissue to plasma; K_CSF‐plasma, rate constant for drug movement from CSF to plasma; K_{plasma‐brain}, rate constant for drug movement from plasma to brain tissue; K_plasma‐CSF, rate constant for drug movement from plasma to CSF; TAU, transit compartment rate constant; Q/V, intercompartmental rate constant.

Table 1.

Model parameters from the final EFV PK model in rhesus macaques and humans

Parameter^a	Geometric mean	Median	CV%
Rhesus macaques
CL/F (L/hour)	8.70	10.74	89.8
V5/F (L)	6.45	5.00	51.2
K_a (1/hour)	0.183	0.17	36.4
V6/F (L)	14.6	13.69	155.0
Q/F (L/hour)	4.66	5.9895	89.1
TAU (1/hour)	0.95	1.16	48.5
M^a	2.63	2.07	103.0
K_plasma‐CSF (1/hour)	1.71E‐06	1.91E‐06	59.5
K_CSF‐plasma (1/hour)	0.18	0.18	27.3
K_{plasma‐brain} (1/hour)	2.42E‐03	2.34E‐03	31.1
K_{brain‐plasma} (1/hour)	0.15	0.14	26.8
K_CSF‐brain (1/hour)	2.56E‐03	0.002779	36.0
K_brain‐CSF (1/hour)	5.58E‐06	4.6E‐06	68.2
V_brain/F (L)	0.037	0.036	21.8
V_CSF/F (L)	0.015 (fixed)	0.015 (fixed)	—
Humans^b
CL/F (L/hour)	12.37	12.20	58.5
V5/F (L)	155.34	147.25	39.1
K_a (1/hour)	0.135	0.025	94.6
V6/F (L)	405.4	200.05	35.8
Q/F (L/hour)	6.31	28.33	142.0
TAU (1/hour)	1.00	1.95	27.8
K_plasma‐CSF (1/hour)	4.27E‐06	4.11E‐06	88.8
K_CSF‐plasma (1/hour)	0.244	0.244	26.0
K_{plasma‐brain} (1/hour)	2.00E‐03	2.00E‐03	30.2
K_{brain‐plasma} (1/hour)	0.175	0.175	31.2
K_CSF‐brain (1/hour)	3.00E‐03	3.00E‐03	40.2
K_brain‐CSF (1/hour)	2.41E‐06	2.41E‐06	70.5
V_brain/F (L)	0.514	0.514	25.1
V_CSF/F (L)	0.15 (Fixed)	0.15 (Fixed)	—

Open in a new tab

CL/F, total apparent clearance; CSF, cerebrospinal fluid; CV%, percentage of coefficient of variation; EFV, efavirenz; K_a, absorption rate constant; K_brain‐CSF, rate constant for drug movement from brain tissue to CSF; K_{brain‐plasma}, rate constant for drug movement from brain tissue to plasma; K_CSF‐brain, rate constant for drug movement from CSF to brain tissue; K_CSF‐plasma, rate constant for drug movement from CSF to plasma; K_{plasma‐brain}, rate constant for drug movement from plasma to brain tissue; K_plasma‐CSF, rate constant for drug movement from plasma to CSF; M, multiplicative term; PK, pharmacokinetic; Q/F, intercompartmental clearance; TAU, transit compartment clearance rate; Q/V, intercompartmental rate constants; V5/F, central compartment volume of distribution; V6/F, peripheral compartment volume of distribution; V_brain/F, brain tissue volume of distribution; V_CSF/F, CSF volume of distribution.

^aM was not incorporated on the clearance term in the human EFV PK model. ^bThe human PK model was developed by a sequential estimation method where the plasma was initially estimated, followed by the central nervous system distributional parameters.

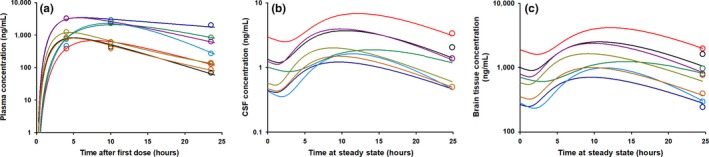
Goodness‐of‐fit spaghetti plots for the rhesus macaque efavirenz (EFV) pharmacokinetic model. Spaghetti plots of the individual model predictions are shown for the eight individual macaques with observations overlaid in the open circles in (a) plasma (b) cerebrospinal fluid (CSF), and (c) brain tissue. Each color represents one individual macaque. Four of the eight macaques had EFV concentrations in the CSF that were below the limit of quantification. Their concentrations were imputed as one‐half of the lower limit of quantification (0.5 ng/mL).

Clinical study demographics

Of the 109 HIV‐positive participants who enrolled into the study across both cohorts, 26 were on EFV‐based regimens. Atripla was the most commonly prescribed regimen (n = 22, 92%). Five participants (18%) were in cohort A, and five (18%) were women. Two treatment‐naive participants were lost to follow‐up after week 2 of the study and were not adherent to therapy as EFV concentrations in plasma and CSF were below the LLOQ. Therefore, their PK samples were excluded from analysis. The complete study demographics are listed in Table 2.

Table 2.

Demographic characteristics of the THINC study population

Demographic characteristic	Cohort A: Treatment‐naive (n = 3)	Cohort B: Treatment‐experienced (n = 21)
Sex, female	0 (0%)	5 (19%)
Age, years	32 (19–53)	54 (42–66)
Weight, kg	65.8 (56.7–110.2)	71.0 (45.4–136.1)
BMI^a	18.5 (17.2–31.2)	21.8 (15.3–48.4)
Race
White	0 (0%)	13 (62%)
African American	3 (100%)	8 (38%)
Combination regimen
Atripla	3 (100%)	16 (76%)
Other 3− drug regimen	0 (0%)	1 (5%)
Other 3+ drug regimen	0 (0%)	4 (19%)
Time on efavirenz treatment,^b years	<1	5 (3–12)
Entry CD4 count, cells/mm³	303 (158–354)	594 (198–1,251)
Entry plasma viral load,^c copies/mL	95,870 (18,334–176,506)	BLQ
Entry CSF viral load,^c copies/mL	15,118 (355–38,400)	BLQ
Entry neurocognitive score
z‐score	−0.8 (−1.3 to 0.13)	−0.43 (−2.8 to 0.86)
GDS	0.88 (0.125–1.31)	0.44 (0.0–3.27)

Open in a new tab

BMI, body mass index; BLQ, viral load lower than 40 copies/ml in the plasma and CSF; CSF, cerebrospinal fluid; GDS, global deficit score; THINC, Tropism of HIV, Persistence, Inflammation, and Neurocognition in Therapy Initiation Cohort. Data are median value (range) or number (%) of subjects.

^aBMI is calculated as the weight in kilograms divided by the height in square meters. ^bInformation was available for 16/24 patients. ^cThe lower limit of quantification for HIV RNA in the plasma and CSF was 40 copies/mL.

PK model of EFV in HIV‐positive participants

A total of 29 paired concentration measurements from 24 participants were available from the plasma and CSF for the clinical PK model.

EFV disposition in the plasma, CSF, and brain tissue in humans was described by an eight‐compartment model (Figure 1). The fitted V_brain, conditioned on the V_CSF was 0.51 L. The geometric mean CL/F was 12.4 L/hour, V5/F was 155 L, and absorption rate constant (K_a) was 0.135 1/hour. Individual parameter estimates were estimated with high precision (overall R ² for plasma and for CSF was 0.97 and 0.92, respectively). Table 1 summarizes the PK parameters. The RSE was > 50% for Ka, intercompartmental clearance and K _brain‐CSF and was 12–40% for the remaining parameters. Figure S4 contains diagnostic plots for the plasma and CSF.

The implications of the final model in the plasma and CSF and the predicted EFV profile in the brain tissue are shown in Figure 3. The 5th to 95th percentile of the 1,000 model replicates captured 88% and 96% of all EFV observations in the plasma and CSF, respectively, suggesting that the model adequately described observations with reasonable partitioning between residual and intersubject variability. Model‐predicted profiles in the CSF and brain tissue were flat, with concentrations of 30 ng/mL (6–170 ng/mL) and 8,000 ng/mL (2,300–29,000 ng/mL), respectively. The predicted brain tissue: plasma AUC_0–24 h ratio was 3.6 (3.2–3.8), whereas the predicted brain tissue: CSF AUC_0–24 h ratio was 213 (23–834).

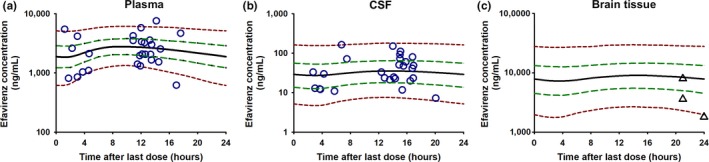
Visual predictive check for the final pharmacokinetic model in the (a) plasma and (b) cerebrospinal fluid (CSF) and (c) model predictions of efavirenz (EFV) in the brain tissue. The purple open circles represent the observations. The dashed red lines represent the 5th and 95th percentiles of the 1,000‐replicate simulations, the dashed green lines represent the 25th and 75th percentiles, whereas the thick solid black line is the median concentration. The 5th to 95th percentile captured 88% of the observations in the plasma and 96% of the observations in the CSF. The model was also overlaid with observations from an external data set from brain tissue samples from the National NeuroAIDS Tissue Consortium (in the black triangles) and was within the range of our model predictions.

Demographic information for the three HIV‐positive patients from the NNTC repository are presented in Table S2. Model overlay with these data (black triangles, Figure 3) showed that the model predictions adequately captured the brain tissue observations (ranging from 1,800−8,000 ng/mL).

Correlation between the model‐predicted C24h and AUC_0–24 h of EFV in the three matrices are shown in Figure 4. The model‐predicted brain tissue C24h and AUC_0–24 h showed stronger correlation with the respective parameters in the plasma (γ = 0.99, P < 0.001 and γ = 0.99, P < 0.001) than with the CSF (γ = 0.42, P = 0.04 and γ = 0.36, P = 0.09).

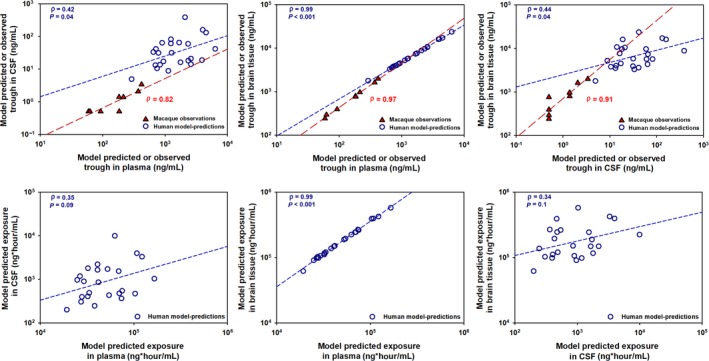
Correlation analysis between model‐predicted efavirenz concentration at 24 hours (C24h) postdose and area under the concentration‐time curve (AUC) in the plasma, cerebrospinal fluid (CSF), and brain tissue in humans and observed concentrations at 24 hours in macaques. The open circles represent the predicted C24h and AUC parameters in humans, whereas the filled triangles (and long dashes) represent observed C24h in the rhesus macaques. Brain tissue C24h and AUC parameters showed better correlation with the plasma parameters (γ = 0.99, P < 0.001 and γ = 0.99, P < 0.001) than with the CSF parameters (γ = 0.44, P = 0.04 and γ = 0.34, P = 0.1).

PK/PD correlation analysis

The z‐score and the GDS did not show any correlation with the model‐predicted EFV AUC_0–24 h in the brain tissue (γ = 0.005, P = 1.0 and γ = 0.045, P = 0.8; Figure 5) or with the model‐predicted EFV AUC_0–24 h in the CSF (γ = 0.05, P = 0.8 and γ = 0.005, P = 1.0).

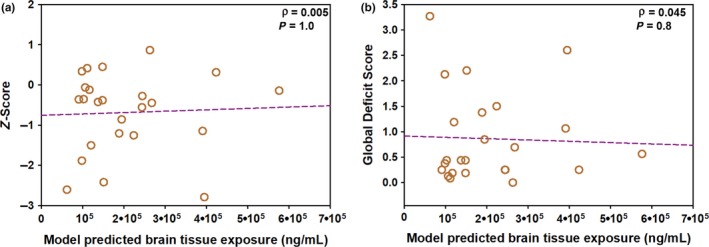
Correlation analysis between model‐predicted efavirenz (EFV) exposure in the brain tissue in humans and neurocognitive scores. The correlation analysis is shown between the model predicted exposure of EFV in the brain tissue and (a) z‐scores and (b) global deficit score. No relationship was noted between model‐predicted brain tissue exposure and either neurocognitive score measurement.

Discussion

In this work, we present a novel framework for analyzing sparse EFV PK data in preclinical species and humans to predict human brain tissue exposure. Because sparse data are available, we developed a PK model for EFV with the knowledge that this drug reaches high tissue concentrations.22 Our analysis showed that the observed C24h in the plasma and brain tissue of macaques were highly correlated (γ = 0.97, P < 0.001), as were C24h in CSF and brain tissue (γ = 0.91, P < 0.001). Similarly, model‐predicted AUC_0–24 h and C24h in human brain tissue were highly correlated with the plasma parameters. These results add credence to previous analyses23, 24 where EFV plasma concentrations may be sufficient to predict brain tissue.

Our data predicted a 10‐fold range in EFV AUC_0–24 h in plasma (19,223–165,487 ng hour/mL) and brain tissue (61,908–576,048 ng hour/mL) and a ~ 50‐fold range in CSF (200–9,940 ng hour/mL) in humans. The wide range in predicted CSF exposures reflects the high variability of observed CSF data in our participants (90% coefficient of variation (CV)). This high variability resulted in the wide range in AUC_brain/AUC_CSF, and lack of correlation between brain tissue and CSF exposure despite a flat EFV profile. High interindividual variability in plasma EFV concentrations has been demonstrated previously,25 and our brain tissue concentration data from our external data set were also highly variable (72% CV). This variability is helpful to quantify, as it is not evident within an approach such as the CPE.

The observed CSF EFV concentrations in humans (30 ng/mL) were 15‐fold higher than the CSF concentrations in the rhesus macaques (~ 2 ng/mL). These differences in concentrations seem to be driven by the higher plasma EFV concentrations in humans (2,100 ng/mL) compared with macaques (200 ng/mL). These species’ differences were also reflected in the brain tissue, and the macaque EFV brain tissue concentrations (775 ng/mL) were ~ 10‐fold lower than our model‐predicted EFV brain tissue concentrations (8,000 ng/mL) in humans. The model‐predicted brain tissue concentrations were 267‐fold higher than CSF, 4‐fold higher than plasma, and 15,000‐fold higher than the protein‐adjusted 90% inhibitory concentration of HIV replication (IC₉₀) of 0.22 ng/mL.26 A 2017 physiologically based pharmacokinetic model27 predicted that EFV accumulated in the brain tissue with a steady‐state concentration of 50,000 ng/mL, which is ~ 10‐fold higher than our model predictions. However, brain tissue PK data recently presented by Nicol et al.28 were within twofold to fourfold of our predictions and concentration data from our external data set showed agreement with our model. As a result, we believe our PK model predictions are biologically plausible.

Our PD measure for the degree of HAND impairment were scores obtained from neurocognitive testing, considered to be the gold standard diagnostic tool.29 The lack of relationship between the model‐predicted exposure in brain tissue and neurocognitive impairment scores may have been due to the small sample size, and/or the limited range of neurocognitive testing and drug exposure. Given the insensitivity of neurocognitive tests to discern mild impairment, future PK/PD studies should explore the relationship between ARV exposure and quantifiable biomarkers of CNS disease. Several biomarkers have been discovered for underlying inflammation and immune activation events in the CNS (neopterin)30 or neuronal injury (neurofilament light chain).31 In our analysis, greater EFV exposure in the brain tissue modestly associated (r = 0.7, P = 0.04) with lower CSF concentration of neurofilament light chain but not neopterin (data not shown). Validation of sensitive biomarkers for HAND may add to the predictability of PK/PD analyses in this setting.

The approach we used in the macaques allowed us to estimate the plasma PK parameters with high precision (high R ² values and low RSEs on the parameters for the individual macaque fits) and leverage data from all animals to estimate CSF and brain tissue profile. We considered simpler CNS model structures, such as the use of intercompartmental clearance values. However, because of the high variability in CSF and brain tissue concentrations, restricting the distribution to clearance values led to model instability and failure of the covariance matrix to converge. Furthermore, characterizing drug distribution into the CNS by rate constants was biologically relevant because different processes govern EFV movement into (passive diffusion) and out of (active efflux by breast cancer resistance protein (BCRP)) the CNS. Similarly, we tried multiple modeling approaches for the clinical PK model. Originally, we considered a maximum a posteriori probability‐Bayesian estimation from a literature model to describe the plasma.20 However, this model did not adequately capture our plasma concentrations and gave us limited confidence to predict brain tissue concentrations. Instead, we performed model fitting using the IT2S estimation method. Given that this tool is also Bayesian in nature and provides valuable individual estimates,6 IT2S is an appropriate method for analyzing sparse data. An important consideration for the use of this method is the accuracy of the initial parameter estimates. For this purpose, we used the published population PK model20 for initial plasma parameter estimates and refined the parameters to better describe the plasma concentrations in our study subjects.

Given the small number of rhesus macaques and humans for model development, we had limited ability to draw population inferences from our data. The results that we present here used NLMEM tools to better characterize individual PK profiles, but are not a substitute for population PK analyses. Indeed, the information gained from prior population PK analyses was invaluable to characterize plasma distribution in our clinical model. Our analysis provides an important proof‐of‐concept approach for the enrichment of sparse data (such as in the setting of therapeutic drug monitoring) with information from data‐rich population PK models. Such an approach allows for the better description of the individual profile and provides the ability to predict PK at otherwise inaccessible sites. Our external validation data set was a unique data source to compare with our model predictions in the brain tissue. Although the observed brain tissue data were all either at, or below, the median concentration of our model predictions, this is not indicative of model misspecification. There were very few brain tissue observations to conclude differences in distribution of the observations and model predictions, and, most importantly, there were no population inferences drawn from our model to assume that the distributions of the external data set and the model predictions had to be similar. Rather, the external data highlight the strength of our approach to predict hard‐to‐obtain clinical data, as well as the accuracy of our individual predictions. Ultimately, high individual precision and satisfactory plasma fit in both macaques and humans were leveraged to estimate CSF and brain tissue PK and provide a novel approach to handle sparse data.

We had a limited ability to identify the mechanism for the increase in CL/F noted in four macaques, and opted for a parsimonious, empiric structural model that fit the data well. Of note, the lowered plasma concentrations were observed 96 hours after the first dose. This is early for EFV auto‐induction (predicted to occur in humans a week after dosing32), although early auto‐induction effect has been shown for some other drugs.33 The four animals that showed lower C24h were predicted to have higher peak concentration after the first dose compared with the other animals (> 2,200 vs. < 1,500 ng/mL), and auto‐induction may occur earlier with higher concentration of the inducing agent. The faster auto‐induction in macaques compared with humans could be attributed to the high variability in cytochrome P450 (CYP)2C9 oxidation in macaques34 and differential drug–enzyme interaction across both species. For example, EFV is also a potent inhibitor of CYP2B6 (Ki = 1.68 μm),35 but CYP2C9 is only moderately inhibited by EFV (Ki = 19.46 μm).35 In our clinical model, because we often had only one plasma concentration per individual, we were not able to estimate the effect of auto‐induction.

Another limitation of our approach is the assumption of the same EFV structural model in both macaques and humans. This approach works best for drugs that do not undergo active influx or efflux by drug transporters and for drugs that are not highly protein bound.36, 37 However, EFV is highly protein bound and is a substrate of the active efflux transporter BCRP,38 which is highly expressed on the blood‐brain barrier.39, 40 Regardless, macaques and humans have similar EFV plasma protein binding (99.4% vs. 99.5%)16 and abundance of BCRP on the blood‐brain barrier.39, 40 These characteristics make our approach suitable.

Finally, the CSF and brain tissue concentrations in the macaques were only collected at the end of the dosing interval at necropsy, and this prevented us from estimating the V_CSF due to identifiability issues. Because we had data on the physiologic volume of CSF17 but not the physiologic brain tissue volume, we conditioned V_brain on a fixed CSF volume in the macaques. For similar reasons, the CSF volume was also fixed in humans. This resulted in the low values of distributional rate constants describing EFV movement into the CSF. With only trough concentration data available, we made limited inferences on time‐dependent EFV profile and performed PK/PD analyses with brain tissue exposure as a more stable model estimate. However, our predicted PK profile in these matrices (no distinction between maximum plasma concentration (C_max) and C24h) agrees with the relatively flat EFV PK profile in the CSF,21 and brain tissue,27 and highlights the utility of EFV C24h.

Conclusions

In conclusion, an eight‐compartment PK model was developed in macaques, and the structural model was translated to humans to determine the CSF and brain tissue distributional parameters of EFV. EFV showed first‐order absorption and linear elimination from the central compartment. EFV brain tissue concentration was predicted to be 8,000 ng/mL with AUC_0–24 h of 150,000 ng hour/mL, and the 5th to 95th percentile model predictions captured postmortem brain tissue concentration data, available from three individuals. The AUC_0–24 h ratio of brain tissue to plasma was 3.6, whereas the AUC_0–24 h ratio of brain tissue to CSF was 212. The brain tissue EFV C24h and AUC_0–24 h were highly correlated (γ = 0.99, P < 0.001) with their respective plasma parameters but were poorly correlated with the CSF parameters (γ = 0.44, P = 0.04 and γ = 0.34, P = 0.09). The individual predictions of EFV AUC_0–24 h in the brain tissue did not correlate with the neurocognitive impairment scores of the study participants, indicating that, in this small study, there may be factors other than EFV exposure in the brain that are responsible for influencing neurological outcomes in individuals with HAND.

Funding

This research was supported by the National Institute of Allergy and Infectious Disease (NIAID) under the R01 grant no. AI111891 and the National Institute of Mental Health (NIMH) under the PO1 grant no. MH094177 along with shared resources from the National Institutes of Health (NIH) funding through the NIMH and the National Institute of Neurological Disorders and Stroke (NINDS) by the following grant: Manhattan HIV Brain Bank (MHBB): U24MH100931. This work was also supported by the Center for AIDS Research under the grant no. P30 AI50410. N. Srinivas was supported by the Royster Society of Fellows, UNC Chapel Hill.

Its contents are solely the responsibility of the authors and do not necessarily represent the official view of the National Neuro‐AIDS Tissue Consortium (NNTC) or NIH.

Conflict of Interest

The authors declared no competing interests for this work.

Author Contributions

N.S., A.F., and A.D.M.K. wrote the manuscript. N.S., S.B.J., K.R., P.M., C.S., P.L., J.J.E., A.F., R.W.P., S.S., R.S., and A.D.M.K. designed the research. N.S., S.B.J., K.R., L.P.K., P.M., L.A., A.P.S., K.H.B., N.W., C.S., and A.F. performed the research. N.S., S.B.J., K.R., A.P.S., K.H.B., N.W., C.S., and A.F. analyzed the data. C.S. and A.F. contributed new reagents/analytical tools.

Supporting information

Figure S1. Efavirenz concentrations in different parts of the brain in the uninfected and infected rhesus macaques.

Figure S2. Individual model predictions vs. observations in the plasma in rhesus macaques.

Figure S3. Goodness‐of‐fit plots for individual model predictions vs. observations in the plasma in rhesus macaques.

Figure S4. Goodness‐of‐fit diagnostic plots for the final clinical PK model in the plasma and CSF.

Table S1. Modeling methods for the preclinical and clinical EFV PK Model.

Table S2. Demographic information from the HIV‐positive patients in the National NeuroAIDS Tissue Consortium repository from whom efavirenz brain tissue concentrations were available.

Click here for additional data file.^{(874.3KB, pdf)}

Acknowledgments

The authors would like to thank Katie Mollan, MS, Senior Biostatistician, at the University of North Carolina (UNC) Center for AIDS Research Biostatistics Core for her advice on the statistical analysis and Julie Dumond, PharmD, MS, Assistant Professor, at the UNC Eshelman School of Pharmacy for her advice on pharmacometric approaches to these data.

This work is dedicated to the memory of Dr Alan Forrest.

References

1. Marra, C.M. HIV‐associated neurocognitive disorders and central nervous system drug penetration: what next? Antivir. Ther. 20, 365–367 (2015). [DOI] [PubMed] [Google Scholar]
2. Tan, I.L. & McArthur, J.C. HIV‐associated neurological disorders: a guide to pharmacotherapy. CNS Drugs 26, 123–134 (2012). [DOI] [PubMed] [Google Scholar]
3. Letendre, S. Central nervous system complications in HIV disease: HIV‐associated neurocognitive disorder. Top Antivir. Med. 19, 137–142 (2011). [PMC free article] [PubMed] [Google Scholar]
4. Srinivas, N. , Maffuid, K. & Kashuba, A.D.M. Clinical pharmacokinetics and pharmacodynamics of drugs in the central nervous system. Clin. Pharmacokinet. 57, 1059–1074 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
5. Letendre, S. Validation of the CNS penetration‐effectiveness rank for quantifying antiretroviral penetration into the central nervous system. Arch. Neurol. 65, 65–70 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
6. Steimer, J.‐L. , Mallet, A. , Golmard, J.‐L. & Boisvieux, J.‐F. Alternative approaches to estimation of population pharmacokinetic parameters: comparison with the nonlinear mixed‐effect model. Drug Metab. Rev. 15, 265–292 (1984). [DOI] [PubMed] [Google Scholar]
7. World Health Organization (WHO) Model List of Essential Medicines (19th List). <http://www.who.int/topics/essential_medicines/en/Last> Accessed June 20, 2018.
8. Gannon, P. , Khan, M. & Kolson, D. Current understanding of HIV‐associated neurocognitive disorders pathogenesis. Curr. Opin. Neurol. 24, 275–283 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
9. Ciccarelli, N. , Fabbiani, M. & Baldonero, E. Efavirenz associated with cognitive disorders in otherwise asymptomatic HIV‐infected patients. Neurology 76, 1403–1409 (2011). [DOI] [PubMed] [Google Scholar]
10. Heaton, R. , Miller, S. , Taylor, M. & Grant, I. Revised comprehensive norms for an expanded Halstead Reitan battery: demographically adjusted neuropsychological norms for African American and Caucasian adults. (Psychological Assessment Resources, Lutz, FL, 2004). [Google Scholar]
11. Blackstone, K. , Moore, D. , Franklin, D. , Clifford, D. , Collier, A. & Marra, C. Defining neurocognitive impairment in HIV: deficit scores versus clinical ratings. Clin. Neuropsychol. 26, 894–908 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
12. Carey, C.L. et al Predictive validity of global deficit scores in detecting neuropsychological impairment in HIV infection predictive validity of global deficit scores in detecting neuropsychological impairment in HIV infection. J. Clin. Exp. Neuropsychol. 26, 307–319 (2004). [DOI] [PubMed] [Google Scholar]
13. Rezk, N.L. , Tidwell, R.R. & Kashuba, A.D.M. High‐performance liquid chromatography assay for the quantification of HIV protease inhibitors and non‐nucleoside reverse transcriptase inhibitors in human plasma. J. Chromatogr. B Anal. Technol. Biomed. Life Sci. 805, 241–247 (2004). [DOI] [PubMed] [Google Scholar]
14. Srinivas, N. et al Antiretroviral concentrations and surrogate measures of efficacy in the brain tissue and CSF of preclinical species. Xenobiotica 10.1080/00498254.2018.1539278. [e‐pub ahead of print]. [DOI] [PMC free article] [PubMed] [Google Scholar]
15. D'Argenio, D.Z. , Schumitzky, A. & Wang, X. ADAPT 5 User's Guide: Pharmacokinetic/Pharmacodynamic Systems Analysis Software. (Biomedical Simulations Resource, Los Angeles, CA, 2009). [Google Scholar]
16. Balani, S.K. , Kauffman, L.R. , Deluna, F.A. & Lin, J.H. Nonlinear pharmacokinetics of efavirenz (DMP‐266), a potent HIV‐1 reverse transcriptase inhibitor, in rats and monkeys. Drug Metab. Dispos. 27, 41–45 (1999). [PubMed] [Google Scholar]
17. Barten, D.M. , Cadelina, G.W. & Weed, M.R. Dosing, collection and quality control issues in cerebrospinal fluid research in animal models. Handb. Clin. Neurol. 146, 47–65 (2017). [DOI] [PubMed] [Google Scholar]
18. Yamaoka, K. , Nakagawa, T. & Uno, T. Application of Akaike's information criterion (AIC) in the evaluation of linear pharmacokinetic equations. J. Pharmacokinet. Pharmacodyn. 6, 165–175 (1978). [DOI] [PubMed] [Google Scholar]
19. Sheiner, L.B. The population approach to pharmacokinetic data analysis: rationale and standard data analysis methods. Drug Metab. Rev. 15, 153–171 (1984). [DOI] [PubMed] [Google Scholar]
20. Kappelhoff, B.S. et al Population pharmacokinetics of efavirenz in an unselected cohort of HIV‐1‐infected individuals. Clin. Pharmacokinet. 44, 849–861 (2005). [DOI] [PubMed] [Google Scholar]
21. Yilmaz, A. , Watson, V. , Dickinson, L. & Back, D. Efavirenz pharmacokinetics in cerebrospinal fluid and plasma over a 24‐hour dosing interval. Antimicrob. Agents Chemother. 56, 4583–4585 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
22. Thompson, C.G. et al Mass spectrometry imaging reveals heterogeneous efavirenz distribution within putative HIV reservoirs. Antimicrob. Agents Chemother. 59, 2944–2948 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
23. Marzolini, C. , Telenti, A. , Decosterd, L. , Biollaz, J. & Buclin, T. Efavirenz plasma levels can predict treatment failure and central nervous system side effects in HIV‐1‐infected patients. AIDS 15, 1193–1194 (2001). [DOI] [PubMed] [Google Scholar]
24. Gutiérrez, F. et al Prediction of neuropsychiatric adverse events associated with long‐term efavirenz therapy, using plasma drug level monitoring. Clin. Infect. Dis. 41, 1648–1653 (2005). [DOI] [PubMed] [Google Scholar]
25. Ståhle, L. , Moberg, L. , Svensson, J.‐O. & Sönnerborg, A. Efavirenz plasma concentrations in HIV‐infected patients: inter‐ and intraindividual variability and clinical effects. Ther. Drug Monit. 26, 267–270 (2004). [DOI] [PubMed] [Google Scholar]
26. Albright, A.V. , Erickson‐Viitanen, S. , O'Connor, M. , Frank, I. , Rayner, M.M. & Gonzalez‐Scarano, F. Efavirenz is a potent nonnucleoside reverse transcriptase inhibitor of HIV type 1 replication in microglia in vitro. AIDS Res. Hum. Retroviruses 16, 1527–1537 (2000). [DOI] [PubMed] [Google Scholar]
27. Curley, P. , Rajoli, R.K.R. , Moss, D.M. , Liptrott, N.J. , Letendre, S. & Owen, A. Efavirenz is predicted to accumulate in brain tissue: an in silico, in vitro and in vivo investigation. Antimicrob. Agents Chemother. 61, 1–10 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
28. Nicol, M . et al Differential Brain Tissue Penetration of Antiretrovirals and Fluconazole. In: Conference on Retroviruses and Opportunistic Infections (CROI); Abstract number: 474; Boston, Massachusetts (2018). <https://www.croiconference.org/sessions/differential-brainissue-penetration-antiretrovirals-and-fluconazole>. Accessed August 10, 2018.
29. Carroll, A. & Brew, B. HIV‐associated neurocognitive disorders: recent advances in pathogenesis, biomarkers, and treatment. F1000Research, 6, 312 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
30. Hagberg, L. et al Cerebrospinal fluid neopterin: an informative biomarker of central nervous system immune activation in HIV‐1 infection. AIDS Res. Ther. 7, 1–12 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
31. McGuire, J.L. , Gill, A.J. , Douglas, S.D. & Kolson, D.L. Central and peripheral markers of neurodegeneration and monocyte activation in HIV‐associated neurocognitive disorders. J. Neurovirol. 21, 439–448 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
32. Ke, A. , Barter, Z. , Rowland‐Yeo, K. & Almond, L. Towards a best practice approach in PBPK modeling: case example of developing a unified efavirenz model accounting for induction of CYPs 3A4 and 2B6. CPT Pharmacomet. Syst. Pharmacol. 5, 367–376 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
33. Shimizu, T. et al Autoinduction of MKC‐963 [(R)‐1‐(1‐Cyclohexylethylamino)‐4‐Phenylphthalazine] metabolism in healthy volunteers and its retrospective evaluation using primary human hepatocytes and CDNA‐expressed enzymes. Drug Metab. Dispos. 34, 950–954 (2006). [DOI] [PubMed] [Google Scholar]
34. Iwasaki, K. et al In vivo individual variations in pharmacokinetics of efavirenz in cynomolgus monkeys genotyped for cytochrome P450 2C9. Biopharm. Drug Dispos. 37, 379–383 (2016). [DOI] [PubMed] [Google Scholar]
35. Xu, C. & Desta, Z. In vitro analysis and quantitative prediction of efavirenz inhibition of eight cytochrome P450 (CYP) enzymes: major effects on CYPs 2B6, 2C8, 2C9 and 2C19. Drug Metab. Pharmacokinet. 28, 362–371 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
36. Sharma, V. & McNeill, J.H. To scale or not to scale: the principles of dose extrapolation. Br. J. Pharmacol. 157, 907–921 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
37. Zou, P. et al Applications of human pharmacokinetic prediction in first‐in‐human dose estimation. AAPS J. 14, 262–281 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
38. Peroni, R.N. et al Efavirenz is a substrate and in turn modulates the expression of the efflux transporter ABCG2/BCRP in the gastrointestinal tract of the rat. Biochem. Pharmacol. 82, 1227–1233 (2011). [DOI] [PubMed] [Google Scholar]
39. Ito, K. et al Quantitative membrane protein expression at the blood‐brain barrier of adult and younger cynomolgus monkeys. J. Pharm. Sci. 100, 3939–3950 (2011). [DOI] [PubMed] [Google Scholar]
40. Uchida, Y. et al Quantitative targeted absolute proteomics of human blood‐brain barrier transporters and receptors. J. Neurochem. 117, 333–345 (2011). [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Figure S1. Efavirenz concentrations in different parts of the brain in the uninfected and infected rhesus macaques.

Figure S2. Individual model predictions vs. observations in the plasma in rhesus macaques.

Figure S3. Goodness‐of‐fit plots for individual model predictions vs. observations in the plasma in rhesus macaques.

Figure S4. Goodness‐of‐fit diagnostic plots for the final clinical PK model in the plasma and CSF.

Table S1. Modeling methods for the preclinical and clinical EFV PK Model.

Table S2. Demographic information from the HIV‐positive patients in the National NeuroAIDS Tissue Consortium repository from whom efavirenz brain tissue concentrations were available.

Click here for additional data file.^{(874.3KB, pdf)}

[cts12620-bib-0001] 1. Marra, C.M. HIV‐associated neurocognitive disorders and central nervous system drug penetration: what next? Antivir. Ther. 20, 365–367 (2015). [DOI] [PubMed] [Google Scholar]

[cts12620-bib-0002] 2. Tan, I.L. & McArthur, J.C. HIV‐associated neurological disorders: a guide to pharmacotherapy. CNS Drugs 26, 123–134 (2012). [DOI] [PubMed] [Google Scholar]

[cts12620-bib-0003] 3. Letendre, S. Central nervous system complications in HIV disease: HIV‐associated neurocognitive disorder. Top Antivir. Med. 19, 137–142 (2011). [PMC free article] [PubMed] [Google Scholar]

[cts12620-bib-0004] 4. Srinivas, N. , Maffuid, K. & Kashuba, A.D.M. Clinical pharmacokinetics and pharmacodynamics of drugs in the central nervous system. Clin. Pharmacokinet. 57, 1059–1074 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]

[cts12620-bib-0005] 5. Letendre, S. Validation of the CNS penetration‐effectiveness rank for quantifying antiretroviral penetration into the central nervous system. Arch. Neurol. 65, 65–70 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]

[cts12620-bib-0006] 6. Steimer, J.‐L. , Mallet, A. , Golmard, J.‐L. & Boisvieux, J.‐F. Alternative approaches to estimation of population pharmacokinetic parameters: comparison with the nonlinear mixed‐effect model. Drug Metab. Rev. 15, 265–292 (1984). [DOI] [PubMed] [Google Scholar]

[cts12620-bib-0007] 7. World Health Organization (WHO) Model List of Essential Medicines (19th List). <http://www.who.int/topics/essential_medicines/en/Last> Accessed June 20, 2018.

[cts12620-bib-0008] 8. Gannon, P. , Khan, M. & Kolson, D. Current understanding of HIV‐associated neurocognitive disorders pathogenesis. Curr. Opin. Neurol. 24, 275–283 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]

[cts12620-bib-0009] 9. Ciccarelli, N. , Fabbiani, M. & Baldonero, E. Efavirenz associated with cognitive disorders in otherwise asymptomatic HIV‐infected patients. Neurology 76, 1403–1409 (2011). [DOI] [PubMed] [Google Scholar]

[cts12620-bib-0010] 10. Heaton, R. , Miller, S. , Taylor, M. & Grant, I. Revised comprehensive norms for an expanded Halstead Reitan battery: demographically adjusted neuropsychological norms for African American and Caucasian adults. (Psychological Assessment Resources, Lutz, FL, 2004). [Google Scholar]

[cts12620-bib-0011] 11. Blackstone, K. , Moore, D. , Franklin, D. , Clifford, D. , Collier, A. & Marra, C. Defining neurocognitive impairment in HIV: deficit scores versus clinical ratings. Clin. Neuropsychol. 26, 894–908 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]

[cts12620-bib-0012] 12. Carey, C.L. et al Predictive validity of global deficit scores in detecting neuropsychological impairment in HIV infection predictive validity of global deficit scores in detecting neuropsychological impairment in HIV infection. J. Clin. Exp. Neuropsychol. 26, 307–319 (2004). [DOI] [PubMed] [Google Scholar]

[cts12620-bib-0013] 13. Rezk, N.L. , Tidwell, R.R. & Kashuba, A.D.M. High‐performance liquid chromatography assay for the quantification of HIV protease inhibitors and non‐nucleoside reverse transcriptase inhibitors in human plasma. J. Chromatogr. B Anal. Technol. Biomed. Life Sci. 805, 241–247 (2004). [DOI] [PubMed] [Google Scholar]

[cts12620-bib-0014] 14. Srinivas, N. et al Antiretroviral concentrations and surrogate measures of efficacy in the brain tissue and CSF of preclinical species. Xenobiotica 10.1080/00498254.2018.1539278. [e‐pub ahead of print]. [DOI] [PMC free article] [PubMed] [Google Scholar]

[cts12620-bib-0015] 15. D'Argenio, D.Z. , Schumitzky, A. & Wang, X. ADAPT 5 User's Guide: Pharmacokinetic/Pharmacodynamic Systems Analysis Software. (Biomedical Simulations Resource, Los Angeles, CA, 2009). [Google Scholar]

[cts12620-bib-0016] 16. Balani, S.K. , Kauffman, L.R. , Deluna, F.A. & Lin, J.H. Nonlinear pharmacokinetics of efavirenz (DMP‐266), a potent HIV‐1 reverse transcriptase inhibitor, in rats and monkeys. Drug Metab. Dispos. 27, 41–45 (1999). [PubMed] [Google Scholar]

[cts12620-bib-0017] 17. Barten, D.M. , Cadelina, G.W. & Weed, M.R. Dosing, collection and quality control issues in cerebrospinal fluid research in animal models. Handb. Clin. Neurol. 146, 47–65 (2017). [DOI] [PubMed] [Google Scholar]

[cts12620-bib-0018] 18. Yamaoka, K. , Nakagawa, T. & Uno, T. Application of Akaike's information criterion (AIC) in the evaluation of linear pharmacokinetic equations. J. Pharmacokinet. Pharmacodyn. 6, 165–175 (1978). [DOI] [PubMed] [Google Scholar]

[cts12620-bib-0019] 19. Sheiner, L.B. The population approach to pharmacokinetic data analysis: rationale and standard data analysis methods. Drug Metab. Rev. 15, 153–171 (1984). [DOI] [PubMed] [Google Scholar]

[cts12620-bib-0020] 20. Kappelhoff, B.S. et al Population pharmacokinetics of efavirenz in an unselected cohort of HIV‐1‐infected individuals. Clin. Pharmacokinet. 44, 849–861 (2005). [DOI] [PubMed] [Google Scholar]

[cts12620-bib-0021] 21. Yilmaz, A. , Watson, V. , Dickinson, L. & Back, D. Efavirenz pharmacokinetics in cerebrospinal fluid and plasma over a 24‐hour dosing interval. Antimicrob. Agents Chemother. 56, 4583–4585 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]

[cts12620-bib-0022] 22. Thompson, C.G. et al Mass spectrometry imaging reveals heterogeneous efavirenz distribution within putative HIV reservoirs. Antimicrob. Agents Chemother. 59, 2944–2948 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]

[cts12620-bib-0023] 23. Marzolini, C. , Telenti, A. , Decosterd, L. , Biollaz, J. & Buclin, T. Efavirenz plasma levels can predict treatment failure and central nervous system side effects in HIV‐1‐infected patients. AIDS 15, 1193–1194 (2001). [DOI] [PubMed] [Google Scholar]

[cts12620-bib-0024] 24. Gutiérrez, F. et al Prediction of neuropsychiatric adverse events associated with long‐term efavirenz therapy, using plasma drug level monitoring. Clin. Infect. Dis. 41, 1648–1653 (2005). [DOI] [PubMed] [Google Scholar]

[cts12620-bib-0025] 25. Ståhle, L. , Moberg, L. , Svensson, J.‐O. & Sönnerborg, A. Efavirenz plasma concentrations in HIV‐infected patients: inter‐ and intraindividual variability and clinical effects. Ther. Drug Monit. 26, 267–270 (2004). [DOI] [PubMed] [Google Scholar]

[cts12620-bib-0026] 26. Albright, A.V. , Erickson‐Viitanen, S. , O'Connor, M. , Frank, I. , Rayner, M.M. & Gonzalez‐Scarano, F. Efavirenz is a potent nonnucleoside reverse transcriptase inhibitor of HIV type 1 replication in microglia in vitro. AIDS Res. Hum. Retroviruses 16, 1527–1537 (2000). [DOI] [PubMed] [Google Scholar]

[cts12620-bib-0027] 27. Curley, P. , Rajoli, R.K.R. , Moss, D.M. , Liptrott, N.J. , Letendre, S. & Owen, A. Efavirenz is predicted to accumulate in brain tissue: an in silico, in vitro and in vivo investigation. Antimicrob. Agents Chemother. 61, 1–10 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]

[cts12620-bib-0028] 28. Nicol, M . et al Differential Brain Tissue Penetration of Antiretrovirals and Fluconazole. In: Conference on Retroviruses and Opportunistic Infections (CROI); Abstract number: 474; Boston, Massachusetts (2018). <https://www.croiconference.org/sessions/differential-brainissue-penetration-antiretrovirals-and-fluconazole>. Accessed August 10, 2018.

[cts12620-bib-0029] 29. Carroll, A. & Brew, B. HIV‐associated neurocognitive disorders: recent advances in pathogenesis, biomarkers, and treatment. F1000Research, 6, 312 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]

[cts12620-bib-0030] 30. Hagberg, L. et al Cerebrospinal fluid neopterin: an informative biomarker of central nervous system immune activation in HIV‐1 infection. AIDS Res. Ther. 7, 1–12 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]

[cts12620-bib-0031] 31. McGuire, J.L. , Gill, A.J. , Douglas, S.D. & Kolson, D.L. Central and peripheral markers of neurodegeneration and monocyte activation in HIV‐associated neurocognitive disorders. J. Neurovirol. 21, 439–448 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]

[cts12620-bib-0032] 32. Ke, A. , Barter, Z. , Rowland‐Yeo, K. & Almond, L. Towards a best practice approach in PBPK modeling: case example of developing a unified efavirenz model accounting for induction of CYPs 3A4 and 2B6. CPT Pharmacomet. Syst. Pharmacol. 5, 367–376 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]

[cts12620-bib-0033] 33. Shimizu, T. et al Autoinduction of MKC‐963 [(R)‐1‐(1‐Cyclohexylethylamino)‐4‐Phenylphthalazine] metabolism in healthy volunteers and its retrospective evaluation using primary human hepatocytes and CDNA‐expressed enzymes. Drug Metab. Dispos. 34, 950–954 (2006). [DOI] [PubMed] [Google Scholar]

[cts12620-bib-0034] 34. Iwasaki, K. et al In vivo individual variations in pharmacokinetics of efavirenz in cynomolgus monkeys genotyped for cytochrome P450 2C9. Biopharm. Drug Dispos. 37, 379–383 (2016). [DOI] [PubMed] [Google Scholar]

[cts12620-bib-0035] 35. Xu, C. & Desta, Z. In vitro analysis and quantitative prediction of efavirenz inhibition of eight cytochrome P450 (CYP) enzymes: major effects on CYPs 2B6, 2C8, 2C9 and 2C19. Drug Metab. Pharmacokinet. 28, 362–371 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]

[cts12620-bib-0036] 36. Sharma, V. & McNeill, J.H. To scale or not to scale: the principles of dose extrapolation. Br. J. Pharmacol. 157, 907–921 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]

[cts12620-bib-0037] 37. Zou, P. et al Applications of human pharmacokinetic prediction in first‐in‐human dose estimation. AAPS J. 14, 262–281 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]

[cts12620-bib-0038] 38. Peroni, R.N. et al Efavirenz is a substrate and in turn modulates the expression of the efflux transporter ABCG2/BCRP in the gastrointestinal tract of the rat. Biochem. Pharmacol. 82, 1227–1233 (2011). [DOI] [PubMed] [Google Scholar]

[cts12620-bib-0039] 39. Ito, K. et al Quantitative membrane protein expression at the blood‐brain barrier of adult and younger cynomolgus monkeys. J. Pharm. Sci. 100, 3939–3950 (2011). [DOI] [PubMed] [Google Scholar]

[cts12620-bib-0040] 40. Uchida, Y. et al Quantitative targeted absolute proteomics of human blood‐brain barrier transporters and receptors. J. Neurochem. 117, 333–345 (2011). [DOI] [PubMed] [Google Scholar]

PERMALINK

Predicting Efavirenz Concentrations in the Brain Tissue of HIV‐Infected Individuals and Exploring their Relationship to Neurocognitive Impairment

Nithya Srinivas

Sarah Beth Joseph

Kevin Robertson

Laura P Kincer

Prema Menezes

Lourdes Adamson

Amanda P Schauer

Kimberly H Blake

Nicole White

Craig Sykes

Paul Luciw

Joseph J Eron

Alan Forrest

Richard W Price

Serena Spudich

Ronald Swanstrom

Angela DM Kashuba

Abstract

Study Highlights.

Methods

ARV dosing in rhesus macaques and preclinical study design

Clinical study participants

Clinical study design

Neuropsychological test evaluations

Quantification of EFV concentration in the fluid and tissue matrices

Development of the preclinical PK model

Development of the clinical PK model

PK/PD correlation analysis

Statistical analysis

Results

PK model for EFV in rhesus macaques

Figure 1.

Table 1.

Figure 2.

Clinical study demographics

Table 2.

PK model of EFV in HIV‐positive participants

Figure 3.

Figure 4.

PK/PD correlation analysis

Figure 5.

Discussion

Conclusions

Funding

Conflict of Interest

Author Contributions

Supporting information

Acknowledgments

References

Associated Data

Supplementary Materials

ACTIONS

PERMALINK

RESOURCES

Similar articles

Cited by other articles

Links to NCBI Databases