Co-occurrence of medical conditions: Exposing patterns through probabilistic topic modeling of snomed codes

Abstract

Patients associated with multiple co-occurring health conditions often face aggravated complications and less favorable outcomes. Co-occurring conditions are especially prevalent among individuals suffering from kidney disease, an increasingly widespread condition affecting 13% of the general population in the US. This study aims to identify and characterize patterns of co-occurring medical conditions in patients employing a probabilistic framework. Specifically, we apply topic modeling in a non-traditional way to find associations across SNOMED-CT codes assigned and recorded in the EHRs of > 13,000 patients diagnosed with kidney disease. Unlike most prior work on topic modeling, we apply the method to codes rather than to natural language. Moreover, we quantitatively evaluate the topics, assessing their tightness and distinctiveness, and also assess the medical validity of our results. Our experiments show that each topic is succinctly characterized by a few highly probable and unique disease codes, indicating that the topics are tight. Furthermore, inter-topic distance between each pair of topics is typically high, illustrating distinctiveness. Last, most coded conditions grouped together within a topic, are indeed reported to co-occur in the medical literature. Notably, our results uncover a few indirect associations among conditions that have hitherto not been reported as correlated in the medical literature.

1. Introduction

Patients associated with multiple co-occurring health conditions often face aggravated complications and less favorable treatment outcomes. The Center for Disease Control and Prevention reports that in the US alone, one in four individuals suffers from multiple health conditions, while the rate is three times higher among individuals 65 or older [1]. Co-occurring conditions are especially prevalent among individuals diagnosed with kidney disease, an increasingly widespread condition affecting 13% of the general population and 18% of hospitalized patients in the US [2]. Kidney disease is associated with a large number of complications, including cardiovascular disease, metabolic bone disease and diabetes [3]. Identifying conditions that tend to co-occur in the context of kidney disease, followed by evidence based interventions, can slow or prevent a patient’s progression to advanced stages of the condition. In this study, we thus aim to identify co-occurrence patterns of medical conditions among individuals who have kidney disease.

We analyzed, in collaboration with physicians and researchers from Christiana Care Health System, Electronic Health Records (EHRs) of > 13,000 patients, gathered over a period of eight years, from primary care and specialty practices across Delaware associated with Christiana Care, the largest health-system in Delaware. We included patients’ records in our dataset, if at any time during follow-up, there was an indication of a decline in kidney function, determined by a lower than normal (< 60 mL/min/1.73m²), estimated Glomerular filtration rate (GFR), a common marker of kidney function. Each record includes attributes such as vital signs, demographics and SNOMED codes for diagnosed conditions, recorded during multiple office visits and hospital stays.

We focus our analysis on the diagnosed conditions attribute in the dataset, represented through the healthcare terminology of SNOMED-CT codes [4]. SNOMED is specifically designed to capture detailed information during clinical care, enabling clinicians to choose appropriate conditions from a predefined fine grained list, and is thus a structured non-text representation of patients’ diagnoses. Ours is the first study that utilizes SNOMED codes for identifying patterns of co-occurring conditions. The large number of patients, the wide timespan in our EHRs and the use of SNOMED codes to represent diagnosed conditions, yield a large scale dataset which supports identifying patterns of co-occurring conditions.

Specifically, we adopt a data driven approach to identify many-to-many associations among a broad group of medical conditions associated with patients who have kidney disease. We apply a probabilistic topic modeling method, Latent Dirichlet Allocation (LDA) to SNOMED codes [5]. Topic modeling has primarily been used for identifying thematic structures (topics) in unstructured text data. In contrast, we apply topic modeling over structured non-text SNOMED codes to automatically organize diagnoses associated with patients’ EHRs into groups of correlated coded conditions, where each group represents a topic, formally defined as a probability distribution over codes. In our study, a patient file, which includes all coded conditions with which the patient has been diagnosed, is viewed as a document, and each code is treated as a word. We hypothesize that a set of coded conditions, tending to co-occur in patients, also demonstrate a high probability to be associated with a specific topic. In preliminary studies (not shown), we employed simpler unsupervised methods such as K-means and co-sine-similarity-based clustering to identify co-occurrence patterns of medical conditions, but unlike topic model those have not revealed meaningful, clinically relevant associations.

Most previous studies, aiming to identify associations among diseases have focused on exposing associations among a few pre-defined specific conditions [6–13]. For instance, Farran et al. targeted association between diabetes and hypertension [12], while a more recent work by Chen et al. explored association between colorectal cancer and obesity [13]. In contrast, ours is the first study aiming to find many-to-many associations among a broad group of conditions, doing so within a specific disease context, namely, kidney disease. Our results thus show highly informative groups of meaningful connections (i.e. informative topics), which manifest themselves within the context of the disease.

A handful of earlier studies explored association among a broad group of conditions [14–16] utilizing textual data present in patient records. In contrast, we utilize non-text SNOMED codes that are designed to unambiguously record diagnosed conditions during clinical care. Hence, using SNOMED as the basis for the analysis can directly expose connections among conditions.

Topic modeling has been broadly used for text analysis [5] and image processing [17] applications. Recently, topic models have also been applied in the biomedical domain [18–23], mostly applying the method to text data (e.g., physicians’ notes, biomedical literature). Only a few studies have applied topic models to non-text data as we do here [24–27]. Most recently, a study by Chen et al. [27] used topic modeling for predicting clinical order-sets from inpatient hospitalization records, with reported performance of 47% precision and 24% recall. In contrast to our study, which aims to expose patterns of co-occurring medical conditions while rigorously assessing topic quality, Chen et al. aimed to predict clinical order-sets using topic modeling as tools without evaluating the obtained topics themselves.

The work most related to ours, a study by Li et al. [26], utilizes topic modeling to cluster patient diagnosis-groups, represented by ICD-9 codes, for identifying comorbidity. Notably, ICD-9 codes are defined at a coarser granularity level than SNOMED codes and thus capture less detailed information during clinical care, than SNOMED codes [28]. Moreover, the dataset used in that work was relatively small, comprising only 4644 patients. Most importantly, unlike our study, the study by Li et al. does not ensure that topics indeed capture clinically-relevant associations; nor evaluates the topics quantitatively.

Preliminary steps of this study were discussed in our earlier extended abstract [29]. Here we present additional experiments and results and extended analysis. Specifically, we conduct a thorough quantitative evaluation of the performance of our model, and an assessment of the medical validity of our results. Moreover, we include results obtained over an additional dataset consisting of many thousands of hospitalization records, which were not available for the preliminary study.

We assess the performance of our method qualitatively as well as quantitatively. For qualitative evaluation, we assess the clinical validity of our results by examining whether the conditions that show high probability to be associated within a topic are known to co-occur according to the medical literature. When applying an unsupervised method such as topic modeling to data, the uncovered groups (topics) may not always carry a useful cohesive semantics. Hence, it is important to quantitatively assess whether the topics are indeed informative. Unlike most other studies on topic modeling, we quantitatively evaluate the topics obtained from our model, by assessing their tightness and distinctiveness.

Tightness signifies that the codes characterizing the topic are highly correlated with each other and thus capture strong non-arbitrary associations. Distinctiveness across topics indicates that codes that are highly probable to be grouped under a specific topic, are unlikely to be associated with other topics. Furthermore, to verify that the topics are informative, we measure the entropy of each topic, and show entropy that is significantly lower than that of the uniform distribution (i.e. high information contents).

We applied our method to two datasets collected from the patients, one comprising office visit records and the other hospitalization records. In both cases, we obtained informative, distinct and tight topics that align well with known co-occurrences among conditions cited in the medical literature. We note that similar disease themes emerge in topics inferred from each of the two sets, but also that the conditions grouped together under topics obtained from the hospitalization dataset typically indicate higher severity than those grouped under topics inferred from office visits. The difference is expected, as patients who are hospitalized often manifest more severe conditions (such as congestive heart failure and renal failure), than patients who are not.

Our method’s ability to generate meaningful topics from both datasets, where one comprises more common conditions (office visits) and the other more severe ones (hospitalization cases), demonstrates its effectiveness in reliably exposing co-occurring conditions. Notably, our results uncover a few indirect associations among conditions that have hitherto gone unreported, suggesting that topic modeling over codes can expose yet unnoticed associations.

2. Material and methods

2.1. Datasets

Our datasets consist of information gathered from office visit records of 13,111 patients in Delaware, who have shown evidence of decreased kidney function during these visits, and from the hospitalization records of a subset of 9,530 patients who had at least one hospital visit. The records included in the office visit set and those included in the hospitalization set do not overlap. Each record contains attributes such as age, ethnicity, and diagnosed conditions, collected between August 2007 and July 2015. As noted, we focus solely on the diagnosed conditions attribute, represented via SNOMED codes.

We extracted the office visit records from the Christiana Care Health System outpatient EHR (Centricity™, GE) and the hospitalization records from the Christiana Care inpatient EHR (PowerChart^R, Cerner Millennium). Patients’ identifiers were removed from records in both the office visit and hospitalization sets. The records were then transformed and standardized into a common data model, the Observational Medical Outcomes Partnership (OMOP) [30]. SNOMED is one of the standardized vocabularies available in the OMOP model. This project was approved by the Christiana Care IRB with a waiver of consent according to 45CFR46.116d.

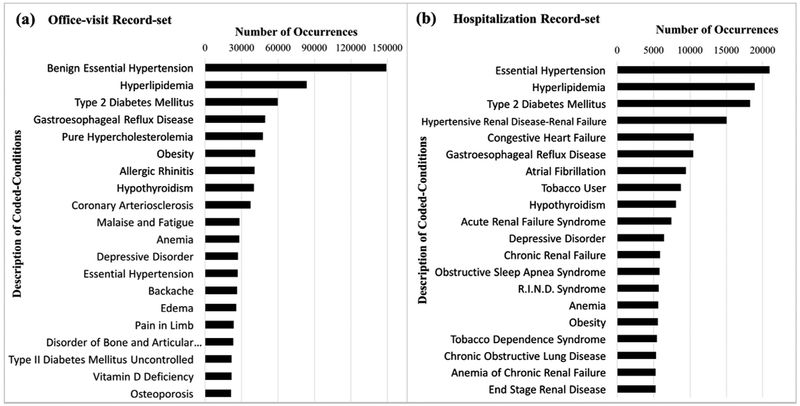
Table 1 summarizes key characteristics of the office visit and the hospitalization datasets. As shown in the table, the patients’ age is quite high; the mean age is 70 (σ = 12) for the office-visit set and 67 (σ = 14) for the hospitalization set. The vast majority of patients (94%) are above 50, 66% above 65, while less than 1% are below 35. Fig. 1 shows descriptions of the twenty most frequent codes appearing in each record set, in decreasing order of occurrence frequency.

Table 1.

Key characteristics of the office visit and hospitalization datasets. The leftmost column lists the characteristics; the middle column shows the corresponding values in the office visit set, while the rightmost column shows the values in the hospitalization set.

	Office visit set	Hospitalization set
Number of Patients	13,111	9,528
Age Range (25th –75th Percentile)	60–80	60–80
Mean Age (σ)	70 (12)	67 (14)
% Female	60%	61%
% Male	40%	39%
Avg. Number of Visits per Patient	17	5

Fig. 1.

Number of occurrences of the twenty most frequent conditions in the office visit record set (a) and in the hospitalization record set (b). Each bar represents the number of occurrences of each condition in the respective record set. For clarity, we show the descriptive name associated with each SNOMED code rather than the code itself.

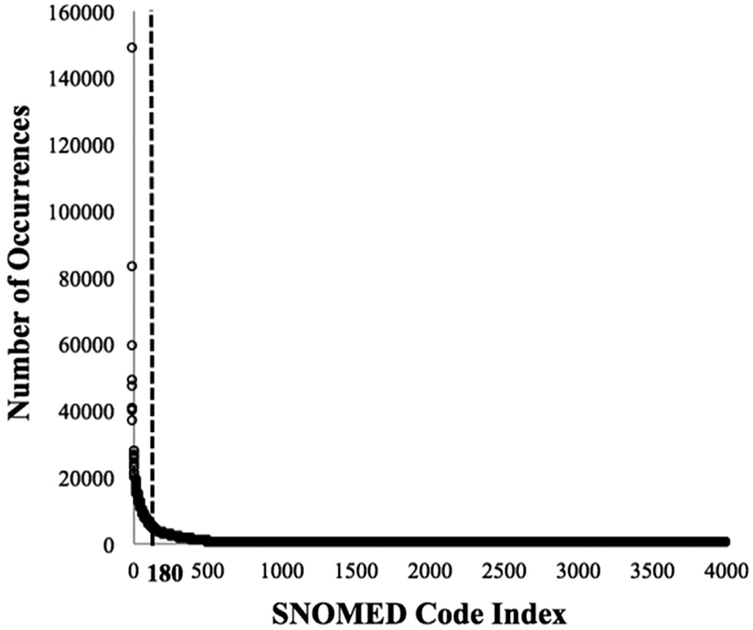
To create a data-matrix that can be processed via topic modeling we make several data organization and preprocessing choices. Traditionally in topic modeling, a natural language word is the basic data unit, while the set of unique words is referred to as the vocabulary. In contrast, in our study, we use coded conditions, represented as SNOMED codes, rather than words, such that the vocabulary is the set of unique codes. To determine the number of unique codes included in our vocabulary, denoted V, we conducted multiple experiments while varying the vocabulary size, considering all codes occurring in the datasets and reduced code sets accounting for 90% and for 80% of the cumulative frequency in each dataset. As further discussed in Section 3, the larger of these vocabularies do not perform as well. We thus focus here on the vocabulary comprising the set of codes accounting for 80% of the cumulative frequency. Of the 4,000 codes in the office visit set, just 180 account for 80% of the cumulative frequency (see Fig. 2). To avoid sparsity in the data-matrix, we limit our vocabulary to these 180 frequent codes (V = 180). Similarly, when working with the hospitalization set, we limit our vocabulary to 250 of the 4,000 codes (V = 250), which accounts again for 80% of the cumulative frequency.

Fig. 2.

Number of occurrences for each of the 4,000 SNOMED codes in the office visit set. The y-axis shows the number of times each SNOMED code occurs in the set; the x-axis corresponds to indices representing the 4,000 SNOMED codes, sorted in decreasing order of number of occurrences.

After defining the vocabulary, we preprocess the original patient files to represent each patient in a bag-of-codes format (analogous to the bag-of-words representation of documents) for applying topic modeling. Bag-of-codes accounts for the number of times a code appears in a patient file. Recurring conditions that persistently recur multiple times in the file (e.g. chronic conditions), and often indicate a higher level of severity, thus incur a higher weight (counts). In contrast, conditions occurring only sporadically in the patient’s history (e.g. occasional cough or headache) receive a lower weight, and as such play a lesser role in the topic profiles. We also experimented with two additional common representations, namely, binary (0/1) and tf-idf (term frequency, inverse document frequency), which proved less effective as we further discuss in Section 3.

Each patient file, F_i (1 ≤ i ≤ M), is converted to a vector of codes, $F_i=\langle c_1^i,\dots ,c_{N_i}^i\rangle$, where M denotes the number of patients in the dataset and N_i is the total number of code occurrences in the i^th patient file. Each code, $c_j^i$, in the vector is one of the V SNOMED codes in our vocabulary, viewed as a value taken by a respective random variable, C_j (1 ≤ j ≤ N_i), denoting the code value occurring in the j^th position of the i^th patient file. We note that any of the V codes in our vocabulary can appear at any position in a patient file.

We process all patient files, F_i, (1 ≤ i ≤ M), to create a data matrix where each row represents a patient, and each column represents a SNOMED code included in the vocabulary, such that each cell <p, c> holds the number of times a patient p was diagnosed with condition c. Each patient in the record set is thus associated with a V-dimensional vector, where V denotes the number of unique codes in our vocabulary and each vector entry corresponds to the occurrence frequency of a condition within the patient’s file. We refer to each such vector as a patient-conditions record, and to the collection of all vectors as the patient-conditions corpus. The latter consists of a 13,111 × 180 matrix for the office visits dataset, and a 9,528 × 250 matrix for the hospitalization dataset.

Studies analyzing clinical data often take into account age as a possible confounding factor affecting disease severity and number of hospitalizations or office visits, and consider stratifying the population by age. In this study we applied similar consideration, and inspected the variation in the total number of code occurrences within patient records as a function of age (data not shown). We have found that the the total number of times coded-conditions are assigned to each patient do not vary significantly with age. This finding is not surprising, because as noted above, the patients in our dataset are predominantly ( > 94%) older than 50, and are all (even the younger ones) at moderate-to-severe stages of the disease. As such, physician visits are frequent and code distributions do not significantly vary by age throughout the population; we thus apply topic-modeling to the population as a whole without any further stratification.

Table 2 shows examples of five patient-conditions records, where each row corresponds to a patient’s record and each column corresponds to a condition. Due to limited space, only eight conditions are shown. Each cell lists the number of times a patient has been diagnosed with the condition.

Table 2.

Examples of five of the 13,111 patient-conditions office-visits records. The leftmost column shows patient IDs and the topmost row shows eight of the 180 conditions. Each cell lists the number of times a patient has been diagnosed with the respective condition, during the eight-year period for which data was gathered.

Patient-ID╲Conditions	Hypertension	Type 2 Diabetes Mellitus	Morbid Obesity	Goiter	Vitamin D Deficiency	Anemia	Pain in Limb	Osteoporosis
1	17	17	10	2	2	9	2	2
2	0	0	0	0	5	0	5	5
3	8	8	8	0	0	8	0	0
4	0	0	0	0	20	0	20	20
5	10	10	10	10	0	10	0	0

2.2. Latent Dirichlet Allocation (LDA)

We employ LDA to model patient records as though they were generated by sampling from a mixture of K underlying topics, where a topic is a multinomial distribution over all coded conditions in our vocabulary [5]. The generative process for each patient file consists of the following steps:

First, a multinomial distribution over V codes for the t^th topic, denoted Φ_t (1 ≤ t ≤ K), is obtained by sampling from a Dirichlet distribution with parameter α; Φ_t represents the conditional probability of a code to occur in the t^th topic. Next, for each patient file, F_i, a multinomial distribution over K topics, denoted θ_i, is sampled from a Dirichlet distribution with parameter β; θ_i represents the conditional probability of the file to be associated with each of the K topics. Subsequently, for each code-position, j, in the file, F_i: (1) A topic is drawn by sampling from θ_i; the selected topic at position j in F_i, is denoted $z_j^i\in \{1,\dots ,K\}$; (2) Given the topic $z_j^i$ a code $c_j^i$ is drawn by sampling the topic-code distribution, ${\Phi }_{z_j^i}$.

The model parameters are learnt iteratively for different values of K, where K ranges from 5 to 100, and the data log-likelihood is calculated for each value of K. To determine the optimal number of topics, we identify the K value that maximizes the data log-likelihood, which is defined as: ${\sum }_{i=1}^M\mathit{log}\int \left\{{\sum }_z[{\prod }_{j=1}^{N_i}\mathit{Pr}(c_j^i\mid z_j^i,{\Phi }_{z_j^i})\mathit{Pr}(z_j^i\mid {\theta }_i)]\right\}\mathit{Pr}({\theta }_i\mid \beta )d{\theta }_i$, (where M denotes the number of patients in the corpus and N_i denotes the total number of code occurrences in the i^th patient file, as defined earlier. See Hornik et al. [31] for details.)

To learn the model parameters based on our data and obtain the data log-likelihood, we employ the R topicmodels library [32], which uses Gibbs sampling. We use the default parameter values, set in the topicmodels library, for the parameter β (0.1) and for the initial value of the parameter α (50/M) [31].

2.3. Jensen-Shannon divergence (JSD)

JSD is a symmetric measure of similarity between two probability distributions [33]. Let $\overrightarrow{X}=\langle x_1,\dots ,x_N\rangle$ and $\overrightarrow{Y}=\langle y_1,\dots ,y_N\rangle$ represent two N-dimensional multinomial distributions. The JSD between $\overrightarrow{X}$ and $\overrightarrow{Y}$ is defined as: $\mathit{JSD}(\overrightarrow{X}\Vert \overrightarrow{Y})=\frac{1}{2}{\sum }_{i=1}^N{x}_i\mathit{log}\left(\frac{x_i}{m_i}\right)+\frac{1}{2}{\sum }_{i=1}^N{y}_i\mathit{log}\left(\frac{y_i}{m_i}\right)$, where the vector $\overrightarrow{m}=\langle m_1,\dots ,m_N\rangle$ represents the mean distribution of $\overrightarrow{X}$ and $\overrightarrow{Y}$, calculated as: $m_i=\frac{1}{2}(x_i+y_i)$ (where 0 ⩽ x_i,y_i ⩽ 1 and ${\sum }_{i=1}^N{x}_i={\sum }_{i=1}^N{y}_i=1$).

The JSD value is 0 for identical distributions, and approaches ln(2) ( ~0.693) as the two distributions become more different from one another. We use JSD to calculate the inter-topic distance between each pair of topics, where the distribution dimension N is the number of coded conditions in our vocabulary. In the work presented here, N = 180 for the office visit dataset and N = 250 for the hospitalization set.

3. Experiments and results

We applied the LDA implementation provided via the R topicmodels library [32], to the patient-conditions corpus, where each of the resulting topics is a distribution over coded conditions. We experimented with different number of topics, K, ranging from 5 to 100. To avoid the use of poor initial estimates as part of the Gibbs sampling process, we discarded 4,000 samples in the burn-in period – the initial stage of the sampling process in which the Gibbs samples are poor estimates of the posterior. We repeated each experiment five times employing different initial seeds, and calculated an average log-likelihood value. We saved the initial seeds so that the results can be reproduced.

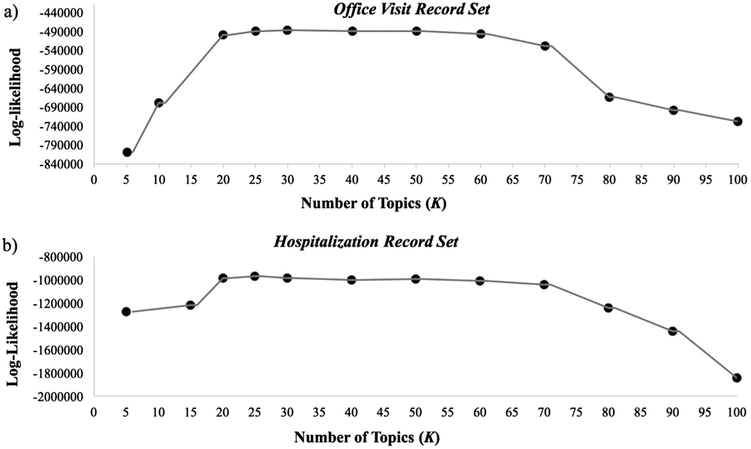
As mentioned in Section 2.2, to determine the optimal number of topics, we identified the value K that maximizes the data log-likelihood. Fig. 3 shows plots of the data log-likelihood as a function of the number of topics (K), for both the office-visit (Fig. 3a) and the hospitalization (Fig. 3b) sets. As demonstrated in the figure, for both record sets, the log-likelihood shows almost no change as K ranges between 20 and 30, while the maximum value log-likelihood is obtained at K = 30 for the office visit set and K = 25 for the hospitalization set. As 20 topics are easier to describe, visualize and evaluate, we report results obtained for K = 20.

Fig. 3.

Data log-likelihood as a function of the number of topics, K, for the office visit record set (a) and for the hospitalization record set (b). The x-axes correspond to the number of topics (K) ranging from 0 to 100; the y-axes correspond to the data log-likelihood values.

Table 3 shows examples of five characteristic topics from the 20 identified by our model from the office visit set. For each of the five displayed topics, we list the conditions that are assigned a probability greater than a threshold value – set here to 0.01, along with their respective probabilities. The term distributions associated with the other 15 topics show similar characteristics. The results obtained over the hospitalization set are similar (Table 4).

Table 3.

Examples of five characteristic topics from among the twenty topics identified by our model over the office visit dataset. Each column lists conditions whose association probability with the respective topic is higher than 0.01, along with the respective probability, Pr(C∣T_i), where C denotes a condition and T_i denotes the i^th topic.

Topic 1	Pr(C∣T1)	Topic 2	Pr(C∣T2)	Topic 3	Pr(C∣T3)	Topic 4	Pr(C∣T4)	Topic 5	Pr(C∣T5)
Type 2 diabetes mellitus	.369	Pain in limb	.195	Hypothyroidism	.400	Allergic rhinitis	.361	Atrial fibrillation	.197
Type II diabetes mellitus uncontrolled	.132	Arthralgia of the lower leg	.166	Disorder of bone and articular cartilage	.229	Osteoporosis	.186	Congestive heart failure	.172
Mixed hyperlipidemia	.099	Low back pain	.144	Vitamin D deficiency	.161	Acute sinusitis	.111	Arthropathy	.112
Disorder associated with type 2 diabetes mellitus	.088	Shoulder joint pain	.128	Anemia	.078	Benign essential hypertension	.110	Peripheral venous insufficiency	.085
Neurologic disorder associated with type 2 diabetes mellitus	.074	Chronic renal failure	.107	Diaphragmatic hernia	.044	Female sexual arousal disorder	.076	Metabolic syndrome	.083
Proteinuria	.064	Arthralgia of the pelvicregion and thigh	.092	Degenerative joint disease of pelvis	.036	Chronic sinusitis	.061	Transient cerebral ischemia	.062
Morbid obesity	.063	Thoracic radiculitis	.071	Abnormal findings on diagnostic imaging of breast	.034	Acute upper respiratory infection	.046	Cerebral infarction due to thrombosis of cerebral arteries	.061
Benign essential hypertension	.038	Joint pain	.036	Goiter	.014	Disease of liver	.043	Syncope and collapse	.050
Vitamin D deficiency	.032	Acute upper respiratory infection	.030	Benign essential hypertension	.002	Acute bronchitis	.004	Conduction disorder of the heart	.049
Diabetic-oculopathy associated with type 2 diabetes mellitus	.029	Chronic rhinitis	.029	Conduction disorder of the heart	.001	Impacted cerumen	.002	Cellulitis-abscess of lower leg	.043
								Type 1 diabetes Mellitus	0.038
								Non-toxic multinodular goiter	0.034
								Gastro intestinal hemorrhage	0.034
	.989		.998		1.00		1.00		.997
CUMULATIVE PROBABILITY

Table 4.

Examples of five characteristic topics from among the twenty topics identified by our model over the hospitalization dataset. Each column lists description of the top-codes whose association probability with the respective topic is higher than 0.01, along with the respective probability, Pr(C∣T_i), where C denotes a coded-condition and T_i denotes the i^th topic.

Topic 1	Pr(C∣T1)	Topic 2	Pr(C∣T2)	Topic 3	Pr(C∣T3)	Topic 4	Pr(C∣T4)	Topic 5	Pr(C∣T5)
Hypertensive Renal Disease with Renal Failure	.211	Chronic Obstructive Lung Disease	.220	Gastroesophageal Reflux Disease	.325	Atrial Fibrillation	.444	Congestive Heart Failure	.325
End Stage Renal Disease	.171	Tobacco User	.192	Osteoarthritis	.139	Patient with Cardiac Pacemaker	.097	Cardiomyopathy	.110
Anemia of Chronic Renal Failure	.149	Dyspnea	.058	Osteoporosis	.089	Benign Prostatic Hypertrophy without Outflow Obstruction	.078	Automatic implantable cardiac defibrillator	.094
Dialysis Finding	.138	Pneumonia	.052	Rheumatoid Arthritis	.067	Hyperlipidemia	.068	Chronic ischemic heart disease	.078
Hyper para-thyroidism due to Renal Insufficiency	.047	Acute Exacerbation of Chronic Obstructive Airways Disease	.046	Anemia	.059	Allergic Reaction	.037	Chronic pulmonary heart disease	.072
Renal Osteodystrophy	.039	Hypoxemia	.040	Glaucoma	.047	Atrial Flutter	.034	Mitral Valve Disorder	.055
Renal Disorder Associated with type 2 Diabetes Mellitus	.028	Chronic Pulmonary Heart Disease	.039	Hearing Loss	.042	Blood Coagulation Disorder	.033	Acute Chronic Systolic Heart Failure	.052
Nephritis	.027	Hyperlipidemia	.034	Systemic Lupus Erythematosus	.031	Sinus Node Dysfunction	.032	Chronic Systolic Heart Failure	.049
Hyperkalemia	0.026	Chronic Asthmatic Bronchitis	.026	Vitamin D Deficiency	.023	Conduction Disorder of the Heart	.021	Left Bundle Branch Block	.029
Hypervolemia	0.017	Acute Respiratory Failure	.024	Diaphragmatic Hernia	.022	Right Bundle Branch Block	.017	Dyspnea	.028
CKD 4	0.017	Chronic Diastolic Heart Failure	.022	Localized Osteoarthrosis	.020	Pleural Effusion	.013	Paroxysmal Ventricular Tachycardia	.024
Complication of Internal Anastomosis	0.016	Acute Chronic Diastolic Heart Failure	.018	Dehydration	.018	Rheumatic Disease of Tricuspid Valve	.013	Hypertensive Heart and Renal Disease with Congestive Heart Failure	.021
Complication of Implant	0.015	Post Inflammatory Pulmonary Fibrosis	.018	Constipation	.018	Chronic Diastolic Heart Failure	.010	Rheumatic Disease of Tricuspid Valve	.016
Disorder of Phosphorus Metabolism	0.015	Congestive Heart Failure	.018	Disorder of Bone and Articular Cartilage	.010	Hypoxemia	.010	Low Blood Pressure	.010
Disorder of Bone and Articular Cartilage	0.015	Acute Chronic Respiratory Failure	.015
CKD 5	0.014	Constipation	.014
CUMULATIVE PROBABILITY	.945		.903		.924		.907		.963

After obtaining the topics, we conducted a thorough evaluation of the performance of our method. First, we surveyed the medical literature by manually searching the PubMed, Google Scholar, WebMD and the Mayo Clinic websites [34–47] to verify whether the most probable conditions within each topic are indeed known to co-occur according to medical literature. We then conducted a rigorous quantitative evaluation by assessing the resulting topics in terms of tightness and distinctiveness.

To assess tightness we inspected, for each topic, the number of codes within it that are assigned a probability greater than 0.01 (the threshold value set here). We refer to each list of coded conditions whose probability is greater than 0.01 as the top-codes for the topic. As shown in Table 3, four of the five topics (Topics 1–4) are associated with 10 top- codes, while the remaining topic (Topic 5) is associated with 13 top-codes. The cumulative probability mass associated with the top-codes accounts for over 0.9 of the total probability mass, as shown at the bottom row of the table. Our results show that for each topic inferred from the office visits set, only a few codes have a probability above 0.01 (at most 15, out of 180 codes); moreover, the cumulative probability mass for these 15 codes is above 0.9.

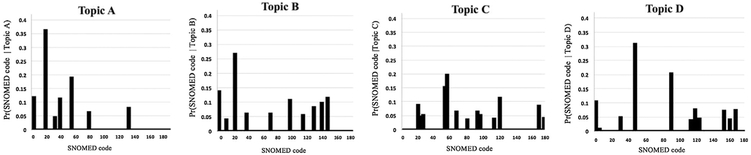
Fig. 4 shows graphs plotting the probability of each of the 180 codes to be associated with each of four example topics. The x-axis corresponds to the 180 codes, while the y-axis corresponds to the conditional probabilities of the codes to occur in the respective topic. As shown in the figure, for each of the four topics, only a few codes (less than 15) are assigned a non-negligible probability of association with the topic, further illustrating tightness of the topics. Likewise, for each topic obtained from the hospitalization set, 25 or fewer codes have a probability higher than the threshold value (0.01), and the cumulative probability of these 25 codes is higher than 0.9.

Fig. 4.

The probability distribution of SNOMED codes in four example topics denoted A-D identified by our model when applied to the office visit set. The x-axes correspond to the 180 codes; the y-axes correspond to the conditional probability of each code to occur in the respective topic.

We also calculated the entropy of each topic and compared the values to the entropy of the uniform distribution (i.e., the maximum possible entropy, log₂N, where N is the number of codes in our vocabulary). The entropy for each of the 20 topics obtained from the office visit set ranges from 1.208 to 3.576; the average entropy value is 2.853 (σ = 0.557), which is much lower than the entropy of the uniform distribution, (log₂N = 7.491, where N = 180). Similarly, for the hospitalization set, the entropy of the 20 topics ranges from 0.849 to 4.907; the average entropy value is 3.507 (σ = 1.049); again, much lower than the entropy of the uniform distribution (log₂N = 7.966, where N = 250).

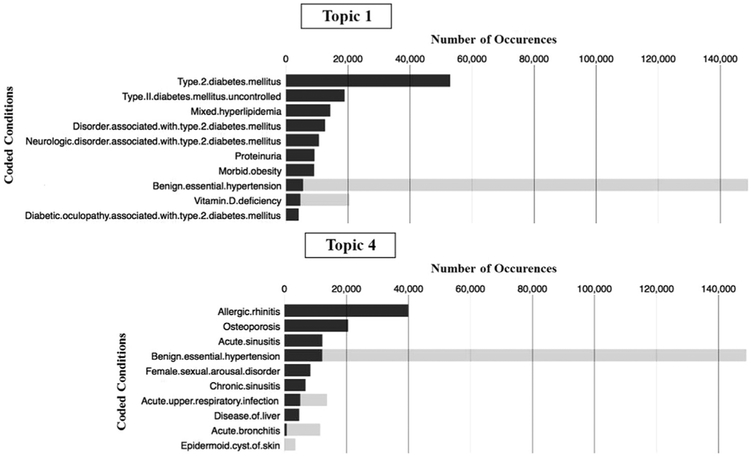
To assess distinctiveness of the topics, we used two approaches. First, we calculated and compared the corpus-wide versus the topic-specific number of occurrences of each top-code associated with each topic. Fig. 5 shows two example plots depicting both the corpus-wide and the topic-specific abundance of top-codes for topics obtained from the office visit set (Topics 1 and 4 in Table 3). For each coded condition, the black bar represents the topic-specific number of occurrences, while the combined black-and-grey bar represents the corpus-wide number of occurrences.

Fig. 5.

Topic-specific and corpus-wide number of occurrences of the top-codes associated with Topics 1 and 4, obtained from the office visit set. Black bars represent topic-specific number of occurrences for each condition. Combined black-and-grey bars represent the corpus-wide number of occurrences for each condition.

We also calculated inter-topic distances between all distinct pairs within the 20 topics inferred from each record set, using Jensen-Shannon divergence [33]. The mean value of the JSD obtained from the office visit set is 0.666 (σ = 0.150), (with median = 0.691 and minimum = 0.483), while for the hospitalization set, the mean is 0.637 (σ = 0.053), with median and min of 0.649 and 0.423, respectively.

While as noted in Section 2.1 we utilized in the above experiments only 180 (or 250) codes accounting for 80% of the cumulative code frequency in the respective dataset, we have conducted additional experiments varying the vocabulary size. Using a vocabulary comprising all 4,000 coded-conditions in the dataset led to very sparse data-matrices and to topics that were neither distinct nor tight. We also used codes accounting for 90% of the respective cumulative frequencies in each dataset, 590 codes to represent the office visit record set and 616 codes for the hospitalization record set. The topics obtained using these vocabularies were as informative and clinically meaningful – but not as tight – as the topics obtained when the vocabulary was smaller and limited to codes comprising 80% of the cumulative frequency. We thus only report here the results obtained using the latter smaller vocabulary.

Last, as also mentioned earlier, in addition to employing bag-of-codes to represent each patient-file, we have experimented using binary (0/1) and tf-idf representations. The former representation does not account for code abundance, while the latter penalizes code abundance if a code occurs in many patient records. While the complete results are not shown here due to space limits, the topics resulting from the 0/1 representation are not as distinct as the ones obtained using bag-of-codes, although topics inferred using each of the two representations capture many similar condition-association patterns. Moreover, since tf-idf penalizes codes that frequently appear within the corpus, this representation loses important information, as a persistently recurring condition (i.e. a code with a high count) is often indicative of a stronger association with other conditions. Hence, topics formed under the tf-idf representation do not capture some of the associations between recurring conditions (e.g. hypertension), and other conditons that are manifested in the disease. We have thus focused our report on the bag-of-codes representation.

4. Discussion

As demonstrated by Tables 3 and 4, the topics obtained from both the office visit and the hospitalization datasets indeed reveal patterns of commonly co-occurring conditions. As mentioned in Section 1, while similar disease themes are found in topics inferred from the hospitalization and from the office visit sets (e.g. Topic 5 in Table 3, and Topics 4 and 5 in Table 4 are all related to Heart disease), disease profiled by topics emerging from hospitalization records reflect a higher level of severity than the topics stemming from office visits. This difference in co-occurrence patterns matches the reality in which hospitalized patients often show more severe manifestations of the disease than non-hospitalized patients. Fig. 1 illustrates this point, where the twenty most frequent codes associated with the hospitalization set denote more severe conditions than those associated with the office visit set. For example, congestive heart failure, atrial fibrillation, and acute renal failure syndrome, are among the most frequent condition codes in the hospitalization list (Fig. 1b) but are not among the most frequent codes in the office visit set (Fig. 1a).

To validate that the condition-association patterns exposed through topic models are meaningful, we verify that the most probable conditions within each topic have indeed been reported to co-occur in the medical literature. For instance, many of the conditions grouped together in the leftmost column of Table 3, (Topic 1), are clearly related to Diabetes – one of the most frequent causes of decline in kidney function [34–37]. Likewise, most of the conditions grouped in Topic 2 (see Table 3) are related to Limb- or Joint-pain, including Chronic Renal-failure, since Metabolic Bone Disease is a frequent complication of advanced kidney disease [3,38]. Similar relationships characterize each of the other topics [34–47].

To further assess the clinical validity of our topics, we selected 10 topics, examining two randomly selected high probability codes from each. We surveyed the medical literature to verify whether these coded conditions are known to co-occur [34–47]. Table 5 shows for each pair of conditions, the PubMed identifier of the paper that establishes the medical connection between them. Most of the condition pairs are well known according to the medical literature, supporting the hypothesis that the model adequately uncovers true associations among coded conditions.

Table 5.

Medical relevance of associations between condition-pairs grouped in topics obtained from the office visits set. Column 1 indicates the topic number; Columns 2 and 3 list two randomly selected conditions that have a high probability to be associated with the topic; Column 4 provides the PUMED identifier and the reference number of the paper establishing the medical conditions as co-occurring.

Topic	Condition 1	Condition 2	Supporting literature
1	Proteinuria	Type 2 diabetes mellitus	7050509 [40]
2	Chronic renal failure	Arthralgia of the lower leg	17251386 [38]
3	Atrial fibrillation	Congestive heart failure	20347787 [41]
4	Allergic rhinitis	Osteoporosis	24090789 [39]
6	Hyperlipidemia	Essential hypertension	1927888 [42]
7	Gastroesophageal reflux	Insomnia	20535322 [43]
8	Hypothyroidism	Disorder of bone and articular cartilage	24783033 [44]
9	Coronary arteriosclerosis	Disorder of kidney and/or ureter	24527682 [45]
10	Anemia	Gout	22906142 [46]
11	Chronic obstructive lung disease	Tobacco dependence syndrome	17040932 [47]

Notably, a few of the coded condition pairs grouped together in our topics are not known to be directly associated with each other. For instance, no direct association is reported between Allergic Rhinitis and Osteoporosis, two conditions grouped under Topic 4. However, a recent study has shown that treating Allergic Rhinitis with depot-steroid injections increases the risk of Osteoporosis [39], which supports the high correlation we find between the two conditions. Similarly, Renal failure and Bone- and Joint-pain are not reported as associated conditions; however, Renal failure causes Osteodystrophy, which in turn causes Bone- and joint-pain [3], explaining the significant association exposed among the conditions in our results. The identification of two indirect medical associations, suggests that our approach is likely to expose yet unnoticed associations among medical conditions when applied to additional datasets.

Our quantitative evaluation of the model performance shows that the obtained topics are indeed tight and distinct. A topic that can be specified by a small number of coded conditions (tightness), is expected to capture meaningful and specific associations, since the codes characterizing the topic are highly correlated with each other.

Fig. 4 shows that each plot contains only a small number of peaks (typically 10), indicating that no more than 10 coded conditions account for most of the topic's probability mass, demonstrating the tightness of our resulting topics. Thus, 10 conditions are typically sufficient for characterizing each topic inferred from the office visit record set, although a few topics are characterized by 11–15 coded conditions (e.g. Topic 5, rightmost column of Table 3).

The probability plots for the other 16 topics show very similar trends, and are not shown here due to limited space. Moreover, the significantly lower entropy of the topic-distributions compared to the entropy of the uniform distribution (the max-entropy distribution) indicates that the topics obtained by our model bear high information contents. The information-based assessment is extended as part of the evaluation of distinctiveness, using the Jensen-Shannon divergence as discussed below.

Topic distinctiveness is established by showing that many of the codes appearing in a topic’s top-codes list are predominantly associated with a specific topic. That is, a top-code corpus-wide abundance is close in count to its topic-specific abundance for one particular topic. For instance, Fig. 5 shows that the majority of the top-codes associated with Topic 1 (eight of ten) and with Topic 4 (six of ten) are all-black, that is, the topic-specific count is the same as the corpus-wide count for these codes. We likewise inspected the other 18 topics (not shown here), observing a similar trend, indicating that the topics capture distict patterns of co-occurrences. While most codes are typically associated with a single topic, a few codes, such as benign essential hypertension, diabetes and vitamin D deficiency, are strongly associated with multiple topics as these conditions co-occur with several different groups of conditions.

The large inter-topic distance between each pair of topics, indicated by high JSD values, further illustrates the distinctiveness of the resulting topics. As discussed earlier, JSD values range from 0 to ln(2) (— 0.693), where 0 indicates identical distributions, and ln(2) indicates orthogonal distributions. The higher the divergence value between two topics, the more distinct they are from one another. The high mean and median values (close to the upper bound of ln(2)) of the inter-topic distances we have obtained indicate that almost all our topic are highly distinct.

The topics obtained from the hospitalization records are also clinically-relevant, tight and distinct. As with the office visit records, we surveyed the medical literature and found that the coded conditions grouped together as topics, inferred from the hospitalization dataset, have been reported to co-occur. Moreover, the observation that only a few coded conditions (25 or fewer, out of 250) characterize each topic, indicates tightness, while the high JSD values of the topics indicate distinctiveness. Furthermore, the low entropy of the topic distributions (compared to that of a uniform distribution), indicates that the topics are indeed informative. The ability of our method to generate clinically-relevant, tight and distinct topics from both datasets, demonstrates its effectiveness in identifying patterns of co-occurring medical conditions.

5. Conclusion

We have employed topic modeling over disease codes using LDA, obtaining probabilistic topics that highlight characteristic patterns of co-occurring medical conditions among patients who have kidney disease. Our results indicate that most coded conditions grouped together within a topic, are indeed reported to co-occur in the medical literature. Our results also uncover several associations among conditions that were hitherto not reported as co-occurring. We quantitatively evaluated the performance of our method and have shown that the topics identified from two different datasets are tight and distinct.

Our approach can also be helpful as a basis for a recommender system, suggesting to the practitioner, conditions that are likely to co-occur with a patient’s current diagnoses. Given a diagnosis code, the topic with which the code is most strongly associated can be identified. Accordingly, the list of the other codes associated with the topic can be shown to the physician, as conditions to be checked for. For instance, if a healthcare provider seeing a patient with decreased kidney function enters Anemia as a diagnosis, the system will prompt checking for Goiter, Hypothyroidism and Hypertension, since these conditions are all strongly associated with the same topic, thus highly likely to co-occur. Last, as conditions associated with other diseases are coded in a similar way within EHRs, we expect that our proposed method can be used to address similar research questions for diseases beyond kidney dysfunction.