Modeling of Myocardium Compressibility and its Impact in Computational Simulations of the Healthy and Infarcted Heart

Abstract

Simulation of heart function requires many components, including accurate descriptions of regional mechanical behavior of the normal and infarcted myocardium. Myocardial compressibility has been known for at least two decades, however its experimental measurement and incorporation into compu‐tational simulations has not yet been widely utilized in contemporary cardiac models. In the present work, based on novel in-vivo ovine experimental data, we developed a specialized compressible model that reproduces the peculiar unim‐odal compressible behavior of myocardium. Such simulations will be extremely valuable to understand etiology and pathophysiology of myocardium remodeling and its impact on tissue-level properties and organ-level cardiac function.

1. Introduction

Myocardial infarction (MI) induces maladaptive remodeling of the left ventricle (LV), causing dilation, wall thinning, change in mechanical properties, and loss of contractile function [1]. Simulation technologies can potentially lead the way for in-silico based models of the heart for many therapeutic applications. One of the truly unique advantages of computational modeling of the heart is its ability to estimate parameters that cannot be measured directly. One of these parameters, ventricular wall stress, may be the single most important indicator of ventricular myocardial function [2]. Specifically, a compu‐tational platform to accurately evaluate the effect of MI on cardiac function impairment, acutely and chronically, would be extremely valuable to understand etiology and path‐ophysiology of myocardium remodeling, its impact on tissue-level properties and organ-level cardiac function, and ultimately, to improve virtual surgery technologies, medical device development, as well as to provide quantitative risk stratification tools for these interventions.

However, material modeling of myocardium, and its critical numerical implemen‐tation, remains an area where much progress is required. One particular challenging feature of functioning myocardium is the interaction of coronary flow with myocardial contractility and compressibility. Increases in perfusion pressure have been shown to increase myocardial tissue volume strain and decrease its compliance [3]. During in vivo function, active muscle contraction influences flow in the coronary vessels, micro-circulation, and venous collection systems embedded in the myocardium. Systole has been shown to inhibit coronary flow perfusion [4], and diastole introduces an “intra‐ myocardial pump” that adds sucking action on arterial blood as a result of the previous systole and compensates for the lower or even retrograde systolic flow [5]. While volu‐ metric changes in the myocardium during the cardiac cycle have been known to occur for at least two decades [6], their incorporation into cardiac simulations and realization of this important effect in cardiac function has yet to be fully accomplished. In the following study we present novel experimental studies, material modeling, and numer‐ical simulations as first step in developing more realistic cardiac models.

2. Methods

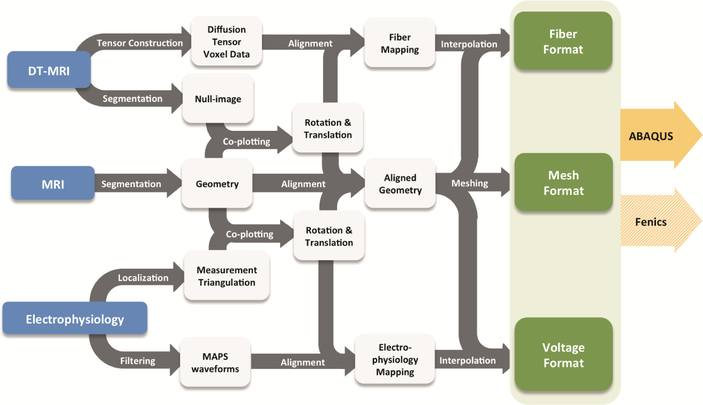
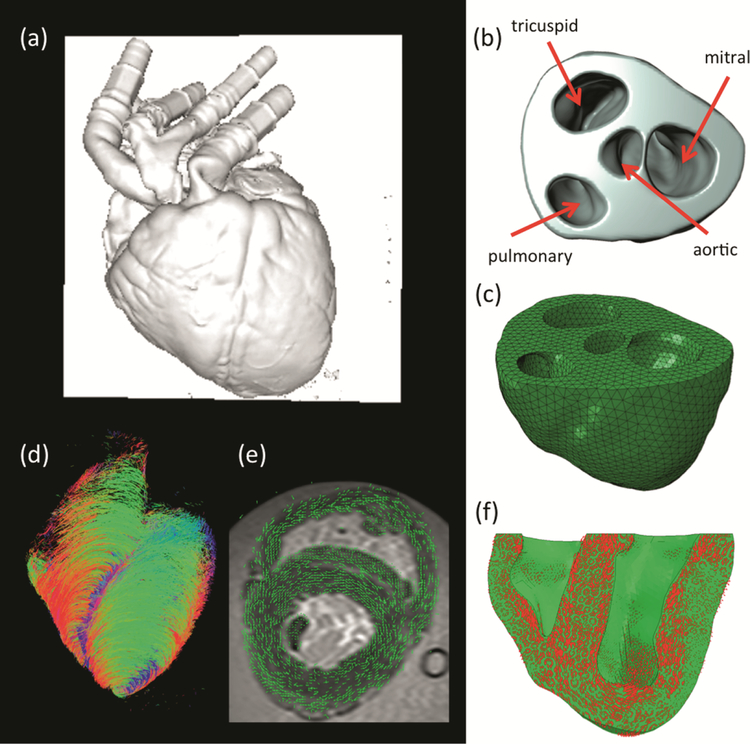
We have developed an in-silico model of MI using a comprehensive model pipeline (Fig. 1) and based on extensive datasets from a single ovine heart collected in vivo and ex vivo. All data collection of this in silico heart model was performed at the Visible Heart Laboratory (VHL, University of Minnesota), in three steps: (1) in vivo, (2) ex situ, and (3) ex vivo. Heart cavity pressures and volumes were acquired in vivo with cathe‐terization and somicrometry. Epicardial electrical activity was measured with mono‐phasic action potentials and diverse 2D echocardiography imaging was conducted to obtain validating datasets of in vivo heart function. The ex situ step was conducted in an isolated heart flow loop replicating in vivo conditions but where much better access was possible for extensive data collection. Subsequently, the heart was fixed under enddiastolic pressures with valves coapted and imaged. Magnetic resonance images (MRI) at end-diastole (Fig. 2a) were segmented (Fig. 2b) to create a finite element (FE) mesh (Fig. 2c). Diffusion tensor MRI (DTMRI) data (Fig. 2d) was aligned with the FE mesh (Fig. 2e) and employed to prescribe principal fiber direction of the FE model for the specification of the anisotropic material law (Fig. 2f).

Fig. 1.

Complete modeling pipeline from the single heart data source.

Fig. 2.

(a) magnetic resonance imaging at the end diastolic configuration; (b) segmentation of the biventricular heart up to the mitral valve plane; (c) FE mesh of the biventricular heart model;(d) diffusion-tensor magnetic resonance imaging; (e) alignment and overlay of the MRI-DTMRI datasets; and (f) determination of principal material directions of the FE model for proper specification of transversely isotropic material properties and active fiber contraction.

As a first step, we utilized a conventional incompressible transversely isotropic Fung-based hyperelastic model for the passive mechanical properties of myocardium of the form

$$T=-\frac{\partial {\text{W}}^{\text{vol}}}{\partial J}+\frac{1}{J}\tilde{F}\frac{\partial {\text{W}}^{\text{dev}}}{\partial \tilde{E}}{\tilde{F}}^{\text{T}}+\frac{1}{J}F{S}^{\text{act}}{F}^{\text{T}}$$ (1)

where the Jacobian of the motion is

$$J=\det F$$ (2)

F is the deformation gradient, the deviatoric deformation gradient is defined as

$$\tilde{F}=J^{-1/3}F$$ (3)

and the deviatoric Green-Lagrange strain is

$$\tilde{E}=\frac{1}{2}\left({\tilde{F}}^{\text{T}}\tilde{F}-1\right)$$ (4)

The passive mechanics of the myocardium is described by its volumetric and devia‐ toric responses, given by respectively

$${\text{W}}^{\text{vol}}=\frac{K}{2}\left(\frac{J^2-1}{2}-\text{ln}J\right)$$ (5)

$${\text{W}}^{\text{dev}}=\frac{c}{2}\left[\text{exp}\left(\alpha \tilde{E}\cdot ℂ\tilde{E}\right)-1\right]$$ (6)

where K is the bulk modulus (with K ≫ c and enforcing material incompressibility), c and α are passive material parameters, and 4^th order tensor ℂ characterizes the transverse isotropy of the material, specifically resulting in

$${\text{W}}^{\text{dev}}=\frac{c}{2}\left[\text{exp}\left(\alpha Q\right)-1\right]$$ (7)

where

$$Q=A_1{E}_{11}^2+A_2\left(E_{22}^2+E_{33}^2+2E_{23}^2\right)+A_3\left(E_{12}^2+E_{13}^2\right)$$ (8)

with A₁ = 12.0 A₂ = 8.0 and A₃= 26.0 [7]. The passive model parameters c and α are calibrated to match the general end-diastolic pressure volume relationship obtained by Klotz et al. [8].

The active stress responsible for myocardium contraction follows Hunter-McCulloch-Ter Keurs model [9] and is given by

$${\text{S}}^{\text{act}}=T_{C{a}^{2+}}\left(X,t\right)\left[1+\beta \left(\lambda -1\right)\right]m\otimes m$$ (9)

where m is the fiber direction and local fiber stretch is

$$\lambda =m\cdot F^{\text{T}}Fm$$ (10)

Time and space-dependent active contraction T_Ca²⁺ (X, t) is driven by epicardial elec‐ trical activity measured with monophasic action potentials (MAP). A total of 71 measurement (over cardiac cycle and synchronized with the QRS complex of ECG) were taken at scattered locations of the LV and RV epicardium. The measurement locations were employed to define an interpolating triangulation, and subsequently, the MAP waveform at each individual FE was obtained with barycentric coordinates in the trian‐ gulation. The pressure-volume (PV) loop, measured through catheterization and sono‐ micrometry, was used to best-fit the modulation of active contraction. We did not perform systematic coupling of the electrical and mechanical aspects of functioning myocardium, but we have used measured electrical data to modulate spatially and temporally the heterogeneity of contraction in active myocardium to simulate the in vivo PV loop.

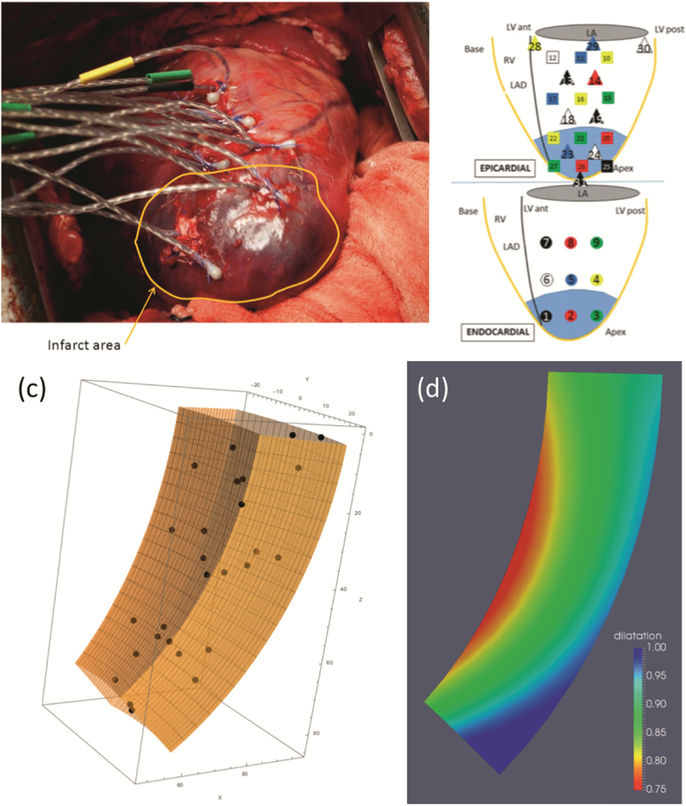
We conducted novel regional experiments using an ovine model with 27 sonocrystals implanted in a 3D array in the LV free wall (Fig. 3a, b) [10]. The positions of the sonoc‐ rystals during the cardiac cycle in vivo can yield a direct measurement of the changes of volume of myocardial tissue. However, a richer analysis can be achieved with a prolate spheroidal coordinate wedge defined in the region delimited by the sonocrystals (Fig. 3c), and the regional strain field is determined from their motion using FE techni‐ ques with Sobolev norm regularization [11]. From the strain field we determined the regional dilatation (normalized volume change, Fig. 3d). Experimental data demon‐ strated a progressive decrease in dilatation from the epi- to the endocardial surfaces, and from the direction of the base to the apex. These results indicated that myocardium does not deform isochorically during systole and myocardial tissue volume decreases (with volumetric changes ranging from 1.0 to ~ 0.75), so that conventional compressible material models cannot be used as J ≤1 still needs to be enforced.

Fig. 3.

(a) sonocrystal study in the ovine model; (b) sonocrystal layout; (c) prolate spheroid wedge used for strain analysis; and (d) regional dilatation for normal myocardium showing regional variations of volume change.

To account for this distinctive type of compressible material behavior (i.e. incom‐ pressible to prevent volume increases but compressible to allow for volume reductions while actively contracting), we have developed a specialized material model that utilized a penalty term allowing for a reduction in volume only and was modulated by the active contraction. Specifically, we have enforced material incompressibility to passive mechanical deformations that involve volumetric changes (i.e. J = 1 is enforced whenever T_Ca²⁺ (X, t) = 0), however a functional form for bulk modulus K dependent on the amount of active contraction was chosen, i.e. K ≡ K(T_Ca²⁺) such that the material becomes compressible during active systole and reductions in volume occur. Because we are interested in modeling changes from end-diastole to peak-systole, a linear form for K (decreasing from K^inc = 10 GPa for nearly-incompressible myocardium) with increasing T_Ca was sufficient to obtain the observed reduction in volume observed from end-diastole to peak-systole, when K^systole = 0.64 GPa.

3. Results

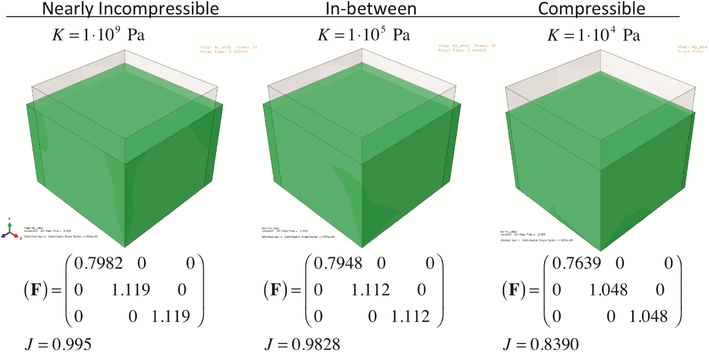
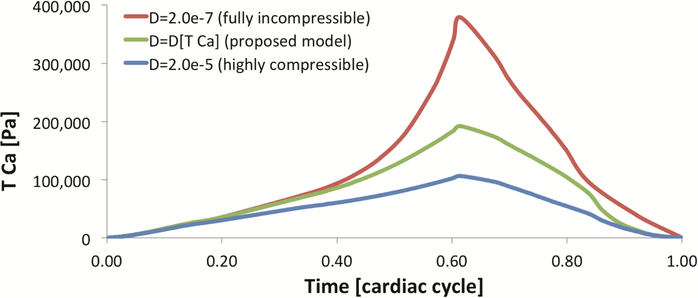
MRI, DTMRI, MAP, and in vivo PV loops allow the construction of a physiologically significant in silico heart model. Passive mechanical properties compared favorably with previous literature, time-modulation of active contraction shows good agreement with typical calcium-activated contraction, and qualitative comparison with in vivo 2D echo validated the baseline healthy model [12]. Testing of the material model was done in several steps, starting with a basic 3D cube to investigate how axial contraction produces transverse expansion (Fig. 4). Note that as the level of compressibility increases, the level of transversal expansion decreases. The impact of myocardial compressibility in active mechanics is substantial – not only incompressible models are unable to replicate the volumetric changes during systole, but also the required activation T_Ca to replicate the experimentally measured PV loop was substantially overestimated (Fig. 5).

Fig. 4.

The effects of the same axial contraction on the corresponding transverse stretches (F₂₂ and F₃₃) and volumetric changes (J). Material compressibility impacts the relationship between active contraction and wall thickening.

Fig. 5.

Active contraction T_Ca inversely determined with the observed PV loop (D = 2/K). Active contraction increases up to a maximum at peak-systole, and relaxes over diastole. Incompressible myocardium requires substantially higher active contractions to achieve similar cavity volumes.

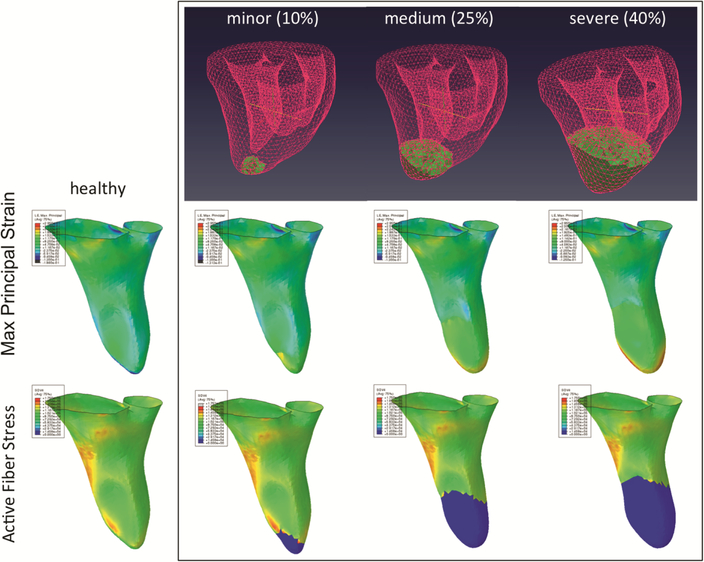
We simulated stiffening and loss of contractility in infarcted myocardium by prescribing a region of infarct observed experimentally in the ovine model of MI (shown as medium MI in Fig. 6) and determined the magnitudes of each effect by inversely matching the infarcted PV loop. In vivo function in the baseline and infarct models was quantitatively validated with the transmural strain smooth fields determined with sonoc‐ rystal arrays. Changes in properties (passive mechanics and active contraction) in infarcted and border-zone regions around the LV apex to best-fit the in vivo MI PV loop resulted in good agreement with transmural strain field observed in vivo and with previous findings. Subsequently, we have conducted a parametric study on the intensity of MI including minor and severe MI case-studies (Fig. 6).

Fig. 6.

Simulations of myocardium using the new material model showing the effects of gradual increases in myocardial infarction and the increase of apical LV chamber dilatation due to the reduction in local active contraction (blue). Accuracy of such simulations are enhanced with appropriate modeling of material compressibility. (Color figure online)

4. Discussion

The employment of a complete dataset from a single heart to develop an in-silico model avoids unnecessary image registration between MRI and DTMRI images. The coupling between electrical activity and active contraction is significant to heart biomechanics and is needed to obtain physiological realistic heart function. Myocardium is extensively perfused with distensible vessels (approximately 10–20% of the total volume). Increases in stiffness/tension of the surrounding tissue, as occurs during muscle contraction, causes the fluid to be extruded from these vessels [6]. Most importantly, the finding that perfused myocardium is compressible implies that results from analyses that assume incompressibility are not realistic. Not only the ventricular walls modeled with incom‐pressible myocardium will be thicker at peak systole (as the relationship between fiber shortening and wall thickening is highly sensitive to volumetric changes) but also ventricular and myofiber stress and active tension will be substantially overestimated – the former is crucial for accurate representation of ventricular kinematics and the latter is a key factor in myofiber stress and ventricular remodeling. To simulate MI, we have found that both impairment of contraction and stiffening of myocardium were necessary to replicate appropriately MI biomechanics. Subsequent remodeling mechanisms of collagen fiber re-orientation that change the material anisotropy locally may be important and are subject of future studies.