Abstract
Purpose
Lung nodules that are missed by radiologists as well as by computer‐aided detection (CAD) systems mostly overlap with ribs and clavicles. Removing the bony structures would result in better visualization of undetectable lesions. Our purpose in this study was to develop a virtual dual‐energy imaging system to separate ribs and clavicles from soft tissue in chest radiographs.
Methods
We developed a mixture of anatomy‐specific, orientation‐frequency‐specific (ASOFS) deep neural network convolution (NNC) experts. Anatomy‐specific (AS) NNC was designed to separate the bony structures from soft tissue in different lung segments. While an AS design was proposed previously under our massive‐training artificial neural networks (MTANN) framework, in this work, we newly mathematically defined an AS experts model as well as its learning and inference strategies in a probabilistic deep‐learning framework. In addition, in combination with our AS experts design, we newly proposed the orientation‐frequency‐specific (OFS) NNC models to decompose bone and soft‐tissue structures into specific orientation‐frequency components of different scales using a multi‐resolution decomposition technique. We trained multiple NNC models, each of which is an expert for a specific orientation‐frequency component in a particular anatomic segment. Perfect reconstruction discrete wavelet transform was used for OFS decomposition/reconstruction, while we introduced a soft‐gating layer to merge the predictions of AS NNC experts. To train our model, we used the bone images obtained from a dual‐energy system as the target (or teaching) images while the standard chest radiographs were used as the input to our model. The training, validation, and test were performed in a nested two‐fold cross‐validation manner.
Results
We used a database of 118 chest radiographs with pulmonary nodules to evaluate our NNC scheme. In order to evaluate our scheme, we performed quantitative and qualitative evaluation of the predicted bone and soft‐tissue images from our model as well as the ones of a state‐of‐the‐art technique where the “gold‐standard” dual‐energy bone and soft‐tissue images were used as the reference images. Both quantitative and qualitative evaluations demonstrated that our ASOFS NNC was superior to the state‐of‐the‐art bone‐suppression technique. Particularly, our scheme was better able to maintain the conspicuity of nodules and lung vessels, comparing to the reference technique, while it separated ribs and clavicles from soft tissue. Comparing to a state‐of‐the‐art bone suppression technique, our bone images had substantially higher (t−test; P < 0.01) similarity, in terms of structural similarity index (SSIM) and peak signal‐to‐noise ratio (PSNR), to the “gold−standard” dual−energy bone images.
Conclusions
Our deep ASOFS NNC scheme can decompose chest radiographs into their bone and soft‐tissue images accurately, offering the improved conspicuity of lung nodules and vessels, and therefore would be useful for radiologists as well as CAD systems in detecting lung nodules in chest radiographs.
Keywords: bone suppression, chest x‐ray, deep learning, neural network
1. Introduction
Chest radiography (chest x‐ray: CXR) is used for diagnosing a wide range of lung diseases including but not limited to lung cancer, pneumonia, tuberculosis, and pulmonary emphysema. More than nine million people die each year worldwide because of chest diseases.1 CXR is the most commonly used imaging technique for diagnosis of lung diseases because of its cost‐effectiveness, availability, and dose‐effectiveness.2 Among different chest diseases, lung cancer is the leading cause of cancer deaths in the world. CXRs are used for detecting lung cancer3, 4, 5 because evidence suggested that the early detection of nodules (i.e., potential lung cancer) may allow a more favorable prognosis.6, 7, 8
Even though CXRs are widely used for detection of pulmonary nodules, nodules can be difficult to detect due to overlap with normal anatomic structures such as ribs and clavicles. A study9 reported that more than 80% of missed lung cancers in CXRs were partly obscured by overlying bones. Similarly, a major challenge in computer‐aided detection (CAD) schemes for nodules in CXRs is the detection of the nodules overlapping with bony structures, because a majority of false positives are caused by these structures.10, 11 To address this issue, a dual‐energy (DE) radiography system12, 13 was developed for separating bones from soft tissue in CXRs by use of two x‐ray exposures at two different energy levels. The technique produces soft‐tissue‐enhanced images from which bones are removed. By using these images, the performance of CAD schemes was improved.14, 15 In spite of the advantages, a limited number of hospitals use DE radiography systems, because specialized equipment is required for obtaining DE x‐ray exposures, and more importantly, the radiation dose can be double in theory, comparing to that in standard CXRs.
A deep‐learning‐based image processing (DLIP) technique for separating bones from soft tissue was first introduced by Suzuki et al.16, 17 The technique employed a DLIP technique called massive‐training artificial neural networks (MTANNs) to find the relationship between CXRs and the corresponding DE bone images, in a supervised learning framework. Once the MTANN was trained, it could produce bone and soft‐tissue images from a single CXR. An observer performance study with 12 radiologists demonstrated that the diagnostic performance of radiologists in the detection of lung nodules was improved significantly by using the soft‐tissue images produced by MTANNs.18 The performance of MTANNs in suppressing bones, in particular the ribs near the lung wall and rib edges, was improved by employing an AS design.19 The method was recently extended for portable CXRs.20 An independent component analysis based technique for the suppression of posterior ribs and clavicles was proposed by Ahmed et al.21 to enhance the visibility of nodules and to aid radiologists during the diagnosis process. A study22 proposed a supervised filter learning technique for the suppression of ribs. The procedure is based on K‐nearest neighbor regression that incorporates the information from a training set of DE soft‐tissue images. Recently, a DLIP technique was proposed by Yang et al.23 to predict bone images from CXRs in a supervised discriminative fashion.
In this study, we extended the MTANNs to formulate a general DLIP framework, which we call neural network convolution (NNC). We developed a “virtual” DE system based on NNC for separating bones from soft tissue in CXRs to improve the performance for nodule delineation and rib edge removal by incorporating a mixture of orientation‐frequency‐specific (OFS) experts together with anatomy‐specific (AS) experts into the NNC framework. Because it is difficult for a single DLIP model to handle ribs and clavicles in various orientations, the OFS expert architecture allows multiple expert models to handle such objects in multiple orientations separately. Also, because the signal and noise statistics vary significantly in different lung regions, the AS expert architecture helps multiple expert models to separate bony structures from soft tissue in different lung segments individually.19 In this work, we mathematically defined the AS NNC model as well as its learning and inference strategies in a probabilistic deep learning framework. We further introduced the OFS architecture to decompose bones and soft tissue into specific orientation‐frequency components of different scales. A major advantage of the anatomy‐specific, orientation‐frequency‐specific (ASOFS) architecture other than its higher performance is that it enables utilizing relatively simple neural network architectures with fewer free parameters, while keeping a large receptive‐field, which would reduce the requirement of a large number of training data. Perfect reconstruction discrete wavelet transform (DWT) was used for OFS decomposition/reconstruction, while we introduced a soft‐gating layer to merge the predictions from AS NNC experts. For evaluation, we used a database of 118 CXRs with pulmonary nodules. We compared our newly proposed ASOFS NNC scheme, through quantitative and qualitative evaluation, with our previous state‐of‐the‐art bone‐suppression technique based on MTANNs.19 An abstract version of our preliminary study was presented at an Annual Meeting of Radiological Society of North America in 2017.24
2. Materials and methods
2.A. Virtual DE imaging based on our ASOFS deep NNC model
Figure 1 shows the schematic diagram of our virtual DE imaging by means of our ASOFS deep NNC in a test stage. To convert an original single CXR image to a bone image, the original image is first decomposed into multiple orientation‐frequency components using a multi‐level multi‐scale OFS decomposition. Each image with a specific component is then decomposed spatially into several anatomic segments using a gating layer. Each of trained NNC experts then process the corresponding regions in a specific lung segment in a particular orientation‐frequency component image to produce component‐wise bone images. The bone predictions by multiple NNC experts for multiple lung segments are then merged using a soft‐gating layer to form an entire bone component image at a specific scale (frequency) in a particular orientation. The final complete bone image is then obtained by using the OFS reconstruction. To obtain the soft‐tissue image, the bone image is subtracted from the original CXR. In a learning stage, we acquired pairs of CXRs and the corresponding “teaching” bone images from a single‐shot DE system. We decomposed the input and the “teaching” (or desired‐output) bone images into their corresponding orientation‐frequency component in a specific lung segment. We trained multiple NNC experts individually with their corresponding components. Both training and test stages can be performed in a fully parallel setting. We now describe the details of our virtual DE system including the NNC model and ASOFS decomposition/reconstruction below.
Figure 1.
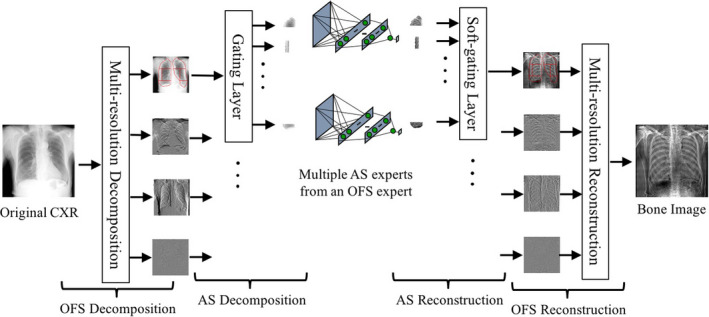
Schematic diagram of our virtual DE system based on our deep ASOFS NNC model in a test stage. The original unseen single CXR is decomposed into specific orientation‐frequency components in multiple anatomic segments. The decomposed components are selectively assigned to corresponding trained NNC experts by the gating layer. The resulting bone predictions from multiple NNC experts are merged by the soft‐gating layer followed by the OFS reconstruction to form a complete bone image where soft‐tissue components are removed, while bone components are maintained. [Color figure can be viewed at wileyonlinelibrary.com]
2.B. Neural network convolution
The root of NNC is neural filters25, 26, 27 and neural edge enhancers28, 29 that are supervised nonlinear convolution filters based on neural networks for noise reduction and edge enhancement, respectively. By extending these filters, MTANNs30 were developed for supervised enhancement of specific patterns in images. In this work, we extended the MTANNs to formulate a general DLIP framework, which we call machine learning convolution (MLC). Given an input image f and the desired output g, the output of an MLC model is defined by
| (1) |
| (2) |
where is the predicted image at spatial coordinates (x, y), f x,y is an input vector to the model defined by an image region (image patch or “kernel”) around (x, y), and , is a continuous function parameterized by , forming a mapping from an N dimensional image patch to a single output pixel. The output image can be obtained by sliding a local window over an image f and applying on the corresponding image regions. To understand the mechanism of MLC, observe that by setting in Eq. (1) to a linear function, the standard definition of convolution in the field of signal processing can be obtained as follows:
| (3) |
| (4) |
where φ is a 2D signal with zero elements outside the region (or the kernel of the convolution), and θ is the vectorized version of the nonzero elements of φ. In general, can be replaced by any regression model, e.g., support vector regression and Gaussian process regression models.31 A special case is when is a neural network, which we call NNC, represented by
| (5) |
| (6) |
where is the main function converting an N i ‐dimensional input to an N o ‐dimensional output, and is a feed‐forward neural network regression model, parameterized by θ. The neural network receives pixel information from an image region (image patch) in the input image f. The input data are subject to the processing in multiple hidden layers, followed by linear transformation in the output layer. Under this terminology, we can construct a variety of early26, 28 and recent32, 33 DLIP models including fully convolutional networks. We applied NNC for radiation dose reduction in CT and breast imaging.32, 34
Given a set of input and desired output (or “teaching”) images, one can extract regions and the corresponding output pixels, from the input and desired output images, respectively. Having this set, the goal of the machine learning is to find the best parameter vector θ of an NNC model so that the predictions are closest to the desired values. Formally, we minimize the mean squared error (MSE) over the empirical distribution, as follows:
| (7) |
where and g(x, y) are an input region and a desired pixel, respectively, and Pdata is the empirical patch‐pixel pair distribution. We call this a region‐based (RB) learning strategy. From a probabilistic viewpoint, Eq. (7) is equivalent to maximizing the conditional log‐likelihood of the parameters θ, assuming that the pixels of the desired images are independent when the corresponding regions in the input images are observed, and the underlying conditional distribution is Gaussian. From an image‐processing perspective, this, in fact, is equivalent to maximizing the peak signal‐to‐noise ratio (PSNR). One can use Eq. (7) in its original form to train an MLC model by replacing with . Gradient‐based optimization can be employed to solve this problem. Particularly we used stochastic gradient descent (SGD) with momentum.35 Using an RB strategy, a mini‐batch of data can be extracted randomly from the set of all region‐pixel pairs. This ensures that the examples in a mini‐batch of data are less dependent, which is a desired property when employing SGD.
2.C. Anatomy‐specific NNC
Even though a single NNC model was able to separate bones from soft tissue in the entire lungs,16 it could not suppress rib edges and the ribs close to the lung wall sufficiently, due to intensity and structural variations of bony structures in different lung segments. Theoretically, one can increase the complexity of a single NNC model to increase its representation capability in order to capture this bone variation. However, this would require a larger number of training examples, which sometimes might not be acceptable due to a sample size limitation and computational limitation. To address this issue, AS decomposition/reconstruction was introduced by Chen et al.19 We used a similar strategy in this study, and we newly defined AS NNC and its corresponding learning and inference strategies formally in a probabilistic deep learning framework. As depicted in Fig. 1, AS decomposition simplifies the bone prediction problem by spatially decomposing the image into different lung segments. Note that we focused on prediction/suppression of bones in the lung field in this study, because this is the most important region in a CXR. One can easily expand this AS strategy to include regions outside the lung field. Correspondingly, the lung field was divided into eight anatomic segments: a left upper segment for suppression of left clavicles and ribs, a left hilar segment for suppression of bone in the hilar area, a left middle segment for suppression of ribs in the middle of the lung field, a left lower segment for suppression of ribs in the left lower lobe, a right upper segment, a right hilar segment, a right middle segment, and a right lower segment. In this fashion, each NNC is trained to learn the relationship between the input CXR and desired (teaching) bone images for a particular anatomy. To formally define AS decomposition/reconstruction using gating and soft‐gating layers, we first redefine the NNC estimation formulation in a probabilistic fashion as a discriminative model as follows:
| (8) |
| (9) |
where P model is the conditional probability distribution of the desired image g given an input image f. As described before, under a patch‐based conditional independence assumption, the image‐to‐image model distribution can be decomposed into a multiplication of the conditional distribution of the pixels given the corresponding image patches, as described in Eq. (10), where S indicates a set of all patch‐pixel pairs in a pair of input‐desired images. When P θ is assumed Gaussian with its conditional expectation being modeled by a neural network, a maximum log‐likelihood estimate of the model parameters from Eq. (10) corresponds to the NNC MSE training in Eq. (7). The basic assumption of the AS model is that the underlying conditional probability distribution changes from anatomy to anatomy, and we can capture this variability by using a mixture model. To represent the AS NNC, we can define
| (10) |
where z is a latent random variable from a categorical distribution from the set of lung anatomic segments (e.g., left upper segment, left hilar segment, etc.) described earlier, and represents the probability of observing an output pixel given an input patch and its corresponding segment category. In Eq. (11), we assumed is a conditional Gaussian model by utilizing a neural network expert to model the conditional expectation. Additionally, we modeled the probability of a lung segment given the input patch, through the segmentation of the lungs into eight anatomic segments. Optimizing the log‐likelihood with the AS assumption of Eq. (11) requires a mutual training of the NNC experts because of the summation over the latent variable z. To simplify the optimization, we assumed the minimum entropy for (i.e., the probability of the most probable outcome is one) which corresponds to the gating layer in Fig. 1. This, in fact, is a reasonable assumption when z represents the lung segments, because z cannot belong to more than one category (except for the segment boundaries). Therefore, the maximum likelihood of the new representation is equivalent to the separate training of eight NNC experts, following our simplification rule. For inference, when the input patch belongs to one specific segment, the processing would be simply the forward propagation of the corresponding NNC expert. When the patch belongs to boundaries, we merge the predictions with a weighted combination of them using Eq. (11). Gaussian smoothing filtering between the lung segment boundaries is used in our implementation, to account for the probability of z given the input patch, which corresponds to the soft‐gating layer in Fig. 1. Equation (11) is described schematically in Fig. 2.
Figure 2.
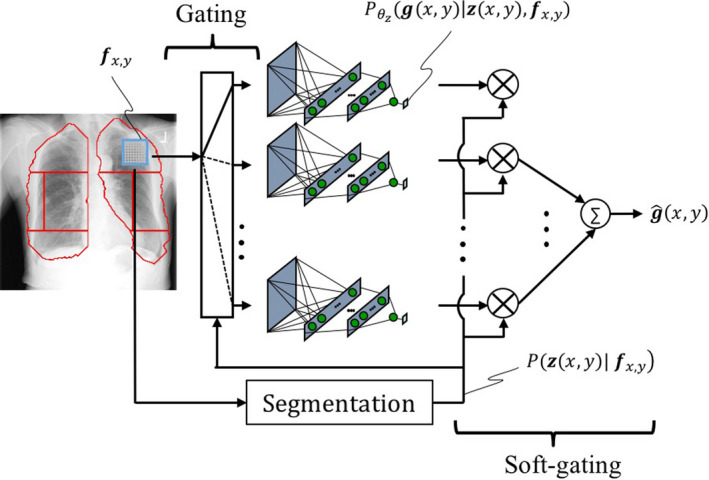
Detailed schematic of our AS NNC with gating and soft‐gating layer. Each NNC is trained through its corresponding patch‐pixel pairs in a specific lung segment. The predictions are combined through a soft‐gating layer by a weighted combination of per‐segment predictions. [Color figure can be viewed at wileyonlinelibrary.com]
2.D. Orientation‐frequency‐specific NNC
To train a DLIP system for bone separation that can generalize well, the receptive‐field should be large enough to cover discriminative information from an input CXR. Intuitively, the receptive‐field should be as large such that it covers bony structures. This can potentially increase the required number of free parameters of a neural network substantially. To address this issue, multi‐resolution‐based technique was proposed.16 A 2‐level pyramidal decomposition was used to address the receptive‐field issue. Additionally, decomposing an input CXR into multiple orientation‐frequency components would potentially result in an easier learning scenario with limited pattern variations, because the orientation and frequency components of bony structures differ significantly from those of soft tissue. A similar assumption was made in a bone suppression study23 by training convolutional neural networks in the gradient domain, and it was shown that the results were improved in comparison to a conventional training in the intensity domain.
We combined the two ideas and proposed a multi‐scale OFS decomposition/reconstruction, to simultaneously address the receptive‐field and pattern variation issues, and train multiple experts for specific orientation‐frequency components. We found DWT as a satisfactory choice for the OFS design, because firstly we were able to employ perfect reconstruction filter banks without loss of information, and secondly the relatively straightforward filtering process of DWT combines well with our DLIP NNC design. Following this design, each decomposition/reconstruction level can double the size of the receptive‐field. As depicted in Fig. 1, a single‐level OFS decomposes a CXR into four frequency components of different orientations: low‐low, low‐high, high‐low, and high‐high components, where the first‐second term corresponds to horizontal‐vertical directions. Following our AS definition in the previous section, each component can be then decomposed spatially into multiple lung segments. Multiple NNC experts are then trained individually for their corresponding particular orientation‐frequency component image in a specific lung segment. The merged predictions of the AS NNCs through the soft‐gating layer are then subject to the OFS reconstruction to form a complete output bone image. From a deep learning perspective, each decomposition level introduces a convolution layer followed by a down‐sampling (or pooling), while each reconstruction level introduces an up‐sampling followed by a convolution layer, where the convolution filters are fixed, and the pooling/un‐pooling layers do not lose information if perfect reconstruction filter banks are used. Figure 3 represents the schematic of OFS NNC (without the AS design) in a deep learning fashion.
Figure 3.
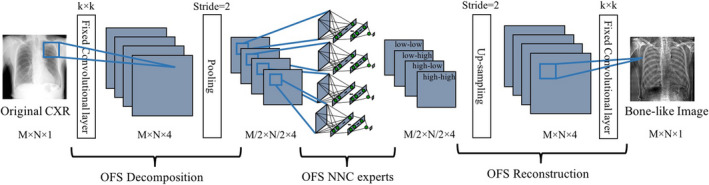
Detailed schematic of our OFS NNC with OFS decomposition/reconstruction. From a deep‐learning perspective, each decomposition corresponds to convolution followed by a pooling layer. Similarly, reconstruction is equivalent to an up‐sampling layer followed by convolution. Each NNC is trained individually through its corresponding patch‐pixel pairs of a specific orientation‐frequency component. [Color figure can be viewed at wileyonlinelibrary.com]
2.E. Implementation
We used a two‐level DWT for the OFS decomposition/reconstruction resulting in seven orientation‐frequency components. We employed the orthogonal Haar wavelet transform for its efficiency and effectiveness. Our preliminary study showed no significant performance difference when employing other variants of wavelet transforms. Specifically, our preliminary evaluations showed similar (no statistically significance differences) quantitative performance for several wavelet types such as Haar, Symlet, Daubechies, and Coiflet. Our previous study16 showed that two levels of decomposition/reconstruction was sufficient to capture the representational information from the input CXRs to discriminate bones from soft tissue. We discuss the choice of OFS levels in a later section. Histogram‐based segmentation was utilized for AS decomposition to segment the lung field. The lung field was then segmented further into eight anatomic segments by selecting the upper third, lower third, and the middle third segments. The middle segment was halved into hilar and middle segments. We extracted 128,000 samples from each particular orientation‐frequency component image and a specific anatomic segment. We trained 56 (seven orientation‐frequency components and eight anatomies each) NNC models with the massive training samples from a relatively small number of cases. Both CXRs and bone images were normalized to a range of approximately between 0 and 1. Because of employing our ASOFS design, we were able to utilize a two‐layer architecture neural network regression including a convolution layer of 9 × 9 filter size and a hidden layer of 64 hidden units with sigmoidal activations, followed by a linear transformation. We consistently used SGD with a learning rate of 0.1, a momentum of 0.9, and a batch‐size of 128, and trained each NNC for 100 epochs to minimize the MSE. No explicit regularization36 was used. We employed a nested two‐fold cross‐validation (CV) strategy as follows: for training, we randomly selected 59 CXR‐bone pairs, from which 50 pairs were randomly chosen for training while the other 9 were used for validation and optimization of the hyper‐parameters. Once the hyper‐parameters were set, the entire 59 pairs were used for training and the corresponding model was tested on the other half of input‐CXR bone‐image pairs. We used the same set of hyper‐parameters to train our model on the second half and test on the first half. We implemented our model using Theano37 running on a workstation with Intel(R) Xeon(R) CPU E5‐1620 v3 @ 3.50 GHz and Nvidia GeForce GTX Titan Z GPU (only one GPU at a time was utilized in our experiments). Because of utilizing relatively simple neural network architectures, we were able to train our models on CPU, while we used GPU implementation for test.
2.F. Dual‐energy database
The database used in this study consisted of 118 posterior‐anterior (PA) CXRs acquired with a computed radiography system with a DE subtraction unit (FCR 9501 ES; Fujifilm Medical Systems, Stamford, CT, USA) at The University of Chicago Medical Center. The DE subtraction unit employed a single‐shot DE subtraction technique where image acquisition is performed with a single exposure that is detected by two receptor plates separated by a filter for obtaining images at two different energy levels.38, 39, 40 All 118 CXRs were abnormal cases with pulmonary nodules (sizes: 5–30 mm). The matrix size of the chest images was 1,760 × 1,760 pixels (pixel size, 0.2 mm; gray scale, 10 bits). The absence and presence of nodules in the CXRs were confirmed by use of CT examinations. Most nodules overlapped with ribs and/or clavicles in CXRs. The registration error between the input images and the teaching images would be minimum because of the use of the single‐shot DE subtraction technique.
3. Results
3.A. Quantitative and qualitative evaluation
We compared our newly developed ASOFS NNC scheme with our previous state‐of‐the‐art bone‐suppression technique, namely AS MTANNs19 quantitatively in terms of PSNR and structural similarity index (SSIM).41 Both PSNR and SSIM have been widely used for quantitative comparisons of pairs of images. The PSNR between two images and g can be calculated as follows:
| (11) |
where p is the peak intensity value of the image, which can be set for the entire database in advance, and MSE is the average squared intensity difference between the two images. For our evaluations, g was set to the “gold‐standard” DE images, while was set to the predictions by our model. Note that the soft‐tissue image and bone image comparisons were performed separately. While the PSNR value can be used to compute the similarity of two images in a pixel‐wise manner, the SSIM considers also the similarity of two images over several regions‐of‐interest (ROI). In fact, to calculate the SSIM between two images, one can first calculate the per‐ROI SSIM values over the entire possible image positions and then take the average of these values over a specific image region. The per‐ROI SSIM for a square ROI consists of a multiplicative combination of the luminance, contrast, and structure similarities which can be simplified as follows:
| (12) |
where a and b are two image ROIs (7 × 7 squares in our experiments), μ a and μ b are the mean intensity of a and b, respectively, σ a , σ b , and σ ab are the standard deviation of a, standard deviation of b, and the covariance between a and b, respectively, and c 1 and c 2 are two constant factors to stabilize the divisions.
The DE bone and soft‐tissue images from our single‐shot DE database were used as the reference standard for the comparisons. We compared the bone predictions of our scheme and those of the reference‐standard technique, with the “real” DE bone images directly. Because of the nonlinear sophisticated contrast enhancement of the commercial DE systems, we applied histogram matching for both our proposed and the reference technique, when comparing the soft‐tissue predictions quantitatively. The comparisons were performed over the lung field of the CXRs because both techniques were designed to suppress the bones in the lung field. Tables 1 and 2 show the corresponding PSNR and SSIM values for bone and soft‐tissue comparisons, respectively. The similarity of the original CXRs with respect to the DE bone images in terms of PSNR and SSIM is also represented in Table 1, as a reference. As seen in Tables 1 and 2, quantitative evaluation showed that our new scheme was superior in terms of PSNR and SSIM. We performed statistical analysis (paired two‐tailed t‐test; a significance level of 0.01) in our evaluation, which revealed that the difference between the two techniques was statistically significant. For a better understanding of the pair‐wise comparison of bone and soft‐tissue images of our new scheme with regards to the reference‐standard technique, we also represented the sorted pair‐wise SSIM and PSNR differences between the two techniques in Fig. 4. As explained in Section 2.5, our results were obtained through a nested two‐fold CV protocol. In order to show the robustness of our scheme to the training and test images, we also showed the per‐fold results, including both PSNR and SSIM values, for two different folds for both bone and soft‐tissue image comparisons in Table 3. The statistical analysis (paired two‐tailed t‐test; a significance level of 0.05), between the results obtained for different folds, showed no statistically significant differences, showing the robustness of our scheme to the training and test images.
Table 1.
Comparison of the bone prediction images of our ASOFS NNC scheme with those of the reference‐standard AS MTANN technique in terms of SSIM and PSNR. DE bone images from our DE database were used as the reference. The original CXRs were also compared to the DE bone images as a reference. Note that the difference between our ASOFS NNC and the state‐of‐the‐art AS MTANN was statistically significant (paired two‐tailed t‐test; a significance level of 0.01)
| Original CXR | AS MTANN | Our ASOFS NNC | |
|---|---|---|---|
| SSIM | 0.604 ± 0.051 | 0.772 ± 0.039 | 0.798 ± 0.034 |
| PSNR | 7.79 ± 1.21 | 22.04 ± 2.56 | 23.62 ± 2.10 |
SSIM, structural similarity index; PSNR, peak signal‐to‐noise ratio.
Table 2.
Comparison of the soft‐tissue prediction images of our ASOFS NNC scheme with those of the reference‐standard AS MTANN technique, in terms of SSIM and PSNR. DE soft‐tissue images from our DE database were used as a reference. Note that the difference between our ASOFS NNC and the state‐of‐the‐art AS MTANN was statistically significant (paired two‐tailed t‐test; a significance level of 0.01)
| AS MTANN | Our ASOFS NNC | |
|---|---|---|
| SSIM | 0.902 ± 0.024 | 0.912 ± 0.027 |
| PSNR | 26.37 ± 1.30 | 29.82 ± 1.50 |
SSIM, structural similarity index; PSNR, peak signal‐to‐noise ratio.
Figure 4.
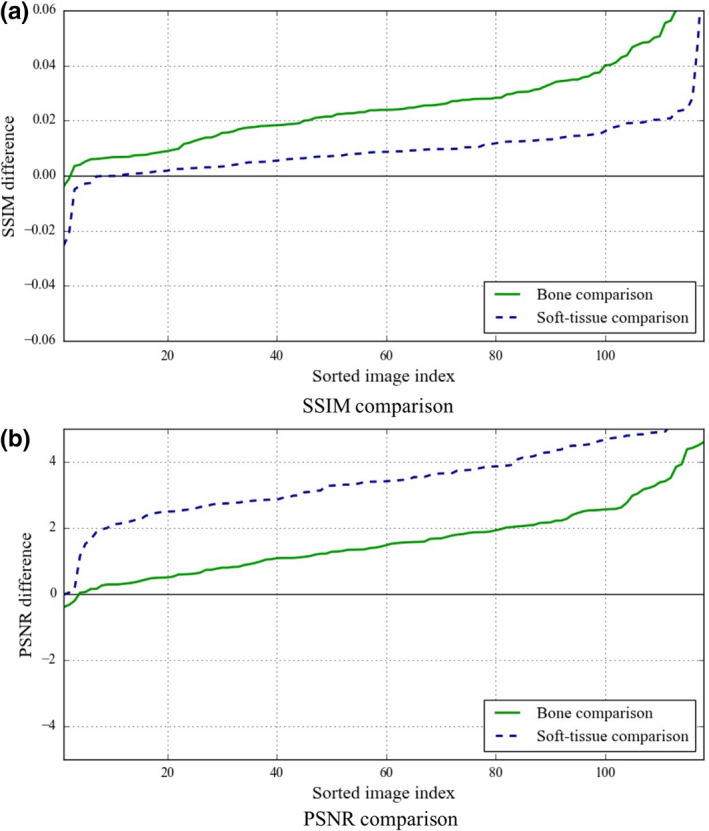
Pair‐wise comparison of our ASOFS NNC scheme with the reference‐standard AS MTANN technique in terms of (a) SSIM and (b) PSNR for both bone and soft‐tissue images. The difference metrics between the two techniques were sorted in an ascending order. Note that the x‐axis is the sorted image index and does not necessarily correspond to the image index. [Color figure can be viewed at wileyonlinelibrary.com]
Table 3.
Quantitative evaluation of the soft‐tissue and bone prediction images of our ASOFS NNC scheme, in terms of SSIM and PSNR, for two different folds in the two‐fold CV. DE images from our DE database were used as a reference. The statistical analysis (paired two‐tailed t‐test; a significance level of 0.05) between the results obtained for different folds showed no statistically significant differences, showing the robustness of our scheme against different training and test images
| Trained on fold 1 Tested on fold 2 | Trained on fold 2 Tested on fold 1 | |
|---|---|---|
| Bone image comparison | ||
| SSIM | 0.798 ± 0.032 | 0.797 ± 0.036 |
| PSNR | 23.87 ± 1.95 | 23.37 ± 2.20 |
| Soft‐tissue image comparison | ||
| SSIM | 0.910 ± 0.032 | 0.914 ± 0.018 |
| PSNR | 29.66 ± 1.60 | 29.98 ± 1.37 |
SSIM, structural similarity index; PSNR, peak signal‐to‐noise ratio.
Figure 5 shows two examples of soft‐tissue images produced from single CXRs with our new ASOFS NNC scheme in comparison with the reference‐standard technique. The original CXRs and the “real” DE soft‐tissue images are also shown as references. As seen, our scheme was better able to suppress bones including the ribs near the lung wall and the clavicles, and specifically rib edges, than the reference technique. Additionally, our new scheme was better able to maintain the conspicuity of soft‐tissue structures such as lung nodules of various sizes and vessels under the clavicles and with overlapping ribs. This was achieved through a more accurate prediction of the bone images by decomposing the prediction task into multiple specific orientation‐frequency component‐wise predictions.
Figure 5.
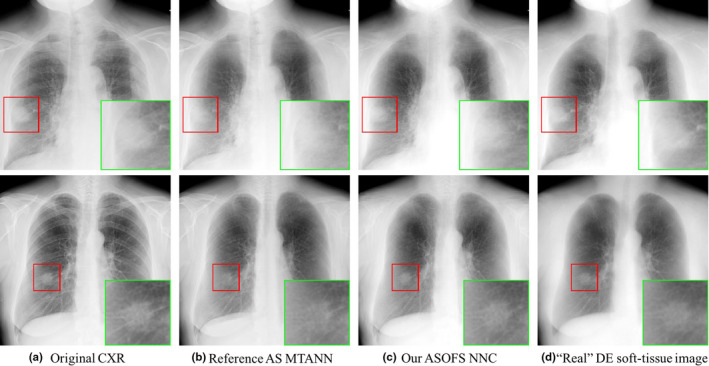
Qualitative comparison of (c) our ASOFS NNC scheme with (b) the reference‐standard AS MTANN for two cases. A region‐of‐interest with a nodule is enlarged in each case for visual assessment. The (a) original CXRs and (d) “real” DE soft‐tissue images from our DE database are shown as references. [Color figure can be viewed at wileyonlinelibrary.com]
3.B. Virtual dual‐energy bone images
To decompose a single CXR using our scheme, we first predicted a bone image and then subtracted the bone image from the input CXR to obtain a soft‐tissue image. It was shown that the performance of a DLIP system was improved by using DE bone images as targets.16 Figure 6 illustrates an example of a bone image produced from a single CXR using our scheme. As seen in Fig. 6, our scheme was able to successfully convert a single CXR to its corresponding bone image. Particularly, our scheme was able to predict both posterior and anterior ribs. Figure 6 also represents how our scheme was able to predict well the bone crossings and the ribs near the lung wall.
Figure 6.
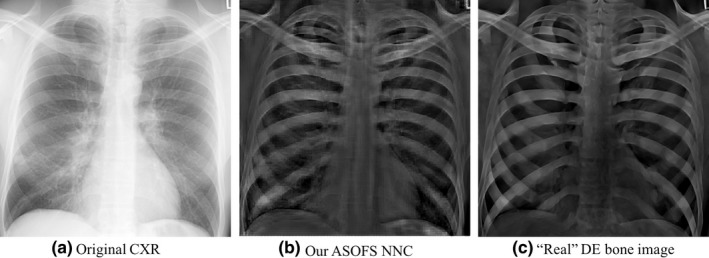
Qualitative assessment of the bone images produced by our (b) ASOFS NNC scheme. (a) The original CXR image and (c) the “real” DE bone image from our DE database are shown as references. Note that the bone images that we used for training were preprocessed in order to reduce the effect of noise of the bone images from the DE system.
We proposed to simplify the learning process by decomposing input CXRs into multiple orientation‐frequency components using our OFS decomposition technique. It would be interesting to visualize the component‐wise bone predictions in the wavelet domain, as depicted in Fig. 7. Our OFS mixture‐of‐experts model was able to predict well the bone components of different frequencies from different orientations.
Figure 7.
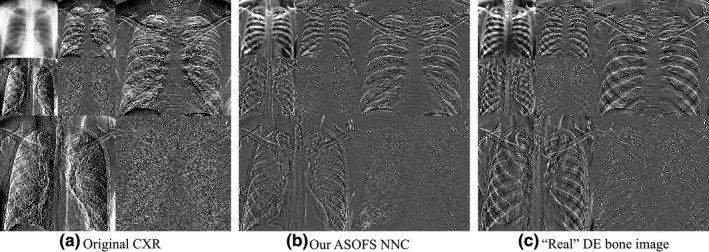
Component‐wise bone predictions using our (b) OFS mixture‐of‐experts deep NNC scheme. Our scheme was able to successfully convert different orientation‐frequency components of (a) the original CXR into its corresponding bone components, which was similar to (c) the wavelet decomposition of the corresponding “real” DE bone image from our DE database.
The previous state‐of‐the‐art bone‐suppression technique, namely, AS MTANNs, used a pyramidal decomposition to both CXRs and bone images. The pyramidal decomposition, however, disregards the orientation information by considering the low‐frequency and high‐frequency components only. In contrast, a wavelet decomposition preserves the orientation information by decomposing an image into multiple orientation‐frequency components of different scales. The intuition behind using the orientation information was to assist the learning process by including the orientation information as the input, because the bony structures contain major dissimilarities to soft tissue in terms of orientations. Our experimental results and comparison to the state‐of‐the‐art demonstrated quantitative and qualitative bone suppression improvements, meaning such decomposition was beneficial.
3.C. Training and processing time
The processing of a single case took less than a second on a regular PC with a GPU (described earlier). This was achieved through the parallel nature of our ASOFS design, and the fact that we were able to use a relatively simple neural network architecture. The training of our 56 NNCs in a serial implementation on CPU took 3.3 hr. Even though we did not found parallel training of the NNC experts necessary, the training time would be decreased by a factor of approximately 56, if all of the NNC experts were trained in parallel, simultaneously.
4. Discussion
We performed an experiment to investigate the effect of the OFS decomposition level. Particularly, we compared our two‐level ASOFS NNC scheme with a three‐level decomposition counterpart. Figure 8 represents an example of a bone image produced by our schemes using two and three levels of decomposition. We found that two levels were sufficient which produced qualitatively more appealing bone images than did the three‐level decomposition. We believe the reason for the failure of the higher level of decomposition is two‐fold: first, with a higher decomposition level, single components contain less spatial information which might be necessary to predict the bones; and second, similar to other mixture‐of‐experts models, it is not a straightforward task to balance the prediction errors, when the number of experts is high.
Figure 8.
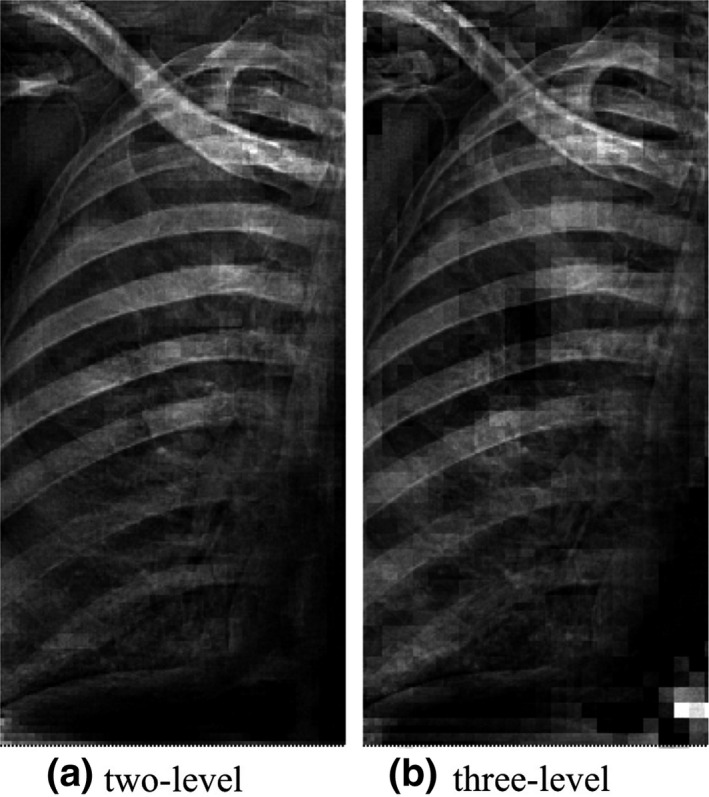
Comparison of (a) two‐level and (b) three‐level OFS decomposition in terms of the bone images using our ASOFS NNC schemes.
Figure 9 represents an example of a lung segment‐wise bone prediction of our scheme through AS decomposition for the lowest resolution/frequency image. See how the NNC expert for each specific segment had a higher performance on the corresponding segment, e.g., the NNC on the left middle section successfully detected the ribs near the left lung wall, while it failed to detect the ribs in the left hilar area, comparing to the NNC expert of the left hilar area. Similar trends can be seen for the experts for the other lung segments.
Figure 9.
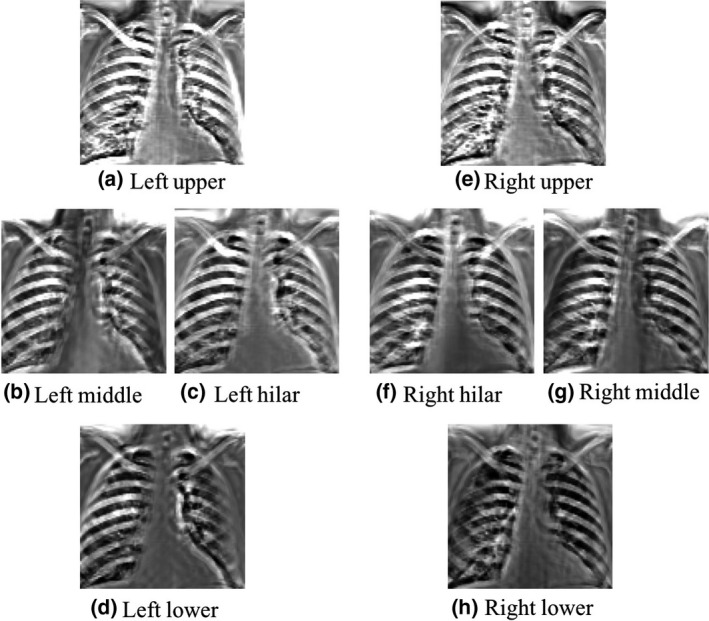
Predictions of the AS NNC experts for different lung segments for the lowest resolution/frequency. Each NNC was trained using the patch‐pixel pairs of its corresponding segment.
Use of DE soft‐tissue images can improve the detection of focal soft‐tissue opacities, such as lung nodules, that may be partly obscured by overlying bony structures.14, 40 Despite the advantages, a very limited number of hospitals use radiography systems with DE subtraction, because specialized equipment for obtaining DE x‐ray exposures is required. More importantly, the radiation dose can be double or more compared with standard chest radiography. In previous studies, the average skin entrance radiation dose with the dual‐shot DE technique was 119–130 mR,42 and that with the single‐shot DE technique was 60–100 mR,38 both of which are greater than the 15–20 mR used in standard chest radiography. In a more recent study, a 2.4 times higher radiation dose was used for DE radiography compared with conventional radiography in order to obtain the same noise level.43 The major advantages of our technique compared to a DE subtraction technique are that our technique requires no additional radiation dose to patients and no specialized equipment for generating DE x‐ray exposures.
A major challenge in current CAD schemes is the detection of nodules overlapping with ribs and clavicles, because most false positives are caused by these structures.9, 10, 11 The distinction between nodules and other anatomic structures such as ribs and clavicles is improved in our soft‐tissue images with our technique; therefore, these images could improve the performance of nodule‐detection CAD schemes.44
There is room for improvement of this study. In this study, we used the same set of hyper‐parameters for all of the 56 NNC experts. Tuning the per‐NNC hyper‐parameters on a validation set can potentially improve the bone‐suppression performance, while it can be potentially a time‐consuming task. In addition, if one or more of the NNC models are not trained sufficiently (e.g., MSE is not converged), fusing them to other experts can decrease the final performance. This can be potentially addressed by combining all NNC experts in a single framework during both the learning and test processes.
A major advantage of single‐shot DE imaging over dual‐shot DE imaging is less motion artifacts in soft‐tissue and bone images. Limitations of single‐shot DE imaging are, in general, a slightly increased noise level and slightly poor energy separation. Because virtual DE imaging based on deep learning16, 17, 18, 19, 20, 21, 22, 23, 24 requires pairs of input chest radiographs and corresponding “teaching” DE bone and/or soft‐tissue images with no/little motion, single‐shot DE imaging is suited for creating images for training deep learning models.
5. Conclusion
We proposed and designed an ASOFS deep NNC scheme to develop a virtual DE imaging system. Acquiring a DE database, our scheme was able to learn to predict bone and soft‐tissue images from single standard CXRs. While the AS was designed previously under the framework of MTANNs, in this work, we newly formally defined the AS decomposition/reconstruction in a probabilistic deep‐learning framework, and showed how it can be optimized and implemented practically using our gating and soft‐gating layers. In addition to that, we newly proposed and developed the novel OFS mixture‐of‐experts models to address the receptive‐field and pattern‐variation issues and to decompose the prediction task into simpler component‐wise predictions. We compared our scheme with a state‐of‐the‐art bone‐suppression technique quantitatively and qualitatively. Our bone and soft‐tissue images had higher PSNR and SSIM values than did those of the reference‐standard technique with a statistically significant difference. In particular, qualitative assessment showed that our scheme suppressed bones more than the reference technique, while it was better able to preserve soft‐tissue structures such as lung nodules and vessels. Therefore, our improved virtual DE system would be beneficial to radiologists as well as CAD schemes in the detection of lung nodules in CXRs.
Acknowledgment
The authors are grateful to all members of Computational Intelligence in Biomedical Imaging (CIBI) Lab at Illinois Institute of Technology, specially Jaimeet Patel for his valuable discussions. This work was done in part at Tokyo Institute of Technology, Yokohama, Japan. This work was supported in part by an NIH grant (1UL1TR002389) with University of Chicago Institute for Translational Medicine.
References
- 1. Murray CJ, Lopez AD. Mortality by cause for eight regions of the world: global Burden of Disease Study. Lancet. 1997;349:1269–1276. [DOI] [PubMed] [Google Scholar]
- 2. Murphy GP, Lawrence W, Lenhard RE. American Cancer Society Textbook of Clinical Oncology. The Society; 1995. [Google Scholar]
- 3. Frost JK, Ball WC Jr, Levin ML, et al. Early lung cancer detection: results of the initial (prevalence) radiologic and cytologic screening in The Johns Hopkins Study 1–3. Am Rev Respir Dis. 1984;130:549–554. [DOI] [PubMed] [Google Scholar]
- 4. Fontana RS, Sanderson DR, Taylor WF, et al. Early lung cancer detection: results of the initial (prevalence) radiologic and cytologic screening in the Mayo Clinic study. Am Rev Respir Dis. 1984;130:561–565. [DOI] [PubMed] [Google Scholar]
- 5. Henschke CI, Miettinen OS, Yankelevitz DF, Libby DM, Smith JP. Radiographic screening for cancer proposed paradigm for requisite research. Clin Imaging. 1994;18:16–20. [DOI] [PubMed] [Google Scholar]
- 6. Flehinger BJ, Kimmel M, Melamed MR. The effect of surgical treatment on survival from early lung cancer. Implications for screening. Chest. 1992;101:1013–1018. [DOI] [PubMed] [Google Scholar]
- 7. Tomotaka S, Takaichiro S, Minoru M, Tetsuo K, Shigeto I, Tsuguo N. Survival for clinical stage I lung cancer not surgically treated comparison between screen‐detected and symptom‐detected cases. Lung Cancer. 1992;4:237. [DOI] [PubMed] [Google Scholar]
- 8. Heelan RT, Flehinger BJ, Melamed MR, et al. Non‐small‐cell lung cancer: results of the New York screening program. Radiology. 1984;151:289–293. [DOI] [PubMed] [Google Scholar]
- 9. Austin JH, Romney BM, Goldsmith LS. Missed bronchogenic carcinoma: radiographic findings in 27 patients with a potentially resectable lesion evident in retrospect. Radiology. 1992;182:115–122. [DOI] [PubMed] [Google Scholar]
- 10. Xu XW, Doi K, Kobayashi T, MacMahon H, Giger ML. Development of an improved CAD scheme for automated detection of lung nodules in digital chest images. Med Phys. 1997;24:1395–1403. [DOI] [PubMed] [Google Scholar]
- 11. Matsumoto T, Yoshimura H, Doi K, et al. Image feature analysis of false‐positive diagnoses produced by automated detection of lung nodules. Invest Radiol. 1992;27:587–597. [DOI] [PubMed] [Google Scholar]
- 12. Glocker R, Frohnmayer W. Über die röntgenspektroskopische Bestimmung des Gewichtsanteiles eines Elementes in Gemengen und Verbindungen. Ann Phys. 1925;381:369–395. [Google Scholar]
- 13. Jacobson B, Mackay RS. Radiological contrast enhancing methods. Adv Biol Med Phys. 1958;6:201–261. [DOI] [PubMed] [Google Scholar]
- 14. Kido S, Nakamura H, Ito W, Shimura K, Kato H. Computerized detection of pulmonary nodules by single‐exposure dual‐energy computed radiography of the chest (Part 1). Eur J Radiol. 2002;44:198–204. [DOI] [PubMed] [Google Scholar]
- 15. Kido S, Kuriyama K, Kuroda C, et al. Detection of simulated pulmonary nodules by single‐exposure dual‐energy computed radiography of the chest: effect of a computer‐aided diagnosis system (Part 2). Eur J Radiol. 2002;44:205–209. [DOI] [PubMed] [Google Scholar]
- 16. Suzuki K, Abe H, MacMahon H, Doi K. Image‐processing technique for suppressing ribs in chest radiographs by means of massive training artificial neural network (MTANN). IEEE Trans Med Imaging. 2006;25:406–416. [DOI] [PubMed] [Google Scholar]
- 17. Suzuki K, Abe H, Li F, Doi K. Suppression of the contrast of ribs in chest radiographs by means of massive training artificial neural network. In: Proc. SPIE Medical Imaging (SPIE MI) 5370.; 2004:1109–1119.
- 18. Oda S, Awai K, Suzuki K, et al. Performance of radiologists in detection of small pulmonary nodules on chest radiographs: effect of rib suppression with a massive‐training artificial neural network. Am J Roentgenol. 2009;193:397–402. [DOI] [PubMed] [Google Scholar]
- 19. Chen S, Suzuki K. Separation of bones from chest radiographs by means of anatomically specific multiple massive‐training ANNs combined with total variation minimization smoothing. IEEE Trans Med Imaging. 2014;33:246–257. [DOI] [PubMed] [Google Scholar]
- 20. Chen S, Zhong S, Yao L, Shang Y, Suzuki K. Enhancement of chest radiographs obtained in the intensive care unit through bone suppression and consistent processing. Phys Med Biol. 2016;61:2283–2301. [DOI] [PubMed] [Google Scholar]
- 21. Ahmed B, Rasheed T, Khan MA, Cho SJ, Lee S, Kim T‐S. Rib suppression for enhancing frontal chest radiographs using independent component analysis. In: International Conference on Adaptive and Natural Computing Algorithms. Berlin, Germany: Springer; 2007:300–308. [Google Scholar]
- 22. Loog M, van Ginneken B, Schilham AMR. Filter learning: application to suppression of bony structures from chest radiographs. Med Image Anal. 2006;10:826–840. [DOI] [PubMed] [Google Scholar]
- 23. Yang W, Chen Y, Liu Y, et al. Cascade of multi‐scale convolutional neural networks for bone suppression of chest radiographs in gradient domain. Med Image Anal. 2017;35:421–433. [DOI] [PubMed] [Google Scholar]
- 24. Zarshenas A, Patel J, Liu J, Forti P, Suzuki K. Virtual Dual‐Energy (VDE) Imaging: Separation of Bones from Soft Tissue in Chest Radiographs (CXRs) by Means of Anatomy‐Specific (AS) Orientation‐Frequency‐Specific (OFS) Deep Neural Network Convolution (NNC). In: Program of Scientific Assembly and Annual Meeting of Radiological Society of North America (RSNA).; 2017.
- 25. Suzuki K, Horiba I, Sugie N, Ikeda S. Improvement of image quality of x‐ray fluoroscopy using spatiotemporal neural filter which learns noise reduction, edge enhancement and motion compensation. In: Proc. Int. Conf. Signal Processing Applications and Technology (ICSPAT) 2.; 1996:1382–1386.
- 26. Suzuki K, Horiba I, Sugie N. Efficient approximation of neural filters for removing quantum noise from images. IEEE Trans Signal Process. 2002;50:1787–1799. [Google Scholar]
- 27. Suzuki K, Horiba I, Sugie N, Nanki M. Neural filter with selection of input features and its application to image quality improvement of medical image sequences. IEICE Trans Inf Syst E85‐D. 2002:1710–1718.
- 28. Suzuki K, Horiba I, Sugie N. Neural edge enhancer for supervised edge enhancement from noisy images. IEEE Trans Pattern Anal Mach Intell. 2003;25:1582–1596. [Google Scholar]
- 29. Suzuki K, Horiba I, Sugie N, Nanki M. Extraction of left ventricular contours from left ventriculograms by means of a neural edge detector. IEEE Trans Med Imaging. 2004;23:330–339. [DOI] [PubMed] [Google Scholar]
- 30. Suzuki K, Armato SG, Li F, Sone S, Doi K. Massive training artificial neural network (MTANN) for reduction of false positives in computerized detection of lung nodules in low‐dose computed tomography. Med Phys. 2003;30:1602–1617. [DOI] [PubMed] [Google Scholar]
- 31. Xu J‐W, Suzuki K. Massive‐training support vector regression and Gaussian process for false‐positive reduction in computer‐aided detection of polyps in CT colonography. Med Phys. 2011;38:1888–1902. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Suzuki K, Liu J, Zarshenas A, Higaki T, Fukumoto W, Awai K. Neural network convolution (NNC) for converting ultra‐low‐dose to “Virtual” high‐dose CT images. In: International Workshop on Machine Learning in Medical Imaging.; 2017:334–343.
- 33. Long J, Shelhamer E, Darrell T. Fully convolutional networks for semantic segmentation. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Vol 07‐12‐June.; 2015:3431–3440.
- 34. Liu J, Zarshenas A, Qadir A, et al. Radiation dose reduction in digital breast tomosynthesis (DBT) by means of deep‐learning‐based supervised image processing. In: Proceedings of SPIE.; 2018.
- 35. LeCun Y, Bottou L, Orr GB, Müller K‐R. Eficient backprop. In: Neural Networks: Tricks of the Trade. Berlin, Germany: Vol Springer B.; 2012:9–48. [Google Scholar]
- 36. Zarshenas A, Suzuki K. Binary coordinate ascent: an efficient optimization technique for feature subset selection for machine learning. Knowledge‐Based Syst. 2016;110:191–201. [Google Scholar]
- 37. Theano Development Team . Theano: A Python framework for fast computation of mathematical expressions. arXiv e‐prints. May 2016:19.
- 38. Ishigaki T, Sakuma S, Horikawa Y, Ikeda M, Yamaguchi H. One‐shot dual‐energy subtraction imaging. Radiology. 1986;161:271–273. [DOI] [PubMed] [Google Scholar]
- 39. Ishigaki T, Sakuma S, Ikeda M. One‐shot dual‐energy subtraction chest imaging with computed radiography: clinical evaluation of film images. Radiology. 1988;168:67–72. [DOI] [PubMed] [Google Scholar]
- 40. Stewart BK. Single‐exposure dual‐energy computed radiography. Med Phys. 1990;17:866–875. [DOI] [PubMed] [Google Scholar]
- 41. Wang Z, Bovik AC, Sheikh HR, Simoncelli EP. Image quality assessment: from error visibility to structural similarity. IEEE Trans Image Process. 2004;13:600–612. [DOI] [PubMed] [Google Scholar]
- 42. Nishitani H, Umezu Y, Ogawa K, Yuzuriha H, Tanaka H, Matsuura K. Dual‐energy projection radiography using condenser x‐ray generator and digital radiography apparatus. Radiology. 1986;161:533–535. [DOI] [PubMed] [Google Scholar]
- 43. Whitman G, Niklason L, Pandit M, et al. Dual‐energy digital subtraction chest radiography: technical considerations. Curr Probl Diagn Radiol. 2002;31:48–62. [DOI] [PubMed] [Google Scholar]
- 44. Chen S, Suzuki K. Computerized detection of lung nodules by means of “virtual dual‐energy” radiography. IEEE Trans Biomed Eng. 2013;60:369–378. [DOI] [PMC free article] [PubMed] [Google Scholar]


