Abstract
Intensity‐based deformable image registration (DIR) requires minimizing an image dissimilarity metric. Imaged anatomy, such as bones and vasculature, as well as the resolution of the digital grid, can often cause discontinuities in the corresponding objective function. Consequently, the application of a gradient‐based optimization algorithm requires a preprocessing image smoothing to ensure the existence of necessary image derivatives. Simple block matching (exhaustive search) methods do not require image derivative approximations, but their general effectiveness is often hindered by erroneous solutions (outliers). Block match methods are therefore often coupled with a statistical outlier detection method to improve results.
Purpose
The purpose of this work is to present a spatially accurate, intensity‐based DIR optimization formulation that can be solved with a straightforward gradient‐free quadratic penalty algorithm and is suitable for 4D thoracic computed tomography (4DCT) registration. Additionally, a novel regularization strategy based on the well‐known leave‐one‐out robust statistical model cross‐validation method is introduced.
Methods
The proposed Quadratic Penalty DIR (QPDIR) method minimizes both an image dissimilarity term, which is separable with respect to individual voxel displacements, and a regularization term derived from the classical leave‐one‐out cross‐validation statistical method. The resulting DIR problem lends itself to a quadratic penalty function optimization approach, where each subproblem can be solved by straightforward block coordinate descent iteration.
Results
The spatial accuracy of the method was assessed using expert‐determined landmarks on ten 4DCT datasets available on www.dir-lab.com. The QPDIR algorithm achieved average millimeter spatial errors between 0.69 (0.91) and 1.19 (1.26) on the ten test cases. On all ten 4DCT test cases, the QPDIR method produced spatial accuracies that are superior or equivalent to those produced by current state‐of‐the‐art methods. Moreover, QPDIR achieved accuracies at the resolution of the landmark error assessment (i.e., the interobserver error) on six of the ten cases.
Conclusion
The QPDIR algorithm is based on a simple quadratic penalty function formulation and a regularization term inspired by leave‐one‐out cross validation. The formulation lends itself to a parallelizable, gradient‐free, block coordinate descent numerical optimization method. Numerical results indicate that the method achieves a high spatial accuracy on 4DCT inhale/exhale phases.
Keywords: deformable image registration, four‐dimensional computed tomography, landmark validation, lung motion, moving least squares, numerical optimization
1. Introduction
Deformable Image Registration (DIR) algorithms determine a spatial transformation that best relates the content depicted within a pair (or sequence) of images, with respect to an intensity and/or physical motion model.1 DIR is essential to a host of medical imaging applications,2 including lung disease analysis,3 strain‐rate imaging,4 and brain morphometry.5 In the specific example of thoracic 4DCT registration, the utility of applications such as CT‐derived ventilation,6 tumor motion assessment,7 and even image reconstruction,8 are dependent on the spatial accuracy of the recovered transformation.9 As such, DIR algorithm development, validation, and applications are all active areas of research.
The image registration problem, despite being conceptually straightforward, is notoriously ill‐posed. DIR problem difficulty can vary greatly according to a number of issues, including the image modalities, the time frame over which the images were acquired, and the nature of the depicted deformation.10 As a result, algorithm development is often focused on specific settings. Just the specific case of thoracic inhale/exhale computed tomography (CT) image pair registration has alone spawned methods based on biomechanical11, 12 and elasticity13, 14, 15 modeling, as well as methods focused on efficient numerical optimization for different parameterizations and image intensity metrics.16, 17 These methods have all demonstrated varying degrees of effectiveness (see Ref. 18 for a thorough review).
Ultimately, regardless of modeling approach, intensity‐based image registration often requires solving an optimization problem defined by an image similarity metric.10 Since imaged anatomy includes a nonhomogeneous collections of bones and vasculature, this optimization problem is typically nonconvex, nonlinear, or possibly discontinuous. Consequently, gradient‐based optimization algorithms, such as Newton's method, require image smoothing, possibly at the expense of degrading fine image features,19 in order to ensure the existence of first or second‐order image derivatives. Moreover, coarse‐to‐fine strategies, such as Gaussian pyramid, are often required to avoid convergence to a local minimum.20
Cognizant of the numerical difficulties associated with intensity‐based DIR, recent gradient‐free methods based on exhaustive block match searches21 and feature extraction22 have achieved high spatial accuracy. In medical imaging in particular, robust statistical regression methods for parametric estimation, such as least squares trimming23 and forward search,24, 25 have demonstrated effectiveness for computing rigid26 and locally affine27 registration from block match data. The purpose of this work is to present a spatially accurate, intensity‐based DIR optimization formulation that can be solved with a straightforward gradient‐free quadratic penalty algorithm. In addition, a novel regularization strategy based on the well‐known leave‐one‐out robust statistical model cross‐validation method is introduced. The spatial accuracy of the proposed Quadratic Penalty DIR method is assessed using expert‐determined landmark point pairs for 10 maximum inhale/exhale 4DCT phases from the publically available www.dir-lab.com validation data repository.9
2. Methods
2.A. DIR problem definition
The DIR algorithms determine a spatial transformation, ϕ(x): , that maps each voxel within a three‐dimensional (3D) reference image, R(x), to its corresponding position within a 3D target image, T(x). Often this relationship is described in terms of a 3D displacement field:
| (1) |
where d k denotes the displacement in the kth spatial dimension. Block matching is a well‐known strategy for finding the optimal displacement of a single voxel with respect to a specified image similarity metric via exhaustive grid search.28 The resulting estimates are robust to image noise, image discontinuities, and large magnitude voxel displacements. However, the `estimates are computed independently from one another, using only a limited amount of localized image information. As a consequence, the spatial accuracy of the estimates is not guaranteed26 and block matching‐based DIR methods must account for erroneous displacement estimates (often referred to as outliers). This is typically accomplished by postprocessing the block match estimates with a robust statistical method for outlier detection, such as median filtering27 or estimated variance thresholding.29 Although such methods have demonstrated a high spatial accuracy, each block match estimate is computed without taking into account the motion of neighboring voxels. This limitation motivates the following general formulation:
| (2) |
where
| (3) |
represents the 3N unknown discretized displacement variables, and the matrix encodes a regularization model, which is enforced as a least squares penalty with strength specified by the regularization parameter α. Image dissimilarity is structured as the sum of the individual dissimilarity contributions associated with each displacement vector, as quantified by the function F. In other words, image dissimilarity is separable with respect to each voxel's unknown displacement vector components.
2.B. Quadratic penalty function formulation
Problem (2) is a nonlinear and nonconvex optimization problem, similar to standard intensity‐based DIR formulations.10 Introducing auxiliary variables z 1, z 2, z 3 and equality constraints:
| (4) |
results in a formulation equivalent to (2), but the structure of the equality‐constrained formulation in (4) is well suited for the quadratic penalty (QP) function optimization method.30 In this instance, the QP method solves a series of subproblems of the form:
| (5) |
for successively smaller values of μ (i.e., successively stronger penalization on equality constraint violations) until convergence to a feasible local minimizer.30 Thus, the effectiveness of the QP method depends almost exclusively on the quality of the subproblem solver.
2.B.1. Block coordinate descent iteration
Subproblem (5) can be solved robustly with straightforward block coordinate descent iteration.
Algorithm 1: block coordinate descent
Given initial displacement estimates z 1, z 2, z 3,
1) Update for i = 1, 2, …, N:
| (6) |
2) Compute:
| (7) |
3) If stop with solutions
Otherwise, set and go back to Step 1.
The block coordinate descent iteration alternates between minimizing with respect to the displacement vectors, and the auxiliary variables until the magnitude difference between successive iterates is zero or less than a specified tolerance. Because the dissimilarity is separable with respect to the individual displacement vectors, the displacement vector update given by Eq. (6) can be computed with an exhaustive grid search, similar to the standard block matching operator. The auxiliary variable updates in Eq. (7) require solving three linear least squares problems. Therefore, the quadratic penalty method and Algorithm 1 can be used to solve Problem (2) without image gradient information.
2.B.2. Convergence of block coordinate descent
Convergence of block coordinate descent iteration is guaranteed when each block coordinate subproblem has a unique and computable global minimizer (see Chapter 8 in Ref. 31). The least squares updates certainly satisfy this condition. The block matching problems are not guaranteed to possess a unique global minimizer, but if they do, the exhaustive grid search will find them. Moreover, the DIR problem can be discretized such that the unknowns [Eq. (3)] correspond to image voxel locations with distinct image features or nonflat regions to reduce the risk of violating the convergence criteria.
2.C. Leave‐one‐out regularization
Leave‐one‐out cross validation (LOOCV) is a well‐known statistical method that quantifies the effectiveness of an approximation model by (a) fitting the model to all but one data point and then (b) evaluating the approximation's error on the remaining (left out) data point. This process is repeated with each data point being left out once. The resulting errors provide an estimate for how well each data point is predicted by the remaining data points.32, 33 In contrast to standard block matching methods, which apply postprocessing statistical methods to detect potential outliers, the goal here is to employ the LOOCV metric as a way to regularize the DIR Problem (2). To do this, the unknown displacement field is modeled with the moving least squares (MLS) approximation.34
The MLS approximation is defined by a set of spatial positions and data values Evaluating the MLS approximation function, f mls (x) requires computing a (proximal distance) weighted least squares polynomial fit to the dataset X, y:
| (8) |
where p is a polynomial parameterized by the vector q and w(·) is the weighting function. In order to formulate an LOOCV regularization metric, the MLS approximation f mls (x) must be expressed as a function of the data vector y.
For specificity, choosing the approximating polynomial in Eq. (8) to have the form results in the following MLS formulation:
| (9) |
where
| (10) |
and W(x) is a diagonal matrix with The normal equations for Eq. (9) dictate that the MLS approximation for X, y can be expressed as:
| (11) |
Equation (11) expresses the MLS approximation as a vector multiplication between the data values, y, and the MLS operator . For each x i , the MLS LOOCV error metric, , is defined as the squared distance between the data estimate for x i and the MLS approximation defined by the data estimates for the remaining points :
| (12) |
where the indexing matrix H (i) is obtained by removing the i th row of the N × N identity matrix. The MLS LOOCV DIR regularization model is defined as the sum of the error metrics for all data points and can be represented as a least squares penalization:
| (13) |
where the N × N matrix A has the form:
| (14) |
Constructing the matrix A requires the same computational workload as evaluating the MLS approximation function, although the MLS operator in Eq. (11) is not typically stored in other applications. Moreover, sparsity can be incorporated into A with a compactly supported or fast decaying weighting function w. For instance, functions of the form
| (15) |
where the parameter σ is set with respect to a maximum distance r max, such that w(r) ≪ 1 for r ≥ r max. These type of weighting schemes are common in MLS applications.35 For instance, assuming the voxel point cloud X possess points that are approximately uniformly spaced h millimeters apart, the MLS weighting function parameter
| (16) |
implies w(r) ≈ 0 for r > 3h.
2.D. Block matching operator
Equation (6) within the block coordinate descent Algorithm 1 requires solving a series of block matching problems with general form:
| (17) |
where . A typical block matching operation is defined by a search window, block window, and image dissimilarity metric F. The image dissimilarity metric is computed with respect to the image intensities contained within block windows:
| (18) |
For instance, F could represent the sum of squared intensity differences between the image intensity blocks R(Ω(x; ε)) and :
| (19) |
However, considering that the test images for this study are inhale/exhale lung CT pairs, the dissimilarity metric should accommodate intensity variations between the inhale and exhale images.36 Such metrics include normalized gradient fields,37 compressible optical flow,27 and those based on the structural similarity index (SSIM)38:
| (20) |
Finally, the search window represents the set of all feasible displacements which, in this case, is represented as a neighborhood of radius l centered on :
| (21) |
The block match estimated displacement for x:
| (22) |
is computed by evaluating the image dissimilarity for each c in the search window. Without loss of generality, it is assumed that F → [0, 1]. Under this assumption, the relationship between the search window radius and the penalty parameter μ for problem Eq. (6) is given as:
| (23) |
This follows from the fact that F (z; x, R , T , ϵ) ≤ 1 and .
2.E. Quadratic Penalty Deformable Image Registration algorithm
The proposed Quadratic Penalty Deformable Image Registration (QPDIR) algorithm solves the formulation in Eq. (2) with the quadratic penalty function optimization method, using the block coordinate descent Algorithm 1 to solve the Eq. (5) subproblem for a series of monotonically decreasing values of μ.
The QPDIR algorithm operates on a subsampling of voxel locations (the voxel set X in Algorithm 2). A point cloud of approximately uniformly spaced voxel locations is determined by a “dart throwing” procedure applied to a simple histogram segmentation of the inhale lung volume (as done in Ref. 21).
3.
Algorithm 2: QPDIR
Given a set of voxel locations with corresponding initial displacement estimates z 1, z 2, z 3, a regularization parameter α, and an initial value for the penalty parameter μ:
1. Compute by solving the QP subproblem defined by μ in Eq. (5), using block coordinate descent (Algorithm 1) and initial guess
2. if μ < 0.5, stop with solution
Otherwise,
set
set μ = 0.5 μ,
go back to Step 1.
3. Apply MLS to compute full displacement field.
As dictated by Eq. (12), the QP stopping criterion μ < 0.5 corresponds to a block match search window with radius <1.00. This reflects the resolution of the block matching operator, considering that it is defined on integer grid values. A flowchart representation of Algorithm 2 is given in Fig. 1.
Figure 1.
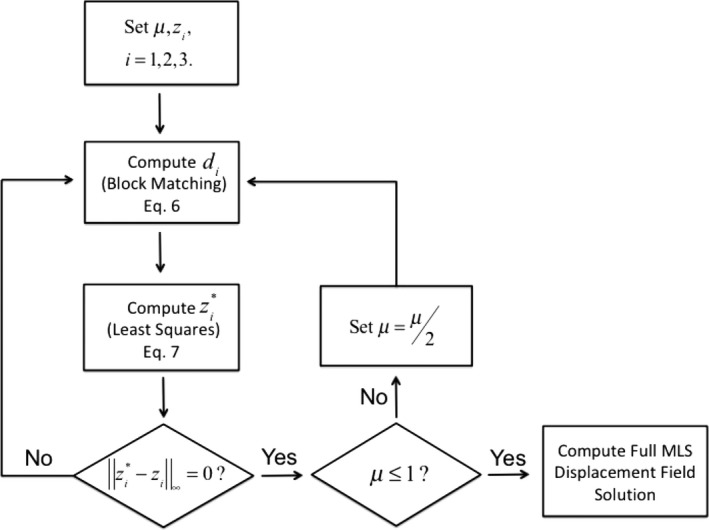
A flowchart representation of the full QPDIR algorithm. For a given penalty parameter μ, the method alternates between the block matching and least squares subproblems until there is no difference between successive iterates. At that point, if the penalty parameter is sufficiently small (less than one), then the full MLS displacement field is computed. Otherwise, the penalty parameter is updated and the process repeats.
2.E.1. Moving least squares displacement field
A full DIR displacement field is obtained from the Algorithm 2 solution, , by applying the MLS approximation. Specifically, for each voxel x within the lung region of interest, the displacement vector is computed as:
| (24) |
where the MLS function f mls is defined according to Eq. (8), using the weighting function defined by Eqs. (4) and (5).
A desirable property of practical DIR algorithms is that the determinant of the transformation's Jacobian is guaranteed to be strictly positive. Physically, this property prevents tissue folding in the resulting DIR solution. As described, the QPDIR algorithm does not explicitly prevent tissue folding, or equivalently, the determinant of the DIR transformation Jacobian is not required to be strictly positive. Although no negative Jacobian determinant values arise in the numerical experiments presented in Section Methods, a nonfolding constraint can be incorporated into the QPDIR numerical implementation (or any DIR method applied to 4DCT inhale/exhale phases) using the postprocessing method described in Ref. 39.
2.E.2. Numerical implementation
The current numerical implementation of QPDIR utilizes the LOOCV regularization metric defined by Eqs. (3) and (4), and minimizes the structural similarity metric defined by (20). The software is implemented in CUDA C++ and utilizes the openMP shared‐memory parallel programming library. Graphics processing unit (GPU) computing handles the bulk of the computational workload, namely the embarrassingly parallelizable block matching minimization (Algorithm 1, Step 1). The least squares updates (Algorithm 1, Step 2) are computed by applying the conjugate gradient method to the normal equations for Eq. (7).
All numerical experiments presented in Section Methods were obtained on a Dell Precision Laptop with an Intel i7‐6920HQ processor (2.90 GHz × 8), a Quadro M5000 Nvidia GPU, and 64GB of RAM.
4. Results
3.A. DIR‐LAB 4DCT cases
A dataset (Table 1) comprised of ten maximum inhale and exhale 4DCT phase pairs, each with a corresponding set of 300 expert‐determined landmark points,9 was used to assess the spatial accuracy of the QPDIR algorithm. All data are available for public download at www.dir-lab.com.
Table 1.
Dataset 4DCT: Ten 4DCT maximum inhale/exhale phase pairs
| Case | Interobserver error (mm) | Average displacement (mm) | QPDIR avg. error (mm) | Best algorithm error (mm) | Best algorithm |
|---|---|---|---|---|---|
| 1 | 0.85 (1.24) | 4.01 (2.91) | 0.71 (0.91) | 0.74 (0.90) | LMP |
| 2 | 0.70 (0.99) | 4.65 (4.09) | 0.69 (0.91) | 0.72 (0.87) | SGM3D |
| 3 | 0.77 (1.01) | 6.73 (4.21) | 0.87 (1.05) | 0.91 (1.05) | isoPTV |
| 4 | 1.13 (1.27) | 9.42 (4.81) | 1.19 (1.26) | 1.21 (1.19) | pTV |
| 5 | 0.92 (1.16) | 7.10 (5.12) | 1.07 (1.50) | 1.07 (1.46) | NGF |
| 6 | 0.97 (1.38) | 11.10 (6.98) | 0.89 (0.94) | 0.85 (0.89) | isoPTV |
| 7 | 0.81 (1.32) | 11.59 (7.87) | 0.80 (0.91) | 0.80 (1.28) | isoPTV |
| 8 | 1.03 (2.19) | 15.16 (9.11) | 1.03 (1.21) | 1.03 (1.19) | NLR |
| 9 | 0.75 (1.09) | 7.82 (3.99) | 0.90 (0.91) | 0.91 (0.93) | SGM3D |
| 10 | 0.86 (1.45) | 7.63 (6.54) | 0.86 (0.91) | 0.83 (0.92) | isoPTV |
isoPTV, Isotropic Total Variation for Parametric Image Registration methods; LMP, LandMark Penalty; NLR, normalized gradient fields; SGM3D, Semi‐Global Scan‐Line Integration method; NGF, Normalized Gradient Field;
A summary of the ten 4DCT inhale/exhale phase test cases provided by www.dir-lab.com, as well as the spatial accuracies achieved by the QPDIR algorithm is detailed. The highlighted entries denote that the algorithm achieved an average error below the interobserver error. For comparison, the lowest average error achieved by a previously published algorithm for each case is also given.
3.B. Parameters
Since 4DCTs are acquired while the patient is free‐breathing, the maximum magnitude displacements for these test cases are generally under 15 voxels. As such, an initial search window size of 15 [Eq. (12)] and initial guess of zero was employed within the QPDIR algorithm to achieve the results in Table 1. Block window size was set to be approximately isotropic in millimeters, which translates into 7 × 7 × 3 voxel windows. The computational point cloud, X, was acquired with the dart throwing method using an approximate isotropic millimeter spacing of 7.5 mm. This resulted in voxel point clouds with 15k–30k points per lung with approximately 3 × 3 × 1 component distance between voxel points, and an MLS weighting parameter [as defined by Eq. (5)] of h = 7.5. The regularization parameter α = 1 [see Eq. (2)] for all cases.
3.C. Spatial accuracy assessment
Spatial error is defined as the Euclidean distance (in millimeters) between the expert‐determined landmark position and the estimated landmark position provided by the DIR. The average interobserver spatial error between three expert readers is also provided with the dir‐lab validation datasets.9, 40 This interobserver error measurement represents the resolution of the landmark error assessment. Concretely, an average DIR spatial error below the interobserver error implies that the DIR algorithm is generating landmarks with an accuracy that is indistinguishable from that of human experts. The spatial accuracy of the QPDIR algorithm and the highest spatial accuracy achieved by a published algorithm (to the best of author's knowledge) for each of the ten 4DCT cases is provided in Table 1. These algorithms include: the LandMark Penalty method,17 Semi‐Global Scan‐Line Integration method,41 Isotropic Total Variation for Parametric Image Registration methods (isoPTV)42 and (pTV),43 Normalized Gradient Field method,44 and diffeomorphic variational normalized gradient fields.45
The QPDIR algorithm achieved an average spatial error (for inhale‐to‐exhale motion recovery) at or below the interobserver variance on six of the ten cases. In aggregate, previous methods achieved this level of accuracy on only five cases. Moreover, the QPDIR achieved an average spatial error at or below those produced by the best previously reported methods on all ten test cases. Moreover, the computation runtimes varied between 1 and 3 min per case.
The Jacobian values (determinant of the first derivative of the spatial transformation) for all ten cases were approximated from the QPDIR displacement fields. As illustrated by Fig. 2, the distribution of Jacobian values indicates that the inhale‐to‐exhale motion is primarily contractive and the QPDIR method did not produce any negative Jacobian values. Figure 3 illustrates the displacement field and Jacobian map for DIR‐LAB Case 6. This particular case is designated as a digital phantom test case by the AAPM Radiation Therapy Committee Task Group on the use of DIR algorithms in radiotherapy.46
Figure 2.
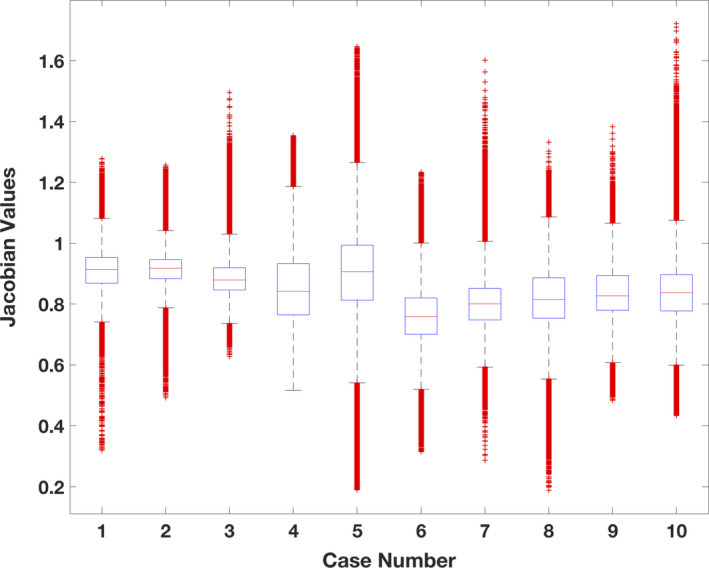
A box plot of the Jacobian values computed from the QPDIR solution for each of the ten cases in Table 1. The plot was created using MATLAB (release 2017b, The Mathworks Inc., Natick, Massachusetts, United States) boxplot function. On each box, the central mark indicates the median, and the bottom and top edges of the box indicate the 25th and 75th percentiles, respectively. The whiskers extend to the most extreme data points not considered outliers. The bulk of the values are all below 1.00, indicating a primarily contractive lung motion from inhale‐to‐exhale.
Figure 3.
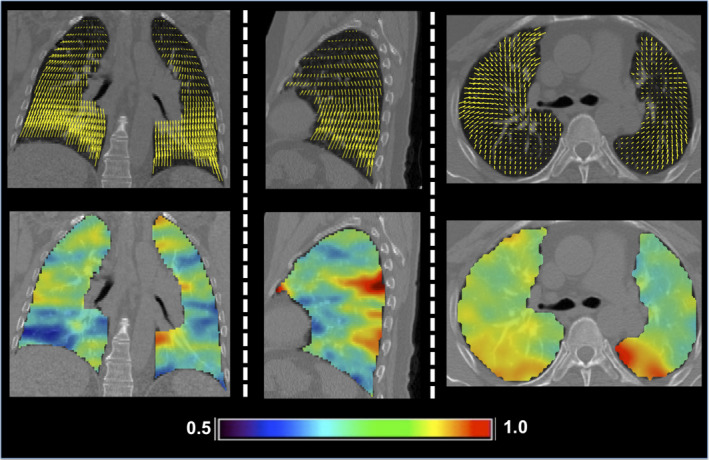
Coronal (left), sagittal (middle), and axial (right) slices of the QPDIR displacement field (top row) and the corresponding Jacobian map (bottom row) for case 6 in Table 1. The color code denotes the Jacobian values for inhale‐to‐exhale lung motion. Most values are less than one, indicating a contractive motion.
5. Discussion
A key difficulty in computing accurate DIR is numerically optimizing a similarity metric defined by the image data. Medical imaging often depicts a nonhomogeneous array of complex anatomical structures. As a result, the similarity objective function can be nonlinear, nonconvex, or discontinuous. These properties are known challenges for numerical optimization algorithms such as gradient descent and Newton's method. In fact, guaranteed convergence for Newton‐type methods requires the existence of smooth objective function derivatives.30 Since this property does not hold for CT images, gradient‐based DIR optimizers require a smooth, continuously defined image interpolant (such as B‐splines or tri‐linear interpolation) on which to operate. Such approximations have the potential to over smooth data, which could possibly lead to poorer accuracy.19 With these issues in mind, the motivation for this work was to develop a robust DIR framework tailored to suit the inherent properties of 4DCT DIR optimization, namely, a discontinuous objective function defined on a discretized digital image grid and moderate (<20 voxel) magnitude displacements.
The QPDIR algorithm is based on reformulating the DIR problem so that it lends itself to the quadratic penalty function optimization method. The formulation utilizes three simple but robust image and data processing methods: block matching, MLS, and LOOCV. While each has been reported on in previous methods, these components have never been incorporated into a single DIR formulation (to the best of the Author's knowledge). The QP framework, therefore, provides a novel mechanism for combining block matching, MLS, and LOOCV into a simple numerical method, specifically designed for 4DCT lung motion. The resulting method achieves accuracies higher than those previously published, indicating that QPDIR is better suited for 4DCT DIR than existing methods.
Quadratic penalty DIR requires the image dissimilarity metric to be separable with respect to individual displacement vectors. In this way, the quadratic penalty subproblems can be solved with a gradient‐free block coordinate descent numerical optimization method. By employing brute‐force exhaustive searches, this approach mitigates the challenges associated with numerically optimizing the similarity metric. However, block match‐generated displacement estimates alone are known to be error prone and insufficient for DIR since the matches rely only on local image information.21 Previous block match DIR algorithms rely on robust statistical methods to filter outliers from block match‐generated data. For simple transformations with few degrees of freedom, such as affine functions, the process of filtering out outliers is straightforward.26 For functions with a large number or parameters, the task becomes computationally burdensome due to the combinatorial nature of outlier detection.47 The QPDIR method, on the other hand, incorporates the outlier detection within the DIR formulation. This is accomplished by reformulating the LOOCV mismatch penalty defined by a MLS parameterization as a matrix‐vector multiplication suitable for optimization. This allows for all displacements to be computed simultaneously with respect to both the image similarity metric and the resulting LOOCV outlier detection penalty. For comparison, on the same ten test cases in Table 1, an algorithm that first applies the least median of squares filter to remove erroneous block match‐generated displacement estimates and then interpolates the trusted estimates with MLS results in average spatial accuracies between 0.74 (0.99) and 1.33 (1.51), while achieving an average mm error below the interobserver variance on only one case.27 The QPDIR algorithm produces average mm errors between 0.69 (0.91) and 1.19 (1.26), and achieves an average mm error below the interobserver variance on six cases. These results imply that incorporating the outlier metric into the DIR minimization problem improves spatial accuracy.
On all ten 4DCT test cases (Table 1), the QPDIR method produced spatial accuracies that are superior or equivalent to those produced by current state‐of‐the‐art methods. Moreover, QPDIR achieved accuracies at the resolution of the landmark error assessment (i.e., the interobserver error) on six of the ten cases, whereas, in aggregate, previous methods achieved this level of accuracy on five cases. Among the most successful of these methods (based on Table 1) is the elegant isoPTV method described in Ref. 42. This method is based on minimizing a computationally intensive isotropic total variation (TV) regularization metric and local block correlation similarity metric. The optimization problem is solved efficiently using the alternating direction method of multipliers (ADMM), which is similar in structure to the QP method, but isoPTV solves the ADMM subproblem with the qausi‐Newton BFGS method. The primary differences between the ADMM and QP optimization algorithms are (1) ADMM estimates the Lagrange Multipliers associated with the equality constraints and (2) the penalty parameter μ is typically held constant. Adjusting the QPDIR algorithm framework (Fig. 1) to accommodate the ADMM method is trivial (the subproblem structure is equivalent). And although the results are not reported in Section Methods, this adaptation does not lead to improved convergence properties or increased spatial accuracy when applied to the DIR‐LAB test cases. In this instance, QP is the more suitable approach because the computational workload of the block coordinate descent iteration is dictated by the block matching search window size, which is proportional to μ. Within the ADMM framework, choosing a small constant μ implies that the optimal displacement values for large magnitude displacements are not contained in the search window radius and will consequently require more iterations to arrive at the solution, thus increasing the chances of converging to an undesirable local minimum. However, choosing a large constant μ implies that the ADMM iterations will be more computationally expensive, due to the increase in block match search window size, whereas the QP algorithm subproblem becomes less computationally intensive as μ decreases (and the block matching search window size decreases). This particular issue is not relevant to the isoPTV algorithm since it relies on gradient‐based optimization to solve the ADMM subproblem. Moreover, the TV regularization strategy allows the isoPTV method to accommodate discontinuities in the displacement field, such as sliding boundaries. While the QPDIR algorithm achieved superior accuracies on the presented test cases, the LOOCV regularization is not suitable for cases with displacement field discontinuities and, consequently, operates on the segmented lung volumes. An immediate area of future research is to implement the TV regularization strategy within the general QP DIR framework, or within an ADMM adaptation, in order to determine if the superior accuracies can be maintained while removing the need for lung segmentation.
Considering that its computational workload is dominated by the block matching operator, as currently implemented, the QPDIR algorithm is ideal for the 4DCT test cases since they depict maximum magnitude displacements on the order of 15 voxels. The algorithm runtime is competitive with the commercially available Velocity (Varian Medical Systems, Palo Alto, CA, USA) B‐spline method, which required an average runtime of approximately 145 s to register the same test cases, albeit with significantly less spatial accuracy.48 However, runtime is highly dependent on the available computational resources. This is especially true for the block matching‐based QPDIR algorithm. Block matching is essentially a stencil operation and its implementation on GPU has been thoroughly investigated.49, 50, 51 Considering that (a) block matching is known to scale well with GPU resources and that (b) the bulk of the computational workload for the QPDIR algorithm is dominated by the block matching operation, QPDIR has the potential to be sped up dramatically using state‐or‐the‐art GPU cards or by adopting a multi‐GPU implementation.
For cases with larger magnitude displacement (on the order of 100 voxels in some cases),40 the block matching operations become computationally intractable. Moreover, such cases often possess extreme deformations, which could impact the convergence requirements (unique global minimizer for each block match) of the QP algorithm. Furthermore, while no negative QPDIR Jacobian values were encountered on the 4DCT test case solutions, the algorithm does not guarantee this property. Intuitively, the likelihood of negative Jacobian values would be higher on cases depicting more exotic deformations. An immediate area of future research is to augment the basic QPDIR framework to account for large magnitude displacements, possibly via standard method such as Gaussian pyramid, and to formulate a separable objective function with more desirable properties (i.e., convexity, provably unique global minimizers) in order to generalize to more complex problems.
6. Conclusions
A gradient‐free optimization algorithm for intensity‐based DIR was presented. The algorithm is designed around a block coordinate descent strategy, which results in a simple iterations of block matching operations and linear least squares solves. In comparison to current state‐of‐the‐art DIR methods, the QPDIR algorithm achieves equivalent or superior spatial accuracies on ten 4DCT inhale/exhale phase test cases. However, additional mathematical modeling and testing is required to extend the utility of the algorithm to more challenging cases. The simplicity of the underlying optimization iteration allows for an efficient parallel numerical implementation. The algorithm runtime ranged between 1 and 3 min for each test case using a Quadro M5000 GPU. Considering the highly parallelizable structure of the QPDIR algorithm, a real‐time implementation is possible on multi‐GPU system architectures. An immediate area of future research is to explore the extent to which the QPDIR's high spatial accuracy improves clinical applications, including CT‐derived ventilation6, 39 and radiotherapy response of the brain as measured by morphometric analysis.52
Ethical approval
This article does not contain any studies with human participants or animals performed by the author.
Conflict of Interest
The author has no conflict to disclose.
Acknowledgments
This work was partially funded through University of Michigan Fast Forward Medical Innovation's MTRAC for Life Sciences Innovation Hub, a partnership with University of Michigan Tech Transfer and the State of Michigan, and NIH grant R01CA200817.
References
- 1. Modersitzki J. Numerical Methods for Image Registration. New York, NY: Oxford University Press; 2004. [Google Scholar]
- 2. Mani VRS, Rivazhagan S. Survey of medical image registration. J Biomed Eng Technol. 2013;1:8–25. [Google Scholar]
- 3. Galban CJ, Han MK, Boes JL, et al. Computed tomography‐based biomarker provides unique signature for diagnosis of COPD phenotypes and disease progression. Nat Med. 2012;18:1711–1715. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Tee M, Noble JA, Bluemke DA. Imaging techniques for cardiac strain and deformation: comparison of echocardiography, cardiac magnetic resonance and cardiac computed tomography. Expert Rev Cardiovasc Ther. 2013;11:221–231. [DOI] [PubMed] [Google Scholar]
- 5. Klein A, Andersson J, Ardekani BA, et al. Evaluation of 14 nonlinear deformation algorithms applied to human brain MRI registration. NeuroImage. 2009;46:786–802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Castillo R, Castillo E, Martinez J, Guerrero T. Ventilation from four‐dimensional computed tomography: density versus Jacobian methods. Phys Med Biol. 2010;55:4661. [DOI] [PubMed] [Google Scholar]
- 7. Boldea V, Sharp GC, Jiang SB, Sarrut D. 4D‐CT lung motion estimation with deformable registration: quantification of motion nonlinearity and hysteresis. Med Phys. 2008;35:1008–1018. [DOI] [PubMed] [Google Scholar]
- 8. McClelland J, Modat M, Arridge S, et al. A generalized framework unifying image registration and respiratory motion models and incorporating image reconstruction, for partial image data or full images. Phys Med Biol. 2017;62:4273–4292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Castillo R, Castillo E, Guerra R, et al. A framework for evaluation of deformable image registration spatial accuracy using large landmark point sets. Phys Med Biol. 2009;54:1849. [DOI] [PubMed] [Google Scholar]
- 10. Modersitzki J. FAIR: Flexible Algorithms for Image Registration. Philadelphia, PA: SIAM; 2009. [Google Scholar]
- 11. Al‐Mayah A, Moseley J, Brock KK. Contact surface and material nonlinearity modeling of human lungs. Phys Med Biol. 2008;53:305. [DOI] [PubMed] [Google Scholar]
- 12. Al‐Mayah A, Moseley J, Velec M, Brock K. Toward efficient biomechanical‐based deformable image registration of lungs for image‐guided radiotherapy. Phys Med Biol. 2011;56:4701. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Werner R, Ehrhardt J, Schmidt R, Handels H. Patient‐specific finite element modeling of respiratory lung motion using 4D CT image data. Med Phys. 2009;36:1500–1511. [DOI] [PubMed] [Google Scholar]
- 14. Werner R, Ehrhardt J, Schmidt R, Handels H. Modeling respiratory lung motion: a biophysical approach using finite element methods. 2008.
- 15. Kabus S, Lorenz C. Fast elastic image registration. Medical Image Analysis for the Clinic: A Grand Challenge. 2010;81–89.
- 16. Kabus S, Netsch T, Fischer B, Modersitzki J. B‐spline registration of 3D images with Levenberg‐Marquardt optimization. 2004.
- 17. Polzin T, Rühaak J, Werner R, et al. Combining automatic landmark detection and variational methods for lung CT registration. Paper presented at: MICCAI Workshop: Pulmonary Image Analysis 2013.
- 18. Sotiras A, Davatzikos C, Paragios N. Deformable medical image registration: a survey. Med Imag IEEE Trans. 2013;32:1153–1190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Bruhn A, Weickert J, Schnörr C. Lucas/Kanade meets Horn/Schunck: combining local and global optic flow methods. Int J Comput Vis. 2005;61:211–231. [Google Scholar]
- 20. Jenkinson M, Bannister P, Brady M, Smith S. Improved optimization for the robust and accurate linear registration and motion correction of brain images. NeuroImage. 2002;17:825–841. [DOI] [PubMed] [Google Scholar]
- 21. Castillo E, Castillo R, Fuentes D, Guerrero T. Computing global minimizers to a constrained B‐spline image registration problem from optimal l1 perturbations to block match data. Med Phys. 2014;41:041904. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Heinrich MP, Handels H, Simpson IJ. Estimating large lung motion in COPD patients by symmetric regularised correspondence fields. In: Medical Image Computing and Computer‐Assisted Intervention–MICCAI 2015. New York, NY: Springer; 2015:338–345. [Google Scholar]
- 23. Rousseeuw PJ, Leroy AM. Robust Regression and Outlier Detection. Hoboken, NJ: John Wiley & Sons; 2005. [Google Scholar]
- 24. Atkinson AC, Riani M. Forward search added‐variable t‐tests and the effect of masked outliers on model selection. Biometrika. 2002;89:939–946. [Google Scholar]
- 25. Atkinson AC, Riani M, Cerioli A. The forward search: theory and data analysis. J Korean Stat Soc. 2010;39:117–134. [Google Scholar]
- 26. Ourselin S, Roche A, Prima S, Ayache N. Block matching: A general framework to improve robustness of rigid registration of medical images. Paper presented at: Medical Image Computing and Computer‐Assisted Intervention–MICCAI 20002000.
- 27. Castillo E, Castillo R, White B, Rojo J, Guerrero T. Least median of squares filtering of locally optimal point matches for compressible flow image registration. Phys Med Biol. 2012;57:4827. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Anandan P. A computational framework and an algorithm for the measurement of visual motion. Int J Comput Vision. 1989;2:283–310. [Google Scholar]
- 29. Garcia V, Commowick O, Malandain G. A robust and efficient block matching framework for non linear registration of thoracic CT images. Paper presented at: Grand Challenges in Medical Image Analysis (MICCAI workshop) 2010.
- 30. Wright S, Nocedal J. Numerical Optimization, vol. 2. New York, NY: Springer; 1999. [Google Scholar]
- 31. Luenberger DG, Ye Y. Linear and Nonlinear Programming. New York, NY: Springer; 2008. [Google Scholar]
- 32. Wahba G. Spline models for observational data. doi: 10.1137/1.9781611970128: Society for Industrial and Applied Mathematics; 1990. [DOI]
- 33. Mongillo M. Choosing basis functions and shape parameters for radial basis function methods. SIAM Undergrad Res Online. 2011;4:190–209. [Google Scholar]
- 34. Levin D. The approximation power of moving least‐squares. Math Comput Am Math Soc. 1998;67:1517–1531. [Google Scholar]
- 35. Most T, Bucher C. A moving least squares weighting function for the element‐free galerkin method which almost fulfulls essesntial boundary conditions. Struct Eng Mech. 2005;21:315–332. [Google Scholar]
- 36. Castillo E, Castillo R, Martinez J, Shenoy M, Guerrero T. Four‐dimensional deformable image registration using trajectory modeling. Phys Med Biol. 2010;55:305. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Haber E, Modersitzki J. Intensity gradient based registration and fusion of multi‐modal images. In: Larsen R, Nielsen M, Sporring J, eds. Medical Image Computing and Computer‐Assisted Intervention – MICCAI 2006: 9th International Conference, Copenhagen, Denmark, October 1‐6, 2006. Proceedings, Part II. 10.1007/11866763_89 Berlin, Heidelberg: Springer Berlin Heidelberg; 2006:726–733. [DOI] [PubMed] [Google Scholar]
- 38. Zhou W, Bovik AC, Sheikh HR, Simoncelli EP. Image quality assessment: from error visibility to structural similarity. IEEE Trans Image Process. 2004;13:600–612. [DOI] [PubMed] [Google Scholar]
- 39. Castillo E, Castillo R, Vinogradskiy Y, Guerrero T. The numerical stability of transformation‐based CT ventilation. Int J Comput Assist Radiol Surg. 2017;12:569–580. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40. Castillo R, Castillo E, Fuentes D, et al. A reference dataset for deformable image registration spatial accuracy evaluation using the COPDgene study archive. Phys Med Biol. 2013;58:2861. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41. Hermann S. Evaluation of scan‐line optimization for 3D medical image registration. Paper presented at: 2014 IEEE Conference on Computer Vision and Pattern Recognition; 23‐28 June 2014, 2014.
- 42. Vishnevskiy V, Gass T, Szekely G, Tanner C, Goksel O. Isotropic total variation regularization of displacements in parametric image registration. IEEE Trans Med Imaging. 2017;36:385–395. [DOI] [PubMed] [Google Scholar]
- 43. Vishnevskiy V, Gass T, Székely G, Goksel O. Total variation regularization of displacements in parametric image registration. In: Yoshida H, Näppi JJ, Saini S, eds. Abdominal Imaging. Computational and Clinical Applications: 6th International Workshop, ABDI 2014, Held in Conjunction With MICCAI 2014, Cambridge, MA, USA, September 14, 2014. 10.1007/978-3-319-13692-9_20 Cham, Switzerland: Springer International Publishing; 2014: 211–220. [DOI] [Google Scholar]
- 44. Konig L, Ruhaak J. A fast and accurate parallel algorithm for non‐linear image registration using Normalized Gradient fields. Paper presented at: 2014 IEEE 11th International Symposium on Biomedical Imaging (ISBI); April 29 2014‐May 2 2014, 2014.
- 45. Rühaak J, Heldmann S, Kipshagen T, Fischer B. Highly accurate fast lung CT registration. Paper presented at: SPIE Medical Imaging; 2013.
- 46. Brock KK, Mutic S, McNutt TR, Li H, Kessler ML. Use of image registration and fusion algorithms and techniques in radiotherapy: report of the AAPM Radiation Therapy Committee Task Group No. 132. Med Phys. 2017;44:e43–e76. [DOI] [PubMed] [Google Scholar]
- 47. Johansen S, Nielsen B. Asymptotic theory of outlier detection algorithms for linear time series regression models. Scand J Stat. 2016;43:321–348. [Google Scholar]
- 48. Kadoya N, Nakajima Y, Saito M, et al. Multi‐institutional validation study of commercially available deformable image registration software for thoracic images. Int J Radiat Oncol Biol Phys. 2016;96:422–431. [DOI] [PubMed] [Google Scholar]
- 49. Li M, Xiang Z, Xiao L, Castillo E, Castillo R, Guerrero T. GPU‐accelerated block matching algorithm for deformable registration of lung CT images [published online ahead of print 06/13]. Proceedings of the IEEE International Conference on Progress in Informatics and Computing IEEE International Conference on Progress in Informatics and Computing. 2015;2015:292–295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50. Mazaré S, Dugelay J, Pacalet R. Using GPU for fast block‐matching. Paper presented at: 2006 14th European Signal Processing Conference; 4‐8 Sept. 2006, 2006.
- 51. Honzátko D, Kruliš M. Accelerating block‐matching and 3D filtering method for image denoising on GPUs. J Real‐Time Image Proc. 2017; 1–15. https://link.springer.com/article/10.1007/s11554-017-0737-9 [Google Scholar]
- 52. Fuentes D, Contreras J, Yu J, et al. Morphometry‐based measurements of the structural response to whole‐brain radiation. Int J Comput Assist Radiol Surg 2014;10:393–401. [DOI] [PMC free article] [PubMed] [Google Scholar]


