Biophysical model‐based parameters to classify tumor recurrence from radiation‐induced necrosis for brain metastases

Abstract

Purpose

Stereotactic radiosurgery (SRS) is used for local control treatment of patients with intracranial metastases. As a result of SRS, some patients develop radiation‐induced necrosis. Radiographically, radiation‐induced necrosis can appear similar to tumor recurrence in magnetic resonance (MR) T ₁ ‐weighted contrast‐enhanced imaging, T ₂ ‐weighted MR imaging, and Fluid‐Attenuated Inversion Recovery (FLAIR) MR imaging. Radiographic ambiguities often necessitate invasive brain biopsies to determine lesion etiology or cause delayed subsequent therapy initiation. We use a biomechanically coupled tumor growth model to estimate patient‐specific model parameters and model‐derived measures to noninvasively classify etiology of enhancing lesions in this patient population.

Methods

In this initial, preliminary retrospective study, we evaluated five patients with tumor recurrence and five with radiation‐induced necrosis. Longitudinal patient‐specific MR imaging data were used in conjunction with the model to parameterize tumor cell proliferation rate and tumor cell diffusion coefficient, and Dice correlation coefficients were used to quantify degree of correlation between model‐estimated mechanical stress fields and edema visualized from MR imaging.

Results

Results found four statistically relevant parameters which can differentiate tumor recurrence and radiation‐induced necrosis.

Conclusions

This preliminary investigation suggests potential of this framework to noninvasively determine the etiology of enhancing lesions in patients who previously underwent SRS for intracranial metastases.

1. Introduction

A common treatment option for intracranial metastases is stereotactic radiosurgery (SRS). SRS helps establish local control, but complications may arise; potential postradiation treatment effects include pseudoprogression and radiation‐induced necrosis.^{1, 2} Pseudoprogression occurs within 3 months of SRS, vs radiation‐induced necrosis which usually appears around 3 months and later.^{1, 2} Radiation‐induced necrosis is an adverse reaction to radiation treatment.^{3, 4} Following SRS, up to 20% of patients exhibit radiation‐induced necrosis,^{4, 5} which often appears as an enhancing lesion in MR T ₁ ‐weighted contrast‐enhanced imaging with accompanying T ₂ ‐weighted and Fluid‐Attenuated Inversion Recovery (FLAIR) abnormalities.^{4, 6, 7} Accurate diagnosis presents enormous clinical challenges as symptoms and radiographic findings for recurrence and radiation‐induced necrosis are often indistinguishable.

Misidentification can have adverse clinical outcomes since treatment and prognosis of radiation‐induced necrosis and tumor progression are different. Treatments for radiation‐induced necrosis include observation and corticosteroids, with symptoms sometimes resolving independently.⁸ These treatments could accelerate tumor progression. Repeat SRS can treat recurrence, but would exacerbate radiation‐induced necrosis and expose patients to unnecessary radiation. Brain biopsies are the diagnostic gold standard, but introduce risk and are often not possible due to patient condition or lesion location. Indeterminate lesions are often followed with costly follow‐up imaging that can cause deleterious outcomes for recurrent tumors with delayed subsequent therapy.⁴ Serial examinations usually include conventional MR with T ₁ ‐weighted contrast‐enhanced imaging and FLAIR imaging, but are diagnostically confounded. Patients that undergo SRS for intracranial metastases would benefit greatly from noninvasive diagnosis.

There is a history of studies attempting to employ quantitative imaging modalities to noninvasively distinguish the etiologies,⁹ with reproducible results proving challenging. Conventional MRI (magnetic resonance imaging) has been studied with mixed interpretations.^{6, 7} There have been studies into mean fractional anisotropy,^{10, 11} perfusion imaging,^{4, 12} positron emission tomography,¹³ magnetic resonance spectroscopy,^{4, 14} and diffusion weighted imaging.^{11, 15} As an overall observation, there remains a lack of consensus in quantitative imaging for diagnosis. Here, a novel framework is introduced that utilizes medical imaging data combined with biophysical models of tumor growth dynamics to noninvasively distinguish between tumor recurrence and radiation‐induced necrosis in a binary classification of enhancing lesion etiology. Congruent with clinical practice, we will not sub‐differentiate pseudoprogression and radiation‐induced necrosis, referring to both as radiation‐induced necrosis.

There is support for patient‐specific tumor growth modeling in clinical settings.^{16, 17} Development and use of tumor growth models within the brain have been investigated,^{18, 19, 20, 21, 22} with work often related to either accurate model development, or its use to assess a potential clinical aspect.^{19, 20, 23} While these are concerned with tumor progression, other work focused on the surrounding environment and its influence. There have been studies investigating the influence of surrounding mechanical environment on tumor growth^{24, 25} and using modeling to predict radiotherapy effect.²² In related work by our group, a mechanically coupled reaction‐diffusion model was used to develop a predictive framework of breast cancer treated with neoadjuvant chemotherapy.^{26, 27, 28} This demonstrated an ability to predict patients’ responsiveness using early cycle treatment changes.²⁸ Building upon these, we use an image‐data‐driven biophysical model of tumor growth as a tool to classify space‐occupying enhancing lesions in the brain following SRS.

In this investigation, we evaluate patient‐specific model parameters by fitting a biomechanically coupled tumor growth model to longitudinal lesion changes observed from MRI data following SRS for brain metastasis and calculate model‐derived measures. We hypothesize the biophysics of the etiologies will result in differences in patient‐specific model parameters and model‐derived measures allowing for noninvasive classification.

2. Materials and methods

2.A. Patient data

Ten de‐identified clinical datasets were obtained under the Vanderbilt University Institutional Review Board approved study to analyze retrospective MR imaging data. Datasets were collected after patients were treated with SRS, ensuring we are modeling effects of recurrent enhancing lesions following SRS. The datasets represent five patients with tumor recurrence and five with radiation‐induced necrosis. Diagnoses were pathologically confirmed or retrospectively determined through long‐term clinical follow‐up, with incidence of all recurrence and three of five radiation‐induced necrosis lesions biopsy confirmed. Data consist of serial MR imaging with standard‐of‐care T ₁ ‐weighted contrast‐enhanced and FLAIR imaging sequences acquired following SRS, prior to diagnosis. To assess longitudinal changes, two time points of T ₁ ‐weighted MR scans obtained immediately prior to diagnosis are used (Fig. 1). Time between scans varied according to the clinician from under 1 month to approximately 9 months, with an average of 3.5 months. Use of sparse MR imaging data from two time points has three purposes: (a) demonstrates use of standard‐of‐care serial imaging data, (b) potentially shows a pathway to replace inconclusive serial imaging, and (c) if it allows earlier detection, it could reduce time between detected changes and clinical action. Note radiographic similarities in T ₁ ‐weighted MR images [Figs. 2(a) and 3(a)]. T ₂ ‐weighted or FLAIR MR images obtained immediately prior to diagnosis were also used (Fig. 1). Due to this retrospective study, T ₂ ‐weighted and FLAIR MR images are used interchangeably to segment edema based on availability.

Figure 1.

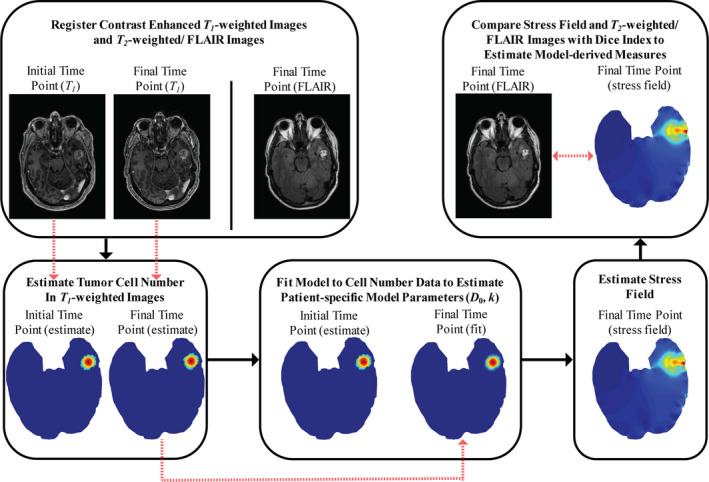
Framework to estimate different patient‐specific model parameters and model‐derived measures for differentiating tumor recurrence and radiation‐induced necrosis. [Color figure can be viewed at wileyonlinelibrary.com]

Figure 2.

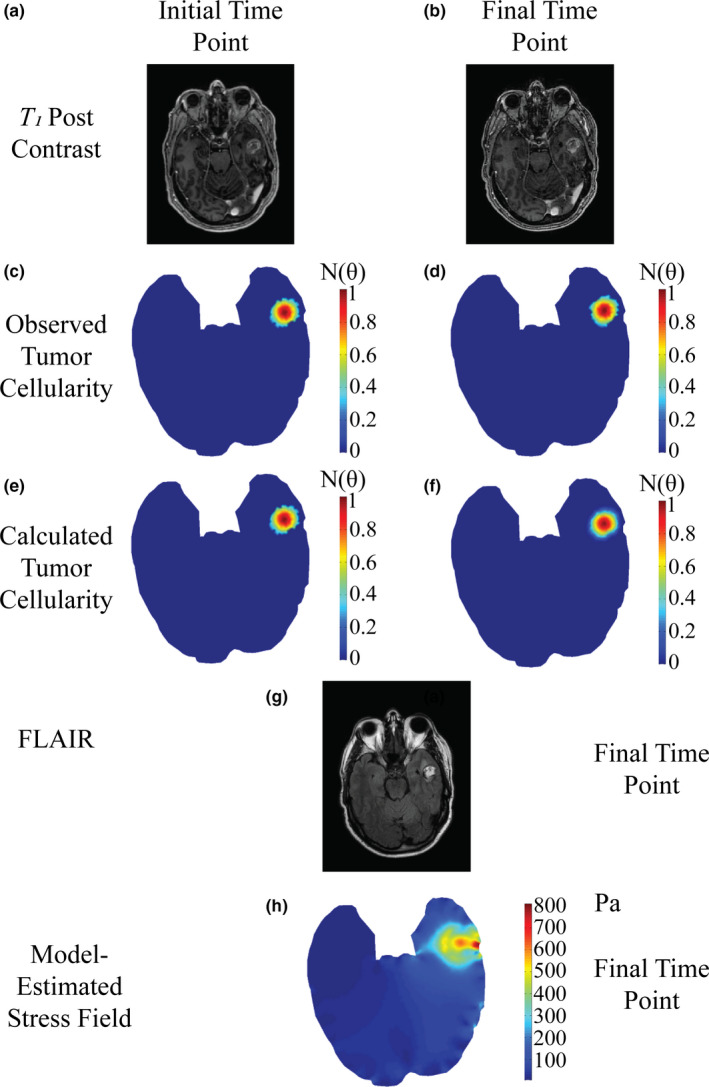
Patient diagnosed with tumor recurrence at starting time point (a,c,e), and final time point taken before diagnosis of lesion etiology (b,d,f,g). Post‐contrast T ₁ ‐weighted MR images (a,b) are used to estimate observed tumor cellularity (c,d) and the model is fit to estimate tumor cellularity (e,f). FLAIR imaging at the time point prior to diagnosis (g) is compared to estimated mechanical stress field (h) at the final time point. [Color figure can be viewed at wileyonlinelibrary.com]

Figure 3.

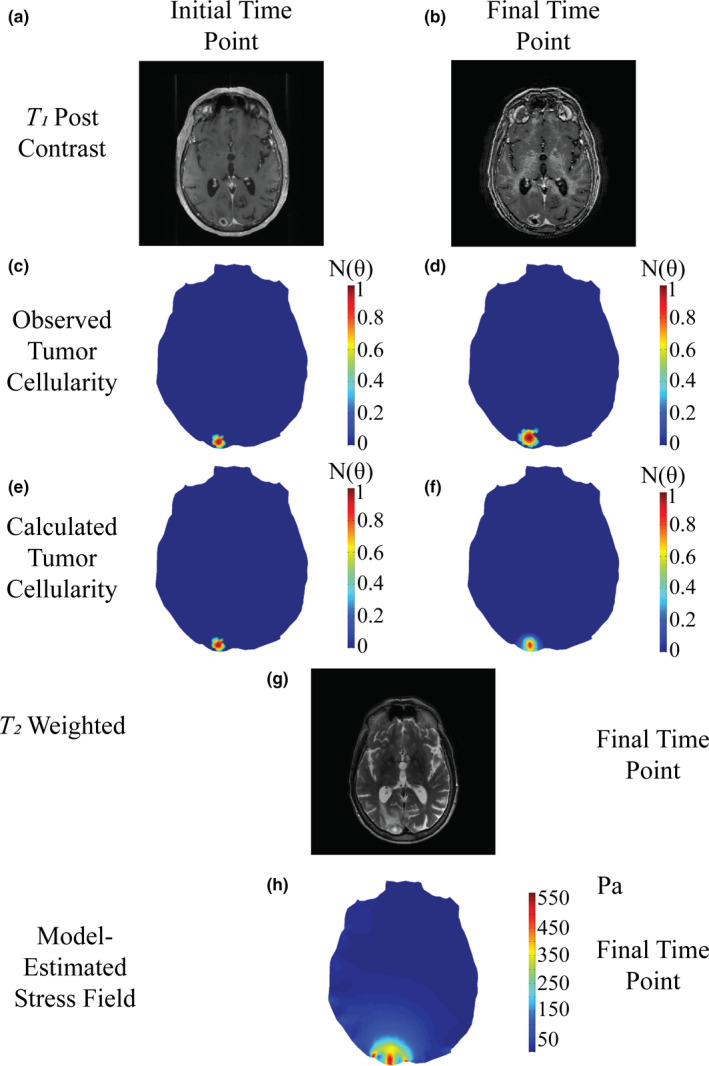
Patient diagnosed with radiation‐induced necrosis at starting time point (a,c,e), and final time point taken before diagnosis of lesion etiology (b,d,f,g). Post‐contrast T ₁ ‐weighted MR images (a,b) are used to estimate observed tumor cellularity (c,d) and the model is fit to estimate tumor cellularity (e,f). T ₂ ‐weighted imaging at the time point prior to diagnosis (g) is compared to estimated mechanical stress field (h) at the final time point. [Color figure can be viewed at wileyonlinelibrary.com]

2.B. Biophysical model of tumor growth

The realistic biomechanically coupled biophysical tumor growth model was adapted from previous work from our group.^{24, 26, 27, 28} A complete description is in previous publications.^{26, 27, 28} The governing equations are:

$$\frac{\partial N\left(\overline{x},t\right)}{\partial t}=\mathrm{\nabla }·\left(D({\sigma }_{\mathit{VM}},\overline{x},t)\mathrm{\nabla }N\left(\overline{x},t\right)\right)+kN\left(\overline{x},t\right)\left(1-\frac{N\left(\overline{x},t\right)}{\theta }\right)$$ (1)

$$D({\sigma }_{\mathit{VM}},\overline{x},t)=D_0{e}^{-\gamma {\sigma }_{\mathit{VM}}\left(\overline{x},t\right)}$$ (2)

$$\mathrm{\nabla }·G\mathrm{\nabla }\overrightarrow{u}+\mathrm{\nabla }\frac{G}{1-2v}\left(\mathrm{\nabla }·\overrightarrow{u}\right)-\lambda \mathrm{\nabla }N\left(\overline{x},t\right)=0$$ (3)

Equation (1) describes rate of tumor cell number change at a given time and location as the sum of random cell diffusion and logistic growth. Equation (2) represents mechano‐inhibition of cellular diffusion coefficient, coupling tumor cell transport to evolving tissue stress state. As tissue distorts due to mass effects, tumor diffusive transport is inhibited. Equation (3) models linear elastic, isotropic mechanical equilibrium in the presence of an external expansive force.^{26, 27, 28} In (1), (2), and (3) $\overrightarrow{u}$ is the displacement vector; $N$ is the spatiotemporal varying cell number. $D$ is the local cellular diffusion coefficient of tumor cells in the presence of mechanical stress; $D_0$ (mm²/day) is the cellular diffusion coefficient without mechanical stress present. Tumor cell proliferation rate is represented by $k$ (day⁻¹), which reflects how proliferative lesion cells are. von Mises stress is represented by ${\sigma }_{\mathit{VM}}$ (Pa). $v$ (0.45) is Poisson's ratio; $G$ (689.66 Pa) represents shear modulus. $\gamma$ (0.0050) and λ (0.010) are empirically derived coupling coefficients. We solve Equations (1), (2), (3) using the Galerkin method of weighted residuals on triangular finite elements described by standard linear Lagrange basis functions.²⁹ Temporal resolution employs a fully explicit forward Euler method. The time step is 1 day, and in work not shown here, stability analysis was performed. Representing the dural surface, the displacement boundary conditions on the mesh outer surface permits surface tangential displacement, but do not allow normal displacement. The cortical surface is treated with a boundary condition of no flux of tumor cells across the boundary. Meshes have a nominal element edge length of 2.5 mm, an average of 7182 elements, and an average of 3700 nodes. We treat the parenchyma as homogenous. The biophysical model is based on a central slice taken through the region‐of‐interest (ROI), and two‐dimensional (2D) plane strain approximation is employed.

As a first‐order approximation for tumor cellular density, we assume the enhancing lesion has a Gaussian distribution of tumor cell density. Maximal cellular carrying capacity, $\theta$, occurs at the enhancing lesion's center. This density decreases outward to a minimum density of 0.25 × θ at the lesion's maximal long axis dimension.

2.C. Patient‐specific model parameters

For each patient, two time points of T ₁ ‐weighted contrast‐enhanced image volumes are selected (scan immediately prior to diagnosis and an earlier scan). Central axial slices with the most radiographic volumetric change with respect to the enhancing portion of the T ₁ ‐weighted MR image were selected. Image volumes are longitudinally rigidly co‐registered to the most recent time point (Fig. 1).³⁰ Enhancing lesions in both T ₁ ‐weighed images are manually segmented. Using the segmentations, the tumor cell number in both T ₁ ‐weighted images are estimated using the Gaussian description and denoted as “observed tumor cellularity” (Figs. 2(c)–2(d) and 3(c)–3(d)]. We fit our tumor growth model to the “observed tumor cellularity”, with the first distribution as the starting point and final distribution as the desired outcome using a custom Levenberg–Marquardt parameter optimization algorithm in MATLAB (MathWorks Inc., Natick, MA, USA) to estimate designated patient‐specific model parameters: tumor cell diffusion coefficient ($D_0$) and tumor cell proliferation rate ($k$). The objective function that was minimized is the sum‐squared error between observed and model‐estimated tumor cellularity. Convergence occurs if one of the following criteria are met. These criteria include: (a) if the absolute objective function value is less than 1e‐4, (b) the relative change in the objective function between iterations is less than 1e‐4, (c) a maximum of 500 iterations occur, or (d) a maximum of 1000 function evaluations occur. In analysis not shown, these proved robust. These are appropriate since we treat all lesions as recurrent tumors [Equations (1), (2), (3)] with estimated parameter set differences guiding diagnosis. We assume model parameters are homogenous over the lesion.

2.D. Model‐derived measures

Based on estimates of patient‐specific model parameters, von Mises stress field due to tumor growth at the final time point is estimated by our mechanically coupled reaction‐diffusion model (Fig. 1). Model‐derived measures were calculated to compare observed edema to model‐estimated stress field. This originates from our previous work, coupling mechanical effects from the surrounding tissue extracellular matrix to tumor growth models.²⁸ Here, von Mises stress is used to describe tissue loading due to lesion growth.²⁸ We hypothesize tissue loading represents an edema‐causative event due to restricted diffusivity in areas with higher stress similar to previous work.³¹ We investigate the relationship between observed edema and model‐calculated von Mises stress fields as a model‐derived measurement. We quantify edema using T ₂ ‐weighted or FLAIR images (based on availability) from the last time point prior to diagnosis. The T ₂ ‐weighted or FLAIR scan is rigidly registered to T ₁ ‐weighted contrast‐enhanced images. Then the enhancing region, associated with edema, is manually segmented. The choice to use manual segmentation in our methodology was based on the heterogeneous nature of clinically acquired imaging data as well as the patient lesions and edema. Therefore, manual segmentation provided the most robust representation of the regions of interest. We quantify regional similarity between edema location and model‐estimated stress field using the Dice similarity index. We designate five isocontours from low stress to high stress at 100, 200, 300, 400, and 500 Pa of the model‐estimated stress field and calculated the Dice index of the segmented edematous region and each mechanical stress isocontour, denoted as Dice₁₀₀, Dice₂₀₀, Dice₃₀₀, Dice₄₀₀, and Dice₅₀₀, respectively.

2.E. Morphometric analysis methods

We evaluated other diagnostic radiologic metrics based on image morphometric analysis, including some used in clinical treatment, to compare our methodology to conventional radiologic assessments. We evaluated the ratio of lesion size in T ₂ imaging to lesion size in T ₁ imaging.³² We performed this by taking the ratio of the edema area (T ₂ ‐weighted or FLAIR MR imaging) to the lesion area (T ₁ ‐weighted MR imaging). As proposed by the Response Assessment in Neuro‐Oncology Brain Metastasis working group, we evaluated the change in the lesion's longest diameter.³³ We calculated longitudinal change in maximum lesion length from outlined lesions of T ₁ ‐weighted images at both time points as percent change from baseline. We performed morphometric analysis evaluating the segmented lesion area and lesion perimeter using the same central axial slice that was used to perform modeling analysis. Finally, we manually segmented the full three‐dimensional (3D) lesion ROI in each image for full volume and surface area morphometric analysis. Full 3D morphometric analysis represents additional data not analyzed under our current 2D framework, extracting additional information from the images. While our work herein compares our analysis to conventional morphometric metrics, it is important to note that this is a limited comparison. These selected conventional analysis metrics represent a good initial evaluation comparison, but other geometric and texture‐based metrics are certainly possible. More extensive comparisons to other types of analysis metrics are warranted in future studies with larger cohorts. Morphometric analysis was performed for both T ₁ ‐weighted and FLAIR images, with T ₁ ‐weighted lesions evaluated as the percent change between the two time points. These measurements are designated as T ₁ Surface Area, T ₁ Volume, FLAIR Surface Area, and FLAIR Volume.

3. Results

Patient‐specific model parameters and model‐derived measures are calculated using our biomechanically coupled tumor growth model fit to serial patient‐specific imaging data. $D_0$ and $k$ are obtained by fitting the tumor growth model to the pairs of longitudinal T ₁ ‐weighted post‐contrast images. Dice₁₀₀, Dice₂₀₀, Dice₃₀₀, Dice₄₀₀, and Dice₅₀₀ are the Dice indices between isocontours of model‐estimated stress field and the segmented edematous region. Examples of the framework execution are in Figs. 2 and 3.

Distribution of patient‐specific model parameters are in Fig. 4(a) and 4(b), reflecting an evident distinction in proliferation rate. Examples of low and high Dice values, in Fig. 4(c) and 4(d), respectively, indicate a distribution difference in the high Dice value. Using the Mann–Whitney U Test, we obtained the results in Table 1. In agreement with Fig. 4(a)–4(d), $k$, Dice₃₀₀, Dice₄₀₀, and Dice₅₀₀ are statistically significantly different with P values of 0.0159, 0.0079, 0.0079, and 0.0159, respectively. We plotted a receiver operating characteristic curve (ROC curve) for model parameters in Fig. 4(e) and model‐derived measures in Fig. 4(f). From Fig. 4(e) and 4(f), we see $k$ and multiple high Dice indexes can classify etiologies. This is verified by observing areas under the ROC curves (Table 1).

Figure 4.

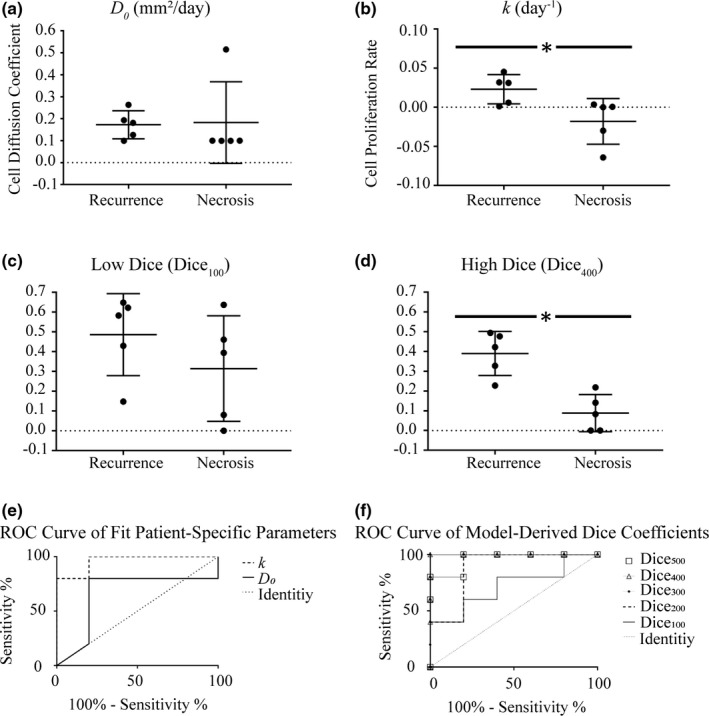
Distribution plots for (a) cell diffusion coefficient (D ₀, mm²/day), (b) cell proliferation rate (k, day⁻¹), (c) low stress isocontour Dice coefficient (Dice₁₀₀), and (d) high stress isocontour Dice coefficient (Dice₄₀₀) for patients with tumor recurrence and radiation‐induced necrosis. The middle horizontal line in both represents the mean value; the outer two lines represent the standard deviations. The ROC curve for (e) cell diffusion coefficient (D ₀) and cell proliferation rate (k) and (f) ROC curve for the Dice correlation coefficients. In both, the dotted line represents the line of identity.

Table 1.

Statistical tests of patient‐specific model parameters, model‐derived measures, and morphometric analysis

Metric	Statistical tests
	Mann–Whitney U test P values	ROC area under curve (AUC)
D 0	0.4603	0.66
k	0.0159a	0.96
Dice100	0.3095	0.72
Dice200	0.0556	0.88
Dice300	0.0079a	1.00
Dice400	0.0079a	1.00
Dice500	0.0159a	0.96
T 1 area	0.3095	0.72
T 1 perimeter	0.0952	0.84
T 1 surface area	0.6905	0.60
T 1 volume	0.4206	0.68
FLAIR area	0.2222	0.76
FLAIR surface area	0.8413	0.56
FLAIR volume	0.8413	0.56
T2/T1 ratio	0.4206	0.68
% change length	0.4206	0.68

^aStatistical significance of P < 0.05.

Conventional metrics of T ₂ /T ₁ ratio and percent change in length are in Figure 5(a)–5(c). We found a lack of diagnostic performance in differentiating etiologies using conventional morphometric analysis, with ROC AUC for T ₂ /T ₁ ratio and percent change in length of 0.68 and 0.68, respectively, and no statistical significance between etiologies. Shown in Table 1, we further assessed input imaging data by analyzing morphometric data in both 2D central slice analysis and 3D full volumetric analysis from segmented lesions. We assessed 2D change in lesion area and perimeter between T ₁ ‐weighted scans as well as the lesion area in FLAIR. We assessed 3D change in lesion volume and surface area between T ₁ ‐weighted scans as well as lesion volume and surface area in FLAIR. The poor performance of conventional image analysis metrics is highlighted by no statistically significant metrics being found.

Figure 5.

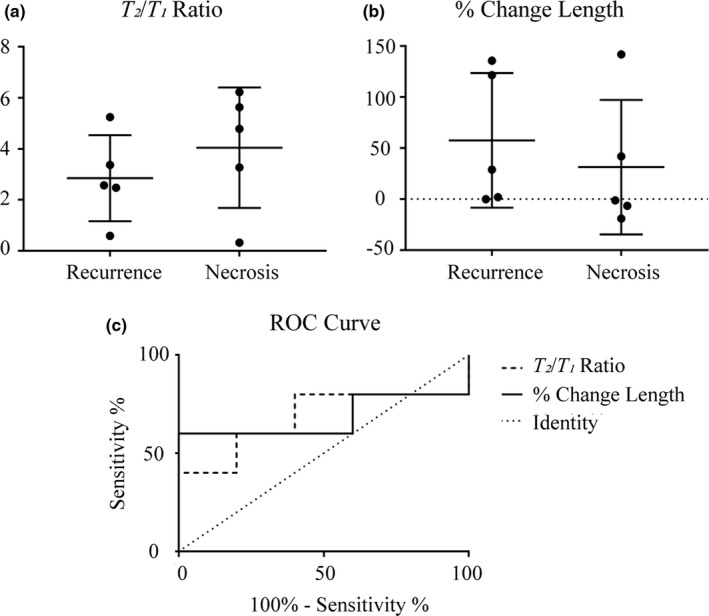
Conventional morphometric assessment methods for determining local control with estimated parameter value distributions for (a) T ₂ /T ₁ ratio and (b) percent change in length. (c) ROC curve for the morphometric assessment methods. The dotted line represents the line of identity.

4. Discussion

We present a framework to estimate patient‐specific model parameters and model‐derived measures based on noninvasive MRI data from patients with brain metastasis treated with SRS. Parameterizing the biophysics of lesion growth could accurately differentiate lesions based on differences in estimated parameters with up to 100% accuracy in our preliminary, initial patient cohort. We compared our modeling results to conventional analysis methods. Our methodology outperformed conventional methods using the same input data, or less input data in the case of 3D image morphometry. It is evident that $k$ and Dice indexes associated with higher stress von Mises isocontours can differentiate etiologies (Table 1). The Dice metrics [Fig. 4(c) and 4(d)] are not independent observations. When estimating $D_0$ and $k$, our model is fit to “observed tumor cellularity”. Based on these fit parameters, the von Mises stress distribution was calculated and compared to observed edema. Therefore our Dice metrics represent linked discriminators permitting mechanistic statistical comparison to additional data. As the von Mises stress isocontour is changed, the statistical relationship with edema is changed, which is why a range of isocontours were compared. Our biophysical model enables proliferative differences to be compared in novel ways capable of accurately differentiating the etiologies.

Speaking to limitations, we used T ₂ ‐weighted and FLAIR imaging interchangeably to indicate edema. Visual confirmation in Fig. 2(g) and 3(g), as well as the Dice indexes differentiating the etiologies, indicate our use of imaging data is reasonable. Next, the brain's heterogeneity has been incorporated into other tumor growth models.²¹ We treated the brain as homogeneous isotropic tissue. In future studies, we intend to increase model specificity by incorporating heterogeneity and anisotropy. Mechanical heterogeneity will result in a spatially varying distribution of mechanical properties throughout tissue types (shear modulus and Poisson's ratio in Eq. (3)). Anisotropy will increase the number of material parameters used to describe the mechanical constitutive behavior in Eq. (3). Since biomechanical coupling enables the surrounding brain tissue to impact the tumor's growth, including heterogeneity and anisotropy will manifest in changes to diffusion via the von Mises stress term in Eq. (2).³⁴ We treated patient‐specific model parameters as homogeneous within the lesion. Our current imaging data constrain us to a global estimate of lesion properties, restricting our classification as entirely tumor recurrence or radiation‐induced necrosis. Biopsies can consist of both recurrence and necrosis.¹⁵ We will address this with additional sources of quantitative imaging to increase specificity. Previously, in other related research we used diffusion weighted MRI (DW‐MRI) to estimate tumor cell density.^{26, 27, 28} In future work, we will acquire DW‐MRI data that would provide improved estimates of tumor cell density from patient scans. Using DW‐MRI, which is a studied surrogate used for estimating tumor cellularity, will result in more accurate estimates of cellular distribution within the patients’ lesion. This will not change the mathematical expression [Eqs. (1), (2), (3)], but rather specifically change the spatial variation of $N\left(\overline{x},t\right)$ defined at imaging times. This will result in the inverse problem being driven by more accurate estimations of “observed tumor cellularity” measurements, but will not change the number of parameters being estimated. Despite this, the standard‐of‐care clinical treatment is a binary diagnosis: no tumor recurrence or partial recurrence. Our framework accomplishes a similar binary classification, making this clinically relevant and amenable to current clinical diagnostic workflows. Given the heterogeneous nature of clinically acquired scans, manual segmentation was used rather than automated segmentation to prevent inaccuracy due to nonuniform intensities across patients and scan time points. In work not shown here, a separate blinded observer performed the same experimental analysis methods on the same patient imaging data (Table S1). Comparing the Mann–Whitney P values and ROC AUC values for the patient‐specific model parameters and model‐derived measures reflected the same trends obtained in this manuscript with average difference in ROC areas under the curve for all metrics of 5% and largest difference of 13% (Table S1). This investigation was performed in 2D; moving forward we will investigate these biophysical model‐based parameters in 3D to capture volumetric changes, similar to our previous work.²⁸ The transition from 2D to 3D is nontrivial but tractable. The results of this 2D investigation indicate a 3D formulation of this framework has the potential to further enhance the noninvasive differentiation between the two etiologies. Furthermore, this preliminary investigation involved a total of 10 patients. For validation, the framework will need to be tested in a larger patient cohort. Finally, the use of edema from T ₂ ‐weighted and FLAIR imaging was incorporated as an external model‐derived feature comparison. It would be interesting to include this data by extending our biomechanical model to include biphasic components that explicitly model the generation of edema from elevated intracranial pressure during tumor expansion, similar to modeling of capillary exchange in other work.³¹

We identified a biophysical model‐based approach to differentiate between the etiologies, whereas traditional image morphometric assessment of the same data was not capable of accurate identification. Patient‐specific geometries varied depending on lesion location (Figs. 2 and 3). Despite this, our framework accurately predicted etiology. There is an intuitive aspect to the parameters which differentiate the etiologies. There was no statistical difference between diffusion coefficients, suggesting diffusion is conserved between etiologies. There is a statistical difference in tumor proliferation rates. This is consistent with radiation‐induced necrosis not being expected to proliferate. Recurrent tumors have model‐estimated mechanical stress fields with significant correlation with the measured edema. We hypothesize this is the result of mechanical stress having a causative edema generation effect associated with recurrent tumor. The success of using patient‐specific image‐data‐driven biophysical modeling to differentiate between both etiologies in patients with brain metastasis treated with SRS shows substantial promise. This is a limited sample size analysis and a larger cohort study is required. The temporal sampling was chosen just prior to diagnosis, but studying the framework's performance at earlier time points is desirable.

5. Conclusions

Results of this study indicate our image‐data‐driven biophysical model‐based analysis framework for estimating patient‐specific model parameters and model‐derived measures has potential to noninvasively differentiate between radiation‐induced necrosis and tumor recurrence. We only used standard‐of‐care imaging scans from the patients’ clinical care, furthering the work's impact. If confirmed, our framework could be used in current clinical workflows to improve diagnosis. It is important to note that results of this investigation are preliminary given the limited number of patients used in this initial investigation. Confirmation of this framework will be needed with a larger patient cohort and further patient statistics. Furthermore, we restricted analysis to metastatic disease, but radiation‐induced necrosis is also found in patients with primary intracranial disease who have undergone SRS,³⁵ making this methodology applicable in patients with primary brain tumors. Our investigation demonstrates the potential of noninvasive differentiation of lesions of unknown etiology in patients who have undergone SRS by means of image‐data‐driven biophysical modeling.

Conflicts of interest

The authors have no conflicts to disclose.

Funding

This work is supported by the National Institutes of Health‐National Institute of Neurological Disorders and Stroke R01NS049251; the National Institutes of Health‐National Cancer Institute K25CA204599, P30CA012197; National Science Foundation Research Experiences for Undergraduates 1559700; and the VISE Seed Grant Program.

Supporting information

Table S1. Sensitivity to manual segmentation.