TROSY Pulse Sequence for Simultaneous Measurement of the ¹⁵N R₁ and {¹H} -¹⁵N NOE in Deuterated Proteins

Abstract

A TROSY-based NMR experiment is described for simultaneous measurement of the ¹⁵N longitudinal relaxation rate constant R₁ and the {¹H}-¹⁵N nuclear Overhauser enhancement. The experiment is based on the observation that the TROSY mixing pulse sequence element symmetrically exchanges ¹H and ¹⁵N magnetizations. The accuracy of the proposed technique is validated by comparison to independent measurements of both relaxation parameters for the protein ubiquitin. The simultaneous experiment is approximately 20-33% shorter than conventional sequential measurements.

The ¹⁵N R₁ and R₂ relaxation rate constants and the steady-state {¹H}-¹⁵N nuclear Overhauser enhancement (NOE) provide vital probes of the picosecond-nanosecond dynamics of backbone amide moieties in proteins ¹. Measurement of these three parameters allows characterization of the spectral density function J(ω) at the frequencies 0, ω_N, ω_N, and ω_H±ω_N (the ¹H single quantum and ¹⁵N single quantum frequencies frequently are approximated by a single effective frequency through reduced spectral density mapping) ². Experimental protocols and approaches for data interpretation are well-established ¹; however, particularly as measurements at multiple static magnetic fields become more commonplace ^3-5, maximizing the efficiency of experimental methods remains essential.

Measurement of the steady-state {¹H}-¹⁵N NOE requires two experiments: one in which the ¹⁵N steady-state magnetization is measured after irradiation of the ¹H spins (saturated), and a second in which the Boltzmann equilibrium ¹⁵N magnetization is measured in the absence of ¹H irradiation (unsaturated or control) ⁶. The ratio of the saturated to the unsaturated intensity is the steady-state {¹H}-¹⁵N NOE. Although simple in the abstract, the steady-state {¹H}-¹⁵N NOE experiment suffers from several factors complicating implementation. Chief among these is the inherent lower experimental sensitivity because starting magnetization originates on the low gyromagnetic ¹⁵N nucleus, rather than ¹H as in the R₁ and R₂ experiments. In addition, the recycle delays must be set long enough (> 7-8/R₁) to ensure complete recovery of equilibrium magnetization in the unsaturated control experiment. Finally, avoidance of saturation transfer through chemical exchange of labile protons requires careful manipulations of the water magnetization. Addressing these concerns to ensure accurate steady-state {¹H}-¹⁵N NOE values results in long experimental times.

The TROSY-based NOE pulse sequence ⁷, performed without ¹H irradiation, shows a unique feature: following the t₁ period, a reverse-INEPT block transfers transverse ¹⁵N magnetization to ¹H for subsequent detection, and simultaneously transfers longitudinal ¹H magnetization to longitudinal ¹⁵N magnetization ⁸. In principle, this polarization-enhanced ¹⁵N magnetization could serve as the starting point for another relaxation experiment. In the present work, a second pulse sequence block utilizes this magnetization to measure the ¹⁵N R₁ relaxation rate constant. Separate storage of decay curves originating with positive or negative values of the initial longitudinal ¹⁵N magnetization also allows the steady-state ¹⁵N intensity to be obtained by extrapolation during data analysis, and hence calculation of the {¹H}-¹⁵N NOE. Thus, an independent measurement of the saturated spectrum is not necessary.

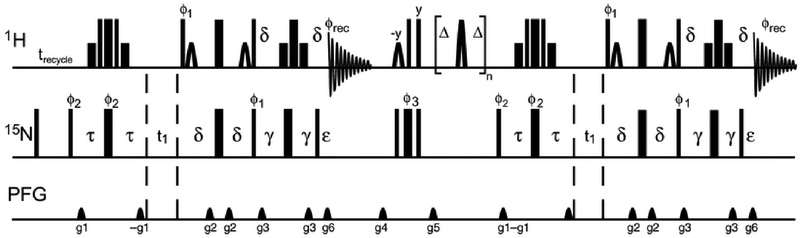
The pulse sequence for the proposed experiment is shown in Figure 1 and is based on the TROSY pulse sequences of Bax and coworkers ⁹. The first part of the experiment is the control measurement of equilibrium ¹⁵N magnetization. In addition, this sequence transfers longitudinal ¹H magnetization to longitudinal ¹⁵N magnetization at the start of the first t₂ acquisition period. Following the t₂ period, two orthogonal ¹H 90° hard pulses are used to purge remaining ¹H magnetization and a composite 0° or 180° ¹⁵N pulse is used to generate positive or negative ¹⁵N longitudinal magnetization. The inversion-recovery relaxation period consists of repeated [Δ - 180°(¹H)- Δ] blocks with Δ = 11 ms ¹⁰. The ¹H 180° pulses are cosine-modulated I-BURP2 pulses to maintain water magnetization on the +z-axis ¹¹. These ¹H 180° pulses serve two purposes: (i) to remove cross-correlated relaxation effects and (ii) to obtain ¹⁵N steady-state magnetization by amide proton saturation. The partially relaxed ¹⁵N magnetization is frequency labeled and transferred to ¹H for detection during the second t₂ period. The experiment is performed twice for each R₁ relaxation delay: the control equilibrium ¹⁵N free induction decays (FID) are co-added while the R₁ FIDs with positive initial ¹⁵N longitudinal magnetization (I₊(t)), or negative initial ¹⁵N longitudinal magnetization (I₋(t)) are stored separately. If the inversion-recovery experiment is performed with N relaxation time points and M scans per complex point in t₁ for each relaxation time point then the final data control unsaturated measurement consists of 2MN co-added FIDs per complex point in t₁. The inversion-recovery curves are fit simultaneously to the equations:

$$\begin{gathered} I_{+}(T)=I_{ss}+\left(I_{+}(0)-I_{ss}\right)e^{-R_{1}T} \\ {I}_{-}(T)=I_{ss}+\left(-I_{-}(0)-I_{ss}\right)e^{-R_{1}T} \end{gathered}$$ (1)

in which I_SS and R₁ correspond to the steady-state ¹⁵N magnetization intensity, and the longitudinal relaxation rate constant, respectively. The initial magnetizations are treated as local variables, while I_SS and R₁ are treated as global parameters. The NOE is calculated as the ratio of I_ss and the average intensity of the control experiment, I₀.

Figure 1.

Pulse sequence for simultaneous measurement of the steady state {¹H}-¹⁵N NOE and the ¹⁵N R₁ relaxation rate constant. Thin and thick solid bars represent high-power 90° and 180° pulses, respectively; short open shapes represent water-selective 90° sinc pulses; short thin solid bars represent rectangular water-selective 90° pulses; thick solid bars flanked by two thin bars indicate a 90_x-210_y-90_x composite pulse; and the open shaped pulses during the T = n(2Δ – τ₁₈₀) relaxation period are cosine-modulated I-BURP2 180° pulses of length τ₁₈₀ crafted to leave the water magnetization unperturbed while maximizing inversion of amide protons. Delays: t_recycle = 11 s, Δ = 11 ms, δ = τ = 2.65 ms, γ = δ – ε/2, and ε > g6. Gradients were applied as square pulses. Gradients g1 and g6 were used for coherence selection and other gradients are used for artifact suppression. Gradients: g1 (600 μs, 21.7 G/cm), g2 (300 μs, 6.8 G/cm), g3 (1000 μs, 32.9 G/cm), g4 (500 μs, 6.8 G/cm), g5 (1000 μs, 13.2 G/cm), g6 (121.60 μs, 21.7 G/cm). All pulses are x-phase unless indicated. Phase cycling: ϕ₁ = y; ϕ₂ = y, −y, and ϕ_rec = y, −y. The phase ϕ₃ = y for I₋(0) and −x for I₊(0) in the R₁ experiment. Echo-antiecho selection is obtained by inverting g1 and ϕ₁. Pulse sequence and acquisition parameter files are provided as Online Resource 1 and 2, respectively

The proposed pulse sequence was used to measure ¹⁵N R₁ and steady-state ¹⁵N-{¹H} NOE for a 1.0 mM sample of [U-²H,¹⁵N] ubiquitin. Sample temperature was calibrated to 298 K using 98% ²H₄-methanol¹². Relaxation data were collected at 14.1 T on a Bruker DRX600 console equipped with a triple-resonance z-axis gradient cryogenic probe. Spectra were recorded using 4 scans per complex t₁ point, and t₂ × t₁ of 512 × 128 complex points. The spectral width was set to 9.3 kHz × 2.4 kHz. Relaxation delays were set to T = n × 22 ms, where n = {2, 4, 10, 18, 44, 88, 240, 464}, giving T = (0.044, 0.220, 0.396, 0.968, 1.936, 5.280, 10.208} s. Spectra were processed using NMRPipe¹³, and in-house Python scripts were used to fit relaxation curves for calculation of R₁ and I_ss values. The proposed pulse sequence was validated by comparison with results from independent conventional measurements of ¹⁵N R₁ and steady-state ¹⁵N-{¹H} NOE using TROSY-based pulse sequences⁹. The conventional NOE experiment used 16 scans per complex t₁ point for the control and the saturated spectra; hard 180° ¹H pulses were used to saturate ¹H magnetization. The conventional R₁ experiment used a recycle delay of 3.5 s, 8 scans per complex t₁ point, and 8 relaxation delays spaced between 0 and 1.6 s. Total acquisition times were 32, 13, and 20 hours for the proposed experiment, conventional NOE experiment, and conventional R₁ experiment, respectively. Experimental uncertainties in relaxation parameters are the standard error in the mean of three replicates.

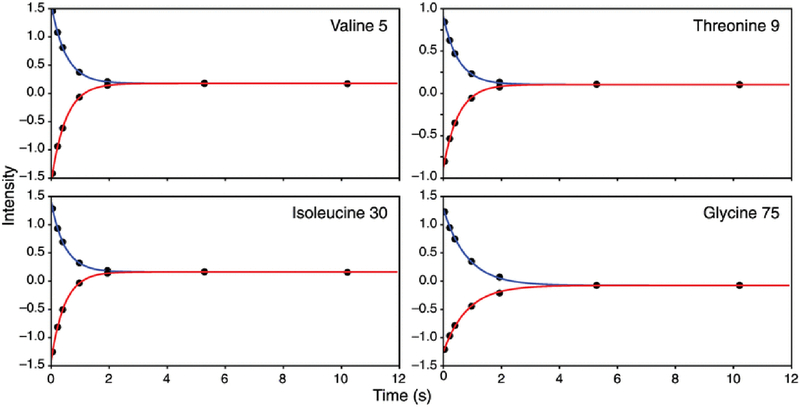
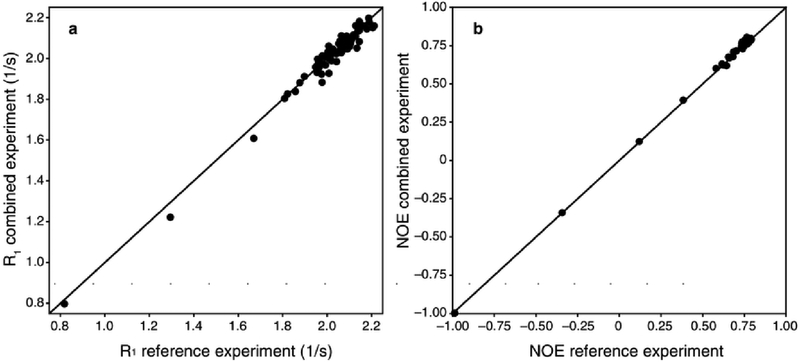
Figure 2 shows representative R₁ relaxation decay curves for Val 5, Thr 9, Ile 30, and Gly 75, which are located in β-sheet, turn, α-helix, and C-terminal regions of ubiquitin, respectively. The absolute value of the initial magnetization for each set of the R₁ curves differed by approximately 2% intensity, with the I₊(T) curve yielding the larger intensity values. As shown in Figure 3, the R₁ and NOE values from the combined experiment are in excellent agreement with reference TROSY-detected experiments for ubiquitin. Comparison of ¹⁵N R₁ values between the two experiments gives a correlation coefficient of 0.974 and an RMSD of 0.032. The mean square errors in the measured R₁ values are 0.012 and 0.010 for the conventional and combined experiments. Comparison of steady-state ¹⁵N-{¹H} NOE values gives a correlation coefficient of 0.998 and an RMSD of 0.016. The mean square errors in the measured NOE values are 0.014 and 0.010 for the conventional and combined experiments. Corrected for differences in acquisition times, the NOE values for the conventional and combined experiments have very similar root-mean-square uncertainties of 0.00925 and 0.0102, respectively.

Figure 2.

¹⁵N R₁ decay curves for Val 5, Thr 9, Ile 30, and Gly 75 in ubiquitin. Data points and fitted decay curves are shown for (blue) positive (I₊(T)) and (red) negative (I₋(T)) initial ¹⁵N magnetization. Data were fit using Eq. 1 using a Levenberg-Marquardt algorithm. Fitted values for R₁ are (Val 5) 2.001 ± 0.001, (Thr 9) 1.927 ± 0.016, (Ile 30) 2.1484 ± 0.016, and (Gly 75) 797 ± 0.009 (uncertainties are standard error in the mean of three replicates)

Figure 3.

Comparison of simultaneous and conventional measurements of (a) ¹⁵N R₁ relaxation rate constant (R² = 0.974, RMSD = 0.032) and (b) steady-state {¹H}-¹⁵N NOE (R² = 0.998, RMSD = 0.016). Uncertainties in measured values are not shown. The mean square errors in the measured R₁ values are 0.012 and 0.010 for the conventional and combined experiments. The mean square errors in the measured NOE values are 0.014 and 0.010 for the conventional and combined experiments. Data values are provided as Online Resource 3

The proposed combined experiment differs from separately acquired NOE and R₁ datasets in three ways. (i) The resonance intensities for the “saturated” spectrum, needed to calculate the NOE, are not directly measured, but are extrapolated during the fitting of the positive and negative R₁ relaxation curves; (ii) longitudinal ¹H magnetization is inverted for a period τ + t₁ prior to the TROSY transfer period; and (iii) non-equilibrium longitudinal ¹⁵N magnetization relaxes during the first acquisition t₂ period prior to the start of the R₁ relaxation delay. Monte Carlo simulations of these effects were simulated for a protein with tumbling time 5 ns and 15 ns, using a 600 MHz spectrometer (full protonation was assumed for simplicity, which should give an upper bound on sensitivity differences). Simulations assumed that the conventional NOE experiments were recorded with 32 scans per FID for each of the control and saturated spectra. The combined experiment used 64 scans to measure the control spectrum and simultaneously used N = 8 time points to measure R₁, with 4 scans for positive initial ¹⁵N magnetization and 4 scans for negative initial magnetization. The simulations indicate that the two different NOE measurements have virtually identical sensitivity per unit time for either the 5 ns and 15 ns rotational diffusion correlation times. The R1 measurement has a lower precision by 15% and ~10% compared with a conventional experiment measured with the same number of scans and time points, for 5 ns and 15 ns tumbling times, respectively. This difference arises from the small relaxation losses noted above. The precision of the R₁ experiment is ~1%, so these small differences are not a major effect on subsequent data analysis. Notably the simulations show that the values of the NOE and R₁ for the combined experiment are uncorrelated, with R² < 0.01. The theoretical calculations are in approximate agreement with the experimental results reported for ubiquitin. The combined experiment yields both the NOE and R₁; thus, R₁ is obtained essentially for free. The time savings afforded by the combined experiment depends on the relative lengths of the conventional NOE and R₁ experiments. For example, savings in experimental time would be 20 or 33% if the conventional R₁ experiment were to be recorded in 1/4 or 1/2 of the experimental time for the conventional NOE measurement.

We have described a TROSY pulse sequence for simultaneous measurement of the intensity of the Boltzmann equilibrium ¹⁵N magnetization and the ¹⁵N longitudinal relaxation rate constant R₁ in a single experiment. Long-time plateau values from fitting of the R₁ data serve as proxies for the usual saturated {¹H}-¹⁵N intensity to allow calculation of the steady-state {¹H}-¹⁵N NOE. Measurements of ¹⁵N R₁ and steady-state ¹⁵N-{¹H} NOE on a ubiquitin sample using both the combined experiment and conventional independent experiments are in very good agreement. The greater efficiency of the proposed pulse sequence should become even more useful for larger bio-molecular systems, for which maximizing sensitivity per unit time is critical.