Chokepoints in Mechanical Coupling Associated with Allosteric Proteins: The Pyruvate Kinase Example

Abstract

Although the critical role of allostery in controlling enzymatic processes is well appreciated, there is a current dearth in our understanding of its underlying mechanisms, including communication between binding sites. One potential key aspect of intersite communication is the mechanical coupling between residues in a protein. Here, we introduce a graph-based computational approach to investigate the mechanical coupling between distant parts of a protein, highlighting effective pathways via which protein motion can transfer energy between sites. In this method, each residue is treated as a node on a weighted, undirected graph, in which the edges are defined by locally correlated motions of those residues and weighted by the strength of the correlation. The method was validated against experimental data on allosteric regulation in the human liver pyruvate kinase as obtained from full-protein alanine-scanning mutagenesis (systematic mutation) studies, as well as computational data on two G-protein-coupled receptors. The method provides semiquantitative information on the regulatory importance of specific structural elements. It is shown that these elements are key for the mechanical coupling between distant parts of the protein by providing effective pathways for energy transfer. It is also shown that, although there are a multitude of energy transfer pathways between distant parts of a protein, these pathways share a few common nodes that represent effective “chokepoints” for the communication.

Introduction

Allosteric regulation of an enzyme can be viewed as an equilibrium process (1, 2) in which an enzyme binds a substrate differently depending on whether an effector is present or absent at a distant site (3, 4). Protein dynamics can influence this process and has recently become a focus in studies of allosteric regulation of an enzyme (5, 6, 7, 8). Indeed, like the contributions of protein dynamics to other biological functions (9, 10, 11, 12, 13), perturbations to an equilibrium protein’s dynamics can influence mechanical coupling between different sites (14). Binding of an effector to an allosteric site (1, 15), electrochemical activity at a given location such as electron transport through respiratory complexes (16), photoisomerization of a cofactor (17), and slow, large-scale motions of flexible moieties (18) can induce changes in the energy distribution of a protein that, in turn, induce an effect in function at a remote site. One way to characterize dynamic contributions to allostery is to evaluate the mechanical coupling between various residues or structural elements through protein motion and the role of the protein scaffold in channeling kinetic energy through these elements.

Understanding mechanical couplings between sites in a macromolecule requires identifying both 1) the coupled sites and 2) plausible networks of residues through which the sites are mechanically coupled. Coupled sites can be identified by conventional methods for assessing macromolecular dynamics, such as root mean-square fluctuation of atomic positions and principal component analysis (PCA) of the covariance of interatomic motions (19, 20), along with systematic mutation studies (21). Normal-mode analysis, whether derived from molecular dynamics (MD) or from coarse-grained models, such as an anisotropic network model (ANM), can provide insight about collective motions capable of transferring energy between sites, as can NMR-derived methods (22). Several methods have been developed for identifying potential allosteric sites based on covariance of atomic motions and normal-mode analysis, including a method by Balabin et al. based on the coupling between local structural perturbations and normal modes (8) and a method by Guarnera and Berezovsky (15) in which potential allosteric sites are stiffened to represent the presence of a ligand and normal-mode free energies are compared. A similar method was also previously reported (23).

A complete characterization of the contributions of mechanical couplings to an allosteric mechanism will require a comparison of the mechanical coupling evaluated for the enzyme in complex with all possible combinations of substrate and allosteric effector binding. For a protein with one active site and one allosteric site, four structures would be required to define the allosteric energy cycle: 1) free enzyme, 2) enzyme-substrate complex, 3) enzyme-effector complex, and 4) the ternary substrate-enzyme-effector complex (2). With such data available, an analysis of mechanical coupling could be initiated for respective cocrystalized enzyme complexes to determine how binding of a ligand alters potential mechanical coupling pathways. However, a key initial step is to evaluate the mechanical couplings that exist in currently available protein structures.

Graph-based methods provide an intuitive route for addressing mechanical coupling. Complex chemical systems can be converted to a reduced, graph-like representation of their connectivity based on interatomic distances and other structural parameters, in which nodes are formed from atoms or collections of atoms (e.g., protein residues), and edges connecting them represent interactions (bonded or noncovalent). The resulting graphs can be traversed to identify local structural features, such as noncovalent clusters (24), cyclic structures in glasses (25), or paths between points that minimize a parameter of interest. Graph-based methods have had a long history in analyzing protein structure (26). For instance, a shortest-path (parameter minimization) approach has been applied by Beratan and co-workers for analyzing electron transfer pathways in proteins (27). Graph-based methods (28) have also previously been used for characterizing allosteric coupling in proteins (7), whether based on normal-mode analysis (29, 30, 31), PCA (32), NMR-derived covariances of interatomic motions (33), discrete MD-derived contacts and covariances of interatomic motions (7), sampling of multiple MD trajectories (6, 17, 34, 35), clustering based on energies of side-chain interactions (36, 37, 38), or evolutionary optimization of ANM-type models (39). Building upon this work, we report a novel, to our knowledge, graph-based method for representing coupling between sites that can be applied to either a crystal structure (via ANM-generated covariances of interatomic motions) or MD data, using either an all-residue or secondary structure representation, that generates a two-dimensional map of mechanical coupling, analogous to those generated by Balabin’s method (8). Our principal goals in developing a new graph-based method were 1) to be able to efficiently determine the extent to which structural elements with correlated motion are mechanically coupled and 2) to identify the key structural elements involved in the transduction of the mechanical force between sites, which may proceed through a large ensemble of pathways involving those residues.

Consistent with our interest in allosteric regulation, our primary model system for evaluating our graph-based method for predicting mechanical coupling through proteins is the allosterically regulated human liver pyruvate kinase (hL-PYK). We chose pyruvate kinase because it is a soluble, globular protein (which avoids having to account for the presence of a membrane in the model) with multiple well-characterized allosteric sites (Fig. 1) (21, 40, 41, 42). Although the enzyme catalyzes a phosphate transfer from phosphoenolpyruvate (PEP) to ADP to form ATP, only the PEP affinity is allosterically regulated. Fructose bisphosphate (FBP) causes increased PEP affinity (43), whereas the alanine effector (Ala^E will be used to distinguish when alanine is the effector ligand) reduces PEP affinity (42). Tang and Fenton recently characterized the contribution of nearly all residues to allosteric regulation in the protein by a systematic mutation study (alanine scan; Ala^M will be used to distinguish when alanine is a replacement amino acid in the protein) (21).

Figure 1.

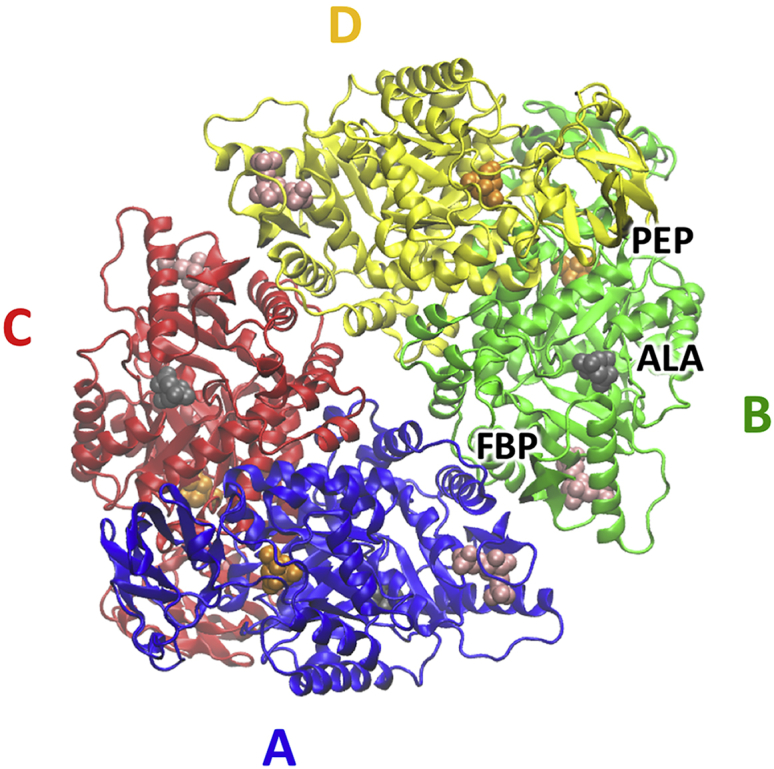
Cartoon representation of the structure of hL-PYK (PDB: 4IMA). The binding sites of the phosphoenolpyruvate substrate (PEP, in orange) and the activator fructose-1,6-bisphosphate (FBP, in pink) and the inhibitor alanine (Ala^E, in gray) binding site are highlighted for each chain. The four chains in the protein are color coded and labeled A, B, C and D on the figure. To see this figure in color, go online.

Using hL-PYK as a testbed, first, we demonstrate how our graph-based representation can identify pairs of residues (protein sites or secondary structure elements) that have correlated motions and are mechanically coupled via specific pathways throughout the protein structure. A key advance of our method is the ability to filter out pairs of residues whose covariant motion is purely coincidental. To examine broader applicability, we also apply our method to two membrane proteins previously examined using Balabin’s method (8). Taking a step further, we will demonstrate how it is possible to identify residues that are critical for mechanical coupling between two distant parts of a protein. Specifically, we will show that mechanical coupling between binding sites occurs through an ensemble of pathways between the sites. These pathways share a few crucial, common nodes that represent effective “chokepoints.” Because these nodes are central to many mechanical coupling pathways, any effort to rationally design proteins with altered dynamics could focus on modifying them. Furthermore, given the observed high correlation between the mechanical couplings and residue positions that contribute to allostery (21), we can speculate that targeting these chokepoints may be an effective way to alter allosteric regulation in enzymes.

Methods

The proposed graph-based representation of the mechanical coupling is introduced using the crystal structure of the hL-PYK tetramer crystallized with FBP bound, with citrate present in the PEP binding site and with the Ala^E site empty (Protein Data Bank (PDB): 4IMA). Because of unresolved residues, particularly in chain D, the crystal structure tetramer was reconstructed and symmetrized based on the nearly complete chain A. Symmetrization has little to no effect on the calculated properties, as discussed in the Supporting Materials and Methods, including Fig. S2.

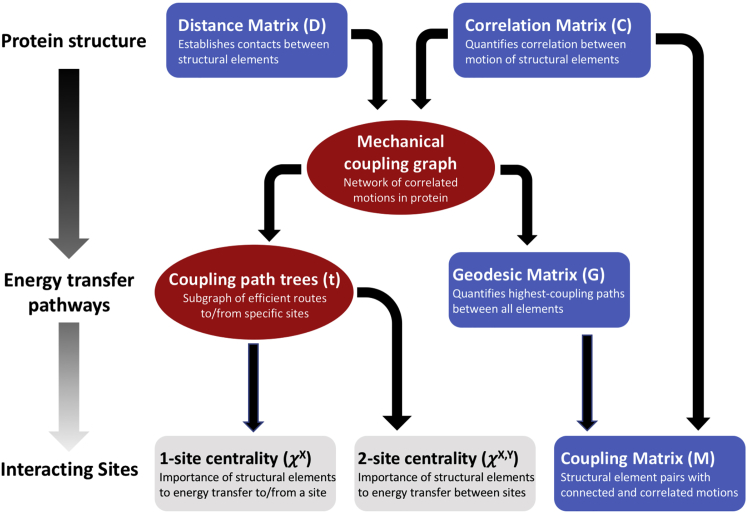
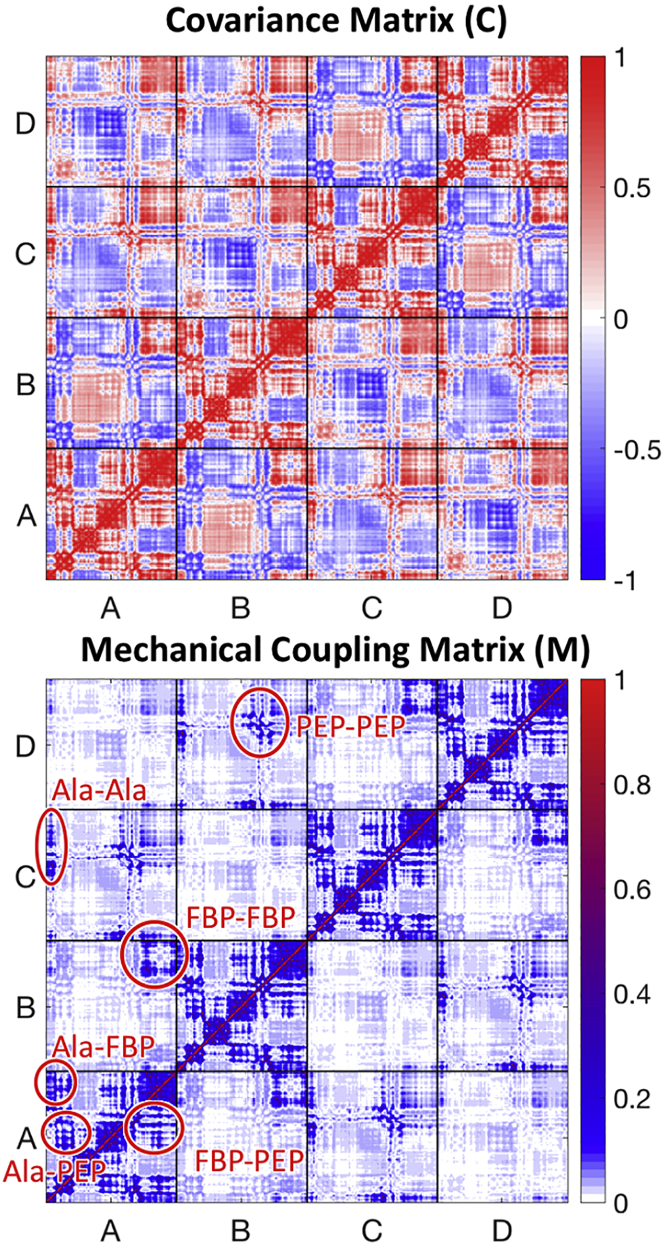
The method treats each residue as a node on a weighted, undirected graph, in which the edges are defined by locally correlated motions of those residues and weighted by the strength of the correlation. The workflow for building such a graph and extracting quantitative information about the mechanical coupling between distant sites is illustrated in Fig. 2. We start from two input quantities: 1) a correlation matrix (normalized covariance matrix of interatomic motions) C (Fig. 3, top) and 2) a minimal (Euclidean) distance matrix D (for example, see Fig. S3, first panel). The correlation matrix can be obtained from an ANM, an MD trajectory, or from experimental (e.g., NMR) data. Thus far, our method has been used with normalized correlation data; however, in principle, it could be used with non-normalized covariances as well. We chose normalized correlation data to facilitate a bounded, linear, and consistent dynamic range that would allow a common set of parameters to be applied to multiple model systems. The correlation matrix elements C_ij represent the extent to which the motion of residues i and j are correlated, with a value of 1 indicating perfectly correlated (parallel) motions, a value of −1 indicating perfectly anticorrelated (antiparallel) motions, and a value of 0 indicating uncorrelated (orthogonal) motion. The correlation matrices discussed here were based on C_α ANM models derived from crystal structures and calculated using ProDy (44) using default settings. The distance matrix is obtained from the same structural data.

Figure 2.

Work flow of the protocol for characterizing the mechanical couplings in protein. The distance matrix (D) and the normalized covariance (correlation) matrix (C) are used to build a mechanical coupling graph. Nodes of the graph represent individual residues, secondary structural elements, or protein domain. The graph can then be traversed to find the highest-coupling (geodesic parameter minimization) route between each pair of nodes (G matrix); the mechanical coupling matrix (M) can then be calculated based on the correlation matrix and path length matrix, as can the one-site and two-site centrality parameters, χ^X and χ^X,Y. To see this figure in color, go online.

Figure 3.

(Top) All-residue covariance matrix (C-matrix) of interatomic motions and (bottom) all-residue coupling matrix, M, for hL-PYK derived from ANM model using crystal structure (PDB: 4IMA). The resulting M-matrix is qualitatively identical with the secondary structure representation (see Supporting Materials and Methods). Coupling can be seen between the alanine and PEP sites, plus between the FBP and PEP sites within each chain, as well as between the FBP sites on two pairs of chains (A and B, C and D), between alanine sites on two pairs of chains (A and C, B and D), and between the PEP sites on two pairs of chains (A and C, B and D). Comparison of two matrices highlights how the path-based weighting (at the heart of the definition of P) substantially reduces noise to better highlight potential allosteric interactions. To see this figure in color, go online.

For a large protein, data on interatomic motions and distances can also be transformed to a further coarse-grained representation, such as using secondary structural elements (identified by STRIDE (45) or similar methods) instead of residues as the matrix elements. Such coarse-graining is motivated by strong internal correlation within structural components in a protein. This allows us to combine many redundant motions into a more readily analyzable set of center-of-mass motions. If a structure is reduced to secondary structural elements, C_ij are averaged for each set of residues being merged to generate the reduced correlation matrix C_red, and the smallest distance matrix element D_ij between residues is selected for each pair of secondary structural elements to generate the reduced distance matrix D_red. All the subsequent steps in the method are identical whether or not reduced representations are used, and from hereon we will refer to the matrices only as C and D.

The first step in the process is the generation of an adjacency matrix A (Eq. 1) that represents the network of correlated motions in the protein, where

$$A_{ij}=1-\left|C_{ij}\right|\text{.}$$ (1)

Our definition of the adjacency matrix A is identical to the definition developed by Dokholyan (7, 46). This initial adjacency matrix includes all covariant motions in the protein, regardless of distance or strength, and needs to be pruned to remove interactions that do not involve strong coupling between adjacent residues or structural elements. The pruning is performed using the rule

$$A_{ij}=0\mathrm{if}{C}_{ij}<\left({\mu }_{\left|\mathbf{C}\right|}+{\sigma }_{\left|\mathbf{C}\right|}\right)\mathrm{or}{D}_{ij}<R_{\text{cut}},$$ (2)

where μ_|C| and σ_|C| are the mean and SD of the elements of C, respectively, and R_cut is the contact distance cutoff. We set R_cut at 7.5 Å based on minimal distance before more than one disconnected node emerges in the graph in any of the systems studied. This distance is consistent with the cutoff distance used by Dokholyan for a related method based on local covariance of interatomic motion (7). Sensitivity analysis to selection of different cutoff distances is reported in Fig. S1. In addition to the minimal correlation and maximal distance cutoffs, our model also applies a maximal coupling threshold in which any correlations |C_ij| > C_thresh are set to C_thresh. We set C_thresh to 0.95, representing an approximate value of the correlation within secondary structural elements. The threshold means that nonzero (connected) elements of the adjacency matrix have a lower bound of A_thresh = 1 − C_thresh, which prevents numerical instabilities when correlations approach unity and enables the coupling matrix (described below) to be normalized. Self-loops (diagonal elements in the adjacency matrix) are also removed.

The adjacency matrix is a two-dimensional representation of an undirected graph of the mechanical coupling within the protein (47). Once the graph is defined (Fig. 4), a standard shortest-path (geodesic) method (for example, the “distances” function in MATLAB; The Mathworks, Natick, MA) can be used to find the paths of maximal local covariance of interatomic motion between each pair of elements in the graph to generate the geodesic matrix G (Fig. S3, lower left), where G_ij is the sum of all edge lengths along the path from element i to element j in the graph. With this information at hand, we can identify structural elements pairs that have correlated and connected motions through the mechanical coupling matrix M (Fig. 3, bottom), whose elements are defined as

$${\text{M}}_{ij}=A_{\text{thresh}}\frac{\left|C_{ij}\right|}{G_{ij}}\text{,}$$ (3)

with the diagonal elements M_ii set to zero to remove trivial coupling of residues with themselves. A maximal M_ij value of unity indicates two adjacent and perfectly correlated residues, whereas a minimal value of zero indicates no significant coupling between residues. The major difference between the M-matrix and simple covariance analysis of the motion is that if two residues have correlated motions but do not have an efficient path for mechanical coupling between them (e.g., a large G_ij), a small (poorly coupled) M_ij will be produced. In this way, geodesic weighting suppresses motions that are merely coincidental. Our process for generating the M-matrix and other descriptors can be applied to any protein for which three-dimensional structural information is available. In addition to generating the M-matrix, the graph can also be used to calculate standard graph theory metrics such as rank, centrality, path trees (shortest path from a node i to all nodes j ≠ i), etc. These metrics can be used in conjunction with the M-matrix to analyze the coupling within a protein, including the cost-weighted betweenness centrality metrics χ^X and χ^X,Y discussed in the next section. The combination of covariance of interatomic motions and contact information from MD trajectories (the information abstracted into the G matrix) have previously been applied to determining mechanical coupling pathways by Vishveshwara et al. (48) Our alternative approach is based on condensing the graph representation of the protein into subgraphs that contain only strongly coupled pathways in or out of a site.

Figure 4.

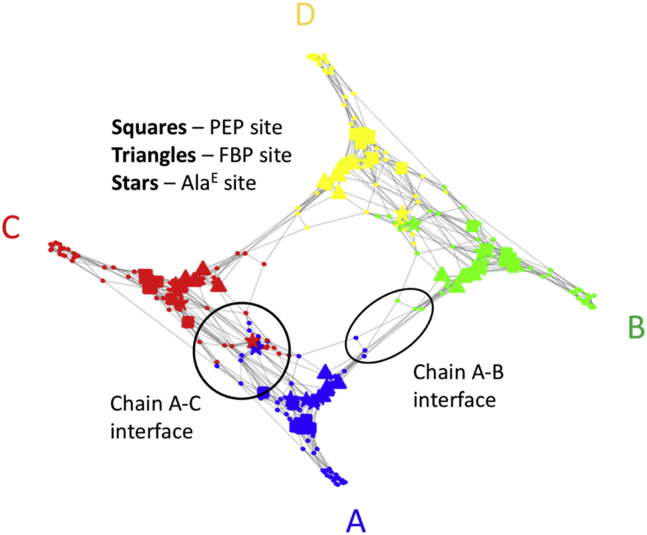
Mechanical coupling graph in hL-PYK. Nodes represent secondary structural elements, and edges represent interactions with high local covariance. The edges of the graph represent interactions with high local covariance. The PEP site is noted by squares, the effector FBP site is noted by triangles, and the inhibitor alanine (Ala^E) site is noted by stars. To see this figure in color, go online.

Results and Discussion

Identification of mechanically coupled sites in proteins

We start our discussion by analyzing the mechanical coupling between distant parts of pyruvate kinase as identified by the M-matrix (lower panel of Fig. 3). Within each chain, the structural elements involved in both allosteric sites are strongly coupled to the active site. In addition, the Ala^E site, which is located between the PEP and FBP sites, couples with both. Comparing the C-matrix and the M-matrix (both shown in Fig. 3), it is evident that the M-matrix filters out coincidental correlations in interatomic motion that are prevalent in the C-matrix. The underlying structure of the coupling can be seen by examining the mechanical coupling graph, shown in Fig. 4 and reduced to secondary structural elements for clarity. In this figure, structural elements comprising the active site (PEP site) on each chain are indicated using squares; the FBP site (40) is indicated with triangles and the Ala^E site (42) with stars. Proximity on the graph indicates strength of interaction between nodes, with clustered nodes having a greater number of strongly coupled paths between them. The corresponding M-matrix for the reduced system of secondary structure elements is shown in Fig. S3, along with the associated C- and G-matrices, and is qualitatively identical to the all-residue matrix shown in Fig. 3. We studied the energy transfer pathways in hL-PYK at two levels of abstraction: 1) treating the α carbon of each residue as a node and 2) coarse-graining the system by treating the center of mass of each secondary structural element as a node. The all-residue and secondary structural analyses were qualitatively equivalent, as can be seen by comparing Figs. 3 and S3. All-residue results are used for comparing with systematic mutation results, whereas the secondary structure representation is adopted for clarity of visualization of the coupling graph.

Communication networks and chokepoints

The M-matrix introduced in the Methods and analyzed in the previous section identifies residues, sites, or secondary structure elements that are mechanically coupled, i.e., parts of a protein or protein complex that have correlated motions and are coupled by efficient (energy transfer) pathways between those endpoints. However, the M-matrix does not directly provide any insight on the identity of the sites (residues or secondary structural elements) that contribute to the mechanical coupling between two distant parts because these quantities are abstracted into the G matrix. It is possible to obtain this crucial information by calculating the shortest-path tree t^(k) (see Fig. S4 for an example) from each residue in the given site X (e.g., the active site X = FBP) to all other residues in the protein and merging the resulting N_trees trees to form a graph of strong coupling routes to or from the site X by summing the inverse of the adjacency matrix elements $t_{ij}^{\left(k\right)}$ of the trees and inverting to form the combined adjacency matrix T,

$$T_{ij}={\left(\sum _{k=1}^{N_{\text{trees}}}\frac{1}{t_{ij}^{\left(k\right)}}\right)}^{-1}\text{.}$$ (4)

The contribution of each residue to conveying a perturbation to or from the site X is then quantified by calculating the betweenness centrality (49, 50) (the ratio of number of shortest paths between nodes i, j ≠ k that pass through node k over the total number of shortest paths between nodes i, j ≠ k) of all residues on the graph, weighted by inverse cost to pass through them given by the elements of the matrix G. We will refer to the resulting quantity as one-site cost-weighted betweenness centrality (χ). Betweenness centrality is a measure of a node’s influence on communication between other nodes (51). It has previously been used as a metric for predicting key proteins in metabolic and protein networks (52). In our work, shortest-path trees and centralities were calculated using the Graph toolbox in MATLAB r2018a; codes for calculating these parameters are included as Data S1, S2, S3, and S4. The one-site cost-weighted betweenness centrality parameter χ^FBP is shown in the upper panels of Fig. 5, mapped onto the underlying graph (left) and the structure of the protein (right). A large ${\chi }_k^{\text{X}}$ value indicates that a large number of pathways pass through node k. Therefore, perturbing that node dramatically influences how the mechanical energy from global motions of the protein is transferred to or from the site X. Similarly, we can define the two-site cost-weighted betweenness centrality ${\chi }_k^{\text{X},\text{Y}}$ between two sites X and Y. A large ${\chi }_k^{\text{X},\text{Y}}$ value indicates that a large number of pathways between those sites pass through node k. Therefore, perturbing that node is expected to dramatically influences how mechanical energy is transferred between the two sites. The two-site cost-weighted betweenness centrality parameter (χ^FBP,PEP) is shown in the middle panels of Fig. 5, mapped onto the underlying graph (left) and the structure of the protein (right). In the rest of the work, we will show how the one-site, χ^X, and two-site, χ^X,Y, cost-weighted betweenness centralities are able to provide a nearly quantitative understanding of the alanine-scanning data for hL-PYK (21).

Figure 5.

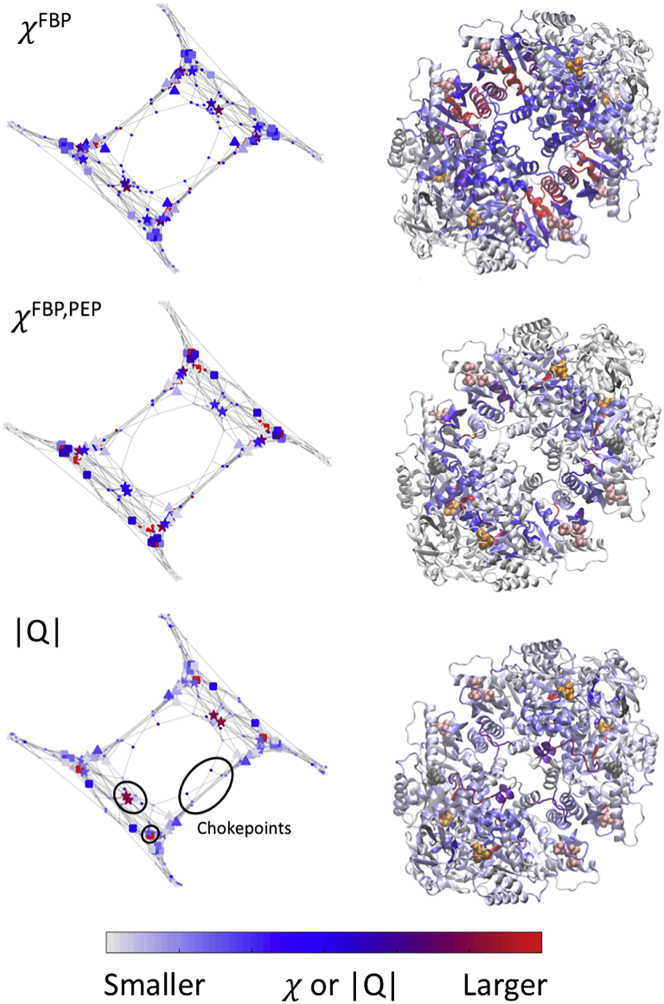
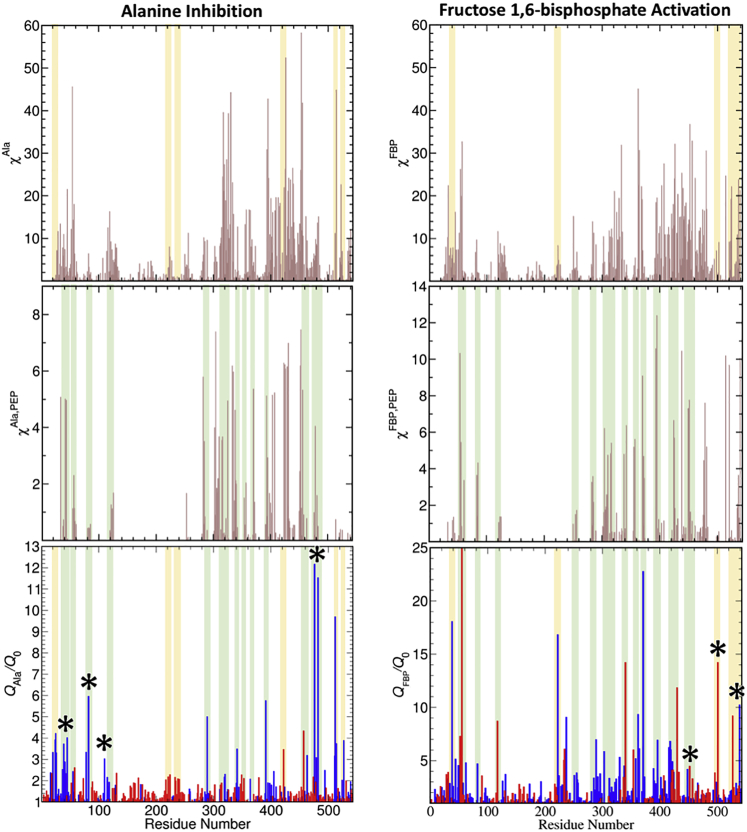
Comparison of cost-weighted betweenness centrality parameters χ^FBP (top row) and χ^FBP,PEP (middle row) for FBP interacting with hL-PYK with the allosteric strength |Q| as derived from an alanine scan (21) mapped onto the secondary structure of the protein. The left column shows the data mapped onto the graph representation of the secondary structure generated using the above methods, and the right column shows the same data mapped onto the protein structure. Because the χ parameters provide no information that would indicate the sign of a potential allosteric effect, the |Q_ax| parameters represent the factor by which the allosteric effect was observed to change. Substantial overlap is observed between χ^FBP,PEP and |Q|, though several structures in the interior of the protein identified as crucial for allostery by the alanine scan are instead highlighted by χ^FBP. Three chokepoint regions highlighted by multiple parameters are also shown, including residues at the A-B and A-C interfaces as well as the ³⁷⁰Cys-³⁷³LEU β-sheet in the PEP site. To see this figure in color, go online.

The lower panel of Fig. 5 shows χ^PEP for the PEP site mapped onto chain A, with the most influential residues noted in red, moderately influential in blue, and noncontributing in white. Coupled residues are observed between the PEP site and both allosteric sites. In addition to the within-chain coupling, the FBP site on each chain is coupled with the neighboring FBP site (chain A to chain B or chain C to chain D). Additionally, the Ala^E site on each chain is coupled with the neighboring Ala^E site (A to C or B to D); couplings are shown in the M-matrix in Fig. 3, and the raw cost-weighted betweenness centrality (without specifying any sites as sources or sinks) is shown in the upper panel of Fig. 5. These interchain couplings involve just a small number of “chokepoints” (purple or red in Fig. 5) that have few or no significant alternative routes. We can speculate that communication across these chokepoints between chains could provide a mechanism for binding cooperativity (53) between the allosteric sites on different chains. An example of modulation across a chokepoint would be a binding event displacing residues, such as motion of the helix that contains Asp⁴⁹⁹, Arg⁵⁰¹, and Trp⁴⁹⁴ in response to an FBP binding that would change the extent of the interaction of this helix with the Trp⁵²⁷ loop on the adjacent subunit, as proposed by Fenton and co-workers (40). This between-chain interaction between FBP sites is shown in the M-matrix in Fig. 3.

Modified allosteric regulation resulting from a whole-protein alanine-scanning study

In an alanine scan, mutants of the protein are produced in which each nonalanine and nonglycine residue is individually mutated to Ala^M and the allosteric coupling of the protein is compared to the wild type. The allosteric coupling is defined as

$$Q_{\text{a}/\text{x}}=\frac{K_{\text{a}}}{K_{\text{a}/\text{x}}},$$ (5)

where K_a is the apparent affinity of the protein for the substrate (e.g., PEP) in the absence of the effector (e.g., FBP or Ala^E) and K_a/x is the apparent affinity of the protein for the substrate at an effector concentration that results in saturation of the allosteric site. The effect of a mutation on one type of allosteric coupling is assessed by the ratio Q_i/Q₀, where Q_i is Q_a/x for a protein with an Ala^M substitution at residue i and Q₀ is Q_a/x for the wild-type protein. For FBP, which allosterically promotes the affinity of hL-PYK for PEP, Q_i/Q₀ < 1 indicates that allosteric promotion by FBP is decreased, and Q_i/Q₀ > 1 indicates that allosteric promotion by FBP is increased by mutation of that residue to Ala^M. Conversely, for Ala^E as a ligand, which allosterically inhibits the affinity of hL-PYK for PEP, Q_i/Q₀ < 1 indicates that allosteric inhibition by Ala^E is increased, and Q_i/Q₀ > 1 indicates that allosteric inhibition by Ala^E is decreased by mutation of that residue to Ala^M.

Because the Q_i/Q₀ quantifies the influence of a single residue mutation on the allosteric regulation between two binding events, this single parameter can easily be correlated with computational metrics based on residue mobility or interactions (i.e., the mechanical coupling metrics discussed in the prior sections). However, whereas the ratio Q_i/Q₀ indicates whether a mutation of a site induces an increase or a decrease of the allosteric effect, the cost-weighted betweenness centrality only informs us that a site is important for the mechanical coupling between distant parts of the protein, and it does not provide any direct information regarding biochemical activity (i.e., increase or decrease). As such, we focus our comparison on the magnitude of the change in allosteric activity |Q|, which is shown for FBP in the lower panels of Fig. 5, mapped onto both the graph representation of the protein (left) and the structure (right), highlighting the regions of the protein that are key to allostery and their correspondence with pathways by which sites can be mechanically coupled. A corresponding representation for Ala^E is shown in Fig. S5; the underlying numerical values are also available as Table S1.

For alanine as an effector (Fig. 6, bottom left), substitutions in the Ala^E binding site (asterisks) reduce the allosteric inhibition, substitutions adjacent to the phosphate binding loop (residues 444–449) in the FBP site enhance the Ala^E allosteric effect, and substitutions adjacent to the allosteric loop (residues 527–533) in the FBP site reduce the Ala^E allosteric effect (inhibition), as do substitutions of some polar residues in the PEP site regions (e.g., at His²⁸⁶, Thr³⁴⁰, and His³⁹¹). Far broader regions of substitution affect FBP (Fig. 6, bottom right) binding, with substantial shifts occurring because of substitutions within the FBP, PEP, and Ala^E sites along with other residues between them.

Figure 6.

Comparison of one-site, χ^X, and two-site, χ^X,PEP, cost-weighted betweenness centrality (likelihood of a node being on a path leading to X = Ala^E and FBP or connecting X to the PEP site, weighted by the degree of coupling along the path) elements for the PEP site on hL-PYK (light red line) with the Q_i/Q₀ values from the alanine scan (bottom panels) (21). In the bottom panels, blue bars for Q_i/Q₀ indicate that the mutant has a reduced response to Ala^E (left) or increased response to FBP (right), whereas red bars are inverse values and indicate that the mutant has an increased response to Ala^E (left) or reduced response to FBP (right). The color convention is from Tang and Fenton and reflects Ala^E as an allosteric inhibitor and FBP as an allosteric activator (21). The green and yellow areas indicate common features between Q_i/Q₀ and χ^X,PEP or χ^X, respectively. Asterisks (^∗) mark residues within either the Ala^E or FBP allosteric site. χ^X and χ^X,PEP values are scaled by a factor of 1/1000. To see this figure in color, go online.

Correlation between mechanical coupling and allostery

A strong Ala^M substitution effect for a residue correlates well with the one-site χ^X and the two-site χ^X,PEP cost-weighted betweenness centralities of that residue with X = Ala^E or FBP (Fig. 6, middle and top panels). As can be seen from Fig. 6, the χ^X,PEP centralities are able to capture nearly the totality of the major features in the Q_i/Q₀ trends for both X = Ala^E and FBP (highlighted as green areas in Fig. 6). Nevertheless, some features in Q_i/Q₀ trends are absent in χ^X,PEP (highlighted as yellow areas in Fig. 6). These features are instead present in χ^X. This finding implies that the majority of the Ala substitutions with strong effects on Q_i/Q₀ are located along pathways of mechanical communication between the effector sites and the PEP site. Interestingly, some Ala^M substitutions that alter the Q_i/Q₀ ratios are located along pathways that convey energy between two Ala^E sites or between two FBP site but are not along paths to the PEP site. These positions are only reflected in χ^Ala or in χ^FBP. This set of Ala^M substitutions are consistent with the hypothesis that an Ala^M substitution can alter the cooperativity of effector binding. It has previously been shown that change in the cooperative binding of either effector or substrate can indirectly influence Q_a/x (54) and therefore the Q_i/Q₀ ratios used in this study. This same type of three-ligand interaction can be observed when the binding of a ligand induces cooperativity in a binding response for a second ligand (55). The possibility of a three-ligand coupling (i.e., Q_a/x dependence on concentration of a third ligand) was also acknowledged in the original whole-protein Ala^M-scanning mutagenesis study (21). Thus, a secondary benefit of the mechanical coupling versus Ala^M-scanning data may be a mechanism to predict these indirect influences on allosteric mechanisms. We also note that the proposed two-site cost-weighted betweenness centralities are able to predict the larger magnitude of the Ala^M substitution effect for FBP than for Ala^E.

Another key observation from the alanine-scanning data that is further backed by cost-weighted betweenness centrality data is a strong degree of complementarity between residues involved in pathways to each allosteric site (e.g., substitutions that reduce the Ala^E allosteric effect often boost the FBP effect and vice versa). This complementarity is further shown in Fig. S6. This observation supports the hypothesis of key “chokepoint” residues influencing allostery by altering mechanical coupling through the protein.

Our results demonstrate that, using readily available structural data, a graph-based method can provide predictions on the importance of residues in allosteric coupling that correlate well with rigorous data from mutation-based studies, both for effects on the active site and between the allosteric sites. However, these correlations come with several caveats, that we discuss below. As previously stated, contributions of mechanical coupling to an allosteric mechanism would best be evaluated by comparing changes in observed mechanical coupling pathways between the four enzyme complexes that define the allosteric energy cycle (i.e., free enzyme, enzyme-substrate complex, enzyme-effector complex, and the ternary substrate-enzyme-effector complex). Those four structures are not currently available for hL-PYK. As an alternative, we evaluated the mechanical couplings in one available crystal structure and compared the identified mechanical couplings to the full-protein alanine-scanning mutagenesis data. Relying on a single crystal structure presents the potential to introduce several biases into the mechanical coupling evaluation. Allosteric coupling (Q_a/x) in the wild-type hL-PYK protein is pH dependent (43), with an increase in regulation as pH increases from 6.0 to 8.0 but negligible allosteric regulation below pH 6.0. The available structures of hL-PYK have been determined at pH below 6.0 (56). The calculations of the mechanical coupling are dependent on the topology included in the structure. Therefore, if the topology of the protein is maintained over the pH range (i.e., the pH dependence of allostery is due to an altered ionization state) and if ligand binding events do not substantially modify that topology, then the mechanical couplings should be maintained. However, ligand-induced changes in topology (and therefore changes in mechanical coupling) could themselves contribute to allosteric mechanisms. Given these considerations, the strength of this study is the correlation of the calculated mechanical couplings with experimental results.

Validation of generality

Although our study primarily focused on hL-PYK, we also performed further validation of the model by comparing prediction of allosteric sites in two G-protein coupled receptors, human β-2-adrenoreceptor (B2AR) and bovine rhodopsin, with predictions from Balabin’s method (8). Like Balabin’s method, this M-matrix approach provides a two-dimensional representation of potential interactions between portions of a protein. M-matrices for B2AR and bovine rhodopsin are shown in Fig. 7. Regions in which both analyses indicated interactions are indicated by orange triangles. Only two regions flagged by the Balabin analysis were not detected by the M-matrix analysis (indicated by red X); however, the M-matrix analysis identified coupling involving residues adjacent to these regions. One significant difference between the methods is that the M-matrix showed far fewer potential interactions in the terminal regions. Because both proteins were modeled in the absence of a membrane environment using both analyses, it is difficult to assign significance to this difference. However, the difference is likely due to the large amplitude of terminal residue motions in the ANM model, which receives much higher weight in a normal-mode-based model as opposed to a local-coupling-based model like the M-matrix.

Figure 7.

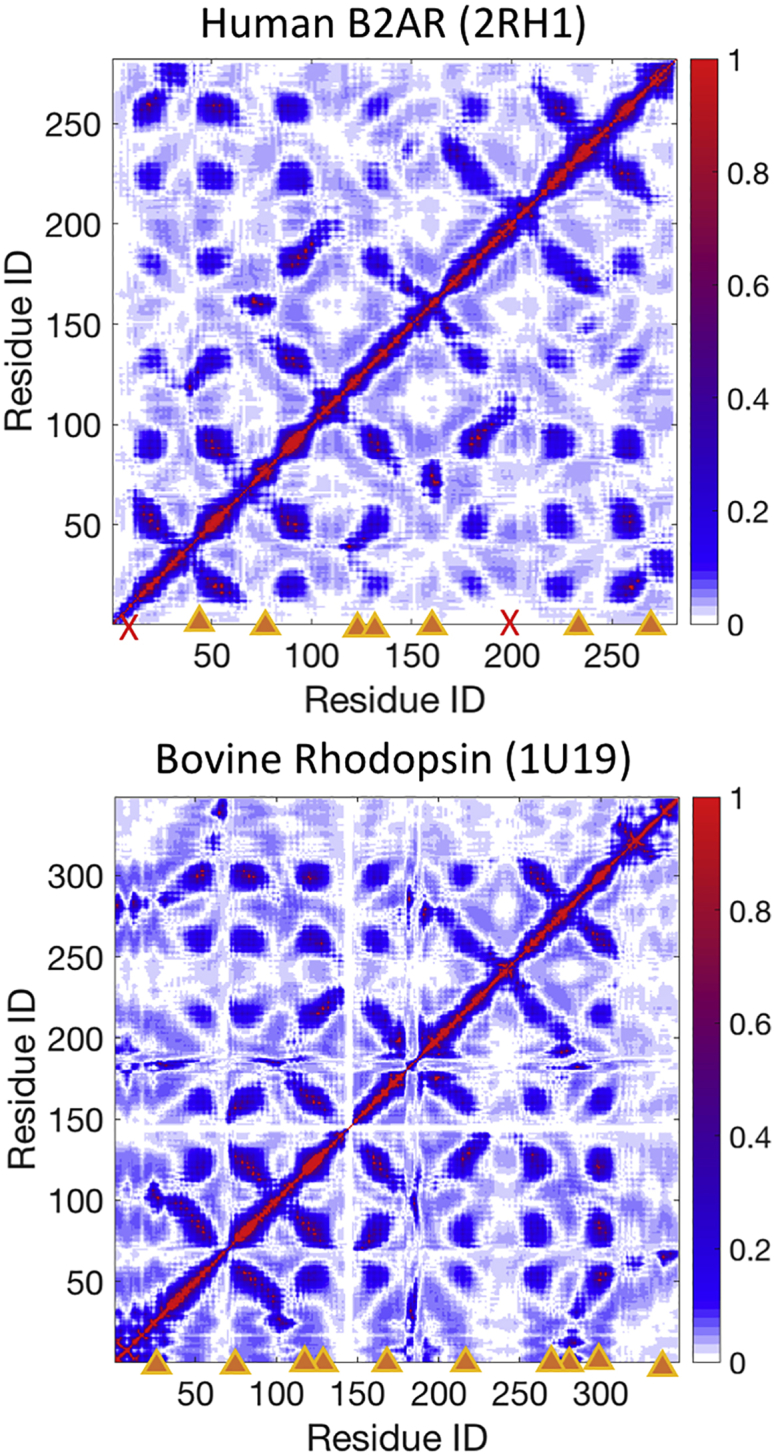
Coupling matrices derived from ANM models of human B2AR (PDB: 2RH1) (top), and bovine rhodopsin (PDB: 1U19) (bottom). Results are consistent with Beratan and co-workers’ method (8), with the exception that the M-matrix method shows less sensitivity to fluctuations of the high-mobility regions near the C- and N- termini of the proteins. Orange triangles indicate regions identified by both methods; red X symbols indicate regions indicated as coupled in (8) that are not found coupled by the M-matrix method. To see this figure in color, go online.

The utility of our method is further illustrated by calculating χ^X,Y between the active site of each receptor (AS) and the G-protein binding site on each receptor. The latter contains a conserved E(D)RY sequence (residues 102–104 (α130–α132) for B2AR and 134–136 for rhodopsin, setting the first residue in the crystal structure as 1) (8). Calculated χ^AS,E(D)RY values are shown mapped onto both an all-residue graph and the protein backbone structure in Fig. 8. Clear coupling pathways are observed in both cases, with a sequence of high-centrality residues propagating up an α-helix from the E(D)RY moiety and bifurcating into multiple routes into the active site (retinal site in rhodopsin, epinephrine site in B2AR). The localization of these pathways is once again suggestive of potential chokepoints whose alteration could disrupt communication between the sites.

Figure 8.

Comparison of cost-weighted betweenness centrality parameters χ^AS,E(D)RY between the active site and the E(D)RY motif on the G-protein binding site for two G-protein-coupled receptors, human B2AR (PDB: 2RH1, top) and bovine rhodopsin (PDB: 1U19, bottom). The ligand in the active site (the β-blocker carazolol for 2RH1 and retinol for 1U19) is shown in green, and the E(D)RY motif is shown in orange. χ^AS,E(D)RY is mapped to an all-residue graph representation on the left and to the protein backbone on the right. Discrete pathways of high-χ residues can be observed for both proteins. To see this figure in color, go online.

Conclusions

Graph-based methods (7) have recently gained popularity as a powerful tool for analyzing biological macromolecules, complementary to conventional metrics such as covariance of interatomic motions and PCA of these correlations. We have developed a novel, to our knowledge, graph-based method that, like several existing methods, is derived from covariance of interatomic motions and, like others, can identify communication pathways within a protein. However, this method combines three crucial advantages into a single approach: 1) it can be performed with arbitrary structural data (e.g., from a crystal structure, NMR, MD, or other simulation techniques); 2) it incorporates the influence of multiple possible paths between sites and produces a simple two-dimensional representation (the M-matrix) of mechanically coupled interactions between residues or secondary structural elements in a protein that can identify sites that may interact with each other; and 3) it can produce simple one-dimensional representations (χ^X and χ^X,Y) of the importance of residues or secondary structural elements for the mechanical coupling with a site. These parameters are calculated from cost-weighted betweenness centralities for pathways involving one or two sites. They provide us with semiquantitative information on the importance of specific structural elements (single residues, secondary structure elements, or full protein domains) to funnel energy between distant parts of a protein or protein complex. The three outputs of our method provide complementary information for determining connected sites and the influence of residues on the strength of those connections.

In summary, our analysis clearly shows that the mechanical communication between remote protein sites is the result of an ensemble of internal motions of a protein, which originate a multitude of energy transfer pathways between sites. However, these pathways share a few common nodes that represent effective “chokepoints” (31). The proposed computational methodology was correlated with outcomes from a full-protein alanine-scanning mutagenesis study for the allosteric regulation of hL-PYK (21). It was further validated against prior computational predictions of allosteric coupling on two G-protein coupled receptors (8). Because of the high correlation between the key residues identified using our method and the mutagenesis study, we propose that the chokepoint nodes identified in this study can be targeted to modulate the protein’s allosteric behavior. Overall, our results are suggestive that the M-matrix and cost-weighted betweenness centralities (x) are useful tools for rapidly predicting sites that can be affected by perturbing a macromolecule motion at a site of interest and for elucidating the key residues involved in the energy transduction between those sites.

Author Contributions

S.R. conceived the idea. L.E.J. and S.R. developed the method. L.E.J. wrote all of the analysis codes. All authors performed research, analyzed data, and wrote the manuscript.

Editor: Monika Fuxreiter.