Skip to main content
PMC home page
Springer logoLink to Springer
. 2018 Dec 5;29(6):2770–2782. doi: 10.1007/s00330-018-5863-7

Technical challenges of quantitative chest MRI data analysis in a large cohort pediatric study

Anh H Nguyen 1,2, Adria Perez-Rovira 1,2,3, Piotr A Wielopolski 2, Juan A Hernandez Tamames 2, Liesbeth Duijts 1,4,5, Marleen de Bruijne 2,3,6, Andrea Aliverti 7, Francesca Pennati 7, Tetyana Ivanovska 8, Harm A W M Tiddens 1,2, Pierluigi Ciet 1,2,9,✉
PMCID: PMC6510873  PMID: 30519932

Abstract

Objectives

This study was conducted in order to evaluate the effect of geometric distortion (GD) on MRI lung volume quantification and evaluate available manual, semi-automated, and fully automated methods for lung segmentation.

Methods

A phantom was scanned with MRI and CT. GD was quantified as the difference in phantom’s volume between MRI and CT, with CT as gold standard. Dice scores were used to measure overlap in shapes. Furthermore, 11 subjects from a prospective population-based cohort study each underwent four chest MRI acquisitions. The resulting 44 MRI scans with 2D and 3D Gradwarp were used to test five segmentation methods. Intraclass correlation coefficient, Bland–Altman plots, Wilcoxon, Mann–Whitney U, and paired t tests were used for statistics.

Results

Using phantoms, volume differences between CT and MRI varied according to MRI positions and 2D and 3D Gradwarp correction. With the phantom located at the isocenter, MRI overestimated the volume relative to CT by 5.56 ± 1.16 to 6.99 ± 0.22% with body and torso coils, respectively. Higher Dice scores and smaller intraobject differences were found for 3D Gradwarp MR images. In subjects, semi-automated and fully automated segmentation tools showed high agreement with manual segmentations (ICC = 0.971–0.993 for end-inspiratory scans; ICC = 0.992–0.995 for end-expiratory scans). Manual segmentation time per scan was approximately 3–4 h and 2–3 min for fully automated methods.

Conclusions

Volume overestimation of MRI due to GD can be quantified. Semi-automated and fully automated segmentation methods allow accurate, reproducible, and fast lung volume quantification. Chest MRI can be a valid radiation-free imaging modality for lung segmentation and volume quantification in large cohort studies.

Key Points

• Geometric distortion varies according to MRI setting and patient positioning.

• Automated segmentation methods allow fast and accurate lung volume quantification.

• MRI is a valid radiation-free alternative to CT for quantitative data analysis.

Electronic supplementary material

The online version of this article (10.1007/s00330-018-5863-7) contains supplementary material, which is available to authorized users.

Keywords: Magnetic resonance imaging, Lung, Lung volume measurements, Phantoms, Imaging

Introduction

Computed tomography (CT) is the most used technique for quantitative lung imaging because of its high spatial resolution and signal-to-noise ratio [1, 2]. Consequently, quantitative imaging analysis using chest CT is better developed and validated compared to chest magnetic resonance imaging (MRI) [3–6]. Nevertheless, MRI is being developed as a feasible radiation-free alternative imaging modality [1, 7].

However, several technical challenges hamper quantitative analysis with MRI, namely protocol standardization, low signal-to-noise ratio, and low spatial resolution. Volume computation in MR is also limited due to geometric distortion (GD) [1, 3], which is mainly caused by magnetic field inhomogeneity and nonlinearity of gradient coils within the scanner [7, 8]. Image processing techniques are available for GD correction and are commonly employed by manufacturers (i.e., “Gradwarp,” General Electric Healthcare). These techniques are particularly important for the delineation of target volumes for radiotherapy of cancer, where several models to correct GD have been analyzed [8–13].

Existing literature has focused on data with relatively small field-of-view (FOV) or on anatomical locations close to the isocenter where GD is minimal, such as in MRI protocols for prostate, brain, and neck tumor size quantification [7, 14, 15]. Conversely, lung imaging requires larger FOV and is therefore more influenced by GD, as magnetic field inhomogeneities make GD more pronounced the farther the object scanned is from the isocenter [7, 10, 16]. Consequently, peripheral lung portions (i.e., costophrenic angles) are most affected by GD. In addition, different MRI settings and patient’s positioning can influence the magnitude of GD [7, 17].

To the best of our knowledge, no previous publications have assessed the effect of GD on lung volume quantification in chest MRI and specifically the validation of lung volume quantification in MRI against CT. This study addresses the problem of correcting for magnetic field inhomogeneity.

In addition, this study evaluates manual, semi-automated, and fully automated methods for lung segmentation and volume quantification with MRI. Lung segmentation is a fundamental step for image analysis and is aimed to extract quantitative information. Although manual segmentation with delineation of lung boundaries on each image can give accurate results, it is laborious. Therefore, various segmentation methods have been developed for CT images. Few studies have been conducted on segmentation methods for MR images [18, 19], because it is believed to be more difficult and to have more variations than CT volumetry. In this study, we assessed segmentation methods in accuracy, reproducibility, and time efficiency to determine the best segmentation strategy for lung volume quantification using MRI in the Generation R Study, a large prospective population-based cohort study, described in detail in the Supplementary material.

In summary, we aimed (1) to quantify GD for different MRI scan settings on volume measurements compared to CT using phantoms and (2) to assess the accuracy, reproducibility, and time efficiency of semi-automated and fully automated lung volume segmentation tools compared to manual segmentations of MRI measurements obtained in children.

Materials and methods

Datasets

Phantom data

A MRI body phantom (Fig. E1), with four bottles filled with potassium sorbate (General Electric Healthcare), was used to assess the effect of GD on volume quantification depending on six different scan settings: (1) reference position with phantom centered in the scanner isocenter, (2) electronic displacement of FOV to simulate incorrect FOV positioning by a MRI technician, (3) manual displacement of phantom to simulate possible patient’s movements in the scanner, (4) table repositioning to simulate whole-body MRI protocol, (5) parallel imaging with different acceleration factors for faster image acquisition, and (6) use of torso coil to replicate the lung MRI protocol of the prospective population-based Generation R cohort study. For settings (2) and (3), eight different phantom positions distanced 5 cm from the isocenter were tested: left (L), right (R), inferior (I), superior (S), left inferior (LI), right inferior (RI), left superior (LS), and right superior (RS). For setting (5), four different acceleration factors were tested (1, 2.25, 4, 5). For setting (6), three positions were tested: torso coil centered on the subject and torso coil distanced 5 cm left or right from the center. All images, except setting (6), were acquired with body coil to obtain the most homogenous signal from the phantom and thus facilitating volume segmentation. Images were collected with in-plane bidimensional (2D Gradwarp) and full three-dimensional (3D Gradwarp) GD correction. These correction techniques correct spatial distortion artifacts and blurring at the extreme margins of MR images determined by only nongradient field nonlinearity [20].

Subjects’ data

To test lung volume segmentation methods, lung MRI data of a subset of 11 anonymized children were randomly selected from the Generation R Study [21, 22]. After written informed consent (METC-2012-165), children underwent whole-body MRI, including brain, heart, hips, and lung MRI acquisitions. The MRI scans were carried out in a specially designed child-friendly MRI research facility. From November 2014 to January 2016, 5000 MRI scans were acquired in the Generation R Study. Each subject underwent two end-inspiratory and two end-expiratory spirometer-guided MRI acquisitions. Data were acquired with 2D and 3D Gradwarp. In particular, 3D Gradwarp of the scanner was applied to one end-inspiratory and one end-expiratory scan (Fig. 1).

Fig. 1.

Fig. 1

Open in a new tab

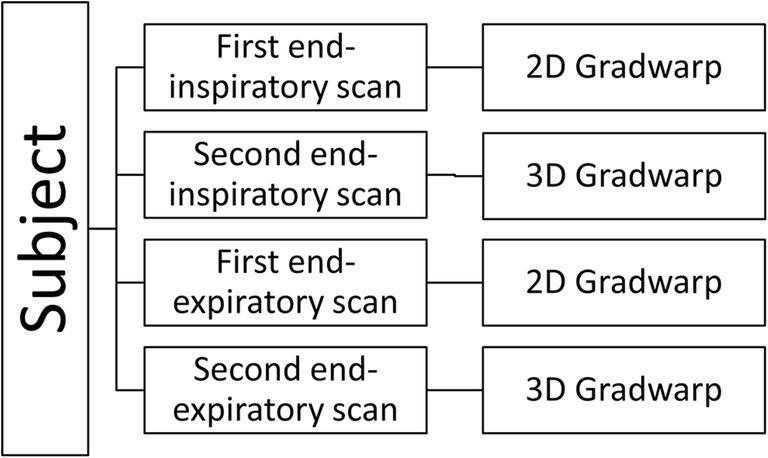
Flowchart of acquisition scheme per subject. Each subject (n = 11) underwent two end-inspiratory and two end-expiratory acquisitions. 2D and 3D Gradwarp correction was applied to one end-inspiratory and one end-expiratory scan. In total, 11 subjects underwent four acquisitions, resulting in 44 scans

More information about the Generation R Study and parameters for MRI and CT acquisitions are presented in the Supplementary material.

Imaging analysis

Phantom segmentation

Phantom volume measurements were manually obtained with MRI and CT through signal intensity thresholding segmentation using AW Server 2 platform (AWS) by GEHC and 3D Slicer software (http://www.slicer.org) by a single observer. Signal intensity threshold was chosen specifically for each scan to include the entire volume of interest, which was visually inspected in multiplanar reformats. All 52 MRI phantom acquisitions were segmented, once with AWS and once with 3D Slicer, making a total of 104 segmentations. Three CT phantom segmentations were performed with 3D Slicer (Fig. 2) to obtain true volumes. A total of 20 out of 52 acquisitions were randomly selected for second segmentation with AWS and 3D Slicer to assess intra- and intermethod agreement.

Fig. 2.

Fig. 2

Open in a new tab

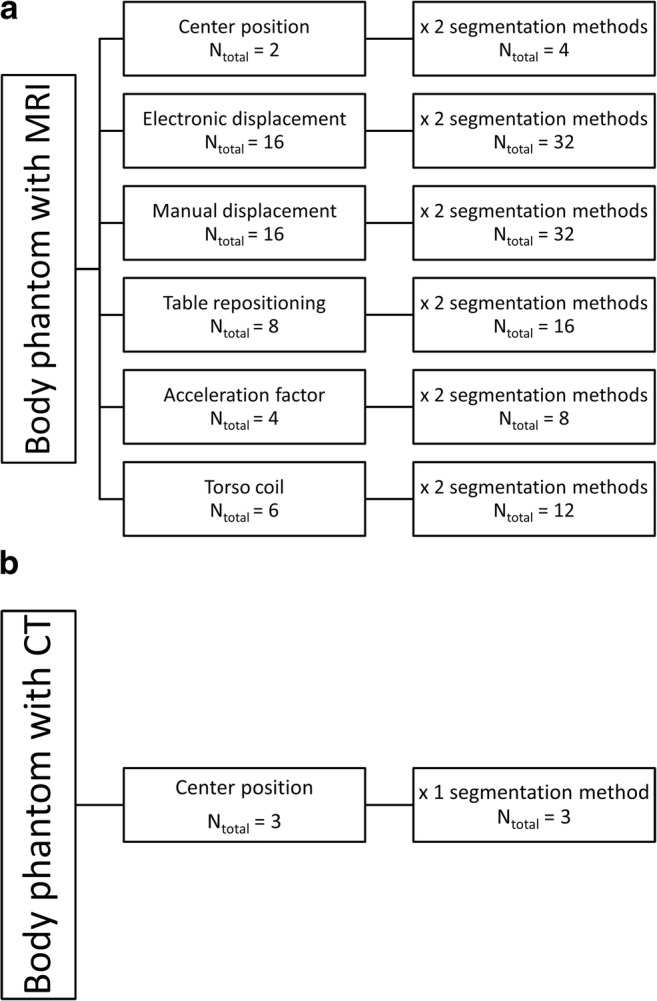
MRI and CT acquisition scheme of body phantom. a Phantom acquisitions with MRI with six different scan settings. b Phantom acquisitions with CT scan as reference images

Subjects’ lung segmentation

Five lung segmentation methods were tested in 44 scans from 11 subjects (Fig. E2): one fully manual (ITK-SNAP) [23], two semi-automated (3D Slicer [24] and GeoS [25]), and two fully automated (Ivanovska [26] and Pennati [27]). Each segmentation method is explained in the Supplementary material.

Five out of 11 Generation R subjects, with four acquisitions for each subject, were randomly selected for second segmentation with manual and semi-automated methods by the first observer and a second observer to assess intra- and interobserver agreement. Both observers were blinded to each other’s segmentations.

Quantification of GD on phantom

MRI volume measurements were compared to CT measurements as the gold standard. The magnitude of GD was quantified as relative volume difference between MRI and CT measurements.

Phantom volume segmentations of the aforementioned MRI scan settings were compared to reference CT images using Dice score after rigid registration. Dice score measures volumetric overlap in the range between 0 (no overlap) to 1 (complete overlap) [28] and can be seen as a measure of shape similarity.

To assess intraobserver agreement, 20 randomly selected phantom acquisitions were segmented twice by the first observer.

Quantification of GD on patient’s data

Volume differences between 2D and 3D Gradwarp datasets were computed as volume difference between the two end-inspiratory scans. Inspiratory scans were used because of easier segmentation of the volume of interest due to more homogeneous lung parenchyma signal intensity levels. As the entire Generation R cohort was only acquired with 2D Gradwarp, 3D Gradwarp correction performed with the built-in software of the scanner (3D GWscanner) was compared with an offline software (3D GWoff-line). Further details are provided in the online supplement.

Comparison of lung segmentation tools on subjects’ data

Lung segmentations from end-inspiratory scans were obtained using 3D Slicer (with threshold painting tool) [24], GeoS [25], Ivanovska [26, 29], and Pennati [27] methods and compared to manual segmentation (MS) to assess their performance. At the time of analysis, the tested fully automated methods were not able to perform segmentation of end-expiratory scans due to decreased contrast differences between lung parenchyma and surrounding tissues. Consequently, only 3D Slicer and GeoS methods were compared to MS for end-expiratory scans. Mean segmentation time for end-inspiratory and end-expiratory images was calculated for each method. Vital capacity (VC) computed with MRI (VCMRI) by segmentation was compared to VC measured by spirometry (VCSPIROMETER) to assess correlation. The smallest measured end-expiratory lung volume was subtracted from the largest measured end-inspiratory lung volume to compute VCMRI. VCMRI was compared to the highest VCSPIROMETER. VCSPIROMETER was obtained from spirometry. VCMRI was calculated as the volume difference between inspiratory and expiratory levels.

Statistical analysis

Descriptive data were reported as means ± standard deviations. Q–Q plots and Shapiro–Wilk tests were used to test normality. Intraclass correlation (ICC) coefficient and Bland–Altman plots were used to assess intra- and interobserver agreement. Paired samples t test, Wilcoxon signed-ranks test, or Mann–Whitney U test was applied to assess differences in lung volume measurements.

To compare semi-automated and fully automated segmentation methods with MS, volume differences were calculated as absolute and relative difference. Dice scores were used to measure overlap in shapes. Pearson correlation coefficient was used to determine correlation between VCMRI and VCSPIROMETER. P values ≤ 0.05 were considered to be statistically significant. Multiple comparisons were adjusted using Bonferroni correction. Statistical analyses were performed using SPSS v.21 (IBM SPSS Statistics).

Results

Quantification of GD on phantom’s data

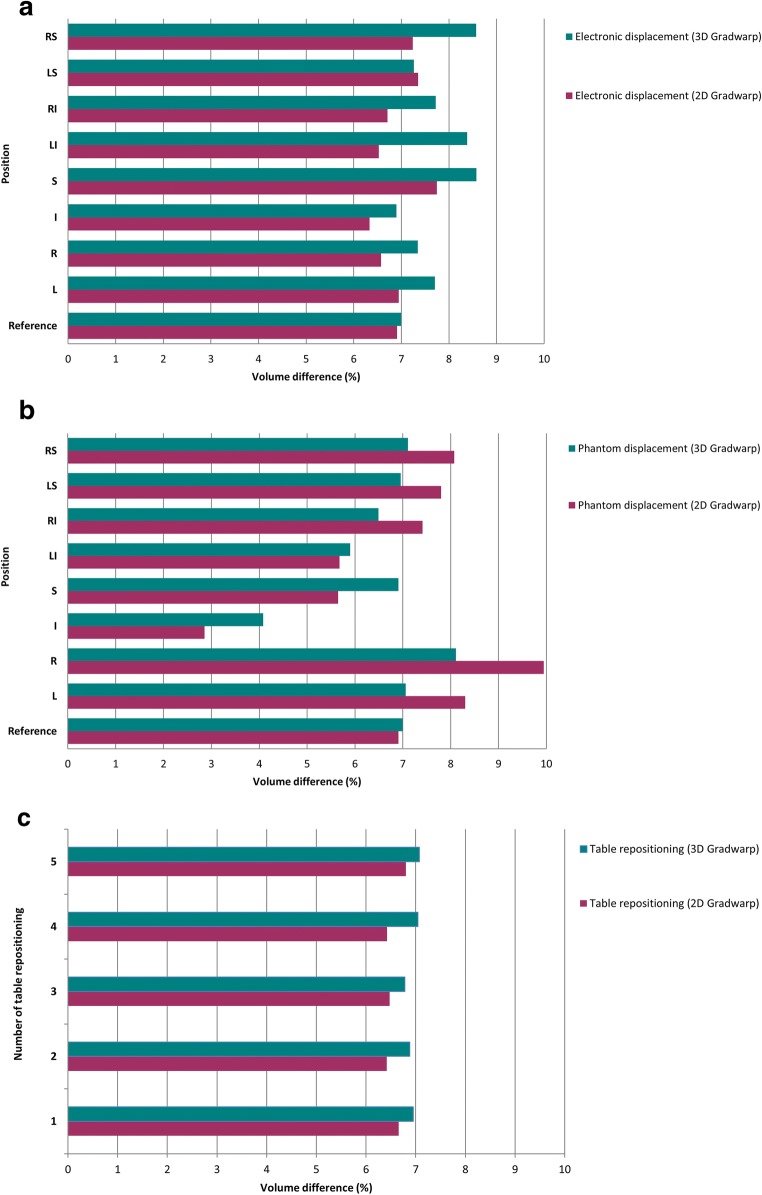
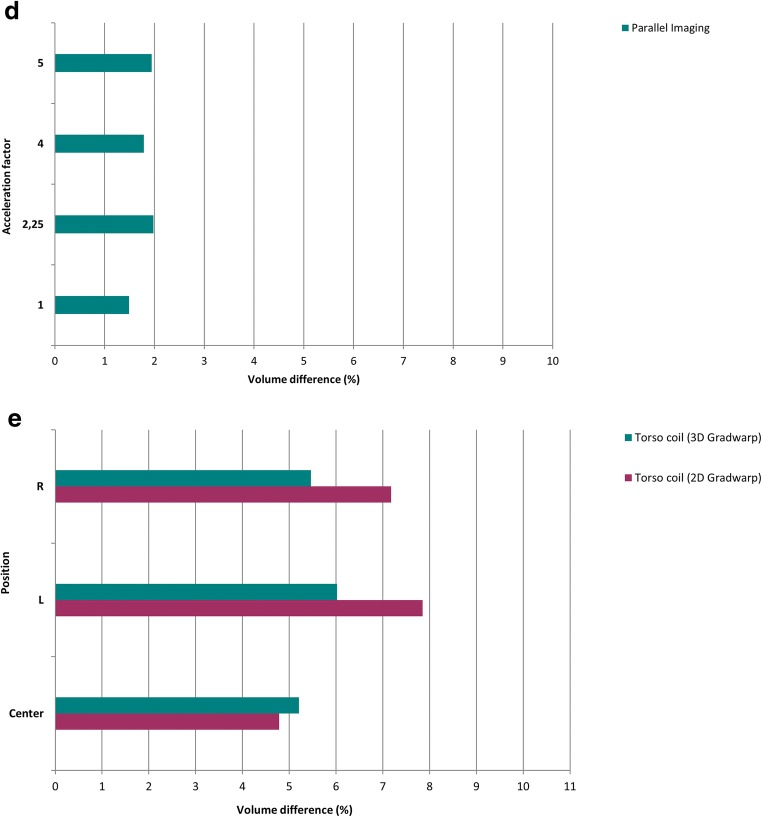
Mean volume of each phantom bottle was 1196.77 ± 77.34 ml measured in CT. Figures 3 and 4 show the effect of GD on volume quantification for different MRI settings. For the reference MRI position with the phantom centered at the isocenter, volume differences were 6.91 ± 0.48 and 6.99 ± 0.22% with 2D and 3D Gradwarp correction, respectively. Electronic displacement of FOV showed volume differences of 6.93 ± 0.57 and 7.81 ± 0.64% with 2D and 3D Gradwarp, respectively. Manual displacement of the phantom showed volume differences of 6.97 ± 8.44 and 6.58 ± 1.42% with 2D and 3D Gradwarp, respectively. Table repositioning showed volume differences of 6.53 ± 0.57 and 6.94 ± 0.25% with 2D and 3D Gradwarp, respectively. Parallel imaging showed a volume difference of 1.80 ± 0.50% with 3D Gradwarp. However, bottles were not completely imaged with this acquisition due to the automatic FOV setting of the scanner, causing an underestimation of the true volume. Imaging using torso coil showed volume differences of 6.61 ± 7.10 and 5.56 ± 1.16% with 2D and 3D Gradwarp, respectively.

Fig. 3.

Fig. 3

Fig. 3

Open in a new tab

Effect of GD on volume quantification with MRI compared to CT according to various MRI scan settings. Relative volume difference (%) for a electronic displacement of FOV, b manual displacement of phantom, c table repositioning, d parallel imaging, and e use of torso coil. Reference = reference MRI isocenter position. Positions distanced 5 cm from isocenter: L = left, R = right, I = inferior, S = superior, LI = left inferior, RI = right inferior, LS = left superior, RS = right superior

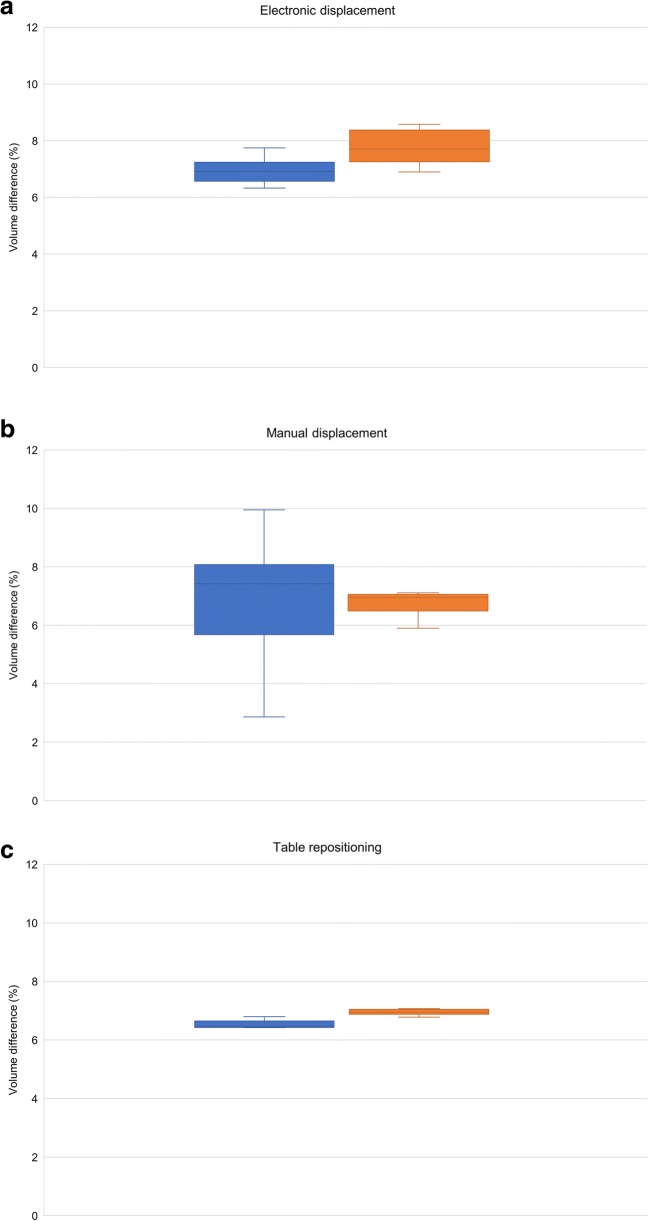
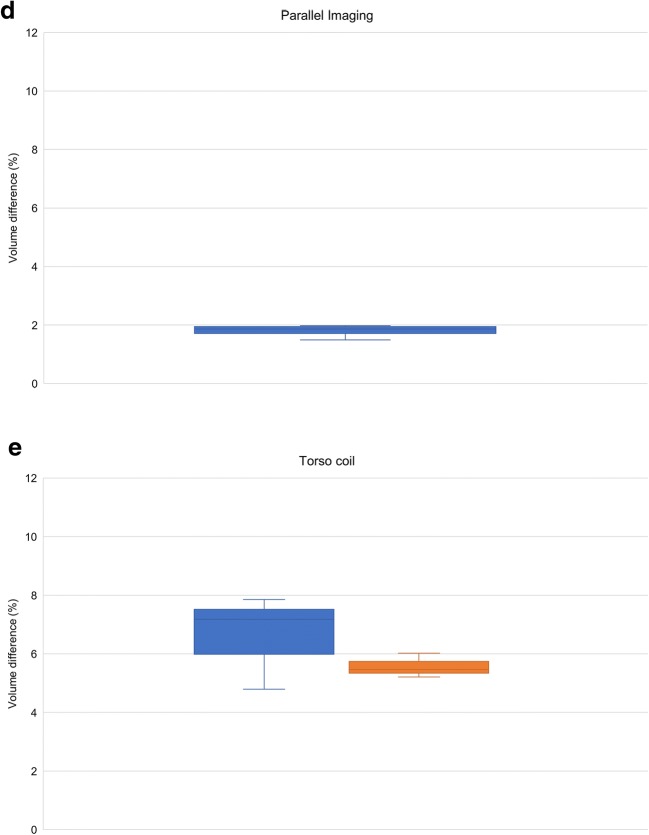
Fig. 4.

Fig. 4

Fig. 4

Open in a new tab

Relative volume difference (%) for a electronic displacement of FOV, b manual displacement of phantom, c table repositioning, d parallel imaging, and e use of torso coil. The horizontal line through each box indicates the median, rectangular boxes represent the interquartile ranges, and whiskers represent minimum and maximum values. Blue = 2D Gradwarp, orange = 3D Gradwarp

For electronic displacement, volumes of bottles on the right side of the phantom were consistently larger, independently of FOV positioning. Range of volume differences within the phantom was smaller with 3D Gradwarp than with 2D Gradwarp for all MRI settings. Figure 5 shows the effect of 2D and 3D Gradwarp. Bottles were more distorted, when distanced farther away from the isocenter.

Fig. 5.

Fig. 5

Open in a new tab

Images illustrate the effect of 2D and 3D Gradwarp. a CT reference image, b MR image with 2D Gradwarp, c MR image with 3D Gradwarp. MR images were obtained with phantom distanced 5 cm to the right of the scanner isocenter. Bending of bottles on the right side of the phantom (blue and green bottles) were seen when the bottles moved further from the scanner isocenter. With 3D Gradwarp, all bottles appear straight

Intra- and intermethod agreement

Phantom volume measurements with 3D Slicer and AWS showed high intra- and intermethod agreement (ICC = 0.991 and ICC = 0.994, respectively). No significant differences between segmentation tools (Z = -0.177, p = 0.86) were found. A Wilcoxon signed-ranks test with Bonferroni-adjusted alpha levels of 0.025 indicated that the first segmentations were significantly higher in volume than the second segmentations of the same data using 3D Slicer (mean difference = 4.48 ± 7.78 ml, Z = -5.450, p < 0.001). Similarly, the first segmentations had significantly higher volumes than the second segmentations using AWS (mean difference = 6.36 ± 5.54 ml, Z = -7.590, p < 0.001). Bland–Altman plots showed that measurements with 3D Slicer and AWS differed very little (Fig. E3).

Figure E4 represents the distribution of Dice scores with 2D and 3D Gradwarp. Mean Dice scores were 0.8593 ± 0.0502 and 0.9298 ± 0.0582 with 2D and 3D Gradwarp, respectively. Range of Dice scores for the MRI settings tested is shown in Table 1. High Dice scores were found for MRI settings using torso coil and table repositioning with 3D Gradwarp. The highest Dice score (0.9611) was found with the torso coil centered on the phantom and with 3D Gradwarp.

Table 1.

Overlapping Dice (0–1) scores between CT and MR images

MRI setting Dice score Dice score
2D Gradwarp 3D Gradwarp
Reference isocenter position 0.8776 0.9554
Electronic displacement 0.8725–0.9532 0.8788–0.9570
Manual displacement 0.7555–0.8906 0.7559–0.9580
Table repositioning 0.8784–0.8805 0.9542–0.9575
Parallel imaging N/A 0.9234–0.9378
Torso coil 0.8726–0.8879 0.9468–0.9611
Open in a new tab

Data are ranges (minimum–maximum) of Dice scores

N/A not available

Quantification of GD on patients’ data

Mean end-inspiratory volume difference between 2D and 3D GWoff-line scans was -0.91 ± 2.08%. Mean end-inspiratory volume difference between 2D and 3D GWscanner was 5.50 ± 9.62%. Mean end-inspiratory volume difference between 3D GWscanner and 3D GWoff-line was 5.90 ± 9.71%. Based on phantom testing, volume difference between 2D and 3D Gradwarp using torso coil was -0.64 ± 5.59%. Therefore, mean volume difference between 3D GWscanner and 3D GWoff-line was around 0.27 ± 11.93%.

Comparison of segmentation methods

A total of 176 segmentations were analyzed for accuracy, reproducibility, and time efficiency, of which 110 were end-inspiratory segmentations and 66 were end-expiratory segmentations.

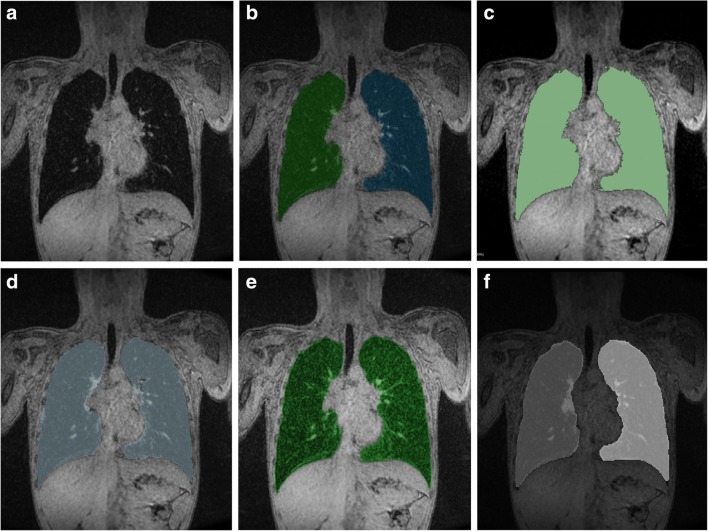
Figure 6 shows an example slice and corresponding segmentations with each tested method. Segmentation of mediastinal structures and peripheral lung portions was found to be the source of variation, leading to volume differences between software measurements. Semi-automated and fully automated methods showed similar segmentation errors, namely inclusion of nonlung tissue (i.e., mediastinum) and exclusion of lung tissue at low signal-to-noise regions (i.e., lung’s apices).

Fig. 6.

Fig. 6

Open in a new tab

Lung volume segmentations with tested segmentation methods. a Exemplary slice with corresponding segmentation results obtained with b MS, c 3D Slicer, d GeoS, e Pennati software, and f Ivanovska software

End-inspiratory segmentations

Semi-automated (ICC = 0.988–0.993) and fully automated segmentation results (ICC = 0.971–0.982) showed high agreement with MS (Tables 2 and 3). Results indicated that segmentations with GeoS, Pennati, and Ivanovska methods were similar to MS, with volume differences ranging from 0.59 to 1.37%. One subject was not segmented by Ivanovska’s method due to motion artifacts. 3D Slicer showed a significant difference (p < 0.001) with volume differences up to 2.89%. Bland–Altman plots showed good agreement between semi- and fully automated methods and MS (Fig. E5).

Table 2.

Segmentation time and intermethod agreement (ICC)

Segmentation method Time (inspiratory) ICC (inspiratory) Time (expiratory) ICC (expiratory)
MS 219 ± 53 149 ± 46
3D Slicer 47 ± 8 0.988 41 ± 7 0.995
GeoS 12 ± 3 0.993 13 ± 4 0.992
Pennati 2 ± 1 0.982 N/A N/A
Ivanovska 3 ± 1 0.971 N/A N/A
Open in a new tab

Data are ± standard deviation in minutes. Semi-automated and fully automated segmentation methods were compared with MS

N/A not available, ICC intraclass correlation coefficient

Table 3.

Comparison of end-inspiratory lung volume segmentations of semi-automated and fully automated methods with MS

Segmentation tool ICC N Absolute difference (ml) p value* Relative difference (%)
3D Slicer (semi-automated) 0.988 22 77.99 ± 55.68 < 0.001 2.89
GeoS (semi-automated) 0.993 22 35.19 ± 62.16 0.020 1.30
Pennati (fully automated) 0.982 22 36.92 ± 113.78 0.223 1.37
Ivanovska (fully automated) 0.971 20 15.86 ± 120.83 0.526 0.59
Open in a new tab

Difference is mean ± standard deviations. Mean inspiratory lung volume obtained with MS was 2702.85 ± 598.51 ml

ICC intraclass correlation coefficient, N number of subjects

*Calculated with Wilcoxon signed-ranks test with Bonferroni-adjusted alpha levels of 0.01 per comparison

End-expiratory segmentations

Both semi-automated methods showed high agreement with MS (ICC = 0.992–0.995) (Table 4). They had similar results as MS with mean differences of -1.27 and 1.81% for 3D Slicer and GeoS, respectively. Bland–Altman plots showed a slightly better performance for 3D Slicer than GeoS (Fig. E6).

Table 4.

Comparison of end-expiratory lung volume segmentations of semi-automated methods with MS

Segmentation tool ICC N Absolute difference (ml) p value* Relative difference (%)
3D Slicer (semi-automated) 0.995 22 -13.63 ± 29.84 0.067 -1.27
GeoS (semi-automated) 0.992 22 19.40 ± 37.65 0.036 1.81
Open in a new tab

Difference is mean ± standard deviations. Mean expiratory lung volume obtained with MS was 1073.69 ± 334.14 ml

ICC intraclass correlation coefficient, N number of subjects

*Calculated with Wilcoxon signed-ranks test with Bonferroni-adjusted alpha levels of 0.025 per comparison

Vital capacity

Spirometry data simultaneously obtained during the MRI scan were available for 8 out of 11 subjects, of which 4 showed large performance variability (Table 5). Association between VCMRI and VCSPIROMETER was similar but not significant for MS (r = 0.444, p = 0.271), GeoS (r = 0.440, p = 0.275), and 3D Slicer (r = 0.423, p = 0.297).

Table 5.

Spirometry data

Subject Vital capacity (ml)
Spirometry MS GeoS 3D Slicer
1 N/A 2310 2313 2230
2 2510 1456 1494 1354
3 1970 605 583 489
4 1790 1828 1816 1752
5 N/A 1852 1888 1784
6 2350 2301 2227 2253
7 N/A 1713 1694 1584
8 1690 1789 1783 1734
9 1520 1486 1453 1357
10 2660 2556 2458 2392
11 2250 1931 1893 1817
Open in a new tab

N/A not available

Segmentation time

Segmentation time for each method is shown in Table 2. Time displayed excludes time needed for file conversion, uploading, and saving steps. Manual segmentation time for end-expiratory images was shorter than end-inspiratory images, because of the shorter scan range due to lower volumes in expiration.

Both observers found MS a laborious task, aside from the considerable amount of time required for segmentation. Among the semi-automated methods, GeoS performed faster and was less laborious than 3D Slicer. Fully automated methods took approximately 2 to 3 min and required minimal user interaction.

Intra- and interobserver agreement

High intraobserver agreements were found for GeoS (ICC = 1.000), 3D Slicer (ICC = 0.999), and MS (ICC = 0.997). Volume differences were 4.81 ml (p = 0.455), 7.49 ml (p = 0.332), and 11.88 ml (p = 0.502), respectively, all not significant. High interobserver agreement was found for GeoS (ICC = 0.994), 3D Slicer (ICC = 0.995), and MS (ICC = 0.989). Volume differences were 92.93 ml (p < 0.001), 52.91 ml (p = 0.030), and 102.03 ml (p = 0.001), respectively. With an adjusted alpha level of 0.017, 3D Slicer showed no significant interobserver difference.

Discussion

We found that mean volume differences from MRI relative to CT due to GD for an object centered at the isocenter of the scanner were 5.56 ± 1.16 and 6.99 ± 0.22% with torso and body coil, respectively. Moreover, we found high Dice overlapping scores for images with 2D Gradwarp and even higher with 3D Gradwarp. We also compared five segmentation methods with different complexity and interaction possibilities. We found that MRI systemically overestimates volume measurements compared to CT due to GD, with varying volume differences according to MRI setting and patient positioning. The range of volume differences within the phantom was always smaller with 3D than 2D Gradwarp, but mean difference was sometimes higher with 3D Gradwarp. This means that 3D Gradwarp normalized the intraobject volume differences but tended to increase volume overestimation.

A discrepancy was found in the expected GD on volume measurements between electronic and manual displacement settings. Previous studies have shown that the greater the distance from the isocenter, the greater the GD [7, 10]. While this was true for the manual displacement setting, it was not for the electronic displacement. Electronic displacement consistently generated a larger volume for bottles on the right side of the phantom. This may be due to asymmetrical inhomogeneity of the magnetic field.

The MRI system changes the FOV from 500 to 600 mm when 3D Gradwarp was applied. When smaller FOV was used with 2D Gradwarp, some bottles were not completely imaged, causing an underestimation of true volume. This problem can explain the lower volume differences found with 2D than with 3D Gradwarp phantom data, for electronic displacement and table repositioning settings.

Finally, end-inspiratory segmentations with GeoS, Pennati, and Ivanovska methods and end-expiratory segmentations with 3D Slicer and GeoS showed similar volume measurements to manual segmentation. Results from the present study suggest that fully automated methods can be used for end-inspiratory lung volume segmentations of large cohort studies, reducing segmentation time and effort without sacrificing accuracy. To date, no fully automated algorithms for end-expiratory images are available. Up to date, GeoS seems the fastest and most accurate semi-automated segmentation method for lung volume segmentation of end-expiratory images.

We acknowledge some limitations to this study: firstly, the small number of subjects. However, each subject had four lung MRI acquisitions, so 44 acquisitions were obtained to test five software methods. Secondly, many missing lung function data hamper data analysis. VCMRI correlated positively with VCSPIROMETER, but analysis of a larger subset is needed to confirm these results. This will be eventually achieved when the entire dataset of Generation R is segmented. Thirdly, only one MRI system was used to acquire the MR images. While this ensured homogeneity in the resulting MR images, this does not reflect the wide range of MRI systems and imaging sequences used in practice. However, our approach can be applied to other vendors and MRI sequences.

Conclusion

MRI systematically overestimates volume compared to CT due to GD. 3D Gradwarp images yield shapes that are similar to reference CT images, but can also determine larger volume overestimation. The effect of GD on volume measurements for images acquired with specific MR settings or in specific patient positions can be quantified and potentially be predicted and corrected.

Semi-automated and fully automated segmentation methods allow accurate, reproducible, and fast lung volume quantification using MRI. We conclude that chest MRI is a valid radiation-free alternative to CT to assess lung volume in large cohort studies.

Electronic supplementary material

ESM 1 (1.8MB, docx)

(DOCX 1799 kb)

Acknowledgements

The Generation R Study is conducted by the Erasmus Medical Center in close collaboration with the School of Law and the Faculty of Social Sciences at the Erasmus University, Rotterdam, the Municipal Health Service, Rotterdam area, and the Stichting Trombosedienst and Artsenlaboratorium Rijnmond (Star-MDC), Rotterdam. We gratefully acknowledge the contribution of children and their parents, general practitioners, hospitals, midwives, and pharmacies in Rotterdam. We thank Mika Vogel (MRI site scientist at Erasmus MC of GEHC) for his technical support.

Abbreviations

2D Gradwarp

2D geometry distortion correction technique

3D Gradwarp

3D geometry distortion correction technique

3D GWscanner

3D Gradwarp correction performed with the built-in software of the scanner

3D GWoff-line

3D Gradwarp correction performed with custom-made offline software

3D Slicer

Threshold painting segmentation method (semi-automated segmentation)

AWS

AW Server (semi-automated segmentation)

CT

Computed tomography

FOV

Field of view

GeoS

Geodesic Image Segmentation (semi-automated segmentation)

GD

Geometric distortion

ICC

Intraclass correlation coefficient

MRI

Magnetic resonance imaging

MS

ITK-SNAP segmentation tool (manual segmentation)

VC

Vital capacity

Funding

The Generation R Study is made possible by financial support from the Erasmus Medical Center, Rotterdam, the Erasmus University Rotterdam, and the Netherlands Organization for Health Research and Development. Dr. Liesbeth Duijts received funding from the European Union’s Horizon 2020 co-funded program ERA-Net on Biomarkers for Nutrition and Health (ERA HDHL) (ALPHABET project (no. 696295; 2017), ZonMW The Netherlands (no. 529051014; 2017)), and the European Union’s Horizon 2020 research and innovation program (LIFECYCLE project, grant agreement no. 733206; 2016). The study sponsors had no role in the study design, data analysis, interpretation of data, writing, or submission of this report.

Guarantor

The scientific guarantor of this publication is Pierluigi Ciet.

Conflict of interest

The authors declare that they have no conflict of interest.

Statistics and biometry

No complex statistical methods were necessary for this paper.

Informed consent

Written informed consent was obtained from all subjects in this study.

Ethical approval

Institutional review board approval was obtained.

Methodology

Performed at one institution.

Footnotes

This paper has been presented to the European Conference of Radiology (ECR 2018) and awarded as the best scientific paper presentation in the section Pediatrics.

References

  • 1.Barreto MM, Rafful PP, Rodrigues RS, et al. Correlation between computed tomographic and magnetic resonance imaging findings of parenchymal lung diseases. Eur J Radiol. 2013;82:e492–e501. doi: 10.1016/j.ejrad.2013.04.037. [DOI] [PubMed] [Google Scholar]
  • 2.Kuo W, Ciet P, Tiddens HA, Zhang W, Guillerman RP, van Straten M (2014) Monitoring cystic fibrosis lung disease by computed tomography. Radiation risk in perspective. Am J Respir Crit Care Med 189:1328–1336 [DOI] [PubMed]
  • 3.Tiddens HA, Stick SM, Davis S. Multi-modality monitoring of cystic fibrosis lung disease: the role of chest computed tomography. Paediatr Respir Rev. 2014;15:92–97. doi: 10.1016/j.prrv.2013.05.003. [DOI] [PubMed] [Google Scholar]
  • 4.van Rikxoort EM, van Ginneken B. Automated segmentation of pulmonary structures in thoracic computed tomography scans: a review. Phys Med Biol. 2013;58:R187–R220. doi: 10.1088/0031-9155/58/17/R187. [DOI] [PubMed] [Google Scholar]
  • 5.Mansoor A, Bagci U, Foster B, et al. Segmentation and image analysis of abnormal lungs at CT: current approaches, challenges, and future trends. Radiographics. 2015;35:1056–1076. doi: 10.1148/rg.2015140232. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 6.Tiddens HA, Rosenow T. What did we learn from two decades of chest computed tomography in cystic fibrosis? Pediatr Radiol. 2014;44:1490–1495. doi: 10.1007/s00247-014-2964-6. [DOI] [PubMed] [Google Scholar]
  • 7.Walker A, Liney G, Metcalfe P, Holloway L. MRI distortion: considerations for MRI based radiotherapy treatment planning. Australas Phys Eng Sci Med. 2014;37:103–113. doi: 10.1007/s13246-014-0252-2. [DOI] [PubMed] [Google Scholar]
  • 8.Langlois S, Desvignes M, Constans JM, Revenu M. MRI geometric distortion: a simple approach to correcting the effects of non-linear gradient fields. J Magn Reson Imaging. 1999;9:821–831. doi: 10.1002/(SICI)1522-2586(199906)9:6&#x0003c;821::AID-JMRI9&#x0003e;3.0.CO;2-2. [DOI] [PubMed] [Google Scholar]
  • 9.Karger CP, Höss A, Bendl R, Canda V, Schad L (2006) Accuracy of device-specific 2D and 3D image distortion correction algorithms for magnetic resonance imaging of the head provided by a manufacturer. Phys Med Biol 51:N253–N261 [DOI] [PubMed]
  • 10.Torfeh T, Hammoud R, McGarry M, Al-Hammadi N, Perkins G (2015) Development and validation of a novel large field of view phantom and a software module for the quality assurance of geometric distortion in magnetic resonance imaging. Magn Reson Imaging 33:939–949 [DOI] [PubMed]
  • 11.Stanescu T, Jans HS, Wachowicz K, Fallone BG. Investigation of a 3D system distortion correction method for MR images. J Appl Clin Med Phys. 2010;11:2961. doi: 10.1120/jacmp.v11i1.2961. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 12.Donato F Jr, Costa DN, Yuan Q, Rofsky NM, Lenkinski RE, Pedrosa I (2014) Geometric distortion in diffusion-weighted MR imaging of the prostate-contributing factors and strategies for improvement. Acad Radiol 21:817–823 [DOI] [PMC free article] [PubMed]
  • 13.Petersch B, Bogner J, Fransson A, Lorang T, Pötter R (2004) Effects of geometric distortion in 0.2T MRI on radiotherapy treatment planning of prostate cancer. Radiother Oncol 71:55–64 [DOI] [PubMed]
  • 14.Sumanaweera T, Glover G, Song S, Adler J, Napel S (1994) Quantifying MRI geometric distortion in tissue. Magn Reson Med 31:40–47 [DOI] [PubMed]
  • 15.Deeley MA, Chen A, Datteri R, et al. Comparison of manual and automatic segmentation methods for brain structures in the presence of space-occupying lesions: a multi-expert study. Phys Med Biol. 2011;56:4557–4577. doi: 10.1088/0031-9155/56/14/021. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 16.Hong C, Lee DH, Han BS. Characteristics of geometric distortion correction with increasing field-of-view in open-configuration MRI. Magn Reson Imaging. 2014;32:786–790. doi: 10.1016/j.mri.2014.02.007. [DOI] [PubMed] [Google Scholar]
  • 17.Baldwin LN, Wachowicz K, Thomas SD, Rivest R, Fallone BG (2007) Characterization, prediction, and correction of geometric distortion in 3 T MR images. Med Phys 34:388–399 [DOI] [PubMed]
  • 18.Kohlmann P, Strehlow J, Jobst B, et al. Automatic lung segmentation method for MRI-based lung perfusion studies of patients with chronic obstructive pulmonary disease. Int J Comput Assist Radiol Surg. 2015;10:403–417. doi: 10.1007/s11548-014-1090-0. [DOI] [PubMed] [Google Scholar]
  • 19.Lui JK, LaPrad AS, Parameswaran H, Sun Y, Albert MS, Lutchen KR (2013) Semiautomatic segmentation of ventilated airspaces in healthy and asthmatic subjects using hyperpolarized 3He MRI. Comput Math Methods Med 2013:624683 [DOI] [PMC free article] [PubMed]
  • 20.Zhuo J, Gullapalli RP. AAPM/RSNA physics tutorial for residents: MR artifacts, safety, and quality control. Radiographics. 2006;26:275–297. doi: 10.1148/rg.261055134. [DOI] [PubMed] [Google Scholar]
  • 21.Kruithof CJ, Kooijman MN, van Duijn CM, et al. The generation R study: biobank update 2015. Eur J Epidemiol. 2014;29:911–927. doi: 10.1007/s10654-014-9980-6. [DOI] [PubMed] [Google Scholar]
  • 22.Kooijman MN, Kruithof CJ, van Duijn CM, et al. The generation R study: design and cohort update 2017. Eur J Epidemiol. 2016;31:1243–1264. doi: 10.1007/s10654-016-0224-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 23.Yushkevich PA, Piven J, Hazlett HC, et al. User-guided 3D active contour segmentation of anatomical structures: significantly improved efficiency and reliability. Neuroimage. 2006;31:1116–1128. doi: 10.1016/j.neuroimage.2006.01.015. [DOI] [PubMed] [Google Scholar]
  • 24.Fedorov A, Beichel R, Kalpathy-Cramer J, et al. 3D Slicer as an image computing platform for the Quantitative Imaging Network. Magn Reson Imaging. 2012;30:1323–1341. doi: 10.1016/j.mri.2012.05.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 25.Criminisi A, Sharp T, Blake A (2008) GeoS: geodesic image segmentation. Computer vision - ECCV 2008, Pt I, proceedings. Springer, Berlin, pp 99–112
  • 26.Ivanovska T, Hegenscheid K, Laqua R, et al. A fast and accurate automatic lung segmentation and volumetry method for MR data used in epidemiological studies. Comput Med Imaging Graph. 2012;36:281–293. doi: 10.1016/j.compmedimag.2011.10.001. [DOI] [PubMed] [Google Scholar]
  • 27.Pennati F, Quirk JD, Yablonskiy DA, Castro M, Aliverti A, Woods JC (2014) Assessment of regional lung function with multivolume (1)H MR imaging in health and obstructive lung disease: comparison with (3)He MR imaging. Radiology 273:580–590 [DOI] [PMC free article] [PubMed]
  • 28.Zou KH, Warfield SK, Bharatha A, et al. Statistical validation of image segmentation quality based on a spatial overlap index. Acad Radiol. 2004;11:178–189. doi: 10.1016/S1076-6332(03)00671-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 29.Ivanovska T, Ciet P, Perez-Rovira A et al (2017) Fully automated lung volume assessment from MRI in a population-based child cohort study. Proceedings of the 12th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications - Volume 6: VISAPP. 10.5220/0006075300530058

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ESM 1 (1.8MB, docx)

(DOCX 1799 kb)

Articles from European Radiology are provided here courtesy of Springer

RESOURCES