Prediction of Potential Disease-Associated MicroRNAs by Using Neural Networks

Abstract

Identifying disease-related microRNAs (miRNAs) is an essential but challenging task in bioinformatics research. Much effort has been devoted to discovering the underlying associations between miRNAs and diseases. However, most studies mainly focus on designing advanced methods to improve prediction accuracy while neglecting to investigate the link predictability of the relationships between miRNAs and diseases. In this work, we construct a heterogeneous network by integrating neighborhood information in the neural network to predict potential associations between miRNAs and diseases, which also consider the imbalance of datasets. We also employ a new computational method called a neural network model for miRNA-disease association prediction (NNMDA). This model predicts miRNA-disease associations by integrating multiple biological data resources. Comparison of our work with other algorithms reveals the reliable performance of NNMDA. Its average AUC score was 0.937 over 15 diseases in a 5-fold cross-validation and AUC of 0.8439 based on leave-one-out cross-validation. The results indicate that NNMDA could be used in evaluating the accuracy of miRNA-disease associations. Moreover, NNMDA was applied to two common human diseases in two types of case studies. In the first type, 26 out of the top 30 predicted miRNAs of lung neoplasms were confirmed by the experiments. In the second type of case study for new diseases without any known miRNAs related to it, we selected breast neoplasms as the test example by hiding the association information between the miRNAs and this disease. The results verified 50 out of the top 50 predicted breast-neoplasm-related miRNAs.

Introduction

The first microRNA (miRNA) named lin-4 was discovered 20 years ago by Victor Ambros.¹ Since then, thousands of currently annotated miRNAs have been discovered in various species of plants, animals, and viruses.² The expression of mRNAs is suppressed in a sequence-specific manner by miRNAs that consist of small endogenous noncoding RNAs.3, 4 Many studies indicated that miRNAs are important cell components and have vital roles in multiple stages of biological processes, such as cell growth,⁵ cell development,⁵ cell cycle regulation,⁶ cell apoptosis,⁷ stress responses,⁸ and tumor invasion.⁹ Furthermore, the strong associations between miRNAs and diseases have been verified by numerous biological studies.10, 11 The accumulating knowledge of disease-related miRNAs could contribute to pathological classifications, individualized diagnoses, and disease treatments.12, 13, 14 However, exploring the underlying miRNA-disease associations still remains a challenge for biologists.15, 16, 17, 18 Powerful computational approaches that could effectively reveal miRNA-disease associations must be urgently developed.

In recent years, many computational prediction methods have been used to identify reliable disease-miRNA candidates for further experimental studies19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30 and achieved excellent performance. Based on the assumptions that miRNAs that have similar functions are more likely associated with similar disease and vice versa, Jiang et al.³¹ estimated the similarity between miRNAs by measuring the similarity of their target genes. The miRNA network based on targets was combined with a disease phenotype network to infer the correlation scores between miRNAs and diseases. In addition, they improved the score calculation by further integrating the similarities of miRNAs with the phenotype similarities of diseases.³² Li et al.³³ collected miRNA targets and measured the function consistency score (FCS) between the target genes and the disease-related genes. However, this method ignored the topological structure when calculating the FCS. Xu et al.³⁴ focused on extracting features from the miRNA-disease network data, which were constructed under two considerations, namely, a feature set primarily related to miRNA information and disease phenotype information. HDMP³⁵ predicted disease-related miRNAs by weighting the most similar neighbors.

In addition, Chen et al.³⁶ presented the random walk with restart for miRNA-disease association (RWRMDA) model to identify potential miRNA-disease pairs by adopting random walks on the miRNA functional similarity network. Shi et al.³⁷ improved the RWRMDA by considering miRNA-target associations, disease-gene associations, and protein-protein interaction networks. Xuan et al.²¹ developed the method miRNAs associated with diseases prediction (MIDP), which utilizes the features of different nodes on the basis of random walks with a restart. Afterward, an extension method, named MIDPE, was proposed by constructing a miRNA-disease bilayer network. This approach was developed because nearly all the previous methods based on random walks could not be applied without any known related miRNA.

Moreover, machine-learning methods have also been considered for identifying miRNA-disease associations. Chen and Yan³⁸ presented regularized least-squares for miRNA-disease association (RLSMDA), in which data from known miRNA-disease associations, disease-disease similarity datasets, and miRNA-miRNA functional similarity networks were integrated. Zou et al.²⁶ introduced two methods to predict miRNA-disease association. CATAPULT²⁶ is a biased support vector machine (SVM) that was trained to classify miRNA-disease pairs. The other method, the KATZ method,²⁶ denotes the associations on the basis of the paths of different lengths in the miRNA-disease network. Based on transduction learning, Luo et al.³⁹ adopted a strategy of collective prediction based on transduction learning (CPTL) to infer potential miRNA-disease associations. Yu et al.⁴⁰ first reconstructed the similarity matrices for miRNAs and diseases and then used label propagation to predict the possible links between miRNAs and diseases. The model of within and between score for miRNA-disease association prediction (WBSMDA)⁴¹ uncovers potential miRNA-disease associations according to the within and between scores for many complex diseases, which could predict the potential related miRNAs of new diseases and new miRNAs without known association information. Chen and Huang⁴² presented a computational model named Laplacian regularized sparse subspace learning for miRNA-disease association prediction (LRSSLMDA), which used Laplacian regularization to preserve the local structures of the training data. Li et al.⁴³ designed the matrix completion for miRNA-disease association prediction model (MCMDA), which could efficiently update the low-rank miRNA-disease matrix to identify their associations. Meanwhile, the path-based miRNA-disease association (PBMDA)²² prediction model is an effective model to predict miRNA-disease association. This model adopts the depth-first search algorithm by integrating the disease semantic similarity, miRNA functional similarity, known human miRNA-disease associations, and Gaussian interaction profile kernel similarity for miRNAs and diseases. inductive matrix completion for miRNA-disease association prediction (IMCMDA)¹⁹ is a matrix computational algorithm that could efficiently update the low-rank miRNA-disease matrix to identify their associations. Chen et al.⁴⁴ presented a computational model of matrix decomposition and heterogeneous graph inference for miRNA-disease association prediction (MDHGI) to find new miRNA-disease associations by integrating the predicted association probability obtained from matrix decomposition through sparse learning method.

All mentioned methods have their own strengths, and these methods can be categorized into five aspects: (1) neighborhood-based methods, such as HDMP³⁵ and CPTL;³⁹ (2) random walk-based methods, such as RWRMDA,³⁶ Shi’s method,³⁷ MIDP, and MIDPE;²¹ (3) machine-learning-based methods, such as Xu et al.’s method³⁴ and RLSMDA;³⁸ (4) path-based methods, such as KATZ²⁶ and PBMDA;²² and (5) matrix-based methods, such as MCMDA,⁴³ IMCMDA,¹⁹ and MDHGI⁴⁴.

Inspired by popular neural-network-based approaches⁴⁵ and the latest advances in network embedding technologies,⁴⁶ we employ NNMDA, which could accurately and efficiently predict miRNA-disease associations by integrating neighborhood information based on neural networks. Specifically, network embedding is an effective approach that aims at converting the network into a low-dimensional space while preserving the structural information of the network.⁴⁶ In this way, nodes and associations of the network can be represented as compacted yet informative vectors in the embedding space.⁴⁶ In the experiment, we use two evaluation methods, namely, leave-one-out cross-validation (LOOCV) and 5-fold cross-validation (5-fold CV), to verify the performance of our method. Compared with existing approach, our method achieves an outstanding performance in identifying potential miRNA-disease associations. For further verification, we used case studies to analyze the performance of NNMDA. Experimental results show that our method has reliable performance on detecting novel associations. We also found that some special associations and corresponding miRNAs require further attention.

Results

In this section, we analyze the performance of NNMDA from several aspects. Evaluation criteria and methods used in this paper are introduced. The performance of NNMDA was compared with those of other methods in identifying potential associations between miRNAs and diseases. Finally, case studies were utilized to further evaluate the reliability of NNMDA.

Evaluation Criteria and Methods

In this paper, area under the curve (AUC), precision (PRE), and recall (REC) were used as evaluation criteria for the performance of models.

AUC is the area under the receiver operating characteristic (ROC) curve and is established by plotting the true positive rate (TPR) against false positive rate (FPR) at various threshold settings.

PRE (also called positive predictive value) is the fraction of relevant instances among the retrieved instances, whereas REC is the fraction of relevant instances that have been retrieved over the total amount of relevant instances. The equations are as follows:

$$PRE=\frac{TP}{TP+FP}$$ (Equation 1)

where TP and FP are the numbers of true positive and false positive samples, respectively, with respect to a specific disease. A large PRE value indicates good prediction accuracy.

$$REC=\frac{TP}{TP+FN},$$ (Equation 2)

where FN is the number of false negative samples with respect to a specific disease.

We evaluated the performance of NNMDA to predict potential disease-related miRNAs by using two evaluation methods (LOOCV and 5-fold CV).

5-fold CV is often used to evaluate the ability of a model to predict potential associations. For a specific disease d, d-related relationships are randomly divided into five subsets, four of which are used as known information, whereas the remaining one is used for testing.

LOOCV is also a widely used evaluation method. For the disease d(i) in our experiment, each known miRNA-disease pair (take miRNA-disease pair (m(j)-d(i)) as an example) was selected as the test sample, whereas all the other known miRNA-disease pairs were considered as training samples. First, we artificially changed the known miRNA-disease pairs (m(j)-d(i)) into unverified miRNA-disease pairs d(i) that were considered as candidate samples. We then ranked the predicted score of the test miRNA-disease pair (m(j)-d(i)) with the candidate samples. If the rank of the test miRNA-disease pair (m(j)-d(i)) exceeded the given threshold, then the model successfully predicted the miRNA-disease pair (m(j)-d(i)).

5-Fold CV

In 5-fold CV, we randomly divided the associations of each disease into five subsets of equal sizes that were used as testing sets.

We compared our method with the following widely applied miRNA-disease prediction algorithms: (1) RWRMDA,³⁶ (2) HDMP,³⁵ (3) IMCMDA,¹⁹ (4) RLSMDA,³⁸ (4) MIDP,²¹ and (5) SPM.²³ Table 1 shows the prediction performance measured as AUC for different diseases.

Table 1.

Comparison of Various Computational Approaches’ AUC Values through 5-Fold Cross-Validation

Method	RWRMDA	HDMP	IMCMDA	RLSMDA	MIDP	SPM	NNMDA
Breast neoplasm	0.785	0.801	0.812	0.832	0.838	0.932	0.968
Hepatocellular carcinoma	0.749	0.759	0.744	0.794	0.807	0.918	0.966
Renal cell carcinoma	0.815	0.833	0.793	0.839	0.862	0.901	0.912
Squamous cell carcinoma	0.819	0.820	0.837	0.849	0.870	0.899	0.924
Colorectal neoplasm	0.793	0.802	0.766	0.831	0.845	0.885	0.927
Glioblastoma	0.680	0.700	0.781	0.714	0.786	0.840	0.911
Heart failure	0.722	0.770	0.924	0.738	0.821	0.950	0.945
Acute myeloid leukemia	0.839	0.858	0.861	0.853	0.915	0.957	0.916
Lung neoplasm	0.827	0.835	0.841	0.855	0.876	0.892	0.943
Melanoma	0.784	0.790	0.761	0.807	0.837	0.951	0.949
Ovarian neoplasm	0.882	0.884	0.875	0.909	0.923	0.949	0.928
Pancreatic neoplasm	0.871	0.895	0.894	0.887	0.945	0.954	0.954
Prostatic neoplasm	0.823	0.854	0.775	0.841	0.882	0.928	0.936
Stomach neoplasm	0.779	0.787	0.783	0.797	0.821	0.859	0.955
Urinary bladder neoplasm	0.821	0.850	0.813	0.845	0.897	0.898	0.920
Average AUC	0.799	0.816	0.817	0.826	0.862	0.914	0.937

Among the 15 algorithms, NNMDA achieved the best performance. Table 1 shows that the average AUC scores of RWRMDA, HDMP, IMCMDA, RLSMDA, SPM, and NNMDA were 79.9%, 81.6%, 81.7%, 82.6%, 86.2%, 91.4%, and 93.6%, respectively. The average AUC score of NNMDA was higher than that of the other methods by 13.8%, 12.1%, 12.0%, 11.0%, 7.5%, and 2.3%, respectively.

In terms of AUC score, NNMDA achieved the highest averaged value but did not exhibit the best performance among all the diseases, particularly in heart failure. Hence, we compared the performance of NNMDA with those of PRE and REC. For a specific disease, we ranked the related candidates according to their scores.

We measured the PRE and REC within the top 20, 40 …, 80, and 100 candidates in the rank list because the top portion of the prediction links is important. PRE indicates the ratio of positive samples in the top-k samples, whereas REC measures how many positive samples are correctly identified within the top-k.

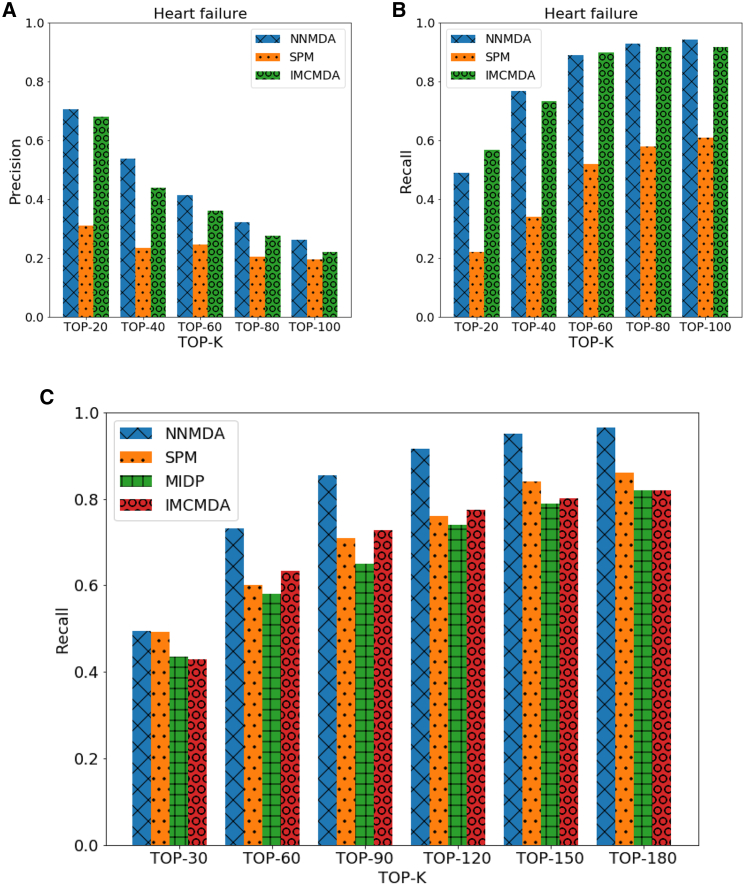
Figures 1A and 1B plot the performance of the three methods that achieved the top three AUC scores in heart failure. We found that NNMDA outperformed the other two methods in terms of PRE (Figure 1A) and REC (Figure 1B), indicating the competitiveness of this approach. We also showed that with the increase in k, REC increased but PRE declined. This finding reveals that the links ranked the top places have a high probability of being potential associations.

Figure 1.

Performances on 5-Fold Cross-Validation Precision

(A) Precision on disease heart failure. (B) Recall on disease heart failure. (C) Average recalls for the 15 tested diseases on four methods (NNMDA, IMCMDA, MIDP, and SPM), which contain the diseases breast neoplasm, hepatocellular carcinoma, renal cell carcinoma, squamous cell carcinoma, colorectal neoplasm, glioblastoma, heart failure, acute myeloid leukemia, lung neoplasm, melanoma, ovarian neoplasm, pancreatic neoplasm, prostatic neoplasm, stomach neoplasm, and urinary bladder neoplasm.

Figure 1C shows the average REC for the 15 tested diseases. Within the top 30, the average RECs of NNMDA, MIDP, SPM, and IMCMDA for all 15 diseases were 49.5%, 43.5%, 49.4%, and 43.0%, respectively. This finding indicates that NNMDA performs slightly better than the other three methods. With the increment of k, the performance of NNMDA remarkably increased for the top 60 to 120 predictions. NNMDA outperformed the other four methods.

LOOCV

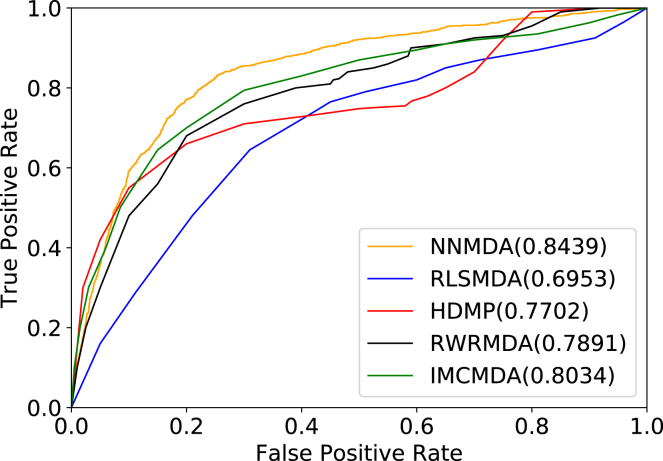
In this section, a ROC curve was plotted by using the results of LOOCV. The x axis of the ROC graph is the TPR, whereas the y axis is the FPR. The ROC curve based on LOOCV is plotted in Figure 2. On the basis of the ROC curve, AUC could be calculated as an evaluation metric for the model.

Figure 2.

Comparison of Performance among NNMDA and Baseline Methods (NNMDA, IMCMDA, RWRMDA, HDMP, and RLSMDA)

Based on the LOOCV results, we compared NNMDA with other four methods, namely, IMCMDA, RWRMDA, HDMP, and RLSMDA. The results showed that NNMDA, IMCMDA, RWRMDA, HDMP, and RLSMDA had obtained AUCs of 0.8432, 0.8034, 0.7891, 0.7702, and 0.6953, respectively. NNMDA achieved the best performance among all these models. Therefore, we can intuitively observe the improved performance of NNMDA in predicting miRNA-disease associations.

Case Study

Two different types of case studies were implemented to validate the performance and evaluate the accuracy of NNMDA for miRNA-disease association prediction.

In the first case study, all the associations between miRNAs and diseases were used to uncover potential associations. For a special disease, we extract the top 30 candidate associations of this disease to determine whether or not these associations can be confirmed by miR2Disease and dbDEMC V2.0 databases. The number of known miRNA-disease associations that are not included in HMDD are used to estimate the performance of NNMDA. Table 2 shows the prediction results of the top 30 predicted lung neoplasm-related miRNAs.

Table 2.

Prediction Results of the Top 30 Predicted Lung Neoplasm-Related miRNAs Based on Known Associations in HMDD V1.0

miRNA	Evidence	miRNA	Evidence
hsa-let-7g	dbDEMC mir2disease	hsa-mir-18b	dbDEMC
hsa-mir-135b	dbDEMC	hsa-mir-17	dbDEMC
hsa-mir-133b	dbDEMC	hsa-mir-21	dbDEMC mir2disease
hsa-mir-200b	dbDEMC mir2disease	hsa-mir-148a	dbDEMC mir2disease
hsa-let-7d	dbDEMC mir2disease	hsa-mir-18a	dbDEMC mir2disease
hsa-mir-181b-1	unverified	hsa-mir-30e	dbDEMC
hsa-mir-29c	dbDEMC mir2disease	hsa-mir-101-1	mir2disease
hsa-mir-98	dbDEMC mir2disease	hsa-mir-30c-2	unverified
hsa-mir-221	dbDEMC mir2disease	hsa-mir-125a	dbDEMC mir2disease
hsa-mir-186	dbDEMC	hsa-mir-200c	dbDEMC mir2disease
hsa-mir-142	unverified	hsa-mir-126	dbDEMC mir2disease
hsa-mir-146a	dbDEMC	hsa-mir-31	dbDEMC mir2disease
hsa-mir-146b	dbDEMC mir2disease	hsa-mir-30c-1	unverified
hsa-mir-101-1	mir2disease	hsa-mir-30a	dbDEMC
hsa-let-7b	dbDEMC	hsa-mir-192	mir2disease dbDEMC

The first column contains the top 1–15 related miRNAs, whereas the third column shows the top 16–30 related miRNAs.

As shown in Table 2, 9 out of the top 10 and 26 out of the top 30 predicted lung-neoplasm-related miRNAs were included. Therefore, most of the potential associations were confirmed by the miR2Disease and dbDEMC V2.0 databases.

An important criterion for evaluating the usefulness of a model is whether or not it can be used to predict potential related miRNAs for a new disease. In the second case study, we evaluated the performance of NNMDA when it was implemented to the new disease without any known related miRNAs. Breast neoplasms were used as an example in our experiment. Therefore, we hid the association information between miRNAs and breast neoplasms by setting all their known associations as unknown ones. We then implemented NNMDA to obtain the ranking list of the association prediction scores for miRNA-breast neoplasms. We analyzed in detail the prediction accuracy on breast neoplasm and mainly focused on the top 50 miRNA candidates. The results for breast neoplasms are represented in Table 3.

Table 3.

Prediction Results of the Top 50 Predicted Breast Neoplasm-Related miRNAs When the Known Associations of Breast Neoplasms Were Considered as Unknown Ones

miRNA	Evidence	miRNA	Evidence
hsa-mir-155	dbDEMC HMDD	hsa-mir-19b-1	HMDD
hsa-mir-21	dbDEMC HMDD	hsa-mir-1-1	HMDD
hsa-mir-146a	dbDEMC HMDD	hsa-mir-145	dbDEMC HMDD
hsa-mir-29b-1	HMDD	hsa-mir-29c	dbDEMC HMDD
hsa-mir-125b-1	HMDD	hsa-mir-199a-2	HMDD
hsa-mir-29b-2	HMDD	hsa-mir-223	dbDEMC HMDD
hsa-mir-34a	dbDEMC HMDD	hsa-mir-126	dbDEMC HMDD
hsa-mir-15a	dbDEMC HMDD	hsa-mir-133a-2	HMDD
hsa-mir-125b-2	HMDD	hsa-mir-19a	dbDEMC HMDD
hsa-mir-20a	dbDEMC HMDD	hsa-mir-199a-1	HMDD
hsa-mir-16-1	HMDD	hsa-let-7b	dbDEMC HMDD
hsa-mir-16-2	HMDD	hsa-mir-26a-1	HMDD
hsa-mir-221	dbDEMC HMDD	hsa-let-7c	dbDEMC HMDD
hsa-mir-29a	dbDEMC HMDD	hsa-mir-142	HMDD
hsa-let-7a-2	HMDD	hsa-mir-146b	HMDD
hsa-mir-26a-2	HMDD	hsa-mir-150	dbDEMC HMDD
hsa-mir-1-2	HMDD	hsa-mir-210	dbDEMC HMDD
hsa-let-7a-1	HMDD	hsa-mir-196a-2	HMDD
hsa-let-7a-3	HMDD	hsa-let-7i	dbDEMC HMDD
hsa-mir-17	dbDEMC HMDD	hsa-let-7d	dbDEMC HMDD
hsa-mir-31	dbDEMC HMDD	hsa-mir-195	dbDEMC HMDD
hsa-mir-92a-1	HMDD	hsa-mir-222	dbDEMC HMDD
hsa-mir-18a	dbDEMC HMDD	hsa-mir-92a-2	HMDD
hsa-mir-122	dbDEMC HMDD	hsa-mir-24-1	HMDD
hsa-mir-133a-1	HMDD	hsa-mir-133b	dbDEMC HMDD

The first column contains the top 1–25 related miRNAs, whereas the third column shows the top 26–50 related miRNAs.

Discussion

Identifying potential disease-related miRNAs could provide new insights into the role of miRNA for its impact on clinical measure, diagnosis, and treatment. However, relying on traditional experimental-based methods, predicting the associations between miRNA and disease seems inefficient. Consequently, great numbers of computational methods have been proposed to solve this challenging problem in recent years. In this paper, we apply a neural-network-based model to predict miRNA-disease associations, which aggregates the neighbor information during the process and preserves the topology of the original network at the same time. After that, to comprehensively verify the performance of our method, 5-fold CV and LOOCV are implemented to evaluate NNMDA in comparison with other state-of-the-art approaches. Compared to the state-of-the-art method, NNMDA performs better in terms of AUC values on the dataset and is able to retrieve more correct associations. In addition, case studies on two common diseases also gave a strong confirmation to the prediction ability of our method. Results show that NNMDA could be a useful tool for studying the miRNA-disease relationship. The success of our method is mainly due to the following two reasons. First, the constructed similarity networks for both miRNAs and diseases are well integrated in the neural network. Second, the imbalance of datasets that we take into consideration helped improve the efficiency. Nonetheless, more informative data sources should be integrated into our model to further improve the prediction performance. The future work may further take more optimization methods into account to accurately uncover associations between miRNAs and diseases.

Materials and Methods

miRNA-Disease Network

Data of known human miRNA-disease associations used in this paper were retrieved from the human miRNA-disease database (HMDDv2.0) to construct the miRNA-disease network.⁴⁷ If a disease is associated with a miRNA, then an edge is added to link them. The miRNA-disease association matrix is asymmetric and binary, i.e., each entry of the association matrix could only be 0 or 1. A total of 6,441 associations between 577 miRNAs and 336 diseases were obtained after duplications were removed.

Disease Functional Similarity

Functionally similar genes exhibit a great probability of regulating similar diseases. Therefore, we used gene functional information to construct a disease similarity network. The data can be downloaded from the HumanNet database,³³ which contains an associated log-likelihood score (LLS) of each interaction between two genes or gene sets. Similarity $DS\left(d_i,d_j\right)$ between diseases $d_i$ and $d_j$ is based on the gene functional information and was calculated as follows:

$$\text{DS}\left({\text{d}}_{\text{i}},{\text{d}}_{\text{j}}\right)=\{\begin{array}{c}\frac{{\sum }_{x\mathit{ϵ}\text{S}\left({\text{d}}_{\text{i}}\right)}LLS\left(x,\text{S}\left({\text{d}}_{\text{i}}\right)\right)+{\sum }_{y\mathit{ϵ}\text{S}\left({\text{d}}_{\text{j}}\right)}LLS\left(y,\text{S}\left({\text{d}}_{\text{j}}\right)\right)}{\left|\left|\text{S}\left({\text{d}}_{\text{i}}\right)\right|\right|+\left|\left|\text{S}\left({\text{d}}_{\text{j}}\right)\right|\right|}\\ \begin{array}{cc}0,& otherwise\end{array}\end{array},\left|\left|\text{S}\left({\text{d}}_{\text{i}}\right)\right|\right|+\left|\left|\text{S}\left({\text{d}}_{\text{j}}\right)\right|\right|\ne 0,$$ (Equation 3)

where $S\left(d_i\right)$ and $S\left(d_j\right)$ represent the gene sets that are related to diseases $,{\text{d}}_{\text{i}}$ and $d_j$, respectively. $S\left(d_i\right)$ and $S\left(d_j\right)$ are the cardinalities of gene sets $,S\left(d_i\right)$ and $S\left(d_j\right)$, respectively. $LLS\left(x,\text{S}\left({\text{d}}_{\text{i}}\right)\right)$ is the LLS between gene x and gene set $S\left(d_i\right)$, where $x\mathit{\epsilon }\text{S}\left({\text{d}}_{\text{i}}\right)$. If $DS\left(d_i,d_j\right)$ > 0, then it can be considered as the weight of the link connecting diseases $d_i$ and $d_j$. Hence, we obtained a weighted disease similarity network containing 112,896 similar associations among 336 diseases.

miRNA Similarity

The miRNA similarity network was constructed by employing four main miRNA similarities, which are based on verified miRNA-target associations, family information, cluster information, and verified miRNA-disease associations. The verified miRNA-target associations can be downloaded from the miRTarBase,⁴⁸ a database of miRNA-target interactions (http://mirtarbase.mbc.nctu.edu.tw/php/index.php) validated by reporter assays and next-generation sequencing experiments. Two miRNA nodes are considered as connected if they share common targets. The edge weight, miRNA similarity based on target, represents the number of shared targets between miRNAs.

We can obtain the family information and cluster information from miRBase.⁴⁹ If two miRNAs belong to the same miRNA family, then the value of miRNA similarity based on family would be set as 1, otherwise 0. We obtained 153 clusters of miRNAs. In terms of miRNA similarity based on cluster, the value would be set to 1 if the two miRNAs belonged to the same cluster. These two matrices were found to both be Boolean types. According to literature,50, 51 functionally similar miRNAs tend to connect with similar diseases and vice versa. We downloaded functional similarity data from http://www.cuilab.cn/files/images/cuilab/misim.zip from a previous study.⁵⁰ With these data, we constructed matrix FMS to represent the miRNA functional similarity. The element $FMS\left(m\left(i\right),m\left(j\right)\right)$ denotes the functional similarity between miRNA $m\left(i\right)$ and $m\left(j\right)$. After a simple combination introduced in Zeng et al.²³, a weighted miRNA similarity network containing 332,928 similar associations among 577 miRNAs was obtained.

Gaussian Interaction Profile Kernel Similarity for Diseases and miRNAs

Considering that similar diseases tend to be related to functionally similar miRNAs and vice versa,50, 52 we calculated Gaussian interaction profile kernel similarities for the miRNAs and diseases’ similarity. First, we used A(i, j) to represent the interaction between disease d(i) and miRNA m(j), where A is the miRNA-disease association matrix. Gaussian interaction kernel similarity between disease d(i) and d(j) was calculated as follows:

$$\text{GS}\left({\text{d}}_{\text{i}},{\text{ d}}_{\text{j}}\right)=\exp \left(-{\text{γ}}_{\text{d}}\sum _{k=1}^{k=nm}{\left(A\left(i,k\right)-A\left(j,k\right)\right)}^2\right),$$ (Equation 4)

where ${\gamma }_d$ is used to control the kernel bandwidth that is obtained by normalizing a new bandwidth parameter ${\text{γ}}_{\text{d}}^{\text{'}}$ by the average number of associations with miRNAs for all the diseases. ${\gamma }_d$ is defined as follows:

$${\text{γ}}_{\text{d}}={\text{γ}}_{\text{d}}^{\text{'}}/\left[\frac{1}{nm}\sum _{k=1}^{k=nm}\sum _{s=1}^{s=nd}A{\left(k,s\right)}^2\right].$$ (Equation 5)

Gaussian interaction profile kernel similarity between miRNA m(i) and m(j) is defined in a similar way:

$$\text{GS}\left({\text{m}}_{\text{i}},{\text{m}}_{\text{j}}\right)=\exp \left(-{\text{γ}}_{\text{m}}\sum _{k=1}^{k=nd}{\left(A\left(k,i\right)-A\left(k,j\right)\right)}^2\right),$$ (Equation 6)

$${\text{γ}}_{\text{m}}={\text{γ}}_{\text{m}}^{\text{'}}/\left[\frac{1}{nd}\sum _{k=1}^{k=nm}\sum _{s=1}^{s=nd}A{\left(k,s\right)}^2\right].$$ (Equation 7)

Schematic Overview

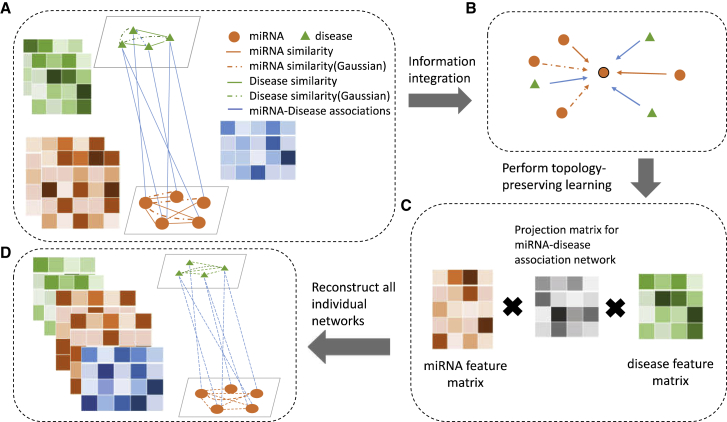
As shown in Figure 3, the framework consists of four major steps: (1; Figure 3A) construct a heterogeneous network based on three miRNA similarity interactions, two disease similarity interactions, and miRNA-disease associations. The similarity matrices are symmetric, whereas the miRNA-disease association matrix is asymmetric and binary, i.e., each entry of the association matrix could be only 0 or 1. (2; Figure 3B) Integrate the neighborhood information of miRNAs and diseases and further embed them into low-dimensional representations in neural network. (3; Figure 3C) Reconstruct miRNA-disease association matrix by using extracted feature vectors and minimize the loss between the new reconstructed matrices and the observed matrices. This step aims to enforce the learned representations as much as it could from the original matrices. (4; Figure 3D) Predict the miRNA-disease associations by ranking and selecting the values in a decreasing order in the reconstructed association matrix.

Figure 3.

Flowchart of NNMDA

(A) NNMDA uses several individual miRNA-related or disease-related networks to construct a heterogeneous network (details of the used datasets are introduced in Materials and Methods). In a heterogeneous network, different types of nodes are connected by distinct types of edges. Two nodes can be connected by more than one edge (e.g., the solid link between diseases representing disease functional similarity and the chain line between them representing disease Gaussian similarity). (B) Each node adopts a neighborhood information aggregation operation to extract information from the neighborhood. Each arrow represents a specific aggregation function with respect to a specific edge type. Each node then updates its feature representation by integrating its current representation with the aggregated information. (C) NNMDA learns the topology-preserving node features that are useful for miRNA-disease interaction prediction by enforcing the node features to reconstruct the original individual networks. (D) Reconstruction of all individual matrices.

Heterogeneous Network

Given a heterogeneous network G = (V, E), V is a node set that contains two kinds of node type, NT = {miRNA, disease}, and E is an edge set with edge types ET = {miRNA-miRNA, miRNA-miRNA-Gaussian, disease-disease-functional, disease-disease-Gaussian, miRNA-disease}. In our framework, each node only belongs to a single node type, whereas the same two nodes can be linked by more than one edge, e.g., two diseases can be simultaneously associated to a disease-disease-functional edge and a disease-disease-Gaussian edge. For each matrix, normalization is first implemented before further processing after data preparation. If $A^{\text{'}}$ is the corresponding normalized matrix of the original matrix A, then it can be formulated as follows:

$${\text{A}}^{\text{'}}\left(\text{i},\text{j}\right)=\frac{A\left(i,j\right)}{{\sum }_{k=1}^{k=Col\left(A\right)}A\left(i,k\right)},$$ (Equation 8)

where Col(A) is the size of A column dimension. A heterogeneous network can be generated using the normalized matrices as association weight.

Neighborhood Information Aggregation and Node Embedding

To develop a network topology-preserving embedding model that can be used to predict miRNA-disease interactions, we adopted the neighborhood information aggregation strategy. For each node u with type $t\in NT$(each node only belongs to a single node type), its features could be aggregated from its neighbors:

$$E{M}_t^{\text{'}}\left(u\right)=concat\left(\sum _{s\in ET}\sum _{e=\left(u,v\right)\in E_s}{A}_s^{\text{'}}\left(;,v\right)\cdot {\sigma }_s,E{M}_t\left(u\right)\right),$$ (Equation 9)

where $E{M}_t^{\text{'}}$ is the embedding of node type t (miRNA or disease), the initial representations of nodes $\left(EM\right)$ are randomly set, v is the neighbor of u with node type ${\text{t}}^{\text{'}}$ $\left({\text{t}}^{\text{'}}\in NT\right)$, and ${\text{σ}}_{\text{s}}$ is defined as follows:

$${\text{σ}}_s=\text{σ}\left({\text{EM}}_{{\text{t}}^{\text{'}}}\cdot {\text{W}}_{\text{s}}+{\text{b}}_{\text{s}}\right),$$ (Equation 10)

where $W_s\left(W_s\in R^{d\times d}\right)$ and $b_s\left(b_s\in R^d\right)$ are the parameters trained in neural network, $W_s$ is the weights parameter, and $b_s$ is the bias term. σ (·) (implemented as RELU(x) = max(x, 0)) is activation function in the neural network. In this step, we further learned node representations into lower dimensional vectors and implement normalization:

$$E^{\text{'}}\left(u\right)=\frac{\sigma \left(E{M}^{\text{'}}\left(u\right)\cdot W_0+b_0\right)}{{\left|\left|\sigma \left(E{M}^{\text{'}}\left(u\right)\cdot W_0+b_0\right)\right|\right|}^2},$$ (Equation 11)

where $E{M}^{\text{'}}\left(u\right)$ is the embedding of node u, $W_0$ $\left(W_0\in R^{2d\times d}\right)$ is the weights, $b_0$ $\left(b_0\in R^d\right)$ is the responding bias term, and σ (·) (implemented as RELU(x) = max(x, 0)) is activation function. Therefore, the new embedding was normalized by its ${\text{l}}_2$-norm. Through neighborhood aggregation, the final neighborhood information is the summation of neighborhood information aggregation with respect to every edge type. We then obtained the representation of each node considering its neighbor information and its own features and learned structural and topological information as the feature vectors.

Topology-Preserving Learning of the Node Embedding

Given the embedding of nodes E(·), topology-preserving learning of the node embedding is defined as:

$$mi{n}_{W,b,P,G}\sum _{t\in ET}{\left(A_t-E_u^{\text{'}}{P}_t{G}_t^T{E}_v^{\text{'T}}\right)}^2,$$ (Equation 12)

where $P,G\in R^{d+k}$ functions are projection matrices that can be used to extract the principle features from node representations. $E_u^{\text{'}}$ and $E_v^{\text{'}}$ are the embeddings of miRNA or disease with $u,v\in NT$. After projections of $E_u^{\text{'}}$ and $E_v^{\text{'}}$ by P and G, the inner product of the two projected vectors should reconstruct the original edge weight. For a symmetric matrix reconstruction (i.e., miRNA-miRNA or disease-disease similarity matrix), matrix P = G was used to enforce symmetry of the recovery. Here, the summation of the squared reconstruction errors was minimized for all edges with respect to all unknown parameters. Given that all operations are differentiable and subdifferentiable, parameters can be trained in an end-to-end manner by performing gradient descent.

After training, each interaction confidence score between miRNA and disease could be predicted by the reconstructed miRNA-disease association matrix. A high score indicates a large probability for the potential association:

$$R{D}_{reconstruct}=E_r^{\text{'}}{P}_{RD}{G}_{RD}^T{E}_d^{\text{'T}},$$ (Equation 13)

where $E_r^{\text{'}}$ represents miRNA feature matrix and $E_d^{\text{'}}$ represents disease feature matrix. In this sense, we can consider our prediction task as a matrix factorization or completion problem. However, our method incorporates a deeper learning model to construct the feature matrices by explicitly defining the construction processes. Through these steps, our method incorporates the prior knowledge of network topology, after which the loss minimization procedure is implemented to prevent the network from arbitrarily factorized.

To further improve the performance of NNMDA, the imbalance of datasets is also taken into consideration. In the process of recovering the associations between miRNAs and diseases, we calculated the loss between prediction matrix and original matrix. To our intuition, the loss obtained from incorrectly predicting a verified entry as an unverified entry (FN) should be different from the loss obtained from wrongly indicating an unknown entry as an verified entry (FP). Because the unknown entries should be considered as unlabeled instead of negative, we redefine loss as follows:

$$Loss=Los{s}_{FN}+\alpha Los{s}_{FP}.$$ (Equation 14)

In our experiment, labeled data are regarded more important than unlabeled. To balance the datasets, in the process of recovering the miRNA-disease matrix, we set parameter α to the ratio of number of entries to size of the matrix, which was finally set to be $\alpha =6441÷577÷336=0.03$ for the experiments. As a result, the method obtained performance improvement in identifying miRNA-disease associations.

Author Contributions

X.Z. conceived the project, designed the experiments, and edited the final paper. W.W. wrote the paper and drafted the figures. G.D. and J.B. contributed to materials and data analysis. W.W., G.D., and J.B. performed the experiments. Q.Z. wrote the paper and edited the paper.

Conflicts of Interest

The authors declare no potential conflicts of interest.