Significance
Structural biology would benefit greatly from having a purely computational means of obtaining protein structural models that rival in accuracy those based on X-ray diffraction experiments. Intermediate resolution structures, with accuracies that are a few angstroms above the experimental uncertainty assigned to X-ray structures, can now be routinely generated. Here, we draw inspiration from blacksmithing to help us devise methods that can refine intermediate resolution models to within experimental accuracy using only modest computational resources. Like the blacksmiths, we use mechanical deformations along collective modes to encourage equilibration. We find that refinement is impeded by slow rotations of bulky side chains in the protein interior and that lowering these barriers while sampling along deformation modes further helps to refine predicted structures.
Keywords: protein structure refinement, principal component analysis, side-chain isomerization, protein blacksmithing, mechanical deformations
Abstract
Refining predicted protein structures with all-atom molecular dynamics simulations is one route to producing, entirely by computational means, structural models of proteins that rival in quality those that are determined by X-ray diffraction experiments. Slow rearrangements within the compact folded state, however, make routine refinement of predicted structures by unrestrained simulations infeasible. In this work, we draw inspiration from the fields of metallurgy and blacksmithing, where practitioners have worked out practical means of controlling equilibration by mechanically deforming their samples. We describe a two-step refinement procedure that involves identifying collective variables for mechanical deformations using a coarse-grained model and then sampling along these deformation modes in all-atom simulations. Identifying those low-frequency collective modes that change the contact map the most proves to be an effective strategy for choosing which deformations to use for sampling. The method is tested on 20 refinement targets from the CASP12 competition and is found to induce large structural rearrangements that drive the structures closer to the experimentally determined structures during relatively short all-atom simulations of 50 ns. By examining the accuracy of side-chain rotamer states in subensembles of structures that have varying degrees of similarity to the experimental structure, we identified the reorientation of aromatic side chains as a step that remains slow even when encouraging global mechanical deformations in the all-atom simulations. Reducing the side-chain rotamer isomerization barriers in the all-atom force field is found to further speed up refinement.
Computational structural biology very much resembles metallurgy. At the heart of both fields is the ability of disordered many-body systems spontaneously to form ordered structures, driven by funneled free-energy landscapes. In structural biology this ability is called “folding,” while in metallurgy it is called “crystallization.” For practical artisans in both areas, however, understanding the thermodynamics is not enough and understanding the timescales of change is important. Metallurgists, and their ancestors, the blacksmiths, exploit the fact that, on the largest length scales, equilibrium is not quickly achieved in a many-body system. They use this nonequilibrium aspect to control the formation of superstructures essential for the strength and flexibility of finished products. In contrast, the smaller biological structures, proteins, at least in vivo, generally, have plenty of time to access their lowest free-energy ensembles. Nevertheless, while equilibrium nearly reigns in vivo, computational structural biologists are presently limited in the amount of computer time they can use to access the lowest free-energy configurations of proteins. This limits our ability to predict the 3D structures of proteins by simulation. A variety of strategies, however, are bearing fruit in the quest for predicting 3D structures from sequence. At the outset, these strategies do not try slavishly to simulate the actual molecular dynamics of proteins at an all-atom level of detail, but rather use several tricks: analogy to known protein structures (1–3), neural nets and other types of machine learning (4–9), evolutionary analysis (10, 11), and coarse-grained simulations using reduced descriptions of protein tertiary structure (12, 13) to produce initial predictions. These methods have grown in power over the last decades, as witnessed by the series of CASP experiments that aim to monitor the community’s progress in protein structure prediction (14). For protein assemblies of modest size, these efforts now make the determination of a moderate resolution predicted structure by computational means viable. After a moderate resolution structure becomes available, however, one could hope to achieve a structural resolution that is comparable to what can be achieved by X-ray diffraction-based structure determination. It is widely thought that such high resolution is a prerequisite to pursuing many practical problems, such as drug design. It is appealing, however, that moderate resolution predicted structures already are proving useful in understanding many questions about biological mechanisms and in designing new laboratory experiments (15, 16).
When trying to refine moderate resolution predictions to structural models comparable in resolution to those determined by experiment, the timescale problems familiar to metallurgists now arrive with a vengeance. While microsecond molecular dynamics runs are now possible for the smaller proteins, such simulations become ever more difficult for larger systems and become more expensive. The natural timescales for equilibration of biomolecular systems lengthen with increasing size—eventually even in vivo: At the cytoskeletal level structure is, in fact, determined by far from equilibrium processes (17, 18). How can this mismatch of timescales between the physical and the practical which grows as the systems grow in size be overcome to allow computational structural studies of larger systems? In this paper we propose to use ideas inspired by the wisdom and artistry of the blacksmiths. Blacksmiths do not limit the ways that they work metals to passively heating and cooling them. The largest-scale structures in metal working are determined not just by thermal equilibration (annealing) but also are made by mechanically deforming the metal and alternating such deformation with heating and cooling. In this same spirit, for proteins we must find the best ways to not only anneal them thermally in a passive fashion but also mechanically deform initially predicted structures to access the appropriate parts of phase space in all-atom simulation. We can then use importance sampling to explore the thermodynamics of subensembles to identify the native ensemble. To design schemes to force equilibration, it helps to know why certain biomolecular motions are slow. Some motions are slow simply because they involve moving many particles at once collectively. These large-scale soft motions are among the slowest to equilibrate. They correspond roughly to the low-frequency normal modes of the protein but of course protein dynamics are anharmonic. Such modes can be found to a good approximation from coarse-grained models (19, 20). These large-scale deformations are further slowed often by the necessity for part of the molecule to “crack,” i.e., locally unfold, to accommodate the large-scale mechanical change (21, 22). Furthermore, like solid on solid friction, fine asperities at the bottom of the energy landscape due to the necessity of appropriately rotating bulky buried side chains can lead to transitions that can be as slow as seconds in the laboratory (23, 24). These motions are slow partly because of the high density of the interiors of proteins but perhaps also because of coupling between side-chain motions that may lead to glassy behavior (25, 26).
These ideas about why the collective motions of proteins are so slow inspire the refinement tools we develop in this paper. The approach we explore has several steps: We first find candidate slow modes by principal component analysis of equilibrium simulations using a fairly accurate coarse-grained model. We then single out those modes that lead to the most cracking, i.e., those modes that change the contact map. Because stabilizing contacts must be broken, these cracking motions are likely to be the slowest and thus limit standard refinement. We then use the chosen modes to characterize the thermally accessible ensembles in an all-atom simulation by using importance sampling along them. We have found that, even when sampling explicitly the chosen large-scale collective motions, fine-grained equilibration still can be slow. Apparently this residual slowness is due to side-chain rotations. We find that these final “polishing steps” can be catalyzed by lowering side-chain dihedral rotation barriers, allowing further refinement.
In this paper, we explore these tools and show how they can be used to refine predicted structures found in CASP12, which have been discussed in other recent works on the refinement problem (27). We show that using very modest computational resources, significant improvements in structural accuracy can be achieved. We also show that not only the final single predictions are improved but also the structural ensembles obtained by molecular dynamics sampling starting from the refined predictions are very close to the ensembles that are obtained if one uses the experimental crystal structure as a starting point.
Results
Overview of the Principal Component-Guided Structure Refinement of CASP12 Targets.
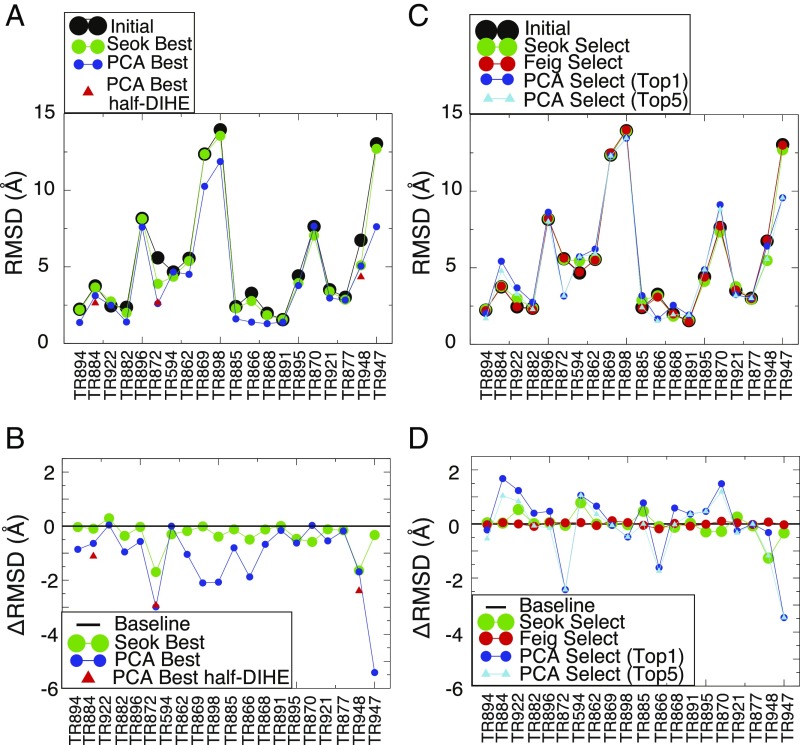
A total of 20 refinement targets were subjected to refinement guided by the principal components found in coarse-grained simulations using the associative memory, water-mediated, structure and energy model (AWSEM). All of the initial structural models were taken from those provided in the refinement category of the CASP12 competition (28). Figs. 1 and 2 and Table 1 provide a summary of the performance of the present refinement protocol, as well as the performance of the two best-performing teams of those that participated in CASP12 (29, 30). Principal component (PC)-guided refinement accelerates the sampling of conformational space (allowing great reduction in computational expense) and thus provides access to parts of conformational space that are significantly closer to the crystal structure than the initial models are. As a result, the structures sampled during PC-guided refinement that are most similar to the crystal structures (denoted “Best” in Table 1) are more similar to the crystal structures than are those that were found by the top-ranked team in the CASP12 competition for 17 of the 20 targets. An analysis of the first round of PC-guided refinement results suggested to us that side-chain rotamer isomerization is involved in the slow motions that are needed for more nearly sampling native structures. We therefore also tested the effects of halving the side-chain rotational barriers in the molecular mechanics force field (see Materials and Methods for details of the implementation) on the ability of the PC-guided scheme to refine structures. Using the reduced side-chain rotation barriers, two of the three targets tested (TR884 and TR948) reached structures with lower rmsds than the best structures that were reached using simulations having the full barrier heights within the same amount of simulation time (Fig. 2 and Table 1). The simulations of the third target that was tested with reduced barriers, TR872, did not reach a lower rmsd than did the full-barrier simulation within 50 ns. Nevertheless, the reduced barrier height simulations for TR872 did show a significant trend toward more native-like structures. When we extended the simulations of TR872 to 200 ns, the rmsd dropped and stayed around ∼2.0 Å after 100 ns, with the lowest rmsd sampled in the run being 1.901 Å (SI Appendix, Fig. S6B), which represents a 0.7-Å improvement over the best structure obtained during the 50-ns full-barrier simulation.
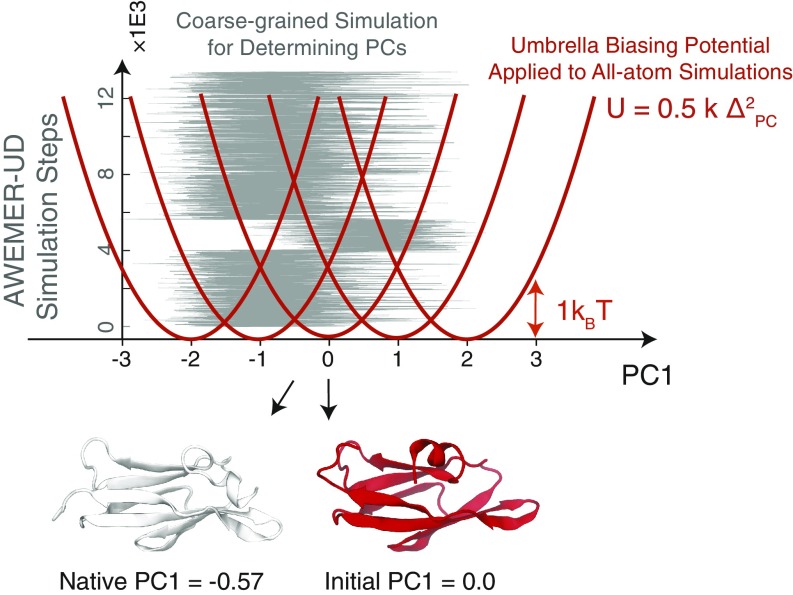
Fig. 1.
Summary of the PC-guided refinement protocol used in this study. The refinement protocol includes a coarse-grained modeling step for determining the mechanical deformations to be made in an all-atom refinement step where the molecule is distorted mechanically. The coarse-grained AWSEM with evolutionary restraints from ultradeep learning (AWSEMER-UD) potential (11) was simulated at a constant temperature of 300 K starting from the initial model structure taken from the CASP12 repository. The coarse-grained trajectory is then used to find the principal components of the backbone motions. A single principal component was then chosen from among those with the largest eigenvalues according to the effect of its motion on the change in the number of contacts (see Materials and Methods for details). These motions would require cracking. The variations of the selected principal component’s value during the constant temperature trajectory are shown in gray. In the five subsequent all-atom explicit-solvent refinement simulations, an umbrella potential was applied to sample along the selected principal component. The reference points of the harmonic biasing potentials were chosen to range from −2 to 2 in units of the SD of principal component values sampled during the coarse-grained AWSEMER-UD simulation. Bottom shows the native and the initial structures with their corresponding principal component values.
Fig. 2.
Summary of the refinement results. (A) The rmsd values of the initial structures (black), the refined structures with the lowest rmsd from the “Seok” group (“Seok Best,” green) (29), and the structures with the lowest rmsd using the AWSEM-PCA protocol (“PCA Best,” blue). Additionally, the lowest rmsd sampled in the simulations of three targets (TR884, TR872, and TR948) where the side-chain barriers were reduced by half [PCA Best half-DIHE (dihedral)] are marked in red triangles. (B) The difference in rmsd values (rmsd; note it is the opposite of the values of −rmsd shown in Table 1) between the initial structures and those in Seok Best (green), the PCA Best (blue), and the “PCA Best half-DIHE” (red). A black line is drawn at the value of as a guide for the eye. (C) The rmsd values of the initial structures (black), the blindly selected structures from the Seok group (green), the “Feig” group (red) (30), PC-guided refinement (“PCA Select (Top1),” blue), and the lowest rmsd structure of the top five selections (“PCA Select (Top5),” cyan). (D) The difference in rmsd values between the initial structures and those in the Seok (green), the Feig (red), the PCA Select (Top1) (blue), and the PCA Select (Top5) (cyan) groups. A black line is shown at rmsd = 0 as a guide for the eye.
Table 1.
A summary of the refinement results
| rmsd, Å | |||||||||||
| Target information | Feig | Seok | AWSEM-PCA | AWSEM-PCA, rmsd, Å | |||||||
| ID | Length | Initial rmsd, Å | Selected | Best | Selected | Best | Selected, top 1 | Selected, top 5 | PCA best | Selected, top 1 | Selected, top 5 |
| TR894 | 54 | 2.231 | 0.03 | 0.035 | -0.042 | 0.861 | 0.223 | 0.545 | 1.37 | 2.008 | 1.686 |
| TR884 | 71 | 3.749 | -0.05 | 0.095 | -0.031 | 0.639 | -1.679 | -1.043 | 3.11 (2.635) | 5.428 | 4.792 |
| TR922 | 74 | 2.45 | 0 | -0.29 | -0.535 | -0.04 | -1.237 | -0.836 | 2.49 | 3.687 | 3.286 |
| TR882 | 79 | 2.357 | 0.09 | 0.358 | -0.008 | 0.957 | -0.396 | 0.069 | 1.4 | 2.753 | 2.288 |
| TR896 | 86 | 8.161 | -0.06 | 0.028 | -0.043 | 0.571 | -0.469 | 0.15 | 7.59 | 8.63 | 8.011 |
| TR872 | 88 | 5.589 | -0.04 | 1.697 | 0.05 | 2.989 | 2.43 | 2.43 | 2.6 (2.659) | 3.159 | 3.159 |
| TR594 | 89 | 4.66 | -0.05 | 0.302 | -0.786 | 0 | -1.058 | -1.058 | 4.66 | 5.718 | 5.718 |
| TR862 | 101 (93) | 5.553 | 0.06 | 0.18 | 0.008 | 1.043 | -0.661 | -0.361 | 4.51 | 6.214 | 5.914 |
| TR869 | 104 | 12.362 | -0.12 | 0.011 | -0.024 | 2.102 | 0.053 | 0.053 | 10.26 | 12.309 | 12.309 |
| TR898 | 106 | 13.944 | -0.05 | 0.39 | 0.025 | 2.074 | 0.483 | 0.483 | 11.87 | 13.461 | 13.461 |
| TR885 | 114 | 2.404 | 0.05 | 0.118 | -0.47 | 0.804 | -0.78 | -0.002 | 1.6 | 3.184 | 2.406 |
| TR866 | 115 (104) | 3.268 | 0.18 | 0.497 | 0.101 | 1.878 | 1.617 | 1.745 | 1.39 | 1.651 | 1.523 |
| TR868 | 130 (106) | 1.964 | -0.02 | 0.123 | 0.123 | 0.674 | -0.59 | 0.022 | 1.29 | 2.554 | 1.942 |
| TR891 | 119 (112) | 1.549 | 0.08 | -0.006 | -0.024 | 0.159 | -0.363 | -0.363 | 1.39 | 1.912 | 1.912 |
| TR895 | 120 | 4.408 | 0.01 | 0.471 | 0.292 | 0.628 | -0.464 | -0.464 | 3.78 | 4.872 | 4.872 |
| TR870 | 123 (110) | 7.625 | -0.1 | 0.584 | 0.273 | -0.025 | -1.486 | -1.191 | 7.65 | 9.111 | 8.816 |
| TR921 | 138 | 3.505 | -0.04 | 0.116 | -0.253 | 0.545 | 0.256 | 0.333 | 2.96 | 3.249 | 3.172 |
| TR877 | 142 | 3.008 | 0.02 | 0.156 | 0.07 | 0.178 | 0.001 | 0.001 | 2.83 | 3.007 | 3.007 |
| TR948 | 161 | 6.737 | -0.07 | 1.642 | 1.263 | 1.687 | 0.316 | 1.173 | 5.05 (4.340) | 6.421 | 5.564 |
| TR947 | 175 | 13.035 | 0.03 | 0.329 | 0.329 | 5.415 | 3.466 | 3.466 | 7.62 | 9.569 | 9.569 |
The proteins are ordered by their sequence length. All of the reported rmsd values are calculated over the CA atoms only. “Initial rmsd” refers to the rmsd of the given initial structure downloaded from the CASP12 official website from the experimentally determined reference structure, which was also obtained from the CASP12 website. The “Feig” and “Seok” columns refer to the results published by the top two best-performing teams in the CASP12 competition (refs. 30 and 29, respectively). “AWSEM-PCA” refers to the performance of the PC-guided refinement protocol. “Best” refers to the structure with the lowest rmsd, and “selected” refers to the rmsd of the structures that were blindly selected. Additional “PCA Best” rmsds are provided in parentheses for three of the targets that were singled out for further detailed study: TR884, TR872, and TR948. The values in parentheses refer to the results of the simulations where the strengths of the side-chain dihedral barriers were halved. Since the lowest rmsd structures are not available in the publication from the team “Feig,” we do not report those values.
PC-Guided Refinement Drives the Structure Toward Its Native State.
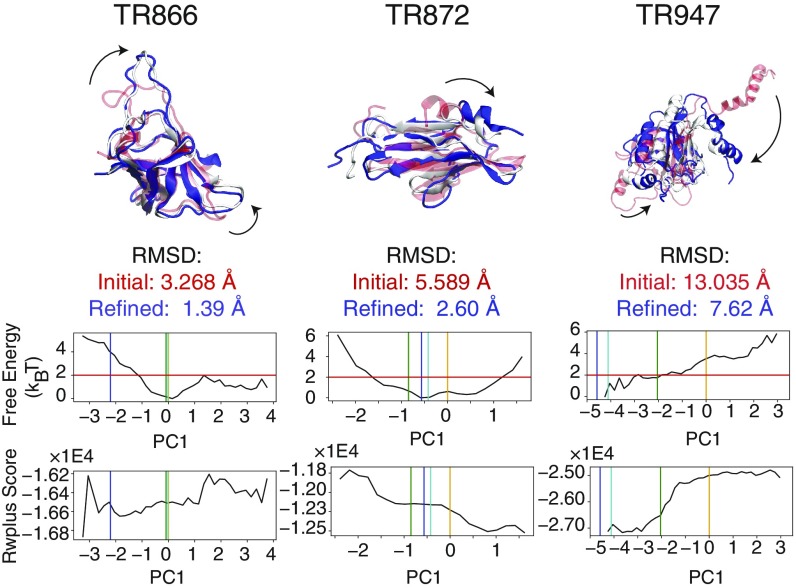
The most striking result from our refinement tests is that the mechanical deformations accessed in PC-guided refinement encourage significant changes of protein structure that do not typically occur in structurally restrained pure molecular dynamics refinement protocols at constant temperature. For almost all of the targets, PC-guided sampling drives some of the trajectories to structures that are closer to the native state than the initial models. Several particularly dramatic structural rearrangements that improve structural accuracy are illustrated in Fig. 3. Fig. 3 shows the structures before and after PC-guided refinement. TR866 underwent relatively large changes of loop structures on two sides of its structure during the refinement simulations. In the PC-guided refinement of TR872, an entire short helix at the N terminus flips into a more native-like conformation than was found in the initial structure. In the refinement of TR947, a multihelix domain that was protruding out into the solvent draws into contact with the rest of the folded domain as is seen in the crystal structure. Such dramatic structural changes over large length scales do not occur on similarly short timescales in conventional fixed restraint-based refinement simulations.
Fig. 3.
Three examples of the conformational changes upon refinement where PC-guided refinement improves the structure significantly: TR866, TR872, and TR947. (Top) In all of these cases, the initial structures (transparent red) have at least one domain that undergoes a significant structural transition (indicated by the arrows). These transitions are encouraged by the PC-guiding potentials. The resulting refined structures are shown in blue. The corresponding experimentally determined structures are shown in white. The structural representations of the complete list of proteins in this study are shown in Figure S7. (Bottom) The reweighted free-energy profiles as a function of the selected principal component are plotted for each set of refinement simulations. The vertical orange, green, cyan, and blue bars indicate the principal component values of the initial, top 1 selected, lowest rmsd, and experimentally determined structures, respectively. The horizontal red line indicates the relative free-energy threshold of from the most probable value of the principal component according to the reweighting of the refinement simulations. In the structure selection scheme, we first applied a “free-energy filter,” which selects structures with PC values in the regions below this threshold. The expectation value of the all-atom statistical potential RWplus (31) is plotted as a function of the principal component value (Bottom).
Summary of the Blindly Selected Models Using a Machine-Learning Scheme with Statistical Energies as Features.
The PC-guided structural refinement scheme samples structures over a wide range of principal component values, some of which are close to the value appropriate for the crystal structure but also other values that are far away and therefore lead structures away from the crystal structures. To limit the initial pool of structures that are to be considered during blind selection, we therefore applied a “free-energy filter.” Because the protocol uses importance sampling, a free-energy profile along the principal component as an approximate “reaction coordinate” can be found. The free-energy filter then selects those structures in regions of principal component space where the relative free energy of the subensemble corresponding to that principal component value is less than higher than the free energy corresponding with the most probable value of the principal component according to the reweighting of the refinement simulations (Fig. 3).
After applying the free-energy filter, the selection protocol continues by applying a machine-learning–based logistic regression scheme that selects five models from the refinement pool for each protein target. As shown in Fig. 2 and Table 1, in terms of the percentage of structures being improved, the top-scoring model obtained by this procedure (Top 1) is competitive with the two best-performing teams of CASP12. Our scheme picks “Top 1” selected structures that are improved in structural accuracy relative to the initial models for 9 of 20 targets, whereas 10 of 20 targets were found to be improved in the top selected structures reported by Seok and by Feig. The best structures found in the Top 5 structures selected from the PC-guided refinement are better than the initial structures for 12 of 20 targets. For those targets that were successfully refined to a lower rmsd than that of the initial model, the magnitude of the rmsd improvement found in the studies of Seok and Feig was typically Å. For the PC-guided refinement protocol, however, the improvements have a considerably larger magnitude on average than those found using the other methods, with the most dramatic improvement from the PC-guided refinement being Å (Fig. 2D). The selected Top 5 structures were further tested for their competence for solving the phasing problem using molecular replacement (MR) based on the existing X-ray diffraction data. The translation-function Z (TFZ) scores were improved by the PC-guided structure refinement scheme for all seven targets in our test (SI Appendix, Table S2). This demonstrates that the blindly selected models from the PC-guided refinement can assist in solving unphased X-ray crystal structures.
Probing the Free-Energy Surface Using Similarity to the Crystal and Initial Structures.
The belief that running all-atom simulations given sufficient time will lead to near-native structures relies implicitly on the notion that the energy landscapes generated by current all-atom force fields are in fact funneled toward the experimentally determined structures for the protein sequences that are being studied (32). Even if current atomistic landscapes, in fact, are sufficiently funneled, sampling challenges with the all-atom models owing to the slow modes of rearrangement complicate the determination of the true minimum free-energy basin for any given protein sequence. To see whether the fully atomistic landscape is indeed appropriately funneled to the X-ray structure, we attempted to determine the relative free energy of the ensemble of structures close to the initial model structures and the ensemble of structures close to the known crystal structures by calculating the relative free energies of different values of the selected principal component used in our refinement simulations. In most cases, the subensemble with the principal component that corresponds with the crystal structure was within 2 of the minimum of the free-energy profile (SI Appendix, Fig. S1), supporting the idea that the current atomistic force field is funneled toward native-like structures. Nevertheless, for several targets, the lowest rmsds that were sampled during the refinement simulations were still above typical crystallographic resolutions of Å; i.e., the immediate vicinity of the experimentally determined structures was not sampled. To sample nearer to the experimentally determined structure, one may need to sample along additional principal components as discussed below. Alternatively, some aspects of the current force field that do not comport with the crystal structure of the monomer may prevent the sampling of such near-native structures. Finally, crystal contacts or the presence of additional interaction partners in the crystal, which were not included in the refinement simulations, might lead to this discrepancy.
To further probe into the folding landscape in the vicinity of the experimentally determined structures, we performed additional umbrella-sampling simulations for one of the refinement targets, TR872. TR872 was chosen for further analysis for several reasons. The experimentally determined structure of TR872 was solved as a monomer, and thus we do not expect complications related to the influence of a missing oligomeric interface on refinement simulations using only the monomer. Although the initial model of TR872 that was provided for refinement during the CASP12 competition has a relatively high rmsd relative to the experimentally determined structure (5.589 Å), the PC-guided refinement was able to substantially refine this initial model into a structure that is, in the best case, just above crystallographic resolution (2.6 Å). Furthermore, this target was studied extensively by Heo and Feig (30) and was found by them to be difficult to refine with typical restraint-based all-atom refinement simulation. They also later showed that the force field did have a minimum free-energy ensemble of structures that is within experimental accuracy (2 Å) according to their extensive simulations, which used the same all-atom potential used in the present study (27).
The simulations designed to probe the free-energy landscape between the model and experimentally determined structures were initialized starting both from the structure that has the lowest rmsd to the native that was sampled during the refinement simulations (the “model” structure) and from the experimentally determined structure. Umbrella sampling was performed along Qdiff, an order parameter that interpolates between two structures (see Materials and Methods for details). The resulting free-energy profiles after reweighting suggest that there is a modest barrier separating the structural ensembles of the model and the experimentally determined structure (Fig. 4 A and B, Top). The structures in the free-energy basin located near the model structure (basin B) are generally more heterogeneous than those in the basin that is nearest to the X-ray structure (basin A), which can be seen in the larger variance in the structures (Fig. 4 A and B, Top) and the order parameters that were used to quantify structural similarity (Fig. 4 A and B, Middle and Bottom). We also observed barriers between the model and experimentally determined structures in the free-energy profiles for several other targets (SI Appendix, Fig. S4). Such a barrier would presumably slow down refinement attempts using only direct molecular dynamics at constant temperature. Below we discuss the apparent origin of this barrier and several ways of overcoming this barrier for the purposes of efficiently refining near-native structures.
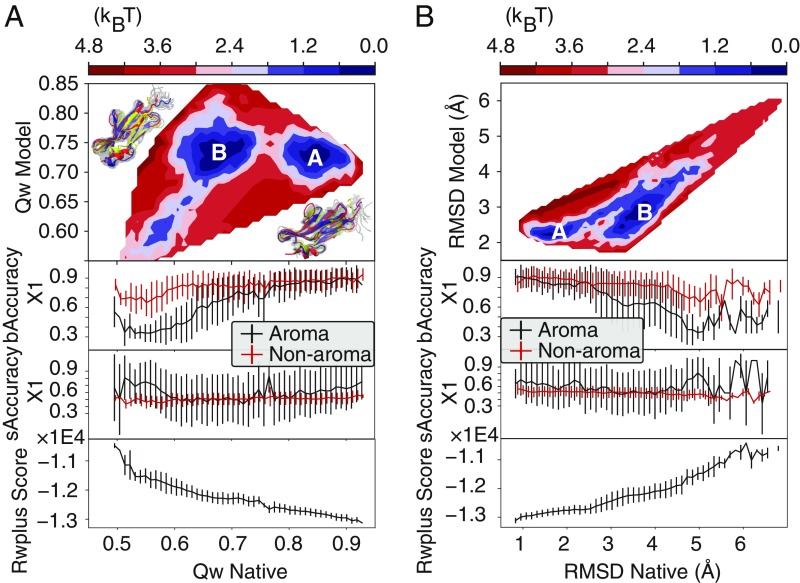
Fig. 4.
Free-energy surfaces constructed from the Qdiff umbrella sampling of TR872. The surfaces are shown with two types of reaction coordinates: rmsds (A) and values (B). Each surface is shown as a function of similarity to both the model structure and the native structure. (A and B, Top) There is an apparent barrier between the basins closest to the experimentally determined structure (basin A) and those closest to the model structure (basin B). (A and B, Middle) The average and the SD of the side-chain accuracy for the buried and surface-exposed residues calculated as a function of these same reaction coordinates. These are shown separately for aromatic residues and for nonaromatic residues. (A and B, Bottom) The expectation value and the SD of the all-atom statistical potential, RWplus, calculated as a function of these same reaction coordinates.
The Accuracy of the Side-Chain Rotamers.
Once the peptide backbone of a predicted structure is within a few angstroms of the experimentally determined structure’s backbone, any significant remaining differences between the predicted and experimental structures are likely to be due to differences in the side-chain orientations. Correct side-chain orientation may play a role in properly configuring binding sites for drugs and catalysis and thus is an interesting measure of the quality of a structure. Sampling of side-chain orientations is slow, particularly within the crowded protein interior. Here, we calculated the fraction of the side-chain rotamer angles that are found within 40○ of their corresponding values in the crystal structures (a value commonly taken for assigning discrete rotamer states). We separately monitor this fraction for the buried residues whose reorientation is strongly coupled to the protein globally and for the surface-exposed residues, which are relatively free to rotate in the solvent. Our calculations suggest that the buried aromatic residues typically are less properly placed than the buried nonaromatic residues as far as their angle is concerned, but the accuracy of the predicted angles is higher for buried aromatic residues than it is for the buried nonaromatic residues (SI Appendix, Fig. S2). The latter observation can be explained by the more restricted prior distribution of angles for aromatic residues than that for nonaromatic residues coming from stereochemistry (33). As a shorthand, we refer to the accuracy of groups of buried residues in a structure as “bAccuracy” and, likewise, refer to the accuracy of groups of surface-exposed residues as “sAccuracy.”
We examined the accuracy of the side-chain orientations in detail for a range of simulated structural ensembles of TR872. The ensembles were generated using biased sampling that was designed to probe the free-energy landscape between two reference structures. One reference structure was the experimentally determined structure. The other reference structure was the structure generated during the PC-guided refinement simulations of TR872 that had the lowest rmsd to the experimental structure. The resulting reweighted free-energy landscapes as a function of similarity to the reference structures can be seen in Fig. 4. When using either rmsds or the fractions of correct pairwise distances, , to the reference structures, two dominant free-energy basins can be seen on the landscape. We denote these basins as “basin A” and “basin B.” Basin A is the basin on the landscape that is nearest to the experimentally determined structure. Basin B is approximately equidistant from the experimentally determined structure and the refined structure.
In basin B, the bAccuracy of the predicted angles for the aromatic residues is found to be lower than what is found for the nonaromatic residues (Fig. 4 A and B, Middle). The average bAccuracy increases on average as the rmsd to the crystal structure decreases, indicating that backbone accuracy and side-chain accuracy are indeed coupled in near-native structural ensembles. The variance of the bAccuracy is smaller in the native basin (basin A) than in basin B: The side-chain conformations are significantly more restricted for backbone conformations near that of the experimentally determined structure. The accuracy of the exposed side chains is lower than that of the buried side chains and shows a higher degree of variation: The rotamer states of surface-exposed residues are less well defined than the rotamer states of buried residues. Taken together, these results indicate that one bottleneck for the refinement of structures when starting from near-native models is the correction of angles of aromatic residues. Since in the laboratory side-chain rotamer flips can take milliseconds or even longer (24), the inability to sufficiently sample the angles of aromatic residues by direct simulation on nanosecond timescales is obviously an issue that must be overcome if molecular dynamics-based structure refinement schemes are to be completely successful.
Reducing the Barrier of Side-Chain Dihedrals Further Improves the PC-Guided Structure Refinement Scheme.
It is possible to imagine multiple ways of accelerating the isomerization of protein side chains. Here, we chose to reduce the energetic barriers between the side-chain rotamers used in the force field for all types of residues by halving the force constant of the dihedral potential (34). There still will be a barrier to reorientation due to elastic deformation of the protein environment much as there is for diffusing interstitials in a metal (35). In the Qdiff sampling simulations of TR872 with reduced barriers, the apparent free-energy barriers separating the model and native basins (basins A and B in Fig. 5A) nevertheless were significantly reduced (Fig. 5B). This reduction of the apparent barrier heights was also seen when the side-chain isomerization barriers for only the aromatic residues were reduced: Aliphatic residues equilibrate well on the present simulation timescales. The slow aromatic side-chain isomerization seems thus to be the main obstacle to further refinement. Steric crowding in the protein interior is another important effect that slows side-chain rotations. Side-chain rotations could therefore be further accelerated by reducing the van der Waals radii of atoms in large side-chain residues. Of course, one must be careful that whatever means are used for accelerating motions do not also unfavorably perturb equilibrium structures.
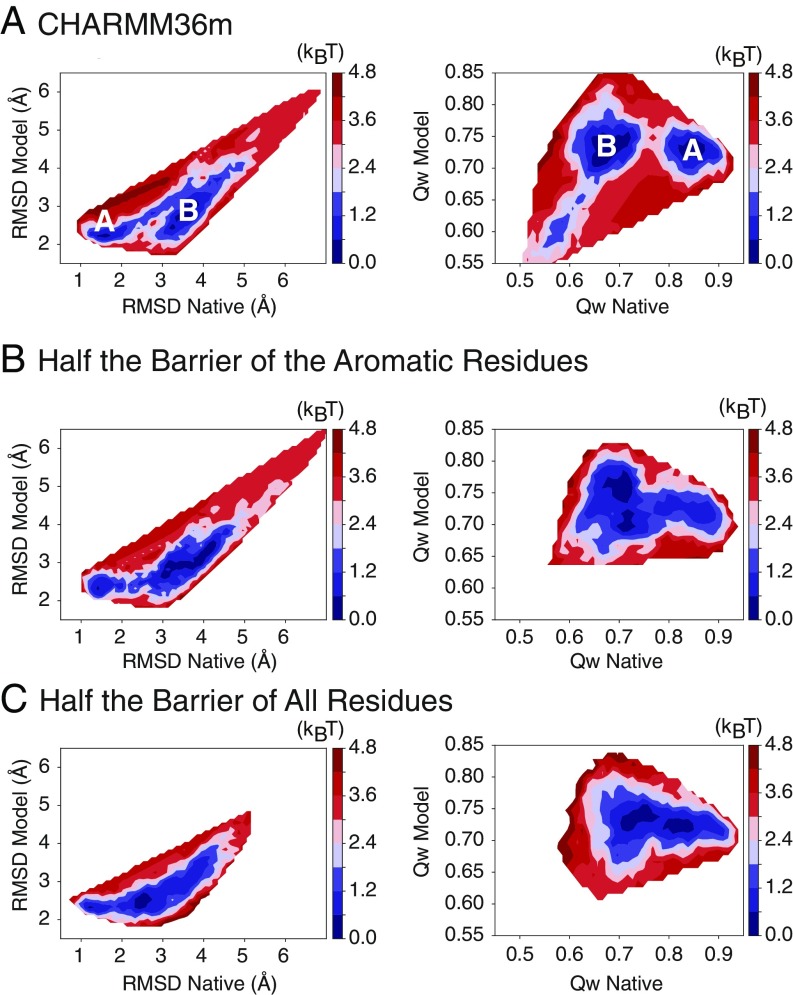
Fig. 5.
Reducing the side-chain dihedral barriers reduces the apparent free-energy barrier between the model structure and the experimental structure. (A–C) The free energy constructed from the Qdiff thermodynamic sampling of TR872 using (A) the CHARMM36m force field, (B) the CHARMM36m force field with the side-chain dihedral barriers of aromatic residues reduced by half, and (C) the CHARMM36m force field with the side-chain dihedral barriers of all residues reduced by half. The apparent free-energy profiles are shown as a function of two types of reaction coordinates, rmsd (A–C, Left) and (A–C, Right). The reduction of the side-chain barriers of aromatic residues reduces most of the apparent free-energy barrier toward the native state that was seen in the full-barrier simulations, while reducing the side-chain barriers of all residue types essentially eliminates the barrier.
We therefore then tested the effect of reducing the side-chain rotamer isomerization barriers on the performance of the PC-guided structure refinement scheme for TR872, carried out as before but with the lower barriers. Within the same amount of simulation time as used before (50 ns), the set of lower barrier refinement simulations generated structures with rmsds similar to those of the best simulations found using the standard force field. The lower barrier refinements also gave significantly improved values (SI Appendix, Fig. S6). We extended the refinement simulations using both the standard and reduced-barrier force fields from 50 ns to 200 ns. The longer 200-ns reduced barrier simulations show clearly better refinement than that provided by the long-timescale simulations with the original barriers. The PC-guided simulations using reduced side-chain isomerization barriers consistently reduce the rmsd of the sampled structures from the experimentally determined structure, finally reaching an rmsd as low as 1.901 Å. We tested the procedure using the reduced barrier force field on an additional two targets, TR884 and TR948. Both of these targets also show improved structural refinement using the reduced barriers (Fig. 2 and Table 1).
It is important to remember that proteins do not stay frozen in a single structure but sample an ensemble on the landscape (26). We therefore examined whether the enhanced sampling that comes from reducing side-chain isomerization barriers allows reconstruction of that ensemble by unrestrained sampling starting from either the model structures or the experimentally determined structures. To this end, we performed an additional set of four 100-ns unrestrained constant temperature (300 K) simulations for TR872 starting from the refined model structure and also from the crystal structure. We used both the half-barrier and full-barrier force fields. The Kolmogorov–Smirnov (KS) test allows one to quantify the similarity of different ensembles (36). The KS test based on the mutual- values of pairs of structures from the simulated ensembles was therefore used to examine the similarity of the different ensembles. The KS test indicates that the ensembles that were generated starting from the model and experimental structures are more similar to each other when one uses a force field with reduced side-chain isomerization barriers than they are when the ensembles are generated using a force field with the full isomerization barriers (SI Appendix, Fig. S5).
Discussion and Conclusion
Experimentally Determined Structures and Native Ensembles.
X-ray diffraction is widely considered to be the gold standard for protein structure determination. Now that simulations and other experimental structure determination techniques can produce structural models that are close to, or even within, the experimental accuracy of X-ray diffraction, it is reasonable to ask whether structures produced by these other methods may be, in some senses, better representations of the structures sampled by the molecule in solution than the X-ray structures are. There are at least two ways, a priori, in which structural ensembles produced by simulation may better represent the molecule than structures reported in X-ray diffraction studies: (i) The simulated ensemble may be a more accurate representation of the thermally sampled ensemble in solution and (ii) even the average structure of the simulated ensemble may be more accurate than the X-ray structure due to extraneous influences in the crystal, e.g., crystal contacts. If consensus between methods is used as a yardstick, crystal effects on the average structure seem to be rather mild. It was shown recently by Heo and Feig (27) that the molecular dynamics force field used in the present study produces minimum free-energy ensembles that are centered within 0.8–2.0 Å rmsd of the experimentally determined structures for all eight refinement targets that they tested. Their analysis, however, also shows that there is substantial structural diversity in the thermally accessible ensembles for these proteins, more diversity perhaps than some would imagine. Both of these results are consistent with our present findings. With some notable exceptions, X-ray diffraction-based protein structures are almost always deposited into structural databases as unique sets of 3D coordinates. Many experiments show that proteins in solution, however, sample numerous conformations (26). Even when determining the structures of proteins in crystals, X-ray diffraction patterns have been shown to be better explained by an ensemble of structures than by a single structure (37, 38).
Although protein backbones seem to be largely unperturbed by crystal effects, the same is not true in general for side-chain orientations. When X-ray diffraction is used to determine the structure of the same protein in different crystal environments, the side-chain orientations of the structures often disagree (39, 40), particularly when the crystals have different space groups. This discrepancy is most noticeable for side chains that are on the surface of the protein, but also exists for side chains that are buried in the protein interior (41). The level of agreement between the side-chain orientations in multiple X-ray structures of the same protein is only slightly higher than the level of agreement that we found between the side-chain orientations of the near-native simulated ensembles and the corresponding crystal structures. In our simulations, the “accuracy” of the surface-exposed side-chain rotamers was found to be as low as 50–60% on average for near-native (1–2 Å rmsd) structures as determined by comparison with a single X-ray structure, whereas the comparison of multiple X-ray structures suggests mutual agreement in the orientations of surface-exposed side chains at the level of 75%. The agreement between the X-ray structures and near-native simulated ensembles for buried side chains is higher, around 90%, still not perfect. When comparing multiple X-ray structures, buried side-chain orientations were found to agree about 95% of the time (41). Thus, the bottom of the folding funnel is better thought of as a caldera (42) with moderate roughness, instead of as a singular point.
We should also remember that the approach we take even under ideal circumstances would predict the structural ensemble of the monomeric protein in solution. Crystal structures apparently lie within or very close to these predicted solution ensembles in most cases, but the structures of monomers in crystals may be influenced by the presence of oligomeric partners. If the structure of one protein depends on its oligomeric partner, the protein complex needs to be simulated in its entirety upon refinement. If cofactors such as ligands, hemes, and ions are present, they also will need to be included in a structural refinement based on purely physical force fields. In our panel of analyses, proteins that contain explicitly bound ions or heme groups, such as TR922 (two calciums bound) and TR891 (heme bound), were not refined as well as those not containing such cofactors. SI Appendix, Table S1 contains a summary of the refinement results and notes for each refinement target indicating whether the target was solved in complex with another protein or in complex with a cofactor.
Search at the Bottom of the Funnel.
Early theoretical considerations of the protein-folding problem confronted the idea that a completely unguided search by a protein for its native state through its entire conformational space would take many times the age of the universe to complete. We now understand that a complete search through conformational space is unnecessary: A biased random search that is guided by the strong native interactions on a funneled energy landscape allows proteins to fold on biological timescales (43, 44). At first glance, it may therefore seem mysterious why it has been so hard to predict and refine protein structures using molecular simulation even when accurate energy functions are available. The resolution of this seeming paradox is that, at the bottom of the funnel, the roughness of the landscape is apparently large enough to give equilibration timescales that challenge current computational resources even though they are not large enough to create a problem for physiology.
We have seen that once a protein structure gets within a small enough rms distance from the experimentally determined structure in terms of the effective reaction coordinate, it will spontaneously continue to a state very close to the crystal structure. Our simulations bridging between the model structure and the experimentally determined structure of TR872 demonstrate this point (Fig. 4A). Once the structure gets to within 2.5 Å(or 0.8) of the experimental structure in terms of CA rmsd, both the statistical potential (RWplus score) and the side-chain accuracy (bAccuracy) acquire a nearly perfect correlation with the rmsd value, and there is almost no barrier between the native and other structures within this “radius.”
Free-energy landscape analysis seems to suggest there is a modest kinetic barrier separating the basin near the experimental structure from other near-native structures. Insufficient sampling during our Qdiff simulations may overestimate the height of such a barrier due to memory of the structures used to initialize the simulations, while the use of imperfect reaction coordinates to bias that sampling probably results in an underestimation of the barrier, so the barrier heights shown here should be considered somewhat uncertain. Importantly, however, we have identified that the corrections of side-chain dihedrals are the motions that contribute to this barrier. The reduction of side-chain dihedral barriers enhances sampling at the bottom of the funnel (Fig. 5 B and C). Indeed, the repetition of several PC-guided structure refinement runs with lower side-chain dihedral barriers reached more native-like protein structures than do the simulations with the full barriers that are ordinarily used.
Tools of the Protein Blacksmith.
There are many prerequisites for successful PC-guided refinements. First, a relatively accurate coarse-grained force field is useful to identify the relevant PC vectors for significantly changing the structures. Here, we have used AWSEMER-UD (11), a coarse-grained force field that has itself been demonstrated to be a successful tool for de novo prediction of protein structures. Given a set of PC vectors, relevant PCs can be identified by checking for cracking along the PC coordinates.
Although this study demonstrates the power of using a PC-guided refinement protocol picking only a single PC vector as the sampling coordinate, further refinements can come by drilling down along additional PC vectors. To demonstrate this possibility, we have geometrically perturbed the structure of TR872 by sequentially swapping the PC values of the initial model into those of the native structure. The resulting curve of rmsd vs. the number of swapped PC values (SI Appendix, Fig. S3) shows that the correction of the 15 PCs with the largest eigenvalues without any further probabilistic sampling results in a structure with a 1.5-Å rmsd from the experimental structure. Further investigations are needed into finding the best way of reordering the PC vectors so that sampling along a minimum number of them would lead to maximum refinement of coarse-grained predicted structures.
In this paper, we illustrated how a PC-guided approach can refine predicted structures of proteins toward their crystal structures. The current method could also be used to refine moderate resolution structures obtained from, e.g., cryo-EM techniques or to sample conformations of proteins undergoing large conformational transitions. The protocol resembles the way blacksmiths forge swords. It proves to be computationally very efficient. In actual blacksmithing, repeated heating and cooling of the sample is an important aspect. A natural extension of the current protocol would be to combine PC-guided mechanical deformations with continuous simulated tempering, which performs a guided random walk in temperature space (45, 46). One might also consider performing Hamiltonian replica exchange simulations with replicas that have different strengths of the side-chain rotamer isomerization barriers to harness the speedup allowed by lowering the barriers without sacrificing the structural specificity attained when using the full barrier heights. By harnessing the power of these orthogonal techniques in refinement, we can soon expect more accurate structures to become routinely available from computational predictions, with fidelity rivaling X-ray diffraction determinations.
Materials and Methods
Principal Component Analysis of AWSEMER-UD Simulations.
Principal component analysis (PCA) is a procedure for finding a set of mutually orthogonal vectors to describe a multidimensional dataset. The coefficients of the first vector are determined such that the variance of the multidimensional input data in that direction is maximum. The second vector is orthogonal to the first one and points in the direction that maximizes the remaining variance of the input data, etc. In the context of protein dynamics, PCA has been used to describe the essential dynamics of a protein based on the correlated fluctuations of atomistic positions (47, 48). To obtain a well-sampled ensemble for PCA analysis, we made use of a coarse-grained force field, AWSEMER-UD (49). AWSEMER-UD was initially described in ref. 11. Here, we adopted a variant of AWSEMER-UD and initialized the simulations from the structures that were provided to participants in the CASP12 structure refinement competition (28). The full Hamiltonian used during the coarse-grained simulations is given in Eq. 1:
| [1] |
The first five terms in Eq. 1 are taken from the standard AWSEM potential described in ref. 12. (Eq. 2) is a harmonic potential based on the pairwise contacts inferred from RaptorX, a deep-learning–based contact inference method (4, 50, 51):
| [2] |
In Eq. 2, the spring constant and is given in Eq. 3:
| [3] |
The sum in Eq. 3 runs over all of the contacts predicted by RaptorX that have a predicted probability larger than 0.5. in Eq. 3 is a prefactor that is proportional to the probability of contact formation as determined by RaptorX (50). is an estimated residue pair-type–dependent distance that was obtained by surveying a database of protein structures (11). Åis a sequence separation-dependent well width.
PC-Guided All-Atom Simulations.
The simulated trajectory from AWSEMER-UD was used for the PCA analysis on the positions of the CA atoms. The calculated PC vectors are ordered by their eigenvalues. The eigenvalue indicates the magnitude of fluctuation of the corresponding PC motion. Since a loop in the terminal end of a protein can exhibit large fluctuations, this type of motion can sometimes show up in the PCs with the largest eigenvalues. Since these kinds of motions are generally irrelevant for structural refinement, we use a “contact filter” to filter out these kinds of motions. The contact filter calculates the SD of contacts for the 10 PCs with the largest eigenvalues. A contact is defined as being formed if the corresponding CA atoms are within 9.5 Å from each other. The contact filter can thus pick out the PCs that change the structure to the greatest extent. We selected the PC with the largest SD of the number of contacts to guide the sampling of the subsequent all-atom simulations.
A set of all-atom explicit solvent PC-guided refinement simulations was then performed. To guide the all-atom simulations along the selected PC vector, we applied an umbrella-sampling potential along the selected PC vector. A total of five windows were used in the umbrella sampling, with reference points at −2.0, −1.0, 0, 1.0, and 2.0 times the SD of the PC values from the AWSEMER-UD simulation that was used to obtain the PCs. This choice of umbrella sampling ensures a wide coverage of the PC space. There were only three cases where the PC value of the experimentally determined structure was beyond the range of this choice (SI Appendix, Fig. S1). In all three of these cases, the starting structure was more than Å away from the experimentally determined structure.
The all-atom simulations were performed using the CHARMM36m (Chemistry at Harvard Macromolecular Mechanics 36m) force field and a time step of 2.0 fs. The total charge of the system was neutralized by adding Na and Cl ions and the final ionic concentration was 0.15 M. The simulations were performed in the constant particle number, volume, and temperature ensemble. The umbrella potentials were gradually increased in strength over time by linearly increasing from 0.0 to a large spring constant of within the first 1 ns and held constant at this large value for 2 ns. The strength was then linearly decreased in time to over 1 ns and held at this value for the rest of the simulation. This procedure ensures a quick structural change of the protein at the start of the simulation. The simulations ran for a total of 50 ns. The simulations were performed using GROMACS 5.1.4 (52) patched with PLUMED-2.3.4 (53, 54). The free energy profiles were reconstructed using the weighted histogram analysis method (WHAM) (55).
Enhancing the Sampling of Side-Chain Rotamers by Reducing the Side-Chain Rotamer Isomerization Barrier.
Side-chain isomerization is slow in the interiors of proteins (24). The explicit barrier to isomerization can be reduced by reducing the force constant of the side-chain dihedral potentials in the molecular force field (34). It is worth noting that the effective barrier to side-chain isomerization is a combination of the explicit barrier in the molecular mechanics force field and an environment-dependent factor arising from steric clashes during rotation attempts (24). Here, we reduced the force constant of dihedral potentials by half compared with the standard values used in the CHARMM36m force field. Two versions of such reduction were tested: (i) reduction only for the aromatic residues (His, Phe, Tyr, and Trp) and (ii) reduction for all types of residues. We found that reducing the barriers of aromatic residues significantly reduces the barrier between the model and experimentally determined structures and that reducing the barriers for all residue types further reduces this barrier (Fig. 5). We tested the effect of reducing the side-chain isomerization barrier by half for all residue types on blind structure refinement by performing PC-guided refinement simulations for three targets: TR884, TR872, and TR948.
Choice of Refinement Targets and Initial Structures.
The refinement targets were all taken from the CASP12 refinement competition. The initial structures were downloaded from the official CASP12 website. The refined structures were compared with either the experimentally determined structures provided on the same website or, if the structure was not available there, to the corresponding experimentally determined structures that were deposited in the Protein Data Bank (PDB) database (56).
Blind Selection of Refined Protein Structures Using a Machine-Learning Scheme.
To select candidate structures from our refinement sampling without using knowledge of the experimentally determined structure, we used a machine-learning–based algorithm based on logistic regression. Details of this method have been given previously (3). Briefly, we used three features capturing the quality of structures for our training and predictions: The “RWplus” energies (31), the total AWSEM energies evaluated based on the backbone structures of proteins with AWSEM Hamiltonian (12), and the term (4) (Eq. 2). A logistic regression algorithm was trained by classifying the top 1% of the structures (those with the lowest CA rmsd to the experimentally determined structure) that were sampled during a set of refinement simulations of one protein (here we used TR866). The cost function to be minimized during the training is given in Eq. 4:
| [4] |
In Eq. 4, is the number of training examples, is the weight vector, and . is the training data, which in this case are the top 1% of structures sampled during the refinement simulations of TR866 as described above. During the training, the weights of these three features were optimized such that the cost function is minimized.
Sampling the Free-Energy Landscapes Between Model Structures and Experimental Structures.
To characterize the free-energy landscape at the bottom of the folding funnel, we performed a set of umbrella-sampling simulations based on the reaction coordinate Qdiff, which interpolates between two given reference structures (57):
| [5] |
The in Eq. 5 is given in Eq. 6:
| [6] |
In Eq. 6, Å and , . The superscripts N1 and N2 indicate the distances as measured in the first and second reference structures, respectively. We selected the structure with the lowest CA rmsd that was sampled during the PC-guided refinement simulations (with full barrier heights) as the first reference structure and the corresponding experimentally determined structure as the other reference structure.
Structure Similarity Evaluation Metrics.
We used two metrics to measure the similarity of the refined structures to the experimentally determined structures. The CA rmsd measures the root-mean-square deviation of the CA atoms of the structure from the corresponding positions of the atoms in the experimentally determined structure after alignment. is computed as shown in Eq. 7:
| [7] |
In Eq. 7, and are the distances between the CA atoms of two residues in the model and experimentally determined structures and N is the total number of residues in the target protein. Å is a sequence separation-dependent well width.
Side-Chain Rotamer Evaluations.
To evaluate the accuracy of side-chain rotamers, we calculated the side-chain accuracy of the buried and surface-exposed residues from our simulations (bAccuracy and sAccuracy) (3). The buried residues are defined as those that have 20% or smaller normalized solvent-exposed areas, while the exposed residues are defined as those that have 50% or larger normalized solvent-exposed areas (58). The side-chain accuracy was measured as the proportion of buried residues that have their side-chain angles falling within 40° of those in the corresponding experimentally determined structures. Both and side-chain angles were analyzed in this study.
Test for Molecular Replacement.
Following commonly used protocols, to maximize the performance of molecular replacement, the flexible parts of the input models (the initial model before refinement and the Top 5 blindly selected models) were deleted according to the predicted secondary structures using RaptorX Property (59), a protein secondary structure prediction algorithm developed using deep learning. All segments predicted to be coils were deleted. These trimmed models were input into the Phaser under Phenix (60) for the calculation of TFZ score. The B factors of all of the models were uniformly set to 0, and the estimated rmsd was set to 2.0 Å. The space groups of the molecules in the crystal were loaded according to the data provided in the PDB website. All other parameters remain at their default values. The number of copies of search was based on the subunit stoichiometry of the crystal structures. Of the 20 proteins used in the PC-guided structure refinement scheme, only 7 proteins were tested for molecular replacement because they had X-ray diffraction data deposited in the database and have relatively simple subunit stoichiometry (monomer or dimer).
Code and Data Availability.
The AWSEM code is available online at https://github.com/adavtyan/awsemmd. The code for performing PC-based biasing in GROMACS is available online at https://github.com/XingchengLin/PC-guided_protein_structure_refinement.git.
Supplementary Material
Acknowledgments
We thank Hans Frauenfelder, whose heroic investigations established the importance and complexity of the energy landscape of folded proteins, ideas that undergird this work. The authors thank George Phillips and Mitch Miller for helpful discussions on molecular replacement and phasing of X-ray diffraction data. This work is supported by the National Science Foundation (NSF)–Center for Theoretical Biological Physics Grants NSF PHY-1427654 and NSF CHE-1614101, and by Grant R01 GM44557 from the National Institute of General Medical Sciences. Additional support was provided by the D. R. Bullard-Welch Chair at Rice University (Grant C-0016 to P.G.W.).
Footnotes
The authors declare no conflict of interest.
Data deposition: The AWSEM code is available online at https://github.com/adavtyan/awsemmd. The code for performing PC-based biasing in GROMACS is available online at https://github.com/XingchengLin/PC-guided_protein_structure_refinement.git.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1900778116/-/DCSupplemental.
References
- 1.Rohl CA, Strauss CE, Misura KM, Baker D. Protein structure prediction using Rosetta. Methods Enzymol. 2004;383:66–93. doi: 10.1016/S0076-6879(04)83004-0. [DOI] [PubMed] [Google Scholar]
- 2.Yang J, et al. The I-TASSER suite: Protein structure and function prediction. Nat Methods. 2015;12:7–8. doi: 10.1038/nmeth.3213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Chen M, et al. Template-guided protein structure prediction and refinement using optimized folding landscape force fields. J Chem Theory Comput. 2018;14:6102–6116. doi: 10.1021/acs.jctc.8b00683. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Källberg M, et al. Template-based protein structure modeling using the RaptorX web server. Nat Protoc. 2012;7:1511–1522. doi: 10.1038/nprot.2012.085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Bohr HG, Wolynes PG. Initial events of protein folding from an information-processing viewpoint. Phys Rev A. 1992;46:5242–5248. doi: 10.1103/physreva.46.5242. [DOI] [PubMed] [Google Scholar]
- 6.Schafer NP, Kim BL, Zheng W, Wolynes PG. Learning to fold proteins using energy landscape theory. Isr J Chem. 2014;54:1311–1337. doi: 10.1002/ijch.201300145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Friedrichs MS, Wolynes PG. Toward protein tertiary structure recognition by means of associative memory Hamiltonians. Science. 1989;246:371–373. doi: 10.1126/science.246.4928.371. [DOI] [PubMed] [Google Scholar]
- 8.Bohr H, et al. A novel approach to prediction of the 3-dimensional structures of protein backbones by neural networks. FEBS Lett. 1990;261:43–46. doi: 10.1016/0014-5793(90)80632-s. [DOI] [PubMed] [Google Scholar]
- 9.Wolynes PG, Papoian GA. AWSEM-MD: From neural networks to protein structure prediction and functional dynamics of complex biomolecular assemblies. In: Papoian GA, editor. Coarse-Grained Modeling of Biomolecules. CRC Press; Boca Raton, FL: 2017. pp. 121–190. [Google Scholar]
- 10.Morcos F, et al. Direct-coupling analysis of residue coevolution captures native contacts across many protein families. Proc Natl Acad Sci USA. 2011;108:E1293–E1301. doi: 10.1073/pnas.1111471108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Sirovetz BJ, Schafer NP, Wolynes PG. Protein structure prediction: Making AWSEM AWSEM-ER by adding evolutionary restraints. Proteins. 2017;85:2127–2142. doi: 10.1002/prot.25367. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Davtyan A, et al. AWSEM-MD: Protein structure prediction using coarse-grained physical potentials and bioinformatically based local structure biasing. J Phys Chem B. 2012;116:8494–8503. doi: 10.1021/jp212541y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Ołdziej S, et al. Physics-based protein-structure prediction using a hierarchical protocol based on the UNRES force field: Assessment in two blind tests. Proc Natl Acad Sci USA. 2005;102:7547–7552. doi: 10.1073/pnas.0502655102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Moult J, Fidelis K, Kryshtafovych A, Schwede T, Tramontano A. Critical assessment of methods of protein structure prediction (CASP)—Round XII. Proteins. 2018;86:7–15. doi: 10.1002/prot.25415. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Potoyan DA, Zheng W, Komives EA, Wolynes PG. Molecular stripping in the NF-B/IB/DNA genetic regulatory network. Proc Natl Acad Sci USA. 2016;113:110–115. doi: 10.1073/pnas.1520483112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Potoyan DA, Bueno C, Zheng W, Komives EA, Wolynes PG. Resolving the NFB heterodimer binding paradox: Strain and frustration guide the binding of dimeric transcription factors. J Am Chem Soc. 2017;139:18558–18566. doi: 10.1021/jacs.7b08741. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Pollard TD, Borisy GG. Cellular motility driven by assembly and disassembly of actin filaments. Cell. 2003;112:453–465. doi: 10.1016/s0092-8674(03)00120-x. [DOI] [PubMed] [Google Scholar]
- 18.Stricker J, Falzone T, Gardel ML. Mechanics of the F-actin cytoskeleton. J Biomech. 2010;43:9–14. doi: 10.1016/j.jbiomech.2009.09.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Bahar I, Atilgan AR, Erman B. Direct evaluation of thermal fluctuations in proteins using a single-parameter harmonic potential. Fold Des. 1997;2:173–181. doi: 10.1016/S1359-0278(97)00024-2. [DOI] [PubMed] [Google Scholar]
- 20.Atilgan AR, et al. Anisotropy of fluctuation dynamics of proteins with an elastic network model. Biophys J. 2001;80:505–515. doi: 10.1016/S0006-3495(01)76033-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Miyashita O, Onuchic JN, Wolynes PG. Nonlinear elasticity, protein quakes, and the energy landscapes of functional transitions in proteins. Proc Natl Acad Sci USA. 2003;100:12570–12575. doi: 10.1073/pnas.2135471100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Whitford PC, Onuchic JN, Wolynes PG. Energy landscape along an enzymatic reaction trajectory: Hinges or cracks? HFSP J. 2008;2:61–64. doi: 10.2976/1.2894846. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Wagner G, DeMarco A, Wüthrich K. Dynamics of the aromatic amino acid residues in the globular conformation of the basic pancreatic trypsin inhibitor (BPTI) Biophys Struct Mech. 1976;2:139–158. doi: 10.1007/BF00863706. [DOI] [PubMed] [Google Scholar]
- 24.McCammon JA, Lee CY, Northrup SH. Side-chain rotational isomerization in proteins: A mechanism involving gating and transient packing defects. J Am Chem Soc. 1983;105:2232–2237. [Google Scholar]
- 25.Stein D. A model of protein conformational substates. Proc Natl Acad Sci USA. 1985;82:3670–3672. doi: 10.1073/pnas.82.11.3670. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Frauenfelder H, Sligar SG, Wolynes PG. The energy landscapes and motions of proteins. Science. 1991;254:1598–1603. doi: 10.1126/science.1749933. [DOI] [PubMed] [Google Scholar]
- 27.Heo L, Feig M. Experimental accuracy in protein structure refinement via molecular dynamics simulations. Proc Natl Acad Sci USA. 2018;115:13276–13281. doi: 10.1073/pnas.1811364115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Hovan L, et al. Assessment of the model refinement category in CASP12. Proteins. 2018;86:152–167. doi: 10.1002/prot.25409. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Lee GR, Heo L, Seok C. Simultaneous refinement of inaccurate local regions and overall structure in the CASP12 protein model refinement experiment. Proteins. 2018;86:168–176. doi: 10.1002/prot.25404. [DOI] [PubMed] [Google Scholar]
- 30.Heo L, Feig M. What makes it difficult to refine protein models further via molecular dynamics simulations? Proteins. 2018;86:177–188. doi: 10.1002/prot.25393. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Zhang J, Zhang Y. A novel side-chain orientation dependent potential derived from random-walk reference state for protein fold selection and structure prediction. PLoS One. 2010;5:e15386. doi: 10.1371/journal.pone.0015386. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Best RB, Hummer G, Eaton WA. Native contacts determine protein folding mechanisms in atomistic simulations. Proc Natl Acad Sci USA. 2013;110:17874–17879. doi: 10.1073/pnas.1311599110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Shapovalov MV, Dunbrack RL. A smoothed backbone-dependent rotamer library for proteins derived from adaptive kernel density estimates and regressions. Structure. 2011;19:844–858. doi: 10.1016/j.str.2011.03.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Endres RG. Accelerating all-atom protein folding simulations through reduced dihedral barriers. Mol Simul. 2005;31:773–777. [Google Scholar]
- 35.Wert C, Zener C. Interstitial atomic diffusion coefficients. Phys Rev. 1949;76:1169–1175. [Google Scholar]
- 36.Lätzer J, Eastwood MP, Wolynes PG. Simulation studies of the fidelity of biomolecular structure ensemble recreation. J Chem Phys. 2006;125:214905. doi: 10.1063/1.2375121. [DOI] [PubMed] [Google Scholar]
- 37.Kuriyan J, et al. Exploration of disorder in protein structures by X-ray restrained molecular dynamics. Proteins. 1991;10:340–358. doi: 10.1002/prot.340100407. [DOI] [PubMed] [Google Scholar]
- 38.Levin EJ, Kondrashov DA, Wesenberg GE, Phillips GN. Ensemble refinement of protein crystal structures: Validation and application. Structure. 2007;15:1040–1052. doi: 10.1016/j.str.2007.06.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.DePristo MA, de Bakker PI, Blundell TL. Heterogeneity and inaccuracy in protein structures solved by X-ray crystallography. Structure. 2004;12:831–838. doi: 10.1016/j.str.2004.02.031. [DOI] [PubMed] [Google Scholar]
- 40.Best RB, Lindorff-Larsen K, DePristo MA, Vendruscolo M. Relation between native ensembles and experimental structures of proteins. Proc Natl Acad Sci USA. 2006;103:10901–10906. doi: 10.1073/pnas.0511156103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Jacobson MP, Friesner RA, Xiang Z, Honig B. On the role of the crystal environment in determining protein side-chain conformations. J Mol Biol. 2002;320:597–608. doi: 10.1016/s0022-2836(02)00470-9. [DOI] [PubMed] [Google Scholar]
- 42.Eastwood MP, Hardin C, Luthey-Schulten Z, Wolynes PG. Evaluating protein structure-prediction schemes using energy landscape theory. IBM J Res Dev. 2001;45:475–497. [Google Scholar]
- 43.Bryngelson JD, Wolynes PG. Spin glasses and the statistical mechanics of protein folding. Proc Natl Acad Sci USA. 1987;84:7524–7528. doi: 10.1073/pnas.84.21.7524. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Leopold PE, Montal M, Onuchic JN. Protein folding funnels: A kinetic approach to the sequence-structure relationship. Proc Natl Acad Sci USA. 1992;89:8721–8725. doi: 10.1073/pnas.89.18.8721. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Zang T, Ma T, Wang Q, Ma J. Improving low-accuracy protein structures using enhanced sampling techniques. J Chem Phys. 2018;149:072319. doi: 10.1063/1.5027243. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Ma T, Zang T, Wang Q, Ma J. Refining protein structures using enhanced sampling techniques with restraints derived from an ensemble-based model: Refining protein structures. Protein Sci. 2018;27:1842–1849. doi: 10.1002/pro.3486. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.García AE. Large-amplitude nonlinear motions in proteins. Phys Rev Lett. 1992;68:2696–2699. doi: 10.1103/PhysRevLett.68.2696. [DOI] [PubMed] [Google Scholar]
- 48.Amadei A, Linssen AB, Berendsen HJ. Essential dynamics of proteins. Proteins. 1993;17:412–425. doi: 10.1002/prot.340170408. [DOI] [PubMed] [Google Scholar]
- 49.Davtyan A. AWSEM-MD. 2011 Available at https://github.com/adavtyan/awsemmd. Deposited February 22, 2011.
- 50.Peng J, Xu J. RaptorX: Exploiting structure information for protein alignment by statistical inference. Proteins. 2011;79:161–171. doi: 10.1002/prot.23175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Wang S, Sun S, Li Z, Zhang R, Xu J. Accurate de novo prediction of protein contact map by ultra-deep learning model. PLoS Comput Biol. 2017;13:e1005324. doi: 10.1371/journal.pcbi.1005324. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Abraham MJ, et al. GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX. 2015;1-2:19–25. [Google Scholar]
- 53.Tribello GA, Bonomi M, Branduardi D, Camilloni C, Bussi G. PLUMED 2: New feathers for an old bird. Comput Phys Commun. 2014;185:604–613. [Google Scholar]
- 54.Lin X. PC-guided protein structure refinement. 2019 Available at https://github.com/XingchengLin/PC-guided_protein_structure_refinement.git. Deposited April 2, 2019.
- 55.Kumar S, Rosenberg JM, Bouzida D, Swendsen RH, Kollman PA. The weighted histogram analysis method for free-energy calculations on biomolecules. I. The method. J Comput Chem. 1992;13:1011–1021. [Google Scholar]
- 56.Berman HM, et al. The protein data bank. Nucleic Acids Res. 2000;28:235–242. doi: 10.1093/nar/28.1.235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Chen M, Schafer NP, Zheng W, Wolynes PG. The associative memory, water mediated, structure and energy model (AWSEM)-Amylometer: Predicting amyloid propensity and fibril topology using an optimized folding landscape model. ACS Chem Neurosci. 2018;9:1027–1039. doi: 10.1021/acschemneuro.7b00436. [DOI] [PubMed] [Google Scholar]
- 58.Fraczkiewicz R, Braun W. Exact and efficient analytical calculation of the accessible surface areas and their gradients for macromolecules. J Comput Chem. 1998;19:319–333. [Google Scholar]
- 59.Wang S, Li W, Liu S, Xu J. RaptorX-property: A web server for protein structure property prediction. Nucleic Acids Res. 2016;44:W430–W435. doi: 10.1093/nar/gkw306. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.McCoy AJ, et al. Phaser crystallographic software. J Appl Crystallogr. 2007;40:658–674. doi: 10.1107/S0021889807021206. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.