Helical nanofiber yarn enabling highly stretchable engineered microtissue

Significance

The challenge in manufacturing stretchable and tough reconstituted tissues lies in the limitation of current approaches to recapitulate the exceptional mechanical properties of native tissues while maintaining cellular functions. Here, we simulate native mechanical complexity by integrating electrospinning and tissue engineering to develop a highly stretchable living tissue consisting of bioinspired hierarchical helical scaffold and seeded cells. The well-organized tissue construct has a toughness of 57 GJ m⁻³ and can be stretched up to 15 times its length while sheltering cells from severe cyclic strains (600%), owing to nonaffine fiber deformation. With the additional ability to promote myogenesis, this hierarchical microtissue designed by leveraging mechanical concepts may be used for applications in tissue engineering, regenerative medicine, and artificial living systems.

Abstract

Development of microtissues that possess mechanical properties mimicking those of native stretchable tissues, such as muscle and tendon, is in high demand for tissue engineering and regenerative medicine. However, regardless of the significant advances in synthetic biomaterials, it remains challenging to fabricate living microtissue with high stretchability because application of large strains to microtissues can damage the cells by rupturing their structures. Inspired by the hierarchical helical structure of native fibrous tissues and its behavior of nonaffine deformation, we develop a highly stretchable and tough microtissue fiber made up of a hierarchical helix yarn scaffold, scaling from nanometers to millimeters, that can overcome this limitation. This microtissue can be stretched up to 15 times its initial length and has a toughness of 57 GJ m⁻³. More importantly, cells grown on this scaffold maintain high viability, even under severe cyclic strains (up to 600%) that can be attributed to the nonaffine deformation under large strains, mimicking native biopolymer scaffolds. Furthermore, as proof of principle, we demonstrate that the nanotopography of the helical nanofiber yarn is able to induce cytoskeletal alignment and nuclear elongation, which promote myogenic differentiation of mesenchymal stem cells by triggering nuclear translocation of transcriptional coactivator with PDZ-binding motif (TAZ). The highly stretchable microtissues we develop here will facilitate a variety of tissue engineering applications and the development of engineered living systems.

Many native tissues such as skin, muscle, and tendon exhibit exceptional mechanical performance, including high stretchability and toughness, to withstand substantial internal and external mechanical loads (1, 2). Fabrication of tissue constructs with comparable mechanical properties to native tissues is desired for applications in translational medicine and tissue engineering (3). Toward this end, a variety of synthetic biomaterials have been developed to achieve high stretchability and toughness. For example, double-network elastomers with both ionic and covalent bonds can be stretched beyond 20 times their initial length (4). Nanocomposite hydrogels can also be highly stretchable and have a fracture energy of ∼10.1 MJ m⁻² (5, 6). The merits of highly stretchable elastomers have aided a myriad of modern technologies, including biomedical devices (7), flexible electronics (8), and soft robotics (9). However, the scope of their application to tissue engineering and regenerative medicine remains limited (3, 10, 11). The challenge is often that the seeded cells are exposed to substantial mechanical loads synchronized with the material, which causes undesirable effects in the cells as a result of them undergoing large deformations, even though the supporting scaffold is capable of withstanding them (11). Indeed, previous studies have shown that the embedded cells in such tough double-network hydrogels undergo elongation when stretched (11), and the corresponding severe stresses experienced by the embedded cells can induce significant consequences such as nuclear envelope rupture (12), DNA damage (13), and apoptosis (14). Therefore, considering only the stretchability of the material itself in designing a microtissue is not sufficient. A highly stretchable microtissue or scaffold with the ability to shelter cells from severe mechanical loads is needed, as it would aid the practical applications in tissue engineering and regenerative medicine.

Native tissues like tendons and muscles, which are composed of stromal cells (15, 16) and protein scaffolds (17, 18), can maintain cell functions even under a severe strain (1, 2, 19). The stretchability of these tissues can be attributed to their crimped fibrous structure that has a hierarchical helix of single protein fibers (at the nanoscale) to tissue bundles (at the mesoscale) (1, 20–26). The aligned fibers follow a sinusoidal waveform along the tissue length, which has been termed fiber crimping (24, 27–29). Such fiber crimping is believed to play an important role in protecting the embedded stromal cells when the native tissues experience in vivo loads and undergo large deformations (25, 30–34); this effect has been attributed to its unique nonaffine deformation, wherein the global macroscopic strain is not identical to the local microscopic strain (35–43). As a result, the cell strain in these native systems differs from tissue strain by a substantial margin, enabling cell survival under severely large deformations.

Inspired by these natural crimped fibrous tissues, we engineer a unique microtissue composed of cells and nanofibers that are arranged in the form of a hierarchical helix. The helix scaffold is fabricated by serially twisting aligned nanofibers into a yarn and then overtwisting them into a helical yarn. This helix scaffold exhibits exceptional stretchability and toughness; it can be stretched up to 15 times its initial length. More importantly, this hierarchical material serving as a fibrous scaffold undergoes nonaffine deformation, where seeded cells stretch substantially less than the overall scaffold, mimicking native crimped fibrous tissues (25, 32, 36, 43–45). As a direct result, cells cultured on this helical scaffold survive cyclic strains up to 600%. We demonstrate the mechanism of the nonaffine deformation involved by deploying both experimentation and mathematical modeling. From an application perspective, we also demonstrate that mesenchymal stem cells (MSCs) cultured on the cellulose-based helix scaffold remain alive for over 7 d with cyclic stretch up to 600% strain. Furthermore, this helix scaffold promotes myogenesis of MSCs by altering cellular physical properties and activating transcriptional coactivator with PDZ-binding motif (TAZ) signaling. We believe this stretchable living microtissue can have broad implications in tissue engineering, regenerative medicine, soft robotics, and engineered living systems.

Results

Fabrication of Helical Nanofiber Yarn Microtissue Scaffold.

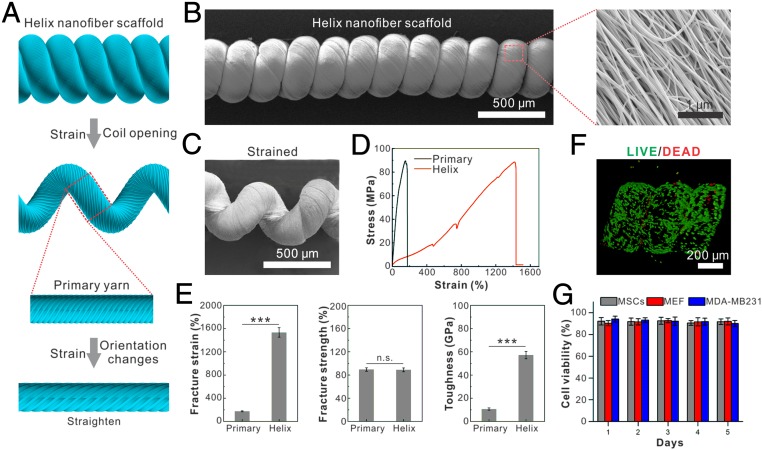
Native stretchable tissues such as muscles, tendons, and vessels usually constitute nanoscale protein fibers and microscale cell fibers. To obtain a synthetic scaffold imitating these stretchable natural fibrous tissues, we first fabricate nanoscale fibers as building blocks, which are subsequently assembled to achieve higher-order hierarchical structures. The original nanofibers are electrospun from either synthetic material [including poly(lactic-co-glycolic acid), polyurethane, and PVDF-hexafluoropropylene (HFP)] or natural material such as cellulose, as shown in SI Appendix, Fig. S1. These nanofibers are aligned and twisted to form primary yarns with a diameter of ∼300 μm and a twist angel of ∼40°, as shown by scanning electron microscopy (Quanta 250 FEG) imaging (SI Appendix, Fig. S1). The primary yarns are further overtwisted to form the final hierarchical helical yarns as shown in Fig. 1 A and B. The resulting hierarchical helix is structurally stable; no obvious partial twisting or untwisting is observed in the relaxed state (Fig. 1B).

Fig. 1.

Fabrication and characterization of helix microtissue fiber. (A) Schematic illustration of the structure of hierarchical helix nanofiber yarn. (B and C) Scanning electron micrographs of an unstrained (B) and a strained (C) hierarchical helix nanofiber yarn. (D) Stress–strain curve of helix nanofiber yarn shows that the helix scaffold can be stretched up to 15 times its initial length under a stress more than 80 MPa. (E) Quantifications of fracture strain, fracture strength, and fracture toughness show that the helix scaffold’s toughness is 6 times larger than the primary yarn by elevating fracture strain rather than facture strength. ***P < 0.001. n.s., not significant. (F and G) Image (F) and quantification (G) of LIVE/DEAD staining of seeded MEFs show that three different types of cells maintain high cell viability on the helix scaffold during 5 d of culturing.

MSCs are then seeded onto the helix yarn to form the microtissue scaffold. These cells fully attach and spread on the helix scaffold in less than 6 h. In 2 d, the seeded cells approach confluence and adapt to the topography of aligned and twisted nanofibers. Thus, we obtain a helix-shaped microtissue constructed from nanofibers as a supporting scaffold along with microscale cells that synergistically align themselves to form a hierarchical helix microtissue.

To test the biocompatibility of these fibers, MSCs are seeded and cultured for 5 d onto the helix scaffold. A high cell viability (>92%) is revealed by the LIVE/DEAD assay on the helix scaffold made from all the aforementioned materials. Cell types other than MSCs, including stromal cells [mouse embryonic fibroblasts (MEFs)] and human breast cancer cells (MDA-MB-231), also show a great cell viability (>93%) in a 5-d culture experiment (Fig. 1 F and G). Interestingly, we find that the proliferation ratio of MEFs on the hierarchical cellulose fiber (∼63%) is even higher compared with that on a 2D substrate made from the same material (∼28%), as indicated by the immunostaining of Ki67 (SI Appendix, Fig. S2). Thus, we demonstrate a living microtissue that recapitulates the structure of native stretchable tissues.

Mechanical Characterization of Helix Scaffold.

As we fabricate the microtissue fibers mimicking structural features of native stretchable tissues, we anticipate that these fibers also would exhibit a superior mechanical performance. To characterize, an individual yarn (10 mm between two clamps) is glued onto two polystyrene clamps and stretched using a tensile machine with a 100-N load cell (Shimadzu AGS-X Tester) at room temperature. Both loading and unloading rates are kept constant at 2 mm min⁻¹. We find that the helix scaffold made from PVDF-HFP nanofibers can be stretched up to 15 times its original length without breakage (Fig. 1 C–E). Furthermore, this highly stretchable helix scaffold exhibits a strong nonlinear elasticity in the form of strain stiffening, which is widely observed in biopolymer networks and is thought to be of importance for tissue mechanical functions (36, 46). The deformation process includes original separation of the adjacent coils and gradual unwinding of the coils until the fiber is free of it. Initially, the helix scaffold requires much smaller stress to stretch, indicating that it is very flexible compared with its primary forms: primary yarn and nanofiber bundle (Fig. 1 D and E). As the strain increases, the helix scaffold stiffens. The stress and strain values at breakage for the hierarchical helix scaffold (Fig. 1E) are 88.7 MPa and 1,420% respectively, and are 88.6 MPa and 174% for the primary yarn (Fig. 1E). As we integrate the stress–strain curve upon fracture to obtain the material toughness (57 GJ m⁻³), we find a 6 times larger toughness over the primary yarn. This is because of elevated fracture strain rather than fracture strength (Fig. 1E). Therefore, the mechanical performance of the helix scaffold significantly exceeds its primary forms by imitating the functional structures of native tissues. To further characterize the mechanical behavior of the scaffold, we perform cyclic loading of various strain amplitudes at a constant loading rate of 10 mm min⁻¹ (SI Appendix, Fig. S2A). We observe clear hysteresis when the material is subjected to cyclic strain, suggesting that the material may have viscoelasticity. To characterize its viscoelasticity, we perform a stress relaxation test and find a characteristic relaxation time of 9.7 ± 1.8 s (SI Appendix, Fig. S2B). Furthermore, we calculate the damping ratio from the cyclic loading by dividing the dissipated energy in a complete loading–unloading cycle by the extension work applied; we find that the damping capacity increases as the strain increases (SI Appendix, Fig. S2C). Moreover, we observe no obvious plastic deformation up to a strain of 200%; all of the fibers recover to their original length after the applied strains are released. When the strain is larger than 200%, the degree of plasticity [defined as the ratio of the residual strain after recovery to the maximum strain applied (47)] gradually increases with an increase in the amplitude of the strain (SI Appendix, Fig. S2 A and D); this is similar to the plastic behavior found in native biopolymers (47, 48). Thus, these mechanical characteristics of our living microtissue fiber are comparable with those of native stretchable tissues.

Helix Scaffold Protects Cells from Damage Under Large Strains.

Even though the helix scaffold we present here has achieved both native structural features and exceptional mechanical performance, whether the seeded cells maintain health and function while the whole microtissue fiber is subjected to large strains remained unknown. Mammalian cells can deform and actively spread from a spherical shape to a spindle shape several times longer (11, 15, 49). However, when cells are forced to deform under large strains, especially at a relatively high strain rate, they often cannot survive. Indeed, several reports have shown that severe deformations can induce cell and nuclear membrane breakage (12), DNA damage (13), and apoptosis (14). In native tissues, the protection of cells under severely large deformation is enabled by the nonaffine deformation of fibrous tissue scaffold, where the cell strain in these native systems significantly differs from the bulk tissue strain (19, 25, 30, 32, 36).

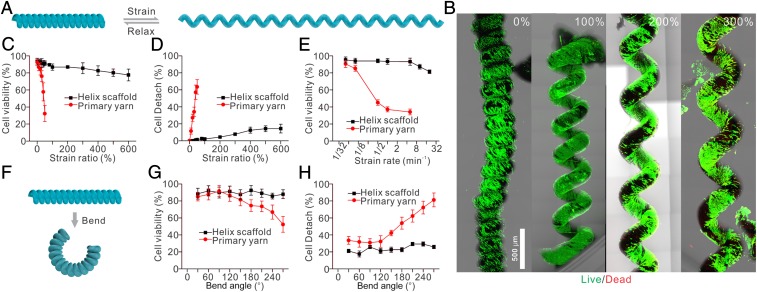
To test whether cells cultured on our helix scaffold survive under large strains, we seed MEFs onto the hierarchical helix scaffold for 2 d until they are fully attached. These scaffolds are then stretched under cyclic load up to 50 times (up to 600%, strain rate of 1/2 min⁻¹) (Fig. 2 A–D). We find that cells maintain high cell viability (85%) after being stretched even over 600% cyclic strain (Fig. 2C) on the helix scaffold as demonstrated by LIVE/DEAD assay. As a comparison, the cell viability dramatically decreases as the strain increases when cells are cultured on the primary yarn: Application of 50% strain leads to more than 70% cell death (Fig. 2C). Moreover, cells on the helix scaffold maintain a spreading morphology and remain attached (>83%) under 600% cyclic strain, while most cells (65%) on the primary yarn round up and detach under 50% cyclic strain (Fig. 2D). Furthermore, to confirm the cell viability under different strain rates, we stretch the helix scaffold and the primary yarn at different strain rates ranging from 1/32 to 16 min⁻¹ at 200% and 50% strain, respectively. Strain rates lower than 1/4 min⁻¹ do not affect cells on either the helix scaffold or the primary yarn (Fig. 2E). Strain rates larger than 1/2 min⁻¹ dramatically reduce the cell viability on the primary yarn (less than 40%), while strain rates only larger than 4 min⁻¹ slightly decrease the cell viability on the helix scaffold (Fig. 2E). Even at a strain rate of 16 min⁻¹, we still observe more than 80% cells survival on the helix scaffold (Fig. 2E). In addition to cyclic stretching, cells on the helix scaffold can sustain large cyclic bending. The helix scaffold (10 mm in length and 500 μm in diameter) is actuated between the straight and bent states at a consistent bending rate to a specified beam bending angle. We find no obvious damage on either the helix scaffold or the primary yarn when the bending angle is lower than 120° (Fig. 2 F and G). Even at a bending angle of 270°, the cell viability on the helix scaffold is above 90%, whereas the cell viability on the primary yarn is less than 75% (Fig. 2G) and a small portion of cells (∼16%) detaches from the primary yarn (Fig. 2H). Overall, these results demonstrate the unique and exceptional cell-deformation buffering effect of the helix scaffold under both bending and stretching, which enables the seeded cells to function as usual despite the fiber being subjected to severe mechanical loads, and thus can potentially promote the practical applications in regenerative medicines.

Fig. 2.

Hierarchical helix scaffold shelters cells from large cyclic straining and bending. (A) Schematic illustration of cycling strain of a hierarchical helix scaffold. (B) LIVE/DEAD staining of seeded cells under cycling strains. The results show that cells maintain a consistently high viability despite different strain ratios. (C) Seeded cells maintain high viability on the helix scaffold under different strains up to 600%. As a comparison, the cell viability dramatically decreases as the strain increases when cells are cultured on the primary yarn. (D) Cells on the helix scaffold maintain a spreading morphology and remain attached (>83%) under 600% cycling strain, while most cells (65%) on the primary yarn round up and detach under 50% cyclic strain. (E) Cells on the helix scaffold maintain high viability at different strain rates ranging from 1/32 to 16 min⁻¹, while cells on the primary yarn round up and detach under 50% cyclic strain. (F) Schematic illustration of cycling bending of a hierarchical helix scaffold. (G) Cells on the helix scaffold maintain high viability under different bend ratios up to 270°. In comparison, cell viability decreases as the bend ratio is larger than 150° when cells are cultured on the primary yarn. (H) Cells on the helix scaffold maintain a spreading morphology and remain attached (>95%) under different bend ratios up to 270°, while cells on the primary fiber round up and detach.

Mathematical Modeling and Simulation.

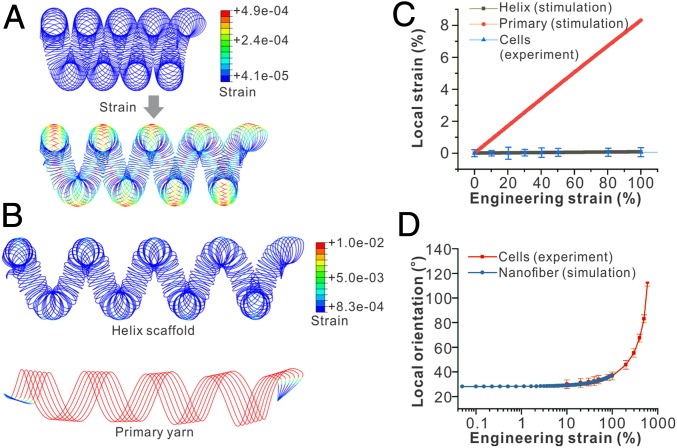
We further explore the underlying reason for the deformation buffering effect of the helix scaffold on seeded cells. Toward this end, simulation of loading of a hierarchical helix scaffold is performed using the finite element software Abaqus. According to the experimentally examined samples, the simulated geometry is generated as an ideal helix with 4.5 strands (Fig. 3A). The precise geometry of the hierarchical helix strand is described by a set of parametric equations, as shown in SI Appendix, Materials and Methods. The scaffold is modeled as an incompressible linear elastic material with a Young’s modulus value of E = 1 and a Poisson’s ratio of 0.5. The loading and unloading of the helix scaffold are simulated by gradually increasing the magnitude of the displacement at both ends of the fiber along the axial direction. The maximum stretch applied is 200% of its initial length. The rotation along the axis, which is perpendicular to the fiber axis and goes through the center of the cross-section, is allowed. We extract the maximal strain on the surface of the scaffold and also compute the fiber angular displacement from the overall displacement field. Since displacement boundary conditions are applied and only dimensionless quantities such as strain and turning angle are studied, the process can be viewed as a geometrical problem and the effects of Young’s modulus can be neglected.

Fig. 3.

Theoretical modeling of straining the hierarchical helix scaffold. (A) Simulated results show the local strain of the hierarchical helix scaffold under an applied 50% engineering strain, showing that the local material strain is much smaller than the applied engineering strain. (B) The field of local material strains on the helix scaffold and primary yarn under the same engineering strains, showing a much larger local material strain on the primary yarn compared with the helix scaffold. (C) The simulated correlations between local strain and engineering strain show that the local strains on the helix scaffold are much smaller than those on the primary yarn under the same engineering strain. Experimental measurements of cell elongation also fit well with the simulated local material strain of the helix scaffold. (D) Local orientations of seeded cells on the helix scaffolds are consistent with simulated local orientations of nanofibers under the same engineering strain.

Our simulation results show that the stress and strain of the material are maximal on the wire surface closest to the outer brim of the helix scaffold (Fig. 3A). As we compare the maximum actual strain as a function of the applied engineering strain of the fiber, we find that the local strain of the wire is 1,000 times smaller than the total engineering strain (Fig. 3 B and C). In comparison, the local strain of the hierarchical helix scaffold is 100-fold lower than those of the primary yarn under the same total engineering strain (Fig. 3C). Indeed, as we estimate the local strains experienced by the seeded cells using their relative length change, we find them nearly zero and consistent with the simulated local material strains (Fig. 3C). The rotation of cell orientation measured in experiments is also consistent with the local rotation of the individual nanofiber wire simulated, showing the structural realignment of the helix scaffold during strain (Fig. 3D). Due to the existence of the coils, the externally applied strain is distinctively different from the actual perceived strain by cells (the former is much larger than the latter), so the cells are almost unaffected in the high tensile state. These simulated results are consistent with previous finite element studies of helical springs (50, 51). Thus, we demonstrate that the cell deformation buffering effect can be attributed to the nonaffine deformation through structural realignment under large strains, which eliminate the local strain applied to individual cells.

Promotion of Myogenesis on Helix Scaffold.

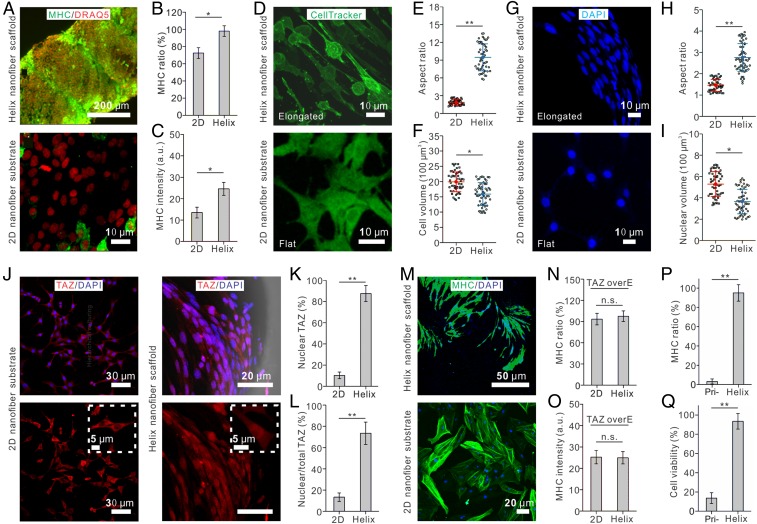
To demonstrate, as proof of principle, that this fibrous microtissue can be used for applications of functional tissue regeneration, we construct a microtissue composed of the helix cellulose scaffold and seeded MSCs. After the MSCs approach confluence, chemical supplements are added to induce myogenesis of the MSCs (see SI Appendix, Materials and Methods). After a 7-d culture, we find that the hierarchical nanofibrous structure largely promotes myogenesis of MSCs compared with the 2D substrate made from the same material (92.0% ± 6.1% vs. 64.4% ± 6.2%), as indicated by myoblast marker myosin heavy chain (Fig. 4 A–C). Furthermore, we find that this is primarily due to the nanotopography rather than the microscale curvature of the helix scaffold, as shown by comparing the myogenesis ratios of MSCs on nanofiber yarn and microfiber yarn with the same overall coil geometry (SI Appendix, Fig. S5).

Fig. 4.

The helix scaffold promotes myogenic differentiation of MSCs via altering physical properties of cells and translocating TAZ. (A–C) Images (A) and quantification of myosin heavy chain (MHC) staining ratio (B) and intensity (C) show that the helix scaffold promotes myogenic differentiation of MSCs. (D–F) Fluorescent images (D) and quantifications show that the helix scaffold elongates the cells to a larger aspect ratio (E) and reduces the cell volume (F) compared with those cultured on a 2D substrate. (G–I) Fluorescent images (G) and quantifications show that the helix scaffold elongates the nucleus to a larger aspect ratio (H) and reduces the nuclear volume (I) compared with those culture on a 2D substrate. (J–L) Fluorescent images (J) and quantifications show that the helix scaffold promotes TAZ nuclear translocation compared with 2D substrate (K and L). (M–O) Overexpression of TAZ in MSCs leads to a comparable myogenesis ratio in cells cultured on the helix scaffold and a 2D substrate. (P and Q) Helix scaffold guarantees a high viability and an elevated myogenic differentiation ratio of MSCs under cycling 600% strains. As a comparison, only a small portion of MSCs on the primary yarn maintains health and goes through myogenic process. *P < 0.05, **P < 0.01. n.s., not significant; overE, overexpression; Pri-, primary.

To explore the underlying mechanism, we find that the helix scaffold modifies the physical properties of cells by aligning and elongating the seeded cells. Whereas cells randomly orient on the 2D membrane made up of nanofibers, they synergistically position in a preferred direction on the helix scaffold (SI Appendix, Fig. S3). The cells also become more elongated on helix scaffolds, as shown by a higher aspect ratio (Fig. 4 D and E), and have a smaller cell volume (Fig. 4 D and F). We characterize the cell nucleus and find that it also has a higher aspect ratio and a smaller volume when cultured on helix scaffolds (Fig. 4 G–I). This behavior of nuclear elongation and organization in a fibrous system is consistent with previous studies (52–54). Moreover, the idea of nuclear deformation regulating gene expression and leading to varied cell functions is also in line with previous observations (55–61). Therefore, the observed biophysical characteristics of both the cytoplasm and nucleus may together promote myogenesis of MSCs on our helix nanofiber yarn, as also suggested by previous reports under various types of material cues (62).

In addition to the biophysical properties of the seeded cells, previous reports have shown that TAZ in myoblasts promotes myogenic gene expression in a MyoD-dependent manner and hastens myofiber formation (63). Meanwhile, TAZ has also been identified as a mechanotransducer that responds to various types of mechanical loadings and extracellular material cues (64). Thus, we further test whether the helix scaffold promotes myogenesis of MSCs via TAZ. Indeed, we find that TAZ translocates into the nucleus from the cytoplasm on the helix scaffold, whereas it remains in the cytoplasm on the 2D nanofiber membrane (Fig. 4 J–L). This TAZ nuclear translocation might be due to cell volume reduction as recently reported (65). Furthermore, overexpression of TAZ leads to higher but comparable myogenesis ratios on both the helix scaffold and the 2D substrate of the same material (Fig. 4 M–O). To summarize, the physical topography of the helix scaffold alters the biophysical properties of seeded cells (aspect ratio and volume), which leads to TAZ nuclear translocation and thus promotes myogenic differentiation of MSCs seeded on the helix scaffold.

Both the helix scaffold and the primary yarn exhibit similar first-order nanoscale topographic features; therefore, as expected, comparable myogenesis ratios are observed on these two types of fibers. However, as we further apply cyclic stretch, we find that 82.3% of MSCs on the helix scaffold go through myogenesis while only 12.7% of seeded MSCs remain healthy, and even less (∼6%) go through myogenesis on the primary yarn (Fig. 4 P and Q). These results show that the hierarchical helix microtissue provides a useful scaffold for muscle regeneration, whose effect can be further harnessed by mechanical loadings.

Discussion

We fabricate a highly stretchable and tough nanofiber helix microtissue that is capable of protecting seeded cells from being damaged under large strains and strain rates. This design is inspired by the structure of muscles and tendons that contributes to its mechanical robustness. The helix microtissue has greatly higher cell viability and proliferation ratio compared with that of a 2D substrate made from the same material. We demonstrate that the helix scaffold has significantly enhanced mechanical performance in comparison with primary yarn, as it can be stretched up to 15 times its original length without rupture. The hierarchical helix scaffold not only mimics the structural and mechanical properties of native tissues but also can protect seeded cells when subjected to both stretching and bending. We use mathematical modeling along with experimental evidence to show that the supporting material, serving as a fiberlike scaffold that enables nonaffine deformation, allows the cells to be stretched substantially less than the overall microtissue. Furthermore, to demonstrate the application of this reconstituted microtissue in regenerative medicine and tissue engineering, we show that it uses its physical structures to regulate the differentiation of the seeded MSCs. The helix scaffold alters the physical properties of cells by stretching both the cytoplasm and the nucleus. We further identify that a transcriptional coactivator (TAZ) serves as the key regulator to transduce the physical information of the hierarchical scaffold to cells by translocating into the nucleus, thus enhancing myogenesis of the seeded MSCs. To summarize, this study provides a microtissue that meets the requirement for regeneration of tough tissues such as muscle, tendon, and bone and offers a pathway for biophysical regulation of stem cell fate using hierarchical structured materials. This work also has the potential to open new technological avenues that can leverage on advances in soft materials, mechanical engineering design, and cell biology to develop new engineered living systems for applications in human health monitoring, wearable and stretchable actuators, bioartificial organs, and so forth.

Materials and Methods

Full materials and methods are described in SI Appendix, Materials and Methods. Briefly, we electrospin nanofibers to form a fibrous membrane and further twist it into a hierarchical helix yarn. Cells are cultured on the helix yarn to form the microtissue. Mechanical loadings on hierarchical helix yarn and microtissue are performed using a mechanical testing machine (U-Stretch; CellScale). Cell survival, proliferation, and differentiation assays are performed using confocal microscropy (Leica SP8).