Significance
The many-body localized phase provides an example of a generic quantum interacting system that does not reach thermal equilibrium and thereby violates the most fundamental principles of statistical physics. For that reason it provides promising pathways to implement robust quantum memory as it is able to retain knowledge of its initial configuration. This breaking of ergodicity, or the emergence of integrability, is due to the essential combination of disorder and interactions in the system. In our work we show, however, that even without disorder one can obtain a system that shows all of the main characteristics of many-body localization, suggesting that there may be easier and more reproducible ways of realizing it.
Keywords: many-body localization, Stark, thermalization, ergodicity
Abstract
In this work we demonstrate that nonrandom mechanisms that lead to single-particle localization may also lead to many-body localization, even in the absence of disorder. In particular, we consider interacting spins and fermions in the presence of a linear potential. In the noninteracting limit, these models show the well-known Wannier–Stark localization. We analyze the fate of this localization in the presence of interactions. Remarkably, we find that beyond a critical value of the potential gradient these models exhibit nonergodic behavior as indicated by their spectral and dynamical properties. These models, therefore, constitute a class of generic nonrandom models that fail to thermalize. As such, they suggest new directions for experimentally exploring and understanding the phenomena of many-body localization. We supplement our work by showing that by using machine-learning techniques the level statistics of a system may be calculated without generating and diagonalizing the Hamiltonian, which allows a generation of large statistics.
Since the phenomenon of many-body localization (MBL) was repostulated more than a decade ago (1–3) it has attracted a great deal of attention. It provides an example of a generic quantum many-body system that cannot reach thermal equilibrium (4–7). In recent years, an enormous theoretical effort was invested in understanding the nature of the MBL transition (8–10), the dynamical (11–13) and entanglement (14–17) properties of these systems, and their response to external probes (18, 19) and periodic driving (20–22). Also, the experimental community (23–27) has found interest in this field, in particular because these systems have the potential of storing information about initial states for long times, and hence may implement quantum memory devices. These systems may also be useful for dynamical quantum control, as they allow the application of driving protocols without heating the system to an infinite temperature.
A key ingredient for achieving the MBL phase is disorder (randomness). The roots of this phase lie within the phenomenon of Anderson localization (1), where noninteracting particles form a localized nonergodic phase. Questioning the fate of Anderson localization in the presence of interactions led to the discovery of the MBL phase.
In this work we ask whether randomness is indeed an essential ingredient in achieving generic nonergodic interacting phases. Viewing MBL as a competition between single-particle localization and interactions, one may wonder whether a localizing mechanism that does not require disorder may produce similar results. It was suggested that quasi-MBL may exist in a translationally invariant quantum system such as a quantum disentangled liquid (28–31), where light particles evade thermalization (for long times) by localizing on heavy particles (32–36). Moreover, it was shown that clean 1D systems with quasi-periodic potentials may host an MBL phase (37–39). While quasi-periodic systems are not considered disordered, they do not respect exactly the discrete translational symmetry of the lattice either and cannot be treated in momentum space. Other proposals (e.g., ref. 40) suggested the appearance of nonergodic dynamics for a large portion of states belonging to the low-energy subspace of the cubic code Hamiltonian which involves eight-spin interaction terms. The model we propose in this work respects the crystal symmetry exactly and hence in that regard it is a realizable and a truly discrete translational invariant model. We show that this model supports a phase that is indistinguishable from the MBL phase based on all of the standard characteristics.
A well-known mechanism for localizing single particles is the Wannier–Stark effect (41), in which particles living on a lattice become localized in the presence of a linear potential. We refer to this phenomenon as Bloch localization. Notice that besides lacking randomness such systems also preserve translation invariance as the linear potential represents a uniform force and may be replaced by a time-dependent vector potential. One may consider the Wannier–Stark effect as a particular case of dynamical localization (42) with linear-in-time vector potential. While no physical difference is expected between the different gauges, the thermodynamic limit in the time-dependent gauge avoids the existence of an infinite energy difference between the edges of the system. Nevertheless, we chose to work in the static gauge since in this work we are only interested in static forces and since it dramatically reduces the numerical effort. In SI Appendix we show that our numerical method is, as expected, indifferent to the choice of gauge. The fate of dynamical localization in the case of time-dependent fields has been discussed in refs. 43 and 44. The interplay between interactions and linear fields has been investigated in the past. It was shown that the oscillatory part of the current, that is, Bloch oscillations (BO), decays as the interaction strength increases (45, 46). It was also shown that the presence of a uniform force changes the nature of the evolution of an initial state under the nonlinear Schrödinger equation (NLSE) as the nonlinearity increases (e.g., for a large nonlinearity the dynamics is localized). However, the ergodic properties and the generality (stability) of these phases cannot be inferred from these works. The absence of BO does not necessarily signify ergodicity and the dynamics of generic interacting models cannot be captured by the NLSE, which is generally valid only as a mean field description of weakly interacting bosons (47). Moreover, only the evolution of low-energy (near ground state) states has been considered and the stability of the above phenomenon was not analyzed. In this work we show that single-particle localization that is not necessarily due to disorder results in a state that is indistinguishable from the MBL state based on the typical tools of assessment. We analyze the spectral and the dynamical properties of 1D interacting fermions and spins in the presence of both disorder and a linear potential. We show that by considering these two different localizing mechanisms, that is, disorder () and linear fields (), one may construct a 2D phase diagram in the space which hosts a connected nonergodic (MBL) phase. We find that above a critical value the MBL phase extends down to the clean limit, that is, the line.
It is worth mentioning that integrable models, such as the 1D Heisenberg and transverse field Ising models, are known examples of clean models that fail to thermalize. While these models fail to thermalize, they are sensitive to the existence of small integrability-breaking terms such as disorder or longer-range interactions and hopping. In this sense the model we suggest is more generic, since the addition of disorder and/or weak longer-range hopping and interactions does not lead to thermalization.
The existence of generic clean models that fail to thermalize may have important implications both theoretically and experimentally. From the theory side, it can simplify dramatically the numerical effort in analyzing these interacting systems. Moreover, the lack of randomness gives hope that the nature of the MBL transition, the emergent conserved quantities, and the generalization to higher dimensions may be approached analytically. From the experimental side the necessity of strong disorder is a major drawback. In intrinsic systems it is not clear whether such strong disorder generically exists. In controlled systems, such as optical lattices, only quasi-random disorder or correlated disorder, for example speckle potentials, may be implemented and a repetition over many realizations is needed due to the small size of the systems (48, 49). In stark contrast, linear field (tilt in optical lattices) may be implemented relatively easily and it provides the ability to experimentally realize these systems in a highly reproducible way, and without the necessity of many repetitions. Unlike integrable models, the inevitable existence of unwanted terms such as weak disorder should not have a dramatic effect on the dynamics.
Background and Model Definition
Bloch Localization.
Our ultimate goal is to understand the fate of Bloch localization in the presence of interactions. In this section we briefly review the properties of noninteracting particles in the presence of a uniform force (linear potential). Consider a 1D lattice model in the presence of a linear potential,
| [1] |
where annihilates a particle from lattice site , is the nearest-neighbor (nn) hopping amplitude, and is the uniform force. The Hamiltonian can be diagonalized by the following transformation:
| [2] |
with being the Bessel functions of the first kind and . Under this transformation Eq. 1 becomes
| [3] |
Since for , all of the eigenstates are localized for any . Each eigenstate, , is localized around site with an inverse localization length given by .
Unlike for Anderson localization, where the localization length is energy-dependent (smaller near the middle of the energy band), for the Bloch localization case the localization length is an energy-independent quantity. Another prominent difference between the two is the form of the density of states, where in the case of Bloch localization the spectrum forms an ordered ladder even deep in the localized phase.
Model Definition.
The basic model we wish to analyze concerns the interplay between the two mechanisms of single-particle localization (disorder and linear field) and interactions. For that, we consider a 1D lattice of interacting spinless fermions in the presence of disorder and a uniform force,
| [4] |
where annihilates a particle from lattice site , is the density, is the nn hopping amplitude, is the uniform force, is a random on-site potential with strength , and is the nn interaction strength.
The above fermionic Hamiltonian may be mapped, via a Jordan–Wigner transformation, into an equivalent spin- chain (Heisenberg),
| [5] |
with and while and are defined as before. In the rest of this paper we will analyze the localization and dynamical properties of these Hamiltonians as a function of the interaction strength, force, and disorder strength. Since the particle number (fermionic model) or the total (spin model) are conserved, we focus our analysis on the half-filled () sector. Regardless, the results do not depend much on the specific sector.
Results and Discussion
Level Statistics.
A well-established signature for the transition from ergodic to nonergodic dynamics is the level statistics of the many-body spectrum. In particular, generic ergodic Hamiltonians belong to the Gaussian orthogonal ensemble (50, 51) and their level spacings, , typically obey the Wigner–Dyson distribution. However, for nonergodic systems the level spacings typically obey the Poisson distribution. It should be pointed out that in both cases symmetries may add high level of degeneracies which lead to deviation from the Wigner–Dyson distribution (nonergodic) and from perfect Poisson distribution (ergodic). However, level spacing obtained from symmetry sectors should not have these additional degeneracies. As in the case of the disordered Heisenberg chain within the sector of zero total magnetization, the transition from ergodic to nonergodic is accompanied by a transition from Wigner–Dyson to Poisson level statistics (9).
Both distributions are often characterized by a single parameter, , which conveniently avoids the need for unfolding the spectrum. For the Wigner–Dyson distribution , and for the Poisson distribution.
We diagonalize the Hamiltonian in Eq. 5 for spins using exact diagonalization, with and for different values of and . In SI Appendix we show that by using machine-learning techniques, statistics for the -value may be generated from directly without the need of diagonalizing the Hamiltonian.
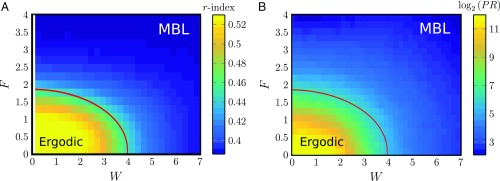
In Fig. 1A we show the value (averaged over different disorder realizations) in the space of . We find that the ergodic phase lives in a dome-shaped region near the origin of the space. The line corresponds to the often-discussed MBL transition near the critical disorder strength . As increases, the value of decreases. Above a critical value of , the critical disorder appears to go to zero and the nonergodic phase appears also in the clean nondisordered limit.
Fig. 1.
These plots constitute the main results of the paper and demonstrate the existence of a potential-gradient-induced MBL phase. (A) The -index as a function of disorder and field strength as calculated for the Hamiltonian in Eq. 5 with and (averaged over 125 realizations). Evidently, a phase boundary exists between a region with (Wigner–Dyson) for small values of and (the ergodic dome) to a region with (Poisson). (B) The averaged participation ratio () as a function of disorder and field strength for the same system as in A. Consistent with the level statistics, inside the ergodic dome the is proportional to the Hilbert space dimension (), while outside the dome it becomes small and independent of . Notice that in B the line is included in the data. In both cases the red line serves only as a guide to eye and is a contour or .
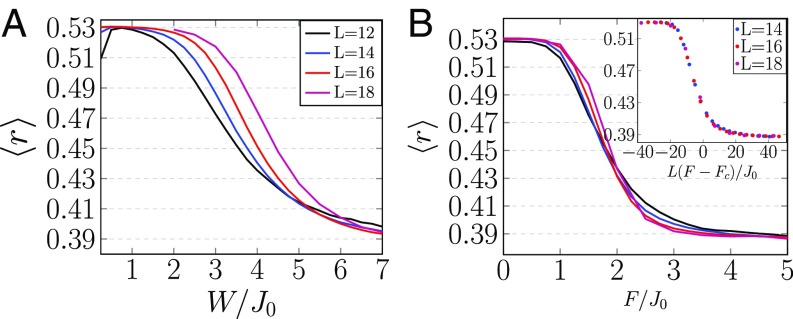
In Fig. 2 we show the value for different system sizes as a function disorder (zero field) and as a function of the field (for a fixed weak disorder). The critical values may be extracted by finite size scaling through a scaling collapse. The case of zero field was analyzed in several works (8, 52–54) in which the critical disorder was found to be in the range (notice a factor of 2 due to a different definition of the spin matrices). For the weak disorder case we plot the data (Fig. 2, Inset) as a function of . We find that the critical exponent is and the critical field is , for which the data collapse on one curve. In SI Appendix we provide more details regarding the finite size scaling and show that the above results are not sensitive to integrability-breaking terms such as next-next-nn hopping and interactions.
Fig. 2.
The -index as calculated for the Hamiltonian in Eq. 5 with for different system sizes, . In A the -index is plotted as a function of for zero linear field. In B the -index is plotted as a function of for a fixed disorder strength . (Inset) The data plotted as a function of with .
Notice that in this part we always considered , since for smal-enough disorder small systems behave as clean systems, which leads to symmetry-related degeneracies in the spectrum.
Inverse Participation Ratio.
Analyzing level statistics of clean systems requires a separation of the Hilbert space into momentum sectors, since degeneracies due to symmetries have to be removed. For finite systems and below a critical disorder strength, the system behaves similar to a clean system. Therefore, the level statistics become a less reliable measure for small disorder strengths since degeneracies start to appear due to the emergence of translation symmetry. A quantity which is less sensitive to symmetries is the inverse participation ratio (IPR). The IPR is also a measure of the long-time return probability of arbitrary initial states. To see that, consider the return probability of a state ,
| [6] |
where is the time evolution operator. The state may be expanded in terms of the Hamiltonian eigenstates, , which allows us to write the IPR (long-time limit of the return probability) as
| [7] |
In the absence of degeneracies, Eq. 7 becomes . Clearly, if the initial state is an eigenstate then , while if the initial states is an equal superposition of all of the eigenstates then , where is the Hilbert space dimension which generically is exponential in the system size. In the following we average the over different initial states which we choose to be eigenstates of some local operators, for example . For ergodic systems, the should be exponentially small in the system size and the system should lose its memory of the initial state. In stark contrast, in the localized phase the converges to a positive system-size-independent constant.
In Fig. 1A we present the averaged and normalized participation ratio, , in the space of . While the IPR is a smooth function, there is a transition between a region where the IPR is exponentially small to a region where the IPR is independent of system size. These regions agree with the results obtained in the previous section. Here also the line behaves in a similar way (cf. Fig. 1B), where the IPR becomes independent of system size as a function of .
Dynamics and Experimental Measurables.
The distinction between ergodic and nonergodic dynamics is well captured by the level statistics and the participation ratio, yet both these measures are hard to access in experiments. As shown in refs. 24, 25, and 27, the nature of the dynamics is examined by tracking the dynamics of an initially prepared out-of-equilibrium density configuration. We numerically show that the existence of a linear field prevents thermalization. For concreteness, we consider a similar out-of-equilibrium initial state as in ref. 24.
The system is prepared in an antiferromagnetic configuration (or charge density wave for the fermions), where the spins on odd sites point down (empty) and on even sites point up (full). We then track the time evolution of the odd–even imbalance, . We use a numerical method based on Krylov subspaces via a reorthogonalized Lanczos implementation to do so (see SI Appendix for more information).
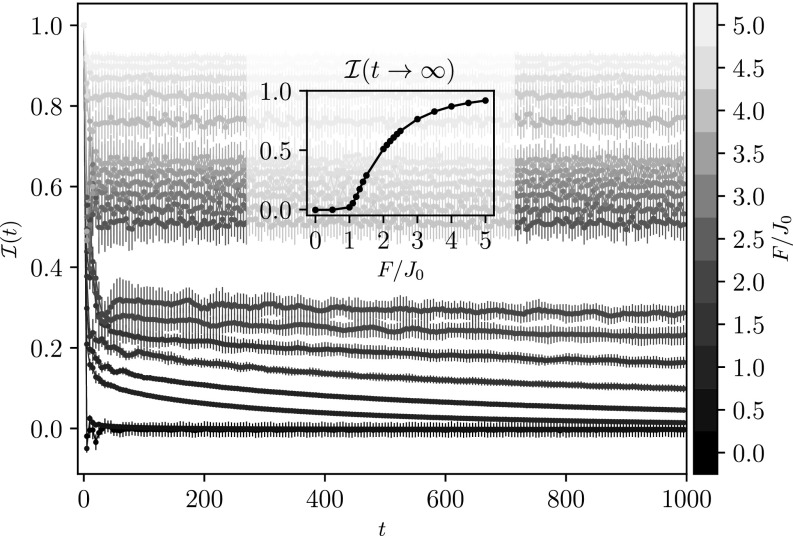
In Fig. 3, Inset we show the resulting long time limit as a function of . Below a critical value the long time limit of tends to zero, while above that value the long time limit tends to a finite value that increases with the field. Computational costs limit the available times we can access, and we remark that not each of these curves has converged yet. Extrapolating the available curves will move the estimated critical field to higher values than suggested by the inset.
Fig. 3.
The imbalance as a function of time for different field strength and for fixed weak disorder , where . At , the imbalance for each field strength starts at . For field strengths above (and including) we cannot identify decaying behavior at these time scales. Error bars show statistical variance over 32 realizations of disorder. (Inset) The long time limit of the imbalance as a function of the field (averaged over the last 50 time steps). Below a critical value the long time limit of tends to zero, while above that value the long time limit tends to a finite value that increases with the field. Notice that some of the lower curves have not yet reached their final value.
In ergodic systems, is expected to decay to zero with a typical relaxation time . We show that while indeed this is the case when the linear field is small, both for the clean case and for weak disorder, beyond a critical field strength the long time limit of is different from zero. In Fig. 3 we show the imbalance in a system of 24 spins (sites) as a function of time for different values of the field and for a fixed weak disorder strength (). The data and code for Fig. 3 are available at GitHub, https://www.github.com/everthemore/krylov-cpp and CaltechData, https://data.caltech.edu/records/1089 (55, 56). It is worth noticing that energetics gives an upper bound to this relaxation process. In the fermionic language, the charge density wave (CDW) configuration and the uniform configuration differ in their dipole moment by an extensive amount . In the absence of a field, the many-body bandwidth of the Heisenberg model with all is . Hence, in the presence of a field, if or the CDW configuration cannot evolve into a uniform configuration at any time. In practice, the critical field obtained from the the level statistics is around , while it seems that the dynamics suggests a slightly lower value (notice that not all of the imbalance curves have converged yet). However, while the true critical field (if it exists) should limit the dynamics of all processes, specific processes like the one considered here may show nonergodic dynamics at lower values. Moreover, one may consider the presence of a prelocalized phase (or prethermal for that matter) that appears in the dynamics. Our numerical data cannot confirm or disprove the existence of such a phase. An analysis of larger systems, and more importantly much longer times, may resolve that issue.
MBL in Two Dimensions
The lesson we learned about the effect of interaction on the Anderson localized (AL) phase in 1D cannot be trivially extended to higher dimensions. The nature, and even the existence, of a many-body-localized phase in is a hotly debated subject. While theoretical works (57–59) showed that locally thermal regions in systems with true random disorder can destabilize the MBL phase in two dimensions, experimental works (24, 26, 27) have shown indications for such a phase in .
Similar questions may be posed in the context of the uniform field as a cause for single-particle localization. In stark contrast to the AL phase, this phase is not sensitive to rare regions. In particular, if the field is applied at an irrational angle, the field is nonzero along all lattice directions. This field can indeed be arbitrarily small for specific lattice directions but can be chosen such that lattice sites along directions at which the field is below the critical value are separated by multiple hops. Since each of these hopping processes has a component against a strong field, and since the bare interaction is local, both the effective hopping coefficient and the effective interaction along these directions may be extremely small. How these renormalized hopping coefficients and interactions scale with the field along these direction, and whether it is possible to choose the field such that along each lattice direction the field is larger than the 1D critical field, is an interesting question worth further investigation. Additionally, along these same lattice directions the linear potential is not perfect and can be regarded as a combination of a linear field and weak quasi-periodic disorder. This quasi-periodic disorder may also help the localization along directions where the field is small. Finally, the absence of rare regions [which are a main reason to exclude MBL in high dimensions (58)] may help the survival of the nonergodic behavior in the thermodynamic limit.
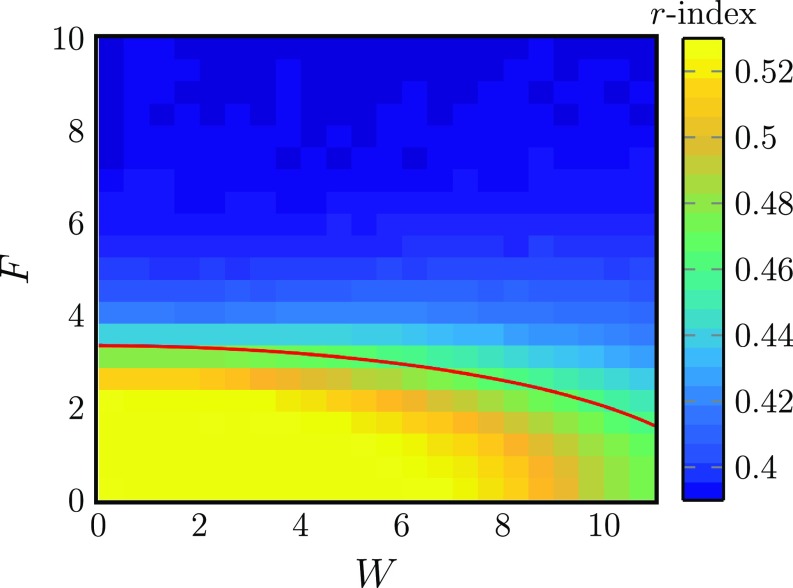
To further speculate on the existence of MBL in 2D, Fig. 4 shows the level statistics (r-index) of a 2D Heisenberg model as a function of the uniform force and disorder. Similar to the 1D case, we see a clear transition from a Wigner–Dyson distribution to Poisson distribution. Since we are restricted to very small system sizes ( lattice), these results should not be taken as a claim of the existence of a 2D MBL phase. However, we hope that these ideas will stimulate further work in this direction.
Fig. 4.
The level statistics ( value) as a function of the field strength, , and disorder strength, , for a disordered 2D system of spins with an incommensurate force (averaged over 32 realizations). The red line is a guide to the eye and is given by a contour of .
Dipole Moment Analysis
Single-particle Wannier–Stark localization may be thought of in terms of energetic constraints imposed by the field. In the many-body case, one may wonder whether interactions can help overcome energetic constraints by reordering of particles. Heuristically, a many-body configuration can be described by its dipole moment (Dynamics and Experimental Measurables), which in the presence of a field is associated with an energy . In order for such a configuration to evolve into a different configuration with dipole moment , the internal structure of the system, that is, hopping and interaction, must be able to supply the energy difference . This condition is captured in the dipole moment structure of the eigenstates. Clearly, in the infinite field limit of our model the dipole moment becomes an exactly conserved quantity. In that case an analogy with ref. 60 can be made, where it was shown that nonergodic dynamics arises in a 1D random quantum circuit model which is constrained to conserve both a charge and the dipole moment of this charge.
The main question is to what extent the dipole moment may be considered as a conserved quantity for finite fields. In SI Appendix we show the results of exact diagonalization of a half-filled fermionic system where each point represents an eigenstate in the space of energy and dipole moment. As expected, in a given energy window and for large field the many body wave functions have well-defined dipole moment. Each dipole moment sector is further split into subsectors of doublon (occupied neighboring sites) number. Hence the dynamics is effectively restricted to preserve the initial dipole moment and the initial doublon number, which is predicted to yield nonergodic dynamics (60). For a weak field, however, this is not the case. The eigenstates in a given energy window span a range of dipole moments and doublon numbers. Around the critical field, we observe that while the eigenstates in a given energy have a finite spread in the dipole moment, the different sectors become distinct and the integer part of the dipole moment behaves as a conserved quantity. Beyond this critical field we also observe a separation into the subsectors of doublon number. While it is hard to pinpoint the exact value of the transition using this approach, the transition can be bounded and is consistent with the value we obtained from the level spacing statistics.
Conclusions
In this work we analyzed the effect of interactions on single-particle localization that arise both from disorder, , and from the existence of linear potentials . With that, we showed that the notion of an MBL phase may be generalized also to a class of clean (nonintegrable) systems. In particular, we find that a phase boundary in the space exists, beyond which the resulting phase fails to thermalize. We find that, unlike in clean integrable models, this nonergodic phase is stable to perturbations and shares all of the familiar fingerprints of the well-studied MBL phase in the presence of disorder.
The existence of such a phase demonstrates that randomness is not an essential ingredient for the emergence of stable nonergodic interacting phases. Such a conclusion may have an impact on the realization of these nonergodic phases. Unlike disorder potentials, linear potentials are relatively easy to implement and are highly tunable and may be controlled dynamically. The ability to realize stable and generic nonergodic phases is an important step toward the realization of quantum memory devices that may store information for long times. Moreover, the lack of randomness and the low sensitivity to dimensionality may render these systems more accessible to a further theoretical investigation, both numerically and analytically. It came to our knowledge that simultaneously to our work, ref. 61 studies the entanglement entropy growth in the presence of a linear field. The results presented in ref. 61 are in agreement with the conclusions we presented in this work.
Supplementary Material
Acknowledgments
This work was supported by Swiss National Science Foundation Grant P2EZP2-172185 (to E.v.N.), Army Research Office Multidisciplinary University Research Initiative W911NF-16-1-0361, “Quantum Materials by Design with Electromagnetic Excitation,” sponsored by the US Army and the Packard Foundation (G.R.), and the Institute for Quantum Information and Matter, an NSF Physics Frontier Center funded in part by the Moore Foundation.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
Data deposition: The C++ code developed for this work has been deposited in GitHub, https://www.github.com/everthemore/krylov-cpp, and the data for Fig. 3 have been deposited in CaltechData, https://data.caltech.edu/records/1089.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1819316116/-/DCSupplemental.
References
- 1.Anderson PW. Absence of diffusion in certain random lattices. Phys Rev. 1958;109:1492–1505. [Google Scholar]
- 2.Basko DM, Aleiner IL, Altshuler BL. Metal–insulator transition in a weakly interacting many-electron system with localized single-particle states. Ann Phys. 2006;321:1126–1205. [Google Scholar]
- 3.Gornyi IV, Mirlin AD, Polyakov DG. Interacting electrons in disordered wires: Anderson localization and low-t transport. Phys Rev Lett. 2005;95:206603. doi: 10.1103/PhysRevLett.95.206603. [DOI] [PubMed] [Google Scholar]
- 4.Nandkishore R, Huse DA. Many-body localization and thermalization in quantum statistical mechanics. Annu Rev Condens Matter Phys. 2015;6:15–38. [Google Scholar]
- 5.Abanin DA, Papić Z. Recent progress in many-body localization. Annalen der Physik. 2017;529:1700169–n/a. [Google Scholar]
- 6.Imbrie JZ. Diagonalization and many-body localization for a disordered quantum spin chain. Phys Rev Lett. 2016;117:027201. doi: 10.1103/PhysRevLett.117.027201. [DOI] [PubMed] [Google Scholar]
- 7.Huse DA, Nandkishore R, Oganesyan V. Phenomenology of fully many-body-localized systems. Phys Rev B. 2014;90:174202. [Google Scholar]
- 8.Oganesyan V, Huse DA. Localization of interacting fermions at high temperature. Phys Rev B. 2007;75:155111. [Google Scholar]
- 9.Pal A, Huse DA. Many-body localization phase transition. Phys Rev B. 2010;82:174411. [Google Scholar]
- 10.Vosk R, Huse DA, Altman E. Theory of the many-body localization transition in one-dimensional systems. Phys Rev X. 2015;5:031032. [Google Scholar]
- 11.Bar Lev Y, Reichman DR. Dynamics of many-body localization. Phys Rev B. 2014;89:220201. [Google Scholar]
- 12.White CD, Zaletel M, Mong RSK, Gil R. Quantum dynamics of thermalizing systems. Phys Rev B. 2018;97:035127. [Google Scholar]
- 13.van Nieuwenburg E, Bairey E, Refael G. December 1, 2017. Learning phase transitions from dynamics. arXiv:1712.00450.
- 14.Bauer B, Nayak C. Area laws in a many-body localized state and its implications for topological order. J Stat Mech Theor Exp. 2013;2013:P09005. [Google Scholar]
- 15.Žnidarič M, Prosen T, Peter P. Many-body localization in the heisenberg magnet in a random field. Phys Rev B. 2008;77:064426. [Google Scholar]
- 16.Bardarson JH, Pollmann F, Moore JE. Unbounded growth of entanglement in models of many-body localization. Phys Rev Lett. 2012;109:017202. doi: 10.1103/PhysRevLett.109.017202. [DOI] [PubMed] [Google Scholar]
- 17.Khemani V, Lim SP, Sheng DN, Huse DA. Critical properties of the many-body localization transition. Phys Rev X. 2017;7:021013. doi: 10.1103/PhysRevLett.119.075702. [DOI] [PubMed] [Google Scholar]
- 18.Gopalakrishnan S, et al. Low-frequency conductivity in many-body localized systems. Phys Rev B. 2015;92:104202. [Google Scholar]
- 19.Berkelbach TC, Reichman DR. Conductivity of disordered quantum lattice models at infinite temperature: Many-body localization. Phys Rev B. 2010;81:224429. [Google Scholar]
- 20.Lazarides A, Das A, Moessner R. Fate of many-body localization under periodic driving. Phys Rev Lett. 2015;115:030402. doi: 10.1103/PhysRevLett.115.030402. [DOI] [PubMed] [Google Scholar]
- 21.D’Alessio L, Polkovnikov A. Many-body energy localization transition in periodically driven systems. Ann Phys. 2013;333:19–33. [Google Scholar]
- 22.Khemani V, Lazarides A, Moessner R, Sondhi SL. Phase structure of driven quantum systems. Phys Rev Lett. 2016;116:250401. doi: 10.1103/PhysRevLett.116.250401. [DOI] [PubMed] [Google Scholar]
- 23.Smith J, et al. Many-body localization in a quantum simulator with programmable random disorder. Nat Phys. 2016;12:907–911. [Google Scholar]
- 24.Choi J-y, et al. Exploring the many-body localization transition in two dimensions. Science. 2016;352:1547–1552. doi: 10.1126/science.aaf8834. [DOI] [PubMed] [Google Scholar]
- 25.Schreiber M, et al. Observation of many-body localization of interacting fermions in a quasirandom optical lattice. Science. 2015;349:842–845. doi: 10.1126/science.aaa7432. [DOI] [PubMed] [Google Scholar]
- 26.Kondov SS, McGehee WR, Xu W, DeMarco B. Disorder-induced localization in a strongly correlated atomic hubbard gas. Phys Rev Lett. 2015;114:083002. doi: 10.1103/PhysRevLett.114.083002. [DOI] [PubMed] [Google Scholar]
- 27.Bordia P, et al. Probing slow relaxation and many-body localization in two-dimensional quasiperiodic systems. Phys Rev X. 2017;7:041047. doi: 10.1103/PhysRevLett.119.260401. [DOI] [PubMed] [Google Scholar]
- 28.De Roeck W, Huveneers F, Müller M, Schiulaz M. Absence of many-body mobility edges. Phys Rev B. 2016;93:014203. [Google Scholar]
- 29.Smith A, Knolle J, Kovrizhin DL, Moessner R. Disorder-free localization. Phys Rev Lett. 2017;118:266601. doi: 10.1103/PhysRevLett.118.266601. [DOI] [PubMed] [Google Scholar]
- 30.Smith A, Knolle J, Moessner R, Kovrizhin DL. Absence of ergodicity without quenched disorder: From quantum disentangled liquids to many-body localization. Phys Rev Lett. 2017;119:176601. doi: 10.1103/PhysRevLett.119.176601. [DOI] [PubMed] [Google Scholar]
- 31.Smith A, Knolle J, Moessner R, Kovrizhin DL. Dynamical localization in lattice gauge theories. Phys Rev B. 2018;97:245137. [Google Scholar]
- 32.Grover T, Fisher MPA. Quantum disentangled liquids. J Stat Mech Theor Exp. 2014;2014:P10010. [Google Scholar]
- 33.Kagan Yu, Maksimov LA. Localization in a system of interacting particles diffusing in a regular crystal. JETP. 1984;60:201–210. [Google Scholar]
- 34.De Roeck W, Huveneers F. Scenario for delocalization in translation-invariant systems. Phys Rev B. 2014;90:165137. [Google Scholar]
- 35.Schiulaz M, Silva A, Müller M. Dynamics in many-body localized quantum systems without disorder. Phys Rev B. 2015;91:184202. [Google Scholar]
- 36.Yao NY, Laumann CR, Cirac JI, Lukin MD, Moore JE. Quasi-many-body localization in translation-invariant systems. Phys Rev Lett. 2016;117:240601. doi: 10.1103/PhysRevLett.117.240601. [DOI] [PubMed] [Google Scholar]
- 37.Iyer S, Oganesyan V, Refael G, Huse DA. Many-body localization in a quasiperiodic system. Phys Rev B. 2013;87:134202. [Google Scholar]
- 38.Lüschen HP, et al. Observation of slow dynamics near the many-body localization transition in one-dimensional quasiperiodic systems. Phys Rev Lett. 2017;119:260401. doi: 10.1103/PhysRevLett.119.260401. [DOI] [PubMed] [Google Scholar]
- 39.Khemani V, Sheng DN, Huse DA. Two universality classes for the many-body localization transition. Phys Rev Lett. 2017;119:075702. doi: 10.1103/PhysRevLett.119.075702. [DOI] [PubMed] [Google Scholar]
- 40.Kim IH, Haah J. Localization from superselection rules in translationally invariant systems. Phys Rev Lett. 2016;116:027202. doi: 10.1103/PhysRevLett.116.027202. [DOI] [PubMed] [Google Scholar]
- 41.Wannier GH. Wave functions and effective Hamiltonian for bloch electrons in an electric field. Phys Rev. 1960;117:432–439. [Google Scholar]
- 42.Casati G, Chirikov BV, Izraelev FM, Ford J. 1979. Stochastic behavior of a quantum pendulum under a periodic perturbation. Stochastic Behavior in Classical and Quantum Hamiltonian Systems, Lecture Notes in Physics, eds Casati G, Ford J (Springer, Berlin), 93, p 93.
- 43.Baum Y, van Nieuwenburg EPL, Refael G. From dynamical localization to bunching in interacting floquet systems. SciPost Phys. 2018;5:017. [Google Scholar]
- 44.Luitz DJ, Bar Lev Y, Lazarides A. Absence of dynamical localization in interacting driven systems. SciPost Phys. 2017;3:029. [Google Scholar]
- 45.Eckstein M, Werner P. Damping of bloch oscillations in the hubbard model. Phys Rev Lett. 2011;107:186406. doi: 10.1103/PhysRevLett.107.186406. [DOI] [PubMed] [Google Scholar]
- 46.Krimer DO, Khomeriki R, Flach S. Delocalization and spreading in a nonlinear Stark ladder. Phys Rev E. 2009;80:036201. doi: 10.1103/PhysRevE.80.036201. [DOI] [PubMed] [Google Scholar]
- 47.Pieri P, Strinati GC. Derivation of the Gross–Pitaevskii equation for condensed bosons from the Bogoliubov–de Gennes equations for superfluid fermions. Phys Rev Lett. 2003;91:030401. doi: 10.1103/PhysRevLett.91.030401. [DOI] [PubMed] [Google Scholar]
- 48.Garreau J-C. Quantum simulation of disordered systems with cold atoms. Comptes Rendus Physique. 2017;18:31–46. [Google Scholar]
- 49.Sanchez-Palencia L, et al. Anderson localization of expanding bose-einstein condensates in random potentials. Phys Rev Lett. 2007;98:210401. doi: 10.1103/PhysRevLett.98.210401. [DOI] [PubMed] [Google Scholar]
- 50.Guhr T, Müller–Groeling A, Weidenmüller HA. Random-matrix theories in quantum physics: Common concepts. Phys Rep. 1998;299:189–425. [Google Scholar]
- 51.Olshanii M, et al. An exactly solvable model for the integrability and chaos transition in rough quantum billiards. Nat Commun. 2012;3:641. doi: 10.1038/ncomms1653. [DOI] [PubMed] [Google Scholar]
- 52.Luitz DJ, Laflorencie N, Alet F. Many-body localization edge in the random-field heisenberg chain. Phys Rev B. 2015;91:081103. [Google Scholar]
- 53.Bertrand CL, García-García AM. Anomalous thouless energy and critical statistics on the metallic side of the many-body localization transition. Phys Rev B. 2016;94:144201. [Google Scholar]
- 54.Kudo K, Deguchi T. Finite-size scaling with respect to interaction and disorder strength at the many-body localization transition. Phys Rev B. 2018;97:220201. [Google Scholar]
- 55.van Nieuwenburg E. 2018 Data from “Time-evolution of a wavefunction using a Krylov subspace expansion.” GitHub. Available at https://www.github.com/everthemore/krylov-cpp. Deposited September 19, 2018.
- 56.van Nieuwenburg E, Baum Y, Refael G. 2018 doi: 10.1073/pnas.1819316116. Data from “Imbalance dynamics for a 24-site quantum spin chain.” CaltechDATA. Available at https://data.caltech.edu/records/1089. Deposited September 25, 2018. [DOI] [PMC free article] [PubMed]
- 57.Chandran A, Pal A, Laumann CR, Scardicchio A. Many-body localization beyond eigenstates in all dimensions. Phys Rev B. 2016;94:144203. [Google Scholar]
- 58.De Roeck W, Huveneers F. Stability and instability towards delocalization in many-body localization systems. Phys Rev B. 2017;95:155129. [Google Scholar]
- 59.De Roeck W, Imbrie JZ. Many-body localization: Stability and instability. Philos Trans R Soc Lond A Math Phys Eng Sci. 2017;375:20160422. doi: 10.1098/rsta.2016.0422. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Pai S, Pretko M, Nandkishore RM. July 25, 2018. Localization in fractonic random circuits. arXiv:1807.09776.
- 61.Schulz M, Hooley CA, Moessner R, Pollmann F. August 3, 2018. Stark many-body localization. arXiv:1808.01250. [DOI] [PubMed]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.