Large bandgap of pressurized trilayer graphene

Significance

The remarkable physical properties of graphene make it a marvel of materials science. However, the gapless character of graphene makes it impossible to be a strong contender for postsilicon electronics. Opening a sizable bandgap in graphene is hence highly desired. We developed a microwiring technique for high-pressure electrical measurement on nanomaterials with only a few layers. Through in situ electrical and absorption studies we demonstrate that an intrinsic bandgap of 2.5 eV is achievable in compressed Bernal-stacked trilayer graphene. The realization of a wide bandgap in compressed graphene stimulates explorations for the practical application of carbon-based electronic devices.

Abstract

Graphene-based nanodevices have been developed rapidly and are now considered a strong contender for postsilicon electronics. However, one challenge facing graphene-based transistors is opening a sizable bandgap in graphene. The largest bandgap achieved so far is several hundred meV in bilayer graphene, but this value is still far below the threshold for practical applications. Through in situ electrical measurements, we observed a semiconducting character in compressed trilayer graphene by tuning the interlayer interaction with pressure. The optical absorption measurements demonstrate that an intrinsic bandgap of 2.5 ± 0.3 eV could be achieved in such a semiconducting state, and once opened could be preserved to a few GPa. The realization of wide bandgap in compressed trilayer graphene offers opportunities in carbon-based electronic devices.

The remarkable physical properties of graphene, such as high carrier mobility, flexibility, and mechanical strength make it a wonder of materials science (1–8). For example, the very high carrier mobility of graphene of 10,000 cm² V⁻¹⋅s⁻¹ has promoted potential applications in high-speed integrated electronic devices. However, unlike silicon semiconductor, the main challenge for graphene-based transistors is the gapless character of graphene (9–19) that results in an impossible on/off field-effect transition and a low I_on/I_off ratio (18, 19). Considerable efforts have been made to increase the bandgap of graphene, using quantum confinement by patterning graphene in the form of a quantum dot (20), nanoribbon (21, 22), and nanomesh (23), or symmetric breaking and selective control of the carrier concentration in graphene layers by an external electric field (9–17). However, these efforts have disappointed as the maximum bandgap opening ever achieved was only several hundred meV in bilayer graphene. Promisingly, a bandgap of ∼1 eV was recently opened in nanoporous graphene (24).

Pioneering studies indicated that the electronic structure of few-layer graphene was highly sensitive to interlayer van der Waals coupling (25–27). Breaking the inversion symmetry of Bernal-stacked bilayer graphene has been shown to open a gap and the possibility of tuning the gap energy. The electronic structure of graphene can also be modified by interlayer hybridization, as exemplified in graphene/h-BN and graphene/SiC multilayers (28–32). We pursued an alternate approach of tuning the interlayer hybridization of few-layer graphene with pressure to modulate the electronic structure. The graphene sample on a different substrate has quite different pressure response (33–36). Furthermore, the behavior of graphene on a substrate at high pressure differs drastically from that of freestanding graphene (37), indicating that substrates obscure the intrinsic properties of graphene significantly.

In our study, we directly transferred the graphene sample onto a diamond surface for measurements to avoid the influence of the substrate. However, pressurizing few-layer graphene and in situ examining the change of the electronic structure, taking the electrical measurements as an example, presents many technical difficulties from preparation of defect-free graphene flakes, the placing of microelectrodes on a tiny piece of atomic layer sample to ensure good contacts in a diamond anvil cell, and the prevention of ultrathin samples from damage under pressure. First, we developed a microwiring technique for in situ high-pressure electrical transport measurements on nanomaterials with only a few layers. A semimetal-to-semiconductor transition was observed in compressed trilayer graphene. Systematic electrical and absorption measurements provide compelling evidence that a large intrinsic bandgap of 2.5 ± 0.3 eV was achieved in mechanically exfoliated Bernal-stacked trilayer graphene under compression.

Results and Discussion

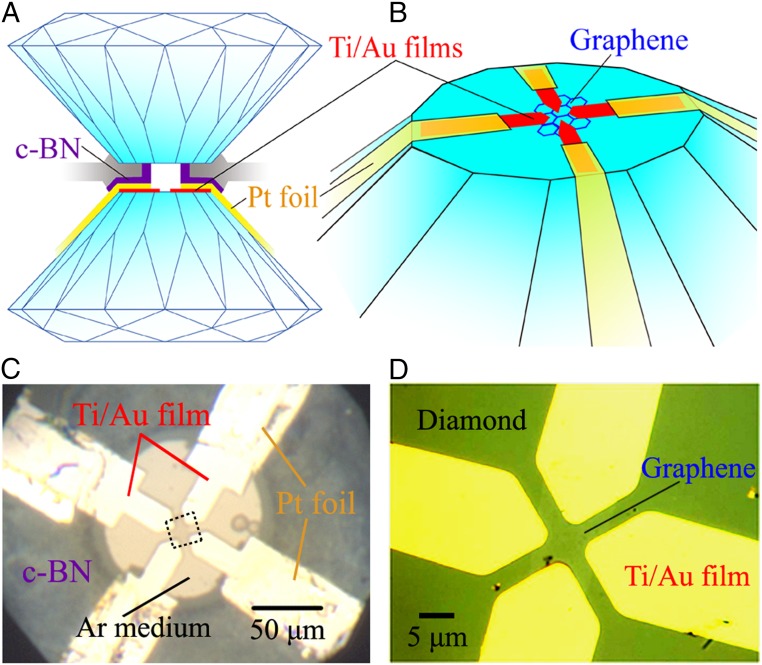
The critical experimental step is the fabrication of probing electrodes with ohmic contact that are suitable for electrical measurements on nanomaterials at high pressure. For this purpose, we used an advanced experimental technique of patterning Ti/Au film as probing electrodes on the diamond culet with an electron beam deposition method. The electrodes were then extended with platinum foils (∼2 μm in thickness) by careful hand-wiring to ensure stability under compression (Fig. 1). More experimental details on our sample preparation, transfer, and identification of the Bernal stacking order can be found in SI Appendix. The resistances of trilayer graphene at ∼0.5 GPa measured by two- and four-terminal electrodes were ∼1.1 kΩ and ∼300 Ω (SI Appendix, Fig. S2), respectively. These values are comparable with previously reported results (14), indicating the good quality of the graphene sheet and contacts.

Fig. 1.

Four-terminal nanodevice of trilayer graphene with Van der Pauw configuration on a diamond culet. (A) Illustration of a cross-sectional view of the designed microcircuit. (B) A perspective view of the designed microwiring setup. (C) Top view of the trilayer graphene sample and probing electrodes in a diamond anvil cell. Daphne 7373 or Argon pressure media were loaded for repeating high-pressure measurements. (D) Optical microscope image of trilayer graphene and Ti/Au film electrodes on the diamond surface.

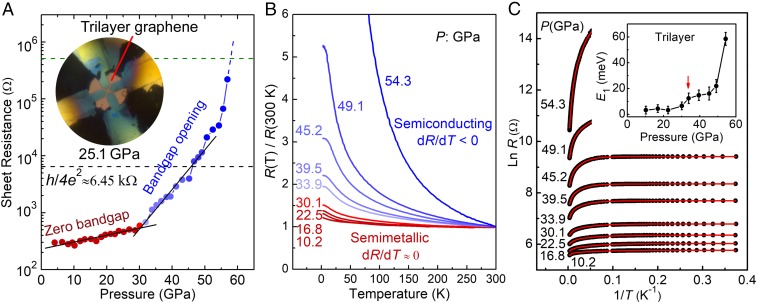
The pressure response of the Bernal-stacked trilayer graphene resistance was investigated at ambient temperature (Fig. 2A). Below 30.1 GPa, the resistance of trilayer graphene varies smoothly with pressure. A break in the trend and a sudden increase in the resistance is observed at about 33.0 GPa. The resistance increases dramatically by more than three orders of magnitudes upon further compression to 59.0 GPa. Above 59.0 GPa, the resistance jumps out of the measurable range of the instrument. This observation is a strong indication of bandgap opening.

Fig. 2.

Sheet resistances of trilayer graphene as functions of pressure and temperature. (A) Resistance–pressure curves of trilayer graphene measured at room temperature (300 K). The solid black lines are guides for the eyes. The black dashed line denotes the resistance quantum, h/4e² ∼ 6.45 kΩ, above which, a disordered conductor would behave as an insulator at low temperatures due to Anderson localization. (B) R-T curves at representative pressures showing the semimetallic–semiconducting transition. (C) Arrhenius plots of the resistance. The solid red lines are fitted to Eq. 1. (Inset) The pressure dependence of the obtained activation energy E₁ is shown. The uncertainties are from the fitting errors and the selection of the critical temperature of these three transport processes.

The sheet resistance of Bernal-stacked trilayer graphene was also investigated as a function of temperature at pressures to check the opening of bandgap (Fig. 2 B and C). At low pressures (<30.1 GPa), the resistance (R) shows a weak temperature dependence (dR/dT ≈ 0), indicative of a semimetallic character. Surprisingly, at 33.9 GPa, the resistance becomes strongly temperature dependent and increases significantly with decreasing temperature (dR/dT < 0). The temperature dependence of resistance becomes even more pronounced at higher pressure up to 54.3 GPa, exhibiting a typical semiconducting behavior.

The temperature dependence of compressed trilayer graphene resistance shows linear trend in the high-temperature range (200–300 K, SI Appendix, Fig. S3), suggesting Arrhenius-like thermally activated conduction. With decreasing temperature, the slope decreases continuously, suggesting another thermally activated conduction process. Below 30 K, the ln R vs. 1/T curves become nearly T-independent, which indicates an alternative conduction mechanism, such as various-range hopping. Such a conduction process was also observed in gapped bilayer graphene (38, 39). Assuming the variable range hopping to be of Mott type, the low-temperature resistance should be proportional to exp[−(T₀/T)^1/3]. Hence, we fitted the R-T curves with the following equation (38):

$$R{\left(T\right)}^{-1}={R_1}^{-1}\exp \left[-E_1/2k_{\mathrm{B}}T\right]+{R_2}^{-1}\exp \left[-E_2/2k_{\mathrm{B}}T\right]+{R_3}^{-1}\exp \left[-{\left(T_3/T\right)}^{1/3}\right],$$ [1]

where E₁, E₂, T₃, R₁, R₂, and R₃ are the two activation energies, hopping energy, and related resistance coefficients, respectively. Our fitted results match the R-T curves well in the whole temperature range (Fig. 2C). The extracted activation energy E₁ varies smoothly with pressure up to 30.1 GPa, followed by a sharp increase above 33.9 GPa (Fig. 2C, Inset), consistent with the onset pressure of the R-P curve.

The gap opening of compressed Bernal-stacked trilayer graphene was further confirmed with infrared-visible-UV (IR-vis-UV) absorption experiments. At ambient conditions (SI Appendix, Fig. S4), a pronounced and asymmetric peak due to excitonic resonance at the photon energy of 4.6 eV is observed in the absorbance pattern of trilayer graphene, similar to that previously reported in mono- and few-layer graphene (40, 41). The transmittance of (95.5 ± 0.5)% at 1.5 eV is comparable with that of suspended trilayer graphene (40, 41). All measurements confirm that the absorption is associated with the intrinsic properties of trilayer graphene.

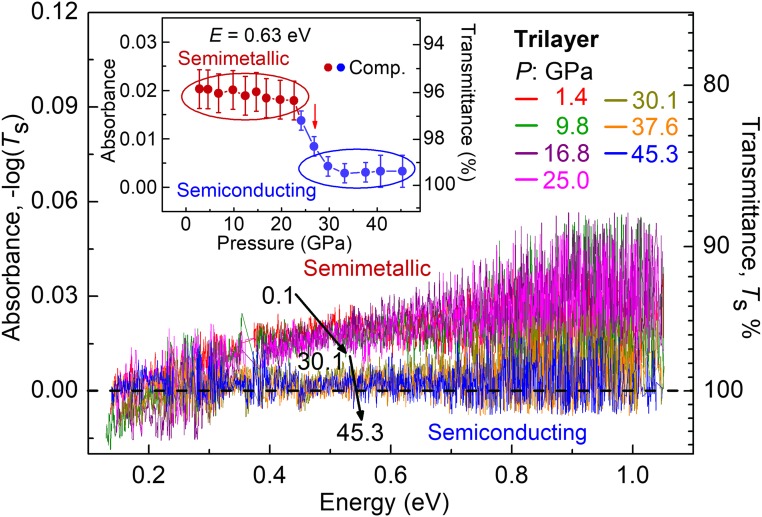
Pressurized Bernal-stacked trilayer graphene was studied with laboratory and synchrotron IR absorption spectroscopy (photon energy range: 0.2 ∼ 1.0 eV, Fig. 3 and SI Appendix, Fig. S5). The absorbance of trilayer graphene [A = −log (T_s), where T_s is the transmittance of sample] varies smoothly with the loading pressure until 26.1 GPa, when it drops suddenly and approaches zero at higher pressure. This observation indicates that the bandgap of compressed trilayer graphene has been opened and is larger than 1.0 eV, the maximum photon energy of IR radiation used in the measurements.

Fig. 3.

IR results of trilayer graphene under compression showing the bandgap opening. (Inset) The pressure dependence of trilayer graphene absorbance at radiation energy of 0.63 eV. The absorbance data at around 0.33 eV are removed due to the influence of C–H bonding absorption in the Daphne 7373 pressure medium.

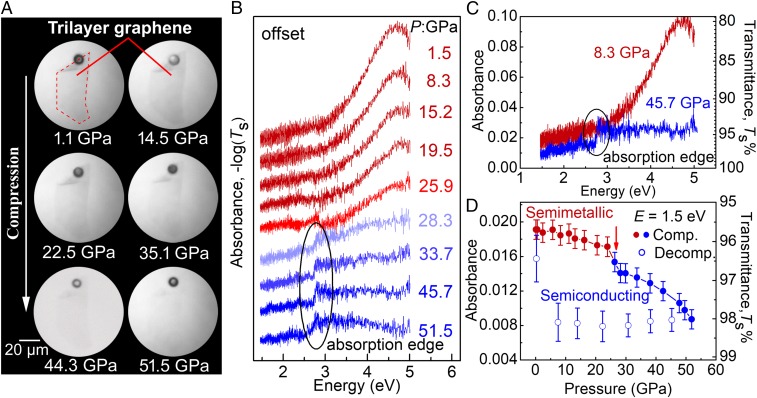
The bandgap energy of pressurized trilayer graphene cannot be accurately determined from the above IR experiments. Therefore, to track the bandgap evolution precisely, we measured the vis-UV transmittance spectra in trilayer graphene under pressure within the energy range of 1.4 ∼ 4.9 eV (Fig. 4B). Below 28.3 GPa, the absorption spectra show no significant change with compression. The main feature is a small blue-shift of the excitonic resonance peak at about 4.6 eV with increasing pressure. At 28.3 GPa, a transition is clearly identified from the absorbance measured with radiation energy of 1.5 eV. As shown in Fig. 4D, the absorbance of trilayer graphene varies smoothly initially up to 25.9 GPa. A sudden drop in the absorbance is observed at 28.3 GPa, followed by a continuous reduction with further compression up to 51.5 GPa. The absorption result suggests that the bandgap is larger than 1.5 eV. The result also agrees well with the optical microscopy observation under white transmitted light where the trilayer graphene becomes increasingly transparent above 28.3 GPa (Fig. 4A). All of the evidence confirms the large intrinsic bandgap in pressurized trilayer graphene. The experimental results suggest that a broad pressure range is needed to make the semimetallic trilayer transform to the semiconducting state completely, i.e., the ratio of semimetallic/semiconducting states is pressure dependent. Such a mixed phase is also observed in compressed substrate-supported two-layer graphene (33, 34). During decompression, the semiconducting phase remains unchanged down to a few GPa, but almost returns to its original state when quenched to ambient pressure, as shown in Fig. 4D. High-pressure Raman characterization confirms the reversible transition as well (SI Appendix, Fig. S6).

Fig. 4.

Bandgap opening in pressurized trilayer graphene. (A) The optical microscope image of trilayer graphene in transmission mode with a white-light source under compression. A ruby ball (black dot) was used as the pressure indicator and visual reference. (B) The optical absorbance patterns of trilayer graphene under compression. The curves are offset for clarity. (C) The absorbance of trilayer graphene at 8.3 and 45.7 GPa without offset. (D) Evolution of absorbance at a photon energy of 1.5 eV during compression and decompression.

The UV absorbance of trilayer graphene shown in Fig. 4B drops above 28.3 GPa. A weak absorption edge starts to appear at 2.5 eV, and concomitantly the excitonic resonance peak is lost. The sharpness of the edge resembles that of an indirect gap material. However, due to the weak absorption signal of trilayer graphene under pressure, it is difficult to ascertain the nature of the gap. To this end, we adopted the Tauc plots to analyze the nature of the bandgap (42):

$${\left(A\cdot E\right)}^{1/2}\sim E-E_{\mathrm{g}}\hspace{0.5em}\text{or}\hspace{0.5em}{\left(A\cdot E\right)}^2\sim E-E_{\mathrm{g}},$$ [2]

where A and E are the absorbance and the incident energy, respectively. The analysis of experimental results reveals a bandgap of 2.5 ± 0.3 eV in compressed trilayer graphene (SI Appendix, Fig. S7). The difference between the optical bandgap and electrical activation energy should be caused by the semimetallic/semiconducting mixed state in compressed trilayer graphene, which is supported by the simultaneously measured electrical and optical absorption results in compressed multilayer graphene (SI Appendix, Fig. S8). The activation energy in compressed multilayer graphene is only dozens of meV, although the multilayer graphene becomes partially transparent. Such a difference is also observed in other materials (43, 44). In the case of trilayer graphene, the semimetallic form starts to transform to a semiconducting state above 30.1 GPa but leaves a large percentage unchanged. The more conductive semimetallic state dominates the electrical properties. Hence, no sharp jump is observed in the resistance and activation energy although the bandgap of the semiconducting area is opened from 0 to 2.5 ± 0.3 eV. An increasing percentage of the semiconducting state forms with further compression, resulting in a dramatic increase of resistance and activation energy with pressure. Above 59.0 GPa, a significant fraction of trilayer graphene becomes semiconducting, dominating the electrical properties. Therefore, the resistance jumps out of the measurable range of the instrument due to the large bandgap.

Previous studies showed that strain/pressure-induced disorder could induce strong Anderson localization and further a metal–insulator transition in materials (14, 45). This type of metal–insulator transition has been observed in graphene when the resistance of graphene is over h/4e² ≈ 6.45 kΩ (45). According to electrical transport results, the semimetallic–semiconducting transition of trilayer graphene occurs at around 33.9 GPa with a sheet resistance of several hundred ohms (Fig. 2A), much smaller than the resistance quantum, h/4e². Furthermore, the present absorption measurements, which are often less affected by the disorder, also confirm the opening of a gap. Hence, the bandgap observed here is not a consequence of the Anderson localization effect.

By comparing the pressure coefficient of the G-band frequency (∂ω_G/∂P) with that of graphite, recent Raman studies showed that a pressure-induced electron transfer occurred in alcohol-immersed monolayer and bilayer graphene, but was absent in trilayer graphene and samples immersed in argon or nitrogen (35, 36). Our Raman results show that the ∂ω_G/∂P of trilayer graphene is about 4.0 ± 0.2 cm⁻¹⋅GPa⁻¹, comparable with that of graphite. Thus, no electron transfer occurs between trilayer graphene and the pressure medium, and consequently the electron transfer effect does not cause the bandgap opening in compressed trilayer graphene.

Strain/stress was also applied to open a bandgap of hundreds of meV in graphene (46, 47). In our experiments, it is possible that the quasi-hydrostatic conditions after the solidification of the pressure medium at high pressure may cause strain/stress in the graphene sample. The broadening of the G band of trilayer graphene after decompression (SI Appendix, Fig. S6) is indicative of residual stress in trilayer graphene. However, the electrical and optical results show that trilayer graphene returns to its semimetallic state after quenching to ambient conditions although considerable residual stress remains in the sample. Furthermore, solidification of Ar and Daphne 7373 occurs at about 1 and 10 GPa, far from the semimetallic–semiconducting transition pressure of 33.9 GPa. Hence, we believe strain/stress induced by the quasi-hydrostatic conditions may affect the onset pressure of the semimetallic–semiconducting transition but does not play a key role in opening of such a large bandgap in trilayer graphene.

Recently, a diamond-like carbon film was observed in two-layer graphene followed by sp²-sp³ rehybridization through nanoindentationand compression methods (33, 34). Previous experimental and theoretical results also demonstrated that graphite transformed into an sp³-bonded carbon phase (48–56) under cold compression, although the structure of the high-pressure phase is still controversial. In addition, the value of the bandgap opened in trilayer graphene is comparable with that of the high-pressure transparent phase of graphite (SI Appendix, Fig. S8). Hence, we infer that the opening of the bandgap is caused by sp²-sp³ rehybridization in pressurized trilayer graphene. Further study is needed to understand the structural evolution of trilayer graphene under compression.

In conclusion, through electrical, IR and vis-UV absorption measurements, we observed an intrinsic bandgap of 2.5 ± 0.3 eV in pressurized Bernal-stacked trilayer graphene by tuning the interlayer coupling with pressure. The high-pressure semiconducting phase could be preserved to a few GPa. The achieved bandgap of 2.5 ±0.3 eV is much larger than previously reported values of several hundred meV. The bandgap of compressed trilayer graphene is larger than silicon (1.1 eV) under ambient conditions. However, the reverse engineering of fabricating a narrower gap graphene sheet is, in principle, comparatively easier. This study may stimulate explorations of practical graphene-based electronic devices.

Materials and Methods

Trilayer graphene flakes were mechanically exfoliated from bulk graphite on Si/SiO₂ surface. In situ high-pressure electrical measurements were conducted in a PPMS-9 system with a temperature range of 2–300 K. High-pressure IR absorption measurements were conducted at Beamline 1.4.3 of the Advanced Light Source, Lawrence Berkeley National Laboratory and the Infrared Lab of National Synchrotron Light Source II at Brookhaven National Laboratory. Vis-UV absorption measurements were conducted on a customized Vis-UV microscope system with a photon energy of 1.4–4.9 eV. More details about the experiments and calculations can be found in SI Appendix.